Transcriptional Coordination of the Metabolic Network in Arabidopsis^,,

Abstract

Patterns of coexpression can reveal networks of functionally related genes and provide deeper understanding of processes requiring multiple gene products. We performed an analysis of coexpression networks for 1,330 genes from the AraCyc database of metabolic pathways in Arabidopsis (Arabidopsis thaliana). We found that genes associated with the same metabolic pathway are, on average, more highly coexpressed than genes from different pathways. Positively coexpressed genes within the same pathway tend to cluster close together in the pathway structure, while negatively correlated genes typically occupy more distant positions. The distribution of coexpression links per gene is highly skewed, with a small but significant number of genes having numerous coexpression partners but most having fewer than 10. Genes with multiple connections (hubs) tend to be single-copy genes, while genes with multiple paralogs are coexpressed with fewer genes, on average, than single-copy genes, suggesting that the network expands through gene duplication, followed by weakening of coexpression links involving duplicate nodes. Using a network-analysis algorithm based on coexpression with multiple pathway members (pathway-level coexpression), we identified and prioritized novel candidate pathway members, regulators, and cross pathway transcriptional control points for over 140 metabolic pathways. To facilitate exploration and analysis of the results, we provide a Web site (http://www.transvar.org/at_coexpress/analysis/web) listing analyzed pathways with links to regression and pathway-level coexpression results. These methods and results will aid in the prioritization of candidates for genetic analysis of metabolism in plants and contribute to the improvement of functional annotation of the Arabidopsis genome.

The advent of whole-system approaches, such as DNA chips and metabolomics, have created new opportunities for studying how metabolic pathways are coordinated to meet cellular demands (Sweetlove and Fernie, 2005). Connectivity in the yeast (Saccharomyces cerevisiae) metabolic network has been explored using gene coexpression data and structural information about the pathways; these studies have revealed fundamental insights into the general properties of metabolic gene networks in eukaryotes (DeRisi et al., 1997; Ihmels et al., 2004b). One early result was that functionally related genes are often coexpressed, and this observation has provided strong motivation for the adoption of expression microarrays in biological research (DeRisi et al., 1997). In addition, it has been shown that many genes encoding metabolic enzymes form modules of coexpression and that coexpressed genes occupy nonrandom positions with respect to the pathway structure (Ihmels et al., 2004a, 2004b). A number of methods based on integration of gene expression data with other data types have been developed, allowing identification of undiscovered modules (Stuart et al., 2003) as well as control elements and transcription factors that regulate their expression (Pilpel et al., 2001). Other important results from the study of biological networks include observations that lethality correlates with high connectivity in the protein interaction and coexpression networks in yeast (Jeong et al., 2001; Carlson et al., 2006), while for mammalian protein interaction networks, the lethality/connectivity correlation is less pronounced (Gandhi et al., 2006). For both network types, connectivity distributions are highly uneven and are well described by power functions of the form f ∼ k^−α, where f is the frequency of nodes having k connections. Although the goodness of fit of power law functions is sometimes controversial, it is clear that most biological networks include a small but significant number of nodes (e.g. genes or proteins) that have a large number of connections, but most nodes have very few (for review, see Albert, 2005). Until recently, the bulk of research done on coexpression networks and metabolism has focused primarily on analysis of data from yeast. However, the accumulation of genomic and metabolic information for more complex eukaryotes, most notably the model dicot Arabidopsis (Arabidopsis thaliana), now allows for analogous studies in higher plants (Minorsky, 2003; Gutierrez et al., 2005).

AraCyc (http://Arabidopsis.org/tools/aracyc/) is a database and visualization system for metabolic pathways in Arabidopsis developed by The Arabidopsis Information Resource (TAIR). The first version of the AraCyc database was based on the MetaCyc compendium of known biochemical pathways and output from the Pathologic software, which uses keyword matching to assign gene products to individual pathway steps recorded in MetaCyc. Since then, AraCyc has undergone continuous improvement through manual editing and literature-based curation (Mueller et al., 2003). However, approximately 40% of the biochemical reactions in AraCyc have no gene annotation, while many others have multiple gene annotations. Because the pathways are based primarily on shared sequence similarity with enzymes from other organisms, it is likely that many annotations will require validation from other sources. In this article, we explore the idea that it may be possible to deepen the annotation of plant metabolic pathways by using coexpression patterns deduced from publicly available DNA microarray datasets to infer functional relationships among genes.

In previous work, we described a method that uses coexpression relationships inferred from regression analysis of DNA microarray data to identify new players in biological pathways (Persson et al., 2005). Using this method, we analyzed quality-screened Affymetrix ATH1 microarray experiments and identified sets of genes that are highly coexpressed with one or more cellulose synthase (CESA) genes in Arabidopsis. The general utility of the approach was demonstrated through mutant analyses of candidate genes: Two genes coexpressed with CESA genes implicated in secondary cell wall formation exhibited cell wall-related phenotypes. Here we further develop the coexpression approach and apply it to metabolic pathways in Arabidopsis. Using the AraCyc database as a starting point, we conducted large-scale coexpression analyses for 1,330 genes encoding metabolic enzymes in Arabidopsis and generated metabolic networks based on the transcriptional relationships between genes. By comparing the AraCyc view of Arabidopsis metabolism with gene expression data, we propose a richer and more detailed picture of metabolic pathways in Arabidopsis and introduce a wealth of candidates for genetic and biochemical analysis.

RESULTS

Genes Belonging to the Same Pathway Are Coexpressed

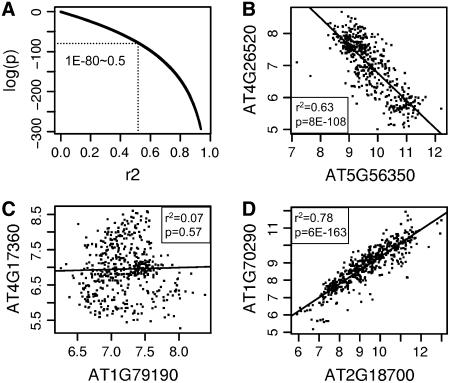
We used publicly available data from 486 quality-screened ATH1 array hybridizations to analyze coexpression patterns for metabolic pathway genes in Arabidopsis. The ATH1 expression microarray from Affymetrix contains over 22,000 probe sets that hybridize to one or more Arabidopsis genes (Redman et al., 2004). Using probe set annotations from Affymetrix, we identified 1,330 nonpromiscuous, nonredundant probe sets that each measure a single gene from the AraCyc database of metabolic pathways. We then performed large-scale linear regression analysis of expression values between these 1,330 probe sets and all other probe sets on the array using the methodology developed previously (Persson et al., 2005). Each regression analysis generates three values useful for evaluating coexpression relationships: a slope parameter that indicates the direction (positive or negative) of coexpression, and p and R-squared (r²) values that indicate the strength of the coexpression relationship. The r² value, also known as the coefficient of determination, is the square of the Pearson's correlation coefficient (r) and is the fraction of variance in one variable that can be explained by variation in the other (Rodgers and Nicewander, 1988). Thus, r² values that are closer to 1 indicate higher correlation and a stronger linear relationship between compared variables. The p value quantifies the confidence in the correlation; it is the probability that the observed value for r² could have been obtained by chance under the null hypothesis that the two variables being compared are not linearly related. Figure 1 describes the relationships between p and r² values obtained in our study and presents illustrative examples of gene pairs that are highly or weakly coexpressed in positive or negative directions. As shown in Figure 1A, a strong relationship exists between p and r² values in our data set; however, because of the greater range among p values, we decided to use primarily the p values to assess coexpression between genes.

Figure 1.

Coexpression p and r² values for genes from the AraCyc database of metabolic pathways. A, Logarithm (base 10) of regression p values plotted against corresponding r² values obtained from regressing expression values for 1,330 AraCyc genes against all genes on the ATH1 expression microarray. B to D, Example plots showing positive (D) and negative (B) linear relationships between normalized expression values (log base 2) for weakly (C) and strongly (B and D) coexpressed genes.

It is generally expected that gene products that are regulated at the level of mRNA abundance and that collaborate in a shared function or pathway are likely to be coexpressed. To assess whether this was the case with Arabidopsis metabolic pathways, we compared r² and p values obtained from linear regressions performed between genes annotated as belonging to the same or different metabolic pathways in AraCyc. In general, the population of within-pathway comparisons contained a higher proportion of high-confidence (low p and high r²) results than did comparisons involving genes from different pathways (Table I). Thus, we found that genes annotated as belonging to the same pathway tend to be more tightly coexpressed than genes from different metabolic pathways, a result that is consistent with results obtained from similar studies in yeast (Ihmels et al., 2004b). Interestingly, we also found that the relative proportion of high-confidence coexpression relationships is also higher among positively coexpressed genes than among negatively coexpressed genes.

Table I.

Gene pairs in the same pathway contain a higher proportion of high-confidence coexpression results

Each row reports the percentage of regression results within each column's category having the p values indicated in the first column. The final row reports the number of pairs (N) considered in each category. The table counts each gene pair once and excludes promiscuous probe sets that match more than one gene.

−Log (p)	Within Pathway, Positive Slope	Across Pathway, Positive Slope	Within Pathway, Negative Slope	Across Pathway, Negative Slope
>200	0.8%	0.05%	0	0
120–200	1.4%	0.53%	0	0.0009%
80–120	2.9%	1.2%	0.28%	0.11%
60–80	2.8%	1.5%	1.2%	0.53%
40–60	5.8%	3.5%	3.3%	2.3%
<40	86%	93%	95%	97%
N (100%=)	4,033	426,724	3,226	434,388

Core Metabolic Pathways Display Tighter Level of Transcriptional Coordination

To investigate whether coexpression levels of genes within pathways vary from one pathway to another, we used a random sampling approach to identify pathways that contained above-average numbers of coexpressed gene pairs. For each gene, we created a list of all other genes represented on the ATH1 array and ordered the list by increasing p (or, equivalently, decreasing r²) values. In this scheme, genes within highly coexpressed pathways should appear near the top of each other's coexpression lists and have small ranks. Moreover, the average of their mutual ranks should be unusually small when compared to samples of genes selected at random without regard to their pathway affiliation. To test this, we selected 10,000 random samples of size N for each pathway having N genes, computed the average rank for each sample, and then compared the distribution of average ranks from the samples to the actual average rank obtained for each pathway. The frequency with which we observed average ranks as small or smaller than the actual observed values thus provided an empirically determined, within-pathway coexpression p value for each pathway.

Table II presents the most tightly coregulated pathways according to this analysis. These tightly coexpressed pathways were enriched in core metabolic pathways such as glycolysis, tricarboxylic acid (TCA) cycle, and the pentose phosphate pathway, which produce precursors for many other pathways. By contrast, pathways involved in noncore or peripheral biochemical pathways were coexpressed to a lesser degree. A full list of the pathways we analyzed, with links to Web pages for individual genes, pathways, probe sets, and plain-text spreadsheets of regression results, is available at http://www.transvar.org/at_coexpress/analysis/web.

Table II.

Most highly coexpressed pathways

Pathways with unusually high levels of coexpression (empirically determined pathway p value < 0.0001) and at least five coexpression links (edges) between genes are listed. The column labeled Genes gives the number of genes per pathway included in the coexpression analysis. The column labeled Edges lists the number of coexpression links in the within-pathway coexpression network, using coexpression cutoff 1E-80. C is the clustering coefficient for the coexpression network; larger values for C indicate a higher degree of connectivity (Watts and Strogatz, 1998). Super-pathway designations are from AraCyc: PME, Generation of precursor metabolites and energy; B, biosynthesis; D/U/A, degradation/utilization/assimilation.

Pathway	Genes	Edges	C	Super Pathway
Photosynthesis, light reaction	10	40	0.923	PME
Carotenoid biosynthesis	10	22	0.754	B
Gly degradation I	8	10	0.604	D/U/A
tRNA charging pathway	44	102	0.412	B
Calvin cycle	36	93	0.399	D/U/A
Photorespiration	29	42	0.318	PME
Chlorophyll biosynthesis	49	105	0.298	B
Gluconeogenesis	55	82	0.288	B
Fru degradation (anaerobic)	57	57	0.266	D/U/A
Glycolysis I	59	57	0.257	PME
Sorbitol fermentation	59	57	0.257	PME
Glycolysis IV	59	57	0.257	PME
Acetate fermentation	60	57	0.252	PME
De novo biosynthesis of purine nucleotides II	29	22	0.22	B
Starch biosynthesis	19	7	0.211	B
Fatty acid biosynthesis—initial steps	30	13	0.156	B
De novo biosynthesis of purine nucleotides I	46	32	0.151	B
TCA cycle—aerobic respiration	42	11	0.111	PME
Acetyl-CoA assimilation	28	6	0.107	PME
Colanic acid building blocks biosynthesis	53	12	0.066	B

Inferring Coexpressed Genes for Metabolic Pathways

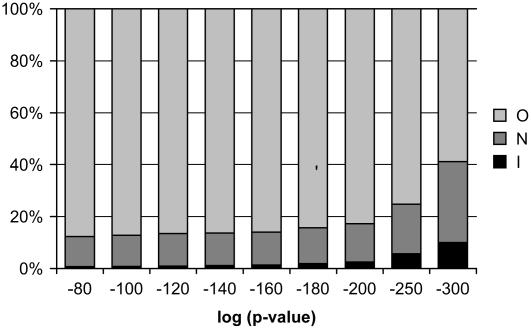
We have shown that pathways are enriched for coexpressed genes, a result that is consistent with the commonly held view that genes involved in related functions are expressed in a coordinate fashion. Previously, we used this aspect of transcriptional regulation to identify new members of cellulose biosynthesis pathways. Using large-scale coexpression results for a group of known CESA genes, we identified candidate genes outside the group that were coexpressed with some or all group members. In this earlier analysis, we observed that although genes in cellulose biosynthesis pathways typically appear near the top of each other's coexpression lists, often there are many more genes that have a higher ranking in terms of coexpression than the other group members. We found that this was also the case for the AraCyc coexpression data set. We found that individual pathway genes are typically coexpressed with tens or sometimes hundreds of genes even at relatively stringent p or r² value coexpression cutoffs and that often these nonpathway genes outrank other members of the pathway in terms of coexpression (Fig. 2).

Figure 2.

Relative proportions of high-confidence coexpression links. Each column reports the relative numbers of coexpression pairs with p values indicated on the x axis, where the paired genes are both in the same AraCyc pathway (I), both are in different AraCyc pathways (N), or only one is in an AraCyc pathway (O).

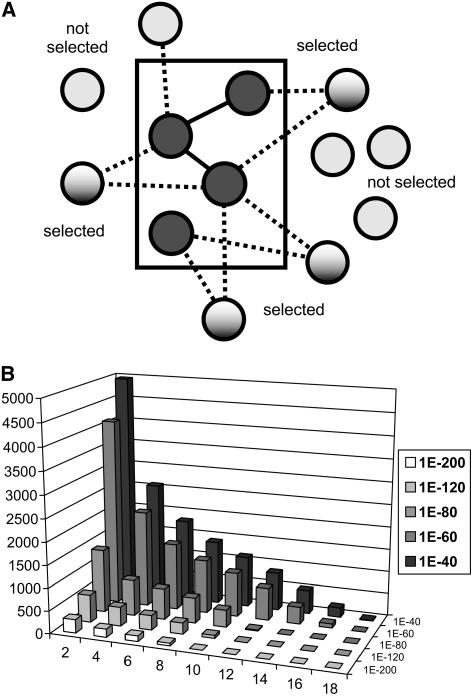
Previously, we narrowed the field of candidate genes for genetic analyses based on the number of CESA bait genes with which the candidates were coexpressed. That is, we chose candidate genes that were tightly coexpressed with as many bait genes as possible. Here, we present a more general version of this approach that uses both the coexpression set size and p values to select and rank candidates (Fig. 3A). The method computes a network structure in which genes are considered linked when their linear regression p and r² values meet a user-defined threshold. It then identifies genes within the network that are linked with multiple members of a given pathway; using graph analysis terminology, this is equivalent to finding genes whose neighborhood of connected genes include multiple genes in the pathway. Next, it ranks these candidate genes based on the number of connected pathway genes (within-pathway neighborhood size) and resolves ties using the product of regression p values between coexpressed gene bait and candidate genes.

Figure 3.

Coexpression network analysis. A, Schematic showing PLC analysis for identifying functionally relevant candidate genes outside a functional grouping (e.g. a metabolic pathway) using their connections to genes within the group. Bait genes that are members of the same functional group (rectangular area) are connected via coexpression relationships (dotted lines) to genes not currently annotated as belonging to the group. Some of the genes outside the group are connected to more than one group member and are selected as candidates for further analysis. B, Numbers of coexpressed genes selected under different coexpression p value cutoffs (ranging from 1E-40 to 1E-120) or requiring increasingly large numbers of coexpression partners within a pathway (2–15). No gene pair is counted more than once per column.

Note that analyzing the network structure in this way does not require that the pathway members themselves be coexpressed (linked) with each other, although this is often the case. In fact, this is a potential strength of the approach in that it can exploit potential redundancies in the system. For example, two isozymes that perform the same pathway step may not necessarily be coexpressed with each other, but they could each require coexpression with a third gene that supplies necessary functionality. Depending on the strength of coexpression, the approach would identify this third gene or any other genes that are connected with multiple genes within the same pathway group. In recognition that this approach is based on coexpression with multiple pathway members, not just single genes, we have termed this approach pathway-level coexpression (PLC) analysis.

We used PLC analysis to survey coexpression relationships for 205 AraCyc pathways, using coexpression p value cutoffs ranging from 1e-40 to 1e-200. Figure 3B summarizes the number of genes identified as being connected to one or more pathway members at different p value cutoffs. A coexpression p value of 1E-80 or better and pathway neighborhoods of two or more pathway genes produces 4,022 candidates connected with 144 pathways. Interestingly, we identified more than 100 genes (using p value cutoff 1E-80) that are coexpressed with pathway neighborhoods containing 15 or more genes. These PLC-identified genes were from two of the most highly coexpressed pathways: chlorophyll biosynthesis and the Calvin cycle. For the Calvin cycle pathway, the highest-ranking PLC-identified gene candidates included several putative chloroplast proteins, including four of unknown function and several more with predicted functions related to electron transport and photosynthesis, such as iron binding and ferrochelatase activity. The highest-ranking PLC result for the chlorophyll biosynthesis pathway is GUN4 (AT3G59400), a well-studied regulator of chlorophyll biosynthesis and a key player in plastid-to-nuclear signal transduction (Larkin et al., 2003).

Further manual and computational inspection of PLC-identified candidate genes reveals many more that appear to be good candidates for biologically meaningful coordinate expression. The flavonoid biosynthesis pathway (PWY1F-FLAVSYN), one of the best-studied pathways in plant secondary metabolism, provides a representative example (Winkel-Shirley, 2001). Table III lists top-ranking genes linked with flavonoid biosynthesis according to PLC. Five of these are already associated with the pathway, a consequence of within-pathway coexpression relationships. Three others have gene ontology (GO) annotations linking them to flavonoid biosynthesis. One of these, At5g17050, was recently identified as a flavonoid 3-O-glucosyltransferase, which influences the flow of metabolites through the flavonoid pathway (Tohge et al., 2005).

Table III.

Genes coexpressed with the flavonoid biosynthesis pathway

Top-ranking genes identified by PLC analysis using p value < 1e-80 are shown with GO annotations. Asterisks indicate genes that are already annotated as members of the flavonoid biosynthesis pathway. The number of coexpressed flavonoid biosynthesis genes is indicated in parentheses in the column labeled Gene ID.

Rank	Gene ID	Annotations (GO ID and Term)
1	AT5G08640 (5)	GO:0008372:cellular component unknown
		GO:0005554:molecular function unknown
		GO:0000004:biological process unknown
2	AT5G17050 (5)	GO:0016757:transferase activity, transferring glycosyl groups
		GO:0008194:UDP-glycosyltransferase activity
		GO:0008152:metabolism
		GO:0016999:antibiotic metabolism
		GO:0009507:chloroplast
3*	AT3G51240 (4)	GO:0009813:flavonoid biosynthesis
		GO:0008372:cellular component unknown
		GO:0045486:naringenin 3-dioxygenase activity
4*	AT5G05270 (4)	GO:0005554:molecular function unknown
		GO:0009813:flavonoid biosynthesis
		GO:0008372:cellular component unknown
5*	AT5G13930 (4)	GO:0009715:chalcone biosynthesis
		GO:0009705:vacuolar membrane (sensu Magnoliophyta)
		GO:0016210:naringenin-chalcone synthase activity
		GO:0005783:endoplasmic reticulum
		GO:0009813:flavonoid biosynthesis
6*	AT3G55120 (4)	GO:0045430:chalcone isomerase activity
		GO:0005783:endoplasmic reticulum
		GO:0009813:flavonoid biosynthesis
		GO:0009705:vacuolar membrane (sensu Magnoliophyta)
		GO:0009411:response to UV
		GO:0042406:extrinsic to endoplasmic reticulum membrane
7*	AT1G65060 (4)	GO:0009698:phenylpropanoid metabolism
		GO:0009411:response to UV
		GO:0016207:4-coumarate-CoA ligase activity
		GO:0008372:cellular component unknown
8	AT1G01280 (3)	GO:0004497:monooxygenase activity
		GO:0019825:oxygen binding
		GO:0005509:calcium ion binding
		GO:0006118:electron transport
		GO:0012505:endomembrane system
9	AT4G20420 (3)	GO:0000004:biological process unknown
		GO:0005554:molecular function unknown
		GO:0012505:endomembrane system
10	AT3G11980 (3)	GO:0009507:chloroplast
		GO:0009522:PSI
		GO:0016628:oxidoreductase activity, acting on the CH-CH group of donors, NAD or NADP as acceptor
		GO:0009556:microsporogenesis

The Trp biosynthesis pathway provides another illustration of how coexpression analysis can lead to new hypotheses regarding gene function. Two genes in the pathway are coexpressed with At3g26830 (PAD3), which encodes a cytochrome p450 monoxygenase and was recently shown to catalyze the final step in the camalexin biosynthesis pathway (Zhou et al., 1999; Schuhegger et al., 2006; note that the version of AraCyc we used predates the latter finding and assigns the PAD3 gene product to the first step of the pathway). Camalexin is the major phytoalexin compound produced in Arabidopsis and plays a role in defense against several pathogens (for review, see Glazebrook, 2005). As it is synthesized from precursors derived from Trp, it is not surprising that we have detected a coexpression relationship between these two pathways (Glawischnig et al., 2004). However, we also found that the two Trp biosynthesis pathway genes coexpressed with PAD3 are also coexpressed with two other genes of unknown function (At2g38860 and At3g46110), which are themselves coexpressed with PAD3. These two genes occupy positions 62 and 137 (out of 22,000) in the sorted list of coexpression results for PAD3, suggesting that they may play a role in linking camalexin and Trp biosynthesis pathways in Arabidopsis.

Using GO Annotations to Evaluate PLC-Identified Candidate Genes

As described above, PLC analysis ranks candidate genes first by the number of coexpressed partners from the bait pathway and second by the p values of the coexpression relationships. Further selection of candidate genes is possible using annotations derived from independent sources unrelated to coexpression data, such as functional information inferred from sequence homology or curated from the literature. For this study, we used GO annotations as a convenient summary of known and predicted functional information for Arabidopsis gene products (Harris et al., 2004). None of the annotations from GO are (thus far) based on large-scale coexpression analysis.

The GO is a structured vocabulary of terms that that organizes knowledge of gene products according to their molecular function, biological role, or cellular localization. GO annotations are associations between terms and gene products, and each GO annotation is tagged with an evidence code indicating the annotation source. The GO annotations can aid the evaluation of PLC analysis results in two ways: First, they can direct attention to particular classes of coexpressed genes, such as transcription factors or protein kinases, and second, they can allow further prioritization of candidate genes based on the similarity of annotations with bait genes from the target pathway. We found that terms appearing frequently among annotations associated with the bait genes also appear frequently among the genes identified in the PLC analysis.

For flavonoid biosynthesis, the term chloroplast is one of the most abundantly used terms for genes within the pathway as well as for the pool of candidate genes identified by PLC analysis (Supplemental Table S1). This annotation derives from electronic annotation by TargetP, a program that uses N-terminal sequence information to predict subcellular localization (Emanuelsson et al., 2000). Although the chloroplast assignment may not be correct given that flavonoid biosynthesis is thought to be associated with the endoplasmic reticulum, it is notable that TargetP assigned the same localization to genes both within the pathway and to coexpressed genes inferred by the PLC method. In addition, 14 PLC-identified genes are annotated with the term transcription factor activity, suggesting a potential role in the regulation of the pathway.

The GO also includes terms indicating that the process, function, or cellular localization of the annotated gene product is currently unknown. We found that a large number of candidate genes identified through PLC analysis are annotated with the unknown function GO terms including 1,205 for biological process unknown; 1,021 for molecular function unknown; and 32 for cellular component unknown out of a total of 4,022 PCL-identified genes. If coexpression patterns can imply functional information, then large-scale coexpression analysis as described here has the potential to contribute to functional annotation of Arabidopsis gene products.

Distance-Dependent Distribution of Coexpressed Metabolic Genes

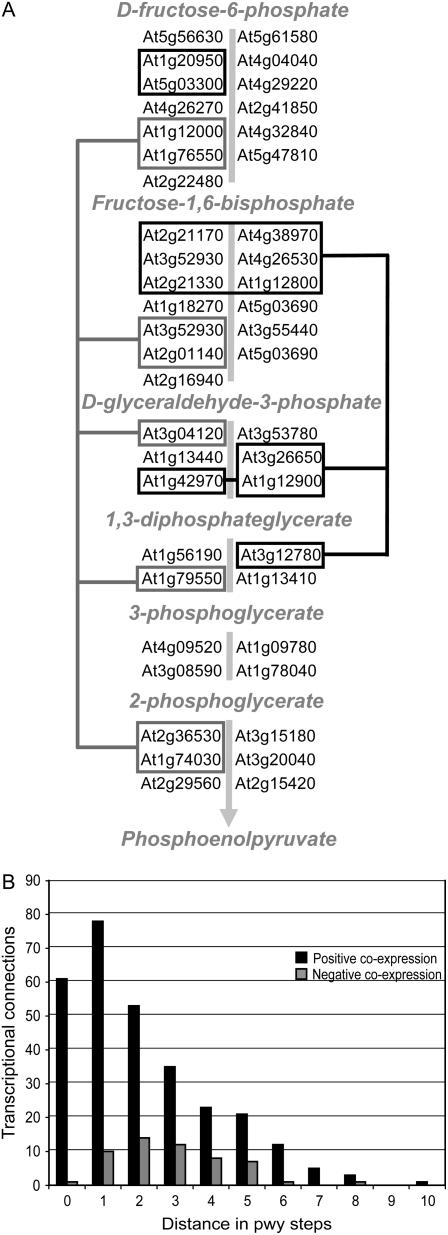
Manual inspection of the coexpression relationships between genes in the same pathway reveals that the distribution of connections between pathway genes appears nonrandom with respect to pathway structure and reaction order. As an example, Figure 4A shows a schematic view of positively coexpressed genes from the glycolysis pathway. Subsets of genes in the pathway form three groups of coexpressed genes, one of which involves nearly every pathway step. Other groups involve genes that catalyze adjacent or nearby reaction steps, which may reflect a general trend. To investigate this possibility, we plotted the number of pathway steps that separate coexpressed gene pairs for pathways containing at least six pathway steps (for a list of these pathways, see Supplemental Table S2). Figure 4B summarizes the results; positive coexpression typically involved genes associated with adjacent pathway steps. Negative coexpression, on the other hand, more often involved genes separated by two to three pathway steps.

Figure 4.

Transcriptional organization of metabolic pathway genes. A, Connectivity in the glycolysis pathway based on coexpression p value threshold 10⁻⁸⁰. Lines connect groups of coexpressed genes. Only genes with nonpromiscuous probe sets are shown. B, Distribution of connections for pathways with six or more pathway steps and at least two coexpressed pathway genes. The x axis shows distance in pathway steps. Genes catalyzing the same step are counted as zero pathway steps, genes catalyzing adjacent steps are counted as one pathway step, and so on. The y axis gives the number of coexpression links for positive (dark) and negative (lighter) coexpression relationships. Pathways included in the analysis are listed in Supplemental Table S2.

Topological Features of the Metabolic Network

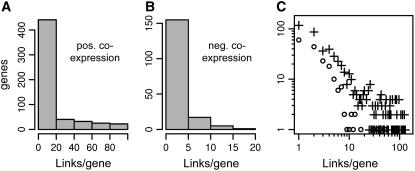
To explore the topology of the metabolic network, we examined the distribution of linked nodes (genes) in networks based on coexpression relationships (Fig. 5, A and B). We found that the distribution of links per node in the coexpression network of metabolic genes in Arabidopsis is highly skewed, with most genes having a small number of connections and a small but significant number having many connections (Fig. 5C). For example, at coexpression p value cutoff 1E-80, over 70% and 95% of linked nodes in the positive and negative AraCyc coexpression networks are connected to 10 or fewer genes/nodes. At this same p value threshold, both positively and negatively connected genes formed large networks of interconnected genes, but many genes (over half) lacked coexpression connections with other genes in the AraCyc data set. Overall connectivity within the positive network was higher than for the negative network: network density (actual links divided by possible links) was larger for the positive coexpression network at coexpression p value cutoffs ranging from 10E-40 to 10E-120.

Figure 5.

Coexpression links per gene. The distributions for positive (A) and negative (B) coexpression links (p < 10⁻⁸⁰) per AraCyc pathway genes are shown. C, Link frequency distribution for positive (+) and negative (o) coexpression networks, p value < 10⁻⁸⁰. The y axis indicates the number of genes that are coexpressed with the number of genes shown on the x axis.

We also investigated correlation between connectivity in the coexpression network (i.e. links per node) and number of paralogous genes per node. We used BLASTp to identify homologous sequences and then asked whether genes with larger numbers of paralogs in the Arabidopsis genome tend to have more or fewer coexpression connections with other genes. For the positive coexpression network (coexpression p value < 1E-80), we found that 65% of the 139 hub genes having 20 or more connections were single-copy genes, but only 37% of genes having fewer than 20 connections were single-copy genes. To assess the significance of this difference, we used random sampling to estimate the probability of obtaining such a high percentage of single-copy genes among the 139 hub genes purely by chance. We generated 100,000 random samples, computed the percentage of single-copy genes for each sample, and found that only four of the random samples contained more than 50% single-copy genes. Thus, we find that the relationship between uniqueness in the genome and status as a hub gene is highly significant. Furthermore, single-copy genes have an average of 11.5 connections, but genes with paralogous copies have an average of five connections per gene. We tested whether this difference in average links per gene is significant using the Wilcoxon rank sum test, which allows an assessment of whether or not two samples come from the same underlying distribution. Using this test, we determined that, on average, genes with paralogs are significantly less well connected (p value = 1.2E-5) than genes with no paralogs. We therefore find that highly connected nodes tend to be single-copy genes, whereas less-well connected genes tend to be present in multiple copies in the genome.

Coexpression Connectivity between Metabolic Pathways

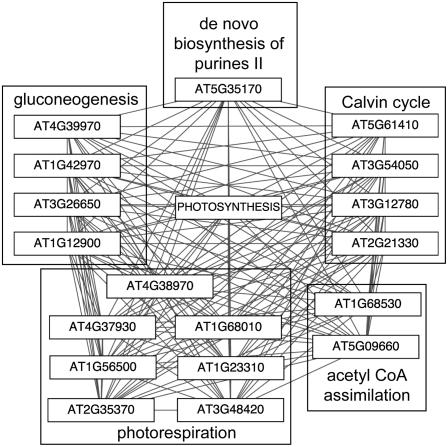
Because pathways are interconnected in the sense that many utilize intermediate metabolites or end products from other pathways, it is likely that some pathways include genes that are highly coexpressed with genes in other pathways. We expect that this would be particularly common for pathways that supply precursors for multiple processes, such as glycolysis or the TCA cycle. We found that this was indeed the case. Figure 6 shows a heatmap visualization in which each cell represents the degree of coexpression (high, medium, and low) between pairs of genes from the different pathways in the corresponding rows and columns. Several pathways contain genes that are highly coexpressed both within and across pathway boundaries. For instance, genes in the photosynthesis light reaction pathway are highly coexpressed with each other and with genes in other pathways, all of which utilize common metabolites, including malate, 3-phosphoglycerate, and Fru-1,6-bisphosphate. Figure 7 diagrams pathways that are linked to the photosynthesis light reaction pathway via coexpressed gene pairs; these include the photorespiration pathway (seven genes), gluconeogenesis (four genes), and the Calvin cycle (four genes). This transcriptional coordination of genes across pathway boundaries suggests corresponding coordination of metabolic flow.

Figure 6.

Within- and across-pathway coexpression patterns. Coexpression relationships are viewed as a grayscale heatmap between a subset of pathways listed in Table I. Cells are shaded according to the negative logarithm (base 10) of coexpression p values between genes from corresponding rows and columns. Coexpression p values less than or equal to 10⁻¹⁰⁰ are shown using the darkest shade. When rows and columns represent the same gene but intersect off the diagonal (due to shared genes across pathways), the corresponding cells are colored using the lightest shade. A version labeled with gene identifiers and pathway names is available as Supplemental Figure S1. Pathway designations and annotations are from AraCyc 2.1.

Figure 7.

Patterns of coexpression with photosynthesis pathway genes. Genes that are coexpressed (p value < 1E-60) with each gene in the photosynthesis light reaction pathway are shown.

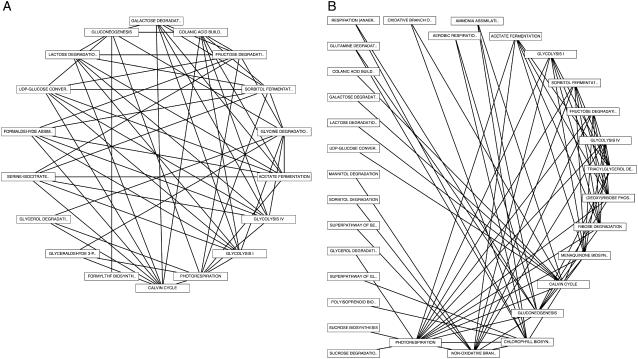
To investigate coregulatory connections between metabolic pathways in greater detail, we computed PLC networks in which each node in the network represents an individual pathway and connections between nodes represent pairs of coexpressed genes in which each member of the pair belongs to one, but not both, of the connected pathway nodes (Fig. 8). We considered negative and positive coexpression links separately because of the different distribution of high-confidence coexpression relationships for positive versus negative coexpression. In this scheme, each node-to-node connection represents a high degree of cross pathway coexpression. We found that pathways with the greatest number of internal coexpression connections are also among the most tightly coregulated across pathway boundaries. These included several core metabolic processes relating to energy metabolism, including the Calvin cycle, gluconeogenesis, Fru degradation, and sorbitol and acetate fermentation (Fig. 8). We found that pathways with large numbers of positive cross pathway connections also possess large numbers of negative cross pathway coexpression links (compare Fig. 8, A and B).

Figure 8.

Metabolic network connectivity. A, Network of positively coexpressed metabolic pathways using a p value cutoff of 1E-200. B, Network of negatively coexpressed metabolic pathways using a cutoff of 1E-80. Connected pathways share at least seven pairs of coexpressed genes.

DISCUSSION

Using linear regression p and r² values to identify and rank coexpression relationships, we showed that, on average, genes involved in the same metabolic pathway are coexpressed to a greater degree than genes involved in different pathways. However, most genes in the AraCyc data set are coexpressed with tens to hundreds of genes, only a small number of which are annotated as belonging to the same pathway or pathways. If understanding a pathway of interest is the main analytical focus, then a method of narrowing the field of candidates is required. To facilitate this type of analysis, we developed a PLC analysis approach that identifies and ranks candidate genes based on coexpression with groups of pathway genes and the relative strength (p and/or r² values) of these coexpression relationships (Fig. 3A).

We used an earlier version of the PLC analysis to identify novel genes involved in cellulose biosynthesis in Arabidopsis (Persson et al., 2005) and here demonstrate a larger-scale application to metabolic pathways in Arabidopsis. Using the method, we identified 4,022 coexpression partners for 144 pathways using a relatively stringent threshold for coexpression. A large proportion of these PLC-identified genes lack GO process, molecular function, or cellular component annotations. Information we have provided regarding their coexpression patterns with pathway genes from the AraCyc database provides new insight into their biological roles by linking these genes to biochemical pathways. Experimental investigation of the coexpressed genes' biological roles is beyond the scope of this current work; however, we have made the results available at our Web site to facilitate exploration and analysis by groups interested in individual pathways. On the Web site, we provide lists of all pathways examined in the study, the genes from each pathway that we included in the analysis, machine-readable spreadsheet files listing regression results for each pathway gene and all other probe sets (genes) on the ATH1 array, and ranked results from PLC using different p values as coexpression cutoffs. In addition, we established a mirror of the AraCyc database version used in our study to allow browsing of pathway structures. For future work, we plan to add tools that will allow users to run the PLC method on gene groupings of their own choosing.

Using random sampling, we computed empirical p values assessing the degree to which genes in each pathway are coexpressed with each other. We found that core metabolic pathways exhibited an unusually high level of within-pathway coexpression. We also identified pathways that possess multiple positive and negative coexpression links across pathway boundaries. These results are based on over 400 individual array hybridizations involving many different cell types, developmental stages, and experimental treatments. Coexpression, in this setting, means that regardless of the experimental condition, high (or low) expression of one member of a coexpression pair (or group) predicts similarly high (or low) expression of the other group members. We do not suggest that the coexpressed genes are expressed in every cell type, only that when they are expressed, they are expressed together. We suggest that the groups of coregulated genes are involved in maintaining and regulating metabolic flow within and across pathways. In addition, we saw that not all genes annotated as belonging to a pathway are involved in within- or across-pathway coexpression relationships. These genes may serve specialized functions that are not apparent when hundreds of experiments are considered. Alternatively, some of these genes may be incorrectly assigned in AraCyc, possibly reflecting the computational origins for AraCyc pathway annotations.

We found that the distribution of positive and negative coexpression relationships is highly skewed; the majority of genes have few links but a small but significant number of genes are very well connected. Similarly skewed distributions have been observed in a number of different biological networks, and it has been proposed that these networks arise in an incremental fashion via two mechanisms: duplication of components of the existing network and random mutation (for review, see Albert, 2005). Both models fit well with what is known about how genomes change over time; new sequences are created from preexisting sequences via duplicative mechanisms that affect regions of many different sizes, and duplicate sequences drift apart through random mutation. In our setting, wholesale duplication of preexisting genes, including both coding and transcriptional control regions, would increase the complexity and size of the coexpression network in that each gene duplication event would add a new node that would connect to the parent node and all its coexpression partners. Unless the presence of both duplicates with identical expression confers a selective advantage, we would expect that over time, the two genes would drift apart with respect to their relative patterns of coexpression. There should be no selective pressure blocking this drift as long as all essential coexpression relationships with either the source gene or its copy are maintained. Our observation that less well-connected nodes are represented by multiple copies in the Arabidopsis genome supports this scenario: We found that genes with one or more paralogs (as detected by blast analysis) are significantly less well connected than single-copy genes that have no within-genome homologs.

We found that the majority of highly connected (20 or more expression links) were single-copy genes. In yeast, single-copy genes exhibit a higher proportion of lethal or reduced-fitness phenotypes than do genes with duplicates (Gu et al., 2003). Similarly, well-connected genes in networks based on protein interactions and/or coexpression are also more likely to exhibit severe phenotypes (Albert et al., 2000; Jeong et al., 2001). It is well known that many genes do not exhibit easily recognized phenotypes, possibly due to functional redundancy or some form of genetic buffering (Cutler and McCourt, 2005). Indeed, we have found that for many pathways, only a subset of the genes annotated as belonging to the pathway exhibit coexpression relationships across a large number of conditions, suggesting that these genes may be the most important players in their respective pathways. Taken together, these results suggest that well-connected genes in Arabidopsis are also likely to be the most promising targets for genetic analysis of metabolic pathways.

An earlier study from Wille et al. (2004) used microarray expression data to examine transcriptional coordination between plastid, mitochondrial, and cytosolic isoprenoid pathways in plants (Wille et al., 2004). The study measured transcriptional coordination using 118 ATH1 arrays and focused on 19 genes in the plastid pathway, 16 genes in the cytosolic pathway, and five genes in the mitochondrial pathway. However, their approach used joint correlation to build the network, whereas ours has used simple linear regression. Despite this difference, we find some interesting similarities in the results. For example, similar to Wille et al. (2004) we found that several genes in the Arabidopsis isopentenyl diphosphate biosynthesis pathway (chloroplast non-mevalonate pathway) are highly coexpressed. In addition, Wille et al. (2004) observed joint regulation of many consecutive and closely positioned genes, which is similar to our finding that genes occupying nearby positions in a pathway tend to be coexpressed.

We believe that the results and methods presented here can aid scientists in choosing candidate genes for genetic analysis based on their position in the coexpression network. We recommend that researchers seeking to characterize any group of functionally related genes perform group- or PLC analysis to identify key players within and outside the group whenever there is good reason to expect that membership in the group will imply coexpression. As demonstrated here, the abundance of microarray expression data for Arabidopsis now available makes this analysis both feasible and productive. Furthermore, the results from coexpression analysis could help to improve annotation of the Arabidopsis genome. Indeed, we propose that lists of high-confidence coexpression partners could be added to gene-level Web pages at sites such as TAIR, providing a new dimension of functional annotation for the Arabidopsis genome.

MATERIALS AND METHODS

Data Files

AraCyc data are from version 2.1 of the database as available in August, 2005. Data were obtained from TAIR (www.arabidopsis.org) as a flat file dump that listed accessions for 221 different pathways associated with 1,612 genes. Affymetrix ATH1 GeneChip probe set and target gene information are from an annotations data file downloaded from the Affymetrix Web site in August, 2005 and dated June 20, 2005. GO annotations are from a file downloaded from TAIR's ftp site September, 2005. Copies of all primary data files are available upon request.

Mapping Gene Identifiers onto Probe Set IDs

To map genes onto probe sets and vice versa, we cross-referenced gene identifiers from the AraCyc database flat file against the AGI and Representative Public ID fields in the Affymetrix ATH1 probe set annotations file. This mapping produced a list of 1,488 probe sets. We purged redundant and promiscuous probe sets, i.e. genes mapped to multiple probe sets and probe sets recognizing more than one gene, to create a list of 1,330 AraCyc-associated probe sets. In a few cases, an AraCyc gene identifier was not represented on the ATH1 array. Visualization of a randomly selected subset of these using the Integrated Genome Browser, which shows the location of ATH1 probe sets alongside Arabidopsis (Arabidopsis thaliana) genome version 5 gene annotations, revealed that these genes are not interrogated on the ATH1 array, most likely because they appeared in the public databases after the ATH1 array entered production. The Integrated Genome Browser is available at http://www.affymetrix.com/support/developer/tools/download_igb.affx. A list of all pathways, probe sets, and gene identifiers is available at http://www.transvar.org/at_coexpress/analysis/web.

Array Processing and Regression Analysis

We obtained 553 CEL files for Affymetrix ATH1 array experiments from the Nottingham Arabidopsis Stock Center AffyWatch subscription service. A number of the files obtained were duplicates; after removing these, we processed the remaining CEL files using the robust multichip average algorithm implementation in Bioconductor (Gentleman et al., 2004). Using the deleted residuals quality control method implemented in the HDBStat! software (Trivedi et al., 2005) and described in detail in Persson et al. (2005), we identified low-quality arrays (Kolmogorov-Smirnov D > 0.15) and removed these from consideration, leaving a total of 486 high-quality array experiments. Linear regression between the 1,330 AraCyc genes and all ATH1 probe sets was then performed as described previously in Persson et al. (2005), using the following procedure.

For each probe set (gene) associated with AraCyc, use simple linear regression to compare its vector of N expression values 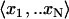with matching expression vectors corresponding to other genes represented on the same array design (Daniel, 2004). For each pairwise comparison of gene X and Y, compute a fitted regression line 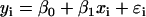where x_i and y_i are expression values for gene X and Y on array i; β_o and β₁ are the intercept and slope; ɛ_i is random error or deviation of y_i from the fitted value; 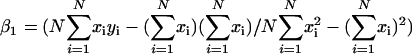and 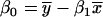. 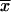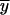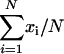The arithmetic means of x_i () and y_i () are and 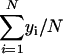, respectively. A p value for a simple linear regression expresses the probability that the slope β₁ of the regression line is equal to zero. In other words, if y varies randomly with x, and vice versa, then the slope of the regression line computed between them will be equal to zero. To compute the probability p that β₁ = 0 for each regression given the data, we use an F test for simple linear regression. For each regression, 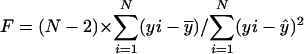, where 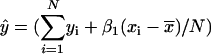, N is the number of arrays (CEL files) or points used in the regression, and 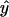is the arithmetic mean of the fitted values for y from the regression. The probability (p value) of β₁ = 0 is the area under the F distribution curve to the right of test statistics F. For each regression, the coefficient of determination 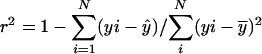, which is also the square of Pearson's correlation coefficient, was calculated (Rodgers and Nicewander, 1988). To perform the linear regressions and compute the F statistic, p values, and r² we used software written in Java and R (http://www.r-project.org). The Java software used a statistical programming library from Visual Numerics Inc. Copies of the code are available upon request. The regression results for all metabolic genes included in the study are available as tab-delimited files from http://www.transvar.org/at_coexpress/analysis/web.

Computing Empirical p Values for Within-Pathway Coexpression

For each AraCyc-associated probe set, we sorted its regression results by increasing p value and computed the average of the mutual ranks for each pathway probe set in the sorted lists of the other pathway probe sets. We used random sampling of probe sets to compute an empirical distribution of average ranks: for each pathway with M probe sets, we selected a random sample of size M from the 1,330 AraCyc probe sets in the study and computed its average rank. We repeated the sampling procedure 10,000 times for each M to develop an empirical distribution of average ranks for pathways including M genes. The average rank for each pathway was then compared to the empirical distribution of average ranks for a pathway of that size to estimate the p value for within-pathway coexpression. The heatmaps showing within- and across-pathway coexpression patterns were generated using matrix2png (Pavlidis and Noble, 2003).

PLC Analysis

Pathway- or group-level coexpression identifies and ranks genes based on their coexpression with a group of genes, such as a metabolic pathway. The procedure operates as follows: Select a subset of functionally related bait genes, B = {g₁, g₂, .., g_M} (e.g. all the members of a metabolic pathway) from the larger set G of all genes g_i and g_j represented on an expression microarray, e.g. ATH1. For every pairwise comparison between g_i and g_j, where one or both are in B, perform linear regression between g_i and g_j, yielding p value p_ij and coefficient of determination r_ij². Use the set of p and r² values obtained from the pairwise regressions to construct an undirected graph, where an edge e_ij connects g_i and g_j whenever p_ij < p_t and r_ij² > r_t² for user-defined thresholds p_t and r_t². Any two genes g_i and g_j that share an edge (link) in the resulting network graph are considered to be coexpressed. Using the coexpression network graph, identify every candidate gene c_i where c_i is coexpressed with two or more bait genes. Define B_i = {g₁, g₂, .., g_K} as the set of K > 1 bait genes coexpressed with candidate gene c_i and P = {p_i1, p_i2, .., p_iK} as the set of p values associated with coexpressed gene pairs {(c_i, g₁), (c_i, g₂),..,(c_i, g_K)}. To prioritize candidates for manual analysis, order the list of candidate genes by the relative sizes of their bait gene sets |B_i|, such that if |B_i| > |B_j| for c_i and c_j, then c_i is listed before c_j. When |B_i| = |B_j|, list c_i first whenever the product of its coexpression p values (p_π) with members of B_i is smaller than for c_j, where (p_π) for c_i is .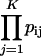

Paralog Identification

We used BLASTp to search the 1,330 Aracyc pathway genes used in the study against a database of Arabidopsis protein sequences obtained from TAIR. We considered hits as paralogs when the query and subject shared greater than 70% amino acid sequence identity across 90% or more of both sequences.

Analyzing Pathway and Coexpression Networks

Networks of coexpressed genes were assembled from pairwise linear regression results comparing AraCyc metabolic pathway genes to each other. We analyzed a number of different networks, which varied by different linear regression p and r² value thresholds used to define coexpression. Depending on the analysis, pathways were considered connected when they shared at least pairs of coexpressed genes, where neither member of a pair was in both pathways and N_p varied from two to seven, depending on the analysis. Coexpression networks were analyzed using the networkx Python toolkit for computing on graphs (https://networkx.lanl.gov/) and visualized using the Cytoscape network visualization software program (Shannon et al., 2003).

Supplemental Data

The following materials are available in the online version of this article.

Supplemental Table S1. GO terms for the flavonoid biosynthesis pathway and genes identified using the PLC algorithm.

Supplemental Table S2. List of pathways analyzed in Figure 4B.

Supplemental Figure S1. Fully labeled heatmap showing coexpression patterns within and across pathways.