Abstract
PDK1 catalyzes phosphorylation of Thr in the conserved activation loop region of a number of its downstream AGC kinase family members. In addition to the consensus sequence at the site of phosphorylation, a number of PDK1 substrates contain a PIF sequence (PDK1-Interacting Fragment), which binds and activates the kinase domain of PDK1 [PDK1(ΔPH)]. To gain further insight to PIF-dependent catalysis, steady-state kinetic and inhibition studies were performed for His6-PDK1(ΔPH)-catalyzed phosphorylation of PDK1-Tide (Tide), which contains an extended ‘PIF’ sequence C-terminal to the consensus sequence for PDK1 phosphorylation. In two-substrate kinetics, a large degree of negative binding synergism was observed to occur on formation of the active ternary complex (αKdATP = 40 μM and αKdTide = 80 μM) from individual transitory binary complexes (KdATP = 0.6 μM and KdTide = 1 μM). On varying ATP concentrations, the ADP product and the (T/E)-PDK1-Tide product analog (p′Tide) behaved as competitive and noncompetitive inhibitors, respectively; on varying Tide concentrations, ADP and p′Tide behaved as noncompetitive and competitive inhibitors, respectively. Also, negative binding synergism was associated with formation of dead-end inhibited ternary complexes. Time progress curves in pre-steady-state studies under ‘saturating’ or kcat conditions showed (i) no burst or lag phenomena, (ii) no change in reaction velocity when ATPγS was used as a phosphate donor, and (ii) no change in reaction velocity on increasing relative microviscosity (0 ≤ η/ηo ≤ 3). Taken together, PDK1-catalyzed trans-phosphorylation of PDK1-Tide approximates a Rapid-Equilibrium Random Bi Bi system, where motions in the central ternary complex are largely rate determining.
Phosphoinsositide-dependent protein kinase-1 (PDK1)4 is a member of the AGC subfamily of serine-threonine protein kinases, which includes different isoforms of cAMP-dependent protein kinase (PKA), protein kinase B (PKB), Ca2+-activated protein kinase (PKC), protein kinase G (PKG), 70 kDa 40S ribosomal protein S6 kinase (S6K), 90 kDa 40S ribosomal protein S6 kinase (RSK), serum- and glucocorticoid-induced protein kinase (SGK), and mitogen- and stress-activated protein kinase (MSK) (1). Among these kinases, amino acid sequences are conserved in a segment of the kinase domain known as the activation loop or T-loop, as well as in a segment C-terminal to the kinase domain known as the hydrophobic motif; and phosphorylation sites or acidic residues in these regions play important roles in their catalytic regulation and/or stability. PDK1 has been termed the ‘master kinase’ (2) in that it has been shown to phosphorylate the critical residue in the activation loops of AGC kinase family members (Fig. 1A) including PKBα (3–6), PKBβ (7), PKBγ (7), SGK1 (8), SGK2 (9), SGK3 (9), S6K (10, 11), PKA (12), PKCα (13), PKCβ II (13), PKCδ (14), PKCζ (14, 15), RSK (16, 17), and protein kinase N (PKN) (18, 19). Whereas the activation loop residue appears to be constitutively phosphorylated in PKA, PKCα, and PKCβ II, PDK1-catalyzed phosphorylation of PKB, SGK, S6K, RSK, PKCδ, and PKCζ occurs in response to cellular agonists acting through a common phosphatidylinositol 3-kinase (PI3K) pathway, albeit with differing temporal regulation (20–23).
Figure 1. Sequence alignment of peptide regions that interact with PDK1.

A, Human AGC kinase family members that have been shown to be substrates for PDK1 show conserved sequences in the segment comprising the VII and VIII subdomains of the catalytic kinase domain, as well as the hydrophobic motif (HM) near the C-terminus. Subdomain VIII is known as the activation loop, and the critical threonine residue that undergoes phosphorylation by PDK1 is indicated by the arrowhead. PI3K-dependent phosphorylation of the critical residue in the HM (arrowhead) enhances PDK1 phosphorylation of the activation loop residue. Identical residues are in bold; and they cluster in the region C-terminal to the threonine phosphorylation site, suggesting a potential consensus motif for PDK1 phosphorylation. B, T308-Tide represents the consensus motif found in subdomain VIII of PKBα, whereby PDK1 phosphorylates Thr-308 (underlined); PIF-Tide represents the consensus HM, which binds the PIF pocket of PDK1 and activates catalysis; PDK1-Tide is generated by joining the T308-Tide and PIF-Tide sequences; and (T/E)PDK1-Tide is a mutant analog of the phospho-PDK1-Tide product.
The common ability of PDK1 to catalyze phosphorylation of the activation loop of its numerous protein targets, but with varying degrees and mechanisms of regulation, has been explained from the intriguing perspective that PDK1 has the ability to ‘sense the conformation’ of many of its substrates (24). PDK1 and other AGC kinases possess a ‘PIF (PDK1-interacting fragment) pocket’ on the catalytic kinase domain (25, 26). In contrast to other AGC kinases, PDK1 does not possess a hydrophobic motif C-terminal to its catalytic domain. Therefore, the PIF pocket of PDK1 is accessible for interaction with the phosphorylated hydrophobic motifs of its target kinases. Such intermolecular interaction promotes activation of PDK1, enabling PDK1-catalyzed phosphorylation of target kinases at the activation loop. Upon phosphorylation of the activation loop, the phosphorylated C-terminal hydrophobic motif of the target kinase is released from the PIF pocket on PDK1, and it forms an intramolecular interaction with its own PIF pocket, which fully stabilizes an active conformation (24). Both in vivo and in vitro studies indicated the important role of intermolecular PIF interactions in activating PDK1-catalyzed phosphorylation of S6K, RSK, and SGK (27–29).
To further investigate the role of PIF interactions, a model ‘PIF-tide’ was synthesized to contain the C-terminal hydrophobic motif region of protein kinase C-related kinase-2 (PRK2). The PIF region in PRK2 contains high sequence homology to the PIF regions of PDK1 protein substrates, except that the Ser/Thr phosphorylation site is replaced by a negatively charged Asp residue (Fig. 1B) (25, 30). Surface plasmon resonance and competition measurements yielded KdPIF values of ~0.8–1.5 μM, indicating a strong binary complex between PIF-Tide and PDK1 (30). In addition, PIF-Tide was found to activate PDK1-catalyzed phosphorylation of the small T308-Tide, which represents the consensus motif near the site of phosphorylation in PKBα (Fig. 1B) (25). By conjugating the PIF-Tide to the C-terminus of T308-Tide, the PDK1-Tide was generated (Fig. 1B) (25). PDK1-Tide remains the prevailing model PDK1 substrate, as it undergoes phosphorylation at a rate >100-fold than T308-Tide, and its Km of ~80 μM is significantly lower than the Km of >10 mM estimated for T308-Tide.
While X-ray structural and mutagenesis studies have clearly defined PIF pocket residues important to catalytic activation of PDK1 (25, 26), a detailed kinetic study of this process awaits description. Here, we report kinetic and chemical/solution perturbation studies aimed to establish the steady-state kinetic mechanism for PDK1-catalyzed trans-phosphorylation of PDK1-Tide. The results of these studies are best approximated a Rapid Equilibrium Random Bi Bi system, where chemical or conformational steps in the central ternary complex are largely rate determining. Most interesting was the apparently large degree of negative binding synergism exhibited between the peptide and nucleotide substrates/products. Such synergism may derive from conformational transitions important to catalytic turnover.
EXPERIMENTAL PROCEDURES
Materials and General Methods
The catalytic kinase domain of PDK1 [His6-PDK1(ΔPH), residues 51–359] (26), containing an N-terminal His6 tag followed by a PreScission protease recognition sequence prior to residue 51, was expressed using the Bac-to-Bac® Baculovirus Expression System (Invitrogen, Inc., Carlsbad, CA) and His6 affinity purified as described (31). Protein concentration was estimated using the Bio-Rad Protein Assay Kit with bovine serum albumin as a standard. PDK1-Tide and (T/E)PDK1-Tide were from 21st Century Biochemicals, Inc. (Marlboro, MA). [γ-32P]ATP and [γ-35S]ATPγS were from MP-Biomedical (Irvine, CA). All other chemicals, salts, and buffers were from Sigma-Aldrich (St. Louis, MO).
Two-Substrate Steady-State Kinetic Assays
Steady-state kinetic assays were carried out for His6-PDK1(ΔPH)-catalyzed trans-phosphorylation of the PDK1-Tide model peptide substrate (Fig. 1B). The 65-μL peptide phosphorylation reactions were performed at 30 °C in reaction buffer containing final concentrations of 50 mM Tris-HCl buffer, pH 7.5, 0.1% 2-mercaptoethanol, 10 mM MgCl2, and 0.2 mM sodium vanadate. Initial velocities were measured for varying PDK1-Tide concentrations (0.3, 1, 3, 10, 30, 100, and 300 μM) at different fixed concentrations of [γ-32P]ATP (~500 cpm/pmol; 0.3, 1, 3, 10, 30, 100, and 300 μM). Data collection in this manner provided all information necessary to construct companion reciprocal plots for the two varied substrates.
After 5 min preincubation of a 60-μL reaction mixture containing both substrates at 30 °C, the assays were initiated by addition of a 5-μL amount of a stock concentration of His6-PDK1(ΔPH) to yield final enzyme concentrations of 5–30 nM. For kinase assays where both the ATP and PDK1-Tide concentrations were ≥3 μM, 20-μL aliquots were removed and quenched at three different times (ranging from 5–60 min). For kinase assays where either the ATP or PDK1-Tide concentration was ≤1 μM, it was necessary to extend some reaction times up to 3 h in order to obtain the minimal detectable amounts of 32P-radiolabeled PDK1-Tide (300–600 cpm) in a 20 μL reaction aliquot (~0.6–1.2 pmol or 30–60 nM). Each 20 μL reaction aliquot was quenched by mixing with 20-μL of 50 mM phosphoric acid, which was then applied to P81 phosphocellulose paper (2 × 2 cm). After 30 s, the papers were washed in 50 mM phosphoric acid for 10 min, then rinsed with acetone, and placed in the hood (≤5 min) to dry. The amount of 32P-labeled peptide was determined by scintillation counting of the paper in 10 mL of scintillation cocktail.
Initial rates for reactions containing ≥1 μM of both substrates were measured under conditions where total product formation represented ≤10% of the initial concentration of the limiting substrate. Due to detection limits, initial rates for reactions containing 0.3 μM of either substrate were measured under conditions where total product formation (30–60 nM) represented 10–20% of the initial limiting substrate concentration. Since it was often necessary to use 30 nM enzyme to catalyze 30–60 nM product under these limiting conditions, it is important to point out these initial velocities were obtained under pre-steady-state conditions. However, the initial velocities obtained under these conditions approximate those obtained under true steady-state conditions, as demonstrated by more rigorous pre-steady-state experiments described later in this paper, which provide no evidence of burst or lag phenomena. Initial velocities (v, M s−1) were normalized to enzyme concentration to yield apparent first-order rate constants (k, s−1), which better facilitate kinetic comparisons between steady-state and pre-steady-state kinetic results.
Control assays were carried out in which either the enzyme or PDK1-Tide were omitted; these values were always ≤5% of the activity measured in the presence of both the lower- and upper-bound concentrations of these reagents (0.3 and 300 μM [γ-32P]ATP; 5 and 30 nM enzyme). Control assays containing the enzyme and only the [γ-32P]ATP substrate were further analyzed to measure ATPase activity. The amount of [32P]inorganic phosphate released from [γ-32P]ATP was determined by addition of 50 μL of the reaction mixture to 100 μL of a quench solution containing a 21% suspension of acid-washed (HCl) activated charcoal in 75 mM phosphoric acid. The quenched solution was mixed and placed on ice for 5 min, which provided for effective removal of the [γ-32P]ATP nucleotide from solution by the charcoal. The charcoal with bound [γ-32P]ATP was pelleted by centrifugation for 10 min, and a 60-μL aliquot of the supernatant was analyzed for [32P]inorganic phosphate. 32P-radioactivity in the supernatant was always ≤5% of the radioactivity measured in the absence of enzyme, indicating that the ATPase activity of His6-PDK1(ΔPH) is significantly lower than activity to the PDK1-Tide substrate.
Product and Dead-End Inhibition Steady-State Kinetic Assays
Diagnostic enzyme inhibition studies were carried out for His6-PDK1(ΔPH)-catalyzed transphosphorylation of PDK1-Tide exactly as described for two-substrate kinetics. ADP was tested as a product inhibitor and a phospho-PDK1-Tide mimetic in which the number two Thr residue that undergoes phosphorylation was replaced by a Glu residue [(T/E)-PDK1-Tide, Fig. 1B) was used as a dead-end product analog inhibitor. In both cases, initial velocities were measured for varying substrate concentrations (0.3, 1, 3, 10, 30, 100, and 300 μM) at different fixed concentrations of the inhibitor (0, 10, 30, 50, 70, and 100 μM) at an unsaturating concentration of the other substrate (30 μM). Data collection in this manner provided information necessary to construct companion plots for ‘diagnostic’ analysis of the effect of either the ADP or (T/E)-Tide inhibitors on the two different varied substrates.
In contrast to the diagnostic inhibition studies, a full array of data sets was collected for product inhibition with ADP. Initial velocities were measured for varying PDK1-Tide concentrations (0.3, 1, 3, 10, 30, 100, and 300 μM) at different fixed concentrations of ADP (0, 1, 3, 10, 30, and 100 μM). In this case, ADP product inhibition was also measured at different fixed concentrations of [γ-32P]ATP (0.3, 1, 3, 10, 30, 100, and 300 μM). Data collection in this manner provided all information necessary to construct companion plots for complete kinetic analysis of the effect of ADP on the two different varied substrates.
Pre-Steady-State Kinetic Assays
Pre-steady-state kinetic assays were carried out for His6-PDK1(ΔPH)-catalyzed transphosphorylation of PDK1-Tide using a KinTek Corporation (Austin, TX) Model RQF-3 rapid-quench-flow apparatus thermostatted at 30 °C. Reaction buffer refers to 50 mM Tris-HCl buffer, pH 7.5, 0.1% 2-mercaptoethanol, 10 mM MgCl2, and 0.2 mM sodium vanadate. The left and right drive syringes in the RQF apparatus were filled with reaction buffer, and the middle (quench) syringe was filled with 75 mM phosphoric acid. One sample loop was loaded with 15 μL of reaction buffer containing 600 μM of both PDK1-Tide and [γ-32P]ATP; and the other sample loop contained 15 μL of varying concentrations of His6-PDK1(ΔPH) enzyme (2, 6, and 10 μM) in reaction buffer. Thio-substitution effects were determined by equivalent substitution of [γ-35S]ATPγS for [γ-32P]ATP. The phosphorylation reaction was initiated by mixing the contents of the sample loops that was allowed to react for a time t (0.05 ≤ t ≤ 10 s) before the reaction was acid quenched. For each time point, two 20-μL aliquots of each quenched reaction solution were individually applied to P81 phosphocellulose paper (2 × 2 cm), and the amount of PDK1-Tide phosphorylation was quantified as described for the steady-state kinetic assays. The time courses were performed in triplicate and the data points represent averaged values ± S.E.
Control assays were carried out in which the PDK1-Tide substrate was omitted for each enzyme concentration in the presence of either [γ-32P]ATP or [γ-35S]ATPγS. The amounts of 32P- or 35S-radioactivity detected on the filter paper were always ≤5% of the measured radioactivity in the presence of PDK1-Tide, indicating that purified active pS241 His6-PDK1(ΔPH) catalyzes little or no nonspecific autophosphorylation during reaction times ≤10 s. In addition, the amounts of 32P- or 35S-radioactivity hydrolyzed from either [γ-32P]ATP or [γ-35S]ATPγS during this time period were shown to be negligible by the charcoal-filtration assay.
Solution Viscometric Studies
Pre-steady-state assays containing either [γ-32P]ATP or [γ-35S]ATPγS as described above were also carried out in reaction buffer containing varying amounts of either microviscogen [0–30% (w/v) glycerol or sucrose] or macroviscogen [0–6.3% (w/v) polyethylene glycol]. The relative viscosities (η/ηo) of reaction buffers containing either a micro- or macroviscogen were calculated at 30 °C, using an Ostwald viscometer to measure transit times and correcting for density. Relative solvent viscosities of 1.0 and 3.0 were obtained for buffers containing 0% and 30% sucrose, respectively. The measurements were made in triplicate and did not deviate by more than 3%.
Data Analysis
Initial rates determined in the two-substrate steady-state kinetic studies were globally fitted to Equation 1,
| (1) |
the general velocity equation derived for a Rapid Equilibrium Random Bi Bi system (32). In this equation, v/[PDK1] = k (s−1) yields the observed pseudo-first-order rate constant as a function of ATP and PDK1-Tide concentrations ([ATP] and [Tide]) according to the dissociation constants of ATP and PDK1-Tide (KdATP and KdTide). The symbol α is a proportionality constant, which quantifies the degree that the binding of one substrate either increases (α < 1) or decreases (α > 1) the affinity of the enzyme for the other substrate. In addition, initial rates for varying the concentrations of either [ATP] or [Tide] were individually fitted to the standard Michaelis-Menten equation to obtain values of appkcat and either appKmATP (at different fixed [Tide]) or appKmTide (at different fixed [ATP]), respectively, which were further analyzed by the appropriate secondary expressions derived from Equation 1. Secondary plots of appkcat versus either [Tide] or [ATP] were fitted to Equations 2 and 3, respectively (32).
| (2) |
| (3) |
Secondary plots of either appKmATP versus [Tide] or appKmATP versus [ATP] were fitted to Equations 4 and 5, respectively (32).
| (4) |
| (5) |
Initial rates determined in steady-state kinetic dead-end inhibition studies were fitted to the general velocity equations derived for competitive and noncompetitive mechanisms of inhibition, respectively (32). In these equations, values of appkcat, appKm, and appKi were determined for varying substrate and inhibitor concentrations at a single fixed concentration of the other substrate.
Initial rates determined in the complete array of ADP inhibition studies were globally fitted to Equation 8,
| (6) |
which is the general velocity equation derived for a Rapid Equilibrium Random Bi Bi system with a dead-end PDK1-ADP-Tide ternary complex (32). In this equation, the parameters are the same as described for Equation 1, but further include KiADP, the dissociation constant of the ADP product inhibitor and β, the proportionality constant to quantify the degree that the binding of Tide substrate either increases (β < 1) or decreases (β > 1) the affinity of the enzyme for ADP. Values of appkcat, appKmATP, appKmTide, and appKiADP that were obtained from fits of individual ADP inhibition data sets to either Equation 6 or 7 were further analyzed by the appropriate secondary expressions derived from Equation 8. In these cases, secondary expressions for appkcat versus either [Tide] or [ATP] are the same as Equations 2 and 3, respectively; and secondary expressions for either appKmATP versus [Tide] or appKmATP versus [ATP] are the same as Equations 4 and 5, respectively (32). Secondary expressions of either appKiADP versus [Tide] or appKiADP versus [ATP] are given by Equations 9 and 10, respectively (32).
| (7) |
| (8) |
All data were plotted and fitted using the GraFit 4.0 software (Erithacus Software, UK), which utilizes an iterative least squares algorithm (33).
RESULTS
Two-Substrate Steady-State Kinetics of His6-PDK1(ΔPH)
As demonstrated in the preceding manuscript, the recombinant catalytic domain construct of PDK1 [His6-PDK1(ΔPH), residues 51–359] was affinity purified (≥95%) from Sf9 insect cell lysate in its Ser-241 phosphorylated and catalytically active form (26). While His6-PDK1(ΔPH) exhibited detectable activity towards trans-phosphorylation of T308-Tide, we confirmed that His6-PDK1(ΔPH), similar to full length PDK1 (25), exhibits very low affinity for T308-Tide with Km ≥ 10 mM. In contrast to T308-Tide, His6-PDK1(ΔPH) exhibited significantly higher activity to PDK1-Tide, which contains the extended PIF residues C-terminal to the sequence of T308-Tide (Fig. 1B). Most important, saturating conditions could be approached with PDK1-Tide enabling steady-state kinetic determinations of values for appkcat, appKmTide, and appKmATP. Therefore, all kinetic studies and mechanistic depictions are given in reference to PDK1-Tide (Tide) as the substrate for phosphorylation by His6-PDK1(ΔPH).
Fig. 2 shows all steady-state kinetic data and secondary plots for titration of His6-PDK1(ΔPH) with varying concentrations of one substrate at different fixed concentrations of the other substrate. During initial attempts to carry out a full titration analysis, it became apparent that titrations using substrate concentrations spanning two log units (3–300 μM) were yielding seemingly parallel lines in double reciprocal plots. Only by spanning substrate concentrations over three log units (0.3–300 μM) was it possible to clearly identify points of reciprocal plot intersection, which lie far to the left of the 1/k- or y-axis and well below the 1/[S]- or x-axis (Figs. 2A and 2B). Such a phenomenon reflects a large negative binding synergism associated between the ATP and Tide substrates. Due to the results obtained in inhibition studies (see below), analysis of these data was best approximated and described for a Rapid Equilibrium Random Bi Bi system (Fig. 2G) (32). Global fitting of the data to Equation 1 yielded values of kcat = 0.356 ± 0.010 s−1, the dissociation constants of ATP (KdATP = 0.57 ± 0.24 μM) and Tide (KdTide = 1.1 ± 0.5 μM) in the absence of the other substrate, and the proportionality constant of α = 77 ± 32. In Equation 1, the calculated dissociation constants of ATP (αKdATP = 44.3 μM) and Tide (αKdTide 84.3 μM) in the ternary complex reflect the large value of α and approximate their appKm values under saturating conditions.
Figure 2. Two-Substrate Steady-State Kinetics.
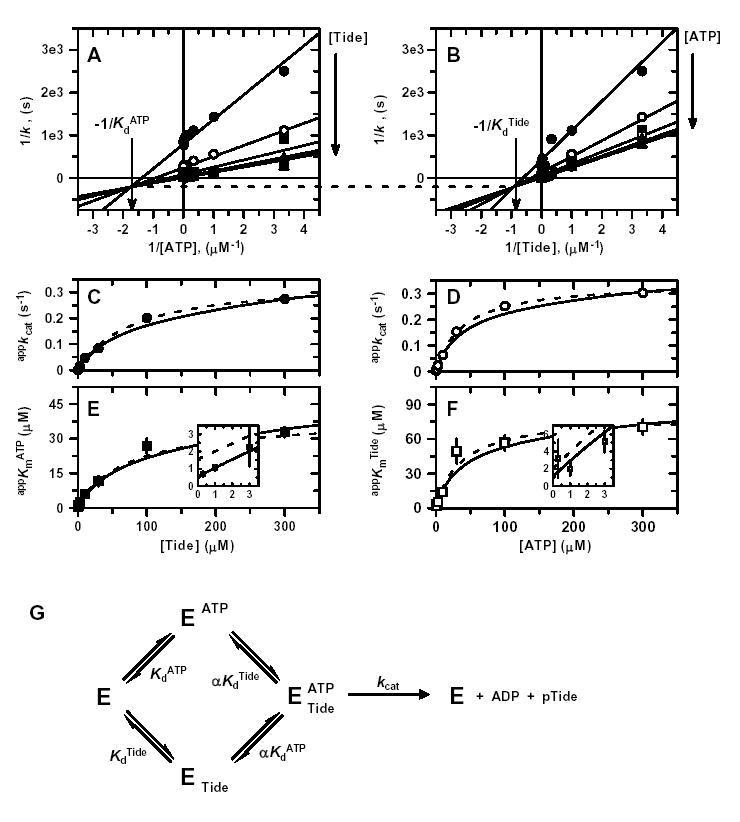
Double reciprocal plots of A, 1/k versus 1/[ATP]; and B, 1/k versus 1/[Tide]. In both reciprocal plots, the concentration of one substrate was varied at seven different concentrations of the fixed substrate [0.3 μM (•), 1 μM (○), 3 μM (▪), 10 μM (□), 30 μM (▴), 100 μM ( ▵), and 300 μM (▾)]. Solid lines indicate the global fit of the data to Equation 1. In addition, values of C, appkcat from varying [ATP]; D, appkcat from varying [Tide]; E, appKmATP from varying [ATP]; and F, appKmTide from varying [Tide] were determined from individual fits of each data set to the Michaelis-Menten equation (Fig. S1) and plotted against the given fixed substrate concentrations. Dashed lines represent direct fits of the secondary plots to C, Equation 2; D, Equation 3; E, Equation 4; and F, Equation 5. Solid lines were generated by these equations using the kinetic constants determined from the global fit of the data in Fig. S1. Insets in panels E and F magnify views of the data and fitted line patterns near the y-axis. G, Equilibria of the Rapid-Equilibrium Random Bi Bi system described by general rate Equation 1. The binding of one substrate changes the dissociation constant, Kd, of the other substrate by the proportionality constant α, which leads to formation of the central ternary complex from which reaction products are catalyzed, kcat.
Since the nature of these data preclude both (i) close examination in double reciprocal plots and (ii) statistical appreciation in global analysis, the data are further displayed in individual plots, where both the global fit to Equation 1 and individual direct fits to the Michaelis-Menten equation are indicated (Fig. S1). To better highlight the effects of the large negative binding synergism (α ≫ 1), values of appkcat and appKmATP (Fig. S1A) and appkcat and appKmTide (Fig. S1B) obtained from individual fits were analyzed in secondary plots, where both global and direct fits are indicated (Figs. 2C–2F). Direct fits of appkcat values obtained for varying [ATP] at different fixed [Tide] (Fig. 2C, Equation 2) and varying [Tide] at different fixed [ATP] (Fig. 2D, Equation 3) yielded well determined values of kcat = 0.351 ± 0.015 s−1 and αKdATP = 39.3 ± 2.2 μM (Fig. 2C) and kcat = 0.346 ± 0.006 s−1 and αKdTide = 80.7 ± 9.2 μM (Fig. 2D). However, the difficulty towards accurate determinations of the dissociation constants of ATP and Tide in each individual binary complex are clearly illustrated by the secondary plots of appKmATP (Fig. 2E, Equation 4) and appKmTide (Fig. 2F, Equation 5), where the corresponding KdATP and KdTide values are given by the y-intercepts (insets). Table 1 summarizes the fitted values ± S.E. of the kinetic constants determined by global and secondary plot data fitting to the equations derived for the Rapid Equilibrium Random Bi Bi system (Fig. 2G).
Figure S1. Two-Substrate Steady-State Kinetics.
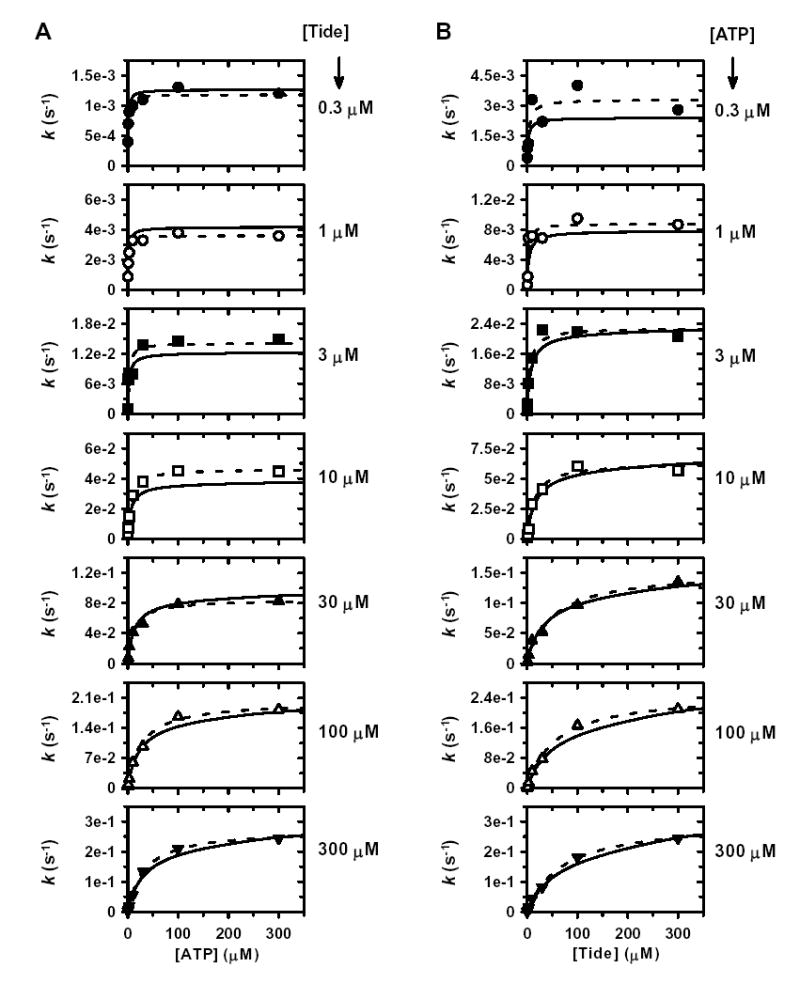
Individual direct plots of A, k versus [ATP]; and B, k versus [Tide]. The concentration of one given substrate was varied at seven different concentrations of the other given fixed substrate [0.3 μM (•), 1 μM (○), 3 μM (▪), 10 μM (□), 30 μM (▴), 100 μM (▵), and 300 μM (▾)]. Dashed lines indicate direct fits of the individual data sets to the Michaelis-Menten equation, which yielded values of appkcat and appKmATP for varying [ATP] and values of appkcat and appKmTide for varying [Tide]. Solid lines indicate the global fit of these data to Equation 1, which describes a Rapid Equilibrium Random Bi Bi system (Fig. 2G).
Table 1.
Steady-State Kinetic Constants for Phosphorylation of PDK1-Tide by His6-PDK1(ΔPH).
| two-substrate a | ADP inhibition b | ||||
|---|---|---|---|---|---|
| parameter | data analyzed | eq | value | Eq | value |
| kcat (s-1) | global | 1 | 0.356 ± 0.010 | 6 | 0.334 ± 0.007 |
| appkcat vs [Tide] | 2 | 0.351 ± 0.015 | 2 | 0.336 ± 0.010 | |
| appkcat vs [ATP] | 3 | 0.346 ± 0.006 | 3 | 0.324 ± 0.014 | |
| KdATP (μM) | global | 1 | 0.57 ± 0.24 | 6 | 0.54 ± 0.15 |
| appKmATP vs [Tide] | 4 | 1.6 ± 1.1 | 4 | 0.804 ± 0.231 | |
| appKmTide vs [ATP] | 5 | 1.0 ± 1.4 | 5 | (1.37) c | |
| αKdATP (μM) | global | 1 | (44.3) c | 6 | (42.6) c |
| appkcat vs [ATP] | 3 | 39.3 ± 2.2 | 3 | 43.4 ± 6.0 | |
| appKmATP vs [Tide] | 4 | 40.8 ± 2.6 | 4 | 42.7 ± 0.9 | |
| appKmTide vs [ATP] | 5 | 25 ± 10 | 5 | 59 ± 32 | |
| KdTide (μM) | global | 1 | 1.1 ± 0.5 | 6 | 1.0 ± 0.3 |
| appKmATP vs [Tide] | 4 | 3.2 ± 2.0 | 4 | (1.52) c | |
| appKmTide vs [ATP] | 5 | 2.1 ± 2.2 | 5 | 1.9 ± 4.6 | |
| αKdTide (μM) | global | 1 | (84.3) c | 6 | (78.2) c |
| appkcat vs [Tide] | 2 | 80.7 ± 9.2 | 2 | 80.2 ± 6.2 | |
| appKmATP vs [Tide] | 4 | 64 ± 13 | 4 | 80.6 ± 5.1 | |
| appKmTide vs [ATP] | 5 | 75.7 ± 7.2 | 5 | 81 ± 13 | |
| α | global | 1 | 77 ± 32 | 6 | 78 ± 21 |
| appKmATP vs [Tide] | 4 | (25.2) c | 4 | (53.1) c | |
| appKmTide vs [ATP] | 5 | (39.3) c | 5 | (42.7) c | |
| KiADP (μM) | global | NA d | NA | 6 | 1.2 ± 0.5 |
| appKiADP vs [Tide] | NA | NA | 7 | 7.5 ± 2.7 | |
| βKiADP (μM) | global | NA | NA | 6 | (58.8) e |
| appKiADP vs [Tide] | NA | NA | 7 | (84) e | |
| appKiADP vs [ATP] | NA | NA | 8 | 19.4 ± 2.8 | |
| β | global | NA | NA | 6 | 49 ± 20 |
| appKiADP vs [Tide] | NA | NA | 7 | 11 ± 4 | |
The steady-state kinetic values ± S.E. were determined for the rapid-equilibrium random-order ternary complex mechanism depicted in Fig. 2G.
The steady-state kinetic values ± S.E. were determined for the rapid-equilibrium random-order ternary complex mechanism with a dead-end E-Tide-ADP complex depicted in Fig. 4G.
This value was calculated from the appropriate relationship given between fitted values of either KdATP, αKdATP, KdTide, αKdTide, or α determined in the indicated method of analysis.
Not applicable.
This value was calculated from the appropriate relationship given between fitted values of KiADP and β determined in the indicated method of analysis.
Dead-End Inhibition Steady-State Kinetics
The pattern of intersecting lines shown in Figs. 2A and 2B provide little evidence towards the steady-state kinetic mechanism of peptide phosphorylation other than ruling out both (i) Ping-Pong and (ii) Rapid-Equilibrium Ordered Bi Bi systems (32). For these mechanisms, respectively, either parallel lines are observed or lines intersect on the y-axis. Discrimination between other possible mechanisms [e.g., Steady-State Ordered, Steady-State Random, or (Partial) Rapid-Equilibrium Random Bi Bi systems] may be achieved by comparing the effects of product (or dead-end) inhibitors in double reciprocal plots constructed for varying each substrate, while the other substrate is fixed at an unsaturated concentration (32).
For His6-PDK1(ΔPH), ADP was shown to be (i) competitive with the ATP substrate (Fig. 3A; appkcat = 0.0939 ± 0.0007 s−1, appKmATP = 11.3 ± 0.4 μM, and appKiADP = 29.6 ± 1.8) and (ii) noncompetitive with the Tide substrate (Fig. 3B; appkcat = 0.145 ± 0.001 s−1, appKmTide = 33.1 ± 0.9 μM, and appKiADP = 73.3 ± 1.9). Since a wide range of concentrations were used for the varied substrate, insets are included in Fig. 3 to magnify views of the line patterns crossing the y-axis. In complementary inhibition studies, the phosphopeptide product analog (T/E)-Tide (p’Tide) was shown to be (i) noncompetitive with the ATP substrate (Fig. 3C; appkcat = 0.0954 ± 0.0009 s−1, appKmATP = 13.6 ± 0.4 μM, and appKip′Tide = 74.2 ± 2.0) and (ii) competitive with the Tide substrate (Fig. 3D; appkcat = 0.142 ± 0.002 s−1, appKmTide = 31.7 ± 1.9 μM, and appKip′Tide = 31.0 ± 2.6).
Figure 3. ADP and pTide Inhibition Kinetics.
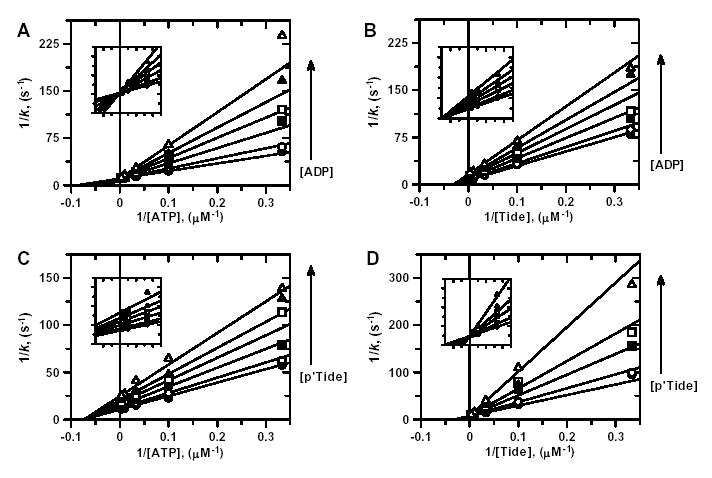
Double reciprocal plots for A, ADP inhibition when ATP is the varied substrate; B, ADP inhibition when Tide is the varied substrate; C, pTide inhibition when ATP is the varied substrate; and D, pTide inhibition when Tide is the varied substrate. For all plots, indicated substrate concentrations were varied at six different concentrations of the indicated inhibitor [0 μM (•), 1 μM (○), 3 μM (▪), 10 μM (□), 30 μM (▴), and 100 μM ( ▵)], while the concentration of the other substrate was fixed at 30 μM. Solid lines represent fits of the data to the equation for either competitive inhibition (A, D) or noncompetitive inhibition (B, C).
The observation of competitive inhibition exhibited between both (i) the ATP substrate and the ADP product inhibitor and (ii) the Tide substrate and the pTide product analog rule out Steady-State Ordered and Steady-State Random Bi Bi systems (32). In a Steady-State Ordered system, competitive inhibition between a given substrate/product pair would be observed only for the substrate that binds first. In a Steady-State Random system, only mixed-type inhibition patterns would be observed. Thus, the line patterns in Fig. 3 remain consistent with either (i) a Rapid-Equilibrium Random Bi Bi system, which can form both E-ADP-Tide and E-ATP-pTide types of dead-end ternary complexes or (ii) a Theorell-Chance system, which is a special case of an Ordered Bi Bi system (32). In a Theorell-Chance system, only the substrate that binds first can form a stable binary complex, while the concentrations of the central substrate and product ternary complexes are essentially zero.
Binding Synergism between ADP and Tide
In order to distinguish between the Rapid-Equilibrium Random and Theorell-Chance Bi Bi mechanisms, the effect of ADP product inhibition was tested for varying one substrate concentration at different fixed concentrations of the other substrate (32). Due to the extensive substrate concentration ranges required in this experiment, the ADP inhibition data are displayed in arrays of individual plots, which permit close inspection of the analyses (Figs. S2 and S3). Similar to Fig. 3A, ADP was shown to be competitive with ATP as the varied substrate (Fig. S2), and values of appkcat (Fig. 4A), appKmATP (Fig. 4C), and appKiADP (Fig. 4E) were obtained for different fixed Tide concentrations. Similar to Fig. 3B, ADP was shown to be noncompetitive with Tide as the varied substrate (Fig. S3), and values of appkcat (Fig. 4B), appKmTide (Fig. 4D), and appKiADP (Fig. 4F) were obtained for different fixed ATP concentrations. The critical observation whereby the appKiADP increases hyperbolically with increasing fixed [Tide] (Fig. 4E) rules out the special case of a Theorell-Chance system, where appKiADP would show no dependence on different fixed [Tide] (32). Thus, the ADP inhibition data can be appropriately analyzed according to equations derived for a Rapid-Equilibrium Random Bi Bi system with a E-ADP-Tide dead-end ternary complex (Fig. 4G, Equation 6) (32).
Figure S2. ADP Product Inhibition (Vary ATP).
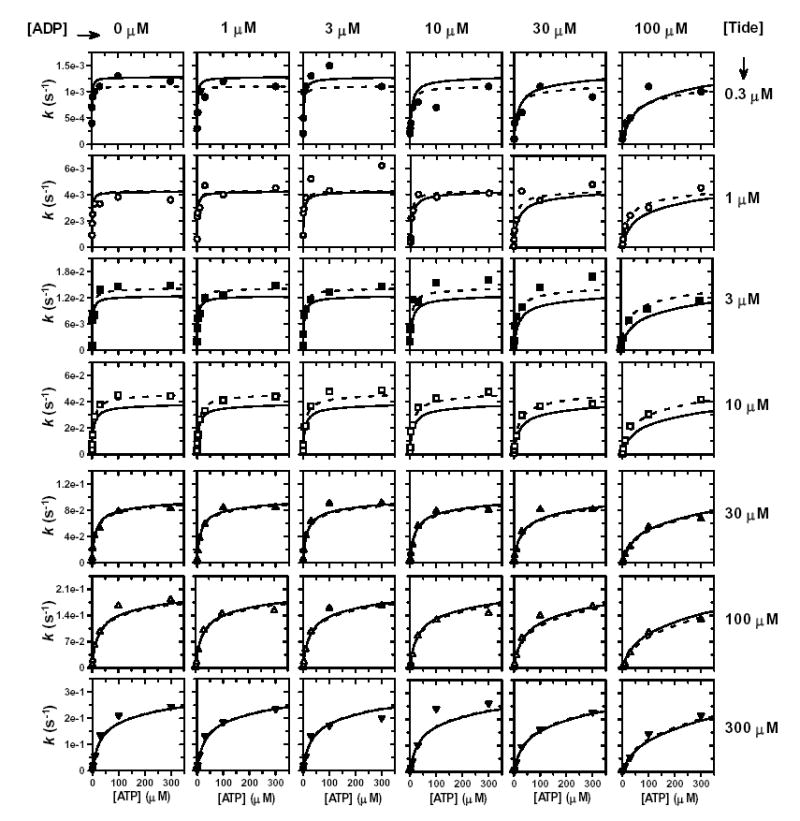
Individual direct plots of k versus [ATP]. The concentration of ATP was varied at six different concentrations of ADP. ADP inhibition studies were carried out at seven different concentrations of Tide [0.3 μM (•), 1 μM (○), 3 μM (▪), 10 μM (□), 30 μM (▴), 100 μM (▵), and 300 μM (▾)]. Dashed lines indicate direct fits of each row of individual data sets to the general velocity equation for competitive inhibition, which yielded values of appkcat, appKmATP, and appKiADP. Solid lines indicate the global fit of these data to Equation 6, which describes a Rapid Equilibrium Random Bi Bi system with a E-ADP-Tide dead-end ternary complex (Fig. 4G).
Figure S3. ADP Product Inhibition (Vary Tide).
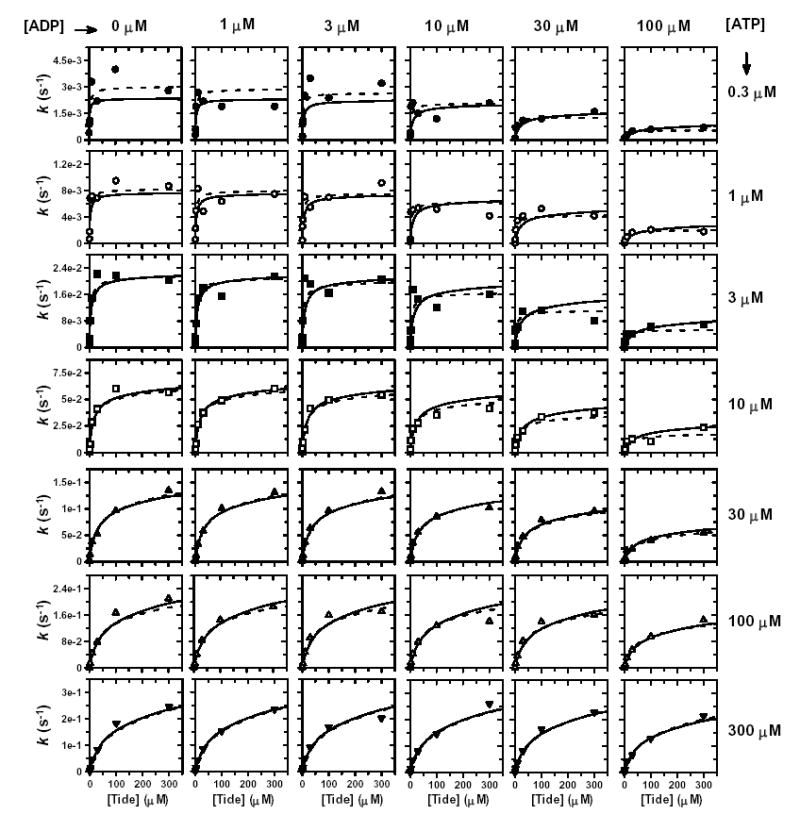
Individual direct plots of k versus [Tide]. The concentration of Tide was varied at six different concentrations of ADP. ADP inhibition studies were carried out at seven different concentrations of ATP [0.3 μM (•), 1 μM (○), 3 μM (▪), 10 μM (□), 30 μM (▴), 100 μM (▵), and 300 μM (▾)]. Dashed lines indicate direct fits of each row of individual data sets to the general velocity equation for noncompetitive inhibition, which yielded values of appkcat, appKmATP, and appKiADP. Solid lines indicate the global fit of these data to Equation 6, which describes a Rapid Equilibrium Random Bi Bi system with a E-ADP-Tide dead-end ternary complex (Fig. 4G).
Figure 4. Binding Synergism between ADP and Tide.
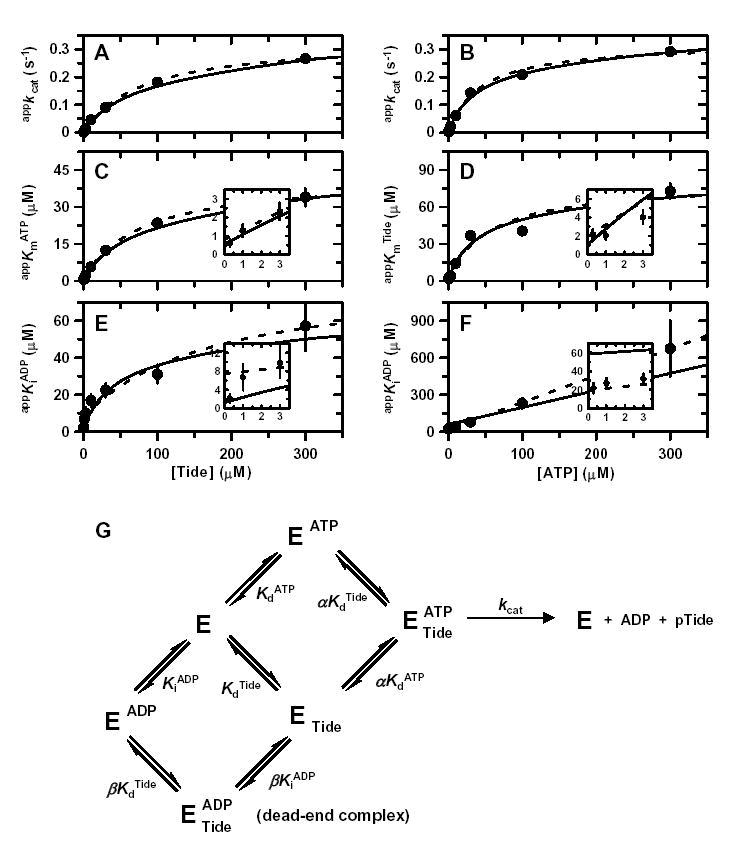
Values of A, appkcat from varying [ATP]; B, appkcat from varying [Tide]; C, appKmATP from varying [ATP]; D, appKmTide from varying [Tide]; E, appKiADP from varying [ATP]; and F, appKiADP from varying [Tide] were determined from fits of ADP inhibition data sets to the equation for either competitive inhibition (Fig. S2) or noncompetitive inhibition (Fig. S3) and plotted against the corresponding fixed substrate concentrations. Dashed lines represent direct fits of the secondary plots to A, Equation 2; B, Equation 3; C, Equation 4; D, Equation 5; E, Equation 7; and F, Equation 8. The solid lines were generated by these equations using the kinetic constants determined from a global fit of the initial rates shown in Figs. S2 and S3. Insets in panels C–F magnify views of the data and fitted line patterns near the y-axis. G, Equilibria of the Rapid-Equilibrium Random Bi Bi system with an E-ADP-Tide dead-end ternary complex according to the general rate Equation 6. The proportionality constants α and β quantify binding synergism exhibited between either ATP and Tide or ADP and Tide, respectively.
Global fitting of the data to the general rate Equation 6 yielded values of kcat, KdATP, KdTide, and α in agreement with those obtained from two-substrate steady-state kinetic analysis (Table 1). In addition, a KiADP = 1.2 ± 0.5 μM was determined for the dissociation constant of ADP, while β = 49 ± 20 indicated large negative binding synergism between ADP product and Tide substrate. The global fitted lines to Equation 6 are indicated for comparison to fitted lines obtained for the competitive (Fig. S2, varying [ATP]) and noncompetitive (Fig. S3, varying [Tide]) individual ADP inhibition data sets.
Table 1 summarizes the fitted values ± S.E. of the kinetic constants determined by both global and secondary plot data fitting to the equations derived for the Rapid Equilibrium Random Bi Bi system with a E-ADP-Tide dead-end ternary complex (Fig. 4G). The primary source of error in the global fitted value of β results from deviations of the appKiADP values obtained at the highest fixed concentrations (300 μM) of both Tide (Fig. 4E) and ATP (Fig. 4F), where little ADP inhibition was detected (Figs. S2 and S3, bottom rows). These relatively small upward deviations cause more dramatic effects on the y-intercepts, which yield the values of KiADP (Fig. 4E, inset) and βKiADP (Fig. 4F, inset).
Pre-Steady-State Thio-Substitution Effects
Since the steady-state kinetic and inhibition results were best approximated by a Rapid Equilibrium Random Bi Bi system, it was of great interest to next investigate the nature of the enzymatic step governing the relatively slow turnover rate of kcat ~ 0.34 s−1. Therefore, His6-PDK1(ΔPH)-catalyzed peptide phosphorylation reactions were carried out under pre-steady-state conditions ([E] = 1–5 μM) with ‘saturating’ amounts (300 μM) of both ATP and Tide. By using enzyme concentrations in this range, it was possible to distinguish whether rates of peptide chemical phosphorylation changed on progressing from the initial turnover (i.e., observed velocity includes all steps leading to and including chemical phosphorylation) to subsequent turnovers (i.e., observed velocity further includes product dissociation steps) (34). Fig. 5A shows the time progress curve of phosphopeptide product (pTide) formed during the first three catalytic turnovers using 5 μM enzyme. No changes in the velocity of pTide formation (slope) could be detected on transition between the initial and subsequent turnovers. If the rate of release of either ADP or pTide product was significantly slower than chemical phosphorylation, then a burst of pTide formation would have been observed during the first turnover, followed by slower linear accumulation of pTide during subsequent turnovers. The constant velocity (i.e., absence of a ‘burst’ of pTide) observed in this pre-steady-state experiment is further supported by the y-intercept, which closely approaches zero (Fig. 5A).
Figure 5. Pre-Steady-State Thio-Substitution and Solution Viscosity Effects.
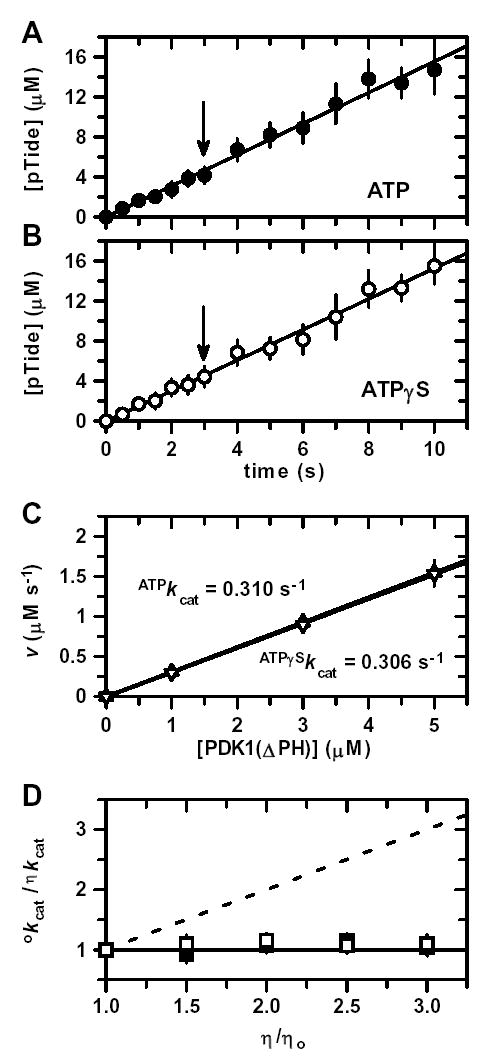
Time progress for pTide formation under ‘saturating’ or kcat conditions using 5 μM enzyme, 300 μM PDK1-Tide phosphate acceptor, and either A, 300 μM ATP as phosphate donor (•) or B, 300 μM ATPγS as thio-phosphate donor (○). Solid lines represent linear fits of the time courses. Since no ‘burst’ or ‘lag’ phenomena were observed, the slopes of these lines yield initial velocities under pre-steady-state conditions. Arrows indicate the common time point at which the concentration of the pTide product equals the given enzyme concentration (i.e., transition point between single and multiple turnovers). C, Plot of pre-steady-state initial velocities, v, versus enzyme concentration (1, 3, and 5 μM) using either ATP (▴) or ATPγS (▿). Solid lines represent linear fits to yield apparent first-order ATPkcat and ATPγSkcat values. D, Plot of relative kcat values, οkcat/ηkcat, versus relative solution viscosity, η/ηo, using either ATP (▪) or ATPγS (□). The solid and dashed lines are drawn for slopes of zero and one, respectively. Bars indicate ±S.E.
In order to more closely probe the nature of the rate-determining step(s), the pre-steady-state time progress curve was also generated using ATPγS as an alternative substrate. If the chemical transfer step were (partially) rate-determining, then such ‘thio-substitutiton’ could lead to either an increased or decreased reaction velocity, depending on the degree of either dissociative or associative character, respectively, which may occur in the chemical step (35). Similar to the ATP reaction (Fig. 5A), pTide showed linear accumulation with time when ATPγS was the substrate (Fig. 5B). Pre-steady-state time progress curves were also generated for [enzyme] = 1 and 3 μM; and the slopes (Δv/Δ[E]) determined from plots of the reaction velocities with either the ATP or ATPγS substrates yielded similar values of ATPkcat = 0.310 ± 0.015 s−1 and ATPγSkcat = 0.306 ± 0.017 s−1 (Fig. 5C). Importantly, these values approximated the kcat values obtained in two-substrate steady-state kinetics (Table 1), indicating that (i) ‘saturating’ conditions are observed in these pre-steady-state experiments, (ii) reaction velocities are linearly proportional over a 103-fold concentration range of His6-PDK1(ΔPH) (0.005 μM ≤ [E] ≤ 5 μM), and (iii) thio-substitution causes no significant change in the magnitude of kcat. While the similar values of ATPkcat and ATPγSkcat suggest that the chemical step is not rate-determining, it cannot be completely ruled out, as small thio-substitution effects may occur if the reaction proceeds with very little change in P–S bond order.
Pre-Steady-State Solution Viscometric Effects
As described in Figs. 5A–5C, pre-steady-state kinetic values of both ATPkcat and ATPγSkcat were also determined in reaction buffers containing increasing amounts of a microviscogen (e.g., glycerol and sucrose). Similar to reaction buffer alone (Figs. 5A and 5B), pTide showed linear accumulations with time, which yielded similar reaction velocities for all viscogen-containing buffers. Fig. 5D highlights the glycerol-independent similar values of °kcat (buffer with no viscogen) and ηkcat (buffer with viscogen) for both the ATP and ATPγS substrates. The observations that all pre-steady-state kinetic time courses remained linear and independent of viscogen indicate that dissociation of both ADP and pTide occur significantly faster than the rate-determining step(s). These results remain consistent with the good approximation of the steady-state kinetic results to a Rapid Equilibrium Random Bi Bi system, where motions in the central ternary complex are largely rate determining (Figs. 2G and 4G).
DISCUSSION
Protein kinases comprise the largest enzyme family, with ~500 being encoded by the human genome (36). The large number of cellular protein kinases reflects the large number of signal transduction pathways required in regulating proper cellular growth, survival, and proliferation. The complexity in elucidating cellular signaling networks is compounded by analyses indicating that individual protein kinases may target and phosphorylate numerous different protein substrates (37, 38). Thus, the mechanisms by which protein kinases selectively recognize protein substrates are of fundamental interest; and only recently, have detailed kinetic, binding, and mutagenesis studies revealed the importance of protein-protein docking complexes in regulating protein phosphorylation specificities (39, 40).
Central to the framework of such mechanistic understanding is development of kinetic mechanisms, describing timescales and equilibria of chemical steps involved in selective substrate recognition, catalytic phosphorylation, and release of products. On review of the steady-state kinetic mechanisms reported for all protein kinases to date, it became apparent that a leading majority of protein kinase reactions best approximate a Rapid Equilibrium Random Bi Bi system (Fig. 2G). In addition, such protein kinases may be further sub-categorized according to whether the ATP and protein substrates exhibit either (i) apparently positive binding synergism [α or Km/Kd < 1), (ii) apparently little binding synergism (α or Km/Kd ~ 1), or (iii) apparently negative binding synergism (α or Km/Kd > 1). Examples of protein phosphorylation reactions exhibiting random type mechanisms with apparently positive binding synergism include PAK24 with myelin basic protein (α ~ 0.5) (41), Csk with Src (α ≤ 0.25) (42), Sky1p with Np13 (α ~ 0.07) (43), and p38α with ATF2Δ115 (α ~ 0.04) (44); apparently little binding synergism (α ~ 1) has been reported for EGFR-TK(+EGF) with GAT-Tide (45), Csk with Poly(Glu,Tyr) (46), and Cak1p with CDK2 (47); while apparently negative binding synergism has been reported for ERK2 with EtsΔ138 (α ~ 2) (48), Sky1p with peptide (α ~ 3) (49), ROCKII with S6 peptide (α ~ 4) (50), and EGFR-TK with GAT-Tide (45). Thus, the α value of ~70 for the reaction of PDK1 with PDK1-Tide represents the largest Km/Kd ratio yet determined for a protein kinase reaction.
Strict interpretation of the α value according the Rapid Equilibrium Random Bi Bi system (Fig. 2G) requires that α quantify the degree that the binding of one substrate either increases (α < 1) or decreases (α > 1) the affinity of the enzyme for the other substrate (i.e., Kd and αKd are true dissociation constants). However, recently reported results of transient kinetic studies have revealed that apparent αKd values obtained in steady-state kinetic analyses may contain terms related to steps occurring in the central ternary complex. For example, pre-steady-state kinetic studies of both Csk with Src (α ≤ 0.25) (42) and Sky1p with Np13 (α ~ 0.07) (43) showed that a rapid burst of chemical phosphorylation precedes steady-state rate-limiting steps involving release of products. For these cases, Adams and coworkers demonstrated how fast and favorable phosphoryl transfer can function as a reversible ‘clamp’ that grasps onto the substrate, pulling it towards product and overcoming weak interactions between the enzyme and substrate (Fig. 6A). Under such conditions (k−3 < k3 > k4), the complex expression relating to the apparent Km (apparent αKd) is reduced to the approximation given by Equation 9 (39, 42, 43).
Figure 6. Docking-Based Substrate Recognition by Protein Kinases.
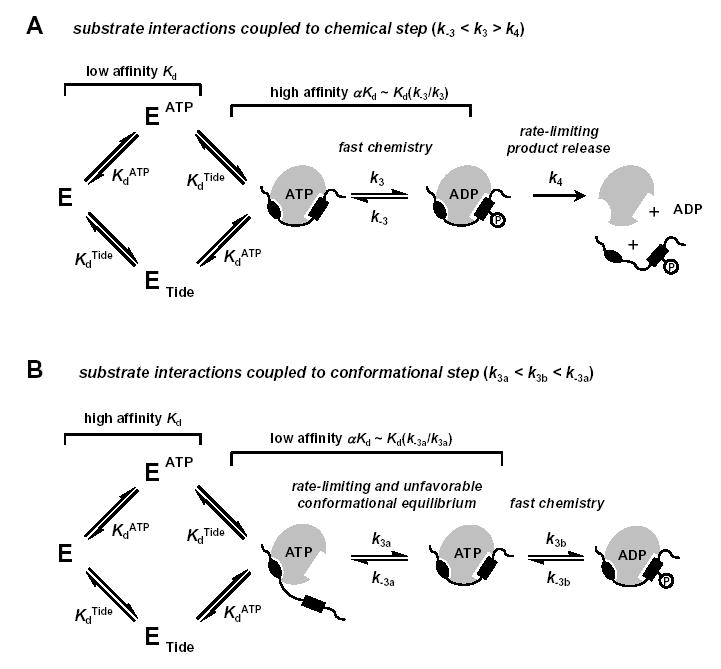
A, Rapid Equilibrium Random Bi Bi kinetic mechanism (KdATP, KdTide) with rapid chemical phosphorylation (k3, k-3) and rate-limiting product release (k4), where (k-3 < k3 > k4) (40). While distal contacts of the protein substrate provide some added binding affinity relative to consensus residues near the site of phosphorylation, the overall affinity of the complex remains weak. However, a fast and highly favorable phosphoryl transfer step can enhance interactions and further increase the apparent affinity according to Equation 9. B, Rapid Equilibrium Random Bi Bi kinetic mechanism (KdATP, KdTide) with a rate-limiting and unfavorable conformational equilibrium (k3b, k-3b) preceding more rapid chemical phosphorylation (k3b, k-3b) and product release steps, where (k3a < k3b < k-3a). In this case, distal contacts of the protein substrate provide very high binding affinity relative to consensus residues near the site of phosphorylation. However, a rate-limiting and unfavorable conformational equilibrium decreases the apparent affinity according to Equation 10. In the case of PDK1, the C-terminal PIF region of the model PDK1-Tide, as well as PDK1 protein substrates, provides a docking site to which PDK1 binds. The docked complex must undergo conformational rearrangement to form a catalytically competent ternary complex.
| (9) |
In contrast to the thermodynamically coupled systems described above (appKm < Kd), Adams and coworkers further explained how uncoupled fast phosphoryl transfer can either lower or raise Km relative to Kd in cases where substrates bind with high intrinsic affinity (39). However, this explanation cannot account for the observed Km > Kd relationship exhibited by PDK1, since pre-steady-state kinetics showed no evidence of a chemical burst preceding rate-limiting product release (Fig. 5). Furthermore, the absence of both thio-substitution and solution microviscosity effects suggested that a rate-limiting conformational change likely precedes chemical phosphorylation (k3a < k3b), as depicted in Fig. 6B. Under conditions where the conformational equilibrium is unfavorable (k3a < k3b < k−3a), the complex expression relating to the apparent Km (apparent αKd) is reduced to the approximation given by Equation 10.
| (10) |
Thus, the high affinity that PDK1 exhibits for both ATP and PDK1-Tide in individual binary complexes (KdATP and KdTide, Table 1) would appear to decrease ~70-fold (αKdATP and αKdTide, Table 1), since formation of the ternary complex may be coupled to both a rate-limiting and a thermodynamically unfavorable conformational transition preceding chemistry. Such a conformational step has been included for the reaction of ERK2 with ETSΔ138, whereby mutagenesis studies revealed the important role of distal contacts in mediating ‘proximity-induced’ catalysis (40, 51, 52). In addition, the apparently negative binding synergism observed between ADP and PDK1-Tide (KiADP < β KiADP) may also reflect a thermodynamically unfavorable conformational transition in the dead-end ternary complex.
Similar to the important role of docking interactions exhibited for the catalytic reactions of Csk, Sky1p, p38α, and ERK2 with their protein substrates, His6-PDK1(ΔPH) reactivity was greatly enhanced by ‘PIF’ docking interactions to the model PDK1-Tide substrate (e.g., where the Km ~ 70 μM observed for PDK1-Tide compared to Km ≥10 mM for T308-Tide). However, the significant effect of this specific interaction has yet to lower the apparent substrate Km (αKd) values to ≤Kd values for the individual binary complexes. Thus, the kinetic constants determined for the PDK1 reaction with PDK1-Tide now serve as a benchmark for future comparisons to kinetic constants determined for reactions of PDK1 with protein substrates (Fig. 1A). Of particular interest will be to identify whether other possible ‘docking’ interactions will serve to overcome the rate-limiting unfavorable conformational transition (Fig. 6B), which currently hinders PDK1-Tide phosphorylation.
In conclusion, the results of steady-state kinetic and inhibition studies for PDK1-catalyzed trans-phosphorylation of PDK1-Tide were best approximated by a Rapid Equilibrium Random Bi Bi system. ATP, PDK1-Tide, ADP, and (T/E)-Tide were shown to form high-affinity binary complexes, which significantly decreased upon formation of either catalytically competent or dead-end inhibited ternary complexes. In addition, time progress curves in pre-steady-state kinetic studies under ‘saturating’ or kcat conditions showed (i) no burst or lag phenomena, (ii) no change in reaction velocity when ATPγS was used as a phosphate donor, and (ii) no change in reaction velocity on increasing relative microviscosity. Taken together, a reaction mechanism is proposed whereby a rate-limiting and unfavorable conformation transition coupled to substrate recognition could account for the large degree of apparently negative binding synergism. In order to further address this phenomenon, extensive transient kinetic and equilibrium binding studies of the coupled interactions will be forthcoming.
Footnotes
This research was supported by grants from the James and Esther King Biomedical Research Program (BM026) and the National Institute of General Medical Sciences (GM69868) to T.K.H.
Abbreviations: ATF2Δ115, activating transcription factor-2 (residues 1–115); ATP, adenosine 5′-triphosphate; ATPγS, adenosine 5′-O-(3-thiotriphosphate); Cak1p, cyclin-dependent kinase-activating kinase of budding yeast; CDK2, cyclin-dependent kinase-2; Csk, C-terminal Src kinase; EGF, epidermal growth factor; EGFR-TK, epidermal growth factor receptor tyrosine kinase; ERK2, extracellular signal-regulated protein kinase-2; EtsΔ138, Ets transcription factor (residues 1–138); His6-PDK1(ΔPH), N-terminal His6 affinity tagged recombinant catalytic domain of PDK1 (residues 51–359); HM, hydrophobic motif; MSK, mitogen- and stress-activated protein kinase; Np13, nuclear protein localization-3; p38α, 38 kDa protein kinase-α; PAK2, p21-activated kinase-2; PDK1, phosphoinositide-dependent protein kinase-1; PH, pleckstrin homology; PIF, PDK1-interacting fragment; PI3K, phosphatidylinositol 3-kinase; PKA, cAMP-dependent protein kinase; PKB, protein kinase B; PKC, Ca2+-activated protein kinase; PKG, protein kinase G; PKN, protein kinase N; ROCKII, human Rho-kinase; RSK, 90 kDa 40S ribosomal protein S6 kinase; Src, SFK from Rous Sarcoma virus; SGK, serum- and glucocorticoid-induced protein kinase; S6K, 70 kDa 40S ribosomal protein S6 kinase; Sky1p, SR protein kinase in yeast.
References
- 1.Peterson RT, Schreiber SL. Curr Biol. 1999;9:R521–R524. doi: 10.1016/s0960-9822(99)80326-1. [DOI] [PubMed] [Google Scholar]
- 2.Mora A, Komander D, van Aalten DM, Alessi DR. Semin Cell Dev Biol. 2004;15:161–170. doi: 10.1016/j.semcdb.2003.12.022. [DOI] [PubMed] [Google Scholar]
- 3.Alessi DR, James SR, Downes CP, Holmes AB, Gaffney PRJ, Reese CB, Cohen P. Curr Biol. 1997;7:261–269. doi: 10.1016/s0960-9822(06)00122-9. [DOI] [PubMed] [Google Scholar]
- 4.Alessi DR, Deak M, Casamayor A, Caudwell FB, Morrice N, Norman DG, Gaffney P, Reese CB, MacDougall CN, Harbison D, Ashworth A, Bownes M. Curr Biol. 1997;7:776–789. doi: 10.1016/s0960-9822(06)00336-8. [DOI] [PubMed] [Google Scholar]
- 5.Stokoe D, Stephens LR, Copeland T, Gaffney PR, Reese CB, Painter GF, Holmes AB, McCormick F, Hawkins PT. Science. 1997;277:567–570. doi: 10.1126/science.277.5325.567. [DOI] [PubMed] [Google Scholar]
- 6.Stephens L, Anderson K, Stokoe D, Erdjument-Bromage H, Painter GF, Holmes AB, Gaffney PRJ, Reese CB, McCormick F, Tempst P, Coadwell J, Hawkins PT. Science. 1998;279:710–714. doi: 10.1126/science.279.5351.710. [DOI] [PubMed] [Google Scholar]
- 7.Walker KS, Deak M, Paterson A, Hudson K, Cohen P, Alessi DR. Biochem J. 1998;331:299–308. doi: 10.1042/bj3310299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kobayashi T, Cohen P. Biochem J. 1999;339:319–328. [PMC free article] [PubMed] [Google Scholar]
- 9.Kobayashi T, Deak M, Morrice N, Cohen P. Biochem J. 1999;344:189–197. [PMC free article] [PubMed] [Google Scholar]
- 10.Alessi DR, Kozlowski MT, Weng QP, Morrice N, Avruch J. Curr Biol. 1998;8:69–81. doi: 10.1016/s0960-9822(98)70037-5. [DOI] [PubMed] [Google Scholar]
- 11.Pullen N, Dennis PB, Andjelkovi M, Dufner A, Kozma SC, Hemmings BA, Thomas G. Science. 1998;279:707–710. doi: 10.1126/science.279.5351.707. [DOI] [PubMed] [Google Scholar]
- 12.Cheng X, Ma Y, Moore M, Hemmings BA, Taylor SS. Proc Natl Acad Sci USA. 1998;95:9849–9854. doi: 10.1073/pnas.95.17.9849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dutil EM, Toker A, Newton AC. Curr Biol. 1998;8:1366–1375. doi: 10.1016/s0960-9822(98)00017-7. [DOI] [PubMed] [Google Scholar]
- 14.Le Good JA, Ziegler WH, Parekh DB, Alessi DR, Cohen P, Parker PJ. Science. 1998;281:2042–2045. doi: 10.1126/science.281.5385.2042. [DOI] [PubMed] [Google Scholar]
- 15.Chou MM, Hou W, Johnson J, Graham LK, Lee MH, Chen CS, Newton AC, Schaffhausen BS, Toker A. Curr Biol. 1998;8:1069–1077. doi: 10.1016/s0960-9822(98)70444-0. [DOI] [PubMed] [Google Scholar]
- 16.Jensen CJ, Buch MB, Krag TO, Hemmings BA, Gammeltoft S, Frödin M. J Biol Chem. 1999;274:27168–27176. doi: 10.1074/jbc.274.38.27168. [DOI] [PubMed] [Google Scholar]
- 17.Richards SA, Fu J, Romanelli A, Shimamura A, Blenis J. Curr Biol. 1999;9:810–820. doi: 10.1016/s0960-9822(99)80364-9. [DOI] [PubMed] [Google Scholar]
- 18.Dong LQ, Landa LR, Wick MJ, Zhu L, Mukai Y, Ono Y, Liu F. Proc Natl Acad Sci USA. 2000;97:5089–5094. doi: 10.1073/pnas.090491897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Torbett NE, Casamassima A, Parker PJ. J Biol Chem. 2003;278:32344–32351. doi: 10.1074/jbc.M303532200. [DOI] [PubMed] [Google Scholar]
- 20.Belham C, Wu S, Avruch J. Curr Biol. 1999;9:R93–R96. doi: 10.1016/s0960-9822(99)80058-x. [DOI] [PubMed] [Google Scholar]
- 21.Vanhaesebroeck B, Alessi DR. Biochem J. 2000;346:561–576. [PMC free article] [PubMed] [Google Scholar]
- 22.Newton AC. Biochem J. 2003;370:361–371. doi: 10.1042/BJ20021626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Biondi RM, Nebreda AR. Biochem J. 2003;372:1–13. doi: 10.1042/BJ20021641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Biondi RM. Trends Biochem Sci. 2004;29:136–142. doi: 10.1016/j.tibs.2004.01.005. [DOI] [PubMed] [Google Scholar]
- 25.Biondi RM, Cheung PCF, Casamayor A, Deak M, Currie RA, Alessi DR. EMBO J. 2000;19:979–988. doi: 10.1093/emboj/19.5.979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Biondi RM, Komander D, Thomas CC, Lizcano JM, Deak M, Alessi DR, van Aalten DMF. EMBO J. 2002;21:4219–4228. doi: 10.1093/emboj/cdf437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Biondi RM, Kieloch A, Currie RA, Deak M, Alessi DR. EMBO J. 2001;20:4380–4390. doi: 10.1093/emboj/20.16.4380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Frödin M, Jensen CJ, Merienne K, Gammeltoft S. EMBO J. 2000;19:2924–2934. doi: 10.1093/emboj/19.12.2924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frödin M, Antal TL, Dummler BA, Jensen CJ, Deak M, Gammeltoft S, Biondi RM. EMBO J. 2002;21:5396–5407. doi: 10.1093/emboj/cdf551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Balendran A, Casamayor A, Deak M, Paterson A, Gaffney P, Currie R, Downes CP, Alessi DR. Curr Biol. 1999;9:393–404. doi: 10.1016/s0960-9822(99)80186-9. [DOI] [PubMed] [Google Scholar]
- 31.Gao X, Yo P, Harris TK. Prot Express Purif. 2005;43:44–56. doi: 10.1016/j.pep.2005.03.017. [DOI] [PubMed] [Google Scholar]
- 32.Segel, I. H. (1975) Enzyme Kinetics, John Wiley & Sons, Inc.
- 33.Leatherbarrow, R. J. (1998) GraFit Version 4.0, Erithacus Software Ltd., Staines, U.K.
- 34.Adams JA. Chem Rev. 2001;101:2271–2290. doi: 10.1021/cr000230w. [DOI] [PubMed] [Google Scholar]
- 35.Herschlag D, Piccirilli JA, Cech TR. Biochemistry. 1991;30:4844–4854. doi: 10.1021/bi00234a003. [DOI] [PubMed] [Google Scholar]
- 36.Manning G, Whyte DB, Martinez R, Hunter T, Sudarsanam S. Science. 2002;298:1912–1934. doi: 10.1126/science.1075762. [DOI] [PubMed] [Google Scholar]
- 37.Manning BD, Cantley LC. Sci STKE. 2002;162:PE49. doi: 10.1126/stke.2002.162.pe49. [DOI] [PubMed] [Google Scholar]
- 38.Obenauer JC, Yaffe MB. Meth Mol Biol. 2004;261:445–468. doi: 10.1385/1-59259-762-9:445. [DOI] [PubMed] [Google Scholar]
- 39.Leiser SA, Aubol BE, Wong L, Jennings PA, Adams JA. Biochim Biophys Acta. 2005;1754:191–199. doi: 10.1016/j.bbapap.2005.07.024. [DOI] [PubMed] [Google Scholar]
- 40.Rainey MA, Callaway K, Barnes R, Wilson B, Dalby KN. J Am Chem Soc. 2005;127:10494–10495. doi: 10.1021/ja052915p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wu H, Zheng Y, Wang ZX. Biochemistry. 2003;42:1129–1139. doi: 10.1021/bi026857l. [DOI] [PubMed] [Google Scholar]
- 42.Leiser SA, Shindler C, Aubol BE, Lee S, Sun G, Adams JA. J Biol Chem. 2005;280:7769–7776. doi: 10.1074/jbc.M411736200. [DOI] [PubMed] [Google Scholar]
- 43.Aubol BE, Ungs L, Lukasiewicz R, Ghosh G, Adams JA. J Biol Chem. 2004;279:30182–30188. doi: 10.1074/jbc.M402797200. [DOI] [PubMed] [Google Scholar]
- 44.Szafranska AE, Dalby KN. FEBS J. 2005;272:4631–4645. doi: 10.1111/j.1742-4658.2005.04827.x. [DOI] [PubMed] [Google Scholar]
- 45.Posner I, Engel M, Levitzki A. J Biol Chem. 1992;267:20638–20647. [PubMed] [Google Scholar]
- 46.Cole PA, Burn P, Takacs B, Walsh CT. J Biol Chem. 1994;269:30880–30887. [PubMed] [Google Scholar]
- 47.Enke DA, Kaldis P, Solomon MJ. J Biol Chem. 2000;275:33267–33271. doi: 10.1074/jbc.M004748200. [DOI] [PubMed] [Google Scholar]
- 48.Waas WF, Dalby KN. J Biol Chem. 2002;277:12532–12540. doi: 10.1074/jbc.M110523200. [DOI] [PubMed] [Google Scholar]
- 49.Aubol BE, Nolen B, Vu D, Ghosh G, Adams JA. Biochemistry. 2002;41:10002–10009. doi: 10.1021/bi020233y. [DOI] [PubMed] [Google Scholar]
- 50.Trauger JW, Lin FF, Turner MS, Stephens J, LoGrasso PV. Biochemistry. 2002;41:8948–8953. doi: 10.1021/bi0258243. [DOI] [PubMed] [Google Scholar]
- 51.Waas WF, Rainey MA, Szafranska AE, Dalby KN. Biochemistry. 2003;42:12273–12286. doi: 10.1021/bi0348617. [DOI] [PubMed] [Google Scholar]
- 52.Waas WF, Rainey MA, Szafranska AE, Cox K, Dalby KN. Biochim Biophys Acta. 2004;1697:81–87. doi: 10.1016/j.bbapap.2003.11.015. [DOI] [PubMed] [Google Scholar]


