Measuring Resistance to Change at the Within-Session Level

Abstract

Resistance to change is often studied by measuring response rate in various components of a multiple schedule. Response rate in each component is normalized (that is, divided by its baseline level) and then log-transformed. Differential resistance to change is demonstrated if the normalized, log-transformed response rate in one component decreases more slowly than in another component. A problem with normalization, however, is that it can produce artifactual results if the relation between baseline level and disruption is not multiplicative. One way to address this issue is to fit specific models of disruption to untransformed response rates and evaluate whether or not a multiplicative model accounts for the data. Here we present such a test of resistance to change, using within-session response patterns in rats as a data base for fitting models of disruption. By analyzing response rate at a within-session level, we were able to confirm a central prediction of the resistance-to-change framework while discarding normalization artifacts as a plausible explanation of our results.

An aspect of behavior that has attracted increasing attention in recent years is the persistence of responding under perturbations such as extinction, satiation, or alternative reinforcement (Nevin & Grace, 2000). The concept of resistance to change addresses the fact that operant behavior can be more or less resilient under such perturbations, depending on previous reinforcement conditions. Thus, studies of resistance to change usually involve a multiple schedule with two or more components that differ in terms of reinforcement rate, delay, or some other parameter (e.g., Nevin, 1974). After establishing a stable baseline, all components are submitted to the same disruptor to evaluate whether response rate will be differentially affected; differences of resistance among components must be attributed to differences in the reinforcement schedules associated with these components.

Because the components arrange different baseline schedules (e.g., variable-interval and variable-ratio schedules: Nevin, Grace, Holland, & McLean, 2001), the results obtained under disruption must be corrected for possible differences in baseline response rates. The correction method most commonly employed is normalization: in each component, the response rate f(x) observed for each quantity x of the disruptor is divided by the baseline response rate, f(0). An additional step is to apply a logarithmic transformation to the f(x)/f(0) ratios and to plot ln(f(x)/f(0)) as a function of x in each component (Nevin, Mandell, & Atak, 1983). The resulting curves all start from the same level, ln(f(0)/f(0))  =  ln 1  =  0, corresponding to a baseline without disruptor (x  =  0), and differences of resistance to change appear as differences in the slope of ln(f(x)/f(0)) as a function of x. The upshot is a fan-like graph in which the normalized and log-transformed rate of response, ln(f(x)/f(0)), decreases less in the component that is more resistant (e.g., Nevin, 2002, Figure 4). Each curve in this graph is known as a resistance function (Nevin & Grace, 2000).

If two components A and B must be compared quantitatively in terms of resistance to change, then straight lines with slopes s_A and s_B may be fitted to the respective curves for A and B. The inverse ratio of the best-fitting slopes, s_B/s_A, provides a quantitative index of relative resistance (Nevin & Grace, 2000). However, this inverse ratio may be statistically unreliable, and in some cases, difficult or impossible to compute (Grace & Nevin, 1997, p. 50). A simpler way to measure relative resistance is to average f(x)/f(0) across various x values and compute how much the logarithm of this average differs among components (Grace & Nevin, 1997, p. 50). Whether a ratio- or difference-based measure is used, the idea is to assess how much the resistance functions diverge in a fan-like graph obtained from normalized and log-transformed test data (Nevin, 2002).

Data Normalization: Background Assumptions

Because data normalization is simple to perform, its theoretical significance and implications are easily missed. Yet, normalization makes sense only if baseline response rate, f(0), is supposed to combine multiplicatively with a function of x that expresses the dynamics of responding under disruption. This multiplicative assumption is explicit in Nevin and Grace's (2000, Equation 15) model of resistance to change. Adjusting these authors' Equation 15 to the present notation, their model implies that during resistance testing:

1

where the m parameter measures resistance to change. Higher resistance means a larger m, which in turns means a shallower slope for the normalized and log-transformed resistance function.

In Equation 1 as it stands, the x/m ratio is dimensionless, which implies that m and x should bear the same units. In studies of resistance to change, however, the units for x can vary widely, depending on which disruptor is used. One way to solve this dimensionality issue is to replace m by a product of the form km, where the units of k and x coincide. In this reformulation of Equation 1, each disruptor is associated with a different parameter k that makes the x/k ratio dimensionless, whereas m (a dimensionless, nonspecific quantity) represents resistance to change across all possible disruptors. Here we shall ignore this complication and absorb both k and m in a single number.

In terms of absolute response rates, Equation 1 is equivalent to:

2

with a  =  f(0) and c  =  1/m. Equation 2 describes a standard exponential model for changes in absolute response rates (Killeen, 2000), and corresponds to the differential equation:

3

The fact that Equation 3 includes c but not a implies that the dynamics of response rate, governed by the resistance parameter c, are independent of the baseline level a  =  f(0). Also, Equation 2 expresses a multiplicative relation between the initial value a and the dynamic factor e^−cx. If Equation 2 is correct, therefore, normalization is an appropriate procedure to evaluate resistance to change independently of the baseline level of responding.

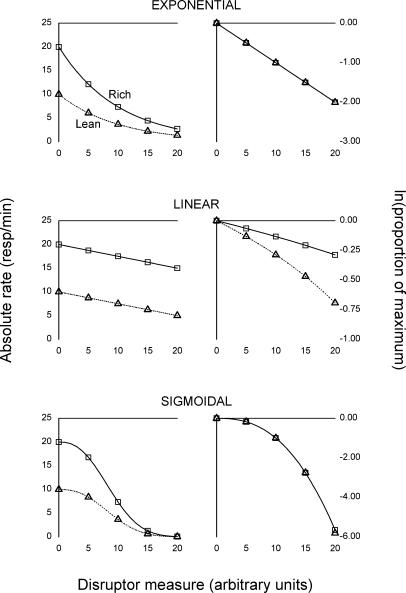
This can be seen in the top row of Figure 1, under the label “exponential.” The left panel (Figure 1, top row) shows a hypothetical case of responding decaying exponentially in two components labelled “Rich” and “Lean” (corresponding, for example, to two variable-interval schedules with different densities of food reinforcement). In drawing this panel, we assumed that the baseline response rate for the rich component (a  =  20) was higher than the baseline response rate for the lean component (a  =  10), as is often the case in resistance-to-change studies. We also assumed the parameter c to be the same in both components (c  =  0.01). That the dynamics of responding, expressed by c, are identical in the rich and lean components is evident once the data are normalized and log-transformed (right panel, top row of Figure 1). Normalizing response rates removes the contribution of the baseline level (a  =  20 versus a  =  10), and the logarithmic transform linearizes the exponential component e^−cx, resulting in two superimposed straight lines (right panel, top row, Figure 1).

Fig 1. Three hypothetical cases of exponential (top row), linear (middle row), and sigmoidal (bottom row) dynamics of responding under disruption.

In each case, absolute response rate in the rich component (squares and solid lines) is supposed to be higher in baseline than absolute response rate in the lean component (triangles and dotted lines). For each model, the panel in the left column shows raw response rates, whereas the panel in the right column shows normalized and log-transformed response rates. The units for disruptor amount are arbitrary. See text for the equations and parameters used to generate the curves.

A problem with this data transformation technique is that normalization can produce artifactual results if absolute response rates do not decay exponentially. This is illustrated in the middle row of Figure 1, under the label “linear.” Here we assume that absolute response rates decrease in a linear fashion over [0, a/c]:

4

and remain equal to 0 thereafter. The corresponding differential equation is simply:

5

with c > 0. Thus, as in the exponential case, the parameter c governs response dynamics (Equation 5) independently of the baseline level a  =  f(0). In drawing the middle row of Figure 1, we assumed a  =  20 and a  =  10 for the rich and lean components, respectively, and c  =  0.25 in both cases. That the dynamics of responding are identical in both components (c  =  0.25) is evident from the raw data (left panel, middle row of Figure 1). Once response rates are normalized and log-transformed, however, the fan-like shape that is typical of resistance-to-change research emerges as a by-product of normalization (right panel, middle row of Figure 1).

That the transformed data appear to be more resistant in the rich component is merely an arithmetical consequence of the fact that during normalization, response rates in the rich component are divided by a larger number (a  =  20) than in the lean component (a  =  10). Therefore, if absolute response rates decay linearly (Equation 4), the data should not be normalized; rather, the baseline level f(0) should be subtracted from f(x), or, equivalently, response functions should be translated vertically until their origins coincide (instead of dividing by f(0), as is usually done in resistance-to-change research).

The third row of Figure 1 illustrates a third possibility, under the label “sigmoidal.” Whereas normalization is adequate for exponential data (Figure 1, top row) and fails in the linear case (Figure 1, middle row), sigmoidal curves raise the possibility that normalization may or may not be appropriate, depending on whether raw response rates are best modelled by a multiplicative equation. The standard logistic equation f(x)  =  a/(1 + be^cx), for example (e.g., Borrelli & Coleman, 1998), cannot be expressed as the product of f(0)  =  a/(1 + b) and of a function that is independent of the baseline level. Indeed, the corresponding differential equation, f ′(x)  =  −c f(x) [1 − f(x)/a], involves a  =  f(0) (1 + b) as well as c; in this context, any attempt at studying behavioral dynamics independently of the baseline level f(0) may lead to misguided or meaningless conclusions. The same issue arises with some, but not all, of the equations that could be applied to sigmoidal curves.

As far as the sigmoidal case is concerned (Figure 1, bottom row), the best way to proceed from a resistance-to-change standpoint may be to model absolute response rates with a sigmoidal equation that also is multiplicative with respect to the baseline level f(0), assume that the equation is correct, and measure resistance on this basis. If the proposed equation describes the data well and if the results derived from it are consistent, then the overall resistance-to-change approach is strengthened (although not proved right). Ideally, the equation in question should extend the exponential model (Equation 2) to the case of sigmoidal curves. The following function fulfills these requirements:

6

with a > 0, c > 0, α ≥ 1, and x in (0, +∞). Because f(x) → a when x → 0, we define f(0) to be a. Thus, Equation 6 expresses a multiplicative relation between the baseline level f(0)  =  a and the dynamic factor exp[−(cx)^α]. We will refer to Equation 6 as a Weibull equation (cf. Tonneau, 2005) or as the generalized model of resistance to change (to be distinguished from the restricted, exponential model of Equation 2). Notice that Equation 6 reverts to Equation 2 when α  =  1. In all cases, the corresponding differential equation is:

7

Increasing α above 1 results in a more pronounced sigmoidal shape, whereas c governs the speed at which decay proceeds, as in the exponential model (Equation 2); larger values of c imply that the sigmoidal function decreases more quickly.

The left panel in the bottom row of Figure 1 was drawn on the basis of Equation 6, with a  =  20 for the rich component, a  =  10 for the lean component, and in both cases, c  =  0.10 and α  =  2.50 (hence the same dynamics). Normalizing and log-transforming the raw data results in two superimposed curves (right panel, bottom row of Figure 1), consistent with the fact that Equation 6 is multiplicative with respect to f(0). In this case, therefore, and contrary to the linear model (middle row of Figure 1), normalization is an adequate method of data analysis. Of course, the normalized and log-transformed curves are not straight lines (due to the non-exponentiality of the raw data), but, as in the exponential model, identical dynamics result in identical normalized curves.

Checking Assumptions

Exponential, linear, or sigmoidal functions (Figure 1) are likely to arise during resistance testing. Depending on the appropriate model for changes in absolute response rates, resistance findings obtained from normalized data may or may not be artifactual. Normalization artifacts, however, can be discarded in some cases. First, a few studies document crossovers between resistance functions: Response rate in the rich component starts above that in the lean component and then decreases until becoming the lower of the two rates (Grimes & Shull, 2001, Figure 2; Nevin, Tota, Torquato, & Shull, 1990, Figure 8). Such crossovers are inconsistent with the artifact shown in the middle row of Figure 1 and provide strong evidence with respect to resistance to change (cf. Nevin & Grace, 2000, p. 122). Second, in studies of resistance in which some of the food deliveries are presented independently of responding, baseline response rate for the rich component is often lower than for the lean component (see Nevin & Grace, 2000). Findings of differential resistance in such conditions cannot be due to normalization artifacts, which arise only if the baseline level is higher in the rich component (Figure 1, middle row). The evidence from response-independent schedules is particularly strong when combined with crossovers (e.g., Grimes & Shull, 2001). Finally, Nevin et al. (2001) found that resistance to change (computed with normalized data) in variable-interval and variable-ratio schedules was higher for lower baseline rates, contrary to what a normalization artifact would imply (Figure 1, middle row).

Despite these positive results, the validity of the multiplicative assumption with respect to baseline rates should be checked as often as possible. Nevin and Grace (2000) recommend checking whether the normalized, log-transformed data are linear, as in the top row of Figure 1 (right panel). A first problem with this recommendation is that even small amounts of noise can make the detection of nonlinearity in the log-transformed data quite difficult. In the right panel of the middle row of Figure 1, for example, the curvature of the log-transformed data is barely perceptible and would easily be masked by perturbations. Conversely, clear evidence of curvature in the log-transformed data refutes the restricted, exponential model of resistance (Equation 2) but remains consistent with the generalized model of resistance to change (Equation 6), as shown in the bottom row of Figure 1 (right panel). For both sets of reasons, checking the linearity of the normalized, log-transformed data may not be the best way to evaluate the assumptions behind normalization.

A more direct way of checking resistance assumptions is to examine the raw data and fit a particular model (Equation 2, 4, or 6) to them; response rates are normalized and log-transformed only after the linear model (Equation 4) is discarded as a plausible account of the untransformed data. Unfortunately, this approach requires a relatively high number of data points to produce orderly results. We addressed this issue by evaluating resistance to change at the within-session level. It is well known that response rate tends to increase, and then decrease, within each operant session (McSweeney & Roll, 1993). Whether these decreases in responding are ascribed to habituation (e.g., McSweeney & Roll, 1998) or to satiation (e.g., Bizo, Bogdanov, & Killeen, 1998), the environmental variable that produces them is the occurrence of the reinforcer in the course of the session (e.g., Cannon & McSweeney, 1995). Hence, the reinforcer functions as a disruptor of responding at the within-session level, just as it does in the between-session tests of resistance that rely on prefeeding (cf. Nevin et al., 1990). In the latter case, the animal is fed before the test session begins, whereas in within-session tests of resistance, the animal feeds itself along the course of the session.

If resistance to change identifies a general property of behavior (Nevin & Grace, 2000), however, resistance should be evident at the within-session level. On a multiple schedule with two components, for example, operant responding should be more resistant to within-session disruption in the rich than in the lean component. Here we report a test of this prediction, discussing methodological and measurement issues along the way.

Method

Subjects

The subjects were 4 naive, male Wistar rats (S1, S2, S3, S4), 5 months old at the beginning of the study. The rats were housed individually and maintained on a 12-hr/12-hr light/dark schedule, with solid food (Purina Chow) continuously available in each rat's home cage. Ten days before the study started, a schedule of water deprivation was progressively established, until the rats had 1 hr of free access to water per day.

Apparatus

Four MED Associates (ENV-007-VP) operant chambers for rats (30 cm wide, 24.5 cm deep, and 30 cm high) were equipped with an aperture (5 cm wide, 5 cm high, 3 cm deep) located 2 cm above the floor at the center of the right panel and giving access to a liquid dipper (ENV-202M with a 0.10-cc cup for water delivery). Water deliveries were signaled by an ENV-135M clicker mounted on the midline of the ceiling, 10 cm from the right panel. On each side of the dipper (3 cm from the aperture, 6.5 cm above the floor) was a retractable lever (4.5-cm wide, 1.5-cm protruding) requiring a minimum force of about 0.18 N to operate. A circular light (28-V, 100-mA, 2.5 cm in diameter) was located 6 cm above each lever. In this study, only the left lever and light were used. A 5 × 6 cm source of white noise was located 20 cm above the floor on the right edge of the left panel; the white noise measured 73 dB against the 62-dB background (scale A) provided by the exhaust fan. The houselight was a 28-V white bulb, located 25.5 cm above the floor at the center of the left panel. A computer controlled stimuli and registered responses through a MED-PC© interface.

Procedure

On the first day of the study, each rat was trained to approach the dipper and drink from it. Training proceeded with both levers retracted. On the second day, the left lever was inserted into the chamber. The session was 45-min long, and each lever press produced 5 s of access to water signaled by a double click. All rats started to press the lever reliably. This session was repeated for two additional days.

Over the next eight days, the rats were exposed to progressively thinner schedules of reinforcement. The schedules used in this study reinforced a lever press with a probability that depended on the length of the preceding interresponse time and on a preset duration t. Reinforcement probability increased linearly from 0 to 1 for the interresponse times that ranged from 0 to t; each interresponse time longer than t produced a reinforcer (see Weiss, 1970). These stochastic schedules mimic variable-interval schedules with a reinforcement rate of 1/t, and produce the within-session response patterns typical of the latter (Tonneau, Ortiz, & Cabrera, 2000). Across four blocks of two days, the parameter t (corresponding to the programmed interreinforcement interval) was extended from 15 s to 60 s. A reinforcer consisted of 5 s of access to water signaled by the double click.

The rats were then exposed to 80 sessions of a multiple schedule to assess resistance to change at the within-session level. Each session, 54 min long, involved 18 components of a rich schedule (t  =  15 s) and 18 components of a lean schedule (t  =  60 s). For Rats S1 and S2, the rich components were signaled by the light above the left lever, and the lean components by the white noise; the reverse assignment held for Rats S3 and S4. There was no intercomponent interval, and all components were 90 s long (including reinforcer access time). Their order in each session was random, with the provisos that each block of six components included three rich and three lean components and that no more than two components of the same type (rich or lean) could occur in succession. Also, in each block of six components, one of the rich components and one of the lean components started with a 15-s period in which no reinforcer could be delivered. The purpose of these probes was to assess discrimination among components unfettered by a possible cueing role of the water deliveries, following Nevin and Grace's (2000) suggestion that resistance to change cannot be evaluated properly in the absence of stimulus control. The rats had one hour of free access to water per day, 30 min after the end of the session.

Results

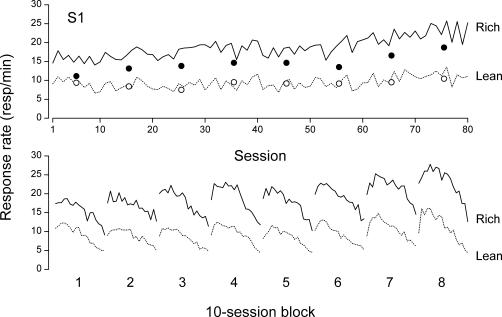
Figure 2 presents the raw data of Rat S1 for illustrative purposes. The solid and dotted lines in the upper panel show daily response rates in the rich and lean components, respectively. (Here and elsewhere, response rates were corrected for reinforcer duration by subtracting out reinforcer access times.) Response rates in the rich and lean components were well differentiated from the start of S1's exposure to the multiple schedule. Response rates during the discrimination probes, averaged by blocks of 10 sessions separately in the rich and lean components (filled and empty circles, respectively) nevertheless show that stimulus discrimination was minimal during the first block of 10 sessions. This rat's discrimination became well established thereafter (filled and empty circles, upper panel). The data for the three other rats, not shown here, revealed adequate stimulus discrimination from the very start of the study.

Fig 2. Upper panel: Daily response rates on the rich schedule (solid line) and on the lean schedule (dotted line) for rat S1.

The filled and unfilled circles show response rates in the discrimination probes for the rich and lean schedules, respectively, averaged by blocks of 10 sessions. Lower panel: Within-session response profiles on the rich schedule (solid lines) and on the lean schedule (dotted lines) for S1. Each profile comprises 18 data points and was obtained by averaging response rates over 10 successive sessions.

The lower panel of Figure 2 shows S1's within-session response profiles on the rich schedule (solid lines) and on the lean schedule (dotted lines). Each profile consists of 18 data points, corresponding to the 18 daily components of each schedule type, averaged by blocks of 10 sessions. In both schedules, response rate increased and then decreased along the course of the session, showing clear within-session dynamics (McSweeney & Hinson, 1992). The shape of the within-session profiles varied across blocks, however, and is often difficult to determine. The decreasing limb of some profiles is consistent with sigmoidal curves, but seems linear in other cases (for example, Block 2, rich component; Block 7, lean component).

Regardless of their shape, S1's within-session profiles for the rich schedule showed no systematic tendency to turn down earlier than S1's within-session profiles for the lean schedule. Measured in number of components, the lag between the two response peaks (component number for the maximum rate on the rich schedule, minus component number for the maximum rate on the lean schedule) ranged from −3 to +3 with a median value of 0. That there was no systematic lag between the peaks for the rich and the lean schedules was confirmed across rats; pooled across rats and 10-session blocks, the lag between peaks ranged from −4 to +4 with a median of 0 and a mean of −0.125.

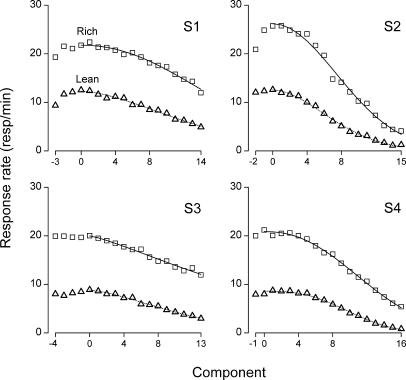
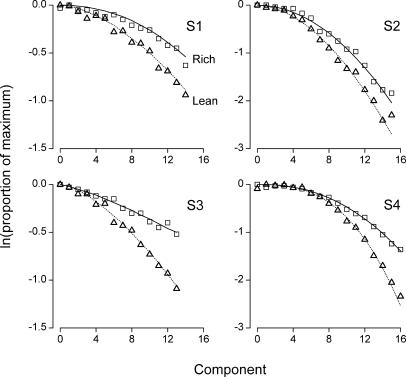
Figure 3 shows each rat's within-session profiles for the rich and lean schedules (squares and triangles, respectively) averaged over the 80 sessions of the study. Measured in number of components, the lag between the peaks of the rich and lean schedules equalled 1, 1, 0, and −1 for Rats S1, S2, S3, and S4, respectively. However small, any lag between the turning points for the rich and lean schedules raises the issue of where to fix the zero value of the horizontal axis (x  =  0) for evaluating within-session resistance functions; the logic of resistance to change implies that the decreasing portions of the rich and lean within-session profiles should be compared along a single scale of disruption (x), even though one of the two profiles may actually start to decrease one component earlier or later than the other (Figure 3). The convention we adopted in each panel of Figure 3 was to set the zero value of the horizontal axis so that it would coincide with the earlier of the two peaks. The initial parts of the profiles (x < 0), corresponding to early-session increases of responding, will not be considered further because with four data points at most, they did not qualify for curve fitting. Thus, the data of interest consist of the portions of the response profiles to the right of zero (x ≥ 0); these late-session curves are clearly sigmoidal for S2 and S4, less so for S1, and appear almost linear in the case of S3 (Figure 3).

Fig 3. Within-session response profiles on the rich schedule (squares) and on the lean schedule (triangles) for each rat.

The profiles were averaged over the 80 sessions of the study, and in each panel the components were renumbered so that the zero of the horizontal axis would coincide with the earlier of the two response peaks (rich or lean). Solid and dotted lines indicate the best-fitting predictions of Equation 6 for the rich and lean schedules, respectively.

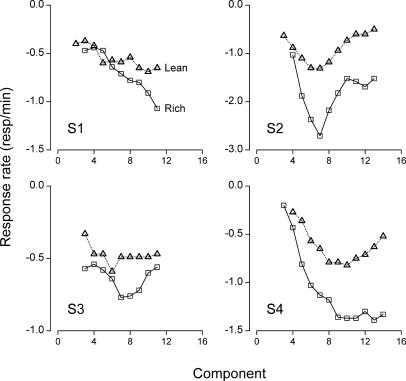
A more precise way of evaluating the shape of the late-session curves is to plot the differences between successive response rates within each component type as a function of component number (x). With small numerical values (range: −4.86 to 0.58 resp/min) and various sign reversals from one data point to the next, however, these differences proved highly sensitive to noise. Hence, we smoothed the late-session curves of Figure 3 with a moving average before computing rate differences. (Notice that smoothing was used not as an antecedent to curve fitting, but only as a step toward a qualitative evaluation of function shape). Following the procedure of Tonneau et al. (2000), the moving average was centered on a window of five points with triangular weights (1/9, 2/9, 3/9, 2/9, 1/9); the first two and last two points on each limb were excluded to avoid distortions at the beginning and end of each data series. For each point y_n on the smoothed late-session curves, we computed the forward difference y_n+1 − y_n and plotted it as a function of component number x (Figure 4).

Fig 4. Forward differences in response rates on the rich schedule (squares and solid lines) and on the lean schedule (triangles and dotted lines) as a function of component number for each rat.

The late-session curves of Figure 3 were smoothed before computing rate differences, the first two and last two data points of each data series being excluded (see text for an explanation of the smoothing method). In each panel, and as in Figure 3, the zero of the horizontal axis coincides with the earlier of the two response peaks. Notice the different vertical scales for each rat.

The difference plots of Figure 4 provide qualitative estimates of the shape of the derivative f ′(x) for each late-session curve in the rich and lean schedules (squares and triangles, respectively). For S2, S3, and S4, the plots decrease and then increase on each schedule (Figure 4), consistent with a sigmoidal resistance function (exponential and linear models predict that the difference plots should be increasing or flat, respectively). The plots for S1, although inconsistent with exponential and linear models, reveal only the decreasing portion of the difference plot predicted by a sigmoidal model. Presumably, extending the graph for S1 to the right (with more components per session) would have revealed an upturn in the difference plot, as in the case of S4, for example.

In any event, all the difference plots in Figure 4 are consistent with sigmoidal functions, and all contradict the linear and exponential models. We conclude that the within-session resistance functions in our study are sigmoidal. Accordingly, the Weibull model of response change (Equation 6) was adjusted to the late-session curves of Figure 3, using the nonlinear fitter of Origin 6.0®. The best-fitting sigmoidal functions are plotted in Figure 3 along with the raw response rates on the rich and lean schedules (solid and dotted lines, respectively). The corresponding values of a, c, and α are presented in Table 1 for each rat and component type, along with the proportion of variance accounted for. Unsurprisingly, the value of a  =  f(0) is larger on the rich schedule than on the lean one for all rats. Whereas α did not seem to vary systematically, in all rats the value of the c parameter increased from the rich to the lean schedule (Table 1), meaning that response dynamics were slower in the former case. The difference in c values between the lean and rich schedules, Δc, equaled 0.012, 0.019, 0.035, and 0.015 for Rats S1, S2, S3, and S4, respectively.

Table 1. Best-fitting Parameters and Proportion of Variance Accounted For (Equation 6) by Subject and Component Type.

Rat	comp	a	c	α	VAC
S1
	Rich	21.77	0.054	2.134	.98
	Lean	12.29	0.066	1.671	.98
S2
	Rich	26.19	0.095	1.997	.99
	Lean	12.56	0.114	1.842	.99
S3
	Rich	19.98	0.045	1.259	.98
	Lean	8.80	0.080	1.520	.99
S4
	Rich	20.87	0.072	2.316	.99
	Lean	8.62	0.087	2.772	.99

The slower dynamics in the rich schedule, corresponding to a smaller value of c in Equation 6, confirm the resistance-to-change findings from studies that varied disruptors between sessions (e.g., Nevin, 1974). Because the linear model has been discarded as an account of the present data (see Figure 4) and because Equation 6 is multiplicative with respect to f(0), the late-session curves of Figure 3 were normalized and transformed logarithmically, as is commonly done in resistance-to-change research. The transformed data, which correspond to within-session resistance functions, are presented in Figure 5 for the rich and lean schedules (squares and triangles, respectively), along with the transformed best-fitting predictions from Equation 6 (solid and dotted lines, respectively). Each panel in Figure 5 reveals the typical fan of differential resistance to change, with a shallower profile for the rich schedule (empty squares and solid lines).

Fig 5. Within-session, decreasing resistance functions on the rich schedule (squares) and on the lean schedule (triangles) for each rat.

The data correspond to the late-session curves of Figure 3, normalized and log-transformed. Solid and dotted lines indicate the normalized, log-transformed, best-fitting predictions of Equation 6 for the rich and lean schedules, respectively. In each panel and as in Figure 4, the zero of the horizontal axis coincides with the earlier of the two response peaks. Notice the different vertical scales for each rat.

The transformed data of Figure 5 are curvilinear (as in the lowest right panel of Figure 1), due to the fact that raw response rates decay in a sigmoidal fashion. Hence, the difference-based measure of Grace and Nevin (1997) should be preferred over the inverse slope ratio as an index of comparative resistance. For each late-session curve in Figure 3 and for all values x (≥ 0) of the component number, we divided the response rate f(x) by its maximal value, averaged these ratios, and computed how much the natural logarithm of the average differed between the rich and the lean components (cf. Grace & Nevin, 1997). The result, which we shall call the resistance differential, equaled 0.13, 0.17, 0.17, and 0.12 for S1, S2, S3, and S4, respectively, confirming that transformed response rates were higher on the rich schedule. Also, the resistance differential and Δc were correlated across rats (R  =  .72), suggesting that the difference measure of Grace and Nevin (1997), adapted to within-session resistance functions, was sensitive to the relative dynamics of the rich and lean schedules as expressed by the parameter c of Equation 6.

To obtain a more detailed view of resistance to change, we computed each rat's resistance differential for late-session curves averaged by blocks of 10 sessions. With a minimum of −0.01, a median of 0.14, and a maximum of 0.36, the resistance differential was positive in 31 of the 32 cases, confirming the tendency of the rich schedule to be more resistant than the lean one. Similarly, we fitted Equation 6 to late-session curves averaged by blocks of 10 sessions, and computed Δc for each block and each rat. Equation 6 gave acceptable fits, with an average proportion of variance accounted for equal to .94. With a minimum of −0.011, a median of 0.020, and a maximum of 0.057, Δc was positive in 31 of the 32 cases, a result consistent with the higher resistance of the rich schedule. The resistance differential and Δc were correlated (R  =  .64), confirming the sensitivity of the former measure to the relative dynamics of the best-fitting Weibull equations. The only negative case of the resistance differential, observed on S2's fifth block of 10 sessions, coincided with the negative case of Δc.

Discussion

Our data extend resistance-to-change findings at the within-session level. The schedule associated with a higher density of reinforcement proved more resistant to disruption than the leaner schedule. Resistance was evaluated in the context of an explicit model for decreases in absolute response rates (Equation 6), which allowed us to correlate the difference measure of comparative resistance (Grace & Nevin, 1997) with variations in the dynamics of the hypothesized process of disruption (expressed by the parameter c of Equation 6).

The most important advantage of our procedure is that discarding the linear model for absolute response rates (Equation 4) becomes feasible, due to the relatively high number of data points present in typical within-session profiles. This does not prove the validity of data normalization or of the whole resistance-to-change framework, but allows additivity artifacts to be discarded as explanation of the results. We emphasize the importance of modeling absolute response rates and checking the dynamic assumptions that underlie response normalization.

One potential problem with the current study is that we used a large difference in interreinforcement interval (15 s versus 60 s) in order to detect a resistance-to-change effect between schedules. Parametric studies might reveal, for instance, that positive results at a within-session level require larger differences of reinforcement rate than positive results in between-session tests of resistance to change. If such is the case, however, then differences in sensitivity between within- and between-session tests will require some explanation and may stimulate further developments in the theory of behavioral resistance.

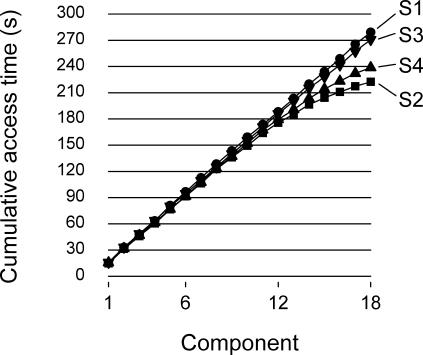
Another problem with within-session measures of resistance is that the frequency or amount of the disruptor (i.e., the reinforcer itself) present during testing is controlled by the animal instead of the experimenter. Figure 6, for example, presents each rat's cumulative seconds of access to water for 18 successive components, access time being averaged over component types (rich or lean) and the 80 sessions of the study. The resulting function is almost linear for rats S1 and S3, but shows clear signs of deceleration after the 12th component for rats S4 and S2, due to the fact that these rats responded at a much lower rate toward the end of the session. Thus, even with interval-like schedules that tend to equalize reinforcement rate (Tonneau et al., 2000, Figure 3), extremely low rates of responding can feed back on the accumulated amount of the reinforcer, hence on the amount of within-session disruption.

Fig 6. Cumulative time of access to water along 18 components for each rat.

The data were pooled across component types (rich or lean) and averaged over the 80 sessions of the study.

This in turn implies that component number (the measure of disruptor amount that appears on the horizontal axis of Figures 3, 4, and 5) is not necessarily proportional to the actual cumulative time of access to the reinforcer. Redoing our analyses with a rescaled horizontal axis (using actual cumulative time of access instead of component number) did not affect our main conclusions regarding the shape of the profiles; in particular, the best-fitting value of the parameter c was still larger in the lean schedule for each rat. In any event, we prefer component number over actual time of access as a measure of disruptor amount because the former defines a true independent variable (determined solely by the experimenter instead of the subject). Furthermore, the framework of resistance to change makes a clear prediction with respect to component number: Within-session response rate should decrease proportionally more slowly in the richer schedule. This prediction was confirmed (Figure 5).

Although of interest in their own right, within-session response patterns also can serve as methodological opportunities for evaluating the effect of independent variables (e.g., Reilly & Lattal, 2004). Aside from the measurement issues discussed above, the main advantage of studying resistance to change at the within-session level is that within-session tests are easily implemented in traditional studies of resistance, with no need for additional sessions or special procedures. Before starting a typical between-session test of resistance with a multiple schedule, numerous sessions are often needed to obtain a stable baseline. The within-session profiles available in these baseline sessions already afford simple tests of resistance to change. Their results could complement at no cost those obtained through explicit, between-session testing.