A New Method for Detecting Human Recombination Hotspots and Its Applications to the HapMap ENCODE Data

Abstract

Computational detection of recombination hotspots from population polymorphism data is important both for understanding the nature of recombination and for applications such as association studies. We propose a new method for this task based on a multiple-hotspot model and an (approximate) log-likelihood ratio test. A truncated, weighted pairwise log-likelihood is introduced and applied to the calculation of the log-likelihood ratio, and a forward-selection procedure is adopted to search for the optimal hotspot predictions. The method shows a relatively high power with a low false-positive rate in detecting multiple hotspots in simulation data and has a performance comparable to the best results of leading computational methods in experimental data for which recombination hotspots have been characterized by sperm-typing experiments. The method can be applied to both phased and unphased data directly, with a very fast computational speed. We applied the method to the 10 500-kb regions of the HapMap ENCODE data and found 172 hotspots among the three populations, with average hotspot width of 2.4 kb. By comparisons with the simulation data, we found some evidence that hotspots are not all identical across populations. The correlations between detected hotspots and several genomic characteristics were examined. In particular, we observed that DNaseI-hypersensitive sites are enriched in hotspots, suggesting the existence of human β hotspots similar to those found in yeast.

Meiotic recombination is one of the major sources of genetic diversity. It has been observed that the occurrence of meiotic recombination in the human genome (and some other genomes) is not uniform, but rather there are regions called “hotspots” (usually 1–2 kb in width) where the frequency of recombination is 10 to several thousand times higher than the average in the background, and almost all recombination events happen within them.^1–6 Recent studies have shown that hotspots are a ubiquitous feature of the human genome,^7,8 and recombination hotspots are also the main contributor of the block-like pattern of haplotypes.⁹ Characterizing these hotspots is of critical importance for understanding molecular mechanisms of meiotic recombination and for designing better strategies in association studies of complex diseases.^10–16 Pedigree analysis can only specify recombination rate on a megabase scale, because of the small number of recombination events that can be observed within a few generations. The first fine-scale description of human recombination hotspots was achieved with the sperm-typing technique,^1–3 which types millions of sperm that contain hundreds of recombination events in the studied region (often ∼10 kb). The resolution of sperm typing is very high, but it is costly and laborious, so it is not yet practical for application to long genomic segments, and it cannot provide any information about females. Up to now, <20 hotspots have been characterized by sperm-typing experiments, and genomewide fine-scale investigations in humans have largely relied on computational analysis of population polymorphism data.^7,8

The problem of estimating a constant recombination rate from population polymorphism data has been intensively studied in recent years.^17,18 Among the many possible methods, likelihood-based methods are the most widely accepted. The basic idea is to search for a recombination rate that maximizes the likelihood of obtaining the observed phased (haplotype) or unphased (genotype) data from the population under the coalescent model.¹⁹ Some methods use all information contained in the data to calculate the full likelihood, which is accurate but extremely expensive to compute.^20–22 Other methods use partial data to calculate approximate likelihoods.^23–26 These likelihoods can approximate the full likelihood well if the methods are designed properly.²⁷

Since a constant recombination rate is rarely the case in the genome, detecting recombination hotspots is more challenging. Zhang et al.²⁸ proposed a nonparametric method based on haplotype-block partitioning, which is computationally effective but cannot give high-resolution prediction of hotspot locations. For more-precise predictions, three major parametric methods based on coalescent models have been developed. Their common basic idea is to compare approximate likelihoods under models with and without hotspot(s). The three methods use different approximations of the full likelihood. The LDhot method⁷ uses a pairwise likelihood that is the product of two-locus likelihoods of all pairs of segregating sites. The Hotspotter method²⁶ defines another kind of likelihood, constructed by multiplying the approximate conditional likelihoods of each haplotype in a specific order. The method by Fearnhead et al.²⁹ and its improved version³⁰ divide a studied region into small subregions and calculate a composite likelihood by multiplying full likelihoods of all subregions.

These three parametric methods are differentiated by their ability to detect multiple hotspots in a genomic segment, the data types to which they can be applied, and the speed of calculation. Both LDhot and Hotspotter assume no more than one hotspot in the studied region, whereas the methods of Fearnhead et al. are able to detect multiple hotspots in a region. Hotspotter and the methods of Fearnhead et al. require phased data, so users need to do haplotype inference first, since almost all available polymorphism data are unphased (Hotspotter has been integrated into the PHASE^26,31–33 program to deal with unphased data). LDhot can be applied to both unphased and phased data directly. The computational costs of these three methods are also quite different. LDhot is very fast because of the use of the pairwise likelihood; therefore, it can be applied to the whole genome.⁸ The methods of Fearnhead et al. are much slower, since they calculate the full likelihood in each of the subregions. Hence, it is very costly to apply them to genome-scale data. The speed of Hotspotter lies between those of LDhot and the methods of Fearnhead et al.

The three parametric methods had been compared on a 206-kb region on human chromosome 1 near the highly variable minisatellite MS32, where the fine-scale recombination-rate variation has been analyzed by sperm-typing experiments.⁵ Of the eight hotspots detected by sperm-typing, LDhot detected four, with no false-positive result; Hotspotter detected five but gave three false-positive predictions; and the first method of Fearnhead et al. detected seven, with only one false-positive prediction, which shows the highest power for this data set.

The major limitations of the methods of Fearnhead et al. are their high computing cost and their inability to directly handle unphased data. To make the method more practical and flexible, we propose, in this article, a new method for hotspot detection. Our method uses a truncated, weighted pairwise log-likelihood (TWPLL) and can be applied to both phased and unphased data with a very fast computational speed. In simulation data, our method shows a high power to detect multiple hotspots, with a considerably low false-positive rate. In the two regions of the human genome where sperm-typing data have been reported, our method gets comparable or even better results than the best results obtained by all those other leading computational methods. We applied the method to the 10 human genome regions known as the HapMap ENCODE regions and identified 172 hotspots that exist in at least one of the three populations.

Nowadays, the mechanism of meiotic recombination is still poorly understood in higher eukaryotes.^34–36 We studied the molecular features of the predicted hotspots in the HapMap ENCODE regions and observed correlations of hotspots with some genomic features. In particular, we observed that DNaseI-hypersensitive sites (DHSSs) are enriched in hotspots. This is a strong sign that there are β hotspots in the human genome similar to those identified in yeast.

Material and Methods

Data

We applied our method to the HapMap ENCODE data as a practical application. The pilot phase of the ENCODE Project focuses on a specified 1% (∼30 Mb) of the human genome, aiming to identify all functional elements in the regions. Some of these regions (known as the HapMap ENCODE regions) have been genotyped by HapMap Centers, and contain 10 genomic segments (500 kb each) from seven chromosomes. The data were genotyped in four populations: Utah residents with northern and western European ancestry (CEU), Han Chinese in Beijing (CHB), Japanese in Tokyo (JPT), and Yoruba in Ibadan, Nigeria (YRI), with diploid population sizes of 90, 45, 44, and 90, respectively. To balance sample size in our experiments, we combined the two East Asian populations (CHB and JPT) into one group and called it “ASI.” Almost all SNPs in these regions have been genotyped. Only those markers with minor-allele frequency (MAF) >0.05 were used to infer hotspots.

After hotspot detection, some genomic features of the HapMap ENCODE regions were downloaded from the ENCODE Project at UCSC Web site to investigate their possible correlations with hotspot locations. These data include DNA sequences, RefSeq genes, CpG islands, repeats, and DHSSs. The total sequence length of the regions is 5 Mb, and we use the sequences to calculate the G+C content. There are 70 CpG islands in these regions, with an average length ∼0.9 kb. Repeats were identified by use of the RepeatMasker software and the repeat libraries available, and they cover 45.6% of the 5-Mb region. Among the ∼30 repeat families, 7 of them (Alu, L1, MIR, Simple_repeat, L2, Low_complexity, and MaLR) occur >500 times in the studied regions. A total of 56 RefSeq genes are found in the studied regions. These gene areas (counted from 1 kb upstream of 5′ sites of the first exons to 1 kb downstream of 3′ sites of the last exons) cover ∼39% of the 5-Mb region. DHSSs are associated with all kinds of gene regulatory regions, including enhancers, silencers, promoters, insulators, and locus-control regions.³⁷ The available data are from four groups: (1) DHSSs identified by DNase-chip in the GM06990 lymphoblastoid cell line, (2) DHSSs identified by DNase-chip in the nonactivated CD4⁺ T cells, (3) DHSSs identified by massively parallel signature sequencing (MPSS) in the nonactivated CD4⁺ T cells, and (4) DHSSs identified by MPSS in the activated CD4⁺ T cells. Among these four groups, 144, 143, 26, and 30 DHSSs were identified in the 5-Mb region, and their average length is ∼0.29 kb. More detailed description about these genomic features can be found at the ENCODE Project at UCSC.

The Pairwise Log-Likelihood (PLL)

Suppose there are S segregating sites in the studied segment, and the recombination rate between site i and site j is ρ_ij. We use L_ij(ρ_ij) to denote the two-locus likelihood between site i and site j, defined as the probability of observing the sample configuration at these two sites in the data, given ρ_ij. This can be easily calculated according to the definition of recombination rate at the two sites. The pairwise likelihood is defined as the product of all pairs of sites in the segment,

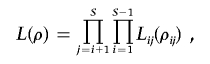and the PLL is defined as

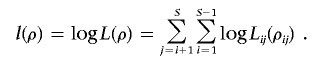There are several advantages of using this likelihood. Since likelihoods of all possible sample configurations at any two sites for a given sample size can be calculated beforehand and stored in a lookup table, calculation of PLL can be extremely fast. Moreover, PLL can be applied to both phased and unphased data directly, since two-locus likelihoods for unphased pairs can be inferred straightforwardly from those of phased pairs.²³ In addition, when two-locus likelihoods are calculated, it is convenient to use different recombination models, such as gene conversion,^25,38 or to calculate under a finite-site mutation model.²⁵ The recombination rate of a region can be estimated as the rate that maximizes the pairwise likelihood. Smith and Fearnhead²⁷ have shown that it is one of the most accurate methods for estimating a uniform recombination rate. When applied to a region with variable recombination rates, the estimated rate will be the average rate across the region.

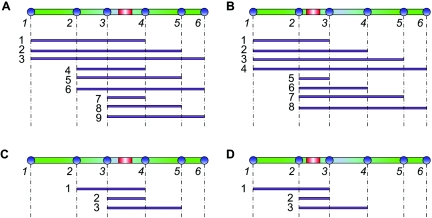
Recombination hotspots can be detected using the likelihood by investigating whether a model with hotspot(s) can produce a higher likelihood of the data than can the uniform-rate model. This can be done by studying the log-likelihood ratio (LLR) of the two models, defined as the log ratio of the likelihood under the model with hotspots to that under the model without hotspots. However, there is a problem if we use PLL for this purpose. Indeed, the PLL is defined on likelihoods of S(S-1)/2 pairs of segregating sites. Suppose there is a hotspot located between the ith and (i+1)th segregating sites; then, this hotspot region will affect i(S-i) terms in the PLL. A simple example with S=6 is illustrated in figure 1A and 1B. Note that i(S-i) depends on the location i, such that it first ascends and then descends with i. Hotspots at different locations in the studied segment will have unequal effects on the likelihood, and hotspots near the center of the segment are more likely to be detected. This will cause a loss of detection power and will also lead to bias in the discovery of hotspots.

Figure 1. .

Subregions covering a hotspot in different log-likelihoods. In each panel, the example region (green bar) contains six segregating sites (blue circles), with a hotspot (red bar) located between a pair of sites. The purple lines indicate the subregions between pairs of sites that cover the hotspot in the log-likelihood. A, With PLL, the hotspot located between the third and fourth sites is covered by nine subregions. B, With PLL, the hotspot located between the second and third sites is covered by eight subregions. C, With TWPLL, the hotspot located between the third and fourth sites is covered by three subregions. D, With TWPLL, the hotspot located between the second and third sites is also covered by three subregions. The number of subregions covering a hotspot depends on the location of the hotspot in PLL, whereas it does not in TWPLL.

The TWPLL

The idea of a weighted PLL that was introduced by Fearnhead³⁹ makes it possible to define a likelihood that is unrelated to the location of hotspots. It was originally defined as

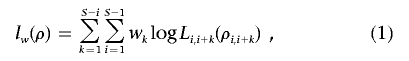where w_k⩾0, k=1,…,S-1, are a set of weights decreasing in k. If we assign w_k=1 for k=1,…,S-1, weighted PLL will degenerate into PLL. Weighted PLL was suggested for the estimation of uniform recombination rates.³⁹ We adopt the idea for estimation of recombination models with hotspots. In our method, we define the weights in equation (1) as

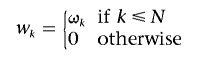and call it the “TWPLL,” where N is the number of segregating sites in the effective neighborhood region (usually N≪S). By defining the distance of two segregating sites as the number of segregating sites between them, only the pairwise likelihoods of pairs of segregating sites with distance no more than N-1 are considered in calculation of the pairwise likelihood. In our experiments, we use N=7. The ω_k should decrease with k, but, currently, the optimal choice of ω_k is still unclear.³⁹ We set ω_k=1/k, k=1,…,N, according to experiments on simulation data, with special attention paid to the balance between precision in detecting hotspot boundaries and sensitivity to noise. With this truncated, weighted pairwise likelihood, for any N⩽i⩽S-N+1, a hotspot located between any site i and the site i+1 will be considered N(N+1)/2 times in equation (1). Since N(N+1)/2 is unrelated to i, it is equally possible to detect hotspots located at different positions. Figure 1C and 1D illustrates the effect of the TWPLL in the simplified example. Only hotspots at the boundaries of the region (i<N or i>S-N+1) are not evenly covered. They usually compose a very small proportion of the region, because N≪S, and we will introduce a compensation for the boundaries when searching for the solutions (see “The Searching Strategy” section).

The Recombination-Rate Model

The models used by LDhot⁷ and Hotspotter²⁶ are all restricted, with at most one hotspot in a data segment. We use a recombination-rate model that allows for multiple hotspots in each studied segment as did the one Fearnhead et al. used.³⁰ The recombination rate as a function of the location x in a region is called the “recombination surface,” denoted ρ(x). A multiple hotspot model has the form

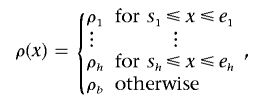where h is the number of hotspots in the region and the kth hotspot extends from position s_k to e_k. Any hotspot does not overlap with or touch the other hotspots. The recombination rates for hotspots are ρ₁,…,ρ_h, respectively, and the background rate of the region is ρ_b.

The Searching Strategy

After defining TWPLL, we need to search for the recombination surface that maximizes the likelihood of the data. We adopted the standard forward-selection procedure to search for the solution. The procedure starts with a model of no hotspot in the region and adds hotspots one by one if adding them increases the likelihood by no less than an LLR threshold T, which is decided by simulation. The searching procedures are as follows:

• Step 1. 

  Assume no hotspot in the region and estimate an average recombination rate as the initial ρ(x) by maximizing the likelihood.

• Step 2. 
  Consider all potential hotspot positions, given the current recombination surface ρ(x). For each potential hotspot, use the following steps to find the best-fit model:

  • (a) 
    Reestimate the background recombination rate that maximizes the likelihood after exclusion of the potential hotspot under current consideration and all hotspots that are already accepted. The recombination surface under this reestimated background rate and accepted hotspots is denoted as ρ^′(x).
  • (b) 
    Assume the current potential hotspot is a real hotspot. Estimate its intensity (recombination rate of the hotspot) that maximizes the likelihood of the whole region. Add this hotspot to the surface ρ^′(x) to get a new surface, ρ^′′(x).
  • (c) 
    Calculate LLR, which is the likelihood under ρ^′′(x) subtracted by the likelihood under ρ^′(x). If the potential hotspot is at one of the boundaries of the studied region, its LLR is amplified by a factor depending on the number of subregions that cover the hotspot, to compensate for its insufficient representation in the likelihood. This set of factors is decided with simulation experiments.
• Step 3. 

  After checking all potential hotspots in step 2, find the one that gives the highest LLR. If this LLR is ⩾T, accept this potential hotspot, refresh the recombination surface, update the set of all potential hotspots, and go to step 2. Otherwise, stop the searching procedures.

In the above procedures, the set of all potential hotspots is collected in the following way. From the beginning of the region, consider every 200-bp position as a possible starting position of a hotspot, if the position is not at a hotspot already detected. From each of these starting positions, we generate a set of potential hotspots with lengths varying from 800 bp to 2.4 kb, with a 200-bp step length. If any potential hotspot thus generated overlaps with or touches any of the hotspots that are already accepted in the prediction, we remove this potential hotspot. This setting considers all possible hotspots of lengths from 800 bp to 2.4 kb, at a resolution of 200 bp.

When we estimate the background rate in step 2(a), some regions are excluded in advance, to avoid estimation of background rates that are too high. For this, we first slide a window of four adjacent SNPs along the whole region and estimate the average recombination rate in each window. If the rate is >10 times the genome average, the sites in this window will not be used for estimating the background rate. A similar strategy was also used by Fearnhead et al.³⁰

It should be noted that the above procedure may not reach the global optimum solution, since it is a greedy forward-selection method. However, since the TWPLL only considers two-locus likelihoods between pairs of segregating sites with distance <N, hotspots will be independent with respect to the TWPLL if they are apart from each other by more than this distance. Therefore, if the distances between hotspots are >N, the greedy searching method can reach the global optimum. When two hotspots are very close to each other—for example, when there are only one or two sites between them—our method will tend to detect them as one larger hotspot. Considering that the average density of SNPs (with MAF >0.05) in the human genome is denser than 1 per kb and that the estimated average density of recombination hotspots is ∼1 hotspot per 50 kb,⁸ global optimum can be reached with this forward-searching strategy in most situations.

The whole method is implemented in a package named “HotspotFisher” that is written in C++ and works on different operation systems. The software is available at Jun Li’s Web site.

Coalescent Simulations

Simulation data based on coalescent models are used for tuning some parameters and for assessing the performance of the method. We used the ^Cosi program⁴⁰ to simulate polymorphism data. ^Cosi is conceptually similar to Richard Hudson’s widely used program,⁴¹ but it has the extra benefit of allowing variable recombination rates—users can set multiple hotspots with different densities and at arbitrary locations. Moreover, ^Cosi calibrates population genetic models with genomewide data and provides users with four detailed human demographic histories that take into consideration events like population splits, admixture, changes in size, bottlenecks, and migration. These four populations include a European population, an Asian population, an African population, and an African American population. We used the first three, since they correspond to the CEU, ASI, and YRI populations in the HapMap ENCODE data.

In most published work on hotspot inference, simulation data were designed such that there is only one hotspot in one data segment.^7,26,29,30 In the study by Zhang et al.,²⁸ multiple hotspots in single segments were simulated, but their locations were fixed and equally spaced, and hotspot widths and intensities were also fixed. To make the simulation data more like the real situation, we simulated long genome regions (200 kb) with multiple hotspots at random locations, with variable widths and intensities. We use our method to estimate the locations of these variable hotspots. The detailed model is as follows:

• (1) The length of each simulated data region is 200 kb. The expected average recombination rate in the simulated segments is set as 1.2 cM/Mb, the same as the human genome average.⁴²
• (2) On each simulated region, a proportion p of recombination events are expected to happen within hotspots. For convenience, we call this proportion the “hotspot quotient” (HQ). Sperm-typing analysis showed that >90% of recombination events in the human genome occur within hotspots (HQ > 90%), and the background recombination rate can be as low as 0.04 cM/Mb.^3,5 We use two HQ values (90% and 70%) in the simulation, to study the performance of the proposed method under different conditions. These two settings give background recombination rates of 0.12 cM/Mb and 0.36 cM/Mb. The model with HQ = 90% is consistent with the results from sperm-typing experiments and appears to be consistent with our results for the 10 HapMap ENCODE regions. The model with HQ = 70% is at the lower end of what is observed for the human genome.^7,8
• (3) The spacing between hotspot centers fits an exponential distribution with the mean of 50 kb, as the suggested average across the whole genome.⁸ We also restrict the spacing between two hotspot centers to be not less than 2 kb.
• (4) The width of hotspots follows a uniform distribution of 1–2 kb. This is in accordance with existing observations of hotspots.^3,5
• (5) The accumulated intensity (defined as the product of the intensity and the width of the hotspot) of each hotspot follows a gamma distribution, with gamma equal to 3 and the mean determined by parameters given in (1), (2), and (3) above. This distribution is chosen arbitrarily, because there is little knowledge about the true distribution of hotspot densities. The hotspot intensity of each hotspot is calculated from its accumulated intensity and width, and, if the resulting intensity is <10 times the background, this hotspot is discarded from the model and replaced by a new one.

We simulated six data sets. Each data set consists of 100 groups of data for estimating the false-positive rate and power, and each group consists of 90 diploid samples, so that the sample size is the same as for the HapMap ENCODE data. Every 90 diploid samples were obtained by combining 180 haplotypes randomly. Data sets 1, 2, and 3 all have HQ = 90% and are generated with the European, Asian, and African demographic histories, respectively. Data sets 4, 5, and 6 have HQ = 70% and are also generated with the three population histories. In the calibrated model of Schaffer et al.,⁴⁰ gene-conversion rate is set at 4.5×10^-9 per bp per generation, with a tract length of 500 bp for all gene-conversion events. This is also what we used in our simulation. ^Cosi assumes an infinite-sites model of mutation, and mutation positions are converted into discrete base-pair positions. A constant mutation rate of 1.0×10^-8 per bp per generation was chosen in our models, so that the average density of SNPs in our simulation data is the same as that in the HapMap ENCODE data.

Results

Hotspot Detection in Simulation Data

We applied our method to each group of the simulation data. The same lookup table was used for the pairwise likelihood in all the experiments. The original table for 192 haplotypes was downloaded from the LDhat version 2.0 (a package for recombination-rate analysis⁷) Web site, and we used the lkgen function in LDhat version 2.0 to convert it to a table for 180 haplotypes. The false-positive rate and power of the hotspot detection were assessed with the simulation experiments. If a detected hotspot overlaps with a hotspot built in the model, we regard it as a true-positive prediction; otherwise, we regard it as a false-positive prediction. Here, we define the false-positive rate as the expected number of false-positive results per Mb and define the power as the proportion of hotspots in the models that are detected by the algorithm.

The LLR threshold T was first estimated on the basis of a given false-positive rate with the data under HQ=90%. It was observed that the false-positive rates are very similar under the two HQ values at the same T values. This is an important property, as it indicates that the same T can be used regardless of the background rate. Finally, T=26 was chosen for all the experiments, which limits the expected false-positives in a 200-kb region to be no more than 0.08, or, equivalently, the false-positive rate is no more than 0.4 per Mb. The results for the simulation data with T=26 are shown in table 1. With this setting, in the total 5 Mb of HapMap ENCODE data, the expected number of false-positive predictions in each population will be no more than 2.

Table 1. .

Hotspot Prediction Performance on Simulation Data (T=26)

	HQ = 90%				HQ = 70%
Population	CEU	ASI	YRI	Totala	CEU	ASI	YRI	Totala
No. of false-positive resultsb	8	5	2	13	3	8	2	13
Power (%)c	69	66	66	87	38	37	35	58
Average position offset (bp)d	360	376	309	…	351	345	258	…
Center coverage (%)e	94	96	98	…	96	98	100	…

^aThe number of hotspots detected in at least one of the populations.

^bThe total number of false-positive predictions in all 100 segments (200 kb each).

^cThe percentage of true hotspots in the models that are correctly detected.

^dAverage offset from the predicted start and end sites to the real start and end sites.

^ePercentage of predicted hotspots that cover centers of corresponding true hotspots in the models.

Table 1 also shows the power reached with different groups of simulation data. It can be seen that almost the same power was reached in different populations, indicating that the method is not sensitive to the population history. With the model of HQ = 90%, the average power for the three populations is as high as 0.67, but, with HQ = 70%, the power decreases to ∼0.37. This indicates that HQ is a major factor that affects the prediction power; the higher the HQ is, the higher the power is. On the human genome, HQ is estimated to be around or more than 90%, according to sperm-typing experiments^3,5 as well as our calculation for the HapMap ENCODE data described below. Some hotspots in the simulation data are not detected in all populations. If we combine the hotspots detected in the three populations together, the power is even higher (0.87 for HQ = 90% and 0.58 for HQ = 70%), whereas the false-positive rate still maintains a low level of 0.65 per Mb, or 3.25 false-positive predictions in a 5-Mb region.

We further examined the accuracy of the hotspot locations that we detected. As shown in table 1, the mean offsets from the predicted start and end locations to the corresponding precise locations in the simulation models are ∼310–380 bp when HQ = 90% and 250–350 bp when HQ = 70%. More than 94% of predicted hotspots cover the center of the corresponding hotspots in the models.

Finally, we examined whether our method is sensitive to some hotspot properties, such as hotspot intensities, hotspot widths, SNP densities in hotspots, and SNP MAFs in hotspots. Spearman's rank correlation coefficients were calculated between each of them and the detection of hotspots (table 2). Hotspot intensities, SNP densities in hotspots, and SNP MAFs in hotspots were weakly but significantly correlated with their detection, suggesting that stronger hotspots with denser SNPs and higher-MAF SNPs inside are easier to detect. Hotspot widths are uncorrelated with the detection of hotspots.

Table 2. .

Spearman's Rank Correlation Coefficients (SCCs) between the Detection of Hotspots and Their Properties

	HQ = 90%			HQ = 70%
Population	CEU	ASI	YRI	CEU	ASI	YRI
SCC with hotspot intensity	.35a	.34a	.34a	.30a	.29a	.34a
SCC with hotspot width	.06	−.01	.05	−.01	−.00	−.01
SCC with SNP density in hotspots	.30a	.27a	.40a	.42a	.45a	.50a
SCC with SNP MAF in hotspots	.35a	.35a	.41a	.32a	.37a	.40a

^aTested significant (P<.05). In calculating the coefficients, we assigned a 1 if a hotspot was detected, and a 0 if it was not.

Hotspot Detection for Experimentally Verified Human Hotspots

To date, there are only two human genome regions for which multiple recombination hotspots have been characterized by sperm-typing experiments. One is a 216-kb segment of the class II region of the major histocompatibility complex (MHC) on chromosome 6, where six hotspots were found by experiments³; the other is a 206-kb segment on chromosome 1 near the highly variable minisatellite MS32, where eight hotspots were reported.⁵ We used these two data sets to validate our method. The first data set contains 247 SNP sites (MAF>0.05) of 50 diploid samples, and the second data set contains 191 SNP sites (MAF>0.05) of 80 diploid samples. We used the diploid data directly. All parameters in our method were set to be the same as in the simulation experiments.

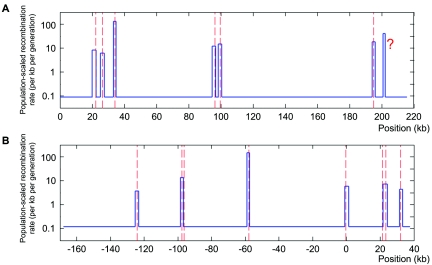
In the first region, our method detected seven hotspots, which included all six true hotspots and an additional one at ∼6.5 kb downstream from the 3′ end of the TAP2 hotspot (fig. 2A). The original sperm-typing data were uninformative about recombination in the 3′ end of the TAP2 hotspot (the area indicated by a question mark in fig. 2A), and it was conjectured by Jeffreys et al.³ that the TAP2 hotspot might be part of a cluster. Fearnhead et al.²⁹ and Zhang et al.²⁸ also applied their methods to this data set. Fearnhead et al. found eight hotspots, including all six true hotspots, a hotspot downstream from the TAP2 hotspot, and an extra hotspot not supported by the sperm-typing experiment.²⁹ Zhang et al. predicted four putative hotspot regions in this data, covering all the known hotspots, and their result also suggested a hotspot downstream from the TAP2 hotspot.²⁸

Figure 2. .

Hotspot detection in the two genomic regions where sperm-typing data are available. The blue lines are the recombination surface we estimated, and peaks in the line are recombination hotspots detected. The centers of true hotspots are shown by red dashed lines. A, The 216-kb segment of the class II region of the MHC. From left to right, the true hotspots are DNA1, DNA2, DNA3, DMB1, DMB2, and TAP2, and the question mark (?) indicates the hotspot that was not observed in sperm-typing experiments but that was conjectured by Jeffreys et al.³ and predicted computationally.^28,29 These hotspots were all detected with our method, in the following order TAP2 (LLR=141.4), DNA3 (LLR=137.2), DMB2 (LLR=99.5), DMB1 (LLR=67.6), DNA2 (LLR=43.6), DNA1 (LLR=30.9), and “?” (LLR=29.3). B, The 206-kb segment on chromosome 1. From left to right, the true hotspots are NID3, NID2a, NID2b, NID1, MS32, MSTM1a, MSTM1b, and MSTM2.⁵ We detected six of them, in the following order: NID1 (LLR=77.0), NID2a (LLR=75.3), MSTM2 (LLR=58.4), MS32 (LLR=41.5), MSTM1b (LLR=36.4), and NID3 (LLR=30.1). In both groups of data, every hotspot we detected contains the center of its corresponding true hotspot.

In the second region, our method correctly detected six true hotspots with no false-positive predictions (fig. 2B). Only two hotspots (NID2b and MSTM1a) were missed in the detection. The NID2b hotspot lies almost entirely within a region of intense marker association, so it is expected that coalescent-based methods would not detect it.⁵ The other hotspot we missed, MSTM1a, was reported to be historically weak and a candidate for a young hotspot.⁴³ It lies very close to a historically strong hotspot, MSTM1b—their centers are only 2.0 kb apart.⁵ As mentioned in our introduction, the methods of Fearnhead et al. showed highest power on this data set among the currently available methods.⁵ It found the six hotspots we detected plus the MSTM1a hotspot, but it made a false-positive prediction between MSTM1b and MSTM2.

In total, our method detected 12 of 14 true hotspots, with zero false-positive results, in these two regions (not considering the putative hotspot in the 3′ region of the TAP2 hotspot). The average offset from the predicted start and end locations to the corresponding true locations decided by the experiments is 409 bp. All predicted hotspots cover the centers of the true hotspots. The performance is consistent with that for the simulation data with HQ = 90%.

Hotspot Detection in the HapMap ENCODE Regions

We applied our method to the HapMap ENCODE regions with the same set of parameters as in the simulation and validation experiments, and we used unphased data directly. Within the 10 500-kb regions, we detected 88, 110, and 87 hotspots in the CEU, ASI, and YRI populations, respectively. This gives us a total of 172 hotspots (or hotspot clusters, defined as sets of hotspots that overlap across populations) that occur in at least one population. The hotspot positions are listed in table 3. The widths of detected hotspots (or hotspot clusters) range from 0.8 kb to 9.8 kb, with average of 2.4 kb, covering ∼8.14% of the studied regions. We downloaded hotspots estimated by LDhot from the ENCODE Project at UCSC, which are also a combination of predictions in the three populations. LDhot reported 95 hotspots (or hotspot clusters) with widths ranging from 2.75 to 16.25 kb, with an average of 4.9 kb. This suggests that the hotspots we identified are at a finer scale, and one hotspot (or hotspot cluster) identified by LDhot may contain several hotspots that we found. The overlapping of the two sets of predicted hotspots (or hotspot clusters) is 75 of the 95 predictions by the LDhot hotspots and 82 of the 172 predictions by our method.

Table 3. .

Hotspots Detected in the HapMap ENCODE Region

A. ENm010 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
				173.929	175.529
177.042	179.442
186.242	188.642			186.129	187.729
247.042	249.442	247.529	249.529	247.729	250.129
263.842	266.242
				283.529	285.929
		289.329	291.729
				356.329	358.529
393.842	396.042	393.529	395.929	394.329	396.529
400.642	403.042
		409.329	411.729
		420.329	422.729
				430.929	432.529
		432.929	435.329	434.529	435.329
		457.729	460.129	456.129	458.529
		471.729	474.129	471.729	474.129
				488.729	489.929
B. ENm013 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
54.407	56.807
		89.552	90.352
		247.752	250.152
				268.248	270.448
		337.552	339.352
415.407	416.407	414.952	417.352	414.248	416.648
				491.648	493.248
C. ENm014 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
				19.692	20.892
55.692	57.492	55.292	57.692	55.492	57.892
66.692	67.892	65.892	68.092	66.892	68.092
				135.892	138.292
				142.692	143.492
210.692	211.692
264.292	266.292
				283.492	285.692
				289.692	292.092
		312.892	313.692	311.092	313.492
				343.692	346.092
364.092	365.692			364.092	365.692
D. ENr112 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
8.498	10.698	8.898	10.898	8.698	9.898
40.498	42.898	41.498	43.898
		58.698	61.098
		80.498	82.698
		86.298	88.698
		97.098	98.898
				102.498	103.498
144.098	146.298	143.698	146.098
				166.098	166.898
				240.098	242.498
268.698	271.098
291.898	294.298
		311.698	313.698
323.298	324.698
		358.698	360.298
360.498	362.898
370.298	372.698
		373.298	375.698
		383.498	385.898	384.898	387.298
400.298	402.698	400.298	402.698	399.698	402.098
414.698	417.098	413.298	415.698	412.898	415.298
		494.698	495.698
E. ENr113 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
66.008	67.608	65.891	68.291
		87.091	89.491
110.608	111.608	110.491	111.691
141.008	142.008	141.291	142.891
153.408	155.808	152.491	154.891
167.408	169.808
176.208	178.208
		181.491	183.891
				225.524	227.324
232.608	234.408	232.691	233.491	232.324	233.924
		270.691	272.891	271.324	273.124
299.408	301.808	300.091	302.491	300.524	302.524
338.208	340.008
				363.124	364.124
371.808	374.208
		409.891	411.091	409.324	411.124
				489.124	490.524
F. ENr123 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
		8.617	11.017
		26.617	28.817
		42.217	44.017	43.440	45.840
		48.617	51.017
		75.217	76.217
		134.417	136.817
		178.417	180.817
		247.817	250.217	246.040	248.440
251.24	252.04			250.840	252.440
		267.217	268.017
		383.617	384.417
		389.617	392.017	389.840	391.440
		428.017	430.417
		447.217	449.617
		464.017	466.217
488.84	490.44	487.017	489.417	488.440	490.840
G. ENr131 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
10.424	12.224	11.337	13.737
				110.824	113.224
184.224	186.424			184.024	186.424
				188.024	190.424
207.024	209.424	208.337	210.737	206.824	209.224
212.424	214.224	212.337	214.337	211.624	214.024
215.024	217.424	216.537	217.337	216.024	217.624
				224.424	225.424
229.024	230.824	228.737	230.337	229.424	230.224
		235.137	237.537
245.024	247.224	244.737	246.737	244.624	247.024
256.424	258.824	256.137	258.537	255.224	257.624
310.824	311.824
382.424	383.624	381.937	384.137
390.024	392.424	389.937	392.337	391.624	394.024
		394.137	395.537
		403.137	405.137	404.624	407.024
414.424	416.824	415.737	416.737
		445.337	446.937	444.224	446.624
450.624	452.224	450.537	452.337	450.624	452.224
455.424	457.424
468.024	469.424
474.824	476.624			475.224	476.824
				498.824	499.624
H. ENr213 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
1.283	2.083	1.083	1.883	1.083	3.483
30.083	32.483	30.083	32.483
63.683	66.083	63.683	66.083	63.083	65.483
		81.683	84.083
93.683	96.083	92.283	94.683	94.683	95.483
206.883	209.283	207.483	209.883
		294.883	296.483
		392.283	393.083
461.683	463.283	460.683	463.083	461.483	463.883
468.083	470.283	468.883	469.683
I. ENr232 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
		103.437	105.837
		151.237	153.637
177.437	178.237
237.837	240.237
257.037	259.437
		280.237	281.437
293.437	295.837	293.037	295.437
302.237	304.637	304.237	306.637	302.237	304.637
310.237	312.637	312.437	314.837	312.637	315.037
				328.637	330.237
334.237	336.237	334.437	336.837	335.437	337.237
		348.037	349.237	346.837	349.237
351.037	353.437
		355.437	357.837	355.837	358.237
362.637	365.037	362.237	364.637	361.037	363.437
367.437	369.437	367.437	369.837	367.437	369.437
				385.037	387.437
390.237	392.637	390.837	392.637	389.237	391.637
399.837	402.237	399.837	402.237	399.237	401.637
		402.837	405.237
				420.237	422.637
429.237	431.637	428.437	430.837
		458.437	460.837	459.437	460.437
		468.837	469.837
479.237	481.637	477.037	479.437	477.037	479.437
482.237	484.637	481.037	483.437	481.237	483.637
		484.437	486.837
491.237	493.637	494.437	496.837	492.437	494.837
J. ENr321 Hotspots
CEU		ASI		YRI
Start	End	Start	End	Start	End
14.645	16.045
43.245	44.845
67.645	69.045	67.601	68.401	67.801	70.201
88.245	89.045
		204.601	207.001
				207.801	208.801
231.245	233.645
247.245	248.045
260.045	262.445
278.645	281.045	278.601	281.001
		289.401	291.801
293.645	294.445	293.601	295.401	293.201	295.601
342.645	344.245			342.401	344.201
364.845	367.245	364.801	367.201	364.201	366.601
		392.001	393.801
396.645	399.045	398.201	400.201	398.401	400.801
				411.401	413.801
		414.801	417.201
		433.801	436.201
461.245	463.645
497.245	499.045			496.601	499.001

According to the simulation results, our method is not sensitive to population histories, so the possible discrepancy between the real histories and the histories estimated by Schaffner et al.⁴⁰ will not lower the power significantly. The power of our method is mainly determined by the background recombination rate. We compared the estimated background rate (after detecting hotspots) in the simulation data and in the HapMap ENCODE data. From the results shown in table 4, it can be observed that the average background rates of the HapMap ENCODE regions are similar to those of simulation data with HQ=90% and are much lower than those of the simulation data with HQ=70%. This suggests that the power of our method for the HapMap ENCODE data is comparable to the power (67%) in the simulation data with HQ=90%. In addition, the estimated background recombination rates of the two regions by sperm-typing experiments (all from the CEU population) are 0.087 and 0.120, which are similar to those of the ENCODE regions. The high power (∼86%) achieved for those data also suggests a high power in the ENCODE regions.

Table 4. .

Estimated Background Recombination Rate for the Simulation Data and the HapMap ENCODE Data

	Simulation Data
	HQ = 90%		HQ = 70%		ENCODE Data
Population	Mean	SEM	Mean	SEM	Mean	SEM
CEU	.078	.030	.202	.055	.059	.029
ASI	.070	.024	.177	.051	.079	.043
YRI	.133	.043	.362	.074	.165	.064

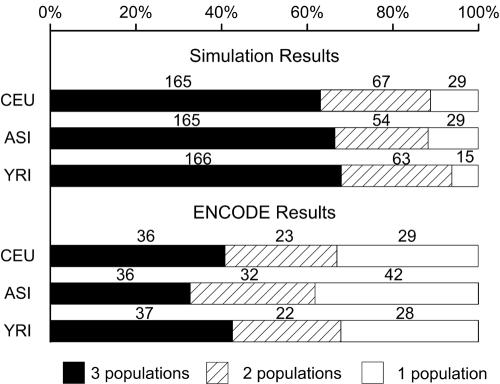
Some of the hotspots are not discovered in all populations. Figure 3 shows the numbers of hotspots detected in one, two, and all three populations in the HapMap ENCODE data and those detected in the three populations in simulation data with HQ = 90%. We observe that, compared with the simulation (in which the three populations have exactly the same hotspots), there are more hotspots in the HapMap ENCODE data that are found only in one population, and there are fewer hotspots that are found in all three populations. This discrepancy is significant by the χ² test (P<1×10^-5), showing a systematic difference between the simulation data and HapMap ENCODE data. We checked known factors that may affect the power of the method, SNP density and SNP MAF, and found no evidence that they cause this difference. There has been a long discussion about whether recombination-rate variations are the same across human populations.^26,30,44,45 If we assume that the recombination rate model and other assumptions underlying the simulation are appropriate for the ENCODE data, the fact that significantly more population-specific hotspots are observed in the real data might be viewed as evidence that the presence of hotspots is not identical in the three populations on the basis of the current data. However, some other possibilities, such as inconsistent intensities of the hotspots in the three populations, may also explain the observed low consensus between the populations.

Figure 3. .

Numbers of hotspots detected in one, two, or all three populations in the simulation study and in the HapMap ENCODE data. The lengths of bars show the percentage of the hotspots in all detected hotspots, and the numbers on the bars are the numbers of hotspots following the corresponding categories. (The numbers of hotspots detected in all three populations are not the same for all populations, since there might be two hotspots in one populations overlapping with single hotspots in other populations.) It can be observed that, in the HapMap ENCODE data, we detected significantly smaller proportion of hotspots shared by all three populations but a larger proportion of hotspots that are detected only in one population, compared with those detected in the simulation data.

Correlation between Hotspot Positions and Genomic Features

Many sequence and gene-related features have been reported to be significantly correlated with hotspot positions at different scales, from several megabases to as fine as ∼5 kb.^8,42,46,47 On the basis of the 172 hotspots we predicted with the HapMap ENCODE data, we investigated the possible correlation of hotspot positions with some major sequence factors and gene annotations. This was done by comparing the distributions of the major factors inside and outside the predicted hotspots, and a significant difference in the distributions may indicate correlation of the factor with the hotspots. The significance was tested with random permutations. First, the occurrence (for discrete features) or average (for continuous features) of a feature in the detected hotspots was counted. Then, we did permutation by randomly relocating the “hotspots” (without changing their widths) within the whole 5-Mb region, keeping in mind that they do not overlap or touch, and counted the occurrence or average of the feature in the permuted “hotspots.” This procedure was done 10,000 times to get the null distribution of the occurrence or average of the feature in the permuted hotspots. The occurrence or average in the true detected hotspots was compared with this null distribution to calculate the P value of observing the occurrence or average solely by chance. If the true occurrence or average was significantly larger or smaller than that in the permuted hotspots, we inferred that the feature is enriched or depleted in hotspots; otherwise, a correlation was not observed.

The features and the test results are listed in table 5. It can be seen that high G+C content was enriched in hotspot regions, consistent with previous reports that hotspots have a weak positive correlation with the G+C content.^{8,28,42,46,47} Significant correlation with the number of CpG islands was not observed. The relation with repeats on the genome was studied by calculating the length of repeat elements located in hotspots normalized by the width of the hotspots. We observed that repeats are significantly depleted in the predicted hotspots when all types of repeats are taken as a whole. This observation is roughly consistent with that in yeast, where Ty elements (the main family of large dispersed natural repeats) tend to have very low recombination rates.⁴⁸ We also studied each family of repeat elements separately by counting the number of repeats that overlap with hotspots. Of the seven most-frequent repeat families that each occur >500 times in the whole 5-Mb region, we observed significant enrichment of Low_complexity, L2, and MIR in hotspots; significant depletion of L1 in hotspots; and no significant correlation with Alu, MaLR, and Simple_repeat. These observations are consistent with those of Myers et al.,⁸ except that they did not observe significant relation with Low_complexity repeats. We also studied the correlation of the detected hotspots with gene annotations. Among the factors we studied, we observed that hotspots tend to avoid gene regions (from 1 kb upstream of the first exons to 1 kb downstream of the last exons). Of the 172 predicted hotspots, 56 are located at ±1 kb from annotated RefSeq genes. Among them, seven hotspots overlap with the ±1-kb areas around annotated transcription start sites. In yeast, there is a category of α hotspots that occur in promoter regions and that are related to certain transcription factor–binding sites. In humans, α hotspots have been reported in a small-scale study²⁸ but have not been found in other studies.^8,30 The observation in the current study does not show the correlation of hotspots with promoters but shows a few examples of hotspots in promoter regions.

Table 5. .

Correlation between Detected Hotspot Positions and Genomic Features in the HapMap ENCODE Regions

	Mean Occurrence or Average Value
Feature	In Putative Hotspots	In Random Hotspots	Enriched or Depleted in Putative Hotspots	P
Basic sequence features:
G+C content	.432	.400	Enriched	<.0001
No. of CpG islands	10	7.78	…	.2587
Genomic repeatsa:
All families of repeats	.396	.456	Depleted	.0014
Alu	143	156.5	…	.2175
L1	117	149.7	Depleted	.0143
MIR	118	90.1	Enriched	.0061
Simple_repeat	78	63.9	…	.0671
L2	90	63.9	Enriched	.0041
Low_complexity	77	57.7	Enriched	.0180
MaLR	56	50.2	…	.2532
RefSeq genes and related features:
Gene regionsb	.2790	.3913	Depleted	.0009
Exonic bases	.0244	.0228	…	.3863
UTRs (5′ + 3′)	.0089	.0127	…	.3288
DHSSs:
Sites in DNase GM069 Chip	26	13.1	Enriched	.0031
Sites in DNase CD4 Chip	24	13.0	Enriched	.0185
Sites in DNase CD4 MPSS	4	2.5	…	.2445
Sites in DNase CD4-act MPSS	4	2.7	…	.2889

^aOnly families of repeats that occur >500 times in the studied regions are listed here. All other repeat families are not tested significantly related with the hotspots.

^bGene regions are calculated as 1 kb upstream of the first exon to 1 kb downstream from the last exon.

The Existence of Human β Hotspots

It is known that in yeast open chromatin structure is necessary for the formation of double-stranded breaks (DSBs), which initiate meiotic crossover events.^35,36 To investigate whether such a relationship persists in humans, we calculated the correlation between hotspot positions and DHSSs, which are strong signals for open chromatin structure. Among 144, 143, 26, and 30 DHSSs in the four groups of DHSS data, 26, 24, 4, and 4 overlap with the detected hotspots, respectively. The lengths of DHSSs are also very short (∼0.29 kb on average). From the results shown in table 5, we observed that the DHSSs from the first two data sets (the one identified by DNase-chip in the GM06990 line and the one identified by DNase-chip in the CD4⁺ T cells) are significantly enriched in the detected hotspots. The other two data sets are rather small, and correlations with DHSSs therein are not significant.

In yeast, the hotspots that require open chromatin structure, which usually show DNaseI hypersensitivity, have been termed “β hotspots.”³⁶ The significant correlation of the detected hotspots with DHSSs we observed suggests the existence of similar β hotspots in humans. If we take all DHSSs in the four groups of data together, they overlap with 26 hotspots among the 172, which indicates that ∼15% of the hotspots in humans could be of the β type. It is interesting to note that, among the seven hotspots that are located at promoter regions, three also overlap with DHSSs where cis-regulatory elements are known to be abundant.

Discussion

In this article, we have presented a new method for detection of recombination hotspots, its validation with simulation and experimentally verified data, and its application to the HapMap ENCODE data. We introduced a TWPLL in the method and adopted models that allow multiple hotspots in a region. Simulation experiments, as well as validation with the two human genome regions that have available sperm-typing data, show that the method is comparable to the best methods, with regard to the detection power and false-positive rate. In addition, the proposed method is computationally fast and can work on both phased and unphased data.

The precision of our method in locating hotspots can be affected by the SNP density, which is high in our study. When the SNP density is low, hotspot locations cannot be determined as precisely, and their lengths should not be limited to 2.4 kb. This can be tackled by adjusting the detected hotspots in the following way. Suppose a hotspot (⩽2.4 kb) is detected whose starting location is between SNPs i and i+1 and whose ending location is between SNPs j and j+1; we adjust its location to be from the position of SNP i to that of SNP j+1. We did simulation with ∼0.7 common SNPs per kb, similar to the SNP density of phase II of the main HapMap project. After the above adjustment to the hotspot boundaries, the power is ∼59% for each population, with the same false-positive rate discussed above. The average position offset is ∼1.5 kb, and >99% of detected hotspots cover the centers of true hotspots in each population. Therefore, the method can surely be applied to phase II HapMap data. When SNP density is too low—for example, 0.2 common SNPs per kb—our method is not recommended.

Another issue is the choice of N and ω_k in TWPLL. Simulations show that our method is not sensitive to either of them. For the data we used, N=5, 7, or 9 results in almost the same power, and, for N=7, ω_k=1/k and ω_k=1-(k-1)/N perform comparably. So, the choice of N and ω_k is not so critical within a certain range, and we suggest that N=7 and ω_k=1/k is generally a good choice for most data sets.

When N and ω_k are fixed, the key parameter to be decided is the threshold T, representing the trade-off between power and false-positive rate. Simulation results show that T can be affected by the SNP density and sample size. A lower T should be chosen for lower SNP density or smaller sample size, to give the same false-positive rate. For example, T=19 is appropriate when the SNP density decreases to the level of the phase II HapMap project, and T=23 is proper if the diploid sample size is 50. Because of the speed of HotspotFisher, it is straightforward to calibrate the choice of T for a specific set of real data by applying HotspotFisher with different values of T to data simulated with features that match the real data.

A single background rate in each region is assumed in our model. In practice, the background rates may vary across the chromosome, so a long chromosome segment should be divided into smaller pieces, to detect hotspots in each piece. Analysis of very small regions would lead to imprecise estimates (large variance), whereas analysis of regions that are too big may lead to poor estimates due to biases from the assumption of a constant background rate. We suggest 100–500 kb to be a good range of choices, and 200 kb may be chosen as the default.

In all our simulations, we applied the proposed method to unphased data directly. An alternative strategy is to detect hotspots on the basis of the haplotypes inferred from genotypes by use of software such as PHASE.^31,32 Since adopting such an additional step often increases the computational cost substantially and since our method can directly handle unphased data, we did not use this strategy in our study. However, it is recommended that others use haplotype data if the data are highly reliable; otherwise, the use of genotypes directly is reliable and convenient.

From another perspective, because the method can work on unphased data efficiently, it can also be incorporated into some haplotype-inference methods. Many current methods for inferring haplotypes from genotypes assume no recombination or minimum recombination events. Users may use the proposed method to detect recombination hotspots first and then use those haplotype-inference methods to infer haplotypes between each pair of adjacent hotspots. This strategy would increase the accuracy of haplotype inference, especially when applied to long genomic regions.

Applying the proposed method to the HapMap ENCODE data, we identified 172 putative hotspots in the 10 500-kb regions. We observed that hotspots are not completely identical across the three populations. Since there are many factors that can affect the prediction in the populations, the observation may indicate the existence of population-specific hotspots and/or that the intensity of the same hotspots in different populations is different, but more data and further experiments are needed to draw a conclusion on this point.

Evidence is accumulating that meiotic crossovers in humans and in yeast may share similar mechanisms—for example, similar short lengths of hotspots and similar correlation with G+C content.^34–36 In yeast, hotspots share no particular sequence features.^34–36 In humans, a recent report has shown that the presence or absence of at least some hotspots is not controlled by the sequence or polymorphisms.⁴³ An important determinant of the β-type hotspots in yeast is the open chromatin structure, and our results show that a significant portion of human hotspots may share a similar mechanism.