Phenomenological theory of mortality evolution: Its singularities, universality, and superuniversality

Abstract

The probability to survive to the age x universally increases with the mean lifespan x̄. For species as remote as humans and flies, for a given x the rate of its evolution with x̄ is constant, except for the narrow vicinity of a certain x̄ = x* (which equals 75 years for humans and 32 days for flies and which is independent of age, population, and living conditions). At x̄ ≅ x* the evolution rate jumps to a different value. Its next jump is predicted at x̄ ≅ 87 years for humans and ≅ 59 days for flies. Such singularities are well known in physics and mathematics as phase transitions. In the considered case different population “phases” have significantly different survival evolution rates. The evolution is rapid—life expectancy may double within a lifespan of a single generation. Survival probability depends on age x and mean longevity x̄ only (for instance, survival curves of 1896 Swedes and 1947 Japanese with approximately equal x̄ are very close, although they are related to different races in different countries at different periods in their different history.) With no adjustable parameters, its presented universal law quantitatively agrees with all lifetable data. According to this law, the impact of all factors but age reduces to the mean lifespan only. In advanced and old age, this law is superuniversal—it is approximately the same for species as remote as humans and flies. It yields survival probability that linearly depends on the mean lifespan x̄. As a result, when human x̄ almost doubles (from 35.5 to 69.3 years), life expectancy at 70 years increases from 8 to 9.5 years only. Other implications of the universal law are also considered.

1. Survival Evolution: Its Universality and Rate

Arguably, mortality is the most universal and, at least for humans, the best quantified phenomenon in biology. The human mortality rate in developed countries is well documented for the last two centuries—see, for example, 494 lifetables (yearly for adults and daily, weekly, and monthly for children) for Sweden (1, 2), Germany (3), and Japan (4). In 1825 Gompertz presented a formula (5) for mortality increase between the ages of 20 and 60 years. Later he argued (6) that there may be four different laws of mortality (for 0–1, 1–20, 20–60, and 60–100 years). Consequently, the Gompertz law was refined to be applicable to the older ages (7–9); Strehler and Mildvan (10) stated that there exists a species-specific lifespan limit (see also refs. 11–13 and reviews in refs. 14–17). Pearl (18) suggested the unitarity of the Gompertz law for different species. However, large fly populations (19–22) demonstrated mortality levelling off and decreasing at older ages, in sharp contrast to the (refined) Gompertz law and to the limited lifespan paradigm. Mortality decrease was related to genetic heterogeneity (19–27). Living conditions affect the mortality laws and their age intervals. During this century human survival curves (1–4) have approached a rectangular shape, and the long quasi-plateau from 20 to 40+ years practically disappeared in the mortality curves. Also, relative mortality increase slowed down in old age (11–13, 28–33), and the probability to survive to 85 years has increased 15-fold (1–4). The changes are country-, time-, and age-specific. This should be anticipated. In a given country in a given calendar year, the probability to die at, for example, 50 years, depends on social, medical, historical, and a variety of other factors, which affected the health and fitness during the previous 50 years. Yet, I prove that the impact of all of these factors on mortality reduces to the mean life expectancy at birth x̄ only. Indeed, consider the probability‡ ℓ_x(x̄) to survive to a given age x as a function of the mean life expectancy at birth x̄ for 1891–1995 Swedish (1, 2), 1871–1994 German (2), and 1981–1990 Japanese (4) male and female lifetables. Independent of calendar year, country, race, and sex, all data (for any given x) follow the same dependence on x̄. (Fig. 1A demonstrates it for x = 30, 60, and 90 years.) The choice of x̄ as a variable allows for the study of the ℓ_x(x̄) universality for any animal species. Fly lifetables (19–22) present the largest nonhuman populations under different conditions. Fly mean lifespan changes with conditions and genotypes almost threefold in the cohorts of different families of medflies (19, 21) (598,118 males and 605,529 females in overcrowded cages; 11,373 males and 12,590 females in individual cells) and fruitflies [three inbred and three F₁ lines in 3 blocks, each with over 550 males (20) in 4-dram shell vials with weekly transfer to fresh medium; 121,894 genetically heterogeneous males (22) in cages]. For a given age, all of these populations follow the same ℓ_x(x̄) dependence on the mean lifespan x̄ at any age x. (Fig. 1A demonstrates it for x = 20 and 40 days.)

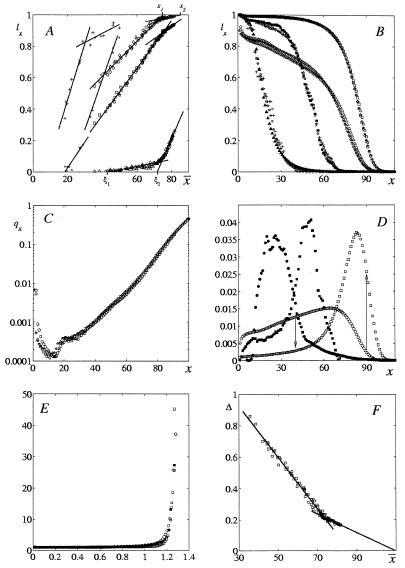
Figure 1.

(A) Evolution of the survival probability ℓ_x(x̄) with the mean lifespan x̄. The age x = 30 (◊), 60 (□), and 90 (▵) for 1890–1995 Swedish, 1871–1994 German, and 1981–1990 Japanese males and females; x = 20 (+) and 40 (x) for heterogeneous male, female, and combined medflies in cages and cells, and genetically heterogeneous and homogeneous fruitflies; top level ages x₁ and x₂ are denoted for human x = 30; bottom level ages ξ₁ and ξ₂ are denoted for human x = 90. In all figures x and x̄ are in years for humans and in days for flies. Straight lines are linear interpolations, whose mean square deviation from experimental data is less than 0.01. (B) Survival curves ℓ_x(x̄) vs. age x for 1896 Swedish (1) (▵, the mean lifespan x̄ = 53.65) and 1947 Japanese (4) (◊, x̄ = 53.96); 1980 Japanese (4) (○, x̄ = 78.77) and 1994 German (3) (□, x̄ = 78.96) females; genetically heterogeneous female medflies (▴) in overcrowded cages (24, 26) (with the mean lifespan x̄ = 18.6) and genetically homogeneous male fruitflies (+) in vials (25) (with x̄ = 19.1); different crosses of male fruitflies (25) with x̄ = 46.3 (■) and x̄ = 46.5 (x); and ℓ_x(x̄) according to the universal law (with no adjustable parameters, ⋆). (C) Mortality rates q_x for 1980 Japanese (4) (○) and 1994 German (3) (□) females from Fig. 1B on a semi-logarithmic scale, which is conventional in demographic studies. Note the mortality minimum, the Gompertz linear region; the slowing down of the mortality rate increases in very old age, and the agreement between experimental and universal data (⋆) over four orders of q_x magnitude. (D) Survival evolution rates a₁ (○, human; ● fly) and a₂ (□, human; ■, fly) vs. age x. The rates are in year⁻¹ for humans, in day⁻¹ for flies. Downward and upward arrows correspondingly demonstrate the decrease (x = 40) and increase (x = 90 years) in human evolution rate at x̄ ≅ x* in Fig. 1A. (E) Human–fly universality: x₁/75 vs. x/75 (○), x₂/82 vs. x/82 (□) for humans, x₁/37 vs. x/37 (●), x₂/56 vs. x/56 (■) for flies; x₁ and x₂ are (top) level ages. (F) Species-specific decrease in the x̄ relative mean fluctuation with the mean longevity x̄ for male and female 1891–1995 Swedes, 1891–1990 Japanese, and 1781–1992 Germans. Straight lines are linear interpolations.

Fig. 1A presents the universal evolution of the survival probability with x̄. The rate of this evolution ℓ_x(x̄)/dx̄ is the slope in Fig. 1A. It is constant for a given age x until a narrow vicinity of a certain x̄ = x*. There it jumps to a significantly different constant value. The survival evolution rate decreases before 68 years for humans (e.g., 5.4-fold for x = 30 years in Fig. 1A) and before 39 days for flies; it increases thereafter (e.g., 15-fold for 90-year-old humans). The change may be nonmonotonic and accompanied by a jump in the survival probability (see, for example, x = 40 days for flies in Fig. 1A). The crossover lifespan x* (75 years for humans and 32 days for flies) is universal and independent of age, population, and living conditions. The better the statistics (e.g., humans vs. flies) and the more homogeneous the population (e.g., Swedish females vs. all humans) are, the narrower the crossover and the more pronounced its singularities are. In physics and mathematics, singularities of static and dynamic characteristics are known as critical phenomena, and phase transitions and are extensively studied. Fig. 1A demonstrates an “evolution phase transition” between population “phases” (with different values of survival evolution rate) at the universal “critical” mean lifespan x*. (Of course, the elucidation of their biological meaning is beyond the scope of phenomenological theory.) The ℓ_x(x̄) linear dependence on the mean value x̄ is unusual for stochastic phenomena [and is presumably related to strong long-range correlation (28, 34–37) between mortality rates at different ages and of different generations of ancestors and their descendants]. It yields, in particular, a weak dependence of the life expectancy in old age on x̄: e.g., at x = 70 years it was 8 years for 1800 Swedish (1) (with x̄ = 35.5) and 9.5 for 1970 Japanese (4) (with almost twice larger x̄ = 69.3 years, in both cases x̄ < x*) males. In the last section, I demonstrate that the universal evolution law predicts the next “evolution phase transition” at human x̄ ≅ 87 years and fly x̄ ≅ 59 days.

Survival evolution is very rapid—Japanese and German x̄ more than doubles (3, 4) in 70 years, i.e., within the mean lifespan of a single generation. According to Fig. 1A, the age x and the mean lifespan x̄ uniquely determine the human and fly ℓ_x(x̄), which is approximated in the next section. So, the populations with the same x̄ should yield identical survival and mortality curves, and the approximation allows one to calculate these curves with no adjustable parameters and provides their change with population and living conditions. This is demonstrated in Fig. 1B with the survival curves of 1896 Swedish (x̄ = 53.65 years) and 1947 Japanese (x̄ = 53.96 years) females (different races in different countries, at half a century different periods of their different history); of 1994 German (2) (x̄ = 78.7 years) and 1980 Japanese (4) (x̄ = 78.8 years) females; of different families of genetically heterogeneous female medflies (19, 21) and inbred (20) (3 × 3, block 2) male fruitflies under different conditions (cages and vials), with x̄ = 18.6 and 19.1 days correspondingly; of different crosses (20) (3 × 2 and 2 × 1, block 1 in both cases) of male fruitflies with x̄ = 46.3 and 46.5 days; and of their calculations according to the universal law. Fig. 1C demonstrates the agreement of experimental and universal human mortality rate q_x over four orders of its magnitude; the deviation determines the upper limit for the premature mortality, which is surprisingly low.

In the next section, I establish the universal ℓ_x(x̄) law. In the last section, I study its implications.

2. Universal Laws of Survival Evolution

The linear approximations ℓ^*_x(x̄) of the ℓ_x(x̄) dependence on the x̄ for all human and fly lifetables yield

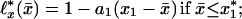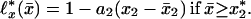1

Here a₁(x), a₂(x) are the approximation slopes and x₁(x), x₂(x) are their “top” level ages: ℓ^*_x(x₁) = ℓ^*_x(x₂) = 1 (see Fig. 1A); for humans x^*₁ = x^*₂ = 75; for flies x^*₁ = 29, x^*₂ = 35; the crossover x* = (x^*₁ + x^*₂)/2. Eq. 1 analytically describes the evolution of survival probability ℓ^*_x(x̄) with x̄. For a given age x, the survival evolution rate dℓ^*_x(x̄)/dx, by Eq. 1 and consistent with Fig. 1A, is constant at x̄ ≤ x^*₁ and equals a₁. At x̄ ≅ x* the rate jumps from a₁ to a different constant a₂. Since‡ ℓ_o(x̄) = 1 and ℓ_∞(x̄) = 0 (nobody lives forever), so, by Eq. 1, a₁(0) = a₂(0) = 0 and a₁(∞) = a₂(∞) = 0. Thus, the evolution rate must be zero for newborns, must reach maximum at a certain age, and then decrease to zero. This is verified with Fig. 1D, which presents a₁(x) and a₂(x) dependencies on x. For humans, for example, the evolutionary rate a₁(x) is maximal at x ≅ 62 years, whereas the rate a₂(x) is maximal at x ≅ 83 years. To compare human and fly mortality, introduce dimensionless variables. Consider, for example, dimensionless level age x₁/x* vs. age x/x* for humans with x̄ < x*; in all other cases chose the variables that provide maximal proximity of human and fly plots. Then Fig. 1E exhibits human–fly superuniversality. Similar superuniversality in advanced and old age (x > 25 years for humans, x > 15 days for flies) is exhibited by the dimensionless “bottom” level ages ξ₁(x), ξ₂(x), where ℓ^*_x(ξ₁) = ℓ^*_x(ξ₂) = 0. The tables of a₁(x), a₂(x), which are plotted in Fig. 1D, and of x₁(x), x₂(x) in Fig. 1E allow one, by Eq. 1, to calculate complete survival ℓ_x(x̄) and mortality q_x(x̄) = ℓn[ℓ_x(x̄)/ℓ_x+1(x̄)] curves, given the values of x and x̄ only. The calculations agree with experimental data with no adjustable parameters (see Fig. 1 B and C). Thus, these (superuniversal in advanced and old age) lifetables may quantitatively replace all hundreds of human and fly lifetables.

3. Universal Law: Implications and Prediction

Universal law (1) of mortality evolution is based on the available data and statistics. Human statistics are rather reliable, except for early ages in developed countries with very low mortality (e.g., 50,208 girls were born and 6 died in their 9th year in 1995 Sweden; ref. 2) and for old ages in the vicinity of and beyond 100 years. Flies allow for genetically homogeneous populations (20), but the latter exceeded a thousand in one case only. Only two (med- and fruitfly) different families were studied. Clearly, comprehensive verification of the implications and predictions of the universal law is important, whereas for young and old ages it may be crucial.

(i) The universality of ℓ_x(x̄) implies another law of mortality evolution—the universal dependence of the x̄ mean square fluctuation Δ₂ on x̄. Fig. 1F demonstrates the universal decrease of the relative fluctuation Δ = Δ₂/x̄ with x̄ for humans (with good statistics). The decrease is linear everywhere, except for the narrow vicinity of the same critical age as in Eq. 1. With the mean accuracy of 0.02, Δ is approximated by the equations

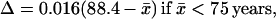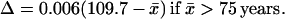2

The slope 0.006 year⁻¹ agrees with the value 0.005 year⁻¹ calculated according to ref. 26. The extrapolation of Eq. 2 to the minimal Δ = 0 yields the maximal mean lifespan x̄_max = 109.7 years, which is consistent with the calculation in ref. 26.

The fluctuations of the mean lifespan of genetically homogeneous populations over 550 fruitflies (20) are ⪝ 10%; in one case only (with the largest Δ), they reach 30%. Together with the universality of Fig. 1 A and F for genetically homogeneous populations, this suggests that under given conditions a genome uniquely determines§ its x̄ and Δ. The validity of Eq. 1 for genetically homogeneous populations implies its validity for a heterogeneous population, where all or almost all genotypes have either x̄ < x^*₁ or x̄ > x^*₂, but may not imply it otherwise. This is consistent with the irregular evolution rate of heterogeneous flies in cups (19, 21) (x̄ ≅ 32). In a heterogeneous population with x̄ < x*, only the subpopulations with progressively larger x̄ > x* survive to the age significantly beyond x*, dominate its mortality, and yield deviations from Eq. 1 in very old age. This is consistent with refs. 26 and 27, with the significant slowing down of the heterogeneous fly a₁(x) decrease in Fig. 1D and x₁ increase in old age (beyond x = 41 days). However, then their x₁ data are statistically unreliable (and are not included in Fig. 1E).

(ii) In human young age ℓ_x(x̄) ≅ 1. Thus, by Eq. 1, ℓnℓ^*_x(x̄) ≅ −a_s(x_s − x̄), where s = 1 or s = 2. In early age, according to Fig. 1 D and E, a_s(x) changes much quicker than x_s(x) does. So,

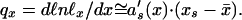3

Thus, the relative mortality q_x/q_y = a′_s(x)/a′_s(y) (where y is a fixed, arbitrarily chosen young age) depends on age x only and is universal. This was indeed demonstrated (27) with all 272 available child lifetables (2–4) (yearly up to 10 years and daily, weekly, and monthly up to 1 year).

(iii) Suppose x̄ in Eq. 1 is less than x^*₁. Because survival probability (for x ≠ 0) never reaches 1, x̄ must always remain smaller than x₁(x) according to Eq. 1. Thus, when x̄ approaches x₁(x), the latter must increase to a different value x₂(x). Indeed, when, for example, x = 40 years, the human x₁ ≅ 76 years. It rapidly switches to x₂ ≅ 87 years at x̄ ≅ 75 years, slightly before x₁ ≅ 76 years. Likewise, at x = 20 days the fly x₁ ≅ 35 days switches to x₂ ≅ 59 days at x̄ ≅ 32 days, somewhat before x₁ ≅ 35 days. Currently, maximal human (1–4) x̄ ≅ 82 years and fly (19–22) x̄ = 49.9 days. I predict the next rapid change from x₂(x) to the larger x₃(x) in the vicinity of x̄ ≅ x₂ ≅ 87 years for humans (if x ∼ 40 years) and x̄ ≅ x₂ ≅ 59 days for flies (if x ∼ 20 days). It may be followed by further jumps at higher x̄.

(iv) Because Fig. 1 A and F and Eq. 1 are universal, all relevant characteristic times—the reproductive age, mean and maximal mean longevity, mean longevity fluctuation, and mean time of mortality evolution adjustment to changing external conditions—must be of the same order of magnitude. Indeed, human x̄/75 years changes from 0.5 to 1.2; fly x̄/32 days increases from 0.6 to 1.7; Japanese and German mean lifespan approximately doubled in 70 years. Eq. 1 universally relates survival probability ℓ_x(x̄) to the mean longevity x̄. Thus, to quantify the evolution of ℓ_x in real time t, it is sufficient to determine the rate dx̄/dt. Phenomenologically, this rate depends on x̄,t. The dependence of dx̄/dt on x̄ is related, in particular, to the properly averaged (with respect to age) ℓ_x(x̄), which is universal and is nonlinear in x̄ in the narrow crossover region x̄ ≅ x*. (The dependence on t is related to changing conditions and is nonuniversal). In mathematics, it is well known that the behaviour of nonlinear equations is very rich. They may have several solutions, which diverge at the branching points. Possibly, human x* ≅ 75 years and fly x* ≅ 32 days in Fig. 1A are such universal branching points (cf. bifurcations in ref. 48). Branching points yield singularities, instabilities and higher fluctuations. These are indeed evident at these ages in Fig. 1A.

(v) The universality of Fig. 1A and F for genetically homogeneous fruitfly populations suggests that the heterogeneous mean lifespan x̄ and its fluctuation are related predominantly to the population genetic composition. [Note that x̄ of different inbred fruitfly lines (20) differs more than 2.5-fold.] I speculate that although individual chances of survival heavily depend on accidental fortunes or misfortunes, the population probability to survive to a given age is strongly correlated with its genetics, which affects immunity, physical fitness, and many other factors. Mortality exterminates genomes (that are “unwanted” under a given set of conditions) on the mean longevity timescale (see point iv) and changes the genetic composition (polymorphism) of the population. This might quantitatively explain very rapid microevolution and is consistent with ref. 49. Rare mutations may be responsible for relatively slower macroevolution on a much larger time scale.

Conclusions

The human and med- and fruitfly probability ℓ_x(x̄) to survive to the age x depends on x and life expectancy at birth x̄ only, and is independent of the population and its living conditions. Fig. 1B demonstrates it for 1896 Swedish (x̄ = 53.65 years) and 1947 Japanese (x̄ = 53.96 years) females (i.e., for different races in different countries at very different periods of their different history), for different families of genetically heterogeneous medfly females (x̄ = 46.3 days) in overcrowded cages, and for inbred fruitfly males (x̄ = 46.5 days) in 4-dram shell vials (i.e., in different conditions).

The universal ℓ_x(x̄) is determined. It yields survival and mortality curves, which agree with all available experimental data for humans and flies—see examples in Fig. 1 B and C (note the agreement between human theoretical and experimental mortality rate q_x over four orders of magnitude; their deviation is a quantitative measure of premature mortality at a given age). Theoretical curves exhibit different mortality regions and their change with populations and living conditions—e.g., human minima; quasi-plateaus, which vanish at sufficiently large human x̄; and the Gompertz ℓnq_x, which linearly increases with x and then slows down at very old age (see, for example, Fig. 1C). Survival evolution with x̄ (for a given age x) proceeds with a constant rate a₁(x) until the narrow vicinity of a certain critical x̄ = x* (which is independent of age, population, and conditions and equals 75 years for humans and 32 days for flies). At x̄ ≅ x* the rate jumps to a different constant value a₂(x) and proceeds with it thereafter (see Fig. 1A). For humans younger than 50 years, a₂(x) ≪ a₁(x); humans older than 70 years have a₂(x) ≫ a₁(x). The rate significantly changes with age and has a maximum at an advanced age. Survival evolution is rapid: x̄ may double within the mean lifespan. Presumably, it is related to the change in the population genetic composition. Such a change may explain a very rapid macroevolution [there were no humans only a few hundred thousand generations ago and no mammals a few dozen million generations ago, whereas a few million billions of intermolecular collisions (“generations”) are needed to cool down a cup of coffee] and is consistent with ref. 49. The singularity at x̄ = x* may manifest the emergence of a new population “phase” (with a significantly different mortality evolution rate) in the course of punctured equilibria (50).

Survival probability as a function of dimensionless age and mean lifespan is superuniversal in advanced and old age for different phyla of human and fly (see Fig. 1E). Probability to survive to old age little depends on the mean lifespan; for example, at 70 years human life expectancy was 8 years for 1800 Swedish (x̄ = 35.5 years) and 9.5 years for 1970 Japanese (x̄ = 69.3 years) males. I predict and verify that the mean quadratic fluctuation of mortality depends on x̄ only (Fig. 1F); that the relative child mortality is independent of conditions. The next jump of the survival evolution rate is predicted in the vicinity of the universal x̄ ≅ 87 years for humans and x̄ ≅ 59 days for flies.

The superuniversality of the survival evolution of species as remote as humans and flies suggests that its law is genetically determined and may be universal for all iteroparous animals. The diversity of life and, in turn, species life histories is so vast that one tends to believe this law is invalid for semelparous species. Yet, one may wildly speculate that it is universal even for animals such as salmon and mayflies, that their survival curves are rectangular at the reproductive age which equals x*, and that their evolution rate is negative and its value is extremely large beyond x̄ = x*.