Abstract
Three-dimensional protein folds were assigned to all ORFs of the recently sequenced genome of the hyperthermophilic archaeon Pyrobaculum aerophilum. Binary hypothesis testing was used to estimate a confidence level for each assignment. A separate test was conducted to assign a probability for whether each sequence has a novel fold—i.e., one that is not yet represented in the experimental database of known structures. Of the 2,130 predicted nontransmembrane proteins in this organism, 916 matched a fold at a cumulative 90% confidence level, and 245 could be assigned at a 99% confidence level. Likewise, 286 proteins were predicted to have a previously unobserved fold with a 90% confidence level, and 14 at a 99% confidence level. These statistically based tools are combined with homology searches against the Online Mendelian Inheritance in Man (OMIM) human genetics database and other protein databases for the selection of attractive targets for crystallographic or NMR structure determination. Results of these studies have been collated and placed at http://www.doe-mbi.ucla.edu/people/parag/PA_HOME/, the University of California, Los Angeles–Department of Energy Pyrobaculum aerophilum web site.
For the nascent field of structural genomics, it is important to know which new protein sequences belong to known three-dimensional folds and which are likely to have previously unobserved folds. The latter proteins present good targets for experimental structure determination because the new structures will likely permit the assignment of other sequences to the novel fold. In this paper we describe methods for whole-genome fold assignment that are statistically validated. We use these methods, in conjunction with homology searches of sequence databases, to determine targets for experimental structure determination of proteins from the newly sequenced hyperthermophilic archaeon Pyrobaculum aerophilum (PA) (1), which is the focus of a structural genomics initiative.
Previous methods of whole-genome fold assignment have used a sharp threshold to separate “confident matches” from “noninformative matches.” How one chooses to define the barrier between confident and noninformative fixes the percentage of a genome that is assigned a fold (sensitivity), and also the percentage that is assigned the correct fold (selectivity). Often, large portions of a genome are ignored because their sequence–structure scores fall below this arbitrary threshold.
An alternative approach is to generate a continuous distribution such that every sequence–structure match is assigned a confidence level describing the likelihood that it is correct. The method proposed in this paper derives these confidence levels by asserting the binary hypothesis that a fold assignment is either correct or incorrect. We have defined structures of our test set as being structurally similar, and thus assigned correctly, if they are in the same dali/FSSP family (2–5), with compatibility Z-scores greater than 2. All other assignments are considered incorrect. As shown below, by treating sequence–structure scores generated by the Sequence Derived Properties (SDP) method (6) with the binary hypothesis we derive continuous probability distributions for how often predictions are correct as a function of the sequence–structure compatibility score.
Materials and Methods
Pyrobaculum Genome.
Predicted coding region sequences of the PA genome were obtained from the Jeffrey H. Miller Laboratory of the University of California Los Angeles Molecular Biology Institute and correspond to the 1/1/99 version of the genome. This version contained 2,681 open reading frames (ORFs) predicted to code for proteins.
Membrane-Spanning Proteins.
Of the 2,681 PA ORFs, 551 contained membrane-spanning α-helices as determined by moment (7) (PA_HOME/TRANSMEMBRANE_HELIX_PREDICTION_RESULTS). These proteins were excluded from fold recognition and novel fold prediction analysis.
Protein Sequence Databases.
The Online Mendelian Inheritance in Man (OMIM) database containing 15,743 sequences was downloaded from the National Center for Biotechnology Information (http://www.ncbi.nlm.nih.gov/Omim/; authored and edited by V. A. McKusick and his colleagues at Johns Hopkins and elsewhere). Similarity searches of the OMIM database were performed by using a local implementation of the Smith–Waterman algorithm (8) with probability values determined by Waterman–Vingron statistics (9, 10).
Additional homology searches were performed against a nonredundant sequence database (NRDB) containing 351,096 sequences, including 18 completed genomes (from The Institute for Genomic Research) plus the databases from SwissProt, TrEMBL, Protein Identification Resource (PIR), and GenPept. The PA genome was excluded from the NRDB. Similarity searches of the NRDB were performed by using the National Center for Biotechnology Information implementation of gapped blast (11, 12) and verified by using the Washington University implementation of gapped blast (13). E values were generated by using standard Karlin–Altschul statistics (14).
Fold Assignment.
Folds were assigned by using the SDP method (6). SDP computes the compatibility of a query sequence to each member of a database of three-dimensional folds. This procedure attempts to match residue type and observed secondary structure of proteins with known three-dimensional structures to these properties predicted from a query sequence. Secondary structure predictions were derived from the PHD server of Sander and Rost (15), which can be accessed at http://dodo.cpmc.columbia.edu/predictprotein/predictprotein.html. The algorithm of the UCLA-DOE-MBI fold recognition server (http://fold.doe-mbi.ucla.edu/) was modified to provide Z-scores for compatibility of the input query sequence with every structure in the fold database. We define Z-max to be the Z-score corresponding to the best sequence–structure match. Sequence similarity searches of the Protein Data Bank (PDB) were also performed by using the Smith–Waterman algorithm to compare pure sequence methods with fold recognition methods.
Position-Specific Iterated blast (psi-blast) Parameters.
Additional searches were performed by using psi-blast (11) for comparison with fold-recognition methods. Library proteins were used to complete the SwissProt database. Searches were allowed 5 iterations to converge with a threshold of 0.0001 per iteration. Seg and Xnu filters were used to screen for low complexity regions within sequences.
Training Set Derivation.
The library of known folds was derived from the PDB SELECT (16, 17) library of Sander (http://www.sander.embl-heidelberg.de/pdbsel). Because the SDP algorithm works more effectively when templates are domains and not full chains, we attempted to find domain definitions for each of the PDB chains. If the selected chain contained a domain definition in the dali Domain Dictionary [DDD (5)], then we chose the definition from DDD. If the PDB file was not found in DDD, we looked for a domain definition in the SCOP database (18). If we were unable to locate a previously defined domain definition, the entire chain was used. Version 2.0 of the DDD was used (http://www2.embl-ebi.ac.uk/dali/domain/2.0/). Version 1.37 of the SCOP database was used (http://scop.stanford.edu/scop/). Our final fold library contains 3,285 domain folds, derived from 2,634 PDB chains.
Correct/Incorrect Matches and “Novel” Fold Classes.
We consider structures to be either similar or dissimilar as evaluated by dali Z-scores (4). Structures are considered to be similar if their pairwise dali Z-score is greater than 2. The authors of dali recommend this cutoff as indicating that the two proteins will share a common architecture and topology.
We recognize that there are many operational definitions of a “novel” fold. We define a fold as “novel” if it is not similar to any fold in our library, as evaluated by the dali Z-score.
Confidence of Assignment.
In fold recognition we observe a continuous distribution of Z-scores for compatibility of an amino acid sequence for a fold (6, 19). We must decide on the basis of the Z-score whether the sequence adopts that fold. A greater Z-score implies a greater compatibility between a sequence and a structure. One can then ask the question “How do we quantify our confidence in our assignment as a function of a sequence–structure compatibility score?” Once we have posed our question in terms of a binary decision problem (correct matches vs. incorrect matches), we can define more precisely what we mean by quantifying prediction confidence. What we really want to know is “How often are we making the assertion that an assignment is correct when the assignment is actually incorrect?” This quantity of incorrect matches above a threshold z represents the probability of false alarm (also known as the occurrence of false positives) and is denoted by Pfa = P (incorrect assignment | Z-score > z). We can express this quantity as a confidence of assignment by realizing that a low probability of false alarm directly corresponds to a high confidence. So we denote assignment confidence = P (correct assignment | Z-score > z) = 1 − Pfa.
Results
Deriving Assignment Confidence.
A confidence curve is a function that maps a sequence–structure compatibility score to a likelihood that the sequence is assigned correctly to a fold. To derive a confidence curve, we first use the SDP method (6) to generate an exhaustive set of sequence–structure compatibility Z-scores between each of the 3,285 sequences and structures in our domain fold library (excluding the true structure of that sequence). The Z-scores describe the compatibility of each sequence with a given fold. Of course, most pairings match the sequence with the wrong structure and have a low Z-score. The dali algorithm is used to determine whether the actual experimental structure of that sequence correctly matches an assigned structure.
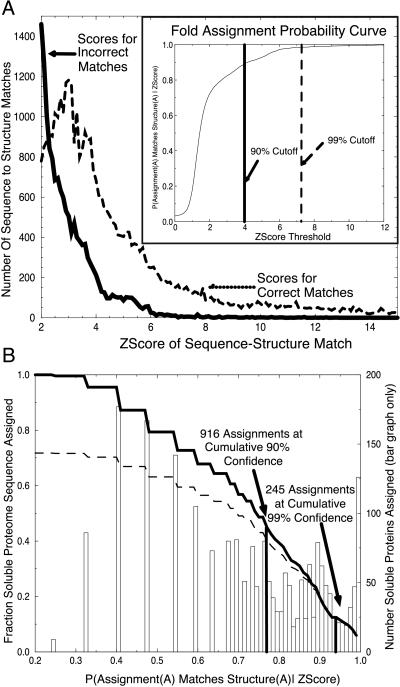
Fig. 1A is a plot of the distribution of Z-scores generated from the training set, for both incorrect matches (dissimilar folds) and correct matches (similar folds). We observe a clear separation between the two distributions; the scores for correct matches shifted to higher scores. The separation of these distributions correlates with the ability of our Z-score to distinguish correct matches from incorrect matches.
Figure 1.
(a) Distributions of fold assignment scores for correct (dashed line) and incorrect (solid line) matches. A test set of 3,285 experimentally determined domain-folds were used to generate an exhaustive set of 10,784,656 (3,285 × 3,284) sequence–structure assignment pairs, excluding the assignment of any sequence to its own structure. Each pair was assigned a sequence–structure compatibility Z-score by the SDP method (6). Structures were compared with the dali algorithm and are designated structurally similar if their dali Z-Score is greater than or equal to 2. We assert the binary hypothesis that an assigned structure for sequence A matches the true structure of A (dashed line) or does not match the true structure of A (solid line). The distributions of scores for the two cases show that similar pairs have higher sequence–structure match scores than do nonsimilar pairs. (Inset) Fold assignment probability curve. These distributions give the likelihood that an assigned fold for a protein A matches the actual structure of protein A as a function sequence–structure Z-score, as explained in the text. (B) Probability of correct fold assignment for fraction of genome proteins assigned. Folds were assigned to each of the predicted soluble 2,130 ORFs within the PA genome. Each sequence within the genome was assigned to the structure with the highest sequence–structure compatibility Z-score. Z-scores map to probability values via the Inset of A. Each bar shows the number of ORFs assigned as a function of probability value. Summing the bar chart (dark line) shows the fraction of the genome assigned a fold as a function of probability value. Summing the bar chart weighted by probability values shows the cumulative number of assignments predicted as a function of probability value (dashed line).
Notice that several of the scores for wrong matches are high. These “wrong” matches tend to be almost correct. We observe that some pairings denoted as dissimilar by our dali cutoff of 2 are actually considered to be similar by other structure comparison sets, such as SCOP and CATH (data not shown). To achieve a completely automated method, all assignments are made automatically by using dali, rather than integrating conflicting results from several different structure comparison methods.
Next we generate a confidence curve from which we can derive the probabilities of false alarm and correct assignment, given a sequence–structure compatibility score, Pfa and P (correct | Z-score > z), as shown in the Inset to Fig. 1A. The probability of false alarm is the probability that a given Z-score belongs to the set of Z-scores for incorrect (dissimilar) sequence–structure matches. Pfa is derived from the percent area under the curve of incorrect predictions that falls above a given Z-score threshold. We observe that the 99% cutoff falls at approximately a Z-score of 7.2 and the 90% cutoff falls at a cutoff around 4.0. The Inset to Fig. 1A allows us to assess our confidence in any sequence–structure match.
Automated Fold Assignment for the Genome of PA.
To assign folds to the genome of PA we must derive sequence–structure compatibility scores for the sequences of PA and then assign probabilities of correctness to each match. We use SDP (6) as described previously (20) to assign sequence–structure compatibility scores from the 2,130 nontransmembrane proteins from the PA genome to each of the 3,285 domain structures within the fold recognition library. Using the function shown in the Inset to Fig. 1A, we map each sequence–structure Z-score to an associated probability of correctness. Sequences were assigned to the fold with the highest Z-score match and hence the highest probability of correctness. The bar graph in Fig. 1B shows the distribution of sequences assigned as a function of probability value.
To give a measure of the fraction of a genome assigned as a function of the probability threshold, we sum the bar chart from the highest Z-score to our threshold, and divide by the number of sequences in the whole genome. Fig. 1B shows the chart of the fraction of the genome assigned as a function of assignment confidence.
We are interested not only in what percentage of assignments are above a given accuracy threshold but also in the cumulative fraction of the genome we expect to have assigned correctly as a function of probability value. We can derive this term by weighting the summed terms from our bar graph by their probability values. The curve showing the fraction of the genome expected to be assigned properly as a function of probability is shown by the dashed line in Fig. 1B. Note that the ratio of the solid line to the dashed line at a particular point is the cumulative confidence in our prediction as a function of probability. As noted on the figure, we were able to assign 916 proteins with a cumulative confidence level of 90% and 245 proteins with a cumulative confidence level of 99%.
Deriving Novel Fold Confidence.
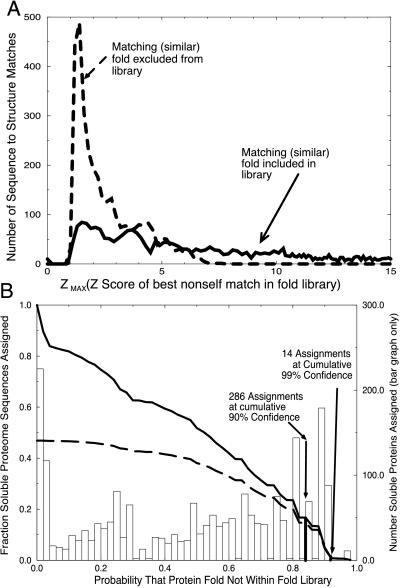
Next we estimate the probability that each sequence represents a novel fold. Our binary hypothesis has two cases, “assignment as novel is true,” or “assignment as novel is false.” To evaluate this hypothesis, we must define what it means for a Z-max score to be “truly novel” or “falsely novel.” To simulate the case of “truly novel” folds, we exclude from our fold library the structure for the given sequence, as well as all other structures that are similar (pairwise dali scores greater than or equal to 2). The distribution of Z-max scores for an exhaustive probing of the fold library where compatible structures have been removed is shown in Fig. 2A (dashed line). This represents what we expect to see for the set of “truly novel” folds.
Figure 2.
(A) Distribution of Z-max scores for similar folds included (solid line) and excluded (dashed line) from the fold library. Two distributions of maximum nonself Z-scores were obtained: one where a similar fold exists in the training set, and a second where similar structures have been excluded from the library. The separation between these two distributions shows that the Z-max score is a good indicator of the presence of similar folds in the library. (B) Probability of correct novel fold assignment for fraction of genome proteins assigned. The probability of a novel fold was determined for each soluble ORF product of PA. The bar chart shows the number of ORFs predicted to have novel folds as a function of probability value. The fraction of the genome predicted to be novel as a function of probability value is given by the solid curve obtained by summing the bar chart. A sum of the bar chart, weighted by probability value, shows the cumulative number of accurate predictions as a function of probability value (dashed line).
For the case of “falsely novel” folds, we exclude only the self structure, and examine the resulting distribution of Z-max scores. In our fold library, each fold was found to have a similar (by dali score) fold present, and therefore all of the sequences were considered “falsely novel.” The exhaustive set of these Z-max scores is shown by the solid line in Fig. 2A, and was used to determine the probability of false alarm (Pfa), which translates to a confidence curve (not shown) similar to the Inset for Fig. 1A. The set of “truly novel” Z-max scores is an essential check of the method, and it shows that the distribution of Z-max scores is greatly shifted to lower values when true structural matches are excluded.
To generate the probability of false alarm (Pfa) we look at Z-max scores that occur below a given threshold, and divide by the total number of Z-max scores. For example, there are 394 false-alarm Z-max scores that occur at or below a value of 1.3, out of a total of 3,285 Z-max scores. Thus, the value of Pfa for a novel fold at this Z-max score is 394/3,285, or 12%. This is the likelihood of falsely predicting a fold to be novel, when it is actually contained in the database. We observe that the 99% cutoff falls at approximately a Z-max score of 1.1 and the 90% cutoff falls at a cutoff around 1.3. Our continuous probability curve allows us to assign automatically a novelty confidence for each sequence in the genome of PA.
Automated Whole-Genome Prediction of Folds as Novel.
SDP sequence–structure compatibility scores from each PA sequence to each structure in our library were calculated for the automated fold assignment shown in Fig. 1B. From this set of sequence–structure scores we extracted the maximal score for each of the 2,130 nontransmembrane proteins within the genome. We next mapped each maximum sequence–structure Z-score to its associated probability of assuming a novel fold. The distribution of the number of PA sequences assigned as novel as a function of confidence is shown in the bar graph of Fig. 2B. As before, we are curious as to how many of the sequences in the PA genome can be assigned at different levels of certainty to be folds that are not represented in our fold library. This is shown by the sum of the bar graph from 1 to a given threshold, the solid line in Fig. 2B.
Also as before, we are interested not only in what percentage of the genome we are assigning as a function of probability value but also in the fraction of the genome that we cumulatively expect to assign correctly as a function of the probability value. We derive this term by weighting the summands from our bar graph by their probability values, as shown by the dashed line in Fig. 2B. We note that the ratio of the dark solid line to the dashed line at a particular point is the cumulative confidence in our prediction as a function of probability. The 90% and 99% cumulative confidence intervals are also indicated in Fig. 2B.
Sequence Analysis: Homology and Transmembrane Searches.
Having now assigned PA sequences to folds and found those PA sequences that most likely assume novel folds, we seek medically relevant sequences and sequences with a large number of homologs by using the Smith–Waterman algorithm against the OMIM disease database of 15,743 disease-related proteins. To find sequences with a large number of homologs a gapped-blast search of a large NRDB was performed.
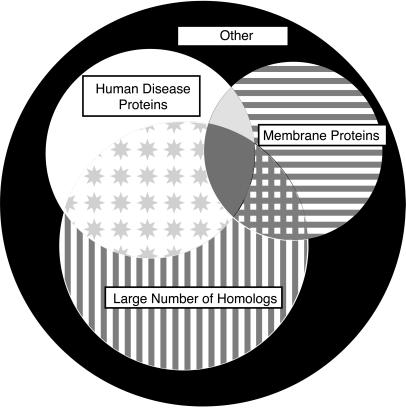
A Venn diagram describing the sequence analysis is shown in Fig. 3. Of the 2,681 PA ORFs, 2,130 (79%) are predicted not to contain membrane-spanning domains; additionally 1,075 (40%) had more than 4 homologs within the NRDB, and 759 (28%) had at least one sequence neighbor within the OMIM database at a significance level of 10−6. An attractive set of targets for structural genomics are those that have a large number of homologs within the NRDB and within OMIM but are not transmembrane proteins. The PA genome contains 422 such targets, representing 16% of the PA sequences.
Figure 3.
The 2,681 ORFs of the genome of PA partitioned into homologs of human disease proteins (208, 8%, white region), membrane-spanning proteins (320, 12%, horizontal line region), and proteins having >4 homologs in other organisms (482, 18%, vertical line region). Attractive initial targets for structural genomics are proteins without transmembrane regions, with human disease relevance, and having many homologs in other genomes (422, 16%, star region). Additional ORFs had both >4 homologs in other organisms and transmembrane helix regions (102, 4%, crosshatch region), or both human disease homologs and transmembrane helix regions (60, 2%, light gray region). A few proteins had >4 homologs in other organisms, and human disease homologs and transmembrane helix regions (69, 3%, darker gray region). There are 1,018 ORFs belonging to none of these categories (37%, black region).
Discussion
Comparison with Other Popular Fold Assignment Methods.
Attaching confidence levels to fold assignments has several advantages. It is not necessary to ignore portions of the genome because scores fall below an arbitrary threshold. Previous genome-wide fold assignment methods have cited percentages of proteins that were “successfully assigned.” We are able to assign a variable fraction of the genome as a function of probability cutoff. This permits independent researchers to weigh each prediction in conjunction with other knowledge about the protein. As the database of experimentally determined structures grows, changes in the confidence levels of assignments will make up-dates of the fold predictions increasingly informative.
In addition, previous methods of whole-genome fold assignment have incorporated “hand pruning” in making assignments (20–22). Although this was an effective initial method, the growing avalanche of sequences renders hand assignment impractical. The assignment scheme presented here was applied in a completely automated fashion, requiring no manual intervention.
For comparison, we also examined fold assignment based solely on sequence similarity. First, we used the optimal alignment algorithm of Smith and Waterman (8) with a GONNET substitution matrix (23). If we look at assignments given correctness estimates above 99% (as derived by SDP sequence–structure compatibility score), we find that Smith–Waterman searches can assign folds to only 50 sequences (data not shown); 8 times as many sequences were assigned by our methods.
Also for comparison, we examined fold assignment by psi-blast. This method, in combination with hand-pruning, has been used for several full-genome fold assignments (21, 24). To compare the SDP method to psi-blast, psi-blast was used to generate an exhaustive set of scores between the sequences of the fold library. The scoring was done in a fully automated fashion, as was the case with the SDP analysis. Standard recommended parameters were used for psi-blast, as described in Materials and Methods.
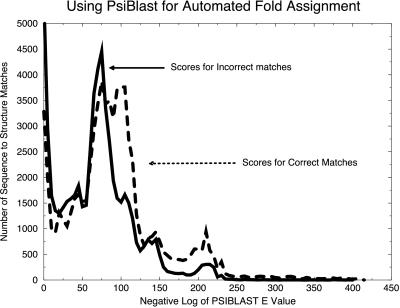
For analysis by binary hypothesis testing, the scores for psi-blast were divided into two sets, as shown in Fig. 4. The first set represents correct (similar) matches (dashed line), where the score represents a pair of sequences whose known structures are similar (dali score greater than 2). The second set of scores represents incorrect (dissimilar) matches (solid line). The separation of the two sets is not as clear as when binary hypothesis testing is applied to the SDP fold assignment method (Fig. 1A). Therefore, the confidence indicators for automated psi-blast assignments would not be as strong as those of the SDP method.
Figure 4.
A test of psi-blast for automated fold assignment. Using psi-blast with the SwissProt sequence database, we used 3,285 sequences from our training set to generate an exhaustive set of 10,784,656 (3,285 × 3,284) nonself sequence–sequence assignment pairs. Using binary hypothesis testing, we divided the resulting set of scores into two cases. For the set of correct matches (dashed line), the actual structures for the two sequences were similar as determined by a dali Z-score greater than or equal to 2. The set of incorrect matches is also shown (solid line). The reduced separation of these cases compared with the results for SDP shown in Fig. 1A implies that confidence intervals may be more difficult to generate by using psi-blast.
Targets for Structure Determination.
Table 1 shows 10 attractive targets for structure determination in the PA genome. They all have a high probability of being novel folds and are either a human disease homolog or posses a large number of NRDB homologs. In addition, they are not expected to contain transmembrane segments. The OMIM homologs of these PA proteins cover a wide range of functions, not simply categories such as metabolic pathways as might be expected. The top hits include homologs such as the small nuclear ribonucleoprotein polypeptide N and a family of ABC transporters. Interestingly, the PA protein GPA2230 has a high degree of homology to two domains of the human protein MDR1 (multidrug-resistance protein 1). Residues 1–65 (of 74 total) of GPA2230 are homologous to MDR1 from residue 541 to 606 (65% similarity) and from residue 1186 to 1252 (66% similarity). The regions of homology are in putative cytosolic regions of the 12-transmembrane-segment protein (25). Also in Table 1 are three PA proteins that are members of large families of conserved hypothetical proteins.
Table 1.
Ten PA proteins that represent attractive targets for structure determination
| PA ID | PA no. of amino acids | Z | P(N) | GenPept no. | OMIM no. | OMIM no. of amino acids | Match no. of amino acids | Function of closest NR/OMIM homolog | NRDB |
|---|---|---|---|---|---|---|---|---|---|
| GPA2549 | 80 | 1.1 | 0.99 | 806564 | 603541 | 80 | 60 (54%) | Small nuclear ribonucleoprotein | 5 |
| GPA2288 | 72 | 1.1 | 0.99 | 1708624 | 125855 | 735 | 30 (73%) | Diacylglycerol kinase, α | 0 |
| GPA2261 | 64 | 1.1 | 0.99 | Hypothetical family | 6 | ||||
| GPA2241 | 155 | 1.1 | 0.99 | Hypothetical family | 8 | ||||
| GPA1339 | 115 | 1.2 | 0.91 | 106985 | 170261 | 703 | 78 (67%) | TAP2 transporter, MHC | 215 |
| GPA2230 | 74 | 1.2 | 0.91 | 34525 | 171050 | 431 | 65 (66%) | Multidrug-resistance protein 1 | 1 |
| GPA2464 | 67 | 1.2 | 0.91 | 539960 | 145505 | 546 | 41 (54%) | Hypertension-associated SA | 15 |
| GPA542 | 135 | 1.2 | 0.91 | 3913830 | 172468 | 172 | 105 (48%) | AMP cyclohydrolase | 36 |
| GPA2413 | 75 | 1.2 | 0.91 | 2342473 | 160776 | 346 | 49 (57%) | Nonmuscle myosin | 0 |
| GPA2606 | 73 | 1.2 | 0.91 | Hypothetical family | 17 |
Each protein has a high probability of being a novel fold [P(N) > 90%]. Also, these proteins either are homologs of human disease-related proteins (OMIM database) or are members of large families of proteins of unknown function.
For some of the homologous human proteins, experimental structural information exists for regions of the protein that do not include the sequence alignment overlap with the PA protein (data not shown). This is true for the v-Jun avian sarcoma oncogene, where the structure (26) covers the DNA-binding region, residues 256–314. The PA protein match to the human protein covers the N terminus, residues 7–60. A similar situation occurs for myosin. The known structure of myosin has revealed the N-terminal “head” portion (27). The overlap of this PA protein with myosin occurs in the rod-like tail domain.
To date, more than 240 PA genes have been cloned for crystallographic analysis. A structure has been published for the PA protein translation initiation factor 5A, PDB code 1bkb (28). The sequence of this protein, GPA1979, scored with an assignment confidence of 48%. The predicted structure, 2rsp, is actually a different fold than the closest structure, 1mjc. 2rspb has a “complex topology,” whereas 1mjc contains a Greek key motif. However, there is still structural similarity between the prediction and the closest structural homolog, 1mjc. Both proteins are all β. 1mjc is a six-stranded β-sheet, whereas 2rsp is a five-stranded β-sheet. The shear number, the extent to which the strands in the sheet are staggered, is 10 in both proteins. Although our prediction is clearly not completely correct, it can be argued that the accuracy associated with the prediction (48%) in a sense describes how correct the prediction is.
An example of our method's success is found in protein GPA2549, a putative small nuclear ribonucleoprotein predicted by these methods to have a 99% chance of being a novel fold (Table 1). Independent of our analysis, the structures of four homologous human proteins were determined by Kambach et al. (29). These human proteins share 45% sequence identity with GPA2549 and form a novel α/β fold with a strongly bent β-sheet. The coordinates of these proteins were not available when the training set was constructed. This example of a correctly predicted novel fold suggests that experimental structures of other proteins from Table 1 may help fill in our universal fold library.
Acknowledgments
We thank Mike Thompson, Melinda Balbirnie, Enoch Huang, Jay Ponder, and Robert Grothe for discussion. This work was supported in part by the Department of Energy. The work of P.M. was funded in part by Institutional National Research Service Award GM08375 from the National Institute of General Medical Sciences.
Abbreviations
- blast
Basic Local Alignment Search Tool
- NRDB
nonredundant sequence database
- OMIM
Online Mendelian Inheritance in Man
- PA
Pyrobaculum aerophilum
- PDB
Protein Data Bank
- psi-blast
position-specific iterated blast
- SDP
Sequence Derived Properties
Footnotes
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.050589297.
Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.050589297
References
- 1.Fitz-Gibbon S, Choi A J, Miller J H, Stetter K O, Simon M I, Swanson R, Kim U J. Extremophiles. 1997;1:36–51. doi: 10.1007/s007920050013. [DOI] [PubMed] [Google Scholar]
- 2.Holm L, Sander C. Trends Biochem Sci. 1995;20:478–480. doi: 10.1016/s0968-0004(00)89105-7. [DOI] [PubMed] [Google Scholar]
- 3.Holm L, Sander C. Nucleic Acids Res. 1996;24:206–209. doi: 10.1093/nar/24.1.206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Holm L, Sander C. Nucleic Acids Res. 1997;25:231–234. doi: 10.1093/nar/25.1.231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Holm L, Sander C. Nucleic Acids Res. 1998;26:316–319. doi: 10.1093/nar/26.1.316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fischer D, Eisenberg D. Protein Sci. 1996;5:947–955. doi: 10.1002/pro.5560050516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eisenberg D, Weiss R M, Terwilliger T C. Proc Natl Acad Sci USA. 1984;81:140–144. doi: 10.1073/pnas.81.1.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Smith T F, Waterman M S. J Mol Biol. 1981;147:195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- 9.Waterman M, Vingron M. Stat Sci. 1994;9:367–381. [Google Scholar]
- 10.Waterman M S, Vingron M. Proc Natl Acad Sci USA. 1994;91:4625–4628. doi: 10.1073/pnas.91.11.4625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Altschul S F, Madden T L, Schäffer A A, Zhang J, Zhang Z, Miller W, Lipman D J. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Altschul S F, Gish W, Miller W, Myers E W, Lipman D J. J Mol Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- 13.Gish W, States D J. Nat Genet. 1993;3:266–272. doi: 10.1038/ng0393-266. [DOI] [PubMed] [Google Scholar]
- 14.Karlin S, Altschul S F. Proc Natl Acad Sci USA. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rost B, Sander C, Schneider R. Comput Appl Biosci. 1994;10:53–60. doi: 10.1093/bioinformatics/10.1.53. [DOI] [PubMed] [Google Scholar]
- 16.Hobohm U, Sander C. Protein Sci. 1994;3:522–524. doi: 10.1002/pro.5560030317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hobohm U, Scharf M, Schneider R, Sander C. Protein Sci. 1992;1:409–417. doi: 10.1002/pro.5560010313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Murzin A G, Brenner S E, Hubbard T, Chothia C. J Mol Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- 19.Bowie J U, Lüthy R, Eisenberg D. Science. 1991;253:164–170. doi: 10.1126/science.1853201. [DOI] [PubMed] [Google Scholar]
- 20.Fischer D, Eisenberg D. Proc Natl Acad Sci USA. 1997;94:11929–11934. doi: 10.1073/pnas.94.22.11929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huynen M, Doerks T, Eisenhaber F, Orengo C, Sunyaev S, Yuan Y, Bork P. J Mol Biol. 1998;280:323–326. doi: 10.1006/jmbi.1998.1884. [DOI] [PubMed] [Google Scholar]
- 22.Rychlewski L, Zhang B, Godzik A. Folding Des. 1998;3:229–238. doi: 10.1016/S1359-0278(98)00034-0. [DOI] [PubMed] [Google Scholar]
- 23.Gonnet G H, Cohen M A, Benner S A. Science. 1992;256:1443–1445. doi: 10.1126/science.1604319. [DOI] [PubMed] [Google Scholar]
- 24.Wolf Y I, Brenner S E, Bash P A, Koonin E V. Genome Res. 1999;9:17–26. [PubMed] [Google Scholar]
- 25.Chen C J, Chin J E, Ueda K, Clark D P, Pastan I, Gottesman M M, Roninson I B. Cell. 1986;47:381–389. doi: 10.1016/0092-8674(86)90595-7. [DOI] [PubMed] [Google Scholar]
- 26.Glover J N, Harrison S C. Nature (London) 1995;373:257–261. doi: 10.1038/373257a0. [DOI] [PubMed] [Google Scholar]
- 27.Rayment I, Rypniewski W R, Schmidt-Base K, Smith R, Tomchick D R, Benning M M, Winkelmann D A, Wesenberg G, Holden H M. Science. 1993;261:50–58. doi: 10.1126/science.8316857. [DOI] [PubMed] [Google Scholar]
- 28.Peat T S, Newman J, Waldo G S, Berendzen J, Terwilliger T C. Structure. 1998;6:1207–1214. doi: 10.1016/s0969-2126(98)00120-8. [DOI] [PubMed] [Google Scholar]
- 29.Kambach C, Walke S, Young R, Avis J M, de la Fortelle E, Raker V A, Lührmann R, Li J, Nagai K. Cell. 1999;96:375–387. doi: 10.1016/s0092-8674(00)80550-4. [DOI] [PubMed] [Google Scholar]