Calcium-sensitive MRI contrast agents based on superparamagnetic iron oxide nanoparticles and calmodulin

Abstract

We describe a family of calcium indicators for magnetic resonance imaging (MRI), formed by combining a powerful iron oxide nanoparticle-based contrast mechanism with the versatile calcium-sensing protein calmodulin and its targets. Calcium-dependent protein–protein interactions drive particle clustering and produce up to 5-fold changes in T2 relaxivity, an indication of the sensors' potency. A variant based on conjugates of wild-type calmodulin and the peptide M13 reports concentration changes near 1 μM Ca²⁺, suitable for detection of elevated intracellular calcium levels. The midpoint and cooperativity of the response can be tuned by mutating the protein domains that actuate the sensor. Robust MRI signal changes are achieved even at nanomolar particle concentrations (<1 μM in calmodulin) that are unlikely to buffer calcium levels. When combined with technologies for cellular delivery of nanoparticulate agents, these sensors and their derivatives may be useful for functional molecular imaging of biological signaling networks in live, opaque specimens.

Calcium ions (Ca²⁺) have been a favorite target in molecular imaging studies because of the important role of calcium as a second messenger in cellular signaling pathways. Fluorescent calcium sensors are used widely in optical imaging, both at the cellular level and at the cell population level. Calcium-sensitive dyes have recently been used in conjunction with laser scanning microscopy to follow neural network activity in small, three-dimensional brain areas (1) and to characterize patterns of interaction among cells in developing vertebrate embryos (2). Because of the scattering properties of dense tissue, high-resolution optical approaches like these are usually limited to superficial regions of specimens and to restricted fields of view (3). To probe calcium dynamics more globally in living systems, a different imaging modality must be used.

Magnetic resonance imaging (MRI) is an increasingly accessible technique for imaging opaque subjects at fairly high spatial resolution, and MRI studies of calcium dynamics could, in principle, complement optical approaches by offering both greatly expanded coverage and depth penetration in vivo (4). Calcium isotopes are unsuitable for direct imaging by magnetic resonance, so attempts to sensitize MRI to calcium have focused around the use of molecular imaging agents. Fluorinated derivatives of the bivalent cation chelator 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA) have permitted calcium measurements in vivo by ¹⁹F MRI but only at ≈10⁻⁵ the sensitivity of standard MRI methods (5, 6). Two potentially more powerful proton T1 relaxation-promoting contrast agents were subsequently introduced. The paramagnetic ion manganese (Mn²⁺) mimics calcium by entering cells through calcium channels. Because it accumulates much faster than it is removed, Mn²⁺ produces an “integral” of calcium signaling history that can be detected as brightening in T1-weighted images (7). A gadolinium complex synthesized by Meade and colleagues (8) acts as a T1 calcium sensor analogous to BAPTA-based probes and may be more compatible with time-resolved calcium imaging than are either Mn²⁺ or ¹⁹F-BAPTA.

A general limitation of MRI molecular imaging strategies is the relative insensitivity of the method to most molecular probes (9). With conventional paramagnetic contrast agents and typical measuring conditions, 10–100 μM concentrations are required for robust visualization (compared with <1 μM for most fluorophores or picomolar quantities for nuclear imaging tracers). For this reason, considerable interest has focused on the use of superparamagnetic iron oxide nanoparticles (SPIOs) (10). SPIO contrast agents are large macromolecules of ≤50 nm radius, containing small crystals of permanently magnetized material. These agents can be detected by T2-weighted imaging at submicromolar particle concentrations and at total iron concentrations an order of magnitude below conventional sensitivity limits. The first SPIO-based MRI sensors were produced by Weissleder and colleagues (11, 12), who synthesized a series of probes for oligonucleotide and protein interactions. These agents produce dramatic T2 contrast changes due to reversible aggregation of appropriately functionalized SPIOs. Here, we describe a potent, tunable MRI calcium sensor family that combines the advantages of SPIO agents with protein-based mechanisms used previously in the construction of fluorescent calcium probes (13).

Results and Discussion

Calcium Sensor Principle.

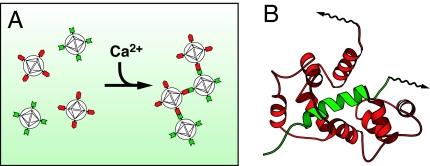
The microscopic spatial distribution of SPIO particles has a great effect on their ability to influence local T2 relaxation rates in aqueous media (11, 14). This principle was used recently to construct a number of SPIO-based sensors for protein and nucleic acid interactions (15). In each case, the formation or disruption of an interaction of interest resulted in a change in the aggregation state of SPIO particles conjugated to the interacting moieties; remarkably large concomitant changes in T2 contrast were observed by MRI. We were interested in whether a similar effect could be coupled to changes in calcium concentration to produce a calcium sensor. A number of proteins are known to associate and dissociate reversibly as a function of calcium concentration (16). Some of the best-studied calcium-dependent interactions take place between the calcium-binding protein calmodulin (CaM) and a series of short basic target peptides (17), most prominently a sequence (M13) derived from rabbit skeletal muscle myosin light chain kinase (18). Reversible calcium-dependent binding of CaM and M13 domains can be detected in cells by fluorescent methods (13, 19). We therefore predicted that if CaM and M13 were conjugated separately to two distinct SPIO populations, a binary mixture of the two species could aggregate selectively in the presence of calcium and could thus constitute an MRI calcium reporter (Fig. 1).

Fig. 1.

Calcium sensor mechanism. (A) SA-MACS-CaM (red) and SA-MACS-M13 (green) nanoparticles form binary aggregates in the presence, but not the absence, of calcium. SPIO aggregation is predicted to lead to T2 changes. (B) The calcium-dependent interaction of CaM (red) and M13 (green) polypeptides underlies the aggregation effect, which requires that each nanoparticle be polydentate in one of these proteins. Protein surfaces are biotinylated (arrows) and attached to SPIOs via tight biotin/streptavidin binding.

We used commercially available SPIO nanoparticles coated with the Streptomyces avidinii protein streptavidin (SA-MACS; Miltenyi Biotec, Auburn, CA). These particles have an overall diameter of 20–100 nm and contain roughly 50% Fe₂O₃ with core diameters of ≈10 nm (20). The particles have a T2 relaxivity (the slope of T2 relaxation rate vs. concentration) of 410 ± 10 s⁻¹ mM⁻¹ Fe (mean ± SEM) at 4.7 T and little measurable T1 relaxivity, and they contain roughly 60 biotin-binding sites per nanoparticle (see Supporting Text, which is published as supporting information on the PNAS web site). To construct calcium sensors based on the SA-MACS nanoparticles, biotin-CaM and biotin-M13 were produced and conjugated to the functionalized SPIOs. To test the generality of the proposed CaM-based sensor mechanism, we also produced conjugates by using a second CaM target peptide, RS20, which is related to M13 but is derived from smooth muscle myosin light chain kinase. Once produced, SA-MACS-CaM, SA-MACS-M13, and SA-MACS-RS20 were stable in 0.1% BSA for up to 1 week at 4°C.

Calcium-Dependent Aggregation of SPIO Conjugates.

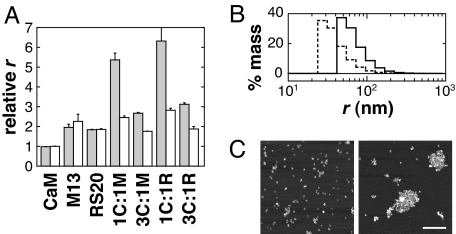
We first characterized calcium-dependent aggregation behavior of the SPIO conjugates by dynamic light scattering (DLS). Fig. 2A shows relative average hydrodynamic radii measured for SA-MACS-CaM, SA-MACS-M13, SA-MACS-RS20, and binary mixtures, recorded in 500 μM CaCl₂ (gray bars) or 500 μM EDTA (white bars), with SPIO concentrations totaling 7.9 mg/liter Fe. In no case did the measured mean radius of the unmixed conjugate species display calcium dependence. M13- and RS20-conjugated particles displayed somewhat larger radii than SA-MACS-CaM, presumably due to a weak tendency of these particles to self-associate in solution. Because of the predicted dependence of binary aggregation phenomena on particle stoichiometry, we made four versions of sensor, varying both the ratio of CaM-conjugate SPIOs to target conjugates and the identity of the CaM target sequence. Sensors 3C:1M and 1C:1M refer to mixtures of SA-MACS-CaM with SA-MACS-M13 in 3:1 and 1:1 molar ratios, respectively; 3C:1R and 1C:1R refer to the corresponding sensors incorporating RS20 instead of the M13 peptide. Under calcium-free conditions, the 1:1 sensors gave rise to mean radii slightly larger than the SA-MACS-M13 or SA-MACS-RS20 particles alone, whereas the 3:1 sensors in EDTA had radii close to the average unmixed particle radius.

Fig. 2.

Light-scattering and AFM analysis of calcium-dependent behavior of the SPIOs conjugates. (A) Mean particle radii are graphed for SA-MACS-CaM, SA-MACS-M13, SA-MACS-RS20, and binary mixtures. CaM conjugates mixed in 1:1 ratio with M13 and RS20 conjugates are denoted 1C:1M and 1C:1R, respectively; 3:1 ratios are denoted 3C:1M and 3C:1R. Radii are expressed relative to the radius of SA-MACS-CaM for each mixture in 500 μM CaCl₂ (gray bars) and 500 μM EDTA (white bars). Error bars denote SEM (n = 3). Strong calcium-dependent effects are observed for all mixed SPIO samples. Ratios of 1:1 produce the largest aggregates but also show a tendency toward calcium-independent clustering. 3:1 binary sensors show little aggregation in the EDTA condition but still display a robust calcium-induced response. (B) Size distributions of the 3C:1M sensor in 500 μM EDTA (dotted line) and 500 μM CaCl₂ (solid line). Distribution histograms were calculated from DLS data, assuming polydisperse but monomodal size populations, and represent the percentage mass estimated in each size interval. (C) Atomic force micrographs of 3C:1M samples obtained after preincubation in 50 μM EDTA (Left) or 50 μM CaCl₂ (Right) and indicating a change in clustering. (Scale bar: 500 nm.)

All of the sensor variants showed a significant increase in relative radius in the presence of 500 μM CaCl₂, compared with the calcium-free condition. Sensors 1C:1M and 1C:1R gave increases approximately by a factor of 2, whereas with 3C:1M and 3C:1R the increase was by a factor of roughly 1.5. The measurements reported in Fig. 2A were obtained after 60-min incubation times; after longer incubations, 1C:1M and 1C:1R continued to aggregate, whereas the 3:1 sensors remained steady. Fig. 2B shows histograms of the (mass-weighted) particle size distributions exhibited by the 3C:1M sensor in the presence and absence of calcium; the distributions were calculated from DLS data, assuming spherical particle geometry and monomodal but polydisperse distribution of sizes. The distribution maximum shifts from a radius of roughly 30 nm to a radius near 50 nm when calcium is added, corresponding reasonably with the increase in mean size reported in Fig. 2A.

These DLS results were reinforced by direct visualization of dissociated and aggregated particles with atomic force microscopy (AFM). Fig. 2C shows AFM images of 3C:1M binary mixtures (20 mg/liter Fe), preincubated for 1 h in 50 μM EDTA or 50 μM CaCl₂ solutions before sample preparation. The image obtained in the absence of calcium (Fig. 2C Left) shows individual nanoparticles and small clusters distributed over the surface of the mica substrate. In the calcium-containing sample (Fig. 2C Right), the mean cluster size is significantly larger, although small clusters are still visible. The clusters are also sparser because a constant number of nanoparticles are now distributed among fewer aggregates than in the calcium-free condition. Similar results were obtained for 3C:1R (data not shown). Note that differences in the precise aggregate size distributions recorded by DLS and AFM could have arisen because of the altered conditions required for optimal AFM imaging: higher SPIO concentration and adhesion to mica. Nonetheless, both of these techniques clearly indicate that the presence of calcium ions drives particle clustering and increases the mean size of SPIO aggregates observed after incubation.

MRI Signal Changes in Response to Calcium.

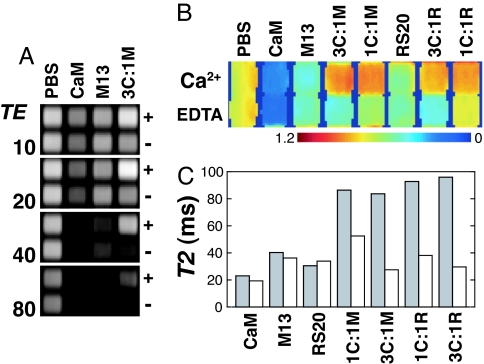
SPIO calcium sensors based on CaM/M13 or CaM/RS20 interactions were investigated by MRI, and extremely robust calcium-dependent contrast changes were observed. We used a spin echo pulse sequence with multiecho acquisition to collect images at several echo times in parallel. Fig. 3A shows images of a microtiter plate containing CaM and M13 conjugates, obtained at echo times of 10, 20, 40, and 80 ms with this approach and with a SPIO concentration again of 7.9 mg/liter Fe. The images indicate that the MRI signal from wells containing 3C:1M is significantly greater when calcium is present and that the effect is most pronounced at longer echo time (TE), while still maintaining excellent signal-to-noise ratio. Wells containing buffer (PBS), CaM conjugates alone, or M13 conjugates alone show signal that is independent of calcium. The MRI signal falls off fastest as a function of TE for SA-MACS-CaM, consistent with the fact that the CaM conjugate SPIOs have the smallest mean radius in solution. Control experiments indicated that the contrast changes were not a function of slice position and are thus unlikely to result from settling or precipitation of particles in the samples for which signal increases were observed (see Fig. 6, which is published as supporting information on the PNAS web site).

Fig. 3.

T2 relaxation rate changes measured by MRI. (A) SPIO conjugates were arrayed into microtiter plates and imaged by MRI. A spin echo pulse sequence was used with Carr-Purcell-Meiboom-Gill (CPMG) acquisition to collect images at multiple echo times for each excitation (see Materials and Methods for details). The four images shown indicate signal dependence on TE for PBS buffer, SA-MACS-CaM, SA-MACS-M13, and a calcium sensor formed by mixing these two species in a 3:1 ratio, each in the presence of either 500 μM Ca²⁺ (+) or 500 μM EDTA (−). Unmixed CaM conjugates have the highest relaxivity and produce the most diminished signal at high echo times. The calcium sensor shows high relaxivity in the absence of calcium but not when calcium is present, where the signal remaining at 80 ms TE for the sensor is comparable to that observed for PBS alone. All SPIO solutions contained 7.9 mg/liter Fe. (B) Normalized T2-weighted MRI signal observed for PBS; for unmixed SPIO conjugates with CaM, M13, and RS20; and for the sensor variants described in Results and Discussion: 3C:1M, 1C:1M, 3C:1R, and 1C:1R. For each species, the top row shows signal observed in the presence of 500 μM CaCl₂, and the bottom row presents signal in 500 μM EDTA. This image was obtained by dividing MRI intensities observed at TE = 30 ms by intensities at TE = 10 ms. (C) T2 values obtained by fitting monoexponential decay curves to MRI signal as a function of TE (odd echoes only: TE = 10, 30, 50, and 70 ms), using the data from A and B. For each solution, the T2 observed in the presence (gray bars) and absence (white bars) of calcium is reported. Calcium-dependent T2 changes are greatest for the 3:1 conjugate ratio calcium sensors 3C:1M and 3C:1R.

Fig. 3B shows the relative T2-weighted MRI signal observed for all of the mixtures we investigated by DLS. This normalized image was obtained by dividing the raw image intensities observed at 30 ms TE by the signal at 10 ms TE and removes potential effects of volume inaccuracies and some sources of MRI sensitivity variation across the field of view (small effects due to excitation inhomogeneity remain, however). The image shows that all sensor variants display significantly greater MRI signal in 500 μM CaCl₂ than in 500 μM EDTA. The signal changes observed for 3C:1M and 3C:1R were greater than those observed for 1C:1M and 1C:1R, mainly because the 1:1 mixtures displayed relatively large signals in EDTA. These data indicate that calcium sensors producing the greatest MRI contrast changes can be formed by mixing CaM and target conjugate SPIO populations in an asymmetric ratio. Fig. 3C shows the T2 values obtained by fitting exponential curves to the multiecho image data from the samples shown in Fig. 3B. The values coincide with the imaging results in showing that the greatest MRI changes are produced by calcium sensors with a 3:1 particle ratio and that the T2 changes by a factor of 2 to 3 for these sensors under the conditions used.

T2 relaxivity (R2) for each sensor variant in the presence and absence of calcium was estimated from the data of Fig. 3 (also see Fig. 7, which is published as supporting information on the PNAS web site). R2 was found to be negatively correlated (r² = 0.84) with increasing mean diameter up to particle clusters about three times the diameter of SA-MACS-CaM; at this size, aggregates have fairly low relaxivity that remains undiminished for larger aggregates. Residual scatter in the data may be due to measurement errors, as well as to variability in the density and geometry of the different aggregates, which are predicted to influence relaxivity. For the 3C:1M sensor, R2 was estimated to be 220 s⁻¹ mM⁻¹ Fe in the calcium-free condition and 45 s⁻¹ mM⁻¹ Fe in 1 mM CaCl₂; for 3C:1R, the R2s were 200 and 34 s⁻¹ mM⁻¹ Fe in calcium-free and calcium conditions, respectively. These roughly 5-fold relaxivity changes are significantly greater than the approximately 2-fold R1 changes reported (8) for T1-based MRI ion sensors.

MRI measurements collectively show that calcium-induced clustering of our sensors corresponds to decreases in T2 relaxivity (producing greater T2-weighted MRI signal), in contrast to results obtained with smaller mononuclear iron oxides (11). This effect was general among variants of our sensor and could also be produced by calcium-independent clustering of the SPIOs we used. In the presence of stoichiometric quantities of polyvalent biotin-dextran, uncomplexed SA-MACS showed a pronounced increase in hydrodynamic radius and a 2- to 3-fold decrease in T2 relaxivity (data not shown). An inverse relationship between iron oxide cluster size and T2 relaxation rates has been described previously (21) and explained by the extensive theoretical work of Gillis and colleagues (22–24). For colloidal suspensions of fixed iron oxide volume fraction, the particle size-dependence of T2 relaxivity depends on the quantity δωR²/D, where δω is the change in (angular) NMR frequency at the particle equator, R is the radius of the cluster, and D is the self-diffusion coefficient. For SPIO solutions in which δωR²/D < 1, both T2 and T2* shorten with increasing R, whereas for δωR²/D > 1 (sometimes referred to as the “static dephasing” regime) T2 increases with R, and T2* remains roughly constant at a minimum value. Three arguments support the conclusion that the aggregation-dependent T2 changes we report correspond to the static dephasing regime. First, our clusters have average radii >25 nm, at which δωR²/D is predicted to be 8.1 or greater, based on a D of 2.3 μm²/ms and δω of 3.4 × 10⁷ rad/s for magnetite and assuming that cores are distributed throughout each particle. Second, we observe a systematic increase in T2 with increasing cluster size, as diagrammed in Fig. 7. Third, we observe negligible differences in T2* between clustered and dispersed SPIOs (see Fig. 8, which is published as supporting information on the PNAS web site), as predicted under static dephasing conditions.

Time Course and Reversibility of Changes in Size and T2 Relaxivity.

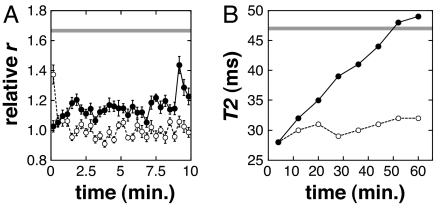
The time course and reversibility of calcium-dependent SPIO conjugate aggregation were investigated by using serial DLS measurements, after manual mixing. Fig. 4A shows a representative series of measurements obtained after dilution of a 3C:1M sensor, preincubated for 1 h in 100 μM EDTA, into a final concentration of 500 μM CaCl₂ (filled circles). An increase in average size of 10–20% in the first few tens of seconds (from the starting value of 1.0) is followed by a slower increase toward the steady-state distribution of hydrodynamic radii. In contrast, EDTA-induced disaggregation of clustered particles preincubated in 100 μM CaCl₂ is significantly faster (open circles) and returns almost completely to a relative r of 1.0 within a few seconds. A control dilution of these clustered particles into 100 μM CaCl₂ results in a steady distribution of clusters, with the mean radius indicated by the horizontal gray line in the figure. Similar results were obtained when aggregation and disaggregation of the 3C:1R sensor were studied by DLS. These data show that the calcium response of CaM-based SPIO aggregation sensors is initiated quickly and is fully reversible but that the aggregation process requires considerable time to reach equilibrium.

Fig. 4.

Time courses and reversibility of calcium-dependent changes. (A) Representative time courses of particle association and dissociation for the 3C:1M aggregation-based calcium sensor. To measure association (filled circles), 3C:1M mixed particles were preincubated in 100 μM EDTA for 1 h before dilution into a final concentration of 500 μM CaCl₂. To measure dissociation (open circles), particles were premixed in 100 μM CaCl₂ and diluted into 500 μM EDTA. The horizontal gray line approximates the starting point for disaggregation, measured by diluting particles preincubated in 100 μM CaCl₂ into the same buffer before DLS. (B) Time courses of changes in T2 relaxation time after calcium-induced aggregation and EDTA-induced disaggregation. Preincubations and dilutions were performed as for the DLS experiments in A, but larger volumes were used. Filled circles correspond to dilution from EDTA into calcium, and open circles correspond to dilution from CaCl₂ to EDTA. Measurements were taken continuously over 1 h using the methods of Fig. 3, with each image requiring 8 min to acquire and a mixing and setup dead time of 4 min. The horizontal gray line approximates the initial T2 of disaggregating SPIOs, again measured by control dilution of particles in 100 μM CaCl₂.

The time courses of calcium-dependent changes in T2 were measured by MRI after mixing, using the same conditions as in Fig. 4A. After dilution of 3C:1M sensors from EDTA into 500 μM CaCl₂, increases in T2 began immediately and continued approximately linearly over the course of an hour (Fig. 4B, filled circles), corresponding to gradually decreasing changes in relaxivity over time. When 3C:1M sensors preincubated in calcium were diluted back into 500 μM EDTA, however, the measured T2 dropped back to near its initial value within the dead time of the experiment (4 min) and then remained roughly constant (Fig. 4B, open circles). Similar evolution of T2 during aggregation and disaggregation was also observed with the 3C:1R sensor. These results show that changes in T2, such as particle aggregation, are reversible but slow to reach equilibrium in the presence of elevated calcium.

Calcium Detection Range and Tuning of the Sensor.

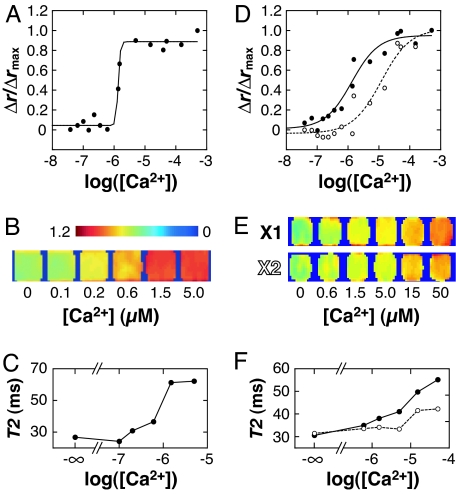
We determined the midpoint (EC₅₀) of the calcium-induced sensor responses by measuring DLS and MRI signals as a function of calcium concentration. Fig. 5A is a representative titration curve showing intensity-weighted mean DLS radii obtained with the 3C:1M sensor; the EC₅₀ observed for this sensor was 1.4 ± 0.1 (n = 3). Samples spanning a range of calcium concentrations were also imaged by MRI (Fig. 5B) using the methods of Fig. 3. The MRI signal and corresponding T2s (Fig. 5C) follow the DLS titration curve fairly closely, with an apparent transition midpoint near 1 μM Ca²⁺. The resting concentration of calcium in most cells is near 0.1 μM, and ionic influx associated with signal transduction typically creates local concentrations from 1 to 10 μM Ca²⁺; therefore, the calcium sensitivity of the described reagent is well suited to detecting concentration fluctuations near the lower end of this range.

Fig. 5.

Calcium sensitivity range and tuning of calcium sensor variants. (A) Calcium titrations were performed to determine the EC₅₀ of the SPIO calcium sensor variants. EGTA-buffered solutions were used for 0–1.35 μM and 39 μM Ca²⁺ concentrations, and unbuffered calcium solutions were used for the remainder of concentrations in the 1.5–500 μM range. The EC₅₀ determined for 3C:1M from three independent titrations (one shown here) was 1.4 ± 0.1 μM Ca²⁺. (B) A normalized MRI image analogous to Fig. 3B, showing relative signal obtained from 7.9 mg/liter 3C:1M sensor in the presence of 0–5.0 μM calcium ions. The transition in signal amplitude occurs near 1 μM, as indicated by the DLS data. (C) T2 values computed from the MRI data of B. (D) Calcium titration of sensors constructed from mutant XCaM proteins 3X1:1M (filled circles) and 3X2:1M (open circles). The mutant CaM used in the 3X2:1M sensor has a lower affinity for the M13 sequence; coupling between calcium sensitivity and binding affinity is likely to reduce this variant's calcium-binding affinity (EC₅₀ of 10 ± 2 μM, n = 2). (E) MRI signal intensity at calcium concentrations from 0 to 15 μM (TE = 40 ms, normalized as in B but with color scale from 0 to 0.8). The 3X1:1M variant shows similar behavior to 3C:1M but with more gradual transition in intensity with increasing [Ca²⁺], as in the DLS titration curve. Variant 3X2:1M shows transition onset at a higher calcium concentration, and even at 15 μM Ca²⁺ has apparently not reached a saturated response. (F) T2 values computed from the image data of E, for sensor variants 3X1:1M (filled circles) and 3X2:1M (open circles).

Manipulation of the calcium sensitivity of our SPIO sensors is convenient because of the ease with which CaM and CaM-target domains can be modified using standard molecular biology techniques. Fig. 5D shows calcium titration curves measured by DLS for SA-MACS-based calcium sensors formed by conjugating two mutants of recombinant Xenopus CaM (XCaM) to SPIOs instead of to the wild-type bovine CaM used in the experiments reported above. The solid curve (filled circles) represents data from a 3:1 binary sensor (3X1:1M) made from conjugates with M13 and XCaM E104Q (13), a CaM mutant with broadened calcium sensitivity (EC₅₀ of 0.8 ± 0.3 μM, n = 3). The dashed curve (open circles) represents data from an analogous sensor (3X2:1M) formed with an XCaM mutant (S81R/E83K/E87R/E104Q) further modified to reduce its affinity for the M13 peptide (25). Because protein complex formation and calcium binding are linked processes, this variant also exhibits lower calcium affinity (EC₅₀ of 10 ± 2 μM, n = 2) than 3X1:1M. Both titration curves for 3X1:1M and 3X2:1M appear to show less cooperative calcium binding (a gentler sigmoidal transition) than is the case for the bovine CaM-based sensor 3C:1M. This difference is probably due to the calcium site substitutions present in the CaM variants used in these sensors. The calcium-binding properties of wild-type and mutant CaM proteins affect the aggregation phenomena we observe by means of kernels for binary aggregation and fragmentation events, which in turn depend on the rate constants for intermolecular association and dissociation between CaM and its targets (26).

The MRI scans in Fig. 5E, and corresponding T2 values in Fig. 5F, show that the sensitivity changes apparent in the DLS titration curves are also reflected in the calcium dependence of T2 relaxation for these conjugates. T2 changes for the 3X1:1M sensor are again apparently less cooperative as a function of [Ca²⁺] than those for wild-type bovine CaM (Fig. 5C), and T2 changes reported for the 3X2:1M variant begin at higher calcium concentrations. The DLS and MRI data from variant sensors, therefore, show collectively that the appropriate incorporation of protein mutations can alter either the cooperativity or the EC₅₀ of calcium binding, optimizing the sensor for reporting in different Ca²⁺ concentration ranges. Mutagenesis of the sensor components may also alter the sensor's propensity to cross-react with endogenous CaM-related proteins in vivo (25).

MRI Applications of SPIO-Based Calcium Sensors.

The absolute T2 relaxivity and calcium-dependent T2 relaxivity changes observed for the described SPIO-based sensors are conducive to applications in MRI studies with <5 mg/liter (90 μM) Fe present, corresponding to particle concentrations on the order of 1 nM and calcium-binding site concentrations of 0.2 μM for the 3C:1M or 3C:1R sensors (assuming optimal conjugation and four Ca²⁺ sites per CaM). The calcium-binding ratio (κ_B) of sensors at this concentration is, therefore, ≈0.2, which is much lower than the endogenous calcium-binding ratios (κ_S ≈ 10–1,000) typically observed in cells (27). The low quantities of agent required for MRI-based detection are, therefore, unlikely to influence endogenous calcium dynamics, in contrast to typical small-molecule calcium sensors (28). On the other hand, the relatively slow response rates of the SPIO sensors to changes in calcium will not permit detection of individual short-lived calcium transients (≈50 ms) or fast fluctuations common to neurons and other signaling cells. Rather, current forms of the sensors may be appropriate for monitoring integrated calcium levels (0.1–1.0 μM Ca²⁺) that vary over several minutes, either in response to slow biological events (e.g., calcium waves in developing embryos) or during relatively long stimulation epochs. To improve the response kinetics, it may be possible to conjugate the same protein moieties to smaller iron oxide particles and to vary the conjugation level (26). Signal processing techniques (high-pass filtering) may also help to resolve more rapid components of the sensors' responses to calcium concentration changes during MRI time series.

Intracellular applications of the SPIO conjugate sensors we describe may initially require microinjection into cells, but several studies show that strategies for less-invasive delivery could soon be practical (29, 30). Once they are in cells, the sensors still face influences that may impede their calcium-dependent response properties. First, the proteins that actuate the agents (CaM, M13, and RS20) could interact with endogenous analogs whose binding to the sensor competes with particle aggregation. Endogenous CaM is expected to pose the greatest “threat” in this regard because its intracellular concentration can sometimes be >1 μM (31–33). To address this problem, our laboratory has adopted a mutational approach similar to one used recently to modify fluorescent CaM-based calcium sensors (25, 34). Second, although the sensors will be targeted to cell cytoplasms, it is possible that some may be trapped in endosomes or other compartments where they cannot function properly. To overcome this barrier, higher concentrations of the sensor may be required, and calcium-dependent signal changes may be attenuated by T2 relaxation resulting from inappropriately localized sensor particles (as well as intrinsic contributions to background T2). Fortunately, because compartmentalized particles often form aggregates and the aggregated forms of our sensor particles have low T2 relaxivity, the influence of compartmentalized particles on cellular calcium imaging may be relatively benign. Concentrations well over 1 nM of the 3C:1M and 3C:1R sensors could also be used if necessary; delivery may be difficult, but serious calcium buffering is unlikely to occur below 1 μM in calcium-binding sites.

In select cases, useful MRI measurements may be possible with the prototype calcium sensors we present here, but it is clear that significant hurdles must be still overcome to apply these contrast agents to a variety of pressing biological problems. Nevertheless, specific molecular strategies can be used to improve the properties of the sensors, including both their slow kinetics and their potential cross-reactivity. The calcium sensitivity and high relaxivity of CaM/target-conjugated SPIOs will then make these sensors and their derivatives potent reporters of calcium-related signaling events for functional MRI studies in vivo.

Materials and Methods

Formation of Bioconjugates.

Biotinylated M13 and RS20 peptides were synthesized by solid-phase methods. Bovine CaM was purchased from Sigma (St. Louis, MO) and biotinylated with NHS-LC-biotin (Pierce Biotechnology, Rockford, IL). Expression vectors for recombinant CaM variants were derived from an XCaM gene (XCaM E104Q; referred to in the text as X1) generously provided by Atsushi Miyawaki (RIKEN Brain Science Institute, Saitama, Japan). The gene was modified to code for a hexahistidine tag and a free cysteine near the N terminus. Sequencing of the clones also indicated the presence of the nonstandard substitution D64Y. The S81R/E83K/E87R/E104Q mutant (referred to as X2) was generated from this template by PCR. Recombinant proteins were expressed in Escherichia coli, biotinylated with biotin-BMCC (Pierce Biotechnology) and purified by nickel-affinity and gel filtration chromatography. Biotinylated polypeptides were mixed in approximately 5-fold excess with streptavidin-coated SPIO particles (SA-MACS; Miltenyi Biotec), incubated for 30 min at room temperature, and purified by magnetic separation. Saturation of biotin-binding sites was confirmed by titration with fluorescent biotin (35). See Supporting Text for further details.

Light-Scattering Experiments.

DLS measurements were performed using a DynaPro DLS system (Wyatt Technology, Santa Barbara, CA). For each sample or condition, a single intensity-weighted value was used to characterize the average size of all particles in the specimen. Throughout this article, mean hydrodynamic radii for individual samples are reported relative to either SA-MACS-CaM or calcium-free binary mixtures of CaM- and target-conjugate SPIOs. Most DLS measurements were obtained after 60 min of incubation in the reported buffer condition, with 200-fold averaging and a 1-s integration time; error bars denote SEM. Time course experiments were initiated by manual 1:1 dilution of premixed CaM- and M13-conjugated SPIOs incubated for 1 h in either 100 μM CaCl₂ or 100 μM EDTA into final concentrations of 500 μM CaCl₂, 500 μM EDTA or control (initial) conditions. Mixing dead time for DLS kinetic experiments was ≈5 s, and each measurement was averaged over a 20-s time window. Calcium titration data were obtained from SPIO suspensions with 7.9 mg/liter Fe, using 0–39 μM Ca/EGTA buffers (Molecular Probes, Eugene, OR) and unbuffered 3–3,000 μM CaCl₂ solutions. Calcium titration was performed in 100 mM KCl/30 mM Mops, pH 7.2; all other measurements were performed in PBS, pH 7.2. Graphing and curve-fitting were performed with Kaleidagraph (Synergy Software, Reading, PA). EC₅₀ for calcium binding were obtained by fitting DLS data to the equation r = c₁[Ca²⁺]ⁿ/(EC₅₀ⁿ + [Ca²⁺]ⁿ) + c₂, where r is the relative radius, c₁ and c₂ are constants, and n is a cooperativity parameter.

AFM.

AFM was performed with a Veeco Instruments (Woodbury, NY) D3000 atomic force microscope in tapping mode, with a silicon cantilever (30 × 125 μm, 265-kHz resonance). SA-MACS conjugates prepared as described above were mixed and incubated in 100 μM CaCl₂ or 100 μM EDTA buffers at room temperature for 1 h. Nanoparticle mixtures were then pipetted onto freshly cleaved mica disks (Electron Microscopy Sciences, Hatfield, PA) and incubated for a further 2 h to allow adhesion to the substrate. The mica samples were then washed with deionized water and dried with air before imaging. To optimize sample loading onto the mica substrates, the SPIO concentrations used for these experiments were 2.5–10 times higher than for DLS experiments.

MRI.

Samples prepared as described above were arrayed into microtiter plates and placed in a 40-cm-bore Bruker (Billerica, MA) Avance 4.7 T MRI scanner. Unused wells were filled with PBS, and imaging was performed on a 2-mm slice through the sample. A T2-weighted spin echo pulse sequence with multiecho acquisition was used; repetition time (TR) was 2 s, and TE ranged from 10 to 80 ms, in 10-ms increments. Data matrices of 512 × 128 points were acquired and zero-filled to 256 points in the second (phase encoding) dimension. Time series images (Fig. 4B) were obtained after a mixing and setup dead time of ≈4 min, with an acquisition time of 8 min per scan. Images were reconstructed and analyzed using custom routines running in Matlab (Mathworks, Natick, MA). Relaxation rates and relaxivities reported here were calculated by exponential fitting to the image data. All data analysis was performed with Matlab and Kaleidagraph.

Abbreviations

CaM

calmodulin

M13

skeletal muscle myosin light chain kinase peptide

RS20

smooth muscle myosin light chain kinase peptide

SPIO

superparamagnetic iron oxide

TE

echo time

XCaM

Xenopus CaM.