Predicting interpretability of metabolome models based on behavior, putative identity, and biological relevance of explanatory signals

Abstract

Powerful algorithms are required to deal with the dimensionality of metabolomics data. Although many achieve high classification accuracy, the models they generate have limited value unless it can be demonstrated that they are reproducible and statistically relevant to the biological problem under investigation. Random forest (RF) generates models, without any requirement for dimensionality reduction or feature selection, in which individual variables are ranked for significance and displayed in an explicit manner. In metabolome fingerprinting by mass spectrometry, each metabolite can be represented by signals at several m/z. Exploiting a prior understanding of expected biochemical differences between sample classes, we aimed to develop meaningful metrics relevant to the significance both of the overall RF model and individual, potentially explanatory, signals. Pair-wise comparison of related plant genotypes with strong phenotypic differences demonstrated that robust models are not only reproducible but also logically structured, highlighting correlated m/z derived from just a small number of explanatory metabolites reflecting the biological differences between sample classes. RF models were also generated by using groupings of samples known to be increasingly phenotypically similar. Although classification accuracy was often reasonable, we demonstrated reproducibly in both Arabidopsis and potato a performance threshold based on margin statistics beyond which such models showed little structure indicative of either generalizibility or further biological interpretability. In a multiclass problem using 25 Arabidopsis genotypes, despite the complicating effects of ecotype background and secondary metabolome perturbations common to several mutations, the ranking of metabolome signals by RF provided scope for deeper interpretability.

Conceptually, the analysis of high dimensional metabolomics data (1–3) is data-driven and dependent on powerful multivariate modeling techniques (4–10). As in proteomics and transcriptomics research (11, 12), there is an imminent need to develop strategies to verify both the reproducibility and significance of such classification results. In the present study, an assumption is made that the goal of any data modeling experiment is not only to attempt to cluster or discriminate sample classes but also to identify the major “explanatory” metabolome signals important in any model construction. Using well characterized plant genotypes, many with known or predictable biochemical differences, we describe a strategy to validate the robustness and interpretability potential of models generated from high dimensional metabolomics data. Metabolite “fingerprinting” (13–16) provides relatively comprehensive metabolome representations, which is especially important when differences between sample classes are unknown. Approaches using mass spectrometry (such as flow infusion electrospray ionization mass spectrometry, FIE-MS) have the advantage that signals (ion mass to charge ratio, m/z) can be linked to candidate metabolites by virtue of atomic mass (3, 17–20).

Data mining techniques build models (classifiers) describing the relationship between a predictor (genotype or cultivar class label for example) and the metabolome fingerprint (21–31). Supervised methods use a range of different strategies including statistical, neural, and rule-based methods (30). Operationally, these approaches build discriminatory models between predefined classes by using training data and then subsequently test models on previously unseen test data, often derived from the same data batch. However, an adequate test of the robustness of any model is only achieved when the same classifier demonstrates high predictive accuracy on validation data derived from an independent experiment. Supervised data mining algorithms may be categorized into those that produce directly interpretable models that represent the data in an explicit way (e.g., as in a mathematical formula or tree structure) and others that cannot easily be described in terms of the original variables. Although many of the former methods can achieve high predictive accuracy, they commonly generate exceedingly complex classification models that are opaque to further interpretability (4, 6–8). When using supervised methods, great care also has to be taken to avoid production of overoptimistic models using essentially variance that is unrelated to the problem under consideration during model construction. Thus, in practical terms, a key attribute of any model is simplicity, both to hopefully avoid irrelevant background noise and to allow for efficient targeting of just a few potentially explanatory variables for further investigation. Decision tree (DT) methods can be very efficient at selecting variables with explanatory power from data sets with high dimensionality (23, 24) and are particularly useful in metabolomics studies where variables may be associated in a nonlinear fashion (i.e., networks). Although accurate DT models can be produced, the resultant tree may miss out on adequate solutions (multiplicity problem) involving alternative explanatory variables to the ones considered in the final tree. To overcome this problem, we describe the use of random forest (RF), an extension of DT methods based on the generation and comparison of an ensemble of trees (28). RF models cope well with high dimensional data sets and multiclass problems and, more importantly, also provide insight into the structure of the data under study by quantifying the confidence in classification voting and by indicating the importance of each variable for the classification task (28, 31, 32).

When high-throughput data analysis is desired, it is important to be able to validate with confidence that any highlighted variables in models with apparently good classification accuracy are truly explanatory. In the present study, we describe a strategy both to validate the explanatory potential of RF models and explore approaches to develop significance metrics appropriate for different types of experimental situations. An initial aim was to define a baseline indicative of a significant difference in models involving binary comparisons of sample classes. Building on this information, a key objective was to develop a rationale for the detection of models with potentially sufficient explanatory power to guide deeper investigation of any significant metabolic phenotype; as part of this process, we evaluated a meaningful threshold for variable significance in ranked lists of potentially explanatory metabolome (m/z) signals generated by RF. Finally, based on these model interpretability measures, we discuss a strategy for the future de novo assessment of phenotype class membership in larger scale genotype screening experiments.

Results

Determining Metrics for Model Significance and Phenotypic Class Membership.

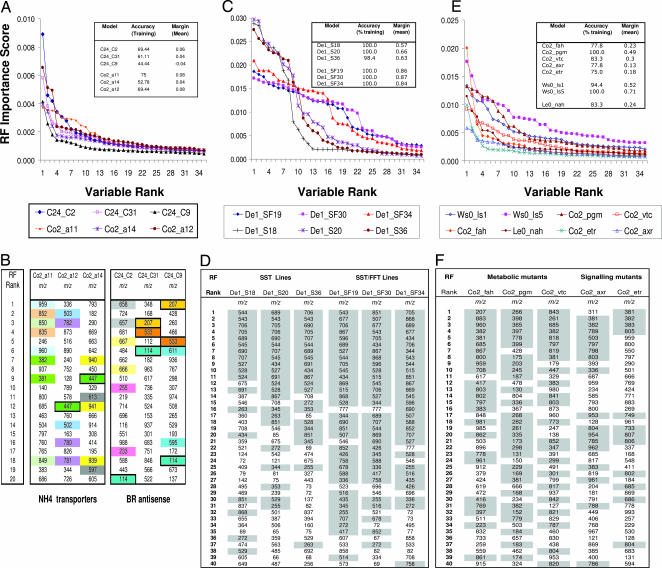
To define a baseline for significance, RF models were developed that attempted to discriminate four near-identical field plots of potato tubers (cultivar Désirée), compare near isogenic lines in two plant species (potato, De1 and De2; and Arabidopsis, Co0 and Co2) and classify samples representing three independent examples each of four classes of genetically modified plants. The internal classification accuracy and average margins computed from the training sample, together with the level of significance determined by permutation testing (11), are compared with those calculated for an independent test set in Table 1. Classification accuracies are almost always not significant at the 0.99 quantile, and margins are <0.1, reflecting a very low confidence in class votes, indicating that lines within the same metaclass had very similar metabolomes. Two types of genetically modified Arabidopsis lines were selected for metabolite fingerprinting that were either not directly effected in metabolism (ammonium transporter T-DNA insertion lines) or effected in metabolites present at concentrations unlikely to be detectable in fingerprinting experiments [brassinosteroid hormone (BR) antisense lines]. Three independent lines of each metaclass were compared with the progenitor ecotypes by RF (Fig. 1A). Only three genotypes (C2 and a11 and a12) had significant accuracies (threshold = 69.4% at P = 0.01), but model margins all fell below 0.1 (significance threshold = 0.09 at P = 0.01). The top 20 variables ranked by importance score in each RF model are shown in Fig. 1B. In classifiers with good generalizibility, it is expected that the same explanatory variables should be highly ranked in all models of the same metaclass and each should be accompanied by other metabolome signals representing isotopes, adducts, or neutral losses of the same metabolite. Very few common features were found between the two weakest models of each metaclasses (m/z boxed in Co2_a12, Co2_a14, C24_C9 and C24_C31), whereas isotope pairs are evident in the two strongest models (Co2_a11 and C24_C2).

Table 1.

Properties of RF models comparing sample classes with little relevant biological differences

Model	Block De	De1_De2	Co2_Co0	SST	SST/FFT	Ammonium transporters	BR antisense
Accuracy (tr)	25	65.6	61.1	55.2	45.8	33.3	57.4
Accuracy (te)	56.3	81.3	58.3	68.8	56.3	38.9	61.1
90%	28.1	57.8	58.3	38.5	38.5	37	37
95%	31.3	62.5	61.1	40.6	41.7	38.9	40.7
99%	37.5	67.2	69.4	44.8	43.8	44.4	46.3
Margin (tr)	−0.092	0.12	0.04	0.02	−0.03	−0.04	0.03
Margin (te)	−0.004	0.15	0.11	0.06	0.02	−0.01	0.08
90%	−0.088	0.03	0.03	−0.05	−0.05	−0.04	−0.04
95%	−0.081	0.05	0.05	−0.04	−0.04	−0.04	−0.04
99%	−0.061	0.09	0.09	−0.03	−0.02	−0.02	−0.03

tr, training; te, test. Numbers in bold represent significance threshold.

Fig. 1.

Determining the characteristics of robust RF models. (A) Variable importance score versus ranking in weak RF models comparing Arabidopsis ammonia transporter mutant lines and brassinosteroid synthesis antisense lines to progenitor ecotypes. (B) Ordered list of top ranking signals from data depicted in A; correlated variables (e.g., isotopes) are color-coded and variables shared between models in the same metaclass are boxed. Variable importance score versus ranking in stronger RF models comparing pair wise with progenitor genotypes in potato transgenic lines (C) and Arabidopsis mutants (E). (D and F) Top ranking signals (descending order) from a selection of models depicted in A and E; m/z representing correlated variables (e.g., isotopes, salt adducts, and common fragments) are shaded in both lists.

Determining Significance Thresholds for Explanatory Variables.

Potato and Arabidopsis lines (see Table 2, which is published as supporting information on the PNAS web site) were selected that had been shown to exhibit detectable changes in metabolism when compared with a progenitor genotype. Two transgenic potato metaclasses (three independent representatives of each in a Désirée background) had been genetically engineered to synthesize fructans of different degrees of polymerization by expression of novel enzyme activity (SST and SST/FFT genotypes; ref. 33). Five Arabidopsis lines in a Co2 background had been mutated in genes coding for specific enzymes in important metabolic pathways (fah, pgm, vtc) or genes involved in hormone signaling (axr and etr). Two spontaneous lesion mutants in a Ws0 background (ls1 and ls5) and a further genotype expressing a transgene coding for salicylate hydroxylase (nah) had strong defense-related phenotypes.

RF discriminated all of the transgenic potato lines with a near perfect classification accuracy, and in each instance the model margin exceeded 0.5 (Fig. 1C Inset). We have demonstrated (19) that these transgenic potato lines contain no detectable metabolome differences except those signals associated with novel fructans, which are shaded in the ranked lists of explanatory signals shown in Fig. 1D (for identity of fructan m/z signals and a confirmatory correlation analysis, see Table 3 and Fig. 4, which are published as supporting information on the PNAS web site). Thus, one logical explanatory “significance” threshold would be the point at which signals not associated with fructans start to enter the list of variables ranked by RF analysis. This point is reached around rank 15–20 in the SST lines and at approximately rank 30 in the SST/FFT lines (Fig. 1D). In models of both genotype classes, this threshold occurs at an importance score of ≈0.003 (see Fig. 1C). Classification accuracies in the Arabidopsis binary comparisons approached or were higher than 80%, and model margins (with the exception of Co2_axr and Co2_etr) were above 0.2 (Fig. 1E Inset). In six of the Arabidopsis lines, an importance score >0.003 was reached at variable rankings from 10 to 30, but in Co2_axr and Co2_etr, the importance scores were generally much lower (Fig. 1E). In the three well studied Arabidopsis Co2 lines mutated in genes coding for key enzymes in specific metabolic pathways (fah, pgm and vtc), almost 80% of the top 20 electrospray ionization (ESI) variables were predicted to be either salt adducts or isotopes of a small number (6–8) of metabolites in both ionization modes (ESI ⁺ m/z are shaded in Fig. 1F; see Table 4, which is published as supporting information on the PNAS web site, for an explanation of signal relationships in both +ve and −ve ion data). As in the potato transgenic lines, many of the top ranking (P = < 0.01) signals in the binary comparison of Arabidopsis lines were highly correlated, suggesting that the proposed isotopes and adducts were indeed likely to be derived from the same metabolite (Fig. 5, which is published as supporting information on the PNAS web site). The lowest ranking signals putatively associated with the biochemical lesions in all three lines (pgm; rank 31 +ve ion; vtc rank 24 +ve ion and fah, rank 20 −ve ion) are located where the importance scores level off at values between 0.002 and 0.003. Permutation testing was applied to determine the significance of the variable importance score in each RF model. In data sets from both plant species, it can be seen that the P value of individual variables start to rise at a different position in the RF ranking, anywhere from rank 2 in Co2_axr to position 26 in De1_SF19 (Fig. 2A and C). A threshold for variable significance in both potato and Arabidopsis RF models was reached at a P value between 0.0025 and 0.01 where a decrease in margin was evident when m/z with larger P values were included in the modeling process (Fig. 2 B and D).

Fig. 2.

Relationship between margin and variable significance in metabolome fingerprint models. Overall model P value (log 10) when including increasing numbers of top ranking variables in RF Analysis of Arabidopsis (A) and potato (C) genotypes. Overall model margins when including variables with increasing P value in RF analysis of Arabidopsis (B) and potato (D) genotypes. A suggested significance threshold is indicated.

Visualization and Interpretation of Phenotypic Relationships in Larger Scale Experiment.

The average margins of all possible pair-wise RF models were projected into a 2D space by non linear mapping to illustrate the relationships between 25 Arabidopsis lines (Fig. 3A). Each Arabidopsis ecotype is generally well separated and genotypes with weak metabolome differences cluster close to their progenitor ecotype (e.g., Co2 with a2, a11, a12, and a14 and C24 with C2, C9, and C31). Similarly, genotypes with increasingly stronger phenotypes are found at increasing distances from the progenitor ecotype (e.g., Co2 with fah, vtc, and pgm and Le0 with uvr, eds, and nah). The metabolome differences with the progenitor ecotype Ws0 in the case of ls1 and ls5 are so great that there is no apparent connectivity. The Arabidopsis genotypes were chosen to include six lines (uvr, eds, vtc, ls1, ls5, and nah) with described defense- or stress-related phenotypes. In a pair-wise comparison to each other all of the defense-related mutants in Le0 and Ws0 backgrounds had much smaller margins than when compared with the progenitor cultivar (data not shown). The uvr, eds, and nah genotypes shared many top-ranking signals (Fig. 3B), whereas phenotypically unrelated mutants such as pgm and fah had little in common. Interestingly, despite being in a different ecotype background vtc also shared many explanatory features with the other defense mutants. The RF models comparing lesion mimic mutants to Ws0 had very large margins, but they were also substantially different from each other (Fig. 3C), and in both cases, 25–30 top ranking variables had importance scores >0.003 (see Fig. 1E). Ls1 and ls5 had a large number of top ranked variables in common (color coded in Fig. 3C); however, each line equally had a large proportion of highly significant (P < 0.001) correlated signals that had no explanatory power in the other line (Fig. 3D).

Fig. 3.

Metabolome modeling with larger multiple class problems. (A) Two-dimensional mapping of 25 Arabidopsis lines using Sammon nonlinear mapping. Control ecotypes are colored blue, and progenitor ecotypes of mutant lines are presented as squares. The ecotype background of mutant lines is depicted by color: red, LeO; yellow, C24; pink, Ws0; green, Columbia. The lines linking phenotypically related genotypes represent margins in pair-wise comparisons and are color coded as follows: black solid line, <0.1; yellow dotted line, 0.1–0.2; blue dashed line, 0.2–0.3. Margins >0.3 have been omitted for the representation. (B) Top ranking signals in common (color coded) between RF models representing pair-wise comparisons between selected defense related and UV sensitive genotypes and their progenitor ecotypes. (C) RF models comparing lesion mimic mutants (ls1 and ls5) with the progenitor genotype (Ws0) indicating the presence of many common signals (color coded). (D) A correlation analysis of variables contributing significantly (P = < 0.005) to models discriminating mutant lines ls1 and ls5 from the progenitor ecotype Ws0.

Discussion

Choice of Data Mining Technique.

There are a range of strategies available to analyze metabolomics data (4–10). In preliminary work (see Table 5, which is published as supporting information on the PNAS web site), we showed that classification accuracies achieved by using RF were equivalent to those obtained by using three common supervised learning algorithms. Feature selection is of primary importance from an interpretation perspective. One problem associated with “naïve” modeling of metabolome fingerprint data are the multiplicity of possible good solutions. It is rarely the case that one unique signal (or combination of very few uncorrelated variables) will adequately describe the property under study. Indeed, previous studies have highlighted the importance of including all variables in the final model to identify “silent phenotypes” or unexpected metabolic pathways (19, 20, 34–36). Several powerful data mining approaches combine feature selection and classification in one analytical run; for example, genetic algorithms or genetic programming evaluate feature subsets by using accuracy estimates provided by a machine learning algorithm (4, 7). These “wrapper” techniques produce parsimonious models using very few variables that are generally dominated by the stronger attributes. Effectively, this means that correlated (essentially redundant) variables are selected only rarely, consequently missing out on potentially informative solutions. We suggest that RF has additional utility because the aim is not to determine the smallest feature set but to identify a complete set of statistically significant explanatory variables.

Assessing Model Robustness.

Validation of a classifier demands not only a consistent predictive power but also that the variables selected for high explanatory potential should be the same in replicate experiments. Thus to achieve an adequate assessment of generalizibility, it is valuable to use algorithms, such as RF, which produce directly interpretable models that represent the data in an explicit way. We suggest that a more stringent representation of class boundary complexity than classification accuracy alone is essential for assessing model quality and further interpretability potential. By definition, the sample margin encompasses a measure of confidence in votes for the right class. In contrast to margin-based classifiers (e.g., support vector machines) or discriminant techniques (such as linear discriminant analysis or partial least squares discriminant analysis), RF does not explicitly maximize the margin, thus making this measure valuable because it is both unbiased and related directly to the generalization error.

In high-throughput metabolite fingerprinting, deciding which models to consider for deeper analysis of signals is usually problem-specific due to constraints associated with sample size (in relation to data variance and dimensionality characteristics) and the lack of prior knowledge about expected margin distributions. Permutation-based tests have been used to provide such information (11). We describe an alternative approach to evaluate any new experimental system based on a combined examination of statistical significance and biological information content to validate robustness and interpretability potential. Thus, using plants of known genotype and predicable biochemical phenotypes, we have explored both margin characteristics and variable behavior in FIE-MS fingerprint models that we expect to be either poor, or possibly adequate or robust in terms of generalizibility. These observations suggest that FIE-MS fingerprinting in combination with RF analysis will be valuable as a prescreen to detect lines with novel metabolic phenotypes in large populations. In model systems, such as Arabidopsis, targeted, even quantitative, profiling approaches using high mass resolution instruments (3, 17, 20) will become more routine as metabolite identity in the sample matrix is better understood, allowing signals relating to specific molecules to be predesignated.

Selecting Significance Thresholds and Evaluating Model Interpretability Potential.

Importance score ranking combined with significance testing of m/z signals provides an excellent metric contributing to a rapid assessment of model robustness and interpretability potential. A standardized significance cutoff based on an arbitrary RF rank was not appropriate, because significance testing revealed that P values for individual variables started to rise at different rank positions in individual models. By generating a series of models using only variables with P values below predetermined thresholds, it was shown that margins began to drop significantly when variables with P values >0.001 were used. Prior knowledge of biochemical difference between genotypes, particularly in the novel fructan-producing transgenic potato lines, allowed us to confirm that signals unrelated to the transgenic phenotype began to populate models if variables with a P value >0.0025 were used. In most instances, for pair-wise comparison of genotypes, this P value threshold (P ≤ 0.001 to P ≤ 0.0025) correlated with an importance score of ≈0.003, below which any variables were unlikely to have any significant explanatory power. Robust models with adequate margins (>0.2) derived from comparison of progenitor genotypes with mutants (or transgenic lines) with strong metabolic phenotypes had a large proportion (>65%) of correlated m/z signals (e.g., potential isotopes, salt adducts, and neutral losses representing the same predicted metabolite) in the top 30 ranked variables. Mutants with pleiotrophic effects lacking a distinct metabolic phenotype, such as auxin (axr-1) or ethylene (etr-1) hormone signaling defective lines, exhibited much lower levels (<35%) of correlated variables. In situations where the metabolic differences between genotypes are more discrete, centering on signals derived from just a small number (2–5) of metabolites, there is clearly a much greater potential for further interpretability. Typically in such models, the top ranking signals are highly correlated and importance scores drop rapidly to the significance threshold.

Interpretation of Phenotypic Relationships in Larger Mutant Genotype Populations.

In large, multiple-class experiments, the meaningful representation of high dimensional multivariate models is problematic, particularly if the objective is to assign any phenotypic relatedness based on separation “distances” that encapsulate the diversity of genotypic differences. Few studies have tackled this problem, and our rather small experiment (considering the number of Arabidopsis mutants available) already illustrates the richness of the information derived from metabolome fingerprints based on mass spectrometry. A traditional approach would be to compare each genotype to a so called progenitor line (e.g., Desiree or Columbia in the present example) and relate phenotypic differences to a representative example of a given species. However, this strategy runs the risk of missing crucial or novel relationships between specific lines. For example, in the present study, we demonstrate that effectively “unlinked” genotypes (e.g., vtc and eds) can, in fact, share many highly ranked explanatory variables; in this case, the ecotype background dominates the modeling process. A further factor impinging on effective phenotyping is the problem of secondary effects of mutations on the metabolome that mask the true explanatory differences between classes; this is demonstrated in the present study by the fact that the defense-related mutants had a large subset of highly ranked variables that were probably associated with their general light (UV) sensitivity. Similarly, the two lesion mimic mutants had a large number of signals in common related to secondary effects after the induction of cell death. However, in both of these situations, by examining the list of top-ranking signals, it is possible to identify real differences between such genotypes.

In conclusion, we suggest that direct interpretability, and a nonbiased capacity to deal with multiple adequate solutions, are just as important as achieving a high classification accuracy in any metabolome modeling procedure using high dimensional data. By representing and ranking all potentially explanatory variables in an explicit way, RF models provide an increased opportunity for assessment of model generalizibility and deeper phenotypic investigation. With more standardized metabolome fingerprinting procedures in the future, we suggest that ranked lists of top explanatory variables (perhaps 20–30 with an adequate model margin) may provide robust, directly comparable representations of sample composition in situations requiring high throughput classification tasks.

Materials and Methods

Plant Material, Sample Preparation, and Metabolite Analysis.

Experimental transgenic potato genotypes engineered to synthesize fructans (33) were derived from the cultivar Désirée and have been described (19). A somaclonal variant (De2) generated via tissue culture provided a near-isogenic line of the commercial Désirée cultivar (De1). Procedures for sample preparation and extraction have been described (19). Information on the Arabidopsis genotypes selected for this study and additional details of metabolite analysis are presented in Supporting Text, which is published as supporting information on the PNAS web site. A minimum of 30 biological replicates were used to develop FIE-MS fingerprints in both ionisation modes.

Data Modeling.

Sample classification, selection, and ranking of potentially explanatory variables in FIE-MS data were achieved by using an implementation of RF as described in Supporting Text. Training/test set partitioning was carried out on the basis of independent analytical batches with 18 and 12 plant replicates selected to form the training and test set, respectively. For each RF model, classification accuracies and average margins were computed from the “out of bag” training samples. One thousand trees were generated in each modeling experiment by using the overall fingerprint if not stated otherwise. The importance score for each m/z for each classification task to define a ranked list of potentially explanatory signals was computed according to Breiman (28). The levels of significance were determined by a permutation test (11, 37) under the null hypothesis that the importance score is not relevant to the classification task. The P value is defined as the fraction of times an importance score in the class-permuted data are greater or equal to the score in the unpermuted data. Two thousand permutations were performed. Average margins (38) of the training samples were used as input for the Sammon nonlinear mapping algorithm (39) using the library “MASS” in the R environment (http://www.r-project.org).

FIE-MS Signal Interpretation.

The initial data analysis by RF produced a list of m/z signals ranked by importance scores or P value for each classification task. The lists of top ranked m/z (generally top 40) were examined for groups of potentially related signals that could represent either the (de)protonated ion (e.g., [M+H]+ = M + 1), salt adducts (both single and double charged e.g., [M+Na]⁺ = M + 23, [M+K]⁺ = M + 39 or [M+Na+K]²⁺ = (M + 23 + 39)/2), common neutral losses (e.g., [M+H-H₂O]⁺ = M-17 and [M+H-HCOOH]⁺ = M-45), the homogeneous dimer ion [e.g., [2M+H]⁺ = 2(M + 1)], and dimer ion pair adducts [e.g., [2M+Na]⁺ = 2(M + 23)] as well as isotopes (M + 2 or M + 3 amu) of a single metabolite. Because several overlapping solutions predicting the presence of different metabolites were often possible, the most likely combination of ions putatively identifying a specific metabolite was confirmed by further examining signal relationships in a correlation analysis using just m/z with an appropriate low P value.

Abbreviations

FIE-MS

flow infusion electrospray ionization mass spectrometry

DT

decision tree

RF

random forest.