Mechanisms and kinetics of β-hairpin formation

Abstract

Thermodynamics and kinetics of off-lattice models with side chains for the β-hairpin fragment of immunoglobulin-binding protein and its variants are reported. For all properties (except refolding time τ_F) there are no qualitative differences between the full model and the Gō version. The validity of the models is established by comparison of the calculated native structure with the Protein Data Bank coordinates and by reproducing the experimental results for the degree of cooperativity and τ_F. For the full model τ_F ≈ 2 μs at the folding temperature (experimental value is 6 μs); the Gō model folds 50 times faster. Upon refolding, structural changes take place over three time scales. On the collapse time scale compact structures with intact hydrophobic cluster form. Subsequently, hydrogen bonds form, predominantly originating from the turn by a kinetic zipping mechanism. The assembly of the hairpin is complete when most of the interstrand contacts (the rate-limiting step) is formed. The dominant transition state structure (located by using cluster analysis) is compact and structured. We predict that when hydrophobic cluster is moved to the loop τ_F marginally increases, whereas moving the hydrophobic cluster closer to the termini results in significant decrease in τ_F relative to wild type. The mechanism of hairpin formation is predicted to depend on turn stiffness.

Fast folding experiments on proteins and their building blocks (α-helices, β-hairpins, and loops) are providing glimpses into the time scales of the early events in the assembly of biomolecules (1, 2). In a recent study, Munoz et al. (3) showed that the 16-residue C-terminal peptide from the protein GB1 forms a β-hairpin in about 6 μs at the folding transition temperature T_F (≈300 K), which is in accord with our earlier theoretical predictions (4, 5). They also proposed a statistical mechanical model to explain the observed thermodynamics and kinetics (6).

The key experimental findings of Munoz et al. (3) are (i) Thermodynamically, the formation of β-hairpin can be described by a two-state process. The transition to the folded state is broad, which is expected for small finite systems. (ii) In the temperature range 15–55°C the folding kinetics (monitored by tryptophan fluorescence) is exponential. This behavior suggests two-state folding kinetics. (iii) β-Hairpins form at rates considerably slower than helices. (iv) The temperature dependence of the measured relaxation rates shows slight curvature and an Arrhenius fit to the data gives negative activation energy.

Before these experiments theoretical and computational studies had demonstrated that generically β-hairpins can form in microseconds (4, 5). There are large variations in the time scales for β-turn formation depending on the underlying sequence-dependent characteristic temperatures (4). All-atom simulations in water have shown that many of the characteristics of folding kinetics in proteins (kinetic partitioning, “mini” hydrophobic core packing, etc.) are found in β-turn forming peptides (7). The experiments (3) raise the need for more realistic models, which are needed to understand the precise mechanisms and structural aspects of the transition states.

The purpose of this paper is to provide a complete picture of the folding of the 16-residue peptide and its variants by using Langevin simulations of minimal off-lattice models. We reproduce, qualitatively, all the major experimental observations. Our studies, based on coarse-grained off-lattice models with side chains, suggest that the zipping of the hydrogen bonds starting from the turn is essential for the assembly of the wild-type (WT) 16-mer peptide. The basic mechanisms are determined by the intrinsic rigidity of the turn which, in this class of peptides, is determined by the location of the hydrophobic cluster.

Methods

Model.

The off-lattice model is a coarse-grained representation of a polypeptide chain, in which only the positions of the C_α carbons and the centers of mass of amino acid residues are retained. The amino acid residues are represented as united side chains around their centers of mass. The hydrogen bonds (HBs) between the backbone carbonyl oxygen CO and amide hydrogen NH groups are mimicked as virtual moieties located between backbone α-carbons (8).

The sets of vectors representing the α-carbon positions {r⃗_b,i} and the side-chain centers of mass {r⃗_s,i}, where i = 1, 2, … , N, specify the conformation of the polypeptide chain. The WT sequence, which corresponds to the C-terminal fragment of the GB1 protein, is GEWTYDDATKTFTVTE.

The potential energy of a conformation is given by E_p({r⃗_b,i}, {r⃗_s,i}) = V_BL + V_SBC + V_BA + V_DIH + V_HB + V_NON, where V_BL, V_SBC, V_BA, V_DIH, V_HB, and V_NON are bond-length potential, side-chain–backbone connectivity potential, bond-angle potential, dihedral angle potential, hydrogen bond, and nonbonded long-range potentials, respectively. The interaction potentials for V_BL, V_BA, and V_HB are given elsewhere (4, 8). Here we give a brief description of the additional terms.

Side-Chain–Backbone Connectivity Potential (V_SBC).

We use V_SBC = ∑_i=1^N (k_s/2)(|r⃗_s,i − r⃗_b,i| − a_s)² with k_s = 200ɛ_h/a² (= k_b, the spring constant used in V_BL) and a_s = a, where a (= 3.8 Å) is the average distance between C_α carbons and ɛ_h is an energy of hydrophobic interactions.

Dihedral Angle Potential and Chirality.

The inclusion of side chains introduces chirality in the native state topology—i.e., the native structure and its mirror image become topologically distinctive. The dihedral angle potential V_DIH is

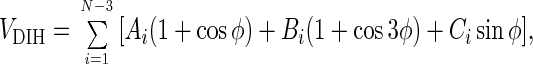1

where A_i = B_i = 1.2ɛ_h and C_i = ±0.6ɛ_h are the values used for the dihedral angles outside the turn region—i.e., for i ranging from 1 to 5 and from 10 to 13. Within the loop (for i = 6 to 9) we choose A_i = 0, B_i = 0.2ɛ_h, and C_i = ±0.3ɛ_h. In Eq. 1 the states g⁻ and g⁺ have different energies and the symmetry in V_DIH with respect to the substitution φ → −φ is broken. This modification is sufficient to distinguish between chiral β-hairpin conformations. We selected the signs of C_i by examining the dihedral angles φ_i^PDB from α-carbon representation of the Protein Data Bank (PDB) native structure (ID code 1gb1) of 16-mer β-hairpin. If φ_i^PDB < 0 (>0), then we chose C_i > 0 (<0). The signs of C_i are altered with i to trace the native fold of the β-hairpin. Other ways of mimicking chiral effects can be found elsewhere (9, 10).

Nonbonded Potential.

The nonbonded potential has three terms V_NON = V_S + V_B + V_BS, where V_S is the interaction between side chains, V_B is the interaction between backbone α-carbons, and V_BS is the potential between backbone α-carbons and side chains (4).

The interactions between side-chain atoms are

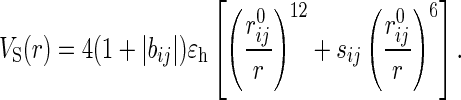2

The residue-dependent term b_ij is the contact interaction matrix taken from table III of Kolinski et al. (KGS) (11). The pairwise contact distances r_ij⁰ (expressed in the units of a = 3.8 Å) are from table I of ref. 11. The parameter s_ij = b_ij/|b_ij| in Eq. 2 controls the nature of the V_S potential. If s_ij < 0, then the interaction is attractive at r ≃ r_ij⁰. If s_ij is positive, V_S is purely repulsive and we replace ɛ_h with ɛ_l = ɛ_h.

The general scheme to develop force fields described above for polypeptide chains is used for the 16-mer fragment. We consider two models. The first, the Klimov and Thirumalai (KT) model, uses the potentials described above. A Gō version of the KT model is constructed, in which the interactions between side chains that are in contact in the PDB native conformation are assumed to be given by Eq. 2. The nonbonded interactions between all other side chains (as well as V_B and V_BS in both models) account only for excluded volume and do not depend on the residue type. The general functional form for these interactions is

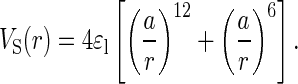3

In our Gō-like model the dihedral angle potentials and HB interactions are the same as in the KT model.

Equilibrium quantities are computed by using the multiple histogram technique (12), and dynamics is obtained from Langevin simulations. The energy scale ɛ_h is typically between 1 and 1.5 kcal/mol. For the purposes of converting to real units we take ɛ_h = 1.25 kcal/mol and time scale τ_L = (ma²/ɛ_h)^1/2 ≃ 3 ps (4), where m (= 5·10⁻²² g) is the average residue mass.

Results

Native State Topologies.

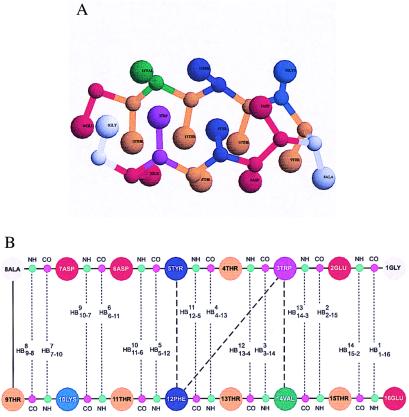
In Fig. 1A the native state, identified as the lowest-energy conformation at T = 0.0 using multiple slow cooling simulations, is shown for the KT model. Fig. 1B shows structural aspects of the hairpin—the HBs and the interaction between the residues constituting the hydrophobic cluster (3W, 5Y, 12F, 14V). The structure is stabilized by 26 (21 in the case of the Gō model) native contacts between side chains (defined with 7.6-Å cut-off distance) and 14 HBs. The angle γ between the planes defined by the two strands (residues 1–6 and 10–16) is 12.1°, and the radius of gyration of the native conformation is R_g,N = 11.9 Å. The corresponding values for the Gō model are 13.4° and 12.2 Å, respectively. The radius of gyration of the PDB native conformation (ID code 1gb1) R_g^PDB is 12.2 Å, and the angle γ is 12.6°. The backbone rms (compared to the PDB structure) of the Gō model is 1.8 Å, whereas the full rms deviation is 2.5 Å. For the KT model the backbone and full rms deviations are 2.6 Å and 3.1 Å, respectively. The contributions to the energy of the native state (per interaction) arising from side-chain contacts (−1.3 kcal/mol) and HB interactions (−0.6 kcal/mol) for the Gō model are in agreement with those derived from the analysis of the energetics stabilizing the WT β-hairpin (stabilization energies due to side-chain interactions ΔG_sc = −2.1 kcal/mol and HB formation ΔH_HB = −1.1 kcal/mol) (3). The results for the KT model are −1.6 and −0.5 kcal/mol.

Figure 1.

(A) The native conformation of the β-hairpin for the KT model. For clarity CO and NH groups are not shown. The figure is created with the program rasmol 2.6 (13). (B) Schematic representation of interactions in the native conformation of a β-hairpin. The 14 HBs are given by dashed lines connecting CO_i (in magenta) and NH_17−i (in green) groups; HB numbering starts with Gly-1 (1GLY). HB labels indicate bond number (superscript) and the pair of residues (subscript). Thick dashed lines show interactions between hydrophobic cluster side chains.

Because only generic functional forms for the interaction potentials with physically reasonable values are chosen and no attempt has been made to optimize them, the agreement between the predicted structures and the PDB data should be considered excellent. We expect that the strategy developed here should provide a good low resolution of the folds of proteins as well.

Thermodynamics of Folding.

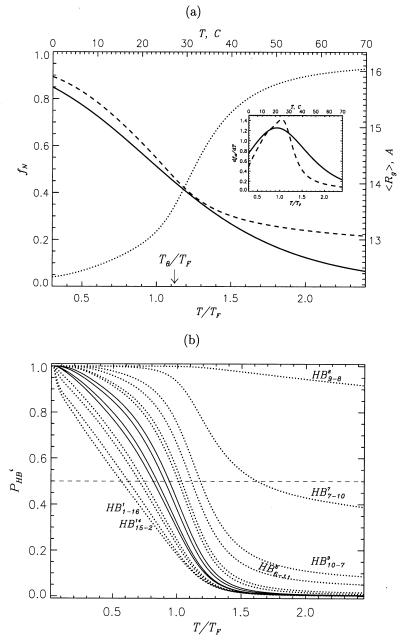
The collapse transition temperature, T_θ, obtained from the peak of specific heat (data not shown) is 346 K for the Gō model. Because this transition corresponds to chain compaction it can also be determined from the temperature dependence of the radius of gyration 〈R_g(T)〉 (Fig. 2A). The derivative d 〈R_g(T)〉/dT has a maximum at T = 365 K ≈ T_θ (data not shown). The value of 〈R_g(T)〉 in the range T_F < T < T_θ changes by less than 10%. Moreover, ΔT = T_θ − T_F (= 0.12T_F) is smaller than the width of folding transition (see Inset to Fig. 2A). Thus, the measurements of T_θ would be difficult, if not impossible, for such a small peptide. The folding transition temperature computed from the fluctuations of the overlap function Δχ (ref. 8) is T_F = 308 K (for the Gō model). For the KT model the peak in Δχ occurs at T_F ≈ 333 K, which is higher than the experimental estimate.

Figure 2.

(A) Temperature dependence of the fraction of native state f_N measured by the fraction of native contacts 〈Q(T/T_F)〉 for the Gō model (dashed curve) and the native hairpin population (solid curve, temperature scale is given at the top) calculated by using the experimental thermodynamic parameters ΔH = −11.6 kcal/mol and ΔS = −39 cal/(mol⋅K) (ref. 3). By fitting 〈Q(T/T_F)〉 to a two-state model we obtained ΔH = −7.0 kcal/mol and ΔS = −22 cal/(mol⋅K). The thermal average of the radius of gyration 〈R_g〉 (in Å, the right-hand vertical axis) vs. T/T_F is plotted (dotted curve). The location of collapse temperature is marked by an arrow. In the temperature range corresponding to that scanned in the experiments (3) the change in 〈R_g〉 is less than 10%. (Inset) Derivatives of 〈Q〉 (dashed curve) and experimental hairpin population (solid curve) with respect to temperature. The temperature scales are the same as in the main figure. It is seen that folding transition in both the experiment and the simulations is very broad. (B) Probabilities of HB formation P_HBⁱ (i gives the HB number) as a function of T/T_F for the Gō model. P_HBⁱ for the HBs proximal to the hydrophobic cluster (HB_3–14³, HB_4–13⁴, HB_12–5¹¹, HB_13–4¹²) are shown by solid curves, other HBs are represented by dotted curves. Terminal HBs and those near the turn are labeled.

The temperature dependence of the probabilities of formation of the HBs P_HBⁱ (i = 1, 2, … , 14) (Fig. 2B) for the Gō model shows that they form over a broad temperature range. Even at relatively high temperatures (T > T_F) HB_9–8⁸ (i.e., a HB labeled 8 formed between CO₉ and NH₈) and HB_7–10⁷ are established with high probability, which is a consequence of their proximity to the turn. We should emphasize that the formation of these HBs does not in any way assist the assembly of the hairpin (Fig. 3B and discussions below). The first HB outside the loop region (namely, HB_10–7⁹) becomes stable at T = 359 K (≈T_θ). As the temperature is lowered the HBs are progressively “zipped” in accordance to their distance from the loop region—i.e., the ones closer to the loop become stable at higher temperatures. Generally, the process of formation of HBs along the hairpin resembles the thermodynamic analog of the recently proposed “kinetic zipper” model for hairpins (3, 14). In both models a hierarchy of structural changes occurs as the temperature is lowered (collapse, folding of the backbone, and ordering of the side chains).

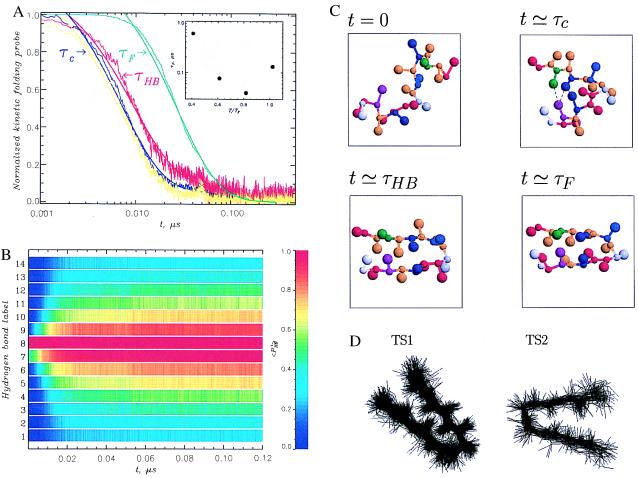
Figure 3.

(A) Plots of the time dependence of the radius of gyration 〈R_g(t)〉 (in blue), the fraction of HBs 〈N_HB(t)〉 (in red), the fraction of unfolded molecules P_u(t) (in green), and the fraction of hydrophobic cluster contacts 〈Q_HC(t)〉 (in yellow) for the Gō model at T = 0.82T_F. The data are shown by dotted lines, and the biexponential fits are shown as solid curves. The collapse time τ_c (coinciding with the time scale for hydrophobic cluster formation), the HB formation time τ_HB, and the folding time τ_F are indicated by arrows. The data are normalized to vary between 1 and 0 and obtained by averaging over 200 trajectories. (Inset) Folding time τ_F vs. temperature. An exponential increase in τ_F is observed at low T. (B) Time evolution of color-coded kinetic probabilities of HB formation 〈P_HBⁱ〉 (the superscript i indicates the HB number as in Fig. 1B) at T = 0.82T_F for the Gō model. The data are averaged over 200 trajectories. This figure shows kinetic zipping of HBs (only for t > τ_c do we observe HB formation away from the turn). The heterogeneity in HB stability after relaxation to equilibrium is also evident: the HBs near the turn are very stable (red color), whereas terminal ones are significantly frayed (light blue). (C) Snapshots from a generic folding trajectory at the three time scales indicated in A. At t = 0 two turn HBs and two intrastrand native contacts are preformed. At t ≃ τ_c the hydrophobic cluster is fully formed (shown by dashed lines) and the size of the hairpin is reduced to its equilibrium collapsed value. There are also four turn HBs. At t ≃ τ_HB all 14 HBs are already formed, but only about 60% of native side-chain contacts (including all in the hydrophobic cluster) is established. At t ≃ τ_F the native structure is reached. (D) Superposition of transition state (TS) conformations for two main TS clusters TS1 and TS2 in the Gō model. The superposition is accomplished by minimizing the rms deviation of structures constituting a given TS cluster. The structural characteristics of TSs are given in the text.

At first glance it may appear that the structural changes that seem to take place over nearly 40°C (308–346 K) is at variance with the apparent two-state transition seen experimentally. However, it should be emphasized that the thermodynamic transition is broad (see below), which is the reflection of the finite size of the chain. To quantitatively assess the degree of cooperativity we compare the theoretical results with experimental data. A measure of the degree of cooperativity of folding is Ω_c = (T_max²/ΔT)(dP_N/dT) (15), where T_max ≈ T_F, ΔT is the full width at half maximum of dP_N/dT, and P_N(T) is a measure of formation of the native state. We find Ω_c ≃ 0.82 when 〈Q(T)〉 = P_N is used. The experimental value of Ω_c, calculated from the temperature dependence of the fraction of the native state (see inset to figure 2 of ref. 3), is 0.14. Typical values of Ω_c for proteins exceed 5 (15). Hence, we find that the degree of cooperativity in the hairpin models and that computed using experimental data are low, as expected.

In the Inset to Fig. 2A, we plot df_N/dT (where f_N is taken to be the fraction of native hairpin for the experiment and 〈Q〉 for simulations). The transition width of the experimental curve is about 40°, and it is also large for our model. It is this large width of the transition that leads to an apparent hierarchy of structural changes. Such changes would be impossible to detect experimentally because they take place within the width of the transition. The low cooperativity and broad transition is consistent with low stability of the hairpin (see legend to Fig. 2A).

Time Scales of Folding.

We have computed the folding time scales at several temperatures T ≲ T_F at the friction coefficient ζ = 50τ_L⁻¹ [corresponding to water viscosity (5)] for the Gō model. Since the foldability index σ [= (T_θ − T_F)/T_θ] is an indicator of the rate of folding (4, 16), we expect σ = 0.11 for the Gō model to be a lower bound. The folding time for the Gō model at T_F is 0.13 μs, which is about a factor of 50 less than the experimental value. Because the computations are considerably more demanding for the KT model, detailed kinetic studies were done only at T ≈ T_F, at which τ_F ≈ 2.2 μs. The complete elimination of nonnative tertiary interactions drastically increases the folding rates.

The folding kinetics is monitored by the time dependence of P_u(t), the fraction of unfolded molecules at time t (i.e., those that have not yet reached the native state). We compute P_u(t), which decays exponentially at T_F, from the distribution of the first passage times. At T = 0.82T_F the folding time τ_F is minimal and the relaxation of P_u(t) has a dominant fast phase (Φ = 0.96) and a very small slow phase (0.04). In the inset to Fig. 3A we display the temperature dependence of τ_F, which is Arrhenius-like with a slight curvature. This trend compares favorably with experiments (see figure 6a of ref. 2).

Folding Mechanism: Collapse, HB Formation, and the Acquisition of Native State.

The mechanism of assembly of the β-hairpin structure is monitored by using several progress variables. It is important to define what is meant by the native structure in our kinetic simulations. Operationally, we assume that the native state is reached when all the HBs and the native contacts between the side chains are established simultaneously, and the instance this occurs for the first time is the first passage time, τ_1i. Steepest descent quenches starting with these structures map onto the low-energy native-like conformations (Fig. 1A), and hence they belong to the native basin of attraction.

A note concerning the definition of the native conformation used in our simulations is in order. In our models and in other studies (3, 17) it is found that the ends are frayed, which is a reflection of the low stability of the folded state. If the contacts corresponding to these terminal residues are excluded from the definition of the first passage time, then τ_F reduces by about 30%. More importantly, we find no change in the mechanism of hairpin formation.

Different scenarios for the relation between collapse and folding emerge depending on the value of foldability index σ (16): Polypeptide chains with small σ collapse and fold almost synchronously. In other words, τ_c/τ_F ≈ O(1), where τ_c is the time scale for collapse. We have computed 〈R_g(t)〉, P_u(t), and the dynamics of the fraction of the native contacts 〈Q(t)〉 by averaging over 200 independent trajectories at temperatures slightly below T_F (T_s = 0.82T_F) for the Gō model. On the time scale τ_c the radius of the gyration decreases sharply (blue curve in Fig. 3A). The initial collapse time τ_c is approximately 0.2τ_F, where the folding time (= 0.04 μs) is computed by using P_u(t) (green curve in Fig. 3A). Thus, the initial event in the refolding process is the collapse of the polypeptide chain.

Additional insight into the mechanism of β-hairpin formation may be obtained by examining the kinetics of formation of the HBs 〈N_HB(t)〉 and the dynamics of contacts between the residues in the hydrophobic cluster (HC) 〈Q_HC(t)〉. It is suspected that much of the inherent stability of this β-hairpin arises from contacts between the residues in the hydrophobic cluster. The time dependence of 〈Q_HC(t)〉 (yellow curve in Fig. 3A) shows that on an average hydrophobic cluster contacts are formed on time scale slightly less than the collapse time τ_c. Only subsequently do the majority of the HBs (on the time scale τ_HB) and other contacts form. A comparison of Fig. 3 A and B (in which the kinetics of formation of all HBs is displayed) shows that the acquisition of contacts in the HC does not lead to the rapid formation of HBs close to these residues. We should also emphasize that although HB_9–8⁸ is preformed it does not lead to rapid assembly of the hairpin (Fig. 3B), i.e., it does not act as a nucleation site. The formation of HBs (to a large extent) starts near the turn and proceeds by a zipping mechanism described by Munoz et al. (3). Formation of all native contacts, leading to the assembly of the hairpin, takes place of the time scale ≈τ_F. Conformations illustrating the structural changes that take place on the time scales τ_c (collapse and formation of HC contacts), τ_HB (formation of HBs by kinetic zipping mechanism), and τ_F (folding time) are shown in Fig. 3C. Animations are available at www.glue.umd.edu/∼klimov.

Identification of Transition State (TS) Structures by Cluster Analysis.

We have used a pattern recognition method based on the cluster analysis technique to identify TS structures in the two models (18). We anticipate (this is explicitly shown in our analysis) that the formation of a stable hairpin should be preceded by the formation of at least a few contacts between the two strands (19), which ensures a rapid access to the native conformation. This kinetic pattern is very reminiscent of a nucleation process. Our method, described in detail elsewhere (18), is readily suited to identify the TS structures that are responsible for interstrand contacts. We should note that although the TS structures are, in general, not unique (20) their number is small (21, 22), especially in a system as simple as the β-hairpin.

Gō model.

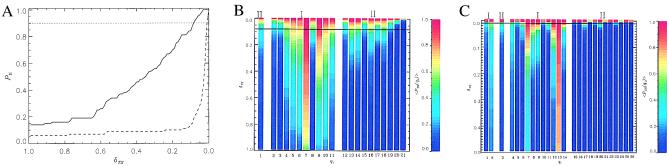
The TS structures were searched at T_s = 0.82T_F, where the folding time is minimal. We generated 100 trajectories so that our results are statistically reliable. We searched for TS structures in every folding trajectory within the time interval (1 − δ_TS)τ_1,i, τ_1,i. We chose δ_TS (= 0.08) from the condition P_II(δ_TS) = ξ (= 0.9), where P_II(δ_TS) is the probability of forming at least one interstrand (type II) contact. The relatively sharp increase in P_II(δ_TS) for δ_TS ≲ 0.5 (see Fig. 4A) ensures us that no qualitative changes are expected upon changing ξ within certain limits. Our identification of TS structures also requires that the contacts be stable (with some tolerance) within the time interval given above. We also varied δ_TS to get a physically reasonable picture of the properties of TS structures which is important because the underlying reaction coordinate is unknown.

Figure 4.

(A) Kinetic probability of forming at least one interstrand contact P_II(t) for the Gō (solid curve) and the KT (dashed line) models as a function of δ_TS, which reflects the progress to the native state. Data are obtained at T = 0.82T_F and T ≈ T_F, respectively, by analyzing 100 trajectories. We assume that the passage of TS occurs at the level of P_II = 0.9 (dotted horizontal line). (B and C) Color-coded kinetic probabilities P_TS(q_i) for the contacts labeled q_i to be formed in the TS for the Gō (B) and KT (C) models. P_TS(q_i) are represented by a color profile at given value of δ_TS. P_TS(q_i) for most intrastrand contacts (type I) rapidly increase, while P_TS(q_i) for interstrand contacts (type II) remain low until the late stages of folding. Then the probabilities P_TS(q_i) for interstrand contacts explosively grow, underscoring the dynamic cooperativity of β-hairpin assembly. For the Gō model the contact labels q_i = 1, … , 21 represent the following native contacts (the numbers in parentheses are residue numbers): 1 (8–9), 2 (15–16), 3 (1–3), 4 (2–4), 5 (3–5), 6 (4–6), 7 (5–7), 8 (9–11), 9 (11–13), 10 (12–14), 11 (13–15), 12 (6–9), 13 (6–11), 14 (5–12), 15 (6–13), 16 (3–12), 17 (4–13), 18 (3–14), 19 (4–15), 20 (2–15), and 21 (2–16). For the KT model (q_i = 1, … , 26) we have 1 (4–5), 2 (5–6), 3 (8–9), 4 (15–16), 5 (1–3), 6 (2–4), 7 (3–5), 8 (4–6), 9 (5–7), 10 (6–8), 11 (9–11), 12 (11–13), 13 (12–14), 14 (13–15), 15 (6–9), 16 (7–10), 17 (6–11), 18 (5–11), 19 (4–11), 20 (5–12), 21 (5–13), 22 (3–12), 23 (4–13), 24 (2–13), 25 (3–14), and 26 (2–15).

By analyzing each trajectory we identified structures in the TS region (δ_TS = 0.08), using the conditions given above. In each trajectory only a subset of native contacts is formed in the TS region. Their formation is preceded by the repeated collisions and break-up of various native contacts. Rather than analyze these trajectories in detail we present in Fig. 4B the color-coded kinetic probabilities P_TS(q_i) (the residues involved in the contacts q_i are given in the legend to Fig. 4 B and C) averaged over 100 trajectories as a function of δ_TS. Even in the early stages of folding (δ_TS ≈ 1.0, t ≪ τ_c or τ_F) certain native contacts form with high probability. These are local intrastrand (type I) contacts, which occur only along the first or the second β-strands. At these early stages of folding P_TS(q_i) for interstrand contacts (type II contacts in Fig. 4B) are negligible. The TS structure cannot involve only local intrastrand contacts, since their formation alone does not lead to a stable native state. The profiles P_TS(q_i) change dramatically as δ_TS decreases. Starting with δ_TS = 0.08 (Gō model), which we identify with a TS region, P_TS(q_i) of certain interstrand contacts (contacts labeled q_i = 13, 14, 16, 18 between residues 6–11, 5–12, 3–12, 3–14) exceed 0.5. Strikingly, three of these contacts belong to the HC (Fig. 1B). Hence, we conclude that formation of the contacts between strands is necessary for subsequent rapid formation of the native state in a dynamically cooperative manner (Fig. 4B).

We computed a number of overall characteristics of the TS conformations, such as the fraction of native contacts 〈Q_TS〉, the radius of gyration 〈R_g,TS〉, and the contact order 〈S_TS〉 (23). These quantities are averaged over the conformations constituting the clusters at the time (1 − δ_TS)τ_1i. On an average the TS structures are compact (〈R_g,TS〉/R_g,N〉 = 1.06) and native-like (〈Q_TS〉 = 0.64). The fluctuations in the distributions are small (unpublished results), implying that there is only a small number of TS structures (see below). The distribution of the contact order 〈S_TS/S_N〉 with respect to the native value is found to be relatively broad with a slight shift toward local interactions. This finding emphasizes the role of both local and nonlocal contacts in the TS.

The diversity of the TS structures and their characteristics can be inferred by applying the cluster analysis to the ensemble of TS conformations. There are two main TS clusters, which are composed of rather compact but structurally different conformations. Approximately two-thirds of folding trajectories pass through the dominant TS (TS1), which is native-like (Fig. 3D). On an average, TS1 contains 15.1 native contacts (of which 7.9 are interstrand) and 10.7 HBs. The hydrophobic cluster is fully formed in TS1. The activation energy for the passage from the unfolded state U to the native state through this TS is negative (E_a,1 ≈ −1.9 kcal/mol). (Note the energy of U is calculated as a thermal weighted average over all conformations with less than 4 HBs at the simulation temperature.) The remaining one-third of unfolded peptides reach the native state through the second TS (TS2), which is less structured than TS1 and has significantly smaller native content. There are, on average, 12.3 native contacts (of which 5.5 are interstrand) and 5.9 HBs, which implies that roughly only half of the native interactions are formed. Interestingly, the hydrophobic cluster contains two of the three contacts formed. The activation energy for TS2 is higher (E_a,2 = 0.18 kcal/mol). The presence of a dominant ordered native-like TS with negative activation energy is consistent with the experiment and statistical mechanical model developed by Munoz et al. However, our results suggest that the dominant hairpin TS1 is more ordered than that predicted by Munoz et al. (3, 6).

KT model.

The major challenge in the analysis of the TS structures in the KT model is the dramatically increased folding time scales. To deal with a manageable number of structures we recorded the instantaneous conformations for cluster analysis at the intervals Δt = 0.6(1 + [τ_1i/6000]) ns. For this analysis we generated 100 trajectories at T_F. The value of δ_TS for the KT model using P_II(δ_TS) = ξ (= 0.9) is 0.01 (Fig. 4A). A comparison of the kinetic probabilities P_TS(q_i) for the Gō (Fig. 4B) and KT (Fig. 4C) models shows that qualitatively these figures are similar. In particular, at times less than τ_c (large δ_TS) only intrastrand contacts are formed. However, rapid assembly of the β-hairpin occurs only when interstrand contacts begin to form. This is seen in the dramatic increase of P_II(δ_TS) at δ_TS ≳ 0.01 (Fig. 4A). Fig. 4C shows that the dynamic cooperativity is much greater in the KT model than in the Gō model. This is seen in the explosive growth of P_TS(q_i) for interstrand contacts and rapid formation of β-hairpin at δ_TS < 0.01. Thus, in complete agreement with the results obtained for the Gō model, we conclude the β-hairpin reaches the TS when the contacts between the strands start to form. Consistent with the results for the Gō model, P_TS(q_i) are not determined by the strength of native contacts (data not shown), which emphasizes the role of topology in selecting the folding pathways.

The structural characteristics of the TS conformations (calculated with δ_TS = 0.01) show that on an average they are highly structured. The TS conformations have on average about 50% of native contacts. The average contact order (more precisely, the ratio of the contact order of the TS ensemble to the native value) 〈S_TS/S_N〉 is equal to 0.80, which implies that local contacts are weakly dominant in the TS.

The comparison of the results for the Gō and KT models gives a consistent picture for TS structures. The TS analysis suggests the following folding scenario for a β-hairpin. The local contacts are formed extremely fast at early stages of folding, but their formation by themselves is not sufficient for reaching the native fold. The β-hairpin passes the TS region at later stages of folding when interstrand contacts form in a dynamically cooperative manner that guarantees quick native state assembly.

Folding Properties of β-Hairpin Mutants: Folding Speed and Mechanism Depend on the Stiffness of the Turn.

We used the Gō model and studied two mutants, M1 and M2, in which the hydrophobic cluster (residues 3W, 5Y, 12F, 14V) is moved either to the loop region (M1) or to sequence termini (M2). The resulting sequences are GEDTWDYATFTVTKTE (M1) and WEYTGDDATKTETFTV (M2). Moving the HC should affect the stiffness of the turn as measured by the bending rigidity κ. We expect that κ_M1 > κ_WT > κ_M2. The relative differences between the values of κ are expected to be small. If a continuum description is used, then the free energy of the polypeptide chain upon forming a hairpin can be written as F ≃ (κ/2)(L/R²) − (l_H/a)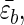 where 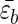is the average gain per residue due to interstrand interactions, l_H is the length of the strand, R is the curvature of the hairpin, and L = 2l_H + πR. Minimizing this with respect to R gives R ≈ (al_pL)^1/3[k_BT/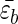]^1/3, where the persistence length l_p = κ/k_B, where k_B is the Boltzmann constant. This suggests that sequences with stiff turns have large turn radius, and hence their formation may require overcoming larger free energy barriers. On the basis of this argument we predict that τ_F^M1 > τ_F^WT > τ_F^M2.

To test this prediction we performed simulations to probe the thermodynamics and kinetics of the two mutant sequences. The collapse temperatures T_θ are 315 K and 340 K for M1 and M2, respectively. The corresponding values for the folding transition temperatures are 264 K and 327 K. The most significant and meaningful changes in folding characteristics are seen in the degree of cooperativity Ω_c and the foldability index σ. Mutant M1 has a lower folding cooperativity (Ω_c = 0.62) and, consequently, stability as indicated by a noticeable decrease in Ω_c derived from 〈Q(T)〉. Recall for the WT Ω_c = 0.82. In contrast, there is an enhancement in cooperativity (and, therefore, stability) in the mutant M2. Indeed, Ω_c = 1.42 for M2 is almost twice as large as for WT. Other studies have reached different conclusion on cooperativity (24).

Changes in cooperativity match those observed for the foldability index (σ = 0.16 for M1, 0.11 for the WT, and 0.04 for M2). Since σ is coupled with the folding rates (4, 16), we expect that M2 sequence should fold faster than WT. Because σ values for WT and M1 are rather close, we expect M1 to fold on similar or slightly larger time scales. These expectations are confirmed by kinetic simulations, in which we calculated folding times τ_F at the constant T_s ≲ T_F. Similar results are obtained at two different temperatures. We found that τ_F^M2 ≃ 0.6τ_F^WT, i.e., M2 folds faster than the WT (τ_F^WT = 0.04 μs). The folding time for M1 is τ_F^M1 ≃ 1.1τ_F^WT. Thus, thermodynamic analysis of WT and both mutants suggests that moving the hydrophobic cluster to the loop compromises the folding cooperativity and stability and leads to somewhat longer folding times. In contrast, placing strong hydrophobic interactions closer to the hairpin ends enhances cooperativity (and stability) and folding rates. We expect these effects to be more dramatic in the real hairpins, where nonnative interactions participate in slowing the folding kinetics. Our findings also suggest that the folding mechanism depends on the rigidity of the hairpin.

Conclusions

Simple off-lattice models (with side chains represented as united atoms) of 16-residue β-hairpin-forming peptide are used to provide description of the kinetic and thermodynamic data. The simulations for the WT qualitatively reproduce all the important experimental observations, including a broad two-state thermodynamic transition, two-state folding kinetics, and the temperature dependence of the folding rates with an apparent negative activation energy. With this calibration we have made a number of theoretical predictions for the WT and two mutants.

(i) The mechanism of β-hairpin formation involves several structural stages. On the collapse time scale τ_c the contacts between the residues in the hydrophobic cluster form. Their formation is followed by zipping of HBs on the time scale τ_HB, predominantly starting from those near the turn. This is in accord with our earlier studies, which showed that nucleation of β-sheet formation starts from the turns (3, 21). Finally, rapid assembly of the hairpin takes place in a dynamically cooperative manner on the folding time scale τ_F. The rate-limiting step is the formation of sufficient number of interstrand contacts, and this is the only kinetic barrier. Estimate for τ_F/τ_c for the Gō model is between 3 and 5 and is expected to be the same for more realistic models as well. The value of τ_HB/τ_c ≈ 1.3. This implies that τ_c ≈ 2 μs and τ_HB ≈ 2.6 μs, assuming that τ_F ≈ 6 μs. Thus, in the experiment it would be hard to draw a distinction between the collapse and folding dynamics in this 16-mer peptide, especially given the low stability of the folded state and the small changes in the radius of gyration. Even in our simulations these changes can be detected only by using averages over hundreds of trajectories, and hence cannot be easily established in all-atom simulations.

(ii) On an average the dominant transition state structures are found to be highly compact, with the radius of gyration being only 6% larger than that for the native conformation. Fluctuations in these quantities are relatively small. The transition states, the number of which is very small, are highly ordered, with a large fraction of native contacts already formed.

(iii) We predict that the folding kinetics of mutants, which were generated by moving the hydrophobic cluster either close to the turn (M1) or near the termini (M2), is determined by the intrinsic stiffness of the hairpin. Both theoretical arguments and explicit simulations suggest that folding times are arranged as τ_F^M1 ≳ τ_F^WT > τ_F^M2. The folding mechanism is determined by the rigidity of the turn. This finding implies that the complex mechanism described for WT may not hold for the mutants M1 and M2.

The models used here are not without limitations. In addition to the obvious limitation of the force fields used (this is also shared in all-atom simulations that rely on transferability of potentials) the neglect of explicit water molecules may be serious. Nevertheless, the combination of simple arguments and detailed simulations using semirealistic models has allowed us to not only reproduce experimental measurements but also make several testable predictions.

Abbreviations

WT

wild type

HB

hydrogen bond

PDB

Protein Data Bank

KT

Klimov and Thirumalai

TS

transition state

Note

After this paper was completed we became aware of two papers on hairpin formation (17, 25). Our results for the folding mechanism, including the importance of hydrophobic cluster formation and folding (for WT) by passing through certain (short-lived) well-defined structures, are in agreement with molecular dynamics simulations (17). The finding that β-hairpins share many features in common with proteins (17) is in agreement with the present study as well as earlier reports (4, 7).