Non-random nature of spontaneous mIPSCs in mouse auditory brainstem neurons revealed by recurrence quantification analysis

Abstract

A change in the spontaneous release of neurotransmitter is a useful indicator of processes occurring within presynaptic terminals. Linear techniques (e.g. Fourier transform) have been used to analyse spontaneous synaptic events in previous studies, but such methods are inappropriate if the timing pattern is complex. We have investigated spontaneous glycinergic miniature synaptic currents (mIPSCs) in principal cells of the medial nucleus of the trapezoid body. The random versus deterministic (or periodic) nature of mIPSCs was assessed using recurrence quantification analysis. Nonlinear methods were then used to quantify any detected determinism in spontaneous release, and to test for chaotic or fractal patterns. Modelling demonstrated that this procedure is much more sensitive in detecting periodicities than conventional techniques. mIPSCs were found to exhibit periodicities that were abolished by blockade of internal calcium stores with ryanodine, suggesting calcium oscillations in the presynaptic inhibitory terminals. Analysis indicated that mIPSC occurrences were chaotic in nature. Furthermore, periodicities were less evident in congenitally deaf mice than in normal mice, indicating that appropriate neural activity during development is necessary for the expression of deterministic chaos in mIPSC patterns. We suggest that chaotic oscillations of mIPSC occurrences play a physiological role in signal processing in the auditory brainstem.

1. Introduction

Miniature spontaneous postsynaptic currents (mPSCs) are thought to represent the spontaneous release of the neurotransmitter contents of individual vesicles from the presynaptic terminal in the absence of presynaptic nerve impulses. Spontaneous release may be influenced by a number of different processes occurring in the presynaptic terminal, and some of these processes may generate distinct oscillations or bursting patterns of release (Abenavoli et al. 2002; Collin et al. 2005). At the neuromuscular junction, miniature endplate currents (mEPCs) were classically thought to be random and memory-less, although some studies have described self-similarity (fractal nature) in mEPC intervals over time, and addition of drugs or pre-stimulation may cause release to be periodic (Lowen et al. 1997; Van der Kloot et al. 1999). Periodicity of spontaneous neurotransmitter release has been described by several authors (Meiri & Rahamimoff 1978; Pawson & Grinnell 1989; Kriebel & Bridy 1996; Lowen et al. 1997), and could be caused by, for example, oscillations in Ca²⁺ in the presynaptic terminal (Melamed et al. 1993; Van der Kloot et al. 1999; Llano et al. 2000; Emptage et al. 2001; Simkus & Stricker 2002; Collin et al. 2005). Detailed investigation of the nature of release, especially periodicity, may provide important insights into processes occurring within the presynaptic terminal. Furthermore, the properties of nerve-evoked synaptic transmission may be influenced by changes in the resting calcium concentration in the presynaptic terminal.

In our previous study of miniature synaptic currents (mIPSCs) in brainstem auditory neurons, we did not observe any effect of depleting internal calcium stores on conventional mIPSC interval histograms (Lim et al. 2003), but this does not rule out the possibility that Ca²⁺ fluctuations may cause or modulate periodicity in mIPSCs. Presynaptic terminals in the CNS are equipped with internal Ca²⁺ stores which may act as coupled-oscillators and generate periodicity or determinism in spontaneous neurotransmitter release. However, with many presynaptic terminals contacting a neuron, and multiple calcium stores in each terminal, it is unlikely that spontaneous neurotransmitter release would follow a simple periodic process. Instead, spontaneous release is more likely to represent the summation of a number of processes with different frequencies, which may also change with time. However, the absence of obvious defined cycles does not necessarily mean that the system is random. It may, for example, be represented by a chaotic system with complex dynamics, or it may exhibit self-similarity (fractal nature; Lowen et al. 1997). Under these circumstances, the use of linear analytical methods (i.e. Fourier transform or autocorrelation) to assess determinism in spontaneous neurotransmitter release is not adequate. Significantly, chaotic behaviour has been shown to enhance information transfer in the central nervous system, and it is important to use methods that are capable of detecting chaos (Schweighofer et al. 2004).

In this work, we have investigated the patterns of inter-event intervals (IeIs) of glycinergic inhibitory mIPSCs in principal cells of the medial nucleus of the trapezoid body (MNTB) using recurrence quantification analysis (RQA; Nieminen & Takala 1996; Faure & Korn 1997; Filligoi & Felici 1999). We also used nonlinear methods to test for chaos and fractal behaviour in the series of IeIs of mIPSCs. We then investigated a possible role of internal calcium stores in generating periodicity in mIPSCs and examined whether developmental deficits observed in glycinergic transmission in MNTB neurons of congenitally deaf mice (dn/dn; Bock et al. 1982; Leao et al. 2004a) alter the dynamics of spontaneous neurotransmitter release. Our results show that RQA is much more sensitive in detecting periodicities in mPSCs than previous linear methods. Importantly, we use RQA to show that, in contrast to our previous conclusion, there are periodicities in mIPSCs in auditory brainstem neurons that are most probably related to oscillations in intra-terminal calcium stores. We further show that these oscillations–which develop in the absence of spontaneous auditory nerve activity–are chaotic, and that this chaotic nature is absent in congenitally deaf mice. We suggest that chaos may play a physiological role in synaptic development, and in signal processing in the auditory brainstem.

2. Material and Methods

(a) Electrophysiology

Normal (CBA strain, 12–14 days postnatal) and congenitally deaf (dn/dn with CBA background, 12–14 days postnatal) mice were decapitated without anaesthetic in accordance with the guidelines Australian National University Animal Experimentation Ethics Committee protocol. The brain was removed and transverse slices (150 μm) were made of the MNTB using an EMS (USA) oscillating tissue slicer, as previously described (Lim et al. 2003; Leao et al. 2004a,b). Data acquisition and analysis was performed using Axograph (Axon Inst.) and Matlab (Mathworks) with the CRP Toolbox (implementation of recurrence analysis can be accessed at http://tocsy.agnld.uni-potsdam.de/crp.php). The amplitudes of spontaneous IPSCs were measured using semi-automated detection procedures (Axograph v. 4.0), as previously described (Clements & Bekkers 1997). Results are expressed as mean±s.e. Significance of results was assessed using a paired t-test, with significance indicated by p<0.05, and the Kolmogorov–Smirnov test.

Drugs were added to the perfusate, as indicated: 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; Tocris), (±)-2-amino-5-phosphonopentanoic acid (D-AP5; RBI), bicuculline methochloride (Tocris), strychnine hydrochloride (Sigma), TTX (Alamone), ryanodine (Sigma). Spontaneous glycinergic mIPSCs were isolated by the use of TTX (1 μM), CNQX (10 μM), D-AP5 (30 μM), and bicuculline methochloride (10 μM). Inhibitory currents were determined by a chloride reversal potential of 0 mV, due to the (symmetrical) chloride concentration in the patch electrode, and −60 mV holding potential. Ruthenium red (100 μM) was added to the extracellular solution to increase the frequency of spontaneous mIPSCs and allow a direct comparison with our previous studies (Lim et al. 2003; Leao et al. 2004a). Recordings were started 10 min after drug application.

(b) Recurrence quantification analysis

RQA is a nonlinear tool used to quantify the amount of deterministic structure in a data series (Nieminen & Takala 1996; Filligoi & Felici 1999), and we have applied RQA in the present study to the analysis of the times of occurrence of spontaneous neurotransmitter release. A number of parameters were calculated from the recurrence plots (RPs) for quantitative comparison: %recurrence, %determinism, maxLine, entropy, %laminarity (%lam) and trapping time (TT). If RQA indicated a non-random structure in mIPSC occurrences, then the Lyapunov exponent and Allan Factor were calculated to test the system for chaotic and fractal behaviour (Rosenstein et al. 1993; Zbilut et al. 2000; Bacchereti 2004). The implementation of RQA and example RPs for random, periodic and complex time series, parameter definitions and a decision tree illustrating the analysis are fully described in the electronic supplementary material, part A. A powerful MATLAB (Mathworks, USA) toolbox used in some of our RQA calculations can be found at http://www.agnld.uni-potsdam.de/˜marwan/toolbox/.

(c) mIPSC model

In order to test the sensitivity of RQA to detect a few rhythmical points embedded in a larger random data series, we modelled mIPSC recordings by summing simulated waveforms (mean peak amplitude=76 pA, mean rise time=0.36 ms, mean decay time constant=2.5 ms; IeIs were randomly selected from an exponential distribution fitted from an experimental dataset; Leao et al. 2004a). Modelled mIPSCs were then added to normally distributed noise and were detected in the resulting trace using the template method (Clements & Bekkers 1997). To introduce periodicity, two or three sinusoids with various frequencies also triggered mIPSCs: three cases were modelled (two low-frequency sinusoids: 0.05 and 0.01 Hz; two ‘high-frequency’ sinusoids: 0.1 and 0.05 Hz; three sinusoids: 0.1, 0.05 and 0.01 Hz).

3. Results

(a) Simulations demonstrate the ability of recurrence plots and recurrence quantification analysis to detect periodicities in mIPSC IeIs

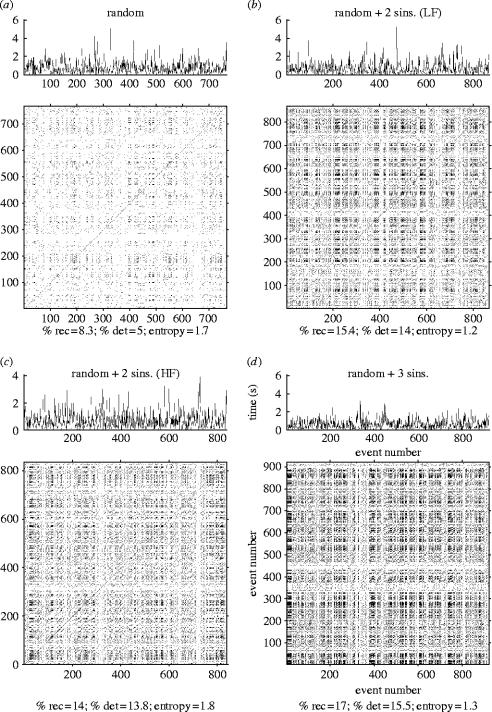
RPs provide a convenient graphical means of revealing patterns in IeIs. As described in §2, we simulated sets of mIPSCs and then analysed the data using the same procedures intended for the experimental data. Figure 1a illustrates the RP for a purely random set of IeIs, showing the expected sparse pattern of dots with little structure. Figure 1b–d shows RPs for the same random dataset but with the addition of small sinusoidal periodicities (see §2). The RPs show an obvious increase in density, suggesting underlying non-random structures. Quantification of %recurrence and %determinism for the examples shown in figure 1a–d revealed respective values of 8.3% and 5% for purely random release (figure 1a), 15.4% and 14% for random plus two low-frequency sinusoids (figure 1b), 14% and 13.8% for random plus high-frequency sinusoids (figure 1c) and 17% and 15.5% for random plus three sinusoids (figure 1d). In order to assess the consistency and reliability of the quantification of %recurrence and %determinism, multiple simulations were performed using different random samples but with the same added sinusoidal parameters. The results gave respective mean±s.e. values (n=5) of %recurrence and %determinism of 9.4±0.5% and 3.9±0.3% (mean sample size=812) for purely random release, 15.7±0.8% and 12.5±0.1% (mean sample size=822) for random plus two low-frequency sinusoids, 21.7±1.2% and 14.2±1.1% (mean sample size=824) for random plus the high-frequency sinusoids, and 22.7±1.6% and 17.6±0.8% (mean sample size=822) for random plus the three sinusoids. All of the %recurrence and %determinism values for the simulations with added sinusoids were highly significantly different (t-test; p<0.001) from the values for purely random release. These simulations demonstrate the potential value of RPs and RQA for the detection and analysis of patterns in mIPSC IeIs.

Figure 1.

Recurrence plots of modelled data reveal embedded periodicity in mIPSC IeIs. mIPSC IeIs (top) and the respective recurrence plots (bottom). Global recurrence quantification analysis variable values are shown below each plot. (a) Purely random release. (b) Random plus two low-frequency (LF) sinusoids (0.05 and 0.01 Hz). (c) Random plus two ‘high-frequency’ (HF) sinusoids (0.1 and 0.05 Hz). (d) Random plus three sinusoids (0.1, 0.05 and 0.01 Hz).

(b) Experimental application of RQA to mIPSCs

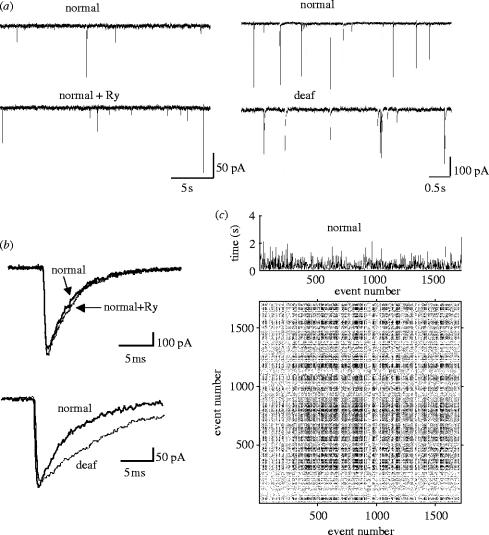
Patch-clamp recordings were made from 52 MNTB neurons. Criteria for accepting mIPSC recordings were: (i) to avoid monotonic trends in the data, the number of events versus time regression should display a correlation coefficient r²<0.05; (ii) mIPSC frequency should be greater than 0.8 Hz, to provide sufficient data points. Twenty-seven cells satisfied these criteria, 18 MNTB principal neurons from normal mice and nine cells from deaf mice. Passive membrane properties did not differ between normal and deaf mice (Leao et al. 2004b). Resting membrane potential, input resistance and membrane capacitance for normal and deaf mice were, respectively: −64±0.3 mV and −64±0.5 mV; 185±3 MΩ and 178±5 MΩ; 27±0.3 pF and 27±0.5 pF (p>0.05 in all cases). Glycinergic mIPSCs were isolated as in §2 (see also Leao et al. 2004a). Addition of 1 μM strychnine abolished all spontaneous mIPSCs, demonstrating that mIPSCs were glycinergic (data not shown). The recording duration for each experimental condition was 10 min. Comparisons between normal and deaf mice were performed using datasets with similar mIPSC frequencies (figure 2a). mIPSC mean amplitude was greater in normal mice than in deaf mice (120±6 pA and 71±2 pA, respectively, p<0.04) and half-width was greater in deaf mice than in normal mice (2.9±0.1 ms versus 2.3±0.1 ms, respectively, p<0.05; figure 2b). mIPSC frequency did not differ significantly between normal and deaf mice (1.6±0.06 Hz and 2.14±0.5 Hz, respectively, p<0.05). Addition of ryanodine in nine neurons (normal mice) did not significantly change mIPSC amplitude, half-width or frequency (figure 2b). Figure 2c illustrates the IeIs (top) and the RP plot for mIPSCs recorded in a normal mouse. The RP shows a high density of dots, suggesting an underlying non-random pattern in the IeIs.

Figure 2.

Glycinergic mIPSC frequency, amplitude and kinetics are not altered by ryanodine. (a) Voltage-clamp recordings showing mIPSC frequency does not change after addition of ryanodine (left). mIPSCs from normal and deaf mice (right). Datasets with similar frequencies in the two groups were used in this study. (b) Overlaid mIPSCs before and after application of ryanodine (top), and overlaid mIPSCs from normal and deaf mice (bottom). mIPSC kinetics and mean amplitude are not affected by ryanodine; however, decay times are slower in deaf mice in comparison to normal mice. (c) Example of a recurrence plot of mIPSC IeIs from a normal mouse. IeIs are shown at the top.

Figure 3a shows the total distribution of mIPSC IeIs for normal mice under control conditions. The Kolmogorov–Smirnov test indicated that this distribution was significantly different from an exponential distribution (p<0.05). mIPSC IeI distributions differed between control and control+ryanodine (figure 3b; Kolmogorov–Smirnov test, p<0.01). IeIs were also different between normal and deaf mice (p<0.05). Figure 3c displays the IeI histogram for mIPSC's recorded in deaf mice. Sherman statistics (ω_n), however, suggested that IeI could be fitted by exponential distributions (Van der Kloot et al. 1999). Exponential data series are expected to have a Sherman statistic mean ω_n of 1/e (0.37). Mean ω_n value for mIPSC IeI for normal mice under control conditions was equal to 0.38±0.002, and addition of ryanodine to the same set of cells did not change ω_n significantly (0.36±0.001). Deaf mice IeI had a mean ω_n=0.0.38±0.002 versus ω_n=0.37±0.001 in normal mice. Gamma renewal processes could also be fitted reasonably well to the IeI distributions (figure 3e). A gamma process is represented by the two-parameter gamma density function $f(x|a,b)=t^{a-1}{\text{e}}^{-x/b}/\Gamma (a)b^a$, where a is the order of the gamma process, b is the characteristic time and Γ(·) is the gamma function. Values of a for normal mice controls and normal mice with ryanodine were the same (both around 1.1±0.01) and normal versus deaf mice values also did not differ significantly (1.1±0.01 versus 1±0.02, respectively). Power spectra of (mIPSC) events per second did not show any periodicity in normal mice (control), normal mice in the presence of ryanodine or deaf mice. In fact, power spectral plots suggested random processes (figure 3d).

Figure 3.

mIPSC IeI histograms. (a) mIPSC IeI histogram from normal mice (13 448 mIPSCs, n=9 cells). Inset: cumulative density function (CDF) of IeI's (solid line, normal mice) and an exponential distribution with the same mean (*; dashed line). (b) mIPSC IeI histograms from normal mice: control (white bars, 8913 mIPSCs, n=9 cells) and following ryanodine (black bars, 8347 mIPSCs, n=9 cells). Inset: CDFs of IeI from control and following ryanodine (*). (c) mIPSC IeI histogram from deaf mice (13 937 mIPSCs, n=9 cells). Inset: cumulative density of IeIs (solid line, deaf mice) and an exponential distribution with the same mean (*; dashed line). (d) Power spectra (db). (i) Power spectra of one normal mouse cell before (1215 mIPSCs, thick solid line) and after ryanodine addition (1285 mIPSCs, thin solid line) and a deaf mouse cell with similar mIPSC frequency (1195 mIPSCs, dashed line). (ii) Modelled mIPSCs power spectra; purely random release (thick solid line), random release plus two periodic oscillators (0.1 and 0.01 Hz sinusoids) and random plus three sinusoids (0.1, 0.05 and 0.01 Hz; see text for explanation). (e) Examples of semilogarithmic plots of IeI histograms (solid lines) and the fit obtained by a gamma distribution (dashed lines; see text for details).

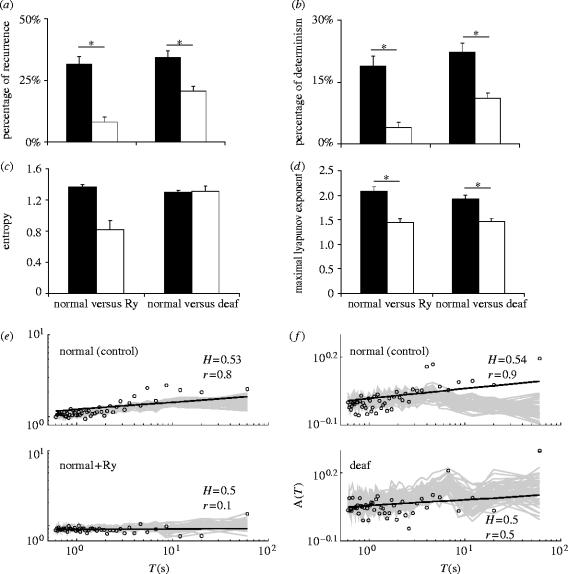
RQA variables, however, revealed a striking difference between normal mice (control) and normal mice+ryanodine. Mean %recurrence values under control conditions and after ryanodine application (normal mice) were 32±3% and 8±2%, respectively (p<0.01), and mean %determinism values were 18±2% and 4±1%, respectively (p=0.01; figure 4a,b). It was not possible to calculate maxLine in most ryanodine cases due to low recurrence. Mean entropy was larger under control conditions, but the difference was not significant (1.4±0.03 and 0.8±0.1 for normal mice before and after ryanodine addition, respectively; figure 4c). Vertical and horizontal structures differed significantly between normal mice control and ryanodine; %lam values were 38.3±3% for normal mice control and 8.5±2% for ryanodine (p<0.02); TT values for normal mice control and ryanodine were 38.3±3% and 12±2.3 s, respectively (p=0.02). Thapsgargin addition in four cells caused a similar change to RQA variables (see electronic supplementary material, part B).

Figure 4.

Recurrence quantification analysis summary for mIPSCs from normal and deaf mice, and following ryanodine. (a) Mean %recurrence, (b) mean %determinism, (c) mean entropy and (d) mean maximal Lyapunov exponent for normal mice control (black bars, left) and following addition of ryanodine (white bars, right); normal (black bars, left) versus deaf mice (white bars, right). (e) Logarithmic Allan factor (A(T) versus T—see text for details) plots of a normal mouse cell before (mIPSC frequency=1.4 Hz; top) and after ryanodine addition (mIPSC frequency=1.4 Hz; bottom). Grey traces represent Allan factors calculated from 100 sets of surrogate data. (f) Same as (e), but the top graph shows a normal mouse cell (mIPSC frequency=1.8 Hz) while the bottom shows a deaf mouse cell A(T) versus T plot (mIPSC frequency=1.9 Hz). (*) denotes significant difference (p<0.05).

Deaf mice RQA also showed significant differences when compared to normal mice. Mean %recurrence values were 34±3% in normal versus 21±2% in deaf mice (p=0.01) and %determinism values were 22±2% in normal versus 11±1% in deaf mice (p=0.02; figure 4a,b). Diagonal line lengths (maxLine) did not differ significantly between normal and deaf mice (25±2 and 30±2 s, respectively). Mean entropy did not differ significantly between normal and deaf mice (1.3±0.02 and 1.3±0.06, respectively; figure 4c). %lam was significantly different between normal mice and control (35±2% and 22.3%, respectively, p=0.01), but not TT (31±2 s versus 25±2 s, respectively). There was no correlation between any of the RQA variables and mean mIPSC amplitude or half-width.

Lyapunov exponents were calculated in order to test whether observed differences in RQA before and after ryanodine (normal mice) and between normal and deaf mice could be due to the presence of chaos in neurotransmitter release. A positive Lyapunov exponent is a strong indicator of a chaotic system. Maximal Lyapunov exponents for normal mice mIPSCs were 2.1±0.1 before and 1.4±0.1 following addition of ryanodine (p<0.01; figure 4d). Normal and deaf mice Lyapunov exponents also differed significantly (1.9±0.07 and 1.5±0.07, respectively; p<0.01; figure 4d). Lyapunov exponents and 1/maxLine displayed strong correlations for both normal and deaf mice (r²=0.8, p=0.04 and r²=0.7, p=0.04, respectively). These results indicate that the determinism in mIPSC event intervals is likely to be due to a chaotic process, which is decreased in MNTB neurons in the presence of ryanodine and in deaf mice.

Allan Factor plots are used to indicate whether a process is random, periodic or fractal. A plot with zero slope indicates a random process, a negative slope indicates a periodic process and a positive slope suggests a fractal process (in which case the value of the slope, α, of the power law relationship indicates the power to which fluctuations in the number of events on one time-scale are proportional, or statistically self-similar, to those on longer time-scales; Fadel et al. 2004). Allan factor plots produced several results (figure 4e,f). Normal mice under control conditions displayed six plots with positive α and r>0.6 and two plots where α was negative and r<−0.6. (In the latter two cases, continuous wavelet transform revealed linear periodicities that were not detected by Fourier transform—see electronic supplementary material, part C.) Results from cells in deaf mice and normal mice with addition of ryanodine displayed five plots each with positive α. However, r was greater than 0.6 only in one plot from a deaf mouse and two plots from normal mice plus ryanodine. The Hurst exponent (H, see electronic supplementary material, part A) was also calculated. H is 0.5 for a series in which events are uncorrelated, and if H>0.5, events are positively correlated. H for results from normal mice under control conditions was 0.52±0.002 (mean r=0.71±0.02). If we ignore the low r values for deaf and control mice with ryanodine (mean r=0.4±0.04 and 0.5±0.04, respectively), H was significantly larger in normal mice (control) when compared to deaf mice and to normal mice plus ryanodine (0.52±0.001, 0.5±0.001 and 0.5±0.001, respectively; p=0.03 and p=0.02, respectively). In summary, our results indicate that there is more structure or determinism in mIPSC event intervals in MNTB neurons under control conditions in normal mice, than in MNTB neurons in the presence of ryanodine or in cells from deaf mice.

4. Discussion

Our results demonstrate the application of RPs and RQA to detect periodicity or deterministic behaviour in spontaneous neurotransmitter release. The application of these nonlinear methods is preferable to conventional methods, and we have used RQA to reveal that calcium stores are involved in generating the pattern of spontaneous mIPSCs in principal cells of the MNTB, and that there is less determinism in mIPSC occurrences in MNTB neurons from congenitally deaf mice. This is significant, particularly since we had previously concluded that calcium stores were not involved, based on simple frequency measurements and IeI histograms (Lim et al. 2003).

(a) Internal calcium stores modulate the deterministic nature of mIPSC's

The results with RQA of mIPSCs from normal mice showed a significant deterministic component in spontaneous neurotransmitter release. This component was disrupted by addition of ryanodine, suggesting that the oscillatory nature of mIPSCs could be modulated by internal Ca²⁺ stores. A similar effect in RQA in four cells from normal mice was observed after addition of thapsigargin (an endoplasmic reticulum Ca²⁺-pump blocker), suggesting that the deterministic nature of mIPSCs may be due to oscillations in Ca²⁺ release from the endoplasmic reticulum. Although this is the simplest explanation, it is also possible that altering calcium homeostasis in the presynaptic terminal disrupts some other factor causing oscillations. Owing to the fact that a number of presynaptic terminals may exhibit oscillations independently of each other, the periodicity observed in this study could be masked by its complexity, causing, therefore, linear methods (such as Fourier transform) to be insensitive to the deterministic nature of the neurotransmitter release. The maximal Lyapunov exponents show in fact that determinism in spontaneous neurotransmitter release is a chaotic process rather than a linear oscillator. These values are in agreement with the RQA analysis, reinforcing the capacity of RQA to detect nonlinear rhythmicity embedded in large random series. The absence of fractal behaviour in release has been observed at neuromuscular junctions (Van der Kloot et al. 1999). In our experiments, we did not consistently observe the presence of fractals in mIPSC patterns.

(b) Cochlear development and mIPSC determinism

The small RQA variables and Lyapunov exponents observed in recordings from deafness mice showed that proper cochlear input may play a role in the development of mIPSC event interval patterns or oscillations. In MNTB principal cells, voltage-dependent Ca²⁺ currents are the same in normal and deaf mice (Leao et al. 2004b), but at the endbulb of Held presynaptic terminal, deaf mice show impaired Ca²⁺ buffering (Oleskevich & Walmsley 2002). It is not known whether there is also impaired buffering in presynaptic glycinergic terminals, but there is evidence for altered development of glycinergic transmission in deaf mice (Leao et al. 2004a). A developmental role for calcium oscillations in presynaptic terminals has been suggested by Spitzer (Spitzer et al. 2000; Spitzer 2002).

(c) Physiological implications of deterministic mIPSC IeIs

Our results show that, under control conditions in normal mice, there is a significant degree of determinism in mIPSC IeIs. This determinism can be periodic, chaotic and/or fractal in nature. This naturally raises the issue about whether or not these patterns are of any physiological significance. First, the observation that blocking intracellular calcium stores reduces the determinism to a more random pattern suggests that there are fluctuations or oscillations in the intra-terminal calcium concentration. Calcium oscillations in synaptic terminals may be a common phenomenon and have been directly observed using fluorescent calcium indicators (Collin et al. 2005). Calcium transients have been implicated in synaptogenesis and stabilization of synaptic connections (Lohmann et al. 2005). Interestingly, Sharma & Vijayaraghavan (2003) have demonstrated that calcium transients in presynaptic terminals in the CA3 region of the hippocampus are sufficient to synchronously increase spontaneous release and actually drive postsynaptic pyramidal cells above firing threshold. Furthermore, intra-terminal calcium fluctuations may directly modulate nerve-evoked release probability, since many steps in the vesicle cycle, including mobilization of vesicles, are calcium dependent. In fact, at the frog neuromuscular junction, Pawson & Grinnell (1989) have shown that there is a relationship between oscillation of mEPP frequency and nerve-evoked release efficacy. This evidence suggests that determinism in spontaneous transmitter release may be of considerable physiological significance. A further issue is whether or not the actual pattern (periodic, chaotic and/or fractal) is of significance. It is conceivable that the pattern of spontaneous release may be generated by the same underlying processes, but that different weightings or initial conditions may give rise to different characteristics. If there is strong coupling between terminals via a mechanism such as calcium-induced calcium release, then a periodic process may emerge, as in the case of loosely coupled oscillators (Van Helden & Zhao 2000). If terminals are independent of each other, then a chaotic process may occur. A hallmark of a chaotic process is sensitivity to slightly different initial conditions, and this may arise, for example, with a positive feedback process such as calcium-induced calcium release. Whether a biological process is periodic or chaotic may be very important. For example, Schweighofer et al. (2004) have shown that chaotic firing patterns may actually enhance information transmission in the inferior olive. In the present study, we have demonstrated that mIPSC occurrences in the MNTB are chaotic, and that furthermore, this chaotic nature depends on normal spontaneous auditory nerve activity during development. Our previous results have shown that inhibitory transmission and connectivity are abnormal in congenitally deaf mice before ear canal opening and the onset of acoustic input (Leao et al. 2004a). We suggest that chaotic mIPSC and presynaptic calcium oscillations are necessary for the normal development of inhibitory synaptic transmission in the MNTB.