Efficiency of carcinogenesis with and without a mutator mutation

Abstract

Carcinogenesis involves the acquisition of multiple genetic changes altering various cellular phenotypes. These changes occur within the fixed time period of a human lifespan, and mechanisms that accelerate this process are more likely to result in clinical cancers. Mutator mutations decrease genome stability and, hence, accelerate the accumulation of random mutations, including those in oncogenes and tumor suppressor genes. However, if the mutator mutation is not in itself oncogenic, acquiring that mutation would add an extra, potentially time-consuming step in carcinogenesis. We present a deterministic mathematical model that allows quantitative prediction of the efficiency of carcinogenesis with and without a mutator mutation occurring at any time point in the process. By focusing on the ratio of probabilities of pathways with and without mutator mutations within cell lineages, we can define the frequency or importance of mutator mutations in populations independently of absolute rates and circumvent the question of whether mutator mutations are “necessary” for cancers to evolve within a human lifetime. We analyze key parameters that predict the relative contribution of mutator mutants in carcinogenesis. Mechanisms of carcinogenesis involving mutator mutations are more likely if they occur early. Involvement of mutator mutations in carcinogenesis is favored by an increased initial mutation rate, by greater fold-increase in mutation rate due to the mutator mutation, by increased required steps in carcinogenesis, and by increased number of cell generations to the development of cancer.

The development of a cancer requires multiple steps as suggested by epidemiologic data and animal models (1–5). At least some of these steps are believed to involve oncogenic mutations or other genetic changes.

The mutator hypothesis originally stated that mutations in DNA polymerases and DNA repair enzymes would play a critical role in carcinogenesis by accelerating the acquisition of oncogenic mutations (6). This concept has been broadened to include a variety of mutator mutations that create genetic instability by mechanisms including microsatellite instability, chromosomal instability, and aberrations of checkpoint control (7–10).

An alternative hypothesis is that enhanced rates of genetic instability are not necessary for carcinogenesis and that cancer arises from mutations occurring at the normal rate followed by multiple rounds of lineage selection and expansion (11–14).

These two hypotheses are not mutually exclusive. Indeed it is likely that carcinogenic pathways corresponding to both hypotheses contribute concurrently. For example, carcinogenesis could involve a mutator mutation and subsequent mutations augmented by lineage selection and expansion.

The common outcome of a malignant lineage is likely approachable by numerous pathways, and we postulate that these pathways will be seen in clinical cancers in proportion to their relative efficiencies, irrespective of whether a given pathway occurs at an absolute rate that could potentially account for observed cancer incidence. Thus, the question of whether mutator mutations are “necessary” can be circumvented.

In this paper, we calculate probabilities of cancer arising at a fixed time within a single cell lineage by pathways with and without a mutator mutation. By focusing on the ratio of probabilities of pathways with and without mutator mutations within cell lineages, we can define the frequency or importance of mutator mutations in populations independent of absolute carcinogenesis rates.

Mutator mutations accelerate the acquisition of oncogenic mutations but need not, in themselves, be oncogenic. In cases in which mutator mutations are not oncogenic, they impose an additional delay required for their acquisition. We evaluate this tradeoff in this paper.

Mutator lineages also are at greater risk of accumulating deleterious mutations that reduce their fitness and could lead to extinction [negative clonal selection (NCS)]. This effect has been studied mathematically (15) and found to be relatively small in most situations.

Simplifying Assumptions

We have used a number of simplifying assumptions to establish a mathematical model for analyzing the role of mutator mutations in carcinogenesis. These assumptions and their limitations are discussed below.

1. We assume that the mutation rate, or probability per unit time in oncogenic or mutator loci, is similar to the average mutation rate throughout the genome and that it is relatively uniform except as affected by mutator mutations. It is nonetheless known that mutation hot spots do indeed occur at specific loci throughout the genome. However, hot spots are not known to be characteristic of oncogenic or mutator loci.

2. It is assumed that a critical number of mutation steps are required for cancer development. Mutations in recessive oncogenes are counted as two steps. This critical number of steps may vary among individual tumor types, as classified either by organ site and histology or by modern molecular classification methods.

3. It is assumed that the critical number of mutations may be acquired in any order and in any combination. In fact, for colon cancer and melanoma there is likely a specific order of acquisition of critical mutations (16, 17), and in animal models only certain combinations of oncogenic mutations lead to malignant transformation (4–5). These assumptions do not affect the key calculation of this paper, the relative efficiency of mutator and nonmutator mechanisms, although they do affect the calculation of absolute rates.

4. The model assumes that the sets of oncogenic and mutator mutation loci are mutually exclusive, which is known not to be true in that the retinoblastoma and p53 gene products are both mutator genes and recessive oncogenes (18). This simplifying assumption will lead to a slight underestimate of the importance of mutator mutations in carcinogenesis, because it does not consider a subclass of mutator mutations, such as the retinoblastoma gene product.

5. We assume that cell proliferation and death are balanced for each cell lineage until the critical number of oncogenic mutations are attained, at which point the lineage is highly selected and expands. Expansion of lineages with only a subset of critical mutations (“premalignant” lineages) is not an explicit part of the model. Mutations affecting cellular fitness may be cooperative in their effects such that the most dramatic increase in cellular fitness occurs only at the point of malignant transformation. The degree to which this assumption is true is unknown.

6. We do not need to assume that the probability of mutation in any given nucleotide locus during the lifetime of a single cell and its progeny is considerably less than 1. This assumption is clearly true for a single cell and its progeny in the absence of lineage expansion as for any given cell most nucleotide loci are unmutated. It would not be true in reference to an overall sufficiently large population of N cells, where N is equal to or greater than the reciprocal of the per nucleotide mutation rate per cell generation times the number of cell generations (19), such as would occur in the case of lineage expansion. However, in that instance the model can be reformulated to address the question of which mechanism will produce the most malignant cells. Relative efficiency would be defined as the “expectation value,” i.e., the mean number of expected malignant cells, of one mechanism compared with another. This definition of relative efficiency may be relevant in vivo, where not every malignant cell necessarily leads to a clinical cancer. Therefore, mechanisms that produce more malignant cells are more likely to lead to clinical cancer. In this regard, it is feasible to broaden this type of model to include premalignant lineage expansion.

7. NCS, i.e., selective extinction of mutator lineages due to accumulation of mutations reducing their fitness, is not considered. An analysis of this effect suggests that it is not quantitatively significant over a broad range of parameter values (15).

8. Only dominant mutator mutations are considered. It is assumed that recessive mutator mutations will be less quantitatively significant because they require two hits to occur. This assumption is different from that for oncogenic mutations, for which we assume that some of the critical oncogenic mutations will be in tumor suppressor genes, therefore requiring two mutations to alter the cellular phenotype.

9. Reversions are expected to be quantitatively significant only at very high mutation frequencies and are not considered.

10. Once the critical number of oncogenic mutations are acquired, the lineage is assumed committed to cancer and will produce a clinical cancer with a constant rate and probability. Whether or not the mutation steps required for commitment are rate limiting, the ratio of clinical cancers occurring by different mechanisms is determined by their ratio at the point of commitment, which is evaluated at fixed time points chosen to correspond to the typical times of onset of most cancers.

Key Parameters and Their Values

N_OL is the number of oncogene loci, the mutation of which could lead to cancer, on a nucleotide basis. N_OL is assumed to be 10², of the approximate order of the number of published oncogenes (4). For dominant oncogenes, we assume that mutations in only a small number of loci result in a gain of function. Although absolute probabilities depend on this number, relative probabilities of mutator and nonmutator pathways do not.

C is the number of oncogene mutations required to produce a cancer and is varied in this paper from 2, as shown in the case of retinoblastoma (20), to 12, as is suggested by epidemiologic data in the case of prostate cancer (21). Based on studies of metabolic pathways involved in cellular transformation, as well as the epidemiologic data, a number of ≈6 is a reasonable expectation (4–5, 22).

k_mut is the spontaneous mutation rate or probability per cell division of a mutation in any one nucleotide locus, estimated at 10⁻¹¹ for stem cells, which are believed to give rise to cancers (23), to 10⁻⁹ in somatic cells (24). k_mut is varied within that range in this paper.

T is the number of cell generations at which the relative efficiency of different mechanisms is evaluated, based on typical times to onset of cancer and cell cycle kinetics. T is varied in this paper from 170 for tissues with a low-cycling fraction (15, 25, 26) to 5,000 for highly proliferative tissues, such as colonic epithelium (27).

p_mut is the spontaneous mutation frequency or probability in the lifetime of the cell lineage that any given critical nucleotide locus in a gene is mutated in the absence of a mutator mutation. (If k_mutT ≪ 1, then p_mut ≈ k_mutT; see Appendix).

The time, in cell generations, when a mutator mutation occurred if it contributed to the pathogenesis of the cancer is t, where 0 < t < T.

N_ML is the number of nucleotides corresponding to critical mutator loci in which a mutator mutation can occur. This parameter affects the calculations of relative efficiencies. Studies in yeast have identified ≈30 potential mutator genes (28), and we assume ≈100 for humans. We vary the number of critical nucleotide loci per mutator gene from 1 to 10. The latter value is still a very conservative estimate given data on loss-of-function mutations (29); therefore, N_ML varies from 100 to 1,000 in this work. If a less conservative, i.e., higher number, were assumed, the estimated relative importance of mutator mechanisms would be increased.

α is the multiplicative factor by which a mutator mutation increases p_mut and k_mut, where α > 1. Mutations in base selection and proofreading generally increase mutation rates 10- to 100-fold (30, 31) but can increase them up to 50,000-fold (31). Thus, after a mutator mutation the spontaneous mutation rate within a lineage would be αk_mut.

The number of the mutation step at which the mutator mutation occurs in the pathogenesis of the tumor is termed k, 1 ≤ k ≤ C. That is, the mutator mutation can occur as the first step in the pathogenesis of the tumor (k = 1), as the second step after one oncogene mutation, (k = 2), all the way up to the second to last step after C − 1 oncogene mutations (k = C).

Results

We see that the relative importance of mutator mutations increases with increasing fold-increase α in mutation rate, increasing number of nucleotide loci available for a mutator mutation N_ML, increasing number of cell generations T, increasing initial mutation rate k_mut, and increasing number of steps C required before commitment to cancer. Depending on the other factors, especially C, a significant increase α in the mutation rate could be required for increased carcinogenic efficiency to be realized from a mutator mutation.

Table 1 shows the value of α_50%, or the minimum fold increase in error rate at which a mutator mutation will contribute to at least 50% of the observed cancers, for different values of T and C assuming the initial mutation rate k_mut = 10⁻¹¹ and the number of nucleotide loci available for a mutator mutation N_ML = 100 or 1,000. Table 1 also shows the same information assuming k_mut = 10⁻⁹. All values of α_50% are within the same orders of magnitude observed for known mutator mutations.

Table 1.

α_50% for various values of T and C

T at various NML and kmut	C
	2	3	4	5	6	8	10	12
NML = 100/kmut = 10−11
170	4,200	287	74	32	19	9.2	6.0	4.5
5,000	775	93	32	16	11	6.1	4.3	3.4
NML = 1,000/kmut = 10−11
170	1,330	133	41	20	13	6.9	4.8	3.7
5,000	245	43	18	10	7.2	4.5	3.4	2.8
NML = 100/kmut = 10−9
170	420	62	23	13	8.6	5.2	3.8	3.1
5,000	77	20	10	6.5	4.9	3.4	2.7	2.3
NML = 1,000/kmut = 10−9
170	133	72	13	8.1	5.9	3.9	3.0	2.6
5,000	24	9.3	5.6	4.1	3.3	2.5	2.2	1.9

The results were calculated by using Eq. 9. The calculations assume that N_ML = 100 or 1,000, as indicated. It is further assumed that k_mut = 10⁻¹¹ or 10⁻⁹, as indicated.

We see as the number of steps required in carcinogenesis decreases, the threshold for α at which a mutator mutation is important in carcinogenesis increases dramatically. Thus, mutator mutations are more likely to play a role as more steps are required in carcinogenesis. Table 1 also shows that the effect of increased T and increased wild-type mutation rate in favoring mutator mechanisms is greater when the number of mutations required for a cancer is small. For example, we see that, for C = 2, α_50% decreases 5- to 6-fold, from 4,200 to 775, when T increases from 170 to 5,000. However, for C = 12, the same change in T leads to only a 24% decrease in α_50%, from 4.5 to 3.4.

Table 2 shows the ratio P_{rel, mut:no mut} of cancers arising with a mutator mutation in their pathogenesis to those without a mutator mutation for various values of T, C, and α, assuming the initial mutation rate k_mut = 10⁻¹¹ and the number of nucleotide loci available for a mutator mutation N_ML = 100 or N_ML = 1,000. Also shown is the same information assuming k_mut = 10⁻⁹. A ratio of >1 indicates a predominance of cancers arising with a mutator mutation, and a ratio of <1 indicates a predominance of cancers arising without it. The fraction of cancers arising with a mutator mutation in their pathogenesis is given by P_{rel, mut:no mut}/(1 + P_{rel, mut:no mut}).

Table 2.

P_{rel, mut:no mut} at various values for T, C, and α

α at various NML and kmut	T = 170			T = 5,000
	C =12	C = 6	C = 2	C = 12	C = 6	C = 2
NML = 100/kmut = 10−11
10	1.5 × 104	2.7 × 10−3	6.3 × 10−6	4.3 × 105	0.79	1.9 × 10−4
20	5.6 × 107	1.6	2.4 × 10−5	1.7 × 109	48	7.0 × 10−4
100	1.3 × 1016	2.5 × 104	5.7 × 10−4	3.9 × 1017	7.2 × 105	1.7 × 10−2
1,000	1.3 × 1028	2.4 × 1010	5.7 × 10−2	3.9 × 1029	7.2 × 1011	1.7
NML = 1,000 and kmut = 10−11
10	1.5 × 105	2.7 × 10−2	6.3 × 10−5	4.3 × 106	7.9	1.9 × 10−3
20	5.6 × 108	16	2.4 × 10−4	1.7 × 1010	480	7.0 × 10−3
100	1.3 × 1017	2.5 × 105	5.7 × 10−3	3.9 × 1018	7.2 × 106	0.17
1,000	1.3 × 1029	2.4 × 1011	0.57	3.9 × 1030	7.2 × 1012	17
NML = 100 and kmut = 10−9
10	1.5 × 106	0.27	6.3 × 10−4	4.3 × 107	79	1.9 × 10−2
20	5.6 × 109	160	2.4 × 10−3	1.7 × 1011	4.8 × 103	7.0 × 10−2
100	1.3 × 1018	2.5 × 106	5.7 × 10−2	3.9 × 1019	7.2 × 107	1.7
1,000	1.3 × 1030	2.4 × 1012	5.7	3.9 × 1031	7.2 × 1013	170
NML = 1,000 and kmut = 10−9
10	1.5 × 107	2.7	6.3 × 10−3	4.3 × 108	790	0.19
20	5.6 × 1010	1.6 × 103	2.4 × 10−2	1.7 × 1012	4.8 × 104	0.7
100	1.3 × 1019	2.5 × 107	0.57	3.9 × 1020	7.2 × 108	17
1,000	1.3 × 1031	2.4 × 1013	57	3.9 × 1032	7.2 × 1014	1.7 × 103

The results were calculated by using Eq. 8. The calculations assume N_ML = 100 or 1,000, as indicated. It is further assumed that the initial mutation rate, k_mut = 10⁻¹¹ or 10⁻⁹, as indicated. Values of P_{rel, mut:no mut} at >1 indicate more than half the cancers arising with a mutator mutation somewhere in their pathogenesis. The fraction of cancers arising via a mutator mutation is given by P_{rel, mut:no mut}/(1 + P_{rel, mut:no mut}).

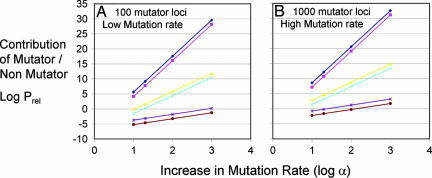
A selection of these results is also represented graphically in Fig. 1, in which the common logarithm of P_{rel, mut:no mut} is plotted on the y axis vs. the common logarithm of α on the x axis for values of C = 2, 6, or 12 and for T = 170 or 5,000, assuming k_mut = 10⁻¹¹ and N_ML = 100 (Fig. 1A) or k_mut = 10⁻⁹ and N_ML = 1,000 (Fig. 1B). As can be seen by taking the logarithm of Eq. 8, these curves represent a family of lines with slope C. We note that the lines in Fig. 1B are parallel to those in Fig. 1A, and indeed any 10-fold increase in either k_mut or N_ML moves the curve up by one logarithm unit without changing its slope. Thus, the slopes and locations of the curves corresponding to data in Table 2 not shown in Fig. 1 can easily be inferred. A positive value of log(P_{rel, mut:no mut}) corresponds to >50% of the cancers arising by a pathway including a mutator mutation, whereas a negative value of log(P_{rel, mut:no mut}) corresponds to <50% of the cancers arising by such a pathway. We observe that under most (but not all) conditions, mutator mutations are favored, in some cases by >30 orders of magnitude.

Fig. 1.

Log(P_{rel, mut:no mut}), the common logarithm of the relative efficiency of carcinogenesis with a mutator mutation compared to that without a mutator mutation, plotted vs. log α, the common logarithm of the fold increase in mutation rate due to a mutator mutation. The graphs were calculated by using Eq. 8 and by assuming that N_ML = 100 (A) or 1,000 (B) and that the initial mutation rate k_mut = 10⁻¹¹ (A) or 10⁻⁹ (B). T = 170 (brown, light blue, and magenta) or 5,000 (purple, yellow, and dark blue). C = 2 (lower lines), 6 (middle lines), or 12 (upper lines).

We see again that when only two steps are required for carcinogenesis (C = 2) mutator mutations are not likely to be important unless the fold increase in error rate caused by them is large (although still within ranges that have been seen). Indeed, the effect of changes in C is dramatic. Overall, we see that the relative importance of mutator mutations can vary widely depending on the parameter values.

Discussion

Cancer is a common endpoint that can likely occur by multiple mechanisms. We have used a direct deterministic mathematical model to assess the importance of mutator mutations in carcinogenesis as a function of a variety of conditions.

By using an approach in which we calculate the ratio of efficiency of carcinogenic mechanisms with a mutator mutation to those without a mutator mutation, we circumvent the debate about whether or not mutator mutations are necessary to produce cancers within a human lifetime. We calculate relative efficiencies rather than absolute rates. We implicitly assume that not every malignant cell develops into a clinical cancer and that the mechanism that produces the greatest number of malignant cells is most likely to be clinically significant. Thus, the focus shifts from evaluating whether steps are rate-limiting to evaluating relative efficiencies of different carcinogenic pathways.

We find that mutator mutations are important in most of the carcinogenic scenarios we analyzed. Mutator mutations are of greatest importance when they occur as an initial step in carcinogenesis.

Our results indicate that the importance of mutator mutations is greatest when more oncogenic mutations are required before commitment to cancer. When only two oncogenic mutation steps are required, mutator mutations are not favored as a pathway to cancer, because they are unlikely to accelerate such a small number of steps sufficiently to offset the time required for acquisition of the mutator mutation itself. As seen in Table 1, however, at as few as three steps, mutator mutations begin to be favored at reasonable fold increases (α) in mutation rates, and, for four or more steps, mutator mutations are clearly favored except for very small α. We note that mutation of both copies of a recessive oncogene would count as two separate events. In the case of embryonal carcinomas, where mutation of both copies of a single recessive oncogene are the only two events required (32), mutator mutations are not likely to play a significant role. Thus, in hereditary, nonpolyposis colon cancer, for which there is a single-copy mutation of a mutator gene and a second mutation is required to lead to a mutator phenotype, there is no increased risk of embryonal cancers despite an increased risk of colon cancer. The case of retinoblastoma (20) is an exception in that the critical oncogene mutation also causes genetic instability; therefore, no extra step is required to acquire the mutator mutation.

The importance of mutator mutations also increases as α increases. The value of α must be greater than a certain minimum for 50% of the cancers to occur via a mechanism that includes a mutator mutation. In this model, the number of nucleotide loci that result in a mutator mutation when mutated is kept fixed. However, in reality, the fraction of mutator loci that result in α above a certain cutoff will be smaller the higher the cutoff is. Mutations of proofreading, base selection, DNA repair, and chromosomal instability can produce values of α within the ranges described in Table 1 (9, 30, 31, 33). Mutations in Escherichia coli DNA polymerase I exhibit up to a 50,000-fold increase in mutation rate (31). Catalytic site mutations of DNA polymerase δ, a major DNA-replicating polymerase, exhibit a 50-fold increase in mutation rate in yeast when substituted for the wild-type gene (33). Moreover mutations that abolish the proofreading activity of DNA polymerase δ resulted in cancers in mice harboring and expressing the mutant gene (33).

The importance of mutator mutations increases with a higher wild-type k_mut and with T in this model, despite acquisition of oncogenic mutations being less “rate limiting” with increasing k_mut and T. This surprising conclusion is a direct result of the focus on relative efficiencies in contrast to calculation of absolute rates and comparison to incidence. The dependence on T suggests a possible importance of mutator mutations in tumors of rapidly proliferating tissues, such as hematologic malignancies or colon cancer, and the effect of the number of oncogenic steps suggests that mutator mutations may play a very significant role in prostate cancer, the development of which may require up to 12 steps (21). Given the relatively late onset of prostate cancer, it is identified as potentially highly susceptible to prevention by agents that inhibit the generation of mutations.

The effect of premalignant lineage expansion on our results will likely depend on its extent and timing relative to the acquisition of oncogenic mutations. The effect of lineage expansion on absolute carcinogenesis rates may also be distinct from that on relative rates. Although lineage expansion affects the absolute rates of developing cancer, preliminary results indicate that the effect on the relative efficiency of mutator and nonmutator mechanisms is less significant.

NCS is not explicitly considered in this model but was considered previously in isolation (15). This work demonstrated that NCS was not quantitatively significant over a broad range of parameters, but it should be noted that the current model may be valid only within that parameter range. In particular, although the results in this article suggest the increasing importance of mutator mutations with increasing k_mut, α, and T, in the presence of NCS these parameters cannot continue to increase indefinitely without the lineages eventually being limited by this effect.

Mutator mutations and lineage expansion of selected premalignant lineages are not mutually exclusive hypotheses, and both likely play significant roles in carcinogenesis, depending on the conditions. Mutator mutations will play a larger role when more oncogenic mutation steps are required for carcinogenesis and when the mutator mutations occur early in carcinogenesis.

Within the limits imposed by NCS, mutations may occur in multiple mutator genes, resulting in an ever-increasing mutation rate and accumulation during tumor progression. Tumors may be considered as a quasispecies, and the evolution of a tumor may depend on multiple mutant cells within the tumor (34) rather than on the emergence of single clones with a proliferative advantage. The genetic variability of tumors produced by mutator mutations increases the likelihood that a clinical tumor will contain one or more cells resistant to any particular therapy, consistent with the observed utility of therapeutic combinations (22).

Methods

The probability of a single cell or its progeny developing cancer in its lifetime without a mutator mutation occurring is

or, equivalently, because p_mut ≈ k_mutT,

The factorial terms are the number of ways C mutations can be selected from a set of N_OL sites without regard to the order of selection, whereas p_mut is the probability of one of these sites being mutated, and p_mut^C is the probability of C sites independently being mutated.

The probability P_{cancer, k} of a single cell or its progeny developing into a cancer in its lifetime with a mutator mutation occurring as the kth step in carcinogenesis at any generation t, 0 < t < T, is given by the integral (from generation 0 to T) of the product of the probability P_{k−1, t} of k − 1 oncogene mutations occurring by generation t, the instantaneous probability of a mutator mutation occurring at generation t (N_ML k_mutdt), and the probability P_{C, k−1, t} of the remaining C − (k − 1) mutations occurring between generation t and T after a mutator mutation at generation t increases the mutation rate α-fold:

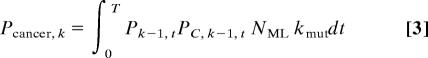where

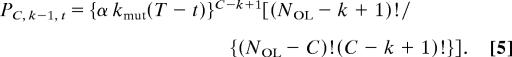Eqs. 3–5 can be shown (see Derivation of Eq. 6 in Appendix) to give an intuitive result regarding the probability of a single cell or its progeny developing into cancer in T generations with a mutator mutation occurring as the kth step:

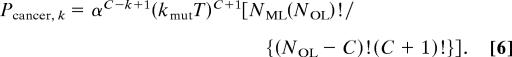We determine the relative probability P_{rel, k:0} of a carcinogenesis pathway with a mutator mutation at the kth step to one without a mutator mutation by dividing Eq. 6 by Eq. 2:

The relative probability P_{rel, mut:non-mut} of a carcinogenic pathway involving a mutator mutation at any step compared with one without a mutator mutation is the sum of Eq. 7 over all integral values of k from 1 to C. This sum can be computed as a geometric series and then approximated to within 1/(α − 1) by the value of the term corresponding to the mutator mutation at the first step (k = 1) when α ≫ 1:

It is apparent from Eqs. 7 and 8 that most of the cancers arising from pathways containing a mutator mutation have that mutation as the first step in their pathogenesis, because that pathway corresponds to the highest power of α in Eq. 7, and α ≫ 1 in most cases. It is clear from Eq. 8 that a mutator mutation must result in a sufficiently large fold increase α in mutation rate to make up for the extra time required to acquire the mutator mutation. For ≥50% of cancers to have a mutator mutation in their pathway, P_{rel, mut: no mut} ≥ 1, or, rearranging Eq. 8,

where α_50% is the minimum value of α that is sufficiently advantageous such that ≈50% of the cancers will have a mutator mutation in their pathogenesis.

Abbreviation

NCS

negative clonal selection.

Appendix

Proof That p_mut ≈ k_mutT When k_mutT ≪ 1.

The rate of decrease in the fraction of unmutated loci is proportional to the mutation rate constant k_mut and the fraction of unmutated loci:

Solving Eq. 10 subject to the boundary condition that p_mut[0] = 0 (i.e., the lineage starts out as wild-type), we obtain

Substituting t = T, expanding the exponential in a Taylor series, and truncating the series after the linear term because k_mutT ≪ 1, we obtain p_mut ≈ k_mutT.

Derivation of Eq. 6.

We start with Eqs. 3–5 for k = 1. Removing terms independent of t from under the integral, we obtain

The integral is solved with the substitution t′ = T − t.

A similar approach is applied to Eqs. 3–5 when k > 1, leading to

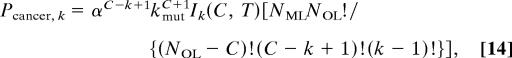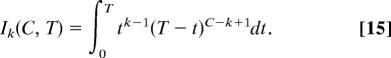Integration of Eq. 15 by parts leads to a recursion relation for I_{k + 1} in terms of I_k:

Repeated application of this recursion relation from the known value of I₁ allows evaluation of I_k for all k, and substitution of those values into Eq. 14 leads to Eq. 6.