Epistasis correlates to genomic complexity

Abstract

Whether systematic genetic interactions (epistasis) occur at the genomic scale remains a challenging topic in evolutionary biology. Epistasis should make a significant contribution to variation in complex traits and influence the evolution of genetic systems as sex, diploidy, dominance, or the contamination of genomes with deleterious mutations. We have collected data from widely different organisms and quantified epistasis in a common, per-generation scale. Simpler genomes, such as those of RNA viruses, display antagonistic epistasis (mutations have smaller effects together than expected); bacterial microorganisms do not apparently deviate from independent effects, whereas in multicellular eukaryotes, a transition toward synergistic epistasis occurs (mutations have larger effects together than expected). We propose that antagonistic epistasis might be a property of compact genomes with few nonpleiotropic biological functions, whereas in complex genomes, synergism might emerge from mutational robustness.

Far from being independent units, genes usually interact in complex networks whose expression is tightly regulated and coordinated. As a consequence, the effect of mutations in different genes often deviates from what would be expected by looking at their separate effects. This deviation, called epistasis, can be antagonistic or synergistic depending on whether mutational effects overlap or reinforce each other, respectively (1). The average direction of epistasis determines the efficiency of natural selection in purging deleterious mutations from populations and hence, is important to many different evolutionary theories, including those seeking to explain the origin of sexual reproduction (2), the evolution of ploidy (3), dominance (4), the accumulation of deleterious mutations in small populations (5), or reproductive isolation (6).

Several studies have measured epistasis for fitness in model organisms, but it is generally believed that no general conclusions about the average direction of epistasis can be drawn. However, it should be noted that the genomic properties of these model organisms widely differ and, therefore, a common pattern of epistasis must not be necessarily expected. Higher complexity, in the form of increased number of genes, modularity, alternative metabolic pathways, or multiple regulatory elements, could modify the effects of mutational perturbations and the properties of genetic interactions. Nonetheless, comparing reported values for epistasis across widely different organisms may provide valuable insights into the evolution of gene interactions. Here, we do this across-species comparison by focusing on average epistasis; this does not preclude that variation in epistasis may also be important for many evolutionary processes, such as narrowing the range of parameter values at which sex and recombination may evolve (7). We first searched the literature for articles that studied epistasis in fitness traits. Then, we analyzed a subset of data that allowed us to obtain a standardized measure of epistasis and thus, to do a quantitative across-species comparison. The results showed that average epistasis correlates to genome complexity. In simpler genomes, such as those of viruses and some bacteria, interactions tend to be antagonistic. In unicellular eukaryotes, there seems to be no average deviation from independent effects, whereas in higher eukaryotes, a transition toward synergism occurs.

Results

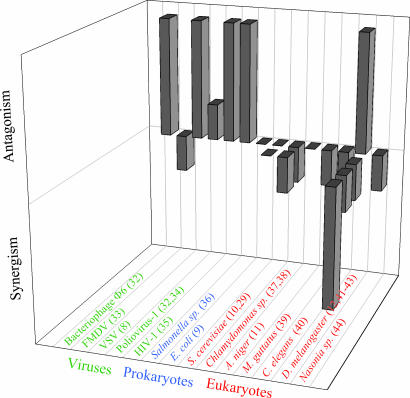
We first compiled information from 21 previous works that sought for epistasis in fitness traits. These studies relied on a variety of strategies. Many were based on mutation accumulation experiments, sometimes combined with chemical mutagenesis, whereas in other cases, site-directed mutagenesis was done. In some cases, mutations were combined by means of the appropriate crosses, whereas in other cases, crosses were done to quantify recombinational load or to characterize the offspring fitness distribution. Fig. 1 and Table 2, which is published as supporting information on the PNAS web site, provide a synopsis of these studies. Among viruses, four of six studies found antagonistic epistasis, one was inconclusive, and one found weak synergistic epistasis. In bacteria, one study found antagonism, whereas another detected no average deviation in either sense. Among unicellular eukaryotes, one-half of the studies concluded that there was no average epistasis, whereas the other half found some synergism. Finally, among pluricellular eukaryotes, seven of nine studies detected variable degrees of synergism in at least some fitness-related traits, one study reported antagonism, and one was inconclusive. Hence, despite the existence of some disparate cases, we found that most studies reporting antagonistic epistasis corresponded to organisms with simple genomes, whereas as complexity increased, cases of synergistic epistasis became more frequent (Kendall's τ_b = −0.5691; 17 df; P = 0.001).

Fig. 1.

Compilation of results from articles that studied epistasis in fitness traits. Each long bar represents a study in which significantly antagonistic or synergistic epistasis was found. Short bars represent cases in which some nonsignificant epistasis was detected. Flat bars represent studies that found no directional epistasis at all. Two studies are not included in the figure. One analyzed data from vaccine design experiments in various RNA viruses and found no general pattern of epistasis (45). The other analyzed data from sexual crosses in several fungi and plant species (46). In fungi, the data were inconclusive, whereas in plants, they indicated synergistic epistasis. More detailed information about all 21 studies can be found in Table 2, which is published as supporting information on the PNAS web site. FMDV, Foot-and-mouth disease virus; HIV-1, HIV type 1; C. elegans, the nematode Caenorhabditis elegans; M. guttatus, the monkeyflower Mimulus guttatus.

However, it could be argued that the validity of the conclusions drawn from the above studies might be limited by their methodological diversity. The most efficient way to avoid this potential problem is probably to focus on data sets for which unambiguous determinations of the number of mutations per genotype were provided and the effect of single mutations is available. When the fitness effects of well defined mutations have been estimated alone and in combination, a quantitative, standardized measure of epistasis can be obtained by calculating the difference between the observed fitness and the product of fitness values associated with the single mutations as:

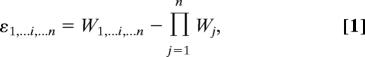where W_j is the relative fitness of the genotype carrying mutation j, W_1,…i,…n is the relative fitness of the genotype carrying mutations 1,…i,…n and ε is the epistasis coefficient between loci 1,…i,…n (1). Positive and negative ε values indicate antagonistic and synergistic epistasis, respectively.

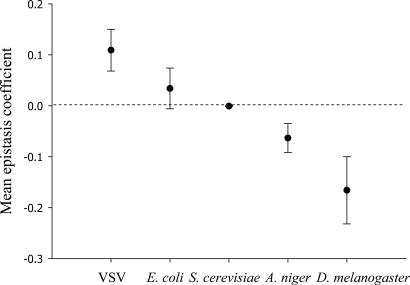
Five data sets provided fitness values for genotypes carrying mutations alone and in combination. The model organisms used in these studies were the vesicular stomatitis virus (VSV) (8), the bacterium Escherichia coli (9), the yeast Saccharomyces cerevisiae (10), the mold Aspergillus niger (11), and the fruit fly Drosophila melanogaster (12). In all cases, mutations were scattered throughout the genome and randomly or systematically combined. After expressing fitness into a common per-generation scale, we calculated the mean epistatic coefficient between deleterious mutations for each species by using Eq. 1. For VSV, the average epistasis coefficient was significantly positive (ε̄ = 0.109 ± 0.041; P = 0.001), whereas for E. coli, ε̄ was also positive but did not significantly differ from zero (0.034 ± 0.040; P = 0.163). For S. cerevisiae, ε̄ was nearly centered on zero (ε̄ = −0.001 ± 0.001; P = 0.633). For A. niger, ε̄ was significantly negative for the whole data set (ε̄ = −0.063 ± 0.029; P = 0.010), which included some presumably lethal genotypes. Even if the putative lethal genotypes were removed from the analysis, epistasis remained significantly synergistic on average (ε̄ = −0.009 ± 0.005; P = 0.046). Finally, for D. melanogaster, two fitness-related traits were measured: productivity and male mating success. Using the product of both parameters as a total fitness measure, we found that epistasis was significantly synergistic on average (ε̄ = −0.166 ± 0.066; P = 0.004).

Some genomic properties of the above five species are shown in Table 1. Whatever measure of complexity is adopted, it seems unquestionable that the rank-order between species genomic complexity is VSV < E. coli < S. cerevisiae < A. niger < D. melanogaster. The magnitude of epistasis strongly differed among the five species (Kruskal–Wallis' H = 21.842; 4 df; P < 0.001) and, using the rank-order classification for genome complexity, a significant negative correlation between the epistasis coefficient and complexity was observed (Fig. 2; Spearman's ρ_S = −0.315; 249 df; P < 0.001). The negative correlation and its statistical significance held regardless (i) the five species were removed from the data set one by one, indicating that our conclusions did not depend on particularities of any single species; (ii) all lethal genotypes were excluded from the analysis; and (iii) for D. melanogaster, only productivity or only male mating success were used instead of the total fitness measure. Finally, although the above data were inevitably collected from experiments varying in some methodological aspects, these factors were very unlikely to have produced an artefactual correlation between complexity and epistasis (Supporting Text, which is published as supporting information on the PNAS web site).

Table 1.

Basic genomic properties for the five species involved in this study, as well as the average selection coefficient against single deleterious mutations (s̄ or h̄s in the case of diploids)

	Genome length, bp	Genes	Ploidy	s̄ (or h̄s)
VSV	1.1 × 104	5	Haploid	0.235
E. coli	4.6 × 106	4,398	Haploid	0.027
S. cerevisiae	1.3 × 107	5,863	Diploid	0.020
Aspergillus*	3.1 × 107	9,457	Diploid	0.019
D. melanogaster	1.8 × 108	14,651	Diploid	0.010

*The data correspond to A. nidulans.

Fig. 2.

Mean per generation epistasis coefficient (ε̄ ± SEM) for five species of increasing complexity.

Discussion

The sign of epistasis should depend on how loci interact to express characters. If each of k loci is necessary for the expression of a fitness trait and, inasmuch as the fitness disadvantage of the kth mutant would be similar to that of each single mutant, epistasis between deleterious mutations should be antagonistic. In general, antagonistic epistasis should preferentially take place in genomes with few genes and little redundancy, or few alternative metabolic pathways, because multiple mutations will often hit essential bits of the same functional module. Genome compactness, with few nonfunctional regions, should enhance this effect. For example, in VSV, two random mutations have more than a one-fifth chance of hitting the same gene. In good agreement with the above hypothesis, it has been shown in silico that reducing genome compactness through the loss of some dispensable functions leads to a shift from antagonistic epistasis toward multiplicative effects (13). Whereas the above multiple-hitting argument should be of clear relevance for short genomes, as those of viruses, its power rapidly vanishes as the number of independent biological functions and genetic redundancy increase. Although it remains unclear whether multiple-hitting could generate observable amounts of antagonistic epistasis in prokaryotes, a recent in silico study of the global transcriptional regulatory network of E. coli suggests that genes can indeed be grouped in very few functional modules (14).

In the contrary, if each of k loci is sufficient for the expression of the character, epistasis should be synergistic, because the fitness of the kth mutant would be disproportionately low compared with that of each single mutant. Therefore, synergistic epistasis could theoretically appear as a consequence of gene duplication and redundancy. However, this mechanism would only be efficient in a system with very few genes. In large genomes, although duplications could have a role in lessening mutational damage (15), they should not generate significant amounts of synergism because the probability of simultaneously hitting two copies becomes vanishingly low as genome size increases. A better clue to how synergistic epistasis can be generated in complex genomes comes from the observation that many genes in higher eukaryotes code for sensors and regulators that confer stability rather than functionality in optimal circumstances. The ability of complex systems to adjust network organization and accommodate perturbation generates robustness to mutational or environmental perturbations (16, 17). As long as a robust genome accumulates a small number of mutations, deleterious effects can be buffered by shuttling the metabolic flux through the unaffected parts of the network, whereas, no matter how robust the system is, for a sufficiently large number of perturbations, buffering mechanisms would become insufficient to prevent the system from collapsing. Therefore, synergistic epistasis can be viewed as an emerging property of complex and robust networks, with high levels of redundancy and frequent alternative pathways (17).

In general, the link between epistasis and complexity can be better understood by acknowledging that epistasis and mutational robustness are probably correlated. Strong mutational effects (low robustness) should be associated to more antagonistic epistasis, whereas mild mutational (robustness) effects should be associated to synergism. This correlation has already been observed in digital organisms (18), in in silico models of bacteriophage T7 infectious cycle (19), and in simulated RNA folding (18, 20, 21). In good agreement, it seems that fitness effects associated with point mutations are larger in RNA genomes than in DNA organisms (22). Table 1 shows estimations of the selection coefficient against deleterious mutations for the five species we analyzed in detail. Although these estimates are difficult to obtain and sometimes controversial, the data seem consistent with an increase in mutational robustness with increasing genomic complexity (ρ_S = −1; 3 df; P < 0.001). In conclusion, we propose that two hallmarks of simple genomes would be that single mutations may have large fitness effects and epistasis among mutations shall be predominantly antagonistic. Conversely, two characteristic properties of complex genomes would be that single mutations may have mild effects on fitness and epistasis among mutations should be predominantly synergistic.

The relationship between epistasis, robustness, and complexity was previously studied by using digital organisms (23). The results of this study can be summarized as follows: (i) simple digital organisms were much more sensitive to mutation than their complex counterparts, in accordance with our above argumentation. This was mainly due to the larger fraction of lethal mutations in simpler digital organisms. (ii) The average intensity of epistasis was weaker in simpler digital organisms. This finding could be explained by noting that, except for compensatory cases, the presence of a lethal mutation in a locus determines the fitness of the organism independently of what alleles are at other loci and, therefore, produces zero epistasis values. It is therefore important to clarify that our multiple-hitting argument does not apply to lethal mutations. (iii) In both types of organism, antagonism was more frequent than synergism. This observation may reflect that even the most complex digital organisms are far less complex than most biological organisms. (iv) In agreement with our results, the frequency of synergistic pairs was larger in complex organisms.

Several complex features of higher eukaryotes, such as large genomes, increased numbers of replication rounds per generation, or small population sizes, may tend to inflate the mutational load, conferring a potential selective advantage to robustness (24, 25). Therefore, mutational robustness might be an adaptive trait of complex organisms. In turn, buffering mechanisms could provide the raw material to create new functions and increase genetic complexity (26). This kind of positive feedback, by which evolution could forge its own path, has been recently proposed to explain the evolution of sexual reproduction in regard to mutational robustness and synergistic epistasis (27).

Data and Methods

VSV Data Set.

Forty-seven combinations of single-nucleotide random, nonlethal mutations were introduced by site-directed mutagenesis in an infectious cDNA template (8). For information about the precise location of each mutation and raw fitness values, see supporting table 1 of ref. 8. It is easy to prove that the fitness of each mutant genotype relative to a wild-type, defined as the size of the progeny per individual per wild-type generation, can be obtained as:

where K is the average per cell progeny for the wild-type and r_i and r₀ stand for the mutant and wild-type growth rates, respectively.

E. coli Data Set.

Twenty-seven random insertions were assayed for fitness alone and in pairs (9). Southern blots confirmed that mutations were dispersed throughout the genome and that there were few, if any, genotypes with identical changes. Raw fitness was calculated as the ratio between the growth rate of the mutant and reference strains by S.F.E. and R. E. Lenski (Michigan State University, East Lansing, MI). All genotypes were viable. The fitness of each genotype was transformed into a per-generation scale by setting K = 2 in Eq. 2.

S. cerevisiae Data Set.

Single-site random mutants were generated by using ethyl methane-sulfonate (EMS) (10). EMS produces a majority of transitions, the remainder being transversions and, sporadically, small deletions (28). The EMS dose was low enough to ensure that no more than one mutation was incorporated per individual. Haploids derived from two different heterozygous clones were mated to recover the wild-type, each single heterozygous mutant, and the double heterozygous mutant. Forty-nine combinations were tested. Raw fitness values were calculated as the ratio of colony growth rates and were provided by R. Korona (Jagiellonian University, Krakow, Poland). Fitness can be rescaled into generation units in the same way as for the E. coli data set.

A. niger Data Set.

Seven phenotypic markers, each located in a different chromosome of the filamentous mold A. niger, were combined by isolating segregants from heterokaryons (11). The markers were five auxotrophic and two antibiotic resistance mutations. Although ≈2,500 haploids were screened, only 186 of 256 possible genotypes were recovered, despite the fact that, because each genotype had the same probability of appearance, ≈10 individuals of each genotype were expected. This finding, together with the observation that the fraction of genotypes successfully isolated decreased with mutation number, indicates that absent genotypes were probably lethal or highly unviable. Raw fitness values were estimated as the increase in mycelial surface and provided by J. A. G. M. de Visser (Wageningen University and Research, Wageningen, The Netherlands). Fitness per generation can be obtained as W_i = (ΔA_i(g)/ΔA_wt(g))^1/g, where ΔA_i and ΔA_wt are the increase in mycelial surfaces for the mutant and the wild type, respectively, and g is the number of generations elapsed during the fitness assay. The number of spores at the initial and final time points were ≈1.2 × 10⁷ and ≈2 × 10⁸, respectively, and therefore, g ≈ log₂(2 × 10⁸/1.2 × 10⁷) = 4. The whole experiment was replicated in two different genetic backgrounds. Fitness values were averaged across the two genetic backgrounds.

D. melanogaster Data Set.

Alleles at five different loci were put together in all 26 different combinations by means of the appropriate crosses (12). All mutations were in the homozygous state. These mutations were black (b) and plexus-speck (px/sp) on the second chromosome and claret (ca), hairy (h), and ebony-stripe (e/sr) on the third chromosome. Two measures of fitness relative to a reference strain were calculated: (i) productivity, which counts viable offspring, and (ii) male mating success, which counts the number of matings per male. Raw fitness measures are available in the supporting table of ref. 8. Given that both fitness components refer to two nonoverlapping and necessary steps of the life cycle of a population, a total fitness can be obtained by multiplying them, which measures the fitness that a population would have if all males and females carried the mutation.

Calculation of Epistasis Coefficients.

Per-generation fitness values for single and multiple mutants were used to calculate the epistasis coefficient (Eq. 1). Only mutants with expected deleterious fitness were considered. Two alternative definitions of the epistasis coefficient were also used: a relative epistasis coefficient (see Supporting Text) and the scaled epistasis coefficient (29). All three definitions led to identical conclusions.

Selection Coefficients per Generation.

Average selection coefficients (s̄) obtained from the above data sets plus mutation accumulation experiments were previously converted into a per-generation scale (22). In diploids, mutational effects against single mutations are measured as hs, where h is the dominance coefficient. For VSV, E. coli, S. cerevisiae, and Aspergillus nidulans (a close relative to A. niger), values in Table 1 are the average of the values reported in the supporting tables of ref. 22. For D. melanogaster, despite intensive work, estimations of the selection coefficient remain controversial. Some authors argue that the homozygous coefficient is in the order of s = 0.2 and the dominance coefficient in the order of h = 0.1 or lower (30), whereas other authors argue that the homozygous coefficient is one order of magnitude lower (s = 0.02) and the dominance coefficient approximately h = 0.5 (31). Therefore, some consensus exists on the value of the selection coefficient against heterozygotes, hs ≈ 0.01.

Statistical Analyses.

Analyses were done with SPSS version 12.0 software. To avoid statistical problems stemming from the fact that some mutations were present in more than one genotype, P values were calculated by the bootstrap method. This latter analysis was done by using a Perl script.

Abbreviation

VSV

vesicular stomatitis virus.