The effect of the Neolithic expansion on European molecular diversity

Abstract

We performed extensive and realistic simulations of the colonization process of Europe by Neolithic farmers, as well as their potential admixture and competition with local Palaeolithic hunter–gatherers. We find that minute amounts of gene flow between Palaeolithic and Neolithic populations should lead to a massive Palaeolithic contribution to the current gene pool of Europeans. This large Palaeolithic contribution is not expected under the demic diffusion (DD) model, which postulates that agriculture diffused over Europe by a massive migration of individuals from the Near East. However, genetic evidence in favour of this model mainly consisted in the observation of allele frequency clines over Europe, which are shown here to be equally probable under a pure DD or a pure acculturation model. The examination of the consequence of range expansions on single nucleotide polymorphism (SNP) diversity reveals that an ascertainment bias consisting of selecting SNPs with high frequencies will promote the observation of genetic clines (which are not expected for random SNPs) and will lead to multimodal mismatch distributions. We conclude that the different patterns of molecular diversity observed for Y chromosome and mitochondrial DNA can be at least partly owing to an ascertainment bias when selecting Y chromosome SNPs for studying European populations.

1. Introduction

Two opposing scenarios have been invoked to account for the spread of agriculture in Europe. The demic diffusion (DD) model assumes that the Neolithic transition diffused in Europe from the Middle East by an important movement of population (Ammerman & Cavalli-Sforza 1984; pp. 78–80), without substantial contact with local Palaeolithic populations. On the contrary, the cultural diffusion (CD) model assumes that the Neolithic transition occurred mainly through the transmission of agricultural techniques (Zvelebil & Zvelebil 1988) without large movements of populations. Archaeological evidence suggests that the dynamics of the spread of agriculture over Europe has been complex, with a succession of migration phases and local admixture (e.g. Zvelebil 1986; Arias 1999; Gronenborg 1999; Mazurié de Keroualin 2003).

Genetic evidence has been inconclusive so far on the amount of Palaeolithic lineage incorporated into the current European gene pool, despite a considerable amount of genetic data available on European populations. This is disappointing since the DD and the CD models lead to quite different predictions concerning the amount of the current European gene pool tracing back to Palaeolithic or Neolithic populations. Under the CD model, the current genetic pool should mainly result from hunter–gatherers lineages, while the Near East Neolithic lineages should be prevalent in the European genetic pool under the DD model. The Neolithic contribution to the current European gene pool has been estimated using various approaches, and has led to contradicting results. Depending on the markers used and the type of analyses performed, it varies from a Neolithic contribution smaller than 25% (Richards 2003), to values larger than 50% (Barbujani & Dupanloup 2002; Chikhi 2002; Dupanloup et al. 2004).

The analysis of classical nuclear markers and Y chromosomes has also often revealed the presence of allele frequency clines (AFCs) along a southeast to northwest axis (Menozzi et al. 1978; Barbujani & Pilastro 1993; Chikhi et al. 1998; Rosser et al. 2000; Sokal et al. 1991). These frequency gradients have been interpreted as a signature of a DD model (Menozzi et al. 1978; Ammerman & Cavalli-Sforza 1984), but some authors have argued they could have been created by the arrival of the first hunter–gatherers in Europe (Richards et al. 1996; Barbujani & Bertorelle 2001), although this hypothesis has never been formally tested. These two causes of gradient formation are actually difficult to distinguish since the first Palaeolithic populations colonized Europe 40 000 years ago using approximately the same path as the Neolithization process 10 000 years ago (Bocquet-Appel & Demars 2000). The pattern of mitochondrial (mt) DNA diversity in European populations has been shown to be compatible with an old Palaeolithic spatial expansion (Ray et al. 2003; Excoffier 2004), while evidence is contradictory for Y chromosome data. On one hand, clines of allele frequencies have been observed for several Y chromosome single nucleotide polymorphisms (SNPs) (Rosser et al. 2000), and a gradient of decreasing Neolithic contribution to the current gene pool has been inferred from the Near East to the West by the analysis of 22 Y chromosome SNPs (Semino et al. 2000; Chikhi et al. 2002), in keeping with the hypothesis of a movement of Neolithic populations from the Near East and a progressive dilution of their gene pool by the incorporation of some Palaeolithic lineages (Dupanloup et al. 2004). On the other hand, the mismatch distributions of European populations inferred from the analysis of 22 Y chromosome SNPs do not show the typical signature of a demographic or spatial expansion (Pereira et al. 2001), which could be owing to a small effective population size of males compared with females (potentially owing to polygyny; Dupanloup et al. 2003), or to reduced male migration rates.

In order to assess the pattern of SNP diversity expected after the Neolithic expansion for various degrees of interactions with Palaeolithic populations, we have carried out simulations of a range expansion in a spatially explicit model of Europe and the Near East. These simulations were used to investigate three particular aspects of SNP diversity that have produced contradictory results discussed above: the existence of gradients of allele frequencies along a European southeast to northwest axis, the proportion of the European gene pool being of Palaeolithic origin, and the mismatch distribution within populations. Because an ascertainment bias in favour of SNPs showing a relatively frequent minor allele is common (i.e. Casalotti et al. 1999) and leads to biased estimates of the past demography of a population (e.g. Wakeley et al. 2001), we have also examined its impact on patterns of molecular diversity.

2. Material and methods

As reported previously (Ray et al. 2003; Excoffier 2004), realistic simulations of genetic diversity were carried out by first generating the forward demographic history (densities and migration rates between adjacent demes) of the populations. These demographic information are stored in a database, which is then used to generate the genealogies of samples of genes drawn in a predefined set of demes using a backward coalescent approach (e.g. Hudson 1990; Nordborg 2001).

a Demographic simulations

While our approach is inspired by previous simulation studies on allele frequencies (e.g. Rendine et al. 1986; Barbujani et al. 1995), we have specifically modelled the occurrence of SNP mutations, and we have added some level of realisms, such as the spatial dynamics of Palaeolithic populations and an explicit competition for local resources between Palaeolithic and Neolithic populations. The spatial expansion of modern humans (Homo sapiens sapiens) in Europe, as well as the Neolithic transition were simulated using a modified version of the Splatche program (Currat et al. 2004) as follows.

(i) Digital model

A digital model of Europe and the Near East has been created by dividing the continental surface in demes arranged on a grid. Each deme covers a surface of 50×50 km² (or 2500 km²), so that the modelled area has slightly more than 7000 demes.

(ii) Range expansions

The colonization of Europe is assumed to have occurred in two phases. The first Palaeolithic wave is assumed to have started some 1600 generations ago (40 000 years ago with a generation time of 25 years) from the Near East (point P on figure 1). This point has been chosen arbitrarily, as the source of modern humans having colonized Europe is not known exactly (Djindjian et al. 1999; Kozlowski & Otte 2000). A second colonization wave is assumed to have started from Anatolia (point N on figure 1; Lev-Yadun et al. 2000) some 400 generations ago (corresponding to 10 000 years ago). At this time, the individuals occupying this deme are assumed to become farmers, and are moved in a new layer of 7000 demes denoted as farmer or F demes, and superimposed on the layer of hunter–gatherers or HG layer.

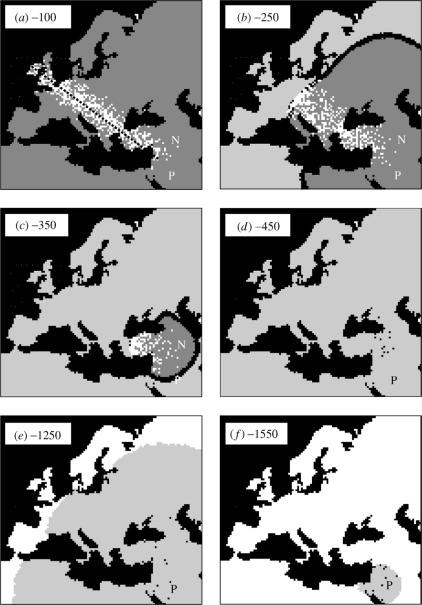
Figure 1.

Spatial and temporal dynamics of the location of ancestral lineages under a double Neolithic and Palaeolithic range expansion from the Near East. The six panes (a)–(f) show the location of ancestral lineages and the area occupied by Neolithic (layer F in dark grey) and Palaeolithic (layer HG in light grey) demes at six different periods before present, under a pure DD model (γ=0). P is the origin of the Palaeolithic expansion and F, the origin of the Neolithic expansion. Dotted lines in (a) represent the axes along which 20 demes are samples for 40 genes. Black spots on the light grey zone represent HG lineages and white spots on the dark grey zone represent F lineages. The black band at the front of the Neolithic expansion represents the cohabitation zone where Neolithic and Palaeolithic populations coexist.

(iii) Demographic regulation

The demography of more than 14 000 demes representing Europe (half in HG and half in F layers) is thus simulated during 1600 generations, according to a model initially developed to describe the interactions between Neanderthals and modern humans (Currat & Excoffier 2004). In brief, density is logistically regulated within each deme (either belonging to the F or HG layer, and noted i below), with intrinsic rate of growth r_i and carrying capacity K_i. The local growth is also regulated by a density-dependent competition exerted by the population from the other layer competing for local resources, according to a modified version of the Lotka–Volterra model (see Currat & Excoffier 2004, for details). Each generation, a proportion m of individuals from any given deme migrates to the neighbouring demes from the same layer. At equilibrium, the local density N_i is equal to K_i, and the number of migrants exchanged between deme is thus equal to K_im, which will be called N_im for coherence with previous work (e.g. Ray et al. 2003). HG contribution to the current genetic pool is simulated by a movement from the HG layer towards the F layer. This movement can be owing to two processes: (i) adoption of Neolithic techniques by HG, a process also-called acculturation (Ammerman & Cavalli-Sforza 1984) or (ii) mating between Palaeolithic and Neolithic individuals. The children resulting from these two processes are assumed to belong to the F layer and have thus an HG ancestor at the former generation. In the case of interbreeding, the amount of gene flow (A) between the two layers depends on the density of the individuals in layer F and HG in a given deme as $A=\gamma (2N_{\text{F}}{N}_{\text{HG}})/{(N_{\text{F}}+N_{\text{HG}})}^2$, where γ controls the fecundity of the mating between individuals of the two layers. As discussed below, a pure DD model assumes that there was no genetic interaction between hunter–gatherers and farmers and, therefore, that γ=0. In that case, previous hunter–gatherers become extinct only owing to their competition with Neolithic people. Less extreme DD models have been implemented, corresponding to different values of $0<\gamma \le 1$, as reported in table 1. The value of γ=1 corresponds to the maximum amount of gene flow that can be simulated in our model and means that HG individuals reproduce indistinctly with HG or F individuals. It corresponds to the movement of 20 HG lineages per deme on average during the whole cohabitation period. As a limiting case, a pure cultural transition was also simulated for which the F layer does not exist and where K_HG was simply multiplied by 20 within each deme. This demographic increase began at time − 400 generations and was applied gradually from the Neolithic source deme at a speed corresponding to the scenario with γ=0. Finally, a scenario without range expansion has been explored by simulating an instantaneous Palaeolithic settlement of Europe, followed by a Neolithic demographic growth (×20) 400 generations before present.

Table 1.

Statistics computed after the simulation of various amount of interactions between Palaeolithic and Neolithic populations.

Palaeolithic contribution		colonization and cohabitation time			Neolithic contributione	allelic frequency clines (AFCs)f
γa	Lb	HG col.c	F col.c	cohab.d	no bias		bias (f≧5%)		bias (f≧10%)
freq.	R2	freq.	R2	freq.	R2
0.00	0	470	260	7.7	1.00 (0.00)	0.03	0.50	0.57	0.60	0.56	0.62
0.05	1	470	260	7.7	0.48 (0.13)	0.03	0.47	0.48	0.54	0.45	0.58
0.10	2	470	255	7.6	0.30 (0.10)	0.03	0.45	0.50	0.56	0.51	0.63
0.15	3	470	250	7.4	0.12 (0.04)	0.04	0.42	0.51	0.58	0.78	0.70
0.25	5	470	245	7.3	0.07 (0.02)	0.03	0.42	0.66	0.59	0.86	0.71
0.50	10	470	240	7.0	0.03 (0.01)	0.02	0.43	0.71	0.58	0.82	0.68
0.75	15	470	230	6.7	0.01 (0.00)	0.02	0.40	0.70	0.58	0.82	0.67
1.00	20	470	220	5.6	0.00 (0.00)	0.02	0.40	0.68	0.59	0.80	0.63
—	—g	470	260h	—	0.00	0.02	0.40	0.68	0.58	0.78	0.66
—	—i	1	1	—	0.00	0.02	0.23	0.08	0.28	0.08	0.28

^aγ is the rate of gene flow between HG and F demes. Minimum=0 (no gene flow) and maximum=1.0.

^bL is the average number of Palaeolithic lineages incorporated per deme over the whole simulation period.

^cColonization time of Europe (in generation) for Palaeolithic and Neolithic range expansions, respectively.

^dMean cohabitation time (in generation) between HG and F within a deme.

^eAverage ‘Neolithic’ contribution to the current European genetic pool (see text) over 10 000 simulations, standard deviation is shown in parentheses.

^fFreq.: proportion of simulation (over 10 000) that shows a significant AFC at the 5% significance level, R²=average determination coefficient for the significant AFCs.

^gSimulation of the Palaeolithic range expansion only, with a progressive demographic increase from the source of the Neolithic (pure acculturation process).

^hTime for cultural diffusion over whole Europe.

ⁱInstantaneous Palaeolithic settlement with a Neolithic increase of the carrying capacity from K=40 to K=800, 400 generations before present (no range expansion).

(iv) Parameter calibration

We gauged the parameters of our model from available palaeo-demographic information. The carrying capacity of male or female hunter–gatherers (K_HG) before the Neolithic was set to 40, corresponding to a density of 0.064 individuals per km² (Steele et al. 1998; Alroy 2001). As it is largely accepted that the Neolithic transition coincides with the beginning of a significant increase in the population size (Hassan 1979; Landers 1992; Bocquet-Appel & Dubouloz 2003; Cavalli-Sforza & Feldman 2003), we have set K_F to 800, a value 20 times larger than K_HG. As K represents here the effective number of gender-specific genes (mitochondrial or Y chromosome), the total density simulated for the 5500 demes constituting Europe is about 880 000 HG and 15 million farmers, which are in broad agreements with the estimated number of people living in the Palaeolithic and the Neolithic in Europe, respectively (Biraben 2003). Note also that K_F values larger than 800 do not affect the results substantially (results not shown). While it has been estimated that 500 generations were necessary for HG to colonize Europe (Bocquet-Appel & Demars 2000), the Neolithic transition was considerably more rapid, and took roughly between 4000 and 8000 years (Price 2000; Mazurié de Keroualin 2003), corresponding to 160 to 320 generations with a generation time of 25 years. These colonization times were used to calibrate the growth (r) and migration (m) rates. Values of r_HG=0.4, r_F=0.8, and m=0.25 give colonization times in good agreement with figures mentioned above (see table 1). Note that a growth rate of 80% per generation is very high but is within the upper range of rates considered as plausible for the human species (Ammerman & Cavalli-Sforza 1984; Young & Bettinger 1995; Pennington 2001). A migration rate of m=0.25 implies the exchange of 10 males or 10 females between neighbouring HG demes per generation and 200 individuals between F demes, two values in broad agreement with those estimated from mt DNA diversity in HG and post-Neolithic populations (N_HGm<10, N_Fm>40; Excoffier 2004).

While the calibrated parameters are considered here as fixed, it is unlikely that small departures from the chosen values would deeply affect our results (Currat 2004). For instance, it has been shown in the case of a single expansion (Ray et al. 2003), that when Nm is larger than about 50, the number of coalescences that occur during the scattering phase S₁ (see figure 2) is relatively insensitive to Nm, because these events will be very rare anyway. As we consider that N_Fm is large (200), we would predict that migration rates higher than or up to four times lower than those presented here should have a negligible impact on the pattern of genetic diversity within and between populations. Note also that r_F mainly controls the speed of the colonization wave in our model, but it can also affect the cohabitation time between the two populations (Currat & Excoffier 2004), smaller values leading to longer cohabitation times and thus to more genetic exchanges between populations. But, a growth rate of 0.6 instead of 0.8 adopted here would only extend the cohabitation time by a single generation on average, and would thus not qualitatively affect our results.

b Genetic simulations

We have simulated the diversity of samples of 40 genes in 20 demes located along an axis between the Near East to Ireland (see figure 1a). For each reconstructed genealogy, the local Neolithic contribution to the current gene pool is measured as the proportion of sampled lineages whose ancestors belong to the source deme F at generation − 400. In order to be able to compare our simulations with the Y chromosome data published for the European populations by Semino et al. (2000) and used in derived analyses (Dupanloup et al. 2003; Pereira et al. 2001), we have simulated 22 linked SNPs assumed to be on the Y chromosome. In order to detect AFCs, the frequency of the SNP is measured in each of the 20 simulated samples, and a linear regression is carried out over geographical distance between samples. If the regression coefficient is statistically significant at the 5% level, we consider this SNP as showing an AFC. The determination coefficient R² of the regression is also calculated for every statistically significant cline. In order to simulate different amounts of ascertainment bias, we have conducted separate analyses on SNPs with overall minor allele frequency among the 20 samples of at least 5% or at least 10%. The molecular diversity of a mtDNA sequence of 300 bp was also simulated for the same samples, assuming a mutation rate of 0.001 25 per generation for the whole sequence (33% of divergence per million years; Heyer et al. 2001; Soodyall et al. 1997). The genetic variability of the samples was analysed using the program Arlequin (Schneider et al. 2000).

3. Results

a Distinction between cultural (CD) and demic (DD) diffusion models

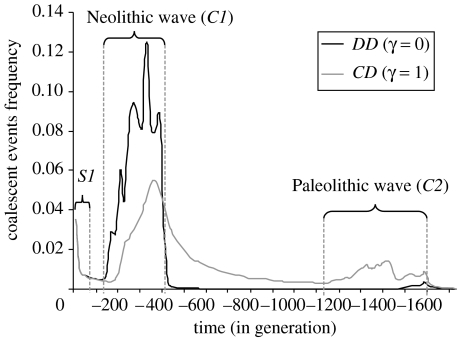
The molecular signature obtained under various scenarios depends on the spatio-temporal dynamics of the sampled lineages. Under a pure DD model (without genetic exchange between Neolithic and Palaeolithic populations, γ=0), and going backward in time, the ancestors of the sampled lineages first coalesce or disperse in the F layer (figure 1a). Then, they are brought back to the place of origin of the Neolithic expansion by the shrinking Neolithization wave (figure 1b,c). Some of them pass through the spatial and demographic bottleneck constituted by the Neolithic source. The lineages that did not coalesce during this bottleneck can disperse again in the HG layer (figure 1d). Finally, the lineages are brought back towards the place of origin of the Palaeolithic expansion (figure 1e,f). This dynamic results in three main periods of coalescent events: the ‘scattering’ phase (sensu Wakeley 1999; S1 in figure 2), followed by two ‘contraction’ phases (corresponding to range expansions when going forward in time), that respectively take place during the Neolithic (C1) and the Palaeolithic (C2) migration waves. As illustrated on figure 2, the relative proportion of coalescent events taking place during the two ‘contraction’ phases C1 and C2 are quite different under the pure DD model (γ=0) and with high Palaeolithic input (γ=1). The number of coalescent events in the scattering phase S1 only depends on the parameter N_Fm, as shown previously (Ray et al. 2003), and it does not allow one to distinguish between the two models. It thus appears that the period C1 is critical to distinguish between models. Under a pure DD model, almost all coalescent events (98%) occur before the lineages reach the initial Neolithic deme (figure 2). In contrast, only about half (49%) of the coalescent events occur between the onset of the Neolithic transition and now, when γ=1. Under this latter case, less than 10% of the coalescent events occur in the layer F, during the Neolithic colonization and 20% within the layer HG during the Paleolithic colonization (figure 2). The remaining 70% occur in the HG layer during or before Neolithic times, after the passage of the Neolithic wave because the lineages evolve in demes with low densities. Note that the number of coalescent events occurring within the Neolithization front depends on γ, the amount of gene flow between the two layers, so that smaller γ values translate into larger numbers of coalescent events within the Neolithization wave. The number of migrants exchanged between demes from the HG layer (N_HGm) does not affect the genetic pattern (results not shown), low N_HGm values only slightly increase the number of coalescent events that occurs within the HG population. The influence of r_HG on the coalescent tree is negligible (results not shown).

Figure 2.

Temporal distribution of the coalescent events over all demes under the pure DD model (γ=0, when there is no genetic interaction between hunter–gatherers and farmers, in black) and when γ=1 (the maximum amount of gene flow allowed, in grey). S1 corresponds to the ‘scattering’ phase (see text), C1 and C2 to the ‘contraction’ phases occurring during the Neolithic and the Palaeolithic expansions, respectively. The small variations in the distributions are owing to spatial bottlenecks (Currat 2004).

b Importance of the migration front

Our simulations underline the role of the range expansion processes for generating AFCs. The colonization process corresponds to a succession of founder effects occurring at the wavefront (Austerlitz et al. 2000). In a coalescent perspective, the lineages that are spread over a wide area are gathered and concentrated by the contracting wavefront, and have thus an increased probability to coalesce during the contraction of the occupied territory. Our simulations reveal that AFCs are extremely rare (<5%) for randomly chosen SNPs, but that they become very frequent in case of an ascertainment bias consisting in selecting SNPs, with minor allele frequencies larger than 5% (table 1). Since gene genealogies resulting from a range expansion have usually long terminal branches (Ray et al. 2003; Excoffier 2004), SNP mutations will most of the time occur on these terminal branches and will consist in singletons when the number of migrants exchanged between neighbouring demes is large, or could reach low frequencies but be geographically restricted when migration is lower. Therefore, randomly chosen SNPs will generally not show clinal patterns since they will be spread over a small region. With ascertainment bias, the fraction of SNPs showing AFCs increases dramatically, and can even be observed in about 50% of the loci (table 1). Interestingly, the AFCs occur at about the same frequency, independently of the amount of incorporation of Palaeolithic lineages into the F layer (table 1), and thus at similar frequencies under a pure DD or a pure CD model. It implies that AFCs cannot be considered as indicative of a range expansion of Neolithic farmers, since they could have been created equally well during the first expansion of modern humans into Europe. Thus, the observation of a high frequency of AFCs in case of ascertainment seems to be a support for some range expansion process. Indeed, as shown on the last line of table 1, the frequency of AFCs remains very low with (8%) or without ascertainment bias (2%) if we simulate an instantaneous settlement without any range expansion.

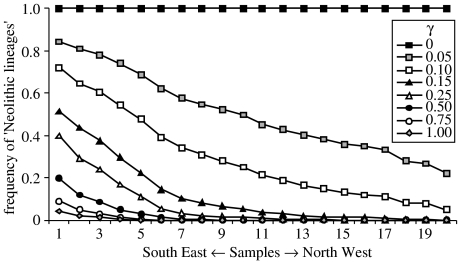
The Neolithization front is also important because it is the region where HG and F demes coexist, and consequently, where genetic exchanges occur between the two layers. Therefore, the probability for a lineage to be of HG ancestry increases with the time spent within the Neolithization front during the contraction periods C1. The proportion of lineages whose ancestors trace back to the F layer diminishes rapidly with increasing distance from the Neolithic source (figure 3). Obviously, when γ increases the total proportion of Neolithic lineages decreases, and these lineages are restricted to the area of the origin of the Neolithic (figure 3). Even when γ=1, there is still 1% of ‘Neolithic lineages’ in the Anatolian sample close to the source of the Neolithic. Note that, under the simulated conditions, a Neolithic cline is observed at the continental level only when γ is non-zero but smaller than 0.15 (corresponding to about 3 HG genes incorporated per deme on average over the whole simulation period). It is also important to note that even for values of γ as low as 0.05 (1 HG incorporated per deme during the whole cohabitation period) the majority of the current European gene pool is of Palaeolithic ancestry (table 1, figure 3). This result is virtually unaffected by the size and the spread of the Neolithic source, for instance, when it consists of a subdivided population of 25 demes (Currat 2004).

Figure 3.

Proportion of ‘Neolithic lineages’ in every sample from the Near East (1) to the North West (20) of Europe, for rates of gene flow between HG and F.

c Molecular diversity within demes

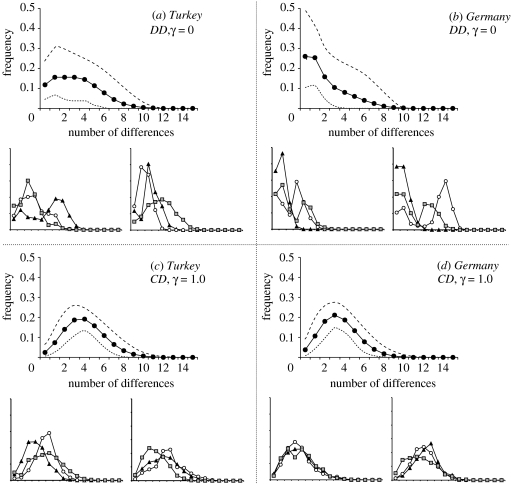
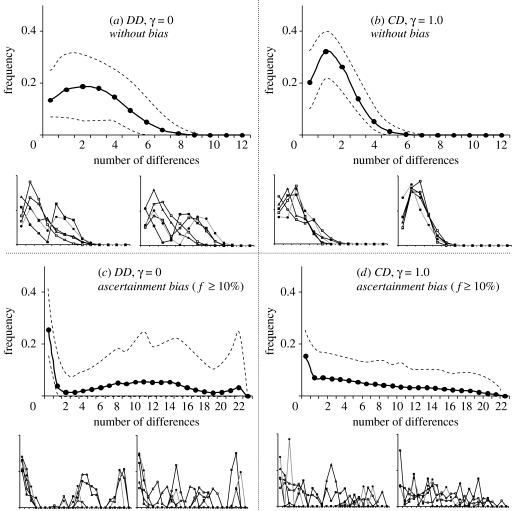
The patterns of molecular diversity can be obtained by adding mutations on top of coalescent trees. Under a pure DD model (γ=0), a large proportion of mismatch distributions are multimodal, have a large variance and present an important proportion of identical pairs of sequences (figure 4a,b). The homozygosity (class 0 in mismatch distributions) increases with the distance between the sampling area and the Neolithic source, because the number of coalescent events occurring during the C1 phase will also increase. When γ increases, the difference between samples located close or far from the Neolithic source disappears, and the proportion of unimodal mismatch distributions quickly increases (∼50% with γ=0.05 and ∼90% with γ=0.15) and is close to 95% when γ>0.5 (figure 4c,d). This increase in the number of unimodal mismatch is faster for populations which are furthest away from the Neolithic source since it is also those integrating the most Palaeolithic genes. The mismatch distributions simulated for 22 SNPs when γ=0 are often bimodal, whereas they are almost always unimodal when γ=1 (figure 5a,b). As soon as ascertainment bias is introduced, the realized mismatch distributions become multimodal under all simulated scenarios (figure 5c,d), even though the average distributions are relatively flat.

Figure 4.

Expected mismatch distributions obtained from 10 000 genetic simulations of 300 bp DNA sequences for samples located in Turkey and in Germany, without (DD) or with maximum (CD) gene flow between HG and F. Dashed lines correspond to the limits of a 90% confidence interval for the mismatch distribution. Small graphs show six independent replicates of each case studied here. N_F m=200.

Figure 5.

Expected mismatch distributions obtained from 10 000 genetic simulations of 22 linked SNPs for samples located in Germany without or with maximum genetic flow between HG and F, with and without ascertainment bias. Dashed lines correspond to the limits of a 90% confidence interval for the mismatch distribution. Small graphs show 10 independent replicates of each case studied here. Ascertainment bias was modelled by selecting SNPs with a minor allele frequency exceeding 10% along the transect shown on figure 1.

4. Discussion

a Simulating a realistic Neolithic range expansion

The degree of realism of our simulations of the colonization of Europe by Homo sapiens sapiens followed by a second Neolithic range expansion is difficult to judge, as the true history of the European population has certainly been even more complex (Mazurié de Keroualin 2003). However, these simulations are more realistic than those done previously (Rendine et al. 1986; Barbujani et al. 1995), and fit the known duration of the Neolithic transition process as well as the duration of the Mesolithic period in several places. Since simulated cohabitation times between HG and F demes vary between 5.6 and 7.7 generations (150–200 years; table 1), they are thus close to documented cases where the two types of economies coexisted over larger areas, like 300 to 700 years in the North of the Alps and the Jura (Gallay 1994), 800 years in Cantabria and 400 years in Portugal (Arias 1999), or 200 years in Franche-Compté (Jeunesse 1998).

Our simulations were performed in a homogeneous environment with γ identical in every deme, regardless of its location. While this assumption may seem unrealistic at a regional scale, it is quite reasonable at a continental scale since the speed of HG colonization and that of the Neolithic transition can be regarded as quite regular at this level (Ammerman & Cavalli-Sforza 1984; Bocquet-Appel & Demars 2000). It would be interesting to test, in future studies, the influence of some heterogeneity of the migration wave, and to incorporate, with considerable additional work and computer power, more realism in the simulation, such as an heterogeneous environment subject to temporal fluctuations (Adams & Faure 1997), spatial heterogeneity in γ inferred from archaeological information (Lahr et al. 2000), maritime migrations along the Mediterranean coasts (Zilhao 2001), or contractions/re-expansion during ice ages and long distance dispersal. It, however, appears necessary to understand the genetic signature expected under a relatively simple demographic scenario, before considering more complex ones.

b AFCs and influence of ascertainment bias

The AFCs can be generated by a succession of founder effects along the axis of diffusion of an expansion wave (Barbujani et al. 1995; Fix 1997; Austerlitz et al. 2000). However, our results show that alleles that are selected to be relatively frequent over the whole range of the studied area are considerably more probable to have a clinal distribution along the axe of the expansion. It, therefore, suggests that the probability of observing a cline is considerably higher for alleles that are older than—or that have occurred in the initial phase of—the expansion (possibly at the front of the wave of advance, Edmonds et al. 2004). In that sense, an ascertainment bias in favour of SNPs with frequent minor alleles will show frequency clines in about 50% of the cases after an expansion (table 1), whereas no or a non-significant number of clines (<5%) will be observed without ascertainment bias. This difference can perhaps explain the fact that AFCs have been commonly observed for classical markers (Menozzi et al. 1978; Sokal et al. 1991), short tandem repeat and SNPs (i.e. Chikhi et al. 1998; Rosser et al. 2000) in Europe, but not for mtDNA when unascertained complete sequence data are used (Richards et al. 1996; Richards et al. 1998). Note that when ascertainment is artificially exerted on mtDNA sequence, for instance by defining haplogroups on the basis of old mutations defining mtDNA lineages, a geographical structure and gradient of haplogroup frequencies begins to be observed (Richards et al. 2002).

Our simulations suggest that AFC from the Middle East to northwestern Europe can be generated equally well by the Neolithic expansion process that occurred 8000 to 3000 BC or by the expansion of the first modern human in Europe ∼45 000 to 30 000 BP. It is important to recognize that AFCs are not generated by the different amounts of Palaeolithic lineages in the current demes along the expansion path (figure 3), since clines are present even in total absence of such lineages, as in the case of a pure DD model (γ=0). In fact, the occurrence of these AFCs is relatively independent of the contribution of Palaeolithic lineages into the current gene pool of Europeans (table 1). The expected frequency of AFCs under a pure CD (when the F layer does not exist, i.e. table 1, last line) is even larger than under the pure DD model (γ=0), owing to the fact that founder effects are stronger in small populations. Since the presence of AFCs is thus independent of the proportion of Neolithic lineages in the population, they cannot be invoked as a pure support to the DD theory (Barbujani et al. 1995; Barbujani & Bertorelle 2001), and only the dating of the AFCs would perhaps allow the support of one model rather than another.

c Palaeolithic contribution to the European genetic pool

The nature of the founders of a population is important to determine its final genetic composition (Heyer 1995; Heyer & Tremblay 1995; Milinkovitch et al. 2004), because the majority of individuals present at equilibrium are descendants from the first colonists (Currat & Excoffier 2004; Edmonds et al. 2004). Our simulations show that a very small initial Palaeolithic contribution in each deme (0.125% on average) is enough to lead to a situation where most of the current gene pool can be traced to the Palaeolithic (table 1). The proportion of Europeans who are descendant from the first farmers from the Levant decreases very quickly with distance from the Neolithic source, as the lineages of Neolithic origin are rapidly diluted along the axis of colonization (figure 3). Under our simulation conditions, an average local Palaeolithic contribution larger than 0.375% will indeed be enough to prevent Neolithic lineages to diffuse over the whole Europe.

These results imply that, under our model of a progressive range expansion of Neolithic farmers with possible genetic exchange and competition with local Palaeolithic hunter–gatherers, it is very unlikely that the Palaeolithic contribution be globally smaller than 50%. If that was the case (e.g. Chikhi et al. 2002; <30%), it would imply that Neolithic would have had virtually no genetic contact with local populations, like under a pure DD model. Global surveys of mtDNA molecular diversity (Richards et al. 1996, 2000), and the simulations of mtDNA mismatch distributions argue against such a low contribution of Palaeolithic populations to the modern gene pool. Indeed, examination of figure 4 reveals that in the absence of exchange with hunter–gatherers, mismatch distributions should often be multimodal, and have a mode closer to zero in populations sampled far from the Neolithic source. On the contrary, most European mismatch distributions are smooth and unimodal (Excoffier & Schneider 1999), and the mode of mismatch distributions is quite homogeneous across Europe (Excoffier 2004), as expected when the contribution of Palaeolithic lineages becomes important. Moreover, previous dating of demographic expansion for European populations has pointed towards 40 000 years ago or more (Comas et al. 1996; Excoffier & Schneider 1999), in keeping with a Palaeolithic expansion.

d Influence of ascertainment bias on SNP diversity

Ascertainment bias has also a drastic effect on the shape of mismatch distributions inferred from linked SNPs, as they become highly multimodal for relatively large amounts of ascertainment bias (minor allele frequency>10%). Therefore, this kind of ascertainment bias can erase a signature of demographic or range expansion in the mismatch. It is interesting to note that the analysis of 22 linked Y chromosome SNPs show bimodal mismatch distributions (Pereira et al. 2001), this absence of expansion signal being attributed to a smaller male than female effective size (Dupanloup et al. 2003). Note, however, that bimodal mismatch distributions can also be obtained under a pure DD model (figure 5a), but this model was shown above to be unlikely from the analysis of mtDNA. It follows that observed differences between the mismatch distributions obtained from mtDNA sequences and from Y chromosome SNPs can be explained by the mere selection of frequent Y chromosome SNPs, which is also supported by the observation of AFC for these markers and not for mtDNA sequences.

Our results underline the fact that ascertainment bias affects levels of genetic diversity, both within and between populations. In particular, the selection of alleles with relatively high overall frequencies will erase the trace of demographic or range expansions in the mismatch distribution. However, because this selection increases the probability of observing AFC after one or a series of range expansion, it enhances the potential of detecting these past range expansions. Therefore, one should not necessarily conclude that markers that could have been selected for their frequency or high heterozygosity would not be suitable for inferring settlement history of human populations, but one should be extremely careful in the interpretation of pattern of diversity, since most theoretical predictions are available for randomly selected markers.