Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2006 Oct;174(2):763–773. doi: 10.1534/genetics.106.060392

The Genetic Architecture of Life Span and Mortality Rates: Gender and Species Differences in Inbreeding Load of Two Seed-Feeding Beetles

Charles W Fox 1,1, Kristy L Scheibly 1, William G Wallin 1, Lisa J Hitchcock 1, R Craig Stillwell 1, Benjamin P Smith 1
PMCID: PMC1602065  PMID: 16888331

Abstract

We examine the inbreeding load for adult life span and mortality rates of two seed beetle species, Callosobruchus maculatus and Stator limbatus. Inbreeding load differs substantially between males and females in both study populations of C. maculatus—life span of inbred females was 9–13% shorter than the life span of outbred females, whereas the life span of inbred males did not differ from the life span of outbred males. The effect of inbreeding on female life span was largely due to an increase in the slope of the mortality curve. In contrast, inbreeding had only a small effect on the life span of S. limbatus—life spans of inbred beetles were ∼5% shorter than those of outbred beetles, and there was no difference in inbreeding load between the sexes. The inbreeding load for mean life span was ∼0.4–0.6 lethal equivalents per haploid gamete for female C. maculatus and ∼0.2–0.3 for both males and females of S. limbatus, all within the range of estimates commonly obtained for Drosophila. However, contrary to the predictions of mutation-accumulation models, inbreeding load for loci affecting mortality rates did not increase with age in either species, despite an effect of inbreeding on the initial rate of increase in mortality. This was because mortality rates decelerated with age and converged to a mortality plateau for both outbred and inbred beetles.

THE evolution of life span, mortality rates, and patterns of senescence is of substantial interest because there is tremendous variation in these traits at all taxonomic levels (Promislow 1991) and because of the medical implications of understanding the genetics underlying mortality rates. Studies on mice, Drosophila, and Caenorhabditis elegans have identified numerous genes that influence life span and/or rates of senescence (Harshman 2002). Recent studies of life span in Drosophila melanogaster indicate that inheritance of life span can be quite complex, with both dominance and epistasis having significant effects on variation in life span (Harshman 2002; Leips and Mackay 2002; Mackay 2002; Spencer et al. 2003; Spencer and Promislow 2005). These studies also show that the genetic architecture (number of genes and degree of allelic and genic interactions) underlying life span differs between the sexes and depends on the environmental conditions in which individuals are reared.

One of the major genetic mechanisms proposed to underlie senescence is the accumulation in populations of late-acting deleterious alleles due to the declining force of selection with increasing age (mutation-accumulation theory) (Hughes and Reynolds 2005). Research has now identified many genes and chromosomal regions (QTL) that affect life span in model organisms but we have few data on the frequency of deleterious alleles affecting life span (De Luca et al. 2003; Carbone et al. 2006). We have less data on the sources of variation in deleterious alleles and the age specificity of expression of those alleles and thus their effects on age-specific mortality rates.

Inbreeding studies are a common method by which we quantify mutational load (inbreeding load) on traits affecting fitness. Inbreeding increases homozygosity and thus increases expression of recessive alleles, allowing us to quantify the degree to which increased expression of recessive alleles reduces fitness. Often these recessive alleles are deleterious and are maintained in populations because their detrimental effects are masked from selection in heterozygous individuals (Carr and Dudash 2003). Because the effects of inbreeding on life span depend on the genetic architecture underlying life span, studies of inbreeding depression can provide insight into the genetics of variation in life span within populations (Swindell and Bouzat 2006). Likewise, quantifying variation in inbreeding load provides a means to study how the genetics of variation in life span vary in response to environmental conditions, among populations or species, and between the sexes. Inbreeding studies can also be used to test predictions of mutation-accumulation theory. In particular, mutation-accumulation theory predicts that inbreeding load increases with age (Charlesworth and Hughes 1996; Hughes and Reynolds 2005). This hypothesis has been tested only with Drosophila and has been generally supported (Snoke and Promislow 2003; Swindell and Bouzat 2006).

Numerous studies have now demonstrated that inbreeding reduces adult life span of a variety of animals, including mice (Miller et al. 2002), carnivores (Laikre and Ryman 1991; Laikre 1999), butterflies (Saccheri et al. 1998; van Oosterhout et al. 2000), hymenopterans (Henter 2003; Luna and Hawkins 2004), and Drosophila. However, many studies have failed to detect inbreeding depression on adult life span (Johnson and Hutchinson 1993; De Clercq et al. 1998; Nieminen et al. 2001; Markert et al. 2004; Prezotti et al. 2004; Radwan et al. 2004; Goncalves and Di Mare 2005) and others have shown that the effect of inbreeding on adult life span varies among lines or populations (Fowler and Whitlock 1999; Swindell and Bouzat 2006) and among rearing conditions (Pray et al. 1994). Unfortunately, most detailed studies of the genetics of life span and mortality rates, and the effects of inbreeding on life span and mortality rates, use Drosophila as a model system (Clarke and Maynard Smith 1955; Hughes 1995; Pletcher et al. 2000; Hughes et al. 2002; Vermeulen and Bijlsma 2004; Swindell and Bouzat 2006). Many of these studies focus on one gender, usually males (Hughes and Charlesworth 1994; Hughes 1995; Snoke and Promislow 2003; Vermeulen and Bijlsma 2004; Swindell and Bouzat 2006), although numerous studies have shown that the genetic architecture underlying adult longevity differs substantially among males and females (Nuzhdin et al. 1997; Vieira et al. 2000; Harshman 2002; Spencer et al. 2003).

Here we examine the effect of inbreeding on adult life span and mortality rates of both males and females of two seed-feeding beetle species, Callosobruchus maculatus and Stator limbatus. We test whether the degree of inbreeding depression, and thus the inbreeding load at loci affecting male and female life span and mortality rates, differs between species and between the sexes. We find that inbreeding load differs substantially between males and females in both study populations of C. maculatus. We also detected significant inbreeding depression for life span of S. limbatus, but inbreeding load was similar between males and females. Contrary to the predictions of mutation-accumulation models, inbreeding load for loci affecting mortality rates did not increase with age in either species.

MATERIALS AND METHODS

The biology of C. maculatus:

C. maculatus is a cosmopolitan pest of stored legumes (Fabaceae). Females cement their eggs to the surface of host seeds (Messina 1991). Eggs hatch 4–5 days later (at 26°–28°) and first instar larvae burrow into the seed. Larval development and pupation are completed within a single seed; beetles emerge as reproductively mature adults.

Because of its ease of laboratory rearing C. maculatus has been widely used as a model organism for the study of mortality patterns (Tatar and Carey 1993, 1994, 1995; Fox et al. 2003a, 2004a, 2004b). Having evolved to use dry seeds, and most recently having evolved in a storage environment, C. maculatus larvae develop and adults mature, mate, and complete reproduction using metabolic water and the resources acquired during larval development (i.e., they are capital breeders) (Messina and Slade 1999). Access to adult resources has a small positive effect on female fecundity and improves adult life span (Fox 1993; Fox and Dingle 1994; Tatar and Carey 1995). However, adults have no access to food or water in a storage environment (they cannot feed externally on seeds) and there is little evidence that they feed as adults outside of a storage environment.

We examined inbreeding effects on two populations of C. maculatus that were collected from and maintained on different legume hosts. The South India (SI) population was collected in 1979 from infested pods of mung bean, Vigna radiata (L.) Wilczek, and the closely related black gram, V. mungo (L.) Hepper, in Tirunelveli, India (Mitchell 1991). The Burkina Faso (BF) population was collected in 1989 from infested pods of cowpea, V. unguiculata (L.) Walp., in Ouagadougou, Burkina Faso (Messina 1993). These two populations differ in body size, lifetime fecundity, patterns of egg dispersion, oviposition preference, and adult life span (Fox et al. 2004a,b; Messina 2004). Both populations were maintained in laboratory growth chambers on seeds of V. radiata (SI) or V. unguiculata (BF) at >1000 adults per generation for >100 generations (BF) or >200 generations (SI) prior to this experiment.

The biology of S. limbatus:

S. limbatus is a seed-feeding beetle native to the southwestern United States and distributed through dry forests and deserts all the way south to northern South America (Morse and Farrell 2005a,b). Eggs of S. limbatus, like those of C. maculatus, are glued to the surface of host seeds and larvae complete development inside a single seed, emerging after pupation as an adult. Adults reproduce using larval resources; they require neither food nor water, making them a very practical laboratory model. S. limbatus uses >70 host species throughout its large geographic range. For these experiments we raised beetles on seeds of the silk tree, Albizia julibrissin. A. julibrissin is not a native host; it is invasive in the United States, but is readily colonized by beetles in the field and is a better host for beetles (i.e., lower mortality) than many of their native hosts. We use A. julibrissin for many laboratory experiments because we can purchase large supplies of seeds from horticultural suppliers.

The study population of S. limbatus used here was collected along Mount Lemmon Highway in Oracle, Pinal County, Arizona (32.61° N, 110.77° W) from >20 Acacia greggii trees as larvae inside of seeds. Beetles emerging from these field-collected seeds were used to establish a laboratory colony (>200 beetles) that was maintained for six generations in the laboratory at >100 families per generation at 26°–28°, light:dark 15:9 hr, prior to this experiment.

Inbreeding depression in C. maculatus and S. limbatus:

Both seed beetle species suffer substantial inbreeding depression throughout development. Eggs produced from inbred matings are less likely to develop and have lower hatch rates, and larvae have reduced hatch-to-adult survival. Eggs from full-sib matings are 17–21% less likely to produce an adult offspring than eggs from outbred matings in the BF and SI populations of C. maculatus (respectively) and 22–41% (depending on the population) less likely to produce an adult offspring in S. limbatus (Fox et al. 2006). Inbred offspring that survive to adults develop more slowly—larval development time is extended by ∼5% (>1 day) in both beetle species (Tran and Credland 1995; Fox and Scheibly 2006; Fox et al. 2006). Inbreeding does not affect adult body size of either sex of S. limbatus (Fox and Scheibly 2006) but has been shown to affect female body size in C. maculatus (Tran and Credland 1995). Inbreeding also negatively affects female fecundity in both C. maculatus (Tran and Credland 1995) and its congener C. chinensis (Tanaka 1990, 1993), although there is no evidence that the effect of inbreeding on fecundity increases with age.

Experimental design:

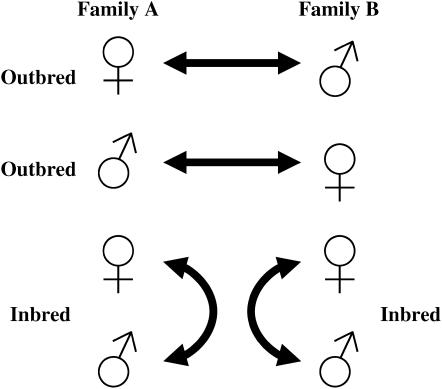
To measure inbreeding depression we used a “block” design (Roff 1998). Each block was created by randomly pairing two families chosen from an outbred population. From each family we randomly chose two females and two males to become parents. We then crossed these two families as shown in Figure 1, creating two inbred and two outbred families. The advantage of this design is that it ensures that inbred families are created from the same set of alleles as are the outbred families to which they are compared (Fox 2005).

Figure 1.—

Figure 1.—

Open in a new tab

The block design used to measure inbreeding depression. Each block is created by crossing beetles from two unrelated families, creating two outbred matings (reciprocal crosses between the two families) and two inbred matings (crosses between full-sibs within each family). Outbreds and inbreds within each block thus have, on average, the same set of alleles but differ in degree of homozygosity due to the mating treatment.

C. maculatus:

Pairs were confined in a 35-mm petri dish with ∼35 seeds of mung, V. radiata. Dishes were checked for eggs twice per day. Larvae were allowed to develop at one egg per seed (excess eggs were scraped from the seed) and one seed per dish inside temperature and photoperiod-controlled growth chambers at 26° (±1°), light:dark 15:9 hr. Dishes were checked twice per day for adult beetles that emerged from a seed. Adults were checked twice per day for the date they died.

The experiment was run in two replicates ∼4 months apart. In replicate 1 we measured adult life span of 2073 adult beetles in 72 blocks, each with two inbred and two outbred families (31 blocks for the BF population and 41 blocks for the SI population). Unfortunately, our sample sizes in replicate 1 were too small for our mortality analyses. We thus repeated the experiment (replicate 2) and raised 12,998 beetles to adult and recorded life span for 12,827 of these (171 beetles were lost or had incomplete data recorded) from 92 blocks (BF population) and 90 blocks (SI population).

Within replicates, beetles from both populations were intermixed on trays in two temperature- and photoperiod-controlled growth chambers with beetles rotated daily between chambers to control for random differences between the chambers.

Stator limbatus:

S. limbatus were handled the same as C. maculatus except that larvae were raised to adults on seeds of A. julibrissin. Because fecundity of S. limbatus females is much lower than fecundity of C. maculatus family sizes are necessarily smaller. We thus created a larger number of blocks. In total we collected 4974 eggs from which we raised 3195 offspring to adult from 167 blocks.

Analyses:

Blocks are the lowest level of independence in this design. Each block contains four means, one for each sex-by-treatment combination (inbred male offspring, outbred males, inbred females, and outbred females). Block means were calculated first by averaging across offspring within a family and then by averaging the families within the block.

Life span data fit assumptions of standard general linear models and are thus analyzed using analysis of variance with life span as the response variable and the block effect (nested within populations and replicates) as the denominator mean square. The magnitude of inbreeding depression was measured as the proportional decrease in life span due to inbreeding, δ = (meanoutbred − meaninbred)/meanoutbred. To test for differences in inbreeding depression between the sexes and among populations (in C. maculatus), we tested for the presence of treatment-by-sex and treatment-by-population interactions.

The age-specific mortality rate was estimated as u(t) = −ln[P(t)], where P(t) is the daily survival rate. As in previous studies (Fox and Moya-Laraño 2003; Fox et al. 2003a,b, 2004a) the mortality rates of both C. maculatus and S. limbatus were best described by a logistic model of the of the form

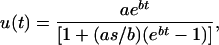graphic file with name M1.gif

where u(t) is the estimated age-specific hazard rate at age t, a is the intercept of the relationship u(t) = aebt (often referred to as the initial mortality rate or the “extrinsic” mortality rate), b is the rate of exponential increase in mortality at young ages, and s describes the degree of deceleration in mortality with increasing age (Vaupel 1990; Pletcher 1999). This model is similar to a Gompertz mortality model except that it incorporates a term, s, to account for the slowing of the increase in mortality rate with age (Pletcher and Curtsinger 1998); when s = 0 the logistic model reduces to the Gompertz model. Both a Gompertz model and a Gompertz–Makeham model provided significantly worse fits to the data (in all analyses) than did the logistic model.

Parameters of the logistic mortality model (a, b, and s) were estimated using the maximum-likelihood estimation procedure of WinModest (Pletcher 1999). We used the log-likelihood-ratio test of WinModest to test whether individual parameter estimates differed significantly between inbred and outbred beetles. This test compares the log-likelihood [L(v)] of models for which parameter estimates are constrained to be equal in the two models with the log-likelihood of the models in which the parameter estimates are unconstrained. Twice the difference between the maximum-log-likelihood estimates of the constrained and unconstrained models is distributed as a χ2-random variable with 1 d.f.

The inbreeding load affecting the age-specific mortality rate was estimated as the number of lethal equivalents per gamete (Lynch and Walsh 1998; Charlesworth and Charlesworth 1999), following the methods in Swindell and Bouzat (2006). The inbreeding load [Lu(t)] affecting age-specific mortality, u(t), was calculated as

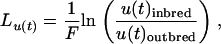graphic file with name M2.gif

where F is the inbreeding coefficient (0.25 in our experiment). The inbreeding load for genes affecting total adult life span was estimated by regressing life span on the inbreeding coefficient, which, for our two-treatment case, is

graphic file with name M3.gif

Inbreeding load for life span was calculated separately for each block and then averaged across blocks within a population/species.

RESULTS

The patterns of life span and mortality for both populations of C. maculatus and S. limbatus were consistent with previous experiments. We thus refer readers to those previous articles for detailed discussions of population differences (Fox et al. 2004a), gender differences (Fox et al. 2003b), and maternal age effects (Fox et al. 2003a) on population demography for both species of beetles. Here we focus only on inbreeding effects.

C. maculatus:

Sex ratio of emerging adults:

The sex ratio of C. maculatus emergers did not differ from 1:1 for any population-by-treatment combination in replicate 1 (male/female ratio between 0.88 and 1.00; sign test P > 0.07 for each population-by-treatment combination), and there was no evidence that sex ratio differed between inbred and outbred beetles (χ2 < 0.71, P > 0.04 for both populations). In contrast, the sex ratio was male biased in three of the four population-by-treatment combinations of replicate 2 (male/female ratio: BF inbred, ratio = 1.25, P < 0.001; BF outbred, ratio = 1.10, P = 0.002; SI inbred, ratio = 1.10, P = 0.006; and SI outbred, ratio = 1.03, P = 0.19). For the BF population, adult sex ratio was significantly more male biased for inbred beetles than for outbred beetles (χ2 = 6.7, P = 0.009), but there was no difference in sex ratio between treatments for the SI population (χ2 = 1.4, P = 0.23).

Life span:

Life span differed between the two replicates of the experiment—beetles lived ∼1 day shorter in replicate 2 than in replicate 1 (F1,251 = 4.49, P = 0.035), although the difference between replicates was larger for females than for males (replicate-by-sex interaction, F1,251 = 5.15, P = 0.024). We thus include a replicate effect and replicate-by-sex interaction in our analyses of variance presented below.

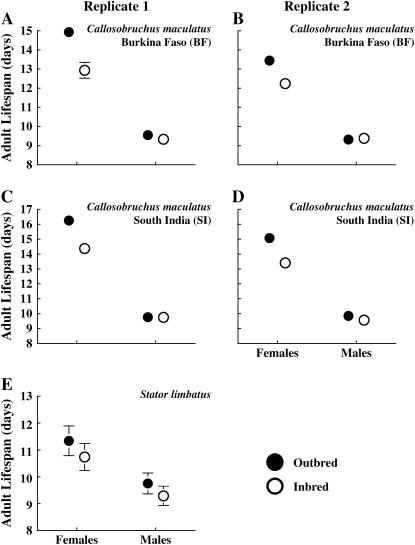
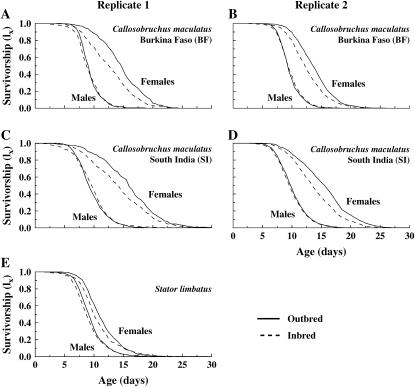
There was a large difference between males and females in the effect of inbreeding on adult life span (significant sex-by-treatment interaction, F1,251 = 13.8, P < 0.001). Females, which lived longer than males (F1,251 = 544, P < 0.001), experienced significant inbreeding depression on life span—inbred females had 11–13% (replicate 1) and 9–10% (replicate 2) shorter life spans than did outbred females (Figure 2; Table 1; F1,251 = 37.4, P < 0.001). This inbreeding effect on life span is evident in the survivorship curve for females of both populations (Figure 3). In contrast, there was no effect of inbreeding on male life span (Figures 2 and 3; Table 1; F1,251 = 0.47, P = 0.49). There was also no difference between populations in the effect of inbreeding on adult life span (there was no significant population-by-treatment interaction, F1,251 = 0.01, P = 0.91) and no difference between populations in the gender effect on inbreeding depression (nonsignificant sex-by-population-by-treatment interaction; F1,251 = 0.05, P = 0.82).

Figure 2.—

Figure 2.—

Open in a new tab

The effect of inbreeding on the adult life span of Callosobruchus maculatus (two replicates) and Stator limbatus. Means (± SEM) are calculated first by averaging across families in a block and then across blocks within a treatment. Each block is treated as an independent data point. Some error bars are smaller than the points.

TABLE 1.

The magnitude of inbreeding depression on adult life span of Callosobruchus maculatus and Stator limbatus

δa
Trait C. maculatus (Burkina Faso) C. maculatus (South India) S. limbatus
Replicate 1
    Females 0.13 ± 0.03 0.11 ± 0.03 0.04 ± 0.01
    Males 0.01 ± 0.03 −0.01 ± 0.04 0.05 ± 0.01
(N = 31) (N = 41) (N = 167)
Replicate 2
    Females 0.09 ± 0.01 0.10 ± 0.01
    Males −0.01 ± 0.01 0.02 ± 0.02
(N = 92) (N = 90)
Open in a new tab

N, the number of blocks where each block contains two inbred and two outbred families; see Figure 1.

a

δ = (meanoutbred – meaninbred)/meanoutbred (the proportional decrease in life span of inbreds relative to outbreds). δ is calculated separately for each block and then averaged across blocks. δ has an expectation of 0 when there is no inbreeding depression and can vary from positive to negative depending on whether inbreds have lower or higher life span than outbreds, respectively.

Figure 3.—

Figure 3.—

Open in a new tab

Survivorship curves for inbred vs. outbred males and females of Callosobruchus maculatus (two replicates) and Stator limbatus.

Mortality rates:

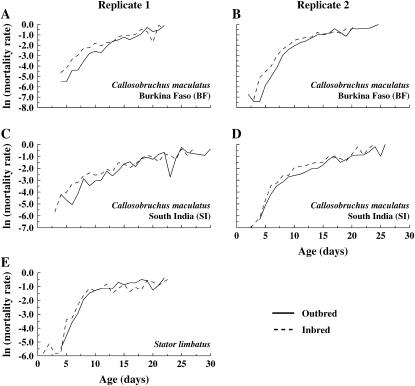
A comparison of the overall shape of the mortality curves [u(t)] between inbred and outbred females was consistent with the ANOVA on life span—mortality curves differed substantially between inbred and outbred females 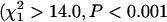Inline graphic for both populations in replicate 1; 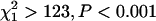Inline graphic for both populations in replicate 2). Unfortunately, our data set in replicate 1 was not large enough to detect significant differences between inbred and outbred females for any of the individual parameters (a, b, or s) of the mortality curve (P > 0.05 for each test; sample sizes ranged between 206 and 324 beetles per population/treatment combination). However, replicate 2 was large enough to provide adequate power for tests of individual model parameters—we averaged 1516 females per treatment/population combination (range 1335–1664). Inbreeding significantly increased the slope (b) of the mortality curve for both populations (Table 2; 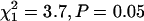Inline graphic for the BF population; 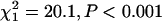Inline graphic for the SI population). The difference in slope (b) between inbred and outbred beetles is clearly visible in the mortality curves for the SI population (Figure 4D) but less clear for the BF population (Figure 4B). However, constraining the mortality curves for inbred and outbred beetles to have equal slopes (b) in the BF population significantly reduces the fit of the logistic model 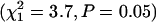Inline graphic whereas constraining the two models to equal intercepts (a) does not 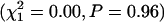Inline graphic, indicating that the two treatments do not differ in their baseline mortality rate for the BF population. 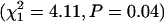In contrast, inbreeding significantly reduced the baseline mortality rate for SI females Inline graphic.

TABLE 2.

Parameter values for the logistic mortality model, u(t) = aebt/[1 + (as/b)(ebt − 1)], for inbred and outbred females of Callosobruchus maculatus

Parameter estimatesa (95% confidence intervals)
a (×10−3) b s
Burkina Faso (BF)
    Inbred 0.15 (0.07–0.29) 0.725 (0.650–0.809) 1.798 (1.475–2.193)
    Outbred 0.14 (0.08–0.26) 0.632 (0.576–0.694) 1.384 (1.142–1.679)
    Likelihood-ratio test (inbred vs. outbred) NS Inbred > outbred, P = 0.05 NS
South India (SI)
    Inbred 0.58 (0.34–0.98) 0.527 (0.469–0.592) 1.638 (1.311–2.046)
    Outbred 1.08 (0.76–1.54) 0.379 (0.347–0.414) 0.923 (0.736–1.159)
    Likelihood-ratio test (inbred vs. outbred) Inbred < outbred, P < 0.001 Inbred > outbred, P < 0.001 Inbred > outbred, P = 0.009
Open in a new tab

a, the initial mortality rate; b, the rate of exponential increase in mortality at young ages; s describes the degree of deceleration in mortality with increasing age; NS, not significant, P > 0.05.

a

Results are presented for replicate 2 only; sample sizes for replicate 1 were small and thus 95% confidence intervals on parameter estimates were very large.

Figure 4.—

Figure 4.—

Open in a new tab

Mortality curves, ln[u(t)], for inbred vs. outbred females of Callosobruchus maculatus (two replicates) and Stator limbatus. Parameter estimates for the logistic mortality curve are presented in Table 2.

Inbreeding load:

Our estimated inbreeding loads on total life span of C. maculatus were 0.61 ± 0.11 and 0.39 ± 0.05 (for replicates 1 and 2, respectively) for BF females and 0.53 ± 0.11 and 0.46 ± 0.06 for SI females, all of which were significantly >0 (P < 0.001) but do not differ significantly between populations. As expected from the lack of significant inbreeding depression for males, the estimates of inbreeding load for males were not significantly different from 0 for either replicate in either population (0.09 ± 0.10 and −0.02 ± 0.04 for BF, 0.06 ± 0.15 and 0.10 ± 0.06 for SI, all P > 0.18).

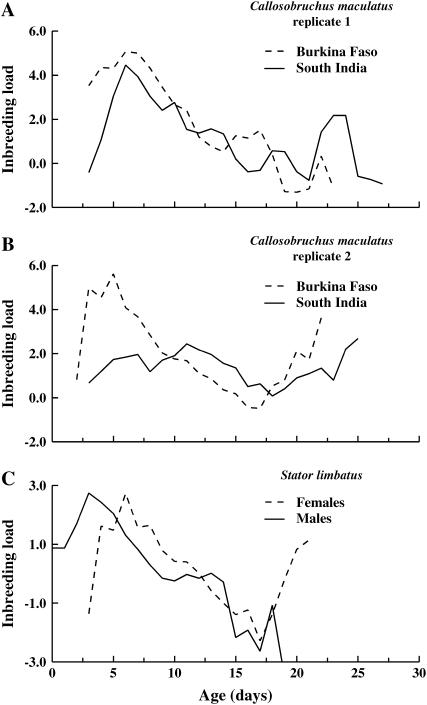
The effect of age on the inbreeding load of C. maculatus females is shown in Figure 5, A and B. In contrast to expectations, we have no evidence that the inbreeding load increases with age. Instead, the slope of the regression of inbreeding load vs. age was significantly negative (ranging between −0.32 and −0.12) for all except SI females in replicate 2, for which the slope did not differ significantly from 0 (slope = 0.01 ± 0.01). Initially, this decline in L with age appears inconsistent with our observation that that there is a significant difference between inbreds and outbreds in the slope (b) of the mortality curve; such a difference suggests that inbreeding depression affecting age-specific mortality increases over the life span of beetles (Swindell and Bouzat 2006). However, this is not necessarily true when the mortality rate does not increase exponentially but instead is best described by a logistic model. Although the mortality rate of Callosobruchus initially increased more quickly for inbred relative to outbred beetles (higher b for inbred beetles), this increase also decelerated more quickly for inbred than outbred beetles such that our estimates of inbreeding load (haploid lethal equivalents) did not increase with age (Figure 5, A and B).

Figure 5.—

Figure 5.—

Open in a new tab

Age-specific inbreeding load for the mortality rate of female Callosobruchus maculatus (two replicates) and both male and female Stator limbatus. The lines are smoothed by averaging 3-day intervals centered on the age on the x-axis.

Stator limbatus:

Sex ratio of emerging adults:

As observed for C. maculatus, the overall sex ratio of emerging adults was significantly male biased (male/female ratio = 1.10, P = 0.02). However, there was no significant difference in sex ratio between the two treatments (χ2 = 1.4, P = 0.24).

Life span:

In contrast to the results for C. maculatus, inbreeding affected adult life span of both sexes of S. limbatus. However, the effect was quite small—in both males and females, outbred S. limbatus lived 4–5% longer than did inbred S. limbatus (Figure 2, Table 1; F1,166 = 8.2, P = 0.005). Note that the large standard errors on life span estimates in Figure 2 are a consequence of a large block effect on life span—life span is heritable, generating substantial variation among blocks in mean life span. Despite this variation in mean life span among blocks, 62% of the blocks showed inbreeding depression in female life span (sign test, P = 0.003) and 68% of blocks showed inbreeding depression in male life span (sign test, P < 0.001). Although the inbreeding effect is small (4–5%; Table 1), inbreeding depression on life span is visible in the survivorship curve for both sexes (Figure 3E).

Although mean adult life span differed between males and females (females live longer; F1,166 = 59.9, P < 0.001), there was no evidence that the magnitude of inbreeding depression differed between the sexes (Table 1; no sex-by-treatment interaction; F1,166 = 0.01, P = 0.99). However, inbreeding depression in males and females appeared to be independent across blocks—although male life span was positively correlated with female life span (among blocks) for outbred beetles (r = 0.36, P < 0.001), male life span was not correlated with female life span for inbred beetles (r = 0.08, P = 0.39) and the magnitude of inbreeding depression (δ) on male life span was not correlated (among blocks) to the magnitude of inbreeding depression on female life span (r = −0.09; P = 0.36).

Mortality rates:

Consistent with the ANOVA results for life span, a comparison of the overall shape of the mortality curves [u(t)] between inbred and outbred beetles indicated that the mortality curves differed significantly between inbred and outbred beetles 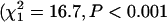Inline graphic for females; 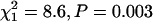Inline graphic for males; Table 3). The trend was for inbred beetles to have higher baseline mortality (a) and a lower increase of the mortality rate with age (b) but none of the individual model parameters were significantly different between inbred and outbred beetles (P > 0.05 for each).

TABLE 3.

Parameter values for the logistic mortality model, u(t) = aebt/[1 + (as/b)(ebt − 1)], for both inbred and outbred females and males of Stator limbatus

Parameter estimates (95% confidence intervals)
a (×10−3) b s
S. limbatus—females
    Inbred 0.11 (0.03–0.43) 0.906 (0.742–1.105) 2.492 (1.831–3.391)
    Outbred 0.02 (0.00–0.12) 1.005 (0.826–1.221) 2.672 (1.976–3.614)
    Likelihood-ratio test (inbred vs. outbred) NS NS NS
S. limbatus—males
    Inbred 0.09 (0.02–0.33) 1.096 (0.906–1.325) 2.502 (1.857–3.371)
    Outbred 0.04 (0.01–0.16) 1.129 (0.954–1.335) 2.369 (1.805–3.108)
    Likelihood-ratio test (inbred vs. outbred) NS NS NS
Open in a new tab

a, the initial mortality rate; b, the rate of exponential increase in mortality at young ages; s describes the degree of deceleration in mortality with increasing age; NS, not significant, P > 0.05.

Inbreeding load:

Our estimated inbreeding loads on total life span of S. limbatus were 0.25 ± 0.08 for females and 0.30 ± 0.08 for males. Both estimates are significantly >0 (t = 2.3, P = 0.02 for females; t = 2.1, P = 0.03 for males) but the estimates of inbreeding load are not significantly different between males and females (z = 0.04, P = 0.97).

As was observed for C. maculatus, but inconsistent with predictions of mutation-accumulation models, we have no evidence that the inbreeding load increases with age for S. limbatus (Figure 5C). Inbreeding load declined by, on average, 0.11 ± 0.05 lethal equivalents per day in females and 0.26 ± 0.03 lethal equivalents per day in males.

DISCUSSION

The most intriguing result of this study is that, for C. maculatus, inbreeding affected life span only of females; female life span was 9–13% lower for inbred beetles whereas male life span was not lower for inbred than outbred beetles. This translated into a significant inbreeding load at loci affecting life span of females, but not males. In contrast, although the effect of inbreeding on S. limbatus life span was small, it was significant and of similar magnitude for both sexes, and thus the estimated inbreeding load was similar for both males and females.

The gender difference in inbreeding load of C. maculatus:

Although numerous studies have shown detectable effects of inbreeding on adult life span (references in the Introduction), we know of only one previous study that has detected a gender difference in the effect of inbreeding on life span—inbreeding has a much larger effect on the life span of females than males in three species of gazelles (Cassinello 2005). However, that study did not distinguish juvenile from adult mortality. To our knowledge, ours is the first study to demonstrate gender-specific effects of inbreeding on adult (postmaturation) life span. However, many studies have demonstrated gender differences in inbreeding depression for other traits. For example, in the butterfly Bicyclus anynana the inbreeding load for male fertility is large whereas the inbreeding load for female fertility is negligible (Saccheri et al. 2005). In mandrills (Mandrillus sphinx), inbreeding affects body size of females, but not males (Charpentier et al. 2006). Inbreeding has also been shown to affect body size of female, but not male, C. maculatus (Tran and Credland 1995). Unfortunately, we did not measure body size in our current experiments. Controlling for the effects of body size in a recent line-cross study reduced the gender difference in dominance affecting population differences in life span (Fox et al. 2004a). In contrast, a previous study has shown that body size is only weakly correlated with female life span for the SI population (R2 < 0.14) and is uncorrelated with female life span in the BF population (Fox et al. 2004a), suggesting that inbreeding effects on body size should have little effect on adult life span. Also, although inbreeding reduced the life span of S. limbatus in this current study, it had no effect on adult body size in any of three replicate populations in a different experiment (Fox and Scheibly 2006). We thus believe that an inbreeding effect on body size is unlikely to be the mechanism causing inbreeding depression in adult life span.

If inbreeding depression on body size is an unlikely explanation, why is there a large gender difference in inbreeding depression in C. maculatus? Possibly larval mortality is nonrandom, with poor-quality inbred males more likely to die before emergence than are poor-quality inbred females. We observed that the sex ratio of emerging adults was slightly male biased in both treatments (for both species) but the degree of male bias differed between inbred and outbred beetles only for the BF population in replicate 2, for which male bias was greater in inbred than in outbred beetles. This indicates that the observed gender difference in inbreeding depression on adult life span is unlikely to be a consequence of gender differences in inbreeding-associated larval mortality—we would expect a more female-biased sex ratio in the inbred relative to outbred treatments if inbreeding-associated larval mortality is removing poor-quality inbred males, but not poor-quality inbred females, from the population.

More likely, the gender difference in inbreeding depression is due to gender differences in which loci affect life span. Studies with Drosophila have demonstrated that many loci have gender-specific effects on adult life span (Nuzhdin et al. 1997; Vieira et al. 2000; Harshman 2002; Leips and Mackay 2002; Spencer et al. 2003). These studies also consistently demonstrate that allelic interactions (e.g., degree of dominance) vary among loci such that gender-specific effects of loci could generate substantial differences between males and females in dominance and thus inbreeding depression. Although detailed QTL studies have been limited to model organisms, especially Drosophila, our results suggest that the loci affecting C. maculatus life span are likewise different between the sexes and that the degree of dominance varies among these loci. Also, although we observed similar amounts of inbreeding depression for both male and female life span of S. limbatus, the magnitude of inbreeding depression for males was not correlated with inbreeding depression for females among experimental blocks. Recall that each block represents crosses between two families such that inbred and outbred offspring will, on average within a block, contain the same set of alleles. The absence of a correlation (among blocks) between the magnitudes of inbreeding depression on S. limbatus males vs. females thus suggests that the loci underlying inbreeding depression in the two genders are different. Results of a recent line-cross study, in which we examined the genetic architecture of differences in life span between the BF and SI populations of C. maculatus, also suggest that differences in the genetic architecture underlie the life span of males and females (Fox et al. 2004b). Specifically, we detected substantial dominance for alleles conferring long adult life span of females, but very little dominance for alleles affecting adult life span of males. Because our line-cross study examined the genetic architecture of differences in life span between populations it does not necessarily demonstrate that dominance differs between males and females within populations, but the results are consistent with the gender difference in inbreeding depression observed in the current study and thus suggest a common underlying genetic mechanism.

Although the gender difference in inbreeding depression in C. maculatus is almost certainly due to gender-specific effects of the loci affecting life span, why is there such a large gender difference in inbreeding load at those loci? Possibly deleterious alleles affecting male life span are rarely hidden in heterozygotes, due to reduced dominance (as observed in our line-cross study), and are thus regularly exposed to selection, reducing inbreeding load for male-specific deleterious alleles in the population. Alternatively, a reduction in the frequency of deleterious recessive alleles in males relative to females, caused by some unknown mechanism, could produce the reduction in inbreeding depression in males relative to females observed in this study and also the reduction in dominance of life span alleles observed in our previous line-cross experiment. However, that still leaves the question of why deleterious alleles are lower in frequency, or less likely to be expressed, in males than in females. Females of C. maculatus are homogametic, whereas males are heterogametic, such that X-linked loci are always hemizygous in males and thus recessive alleles at X-linked loci are always exposed to selection in males. If sex-linked deleterious alleles have gender-specific expression, then sex linkage would lead to gender-specific purging of these alleles. However, we did not detect any sex linkage for loci affecting life span in our crosses between SI and BF beetles (Fox et al. 2004b). Also, there is no evidence that genes affecting Drosophila life span are frequently sex linked. However, a QTL study is required to map loci affecting life span in C. maculatus before we can test hypotheses regarding sex linkage.

Alternatively, the gender difference in inbreeding load of C. maculatus may be due to gender-specific effects of loci affecting allocation of resources between reproduction and somatic maintenance. To avoid complications due to a cost of reproduction (Tatar et al. 1993) all of our beetles were virgin during the experiment, an uncommon situation in nature, especially in a storage environment. Mating and reproduction affect life span and mortality rates in C. maculatus (Tatar et al. 1993). If loci controlling allocation of resources between reproduction (female eggs or male spermatophores) and somatic maintenance have gender-specific effects, then gender differences in the reallocation of resources could generate the gender difference in inbreeding depression. We are currently examining inbreeding depression in C. maculatus that have access to mates and oviposition substrates (seeds) to test this hypothesis.

Age-specific inbreeding load and mutation accumulation:

We estimated that the inbreeding load affecting average life span of females was between ∼0.4 and 0.6 lethal equivalents per haploid gamete for female life span in both populations of C. maculatus, a little less than double the estimated inbreeding load observed for male and female S. limbatus (∼0.2–0.3). These estimates all fall in the range of estimates obtained in studies of male D. melanogaster (Swindell and Bouzat 2006). However, contrary to many previous studies with Drosophila (Snoke and Promislow 2003; Swindell and Bouzat 2006), although the inbreeding load for loci affecting mortality fluctuated with age we did not find that inbreeding load consistently increased with age, a result inconsistent with one prediction of mutation-accumulation theory (Charlesworth and Hughes 1996; Hughes et al. 2002; Hughes and Reynolds 2005) but consistent with a previous study of another species of Callosobruchus (C. chinensis) that found no effect of female age on the magnitude of inbreeding depression on fecundity (Tanaka 1990, 1993). Our result that inbreeding load for the mortality rate does not increase with age initially appears inconsistent with the observed effect of inbreeding on the slope of the mortality curve—inbred females had significantly higher initial slopes (i.e., the mortality rate increased more quickly with age) than did outbred females. However, mortality did not increase exponentially beyond the first few days. Instead, the rate of increase in mortality quickly decelerated and reached a plateau, as observed in many other studies (Carey et al. 1992; Mueller and Rose 1996; Pletcher and Curtsinger 1998; Wachter 1999) and observed previously for both C. maculatus and S. limbatus (Fox and Moya-Laraño 2003; Fox et al. 2003b, 2004a). This deceleration in the rate of increase in mortality reduced the relative difference between inbred and outbred beetles, reducing the estimated inbreeding load at older ages.

Our result that inbreeding load for the mortality rate does not increase with age is inconsistent with the prediction from mutation-accumulation models (Charlesworth and Hughes 1996). However, this prediction assumes that mutational effects are independent across ages. It is possible that the large inbreeding depression observed for female C. maculatus may be caused by a small number of deleterious alleles of large effect that act across many or all age classes. Also, the cumulative effect of multiple deleterious alleles could quickly remove poor-quality females from the population such that the population of beetles left alive at older ages in the inbred treatment represents those with lower overall mutational loads, such that the difference in mortality rate between inbred and outbred beetles declines with age and thus inbreeding load declines with age. Finally, the sampling variance for estimates of inbreeding load is dependent on both the inbreeding coefficient (F) and the magnitude of inbreeding depression (Lynch and Walsh 1998). Although our sample sizes are large, especially for replicate 2 of the C. maculatus study, we have only one level of inbreeding that is fairly low (F = 0.25) and a moderately small effect of inbreeding depression on life span (δ ∼ 0.05 for S. limbatus and δ ∼ 0.09–0.13 for C. maculatus). Thus, our estimates of age-specific inbreeding load (L) may be very sensitive to environmental variance, possibly obscuring an increase in L with age. These hypotheses have yet to be tested.

Acknowledgments

We thank Frank Messina for providing the SI and BF colonies used in this experiment. We thank A. Amarillo-Suárez and J. Moya-Laraño for help collecting S. limbatus and M. E. Czesak, F. J. Messina, J. J. Obrycki, and two anonymous reviewers for comments on previous versions of this manuscript. This work was funded in part by the National Science Foundation (DEB-0271929 to C.W.F.). This article is publication 06-08-088 of the Kentucky Agricultural Experiment Station.

References

  1. Carbone, M. A., K. W. Jordan, R. F. Lyman, S. T. Harbison, J. Leips et al., 2006. Phenotypic variation and natural selection at Catsup, a pleiotropic quantitative trait gene in Drosophila. Curr. Biol. 16: 912–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Carey, J. R., P. Liedo, D. Orozco and J. W. Vaupel, 1992. Slowing of mortality-rates at older ages in large medfly cohorts. Science 258: 457–461. [DOI] [PubMed] [Google Scholar]
  3. Carr, D. E., and M. R. Dudash, 2003. Recent approaches into the genetic basis of inbreeding depression in plants. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 358: 1071–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cassinello, J., 2005. Inbreeding depression on reproductive performance and survival in captive gazelles of great conservation value. Biol. Conserv. 122: 453–464. [Google Scholar]
  5. Charlesworth, B., and D. Charlesworth, 1999. The genetic basis of inbreeding depression. Genet. Res. 74: 329–340. [DOI] [PubMed] [Google Scholar]
  6. Charlesworth, B., and K. A. Hughes, 1996. Age-specific inbreeding depression and components of genetic variance in relation to the evolution of senescence. Proc. Natl. Acad. Sci. USA 93: 6140–6145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Charpentier, M., J. M. Setchell, F. Prugnolle, E. J. Wickings, P. Peignot et al., 2006. Life history correlates of inbreeding depression in mandrills (Mandrillus sphinx). Mol. Ecol. 15: 21–28. [DOI] [PubMed] [Google Scholar]
  8. Clarke, J. M., and J. Maynard Smith, 1955. The genetics and cytology of Drosophila subobscura XI. Hybrid vigour and longevity. J. Genet. 53: 172–180. [Google Scholar]
  9. De Clercq, P., M. Vandewalle and L. Tirry, 1998. Impact of inbreeding on performance of the predator Podisus maculiventris. Biocontrol 43: 299–310. [Google Scholar]
  10. De Luca, M., N. V. Roshina, G. L. Geiger-Thornsberry, R. F. Lyman, E. G. Pasyukova et al., 2003. Dopa decarboxylase (Ddc) affects variation in Drosophila longevity. Nat. Genet. 34: 429–433. [DOI] [PubMed] [Google Scholar]
  11. Fowler, K., and M. C. Whitlock, 1999. The variance in inbreeding depression and the recovery of fitness in bottlenecked populations. Proc. R. Soc. Lond. Ser. B Biol. Sci. 266: 2061–2066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fox, C. W., 1993. Multiple mating, lifetime fecundity and female mortality of the bruchid beetle, Callosobruchus maculatus (Coleoptera: Bruchidae). Funct. Ecol. 7: 203–208. [Google Scholar]
  13. Fox, C. W., 2005. Problems in measuring among-family variation in inbreeding depression. Am. J. Bot. 92: 1929–1932. [DOI] [PubMed] [Google Scholar]
  14. Fox, C. W., and H. Dingle, 1994. Dietary mediation of maternal age effects on offspring performance in a seed beetle (Coleoptera: Bruchidae). Funct. Ecol. 8: 600–606. [Google Scholar]
  15. Fox, C. W., and J. Moya-Laraño, 2003. Why organisms show late-life mortality plateaus: a null model for comparing patterns of mortality. Evol. Ecol. Res. 5: 999–1009. [Google Scholar]
  16. Fox, C. W., and K. L. Scheibly, 2006. Variation in inbreeding depression among populations of the seed beetle, Stator limbatus. Entomol. Exp. Appl. (in press).
  17. Fox, C. W., M. L. Bush and W. G. Wallin, 2003. a Maternal age affects offspring lifespan of the seed beetle, Callosobruchus maculatus. Funct. Ecol. 17: 811–820. [Google Scholar]
  18. Fox, C. W., L. Dublin and S. J. Pollitt, 2003. b Gender differences in lifespan and mortality rates in two seed beetle species. Funct. Ecol. 17: 619–626. [Google Scholar]
  19. Fox, C. W., M. L. Bush, D. A. Roff and W. G. Wallin, 2004. a Evolutionary genetics of lifespan and mortality rates in two populations of the seed beetle, Callosobruchus maculatus. Heredity 92: 170–181. [DOI] [PubMed] [Google Scholar]
  20. Fox, C. W., M. E. Czesak and W. G. Wallin, 2004. b Complex genetic architecture of population differences in adult lifespan of a beetle: nonadditive inheritance, gender differences, body size and a large maternal effect. J. Evol. Biol. 17: 1007–1017. [DOI] [PubMed] [Google Scholar]
  21. Fox, C. W., K. L. Scheibly, B. P. Smith and W. G. Wallin, 2006. Inbreeding depression in two seed-feeding beetles, Callosobruchus maculatus and Stator limbatus. Bull. Entomol. Res. (in press). [DOI] [PubMed]
  22. Goncalves, R. R., and R. A. Di Mare, 2005. Biology of crucifer moth, Plutella xylostella Linnaeus (Lepidoptera, Yponomeutidae), under controlled temperature conditions, and parasitoids associated. Part III. Study on the biology of Apanteles piceotrichosus (Blanchard) (Hymenoptera, Braconidae): analysis of the inbreeding effect. Rev. Bras. Zool. 22: 806–809. [Google Scholar]
  23. Harshman, L. G., 2002. Life span extension of Drosophila melanogaster: genetic and population studies. Popul. Dev. Rev. 29: S99–S126. [Google Scholar]
  24. Henter, H. J., 2003. Inbreeding depression and haplodiploidy: experimental measures in a parasitoid and comparisons across diploid and haplodiploid insect taxa. Evolution 57: 1793–1803. [DOI] [PubMed] [Google Scholar]
  25. Hughes, K. A., 1995. The inbreeding decline and average dominance of genes affecting male life-history characters in Drosophila melanogaster. Genet. Res. 65: 41–52. [DOI] [PubMed] [Google Scholar]
  26. Hughes, K. A., and B. Charlesworth, 1994. A genetic analysis of senescence in Drosophila. Nature 367: 64–66. [DOI] [PubMed] [Google Scholar]
  27. Hughes, K. A., and R. M. Reynolds, 2005. Evolutionary and mechanistic theories of aging. Annu. Rev. Entomol. 50: 421–445. [DOI] [PubMed] [Google Scholar]
  28. Hughes, K. A., J. A. Alipaz, J. M. Drnevich and R. M. Reynolds, 2002. A test of evolutionary theories of aging. Proc. Natl. Acad. Sci. USA 99: 14286–14291. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Johnson, T. E., and E. W. Hutchinson, 1993. Absence of strong heterosis for life span and other life-history traits in Caenorhabditis elegans. Genetics 134: 465–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Laikre, L., 1999. Conservation genetics of Nordic carnivores: lessons from zoos. Hereditas 130: 203–216. [DOI] [PubMed] [Google Scholar]
  31. Laikre, L., and N. Ryman, 1991. Inbreeding depression in a captive wolf (Canis lupus) population. Conserv. Biol. 5: 33–40. [Google Scholar]
  32. Leips, J., and T. F. C. Mackay, 2002. The complex genetic architecture of Drosophila life span. Exp. Aging Res. 28: 361–390. [DOI] [PubMed] [Google Scholar]
  33. Luna, M. G., and B. A. Hawkins, 2004. Effects of inbreeding versus outbreeding in Nasonia vitripennis (Hymenoptera: Pteromalidae). Environ. Entomol. 33: 765–775. [Google Scholar]
  34. Lynch, M., and B. Walsh, 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA.
  35. Mackay, T. F. C., 2002. The nature of quantitative genetic variation for Drosophila longevity. Mech. Ageing Dev. 123: 95–104. [DOI] [PubMed] [Google Scholar]
  36. Markert, J. A., P. R. Grant, B. R. Grant, L. F. Keller, J. L. Coombs et al., 2004. Neutral locus heterozygosity, inbreeding, and survival in Darwin's ground finches (Geospiza fortis and G. scandens). Heredity 92: 306–315. [DOI] [PubMed] [Google Scholar]
  37. Messina, F. J., 1991. Life history variation in a seed beetle: adult egg-laying vs larval competitive ability. Oecologia 85: 447–455. [DOI] [PubMed] [Google Scholar]
  38. Messina, F. J., 1993. Heritability and evolvability of fitness components in Callosobruchus maculatus. Heredity 71: 623–629. [Google Scholar]
  39. Messina, F. J., 2004. Predictable modification of body size and competitive ability following a host shift by a seed beetle. Evolution 58: 2788–2797. [DOI] [PubMed] [Google Scholar]
  40. Messina, F. J., and A. F. Slade, 1999. Expression of a life-history trade-off in a seed beetle depends on environmental context. Physiol. Entomol. 24: 358–363. [Google Scholar]
  41. Miller, R. A., J. M. Harper, R. C. Dysko, S. J. Durkee and S. N. Austad, 2002. Longer life spans and delayed maturation in wild-derived mice. Exp. Biol. Med. 227: 500–508. [DOI] [PubMed] [Google Scholar]
  42. Mitchell, R., 1991. The traits of a biotype of Callosobruchus maculatus (F) (Coleoptera: Bruchidae) from south India. J. Stored Prod. Res. 27: 221–224. [Google Scholar]
  43. Morse, G. E., and B. D. Farrell, 2005. a Ecological and evolutionary diversification of the seed beetle genus Stator (Coleoptera: Chrysomelidae: Bruchinae). Evolution 59: 1315–1333. [PubMed] [Google Scholar]
  44. Morse, G. E., and B. D. Farrell, 2005. b Interspecific phylogeography of the Stator limbatus species complex: the geographic context of speciation and specialization. Mol. Phylogenet. Evol. 36: 201–213. [DOI] [PubMed] [Google Scholar]
  45. Mueller, L. D., and M. R. Rose, 1996. Evolutionary theory predicts late-life mortality plateaus. Proc. Natl. Acad. Sci. USA 93: 15249–15253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Nieminen, M., M. C. Singer, W. Fortelius, K. Schops and I. Hanski, 2001. Experimental confirmation that inbreeding depression increases extinction risk in butterfly populations. Am. Nat. 157: 237–244. [DOI] [PubMed] [Google Scholar]
  47. Nuzhdin, S. V., E. G. Pasyukova, C. L. Dilda, Z. B. Zeng and T. F. C. Mackay, 1997. Sex-specific quantitative trait loci affecting longevity in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 94: 9734–9739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Pletcher, S. D., 1999. Model fitting and hypothesis testing for age-specific mortality data. J. Evol. Biol. 12: 430–439. [Google Scholar]
  49. Pletcher, S. D., and J. W. Curtsinger, 1998. Mortality plateaus and the evolution of senescence: Why are old-age mortality rates so low? Evolution 52: 454–464. [DOI] [PubMed] [Google Scholar]
  50. Pletcher, S. D., A. A. Khazaeli and J. W. Curtsinger, 2000. Why do life spans differ? Partitioning mean longevity differences in terms of age-specific mortality parameters. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 55: B381–B389. [DOI] [PubMed] [Google Scholar]
  51. Pray, L. A., J. M. Schwartz, C. J. Goodnight and L. Stevens, 1994. Environmental dependency of inbreeding depression—implications for conservation biology. Conserv. Biol. 8: 562–568. [Google Scholar]
  52. Prezotti, L., J. R. P. Parra, R. Vencovsky, A. S. G. Coelho and I. Cruz, 2004. Effect of the size of the founder population on the quality of sexual populations of Trichogramma pretiosum, in laboratory. Biol. Control 30: 174–180. [Google Scholar]
  53. Promislow, D. E. L., 1991. Senescence in natural populations of mammals: a comparative study. Evolution 45: 1869–1887. [DOI] [PubMed] [Google Scholar]
  54. Radwan, J., J. Unrug, K. Snigorska and K. Gawronska, 2004. Effectiveness of sexual selection in preventing fitness deterioration in bulb mite populations under relaxed natural selection. J. Evol. Biol. 17: 94–99. [DOI] [PubMed] [Google Scholar]
  55. Roff, D. A., 1998. Effects of inbreeding on morphological and life history traits of the sand cricket, Gryllus firmus. Heredity 81: 28–37. [Google Scholar]
  56. Saccheri, I., M. Kuussaari, M. Kankare, P. Vikman, W. Fortelius et al., 1998. Inbreeding and extinction in a butterfly metapopulation. Nature 392: 491–494. [Google Scholar]
  57. Saccheri, I. J., H. D. Lloyd, S. J. Helyar and P. M. Brakefield, 2005. Inbreeding uncovers fundamental differences in the genetic load affecting male and female fertility in a butterfly. Proc. R. Soc. Lond. Ser. B Biol. Sci. 272: 39–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Snoke, M. S., and D. E. L. Promislow, 2003. Quantitative genetic tests of recent senescence theory: age-specific mortality and male fertility in Drosophila melanogaster. Heredity 91: 546–556. [DOI] [PubMed] [Google Scholar]
  59. Spencer, C. C., and D. E. L. Promislow, 2005. Age-specific changes in epistatic effects on mortality rate in Drosophila melanogaster. J. Hered. 96: 513–521. [DOI] [PubMed] [Google Scholar]
  60. Spencer, C. C., C. E. Howell, A. R. Wright and D. E. L. Promislow, 2003. Testing an ‘aging gene’ in long-lived Drosophila strains: increased longevity depends on sex and genetic background. Aging Cell 2: 123–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Swindell, W. R., and J. L. Bouzat, 2006. Inbreeding depression and male survivorship in Drosophila: implications for senescence theory. Genetics 172: 317–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Tanaka, Y., 1990. Age specificity of inbreeding depression during a life cycle of Callosobruchus chinensis (Coleoptera: Bruchidae). Res. Popul. Ecol. 32: 329–335. [Google Scholar]
  63. Tanaka, Y., 1993. A genetic mechanism for the evolution of senescence in Callosobruchus chinensis (the azuki bean weevil). Heredity 70: 318–321. [Google Scholar]
  64. Tatar, M., and J. R. Carey, 1994. Genetics of mortality in the bean beetle Callosobruchus maculatus. Evolution 48: 1371–1376. [DOI] [PubMed] [Google Scholar]
  65. Tatar, M., and J. R. Carey, 1995. Nutrition mediates reproductive trade-offs with age-specific mortality in the beetle Callosobruchus maculatus. Ecology 76: 2066–2073. [Google Scholar]
  66. Tatar, M., J. R. Carey and J. W. Vaupel, 1993. Long-term cost of reproduction with and without accelerated senescence in Callosobruchus maculatus: analysis of age-specific mortality. Evolution 47: 1302–1312. [DOI] [PubMed] [Google Scholar]
  67. Tran, B. M. D., and P. F. Credland, 1995. Consequences of inbreeding for the cowpea seed beetle, Callosobruchus maculatus (F) (Coleoptera: Bruchidae). Biol. J. Linn. Soc. 56: 483–503. [Google Scholar]
  68. van Oosterhout, C., W. G. Zijlstra, M. K. van Heuven and P. M. Brakefield, 2000. Inbreeding depression and genetic load in laboratory metapopulations of the butterfly Bicyclus anynana. Evolution 54: 218–225. [DOI] [PubMed] [Google Scholar]
  69. Vaupel, J. W., 1990. Relatives risks: frailty models of life history data. Theor. Popul. Biol. 37: 220–234. [Google Scholar]
  70. Vermeulen, C. J., and R. Bijlsma, 2004. Changes in mortality patterns and temperature dependence of lifespan in Drosophila melanogaster caused by inbreeding. Heredity 92: 275–281. [DOI] [PubMed] [Google Scholar]
  71. Vieira, C., E. G. Pasyukova, Z. B. Zeng, J. B. Hackett, R. F. Lyman et al., 2000. Genotype-environment interaction for quantitative trait loci affecting life span in Drosophila melanogaster. Genetics 154: 213–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Wachter, K. W., 1999. Evolutionary demographic models for mortality plateaus. Proc. Natl. Acad. Sci. USA 96: 10544–10547. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES