Genetic and Environmental Effects on Complex Traits in Mice

Abstract

The interaction between genotype and environment is recognized as an important source of experimental variation when complex traits are measured in the mouse, but the magnitude of that interaction has not often been measured. From a study of 2448 genetically heterogeneous mice, we report the heritability of 88 complex traits that include models of human disease (asthma, type 2 diabetes mellitus, obesity, and anxiety) as well as immunological, biochemical, and hematological phenotypes. We show that environmental and physiological covariates are involved in an unexpectedly large number of significant interactions with genetic background. The 15 covariates we examined have a significant effect on behavioral and physiological tests, although they rarely explain >10% of the variation. We found that interaction effects are more frequent and larger than the main effects: half of the interactions explained >20% of the variance and in nine cases exceeded 50%. Our results indicate that assays of gene function using mouse models should take into account interactions between gene and environment.

IT is widely recognized that environmental variables, such as who carries out the experiment and when, and physiological variables, such as sex and weight, are confounds that need to be accounted for during the collection of mouse phenotypes. Many articles attest to the effect of these variables on phenotypic values (e.g., Chesler et al. 2002a; Champy et al. 2004) and point out the need for rigorous standardization of laboratory practice (Henderson 1970; Crabbe et al. 1999; Brown et al. 2005). It is also acknowledged that the size and even direction of environmental effects on a phenotype can vary with genotype, a phenomenon known as gene-by-environment interaction, and this has been documented in studies of rodents over the past 50 years (e.g., Cooper and Zubek 1958).

Following a report on the importance of laboratory-by-strain interaction (Crabbe et al. 1999), recent interest has focused on the prevalence and size of such interactions, as well as their ability to increase power in genetic mapping experiments (Wang et al. 2006). Table 1 summarizes the available data and shows that the picture of how much genetic and environmental factors interact is piecemeal: our knowledge of the relative size of interaction and main effects is limited to a handful of phenotype–covariate combinations.

TABLE 1.

Recent reports of gene-by-environment interactions in mouse

Covariate	Phenotype	QTL (i.e., single locus) or polygenic (e.g., strain) effect	Main-effect variancea (%)	Interaction-effect variancea (%)	Reference
Laboratory	Elevated plus maze	Polygenic	32.7b	21b	Crabbe et al. (1999)
	Body weight	Polygenic	20.4b	7.1b
	Cocaine-induced activity	Polygenic	5.3b	8.6b
Sex	Body weight	Polygenic	63.7b	7b
	Open field test	Polygenic	—	4.5b
Diet	Obesity	QTL	—	—	York et al. (1999)
Diet (food shortage)	Amphetamine-induced activity		—	—	Cabib et al. (2000)
Maternal lactational environment	Plasma glucose	Polygenic	—	—	Reifsnyder et al. (2000)
Experimenter	Tail-withdrawal latency	Polygenic	42	18	Chesler et al. (2002)
Sex
Testing order
Time of day
Laboratory	Locomotion	Polygenic	11.9–28.4b	10.9–16.5b	Wahlsten et al. (2003)
	Elevated plus maze	Polygenic	25.2–30b	13–14.3b
Diet	Agressiveness	Polygenic	—	—	Nyberg et al. (2004)
Diet	Liver weight	QTL	—	—	Ehrich et al. (2005)
	Serum insulin	QTL	—	—
	Fat pad	QTL	—	—
Diet	Liver weight	Polygenic	—	—	Biddinger et al. (2005)
	Leptin	Polygenic	—	—
	Glucose tolerance test	Polygenic	—	—
Laboratory	Open field test	Polygenic	0–20.3	0.1–8.7	Kafkafi et al. (2005)
Sex	Gonadal fat mass	QTL	—	—	Wang et al. (2006)

^aThe proportion of variance attributable to the main or interaction effect of the covariate, with “—” representing cases where this figure was not reported.

^bThe proportion of variance is given as the partial ω²-statistic.

During an investigation of the genetic basis of complex traits in 2448 genetically heterogeneous stock (HS) mice (1220 female, 1228 male) (Solberg et al. 2006), we collected environmental and physiological covariates. The mice we used were descended from eight inbred strains (A/J, AKR/J, BALBc/J, CBA/J, C3H/HeJ, C57BL/6J, DBA/2J, and LP/J) (Demarest et al. 2001), incorporating more genetic variation from a single cross than has hitherto been assessed in mice. The generality of our findings is enhanced by our use of a battery of tests that includes both behavioral and a broad range of physiological phenotypes (Solberg et al. 2006), summarized in Table 2 (the names of all phenotypes are given in Table 3).

TABLE 2.

Summary of phenotypes analyzed, number of animals, and mean age (in days) at which the animals were analyzed

Phenotype	Description	No. of animals	Mean age (days)
Weight, 6 wk	Body weight at the beginning of testing.	2516	42
Immunology	CD4, CD3, CD8, and B220 antibody staining.	1872	42
OFT	Open field arena: distance in the perimeter, the center, and total distance in 5 min.	2504	45
EPM	Elevated plus maze: distance traveled, time spent, and entries into closed and open arms.	2452	46
FN	Food hyponeophagia: time taken to sample a novel foodstuff (overnight food deprivation).	2474	47
Burrowing	No. of pellets removed from burrow in 1.5 hr.	2455	48
Activity	Activity measured in a home cage in 30 min.	2445	48
Startle	Startle to a loud noise.	1948	52
Context freezing	Freezing to the context in which a tone is associated with a foot shock.	2070	55
Cue freezing	Freezing to a tone after association with a foot shock.	2110	56
Plethysmography	Animals sensitized by injection with ovalbumin inhale metacholine and changes in lung function are measured by plethysmography (a model of asthma). Respiratory rate, tidal volume, minute volume, expiratory time, inspiratory time, and enhanced pause are recorded with and without exposure to metacholine.	2304	63
IPGTT	Glucose and insulin values taken at 0, 15, 30, and 75 min after i.p. glucose injection (a model of type 2 diabetes mellitus).	2334	68
Weight, 10 wk	Body weight at the end of testing.	2319	70
FBC	Full blood count (hematocrit, Hb concentration, mean cellular volume, mean cellular Hb concentration, white cell count, platelet count).	1892	71
Tissue harvest	Adrenal weight.	2309	71
Wound healing	Reduction in size of a 2-mm ear punch hole.	2273	71
Biochemistry	Albumin, alkaline phosphatase, alanine transaminase, aspartate transaminase, calcium, chloride, creatinine, high-density lipoprotein, low-density lipoprotein, phosphorous, sodium, total cholesterol, total protein, triglycerides.	1890	71

TABLE 3.

Phenotypes assessed in the project

Test	Measure
Open field arena	Total activity
	Fecal boli
Elevated plus maze	Closed-arm distance
	Open-arm distance
	Closed-arm time
	Open-arm time
	Closed-arm entries
	Open-arm entries
New home-cage activity	Total beam breaks (30 min)
	Total beam breaks (first 5 min)
	Total beam breaks (last 5 min)
	Fine movement
Context freezing	Time freezing to context (sec)
Cue conditioning	Time freezing during cue (sec)
	Time freezing after cue (sec)
	Fecal boli
Fear-potentiated startle	Startle response
	Change in startle after training
Plethysmography	Enhanced pause (baseline)
	Enhanced pause (metacholine)
	Expiratory time (baseline)
	Expiratory time (metacholine)
	Inspiratory time (baseline)
	Inspiratory time (metacholine)
	PenH difference
	Respiratory rate (baseline)
	Respiratory rate (metacholine)
	Tidal minute volume (baseline)
	Tidal minute volume (metacholine)
	Tidal volume (baseline)
	Tidal volume (metacholine)
IPGTT	AUC-G (mg/dl)
	AUC-IRI (ng/ml)
	AUC-IRI/AUC-G
	DG (mg/dl)
	DIRI (ng/ml)
	DIRI/DG
	Glucose 0 (mg/dl)
	Glucose 15 (mg/dl)
	Glucose 30 (mg/dl)
	Glucose 75 (mg/dl)
	Insulin 0 (ng/ml)
	Insulin 15 (ng/ml)
	Insulin 30 (ng/ml)
	Insulin 75 (ng/ml)
	Insulin slope
	K (glucose slope)
Immunology	%B220+
	%CD3+
	%CD4+
	%CD4+/CD3+
	%CD8+
	%CD8+/CD3+
	%NK cells
Hematology	Hematocrit (%)
	Hemoglobin (g/dl)
	Mean cellular volume (fl)
	Platelets (n/μl)
	Red blood cell count (n/μl)
	White blood cell count (n/μl)
	Mean cellular Hb concentration (%)
	Red cell distribution width
	Mean corpuscular hemoglobin (pg)
	Lymphocytes
	Plateletcrit (%)
Biochemistry	Alkaline phosphatase (units/liter)
	Alanine transaminase (units/liter)
	Aspartate transaminase (units/liter)
	Albumin (g/liter)
	Calcium (mmol)
	Chloride (mmol)
	High-density lipoproteins (mmol)
	Low-density lipoproteins (mmol)
	Phosphorous (mmol)
	Sodium (mmol)
	Total cholesterol (mmol)
	Total protein (g/liter)
	Triglycerides (mmol)
	Urea (mmol)
Weight, length, and growth	Body length
	Body mass index
	Growth slope
	Weight, 10 wk
	Weight, 6 wk
	Weight, 7 wk
	Weight, 8 wk
Adrenal weight	Adrenal weight (g)
Wound healing	Ear hole area (from ear punch) (mm2)

METHODS

Animals:

Original Northport HS mice were obtained from Robert Hitzemann at the Oregon Health Sciences Unit, Portland, Oregon. At the time the animals arrived they had passed 50 generations of pseudorandom breeding (Demarest et al. 2001). A breeding colony in open cages was established at Oxford University to generate animals for phenotyping. The animals' pedigree comprising the parents and grandparents of the phenotyped animals was recorded.

Phenotypes and covariates:

The phenotypes used in this study and the protocol used to collect them are fully described in Solberg et al. (2006) and summarized in Table 2. We collected 15 covariates (Table 4). Seven are mouse-specific covariates (short names quoted in brackets where needed): sex, age, cage identifier (i.e., a unit of shared environment), weight at 9 weeks (“weight”), number of animals in a cage (“cage density”), sibship (“family”), and which litter the mouse came from (“litter”; e.g., “3” means the animal came from his parents' third litter); three are test-specific covariates: experimenter, test order, and apparatus (if more than one was used); and five covariates are for the time of the experiment: year, season (the group of three months), month, hour (time rounded to the nearest hour), and “study day,” defined as the number of days from start of the study on January 20, 2003.

TABLE 4.

Covariates used in the study

Covariate	Encoding	Description	Summary
Age	Integer	Age in days	Mean = 61, SD = 4, 31–85
Apparatus	Categorical	Experimental unit used	Groups = 4, size = 348–526
Cage	Categorical	Cage in which animal was housed	Groups = 435–549, size = 1–7
Cage density	Integer	No. of animals in a cage	Mean = 4.7, SD = 1.1, 2–7
Experimenter	Categorical	Who performed the test	Groups = 2–12, size = 7–457
Family	Categorical	Sibship of animal	Groups = 160–180, size = 1–52
Hour	Categorical	Hour of the day test was performed	Groups = 1–11, size = 1–2307
Litter	Integer	No. litter the animal came from	Mean = 2.2, SD = 1.3, 1–8
Month	Categorical	Month test was performed	Groups = 12, size = 32–314
Season	Categorical	Season test was performed	Groups = 4, size = 284–788
Sex	Categorical	Sex of the animal	Groups = 2, size = 806–1293
Study day	Integer	Day into study that test was performed (day 1 is Jan. 20, 2003)	Mean = 306, SD = 160, 1–621
Test order	Integer	Order in which animal was tested that day	Mean = 2.8, SD = 1.4, 1–7
Weight	Real no.	Body weight (g) at 9 wk	Mean = 23.9, SD = 4.2, 12–39.1
Year	Categorical	Year of test	Groups = 2, size = 711–1517

“Encoding” refers to how a covariate was modeled statistically. For numerical covariates, the column headed “Summary” gives the grand mean and standard deviation over all phenotypes, followed by the minimum and maximum values observed for any given phenotype. For categorical covariates Summary gives the number and size of categories seen for a typical phenotype. For example, for phenotypes in which the experimenter covariate was present, there were between 2 and 12 experimenters who each recorded data for between 7 and 457 mice.

In the analysis, we fitted statistical models for each phenotype, first testing the significance of each covariate as a main effect and then its interaction with genetic background. Covariates were either treated as continuous variables [age, cage density, litter, study day (continuous), weight] or encoded as categorical factors taking discrete levels (apparatus, cage, experimenter, sex, hour, month, season, year, and family). Note that although hour could have been treated as continuous, that would have allowed detection of only linear trends between time and phenotype, whereas as a factor it can be used to detect nonlinear relationships.

Statistical analysis:

All analysis was carried out using the R statistical package (R Development Core Team 2004), along with the add-on packages lme4 (Pinheiro and Bates 2000), MASS (Venables and Ripley 2002), and regress (Clifford and McCullagh 2005).

We applied normalizing transformations to each phenotype, guided by the Box–Cox procedure (Venables and Ripley 2002), and in most cases this comprised a simple exponentiation or log transform to correct skewness (see Table 5). Phenotypes with symmetrical but highly long-tailed distributions were corrected with a simplified Blom transformation (Blom 1958), in which the value is replaced by the probit of its empirical distribution function probability. Asymmetric highly skewed long-tailed distributions best modeled as exponential or gamma distributions were excluded from the analysis, as were categorical phenotypes and latency phenotypes that require survival analysis. After transformation, each phenotype was trimmed by removing values more than 3 standard deviations from the mean to moderate the effects of outliers.

TABLE 5.

Transformations, heritabilities, and common environment effects for 88 phenotypes listed in order of heritability

Phenotype	Transformation	Category	% variance due to additive genetic variation (i.e., heritability)	% variance due to common environment
%CD8+	x	Physiological	88.91	11.09
CD4+/CD8+	x−(1/3)	Physiological	80.48	14.59
Weight, 7 wk (g)	x1/3	Physiological	79.36	20.64
Weight, 6 wk (g)	x1/3	Physiological	74.48	25.52
%CD4+/CD3+	x2	Physiological	72.73	18.48
Weight, 8 wk (g)	x1/3	Physiological	71.99	18.29
High density lipoproteins (mmol)	x	Physiological	69.11	17.01
Alkaline phosphatase (units/liter)		Physiological	62.83	20.47
Weight, 10 wk (g)	x1/3	Physiological	62.35	18.02
%B220+		Physiological	59.86	24.66
Glucose 0 (mg/dl)		Physiological	55.33	32.08
Red cell distribution width	x−2	Physiological	55.29	12.98
Mean cellular Hb conc. (%)	x	Physiological	52.16	39.97
%CD3+	x2	Physiological	51.30	22.51
Ear hole area (mm2)		Physiological	51.02	14.46
Mean cellular volume (fl)	x	Physiological	50.89	20.60
Calcium (mmol)	x	Physiological	48.89	31.39
Lymphocytes		Physiological	48.29	17.85
Mean corpuscular hemoglobin (pg)	x	Physiological	47.94	20.24
Inspiratory time (metacholine)	x−1	Physiological	44.96	10.81
Chloride (mmol)	x	Physiological	44.78	38.43
Open-arm distance	x1/3	Behavioral	42.06	6.19
%CD4+	x	Physiological	40.70	26.46
Startle response	x1/3	Behavioral	40.67	4.20
White blood cell count (n/μl)	log10(x + 1)	Physiological	40.65	23.15
Sodium (mmol)	x	Physiological	39.34	37.83
Closed-arm distance	x	Behavioral	38.81	7.95
Open-arm entries		Behavioral	38.57	5.46
Open-arm time		Behavioral	37.92	6.08
Enhanced pause (baseline)	log10(x)	Physiological	37.81	26.70
Total cholesterol (mmol)	x	Physiological	37.50	17.62
Total beam breaks (30 min)		Behavioral	37.17	11.14
Respiratory rate (metacholine)	log10(x)	Physiological	36.13	12.81
Expiratory time (metacholine)	log10(x)	Physiological	35.00	13.94
Glucose 15 (mg/dl)		Physiological	34.83	29.86
Total activity	x	Behavioral	33.86	5.81
Inspiratory time (baseline)	x−2	Physiological	32.76	16.55
Alanine transaminase (units/liter)	log10(x + 3)	Physiological	32.20	29.18
Respiratory rate (baseline)	x	Physiological	31.57	18.95
Tidal volume (metacholine)	x1/3	Physiological	30.95	21.69
Low density lipoproteins (mmol)	log10(x)	Physiological	30.70	18.25
Urea (mmol)	log10(x + 1)	Physiological	30.59	21.54
Growth slope	x	Physiological	30.52	37.39
Time freezing during cue (sec)	x	Behavioral	30.51	0.00
Expiratory time (baseline)	log10(x)	Physiological	29.52	21.37
Fine movement	x2	Behavioral	29.45	10.04
Total beam breaks (first 5 min)		Behavioral	29.27	12.26
Enhanced pause (metacholine)	log10(x)	Physiological	27.30	28.26
Adrenal weight	log10(x)	Physiological	27.00	36.09
Closed-arm time		Behavioral	26.65	7.47
Tidal minute volume (metacholine)	x1/3	Physiological	26.59	20.01
Albumin (g/liter)	x	Physiological	26.42	22.42
Insulin 30 (ng/ml)	x1/4	Physiological	26.34	21.62
Glucose 75 (mg/dl)		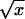Physiological	26.28	22.94
Insulin 15 (ng/ml)	log10(x)	Physiological	25.85	22.24
Time freezing to context (sec)		Behavioral	25.23	12.09
PenH difference	x1/3	Physiological	25.20	28.85
Platelets (n/μl)	x	Physiological	25.07	19.94
DIRI/DG	x1/4	Physiological	24.61	23.89
Triglycerides (mmol)	log10(x)	Physiological	22.55	21.94
AUC-IRI/AUC-G	x1/4	Physiological	22.48	22.86
Total beam breaks (last 5 min)		Behavioral	22.39	7.58
Glucose 30 (mg/dl)		Physiological	22.18	27.00
% NK cells	x−(1/2)	Physiological	21.88	30.24
DG (mg/dl)	x	Physiological	21.82	24.96
Body length (cm)	x	Physiological	21.34	19.92
AUC-G (mg/dl)	x	Physiological	21.24	24.88
DIRI (ng/ml)	x1/3	Physiological	21.02	19.04
Aspartate transaminase (units/liter)	x−(1/2)	Physiological	20.96	18.47
AUC-IRI (ng/ml)	x1/2	Physiological	19.24	18.87
Closed-arm entries	x	Behavioral	19.20	7.00
Tidal volume (baseline)	x1/3	Physiological	18.56	25.07
Insulin 0 (ng/ml)	log10(x)	Physiological	17.83	26.01
Tidal minute volume (baseline)	x1/3	Physiological	16.51	22.21
Phosphorous (mmol)	log10(x + 1)	Physiological	16.10	28.41
Insulin slope	x1/3	Physiological	15.21	6.49
Red blood cell count (n/μl)	x3	Physiological	15.14	18.00
Hemoglobin (g/dl)	x3	Physiological	15.12	17.83
Time freezing after cue (sec)	x	Behavioral	13.81	0.00
Change in startle after training	Blom(x)	Behavioral	13.61	4.48
Fecal boli		Behavioral	13.38	13.02
Body mass index	x	Physiological	13.21	14.75
Insulin 75 (ng/ml)	x1/3	Physiological	13.11	26.72
Plateletcrit (%)		Physiological	12.91	20.24
Hematocrit (%)	x3	Physiological	10.86	18.98
Fecal boli after cue		Behavioral	9.91	6.97
Total protein (g/liter)	x2	Physiological	8.51	28.59
K (glucose slope)	x1/2	Physiological	7.60	10.28

Transformations use the following conventions: x = phenotype; log₁₀, log to base 10; Blom, replace each point with the probit of its relative cumulative frequency.

Modeling the heritability and the effect of common environment:

We used a variance-components approach to model the effect of genetic background. Here the genetic effect on an animal's phenotype is a value drawn from a normal distribution constrained such that the genetic effects of different animals correlate with their relatedness. First we fitted a standard additive genetic, common environmental error, unique environmental error (ACE) model to obtain estimates of the proportion of phenotypic variance attributable to additive genetic effects (i.e., the heritability) and to shared environmental effects. Second, we used an approximation to the ACE model that could be extended to test for the effect of individual environmental covariates.

We formulated the ACE model as follows. Let n be the total number of animals, be the number of cages, μ be the grand mean, 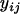be the phenotype of the ith animal in the jth cage, 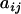be that animal's additive genetic random effect, be its value for covariate c, be the fixed effect associated with covariate c, C be the set of fixed-effect covariates, be the random effect of cage j, and be the random effect of uncorrelated environmental noise. Then

(1)

where, the n-vector , the -vector , and the n-vector , where is the additive genetic relationship matrix (e.g., see Lynch and Walsh 1998) computed from the pedigree. We estimated the heritability of each phenotype, i.e., the proportion of variance attributable to additive genetic variation, as and the size of the common environmental effect as 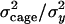, where is the phenotypic variance. The set of covariates chosen for C was sex, litter, and, for phenotypes not directly related to body mass, weight. Fitting was done by restricted estimate maximum likelihood (REML), using the R package regress.

Testing main effects of covariates:

For each phenotype we tested the significance of individual covariates using an approximation to the ACE model above. We employed a random family effect as a surrogate for the genetic effect, replacing the random effect 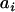, specific to individual i, with a random effect , specific to family q. As explained below, this substitution amounts to a reparameterization that affects in a predictable fashion only the estimated variance of random terms. Also, because we wish to examine the effects of individual environmental covariates, we excluded a catch-all random effect for cage, which would otherwise be heavily confounded with any individual environmental covariate. Using notation similar to that above, the model for testing the significance of covariate was

(2)

where are the fixed effects associated with covariate c, 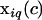is the component of the design matrix representing the ith animal's value for covariate c, 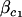and are defined similarly for , and 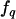is such that if there are nuclear families then the . We measured the significance of the covariate as the improvement in fit conferred by covariate 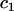after certain basic covariates (C) had already been included. The set C usually comprised sex and, for phenotypes not directly related to body mass, weight. When was weight, C comprised only sex; when was sex, C was empty. The significance of the fixed effect was assessed using an approximation to the sequential F-test based on the Wald test (Pinheiro and Bates 2000). We fit all models by REML using the lmer function from the R package lme4 (Pinheiro and Bates 2000).

Testing interaction effects between covariates and family:

We define the “interaction model” for the covariate 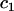and family by adding a term to the main-effects model in Equation 3 to allow each family to have its own effect for that covariate. For factor covariates, the interaction model included a random intercept nested within family, i.e.,

(3)

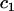where is the fixed effect associated with category k of covariate , and 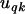is the random effect for category k in family q, such that if there are unique combinations of category and family then the -vector . For continuous covariates, the interaction model included a random slope for conditioned on family, i.e.,

(4)

where 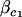is the fixed coefficient of covariate 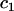, 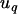is the random deviation from that coefficient in family q, and the correlation between the random intercept f and slope u is unrestricted. We assessed the significance of the interaction model (Equation 3 or Equation 4) by a likelihood-ratio test (LRT) with the corresponding main-effects model. Note that by using the change in the number of degrees of freedom to parameterize the chi-square distribution used for the LRT, our P-values for interaction effects are slightly conservative (Self and Liang 1987). We used the Dunn–Šidák correction, an exact form of the Bonferroni correction (Sahai and Ageel 2000), to take account of the number of tests performed. For N tests, the corrected 5% threshold is .

The magnitude of a covariate's effect is defined as the percentage of phenotypic variance it explains, estimated in the model used to test its significance. For fixed effects, this is the percentage of the total sum of squares attributable to the effect in a sequential ANOVA table after fitting the other covariates (known in some literature as η²; Olejnik and Algina 2003). For random effects, it is the estimated variance of the effect expressed as a percentage of the total phenotypic variance. Where the random effect is based on an interaction with family, we report the percentage variance as twice that of the estimated amount, in accordance with the reparameterization formulas described below.

Our use of family as a surrogate for the genetic effect means we underestimate the effect size of interactions by a factor of two. However, this difference is entirely superficial. Suppose the n animals are sorted in order of their nuclear families. When fitting the family effect, the n-vector of random effects is distributed as , where the matrix F is block diagonal such that 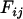is 1 if i and j are in the same sibship and 0 otherwise (note that parents are not included in the analysis because phenotypes were collected only on the offspring). The covariance matrix for all random effects is therefore

(5)

where 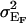is the environmental variance when using family for the genetic effect. This models all animals within a sibship as if they were genetically identical and all sibships as nuclear. Treating sibships as nuclear is reasonable in our case since the sparsity of our additive genetic relationship matrix means that , where when i = j, 0.5 when i and j are sibs, and 0 otherwise, and we found empirically that in this data set the likelihood ratios using the full pedigree A matrix were very close to those obtained using the nuclear approximation S. Using the approximation S for A, our heritability models a covariance matrix

(6)

Substituting the equality and equating the coefficients of F and I, it follows that such that when estimated, , which agrees with our observed discrepancy between family-effect size and heritability. Similarly . Thus the two models are reparameterizations of each other. When fitted, they have identical likelihood ratios, and hence is an estimate of the true additive genetic variance.

Our estimates of the variance attributable to gene-by-environment effects also rely on the use of the family surrogate. Applying a similar argument to that above we can show that those variance estimates are also half what they would be if we used the S matrix. The variance of the interaction model for categorical covariates (Equation 4) is

(7)

where 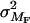is the variance of the interaction and is its correlation matrix, which is simply F but with when animals i and j are in different categories. If we were to use S (an approximation for A) in place of F we would have

(8)

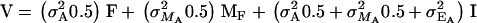with being the interaction between the categorical covariate and the additive genetic effect. However, since and , it follows that and therefore . For interactions between a continuous covariate x and family (Equation 5) the variance is

(9)

where when x is the n-vector of x for the n animals. If we were to use S-approximation for A the variance would be

(10)

Substituting as before, 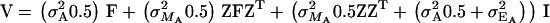, which implies . Hence, in all cases the estimated variance of an additive genetic component is simply twice that of the corresponding family component.

RESULTS

Of the 102 phenotypes available for analysis (Solberg et al. 2006), 88 could be accommodated in our linear mixed modeling framework (see methods). We obtained data for 15 covariates (Table 4): age, apparatus (for those tests where multiple units were used), cage (a variable indicating animals that were housed in the same cage), cage density (the number of animals in a cage), experimenter, family (defined as the offspring of two parents), sex, hour, litter (a number representing the birth order of each litter for a given sire and dam), month, season, study day, test order, weight, and year. An average of 10.3 covariates were recorded per phenotype (since not all phenotype–covariate combinations were available), leading to an average of 69.4 phenotypes measured per covariate. In total, we performed 1804 statistical tests. The significance of results is reported as the negative base 10 logarithm of the P-value (log P) of the relevant test. We took account of multiple testing by using the Dunn–Šidák correction, which for α = 5% comparisonwise error rate yielded a significance threshold of log P = 4.55.

We assessed initially the importance of three physiological covariates (sex, weight, and age). We fitted the covariates sequentially in the order sex, then weight, then age, so that, for instance, our reported significance for weight refers to how much it improved the fit of a model that already included sex. We included family in all models to ensure tested covariates were significant over and above genetic effects. Family, modeled as a random effect, is highly correlated with heritability (correlation of 0.89) and so acts a surrogate for the effect of additive genetic variation (see methods). We report estimates of heritability for all phenotypes in Table 5.

The effects of sex, weight, and age were relatively small (Figure 1b, “main effect” rows): sex effects explained >10% of the variance for 14 phenotypes; in more than half of the cases the effect was <5%; weight accounted for >10% of the variance for three phenotypes; all age effects were <2% (see appendix).

Figure 1.—

Main effects and interactions. (a) The log P (i.e., the −log₁₀ of the P-value) for main and interaction effects of 12 covariates. Each box shows significance scores for one covariate on all applicable phenotypes. The shaded bar marks the corrected 5% threshold for significance (log P = 4.55). For example, Apparatus has significant main effects for a few phenotypes but significant interactions for none, whereas Hour has few significant main effects but has significant interaction effect for a number of phenotypes. (b) The estimated percentage of variance significant effects contributed to the phenotype. Note that log P's are capped at 20 for display purposes and that results for test order, which had no significant effects, are not shown.

Appendix.

Significant main effects and interactions of 13 covariates in 88 phenotypes

				Main effects		Interactions
Test	Phenotype	Covariate	No. observed	log P	% variance explained	log P	% variance explained
Adrenal weight	Adrenal weight	Age	2256	—	—	7.15	0.03
Adrenal weight	Adrenal weight	Cage density	2256	9.18	0.71	10.65	7.33
Adrenal weight	Adrenal weight	Experimenter	2257	11.79	1.02	7.11	21.28
Adrenal weight	Adrenal weight	Litter	2244	—	—	19.45	13.99
Adrenal weight	Adrenal weight	Month	2256	12.46	1.53	38.39	28.19
Adrenal weight	Adrenal weight	Season	2256	—	—	27.85	28.39
Adrenal weight	Adrenal weight	Sex	2257	306.75	36.47	31.10	29.83
Adrenal weight	Adrenal weight	Study day	2256	—	—	20.21	0.03
Adrenal weight	Adrenal weight	Weight	2257	18.91	1.57	19.96	0.68
Adrenal weight	Adrenal weight	Year	2256	5.75	0.43	7.37	26.54
Biochemistry	Alanine transaminase (units/liter)	Cage density	1897	—	—	6.90	11.83
Biochemistry	Alanine transaminase (units/liter)	Litter	1887	—	—	21.79	18.17
Biochemistry	Alanine transaminase (units/liter)	Month	1589	24.03	6.70	25.21	48.49
Biochemistry	Alanine transaminase (units/liter)	Season	1589	14.47	3.36	18.73	45.51
Biochemistry	Alanine transaminase (units/liter)	Sex	1897	9.11	1.53	6.29	19.04
Biochemistry	Alanine transaminase (units/liter)	Study day	1589	26.68	5.81	—	—
Biochemistry	Alanine transaminase (units/liter)	Weight	1897	—	—	6.55	0.51
Biochemistry	Alanine transaminase (units/liter)	Year	1589	8.30	1.70	4.97	31.62
Biochemistry	Albumin (g/liter)	Cage density	1999	—	—	6.52	11.16
Biochemistry	Albumin (g/liter)	Litter	1990	—	—	9.08	12.27
Biochemistry	Albumin (g/liter)	Month	1680	20.84	5.74	11.81	31.16
Biochemistry	Albumin (g/liter)	Season	1680	11.81	2.66	9.37	31.15
Biochemistry	Albumin (g/liter)	Sex	1999	25.05	4.44	4.93	16.30
Biochemistry	Albumin (g/liter)	Study day	1680	15.31	3.12	—	—
Biochemistry	Albumin (g/liter)	Year	1680	11.51	2.31	4.87	24.13
Biochemistry	Alkaline phosphatase (units/liter)	Age	1701	7.71	1.16	11.99	0.93
Biochemistry	Alkaline phosphatase (units/liter)	Litter	2011	—	—	10.65	10.17
Biochemistry	Alkaline phosphatase (units/liter)	Month	1701	8.93	2.35	17.78	31.72
Biochemistry	Alkaline phosphatase (units/liter)	Season	1701	—	—	10.64	26.09
Biochemistry	Alkaline phosphatase (units/liter)	Sex	2021	11.28	1.49	11.77	23.24
Biochemistry	Alkaline phosphatase (units/liter)	Study day	1701	—	—	6.20	0.02
Biochemistry	Alkaline phosphatase (units/liter)	Year	1701	—	—	4.95	24.45
Biochemistry	Aspartate transaminase (units/liter)	Litter	1933	—	—	9.83	10.96
Biochemistry	Aspartate transaminase (units/liter)	Month	1629	9.03	3.02	8.89	25.09
Biochemistry	Aspartate transaminase (units/liter)	Season	1629	5.73	1.35	10.02	27.87
Biochemistry	Aspartate transaminase (units/liter)	Sex	1942	27.03	4.91	—	—
Biochemistry	Aspartate transaminase (units/liter)	Study day	1629	25.52	5.27	—	—
Biochemistry	Aspartate transaminase (units/liter)	Weight	1942	10.20	1.72	—	—
Biochemistry	Aspartate transaminase (units/liter)	Year	1629	7.03	1.35	5.49	27.42
Biochemistry	Calcium (mmol)	Age	1688	—	—	4.70	0.77
Biochemistry	Calcium (mmol)	Cage density	2004	—	—	4.72	8.84
Biochemistry	Calcium (mmol)	Litter	1994	—	—	13.69	15.89
Biochemistry	Calcium (mmol)	Month	1688	12.22	3.66	14.95	35.51
Biochemistry	Calcium (mmol)	Season	1688	6.95	1.59	13.60	38.72
Biochemistry	Calcium (mmol)	Sex	2004	11.48	1.65	15.18	32.18
Biochemistry	Calcium (mmol)	Study day	1688	13.11	2.55	10.28	0.02
Biochemistry	Calcium (mmol)	Weight	2004	10.36	1.48	11.42	0.83
Biochemistry	Calcium (mmol)	Year	1688	11.79	2.26	—	—
Biochemistry	Chloride (mmol)	Age	1744	—	—	13.36	2.21
Biochemistry	Chloride (mmol)	Cage density	2068	—	—	7.82	11.10
Biochemistry	Chloride (mmol)	Litter	2058	—	—	26.60	38.71
Biochemistry	Chloride (mmol)	Month	1744	7.69	2.39	43.88	69.06
Biochemistry	Chloride (mmol)	Season	1744	—	—	30.28	70.86
Biochemistry	Chloride (mmol)	Sex	2068	23.74	3.32	20.74	35.48
Biochemistry	Chloride (mmol)	Study day	1744	8.33	1.42	14.12	0.02
Biochemistry	Chloride (mmol)	Weight	2068	10.63	1.40	14.04	0.78
Biochemistry	High-density lipoproteins (mmol)	Age	1612	—	—	5.36	0.45
Biochemistry	High-density lipoproteins (mmol)	Month	1612	—	—	5.86	12.67
Biochemistry	High-density lipoproteins (mmol)	Sex	1912	173.55	22.74	14.96	21.61
Biochemistry	High-density lipoproteins (mmol)	Study day	1612	4.58	0.49	—	—
Biochemistry	High-density lipoproteins (mmol)	Weight	1912	19.46	2.01	14.86	0.71
Biochemistry	High-density lipoproteins (mmol)	Year	1612	5.34	0.58	—	—
Biochemistry	Low-density lipoproteins (mmol)	Cage density	1947	—	—	4.77	8.53
Biochemistry	Low-density lipoproteins (mmol)	Month	1646	9.20	3.05	5.54	18.53
Biochemistry	Low-density lipoproteins (mmol)	Sex	1947	13.44	2.32	7.73	19.19
Biochemistry	Phosphorous (mmol)	Age	1495	6.27	1.41	—	—
Biochemistry	Phosphorous (mmol)	Month	1495	—	—	12.77	40.25
Biochemistry	Phosphorous (mmol)	Season	1495	—	—	5.77	26.54
Biochemistry	Phosphorous (mmol)	Sex	1783	—	—	5.21	24.81
Biochemistry	Phosphorous (mmol)	Study day	1495	4.86	1.05	—	—
Biochemistry	Phosphorous (mmol)	Year	1495	8.05	1.84	—	—
Biochemistry	Sodium (mmol)	Age	1734	—	—	9.72	1.85
Biochemistry	Sodium (mmol)	Litter	2048	—	—	28.54	33.14
Biochemistry	Sodium (mmol)	Month	1734	6.63	2.10	37.62	62.02
Biochemistry	Sodium (mmol)	Season	1734	—	—	21.62	50.65
Biochemistry	Sodium (mmol)	Sex	2058	34.14	5.01	17.45	31.96
Biochemistry	Sodium (mmol)	Study day	1734	7.04	1.17	11.85	0.02
Biochemistry	Sodium (mmol)	Weight	2058	14.14	1.96	12.64	0.76
Biochemistry	Sodium (mmol)	Year	1734	7.08	1.17	—	—
Biochemistry	Total cholesterol (mmol)	Month	1704	15.12	3.48	6.68	16.02
Biochemistry	Total cholesterol (mmol)	Season	1704	11.76	2.09	—	—
Biochemistry	Total cholesterol (mmol)	Sex	2018	97.59	15.23	5.81	14.08
Biochemistry	Total cholesterol (mmol)	Weight	2018	5.43	0.66	—	—
Biochemistry	Total protein (g/liter)	Cage density	1882	—	—	5.86	10.40
Biochemistry	Total protein (g/liter)	Month	1565	16.74	5.29	12.86	40.36
Biochemistry	Total protein (g/liter)	Season	1565	12.91	3.23	8.38	40.76
Biochemistry	Total protein (g/liter)	Sex	1882	12.49	2.34	5.71	20.71
Biochemistry	Total protein (g/liter)	Study day	1565	—	—	5.86	0.02
Biochemistry	Total protein (g/liter)	Weight	1882	8.64	1.57	—	—
Biochemistry	Triglycerides (mmol)	Cage density	1738	—	—	7.30	10.48
Biochemistry	Triglycerides (mmol)	Month	1448	—	—	6.31	20.79
Biochemistry	Triglycerides (mmol)	Sex	1738	85.67	16.34	—	—
Biochemistry	Urea (mmol)	Cage density	1992	—	—	8.79	13.88
Biochemistry	Urea (mmol)	Litter	1982	—	—	10.54	11.86
Biochemistry	Urea (mmol)	Month	1673	6.80	2.44	8.58	24.17
Biochemistry	Urea (mmol)	Season	1673	5.68	1.35	—	—
Biochemistry	Urea (mmol)	Sex	1992	—	—	10.62	27.54
Context freezing	Time freezing to context (sec)	Apparatus	1671	18.88	4.13	—	—
Context freezing	Time freezing to context (sec)	Experimenter	1671	5.22	1.70	—	—
Context freezing	Time freezing to context (sec)	Sex	1671	24.20	5.14	—	—
Context freezing	Time freezing to context (sec)	Weight	1671	6.04	1.14	—	—
Cue conditioning	Fecal boli after cue	Sex	1768	4.80	0.98	—	—
Cue conditioning	Time freezing after cue (sec)	Age	1791	5.08	1.05	—	—
Cue conditioning	Time freezing after cue (sec)	Apparatus	1665	43.68	10.98	—	—
Cue conditioning	Time freezing during cue (sec)	Apparatus	1665	46.03	10.54	—	—
Elevated plus maze	Closed-arm entries	Experimenter	2229	4.57	1.44	—	—
Elevated plus maze	Closed-arm entries	Weight	2229	5.68	0.89	—	—
Elevated plus maze	Closed-arm time	Month	2221	—	—	4.98	15.61
Elevated plus maze	Open-arm distance	Experimenter	2261	7.14	1.71	—	—
Elevated plus maze	Open-arm distance	Month	2260	—	—	7.52	17.06
Elevated plus maze	Open-arm distance	Weight	2261	4.82	0.63	—	—
Elevated plus maze	Open-arm entries	Weight	2261	5.90	0.80	—	—
Elevated plus maze	Open-arm time	Experimenter	2261	6.78	1.69	—	—
Elevated plus maze	Open-arm time	Month	2260	—	—	7.18	17.03
Elevated plus maze	Open-arm time	Weight	2261	5.30	0.72	—	—
Fear potentiated startle	Startle response	Age	2005	5.40	0.82	—	—
Fear potentiated startle	Startle response	Apparatus	2005	31.59	5.54	—	—
Fear potentiated startle	Startle response	Sex	2005	15.69	2.65	—	—
Fear potentiated startle	Startle response	Study day	2005	4.86	0.73	—	—
Fear potentiated startle	Startle response	Weight	2005	7.53	1.19	—	—
Fear potentiated startle	Startle response	Year	2005	5.60	0.85	—	—
Glucose tolerance test	AUC-G (mg/dl)	Age	2130	—	—	5.36	0.94
Glucose tolerance test	AUC-G (mg/dl)	Cage density	2130	—	—	8.35	12.51
Glucose tolerance test	AUC-G (mg/dl)	Experimenter	2130	9.45	2.11	8.77	26.37
Glucose tolerance test	AUC-G (mg/dl)	Hour	2130	—	—	5.04	16.56
Glucose tolerance test	AUC-G (mg/dl)	Litter	2117	—	—	12.48	11.96
Glucose tolerance test	AUC-G (mg/dl)	Month	2130	4.74	1.59	18.71	36.65
Glucose tolerance test	AUC-G (mg/dl)	Season	2130	5.10	1.01	7.80	25.18
Glucose tolerance test	AUC-G (mg/dl)	Study day	2130	—	—	5.60	0.01
Glucose tolerance test	AUC-G (mg/dl)	Weight	2130	—	—	6.26	0.53
Glucose tolerance test	AUC-IRI (ng/ml)	Cage density	2105	—	—	5.10	7.54
Glucose tolerance test	AUC-IRI (ng/ml)	Month	2105	—	—	10.38	24.65
Glucose tolerance test	AUC-IRI (ng/ml)	Season	2105	—	—	4.63	16.35
Glucose tolerance test	AUC-IRI (ng/ml)	Sex	2105	—	—	7.95	21.33
Glucose tolerance test	AUC-IRI (ng/ml)	Weight	2105	6.66	1.07	—	—
Glucose tolerance test	AUC-IRI/AUC-G	Cage density	1982	—	—	6.51	10.92
Glucose tolerance test	AUC-IRI/AUC-G	Litter	1970	—	—	5.85	8.22
Glucose tolerance test	AUC-IRI/AUC-G	Month	1982	—	—	10.08	26.85
Glucose tolerance test	AUC-IRI/AUC-G	Season	1982	—	—	5.08	19.65
Glucose tolerance test	AUC-IRI/AUC-G	Sex	1982	—	—	6.70	19.96
Glucose tolerance test	DG (mg/dl)	Age	2131	—	—	5.88	1.01
Glucose tolerance test	DG (mg/dl)	Cage density	2131	—	—	8.53	12.82
Glucose tolerance test	DG (mg/dl)	Experimenter	2131	11.18	2.43	9.80	28.15
Glucose tolerance test	DG (mg/dl)	Hour	2131	—	—	5.36	17.29
Glucose tolerance test	DG (mg/dl)	Litter	2118	—	—	12.75	12.24
Glucose tolerance test	DG (mg/dl)	Month	2131	5.15	1.68	18.64	36.72
Glucose tolerance test	DG (mg/dl)	Season	2131	5.79	1.13	7.61	25.02
Glucose tolerance test	DG (mg/dl)	Study day	2131	—	—	5.87	0.01
Glucose tolerance test	DG (mg/dl)	Weight	2131	—	—	6.62	0.56
Glucose tolerance test	DIRI (ng/ml)	Cage density	2107	—	—	5.14	7.64
Glucose tolerance test	DIRI (ng/ml)	Litter	2095	—	—	5.02	6.49
Glucose tolerance test	DIRI (ng/ml)	Month	2107	—	—	9.93	24.02
Glucose tolerance test	DIRI (ng/ml)	Season	2107	—	—	4.85	17.02
Glucose tolerance test	DIRI (ng/ml)	Sex	2107	—	—	7.48	20.05
Glucose tolerance test	DIRI (ng/ml)	Weight	2107	6.66	1.06	—	—
Glucose tolerance test	DIRI/DG	Cage density	1984	—	—	6.53	10.85
Glucose tolerance test	DIRI/DG	Litter	1972	—	—	6.95	9.39
Glucose tolerance test	DIRI/DG	Month	1984	4.86	1.71	11.17	28.02
Glucose tolerance test	DIRI/DG	Season	1984	—	—	6.05	21.73
Glucose tolerance test	DIRI/DG	Sex	1984	—	—	6.74	19.65
Glucose tolerance test	Glucose 0 (mg/dl)	Age	2225	4.66	0.43	22.81	1.50
Glucose tolerance test	Glucose 0 (mg/dl)	Cage density	2225	4.71	0.43	18.00	12.92
Glucose tolerance test	Glucose 0 (mg/dl)	Experimenter	2225	23.96	2.95	24.04	34.21
Glucose tolerance test	Glucose 0 (mg/dl)	Hour	2225	—	—	12.95	22.62
Glucose tolerance test	Glucose 0 (mg/dl)	Litter	2212	13.63	1.38	19.37	19.71
Glucose tolerance test	Glucose 0 (mg/dl)	Month	2225	8.09	1.42	46.92	41.41
Glucose tolerance test	Glucose 0 (mg/dl)	Season	2225	5.89	0.72	26.62	39.04
Glucose tolerance test	Glucose 0 (mg/dl)	Sex	2225	158.57	20.42	16.37	24.82
Glucose tolerance test	Glucose 0 (mg/dl)	Study day	2225	14.64	1.51	24.49	0.01
Glucose tolerance test	Glucose 0 (mg/dl)	Weight	2225	—	—	15.79	0.72
Glucose tolerance test	Glucose 0 (mg/dl)	Year	2225	28.29	3.09	10.67	30.40
Glucose tolerance test	Glucose 15 (mg/dl)	Age	2204	—	—	11.08	1.30
Glucose tolerance test	Glucose 15 (mg/dl)	Cage density	2204	—	—	15.31	18.04
Glucose tolerance test	Glucose 15 (mg/dl)	Experimenter	2204	53.70	8.43	16.69	30.82
Glucose tolerance test	Glucose 15 (mg/dl)	Hour	2204	5.29	1.16	6.02	19.58
Glucose tolerance test	Glucose 15 (mg/dl)	Litter	2192	8.02	1.12	9.18	15.06
Glucose tolerance test	Glucose 15 (mg/dl)	Month	2204	4.72	1.40	31.77	44.55
Glucose tolerance test	Glucose 15 (mg/dl)	Season	2204	5.54	0.96	19.27	40.90
Glucose tolerance test	Glucose 15 (mg/dl)	Sex	2204	15.01	2.21	7.35	21.40
Glucose tolerance test	Glucose 15 (mg/dl)	Study day	2204	4.79	0.63	18.57	0.01
Glucose tolerance test	Glucose 15 (mg/dl)	Weight	2204	—	—	5.56	0.55
Glucose tolerance test	Glucose 15 (mg/dl)	Year	2204	12.49	1.82	5.74	36.94
Glucose tolerance test	Glucose 30 (mg/dl)	Age	2187	—	—	6.94	0.94
Glucose tolerance test	Glucose 30 (mg/dl)	Cage density	2187	—	—	11.78	16.14
Glucose tolerance test	Glucose 30 (mg/dl)	Experimenter	2187	21.23	4.04	11.68	29.41
Glucose tolerance test	Glucose 30 (mg/dl)	Hour	2187	—	—	5.59	20.08
Glucose tolerance test	Glucose 30 (mg/dl)	Litter	2174	4.68	0.67	8.05	11.02
Glucose tolerance test	Glucose 30 (mg/dl)	Month	2187	5.03	1.59	19.07	34.35
Glucose tolerance test	Glucose 30 (mg/dl)	Season	2187	5.72	1.08	11.18	31.27
Glucose tolerance test	Glucose 30 (mg/dl)	Sex	2187	9.87	1.53	4.84	18.00
Glucose tolerance test	Glucose 30 (mg/dl)	Study day	2187	—	—	10.33	0.01
Glucose tolerance test	Glucose 30 (mg/dl)	Weight	2187	—	—	5.30	0.63
Glucose tolerance test	Glucose 30 (mg/dl)	Year	2187	—	—	4.79	35.33
Glucose tolerance test	Glucose 75 (mg/dl)	Age	2153	—	—	7.87	1.02
Glucose tolerance test	Glucose 75 (mg/dl)	Cage density	2153	—	—	4.99	7.52
Glucose tolerance test	Glucose 75 (mg/dl)	Experimenter	2153	10.63	2.14	17.74	37.77
Glucose tolerance test	Glucose 75 (mg/dl)	Hour	2153	—	—	7.83	20.67
Glucose tolerance test	Glucose 75 (mg/dl)	Litter	2140	—	—	10.28	10.05
Glucose tolerance test	Glucose 75 (mg/dl)	Month	2153	5.90	1.70	18.07	32.97
Glucose tolerance test	Glucose 75 (mg/dl)	Season	2153	7.51	1.33	7.83	23.33
Glucose tolerance test	Glucose 75 (mg/dl)	Sex	2153	34.87	5.67	5.24	15.93
Glucose tolerance test	Glucose 75 (mg/dl)	Study day	2153	—	—	6.82	0.01
Glucose tolerance test	Glucose 75 (mg/dl)	Weight	2153	—	—	9.78	0.69
Glucose tolerance test	Insulin 0 (ng/ml)	Cage density	2206	—	—	11.14	14.52
Glucose tolerance test	Insulin 0 (ng/ml)	Experimenter	2206	—	—	12.19	28.49
Glucose tolerance test	Insulin 0 (ng/ml)	Hour	2206	—	—	11.02	32.11
Glucose tolerance test	Insulin 0 (ng/ml)	Litter	2193	—	—	9.26	15.06
Glucose tolerance test	Insulin 0 (ng/ml)	Month	2206	11.67	2.91	26.56	42.42
Glucose tolerance test	Insulin 0 (ng/ml)	Season	2206	7.28	1.37	15.28	34.80
Glucose tolerance test	Insulin 0 (ng/ml)	Sex	2206	12.78	2.05	9.06	24.42
Glucose tolerance test	Insulin 0 (ng/ml)	Weight	2206	5.08	0.74	—	—
Glucose tolerance test	Insulin 15 (ng/ml)	Cage density	2197	—	—	6.44	10.52
Glucose tolerance test	Insulin 15 (ng/ml)	Experimenter	2197	—	—	7.73	20.84
Glucose tolerance test	Insulin 15 (ng/ml)	Litter	2185	—	—	9.16	10.53
Glucose tolerance test	Insulin 15 (ng/ml)	Month	2197	8.96	2.37	13.45	27.78
Glucose tolerance test	Insulin 15 (ng/ml)	Season	2197	5.95	1.12	6.03	20.13
Glucose tolerance test	Insulin 15 (ng/ml)	Sex	2197	—	—	7.91	20.73
Glucose tolerance test	Insulin 15 (ng/ml)	Weight	2197	4.96	0.72	5.71	0.57
Glucose tolerance test	Insulin 30 (ng/ml)	Cage density	2178	—	—	6.23	9.10
Glucose tolerance test	Insulin 30 (ng/ml)	Experimenter	2178	—	—	5.51	16.19
Glucose tolerance test	Insulin 30 (ng/ml)	Litter	2166	—	—	7.56	9.10
Glucose tolerance test	Insulin 30 (ng/ml)	Month	2178	7.05	2.03	14.18	29.40
Glucose tolerance test	Insulin 30 (ng/ml)	Season	2178	—	—	8.50	24.71
Glucose tolerance test	Insulin 30 (ng/ml)	Sex	2178	—	—	7.23	18.84
Glucose tolerance test	Insulin 30 (ng/ml)	Weight	2178	4.62	0.67	—	—
Glucose tolerance test	Insulin 75 (ng/ml)	Cage density	2112	4.88	0.70	7.15	9.48
Glucose tolerance test	Insulin 75 (ng/ml)	Experimenter	2112	—	—	5.65	17.04
Glucose tolerance test	Insulin 75 (ng/ml)	Hour	2112	—	—	8.55	22.87
Glucose tolerance test	Insulin 75 (ng/ml)	Litter	2100	—	—	6.11	12.60
Glucose tolerance test	Insulin 75 (ng/ml)	Month	2112	6.86	1.96	16.98	30.66
Glucose tolerance test	Insulin 75 (ng/ml)	Season	2112	—	—	6.91	21.29
Glucose tolerance test	Insulin 75 (ng/ml)	Sex	2112	30.76	5.18	7.85	18.15
Glucose tolerance test	Insulin 75 (ng/ml)	Weight	2112	11.85	1.87	—	—
Glucose tolerance test	Insulin slope	Sex	1122	5.58	1.83	—	—
Glucose tolerance test	K (glucose slope)	Sex	1953	11.19	2.22	—	—
Glucose tolerance test	K (glucose slope)	Year	1953	4.83	0.87	—	—
Growth	Growth slope	Cage density	2418	—	—	20.00	15.53
Growth	Growth slope	Litter	2462	—	—	26.05	20.10
Growth	Growth slope	Sex	2474	135.72	17.45	19.14	26.19
Hematology	Hemoglobin (g/dl)	Month	1870	—	—	8.59	23.95
Hematology	Hemoglobin (g/dl)	Season	1870	—	—	5.06	18.96
Hematology	Hemoglobin (g/dl)	Sex	1870	9.07	1.73	—	—
Hematology	Hemoglobin (g/dl)	Weight	1870	6.22	1.14	4.86	0.40
Hematology	Lymphocytes	Age	1833	4.58	0.70	—	—
Hematology	Lymphocytes	Litter	1822	7.18	1.15	7.79	8.82
Hematology	Lymphocytes	Month	1833	—	—	10.72	25.40
Hematology	Lymphocytes	Season	1833	—	—	10.24	25.19
Hematology	Lymphocytes	Sex	1833	—	—	5.90	18.71
Hematology	Lymphocytes	Study day	1833	14.16	2.40	—	—
Hematology	Lymphocytes	Year	1833	6.04	0.96	—	—
Hematology	Mean cellular Hb concentration (%)	Age	1863	9.85	1.40	26.04	1.83
Hematology	Mean cellular Hb concentration (%)	Cage density	1862	—	—	33.52	29.32
Hematology	Mean cellular Hb concentration (%)	Litter	1852	—	—	39.31	35.19
Hematology	Mean cellular Hb concentration (%)	Month	1863	68.92	11.39	58.19	54.51
Hematology	Mean cellular Hb concentration (%)	Season	1863	28.14	4.54	40.00	58.58
Hematology	Mean cellular Hb concentration (%)	Sex	1863	6.02	0.84	19.55	39.16
Hematology	Mean cellular Hb concentration (%)	Study day	1863	5.96	0.82	19.79	0.07
Hematology	Mean cellular Hb concentration (%)	Weight	1863	—	—	14.68	0.92
Hematology	Mean cellular Hb concentration (%)	Year	1863	—	—	31.10	82.94
Hematology	Mean cellular volume (fl)	Cage density	1875	—	—	7.63	12.47
Hematology	Mean cellular volume (fl)	Litter	1865	—	—	4.68	5.79
Hematology	Mean cellular volume (fl)	Month	1876	13.39	3.18	15.63	30.61
Hematology	Mean cellular volume (fl)	Season	1876	—	—	7.50	21.56
Hematology	Mean cellular volume (fl)	Sex	1876	—	—	8.89	20.90
Hematology	Mean cellular volume (fl)	Study day	1876	6.15	0.90	—	—
Hematology	Mean cellular volume (fl)	Weight	1876	—	—	5.16	0.45
Hematology	Mean cellular volume (fl)	Year	1876	6.67	0.99	—	—
Hematology	Mean corpuscular hemoglobin (pg)	Age	1871	—	—	15.80	1.25
Hematology	Mean corpuscular hemoglobin (pg)	Cage density	1870	—	—	13.30	16.26
Hematology	Mean corpuscular hemoglobin (pg)	Litter	1860	—	—	16.42	16.51
Hematology	Mean corpuscular hemoglobin (pg)	Month	1871	32.68	6.77	10.21	22.91
Hematology	Mean corpuscular hemoglobin (pg)	Season	1871	19.94	3.62	8.85	25.86
Hematology	Mean corpuscular hemoglobin (pg)	Sex	1871	—	—	11.35	27.44
Hematology	Mean corpuscular hemoglobin (pg)	Study day	1871	—	—	9.47	0.04
Hematology	Mean corpuscular hemoglobin (pg)	Weight	1871	—	—	5.59	0.55
Hematology	Mean corpuscular hemoglobin (pg)	Year	1871	—	—	8.52	44.24
Hematology	Plateletcrit (%)	Age	1839	—	—	5.10	0.73
Hematology	Plateletcrit (%)	Month	1839	14.39	4.06	6.26	19.33
Hematology	Plateletcrit (%)	Season	1839	4.85	1.11	4.59	19.65
Hematology	Plateletcrit (%)	Sex	1839	36.50	7.50	8.92	27.53
Hematology	Platelets (n/μl)	Month	1863	16.43	4.18	10.19	24.81
Hematology	Platelets (n/μl)	Season	1863	6.62	1.36	7.75	26.64
Hematology	Platelets (n/μl)	Sex	1863	30.92	5.76	10.78	27.67
Hematology	Platelets (n/μl)	Study day	1863	9.44	1.60	—	—
Hematology	Platelets (n/μl)	Weight	1863	5.77	0.93	5.54	0.50
Hematology	Platelets (n/μl)	Year	1863	5.56	0.89	—	—
Hematology	Red blood cell count (n/μl)	Month	1870	—	—	11.88	29.98
Hematology	Red blood cell count (n/μl)	Season	1870	—	—	5.84	21.52
Hematology	Red blood cell count (n/μl)	Sex	1870	9.32	1.77	4.95	19.31
Hematology	Red blood cell count (n/μl)	Weight	1870	5.90	1.07	4.94	0.48
Hematology	Red cell distribution width	Litter	1850	—	—	4.64	8.40
Hematology	Red cell distribution width	Month	1861	8.27	2.18	10.68	23.56
Hematology	Red cell distribution width	Season	1861	—	—	5.74	17.99
Hematology	Red cell distribution width	Sex	1861	12.88	1.99	—	—
Hematology	Red cell distribution width	Weight	1861	—	—	4.86	0.42
Hematology	White blood cell count (n/μl)	Cage density	1875	—	—	5.44	12.88
Hematology	White blood cell count (n/μl)	Litter	1865	6.24	1.00	11.57	12.54
Hematology	White blood cell count (n/μl)	Month	1876	—	—	15.14	33.46
Hematology	White blood cell count (n/μl)	Season	1876	—	—	15.64	36.77
Hematology	White blood cell count (n/μl)	Sex	1876	—	—	6.89	23.62
Hematology	White blood cell count (n/μl)	Study day	1876	10.18	1.71	6.86	0.03
Hematology	White blood cell count (n/μl)	Weight	1876	—	—	5.48	0.58
Hematology	White blood cell count (n/μl)	Year	1876	—	—	6.33	42.86
Hematology	Hematocrit (%)	Month	1873	—	—	10.13	27.26
Hematology	Hematocrit (%)	Season	1873	—	—	4.92	19.31
Hematology	Hematocrit (%)	Sex	1873	12.18	2.39	5.01	18.41
Hematology	Hematocrit (%)	Weight	1873	5.59	1.02	6.60	0.48
Immunology	%B220+	Age	1723	—	—	9.73	2.70
Immunology	%B220+	Cage density	1677	—	—	7.72	10.49
Immunology	%B220+	Litter	1713	—	—	9.38	14.26
Immunology	%B220+	Month	1723	11.68	2.84	28.30	41.28
Immunology	%B220+	Season	1723	—	—	23.99	46.06
Immunology	%B220+	Sex	1723	13.02	2.07	10.71	28.81
Immunology	%CD3+	Litter	1723	5.00	0.78	6.68	13.19
Immunology	%CD3+	Month	1733	16.65	4.07	19.89	37.17
Immunology	%CD3+	Season	1733	5.47	1.12	14.69	35.98
Immunology	%CD3+	Sex	1733	—	—	11.57	30.57
Immunology	%CD4+	Cage density	1673	—	—	4.92	8.94
Immunology	%CD4+	Litter	1721	—	—	11.42	18.10
Immunology	%CD4+	Month	1731	14.99	3.94	23.00	44.64
Immunology	%CD4+	Season	1731	—	—	18.16	44.24
Immunology	%CD4+	Sex	1731	—	—	9.74	28.88
Immunology	%CD4+/CD3+	Age	1732	—	—	6.12	1.24
Immunology	%CD4+/CD3+	Cage density	1674	—	—	5.40	6.88
Immunology	%CD4+/CD3+	Litter	1722	—	—	15.81	10.27
Immunology	%CD4+/CD3+	Month	1732	25.71	4.65	13.23	21.82
Immunology	%CD4+/CD3+	Season	1732	8.50	1.35	8.04	17.89
Immunology	%CD8+	Age	1733	—	—	5.32	1.08
Immunology	%CD8+	Month	1733	14.17	2.57	7.57	14.65
Immunology	%CD8+	Season	1733	10.53	1.46	—	—
Immunology	%CD8+	Sex	1733	—	—	5.30	12.61
Immunology	%NK cells	Cage density	1667	—	—	5.29	10.41
Immunology	%NK cells	Litter	1714	—	—	11.43	16.79
Immunology	%NK cells	Month	1724	35.27	8.68	16.15	32.91
Immunology	%NK cells	Season	1724	9.04	2.06	16.04	37.88
Immunology	%NK cells	Sex	1724	5.22	0.95	—	—
Immunology	CD4+/CD8+	Age	1729	—	—	6.02	1.07
Immunology	CD4+/CD8+	Cage density	1671	—	—	4.85	5.83
Immunology	CD4+/CD8+	Litter	1719	—	—	10.62	7.45
Immunology	CD4+/CD8+	Month	1729	17.55	3.26	9.38	17.39
Immunology	CD4+/CD8+	Season	1729	8.52	1.29	4.78	12.21
Length	Body length (cm)	Age	1942	—	—	7.56	0.81
Length	Body length (cm)	Litter	1932	—	—	10.25	8.30
Length	Body length (cm)	Month	1942	16.46	3.22	11.29	21.08
Length	Body length (cm)	Season	1942	5.61	0.91	13.42	24.69
Length	Body length (cm)	Sex	1942	35.12	5.17	—	—
Length	Body length (cm)	Study day	1942	—	—	4.91	0.02
Length	Body length (cm)	Weight	1942	87.23	13.94	—	—
Length	Body length (cm)	Year	1942	5.94	0.76	—	—
New home-cage activity	Fine movement	Age	2294	5.14	0.72	—	—
New home-cage activity	Fine movement	Sex	2294	7.62	1.13	—	—
New home-cage activity	Total beam breaks (30 min)	Experimenter	2290	—	—	6.49	17.79
New home-cage activity	Total beam breaks (30 min)	Month	2290	—	—	7.05	18.22
New home-cage activity	Total beam breaks (30 min)	Season	2290	—	—	4.87	16.40
New home-cage activity	Total beam breaks (first 5 min)	Experimenter	2289	11.94	2.90	5.06	15.50
New home-cage activity	Total beam breaks (first 5 min)	Month	2289	—	—	11.44	24.53
New home-cage activity	Total beam breaks (first 5 min)	Season	2289	—	—	9.49	23.45
New home-cage activity	Total beam breaks (last 5 min)	Hour	2275	4.99	1.41	—	—
Open field	Fecal boli	Month	2304	5.34	1.75	—	—
Open field	Fecal boli	Sex	2304	—	—	5.40	16.38
Open field	Total activity	Experimenter	2302	4.99	1.34	—	—
Open field	Total activity	Season	2302	—	—	6.11	16.96
Open field	Total activity	Sex	2302	7.60	1.07	—	—
Plethysmography	Enhanced pause (baseline)	Age	2169	—	—	15.55	2.18
Plethysmography	Enhanced pause (baseline)	Cage density	2169	—	—	7.42	8.81
Plethysmography	Enhanced pause (baseline)	Hour	2169	—	—	18.39	31.96
Plethysmography	Enhanced pause (baseline)	Litter	2157	6.97	0.91	24.63	25.45
Plethysmography	Enhanced pause (baseline)	Month	2169	77.44	11.87	24.29	31.43
Plethysmography	Enhanced pause (baseline)	Season	2169	48.57	7.17	13.71	27.43
Plethysmography	Enhanced pause (baseline)	Sex	2169	15.80	2.24	11.77	25.38
Plethysmography	Enhanced pause (baseline)	Study day	2169	—	—	20.59	0.09
Plethysmography	Enhanced pause (baseline)	Year	2169	5.51	0.72	12.08	48.49
Plethysmography	Enhanced pause (metacholine)	Age	1943	—	—	7.64	1.41
Plethysmography	Enhanced pause (metacholine)	Hour	1943	—	—	20.37	36.68
Plethysmography	Enhanced pause (metacholine)	Litter	1931	—	—	10.94	20.86
Plethysmography	Enhanced pause (metacholine)	Month	1943	16.72	3.76	19.83	37.13
Plethysmography	Enhanced pause (metacholine)	Season	1943	11.87	2.12	15.67	36.31
Plethysmography	Enhanced pause (metacholine)	Sex	1943	21.63	3.56	9.84	26.78
Plethysmography	Enhanced pause (metacholine)	Weight	1943	6.51	0.97	—	—
Plethysmography	Enhanced pause (metacholine)	Year	1943	—	—	8.18	50.39
Plethysmography	Expiratory time (baseline)	Hour	2165	—	—	17.65	34.38
Plethysmography	Expiratory time (baseline)	Litter	2153	—	—	9.09	10.52
Plethysmography	Expiratory time (baseline)	Month	2165	17.72	3.94	11.84	26.41
Plethysmography	Expiratory time (baseline)	Season	2165	13.74	2.42	10.14	26.77
Plethysmography	Expiratory time (baseline)	Sex	2165	—	—	9.43	25.60
Plethysmography	Expiratory time (baseline)	Study day	2165	—	—	5.30	0.03
Plethysmography	Expiratory time (baseline)	Weight	2165	4.77	0.68	6.66	0.57
Plethysmography	Expiratory time (baseline)	Year	2165	9.98	1.53	—	—
Plethysmography	Expiratory time (metacholine)	Hour	1935	—	—	5.56	15.75
Plethysmography	Expiratory time (metacholine)	Month	1935	5.31	1.78	—	—
Plethysmography	Expiratory time (metacholine)	Sex	1935	—	—	6.15	17.12
Plethysmography	Inspiratory time (baseline)	Cage density	2174	5.18	0.74	—	—
Plethysmography	Inspiratory time (baseline)	Hour	2174	—	—	17.02	32.09
Plethysmography	Inspiratory time (baseline)	Litter	2162	—	—	12.07	12.87
Plethysmography	Inspiratory time (baseline)	Month	2174	15.47	3.57	9.87	24.28
Plethysmography	Inspiratory time (baseline)	Season	2174	10.83	1.95	10.09	27.17
Plethysmography	Inspiratory time (baseline)	Sex	2174	12.32	1.95	12.50	29.61
Plethysmography	Inspiratory time (baseline)	Study day	2174	—	—	4.99	0.03
Plethysmography	Inspiratory time (baseline)	Weight	2174	—	—	9.22	0.71
Plethysmography	Inspiratory time (metacholine)	Hour	1946	—	—	7.07	18.98
Plethysmography	Inspiratory time (metacholine)	Month	1946	5.41	1.64	—	—
Plethysmography	Inspiratory time (metacholine)	Season	1946	4.58	0.86	—	—
Plethysmography	Inspiratory time (metacholine)	Sex	1946	20.64	3.33	—	—
Plethysmography	Inspiratory time (metacholine)	Weight	1946	6.35	0.93	—	—
Plethysmography	PenH difference	Age	1934	—	—	7.34	1.63
Plethysmography	PenH difference	Cage density	1934	—	—	5.67	9.31
Plethysmography	PenH difference	Hour	1934	—	—	19.08	35.57
Plethysmography	PenH difference	Litter	1922	—	—	9.53	18.03
Plethysmography	PenH difference	Month	1934	8.20	2.32	21.79	42.75
Plethysmography	PenH difference	Season	1934	5.00	1.00	17.35	42.74
Plethysmography	PenH difference	Sex	1934	14.92	2.52	12.02	29.38
Plethysmography	PenH difference	Weight	1934	—	—	6.27	0.60
Plethysmography	PenH difference	Year	1934	—	—	10.72	58.13
Plethysmography	Respiratory rate (baseline)	Cage density	2163	4.82	0.69	—	—
Plethysmography	Respiratory rate (baseline)	Hour	2163	—	—	18.19	33.50
Plethysmography	Respiratory rate (baseline)	Litter	2151	—	—	11.93	12.53
Plethysmography	Respiratory rate (baseline)	Month	2163	21.39	4.60	10.40	24.62
Plethysmography	Respiratory rate (baseline)	Season	2163	16.14	2.84	9.65	26.40
Plethysmography	Respiratory rate (baseline)	Sex	2163	6.22	0.92	11.01	27.80
Plethysmography	Respiratory rate (baseline)	Study day	2163	—	—	6.20	0.04
Plethysmography	Respiratory rate (baseline)	Weight	2163	—	—	6.07	0.57
Plethysmography	Respiratory rate (baseline)	Year	2163	6.34	0.94	—	—
Plethysmography	Respiratory rate (metacholine)	Hour	1928	—	—	5.87	17.38
Plethysmography	Respiratory rate (metacholine)	Season	1928	5.21	1.08	—	—
Plethysmography	Tidal minute volume (baseline)	Age	2158	—	—	5.04	0.68
Plethysmography	Tidal minute volume (baseline)	Cage density	2158	7.51	0.89	—	—
Plethysmography	Tidal minute volume (baseline)	Hour	2158	—	—	11.54	19.48
Plethysmography	Tidal minute volume (baseline)	Litter	2146	—	—	6.21	7.69
Plethysmography	Tidal minute volume (baseline)	Month	2158	13.49	2.54	12.97	20.28
Plethysmography	Tidal minute volume (baseline)	Season	2158	—	—	8.70	19.41
Plethysmography	Tidal minute volume (baseline)	Sex	2158	64.43	9.12	—	—
Plethysmography	Tidal minute volume (baseline)	Weight	2158	68.90	9.81	—	—
Plethysmography	Tidal minute volume (metacholine)	Hour	1930	—	—	6.17	11.81
Plethysmography	Tidal minute volume (metacholine)	Litter	1918	—	—	5.61	5.33
Plethysmography	Tidal minute volume (metacholine)	Month	1930	18.51	3.03	4.64	10.60
Plethysmography	Tidal minute volume (metacholine)	Season	1930	10.81	1.45	—	—
Plethysmography	Tidal minute volume (metacholine)	Sex	1930	105.05	14.76	5.95	12.00
Plethysmography	Tidal minute volume (metacholine)	Weight	1930	71.25	9.55	5.82	0.35
Plethysmography	Tidal volume (baseline)	Age	2149	—	—	16.84	1.43
Plethysmography	Tidal volume (baseline)	Cage density	2149	—	—	6.01	4.08
Plethysmography	Tidal volume (baseline)	Hour	2149	—	—	20.24	22.32
Plethysmography	Tidal volume (baseline)	Litter	2137	—	—	16.96	16.06
Plethysmography	Tidal volume (baseline)	Month	2149	39.79	5.07	20.32	22.38
Plethysmography	Tidal volume (baseline)	Season	2149	20.90	2.41	10.96	20.87
Plethysmography	Tidal volume (baseline)	Sex	2149	131.89	16.98	7.75	13.06
Plethysmography	Tidal volume (baseline)	Study day	2149	—	—	7.27	0.03
Plethysmography	Tidal volume (baseline)	Weight	2149	87.94	10.73	6.12	0.32
Plethysmography	Tidal volume (metacholine)	Age	1932	—	—	9.74	0.80
Plethysmography	Tidal volume (metacholine)	Hour	1932	—	—	10.72	15.83
Plethysmography	Tidal volume (metacholine)	Litter	1920	—	—	8.86	7.08
Plethysmography	Tidal volume (metacholine)	Month	1932	26.81	3.64	5.22	10.32
Plethysmography	Tidal volume (metacholine)	Season	1932	18.02	2.07	—	—
Plethysmography	Tidal volume (metacholine)	Sex	1932	141.45	18.43	6.03	11.35
Plethysmography	Tidal volume (metacholine)	Weight	1932	85.28	10.30	—	—
Plethysmography	Tidal volume (metacholine)	Year	1932	6.15	0.59	—	—
Weight	Body mass index	Age	1925	5.87	0.79	—	—
Weight	Body mass index	Month	1925	8.83	2.16	7.41	16.75
Weight	Body mass index	Season	1925	6.21	1.07	9.93	21.20
Weight	Body mass index	Sex	1925	113.93	20.32	—	—
Weight	Body mass index	Weight	1925	19.91	3.03	—	—
Weight	Weight, 10 wk (g)	Cage density	2319	—	—	5.37	3.29
Weight	Weight, 10 wk (g)	Litter	2307	—	—	10.27	6.10
Weight	Weight, 10 wk (g)	Sex	2320	Inf	41.37	—	—
Weight	Weight, 6 wk (g)	Cage density	2432	5.57	0.32	20.89	9.30
Weight	Weight, 6 wk (g)	Litter	2498	—	—	39.27	16.69
Weight	Weight, 6 wk (g)	Sex	2511	Inf	30.63	12.63	12.87
Weight	Weight, 7 wk (g)	Cage density	2405	5.04	0.26	8.22	4.40
Weight	Weight, 7 wk (g)	Litter	2457	6.16	0.32	21.11	7.79
Weight	Weight, 7 wk (g)	Sex	2470	Inf	35.40	7.13	8.27
Weight	Weight, 8 wk (g)	Litter	2290	—	—	10.46	2.53
Weight	Weight, 8 wk (g)	Sex	2302	Inf	44.52	—	—
Wound healing	Ear hole area (mm2)	Cage density	2185	10.45	1.37	9.10	9.56
Wound healing	Ear hole area (mm2)	Litter	2172	6.00	0.76	9.72	10.59
Wound healing	Ear hole area (mm2)	Month	2185	24.17	4.34	9.94	18.33
Wound healing	Ear hole area (mm2)	Season	2185	17.81	2.67	6.08	14.33
Wound healing	Ear hole area (mm2)	Sex	2185	13.93	1.91	4.87	12.85
Wound healing	Ear hole area (mm2)	Study day	2185	—	—	9.67	0.04
Wound healing	Ear hole area (mm2)	Year	2185	—	—	6.42	32.64

Note that not all combinations of phenotype and covariate were available in the study. Log P denotes the logarithm to the base 10 of the P-value. Inf denotes a P-value that was computationally indistinguishable from zero. For brevity, results are omitted for effects with log P's of <4.55 (i.e., the corrected 5% significance level).

We estimated the significances and effects of the remaining covariates by adding each to a model that already included family, sex, and weight. Significant main effects of covariates were more common in physiological than behavioral phenotypes (33% of the time vs. 13%; see Table 6). Overall, 21 of the 258 significant effects explained >10% of the variance; the five cases of when a covariate explained >25% of the variance involved sex. Table 6 provides a summary for each covariate, splitting results by category of phenotype. Figure 1 plots log P-values and the percentage of phenotypic variance explained by significant covariates. Figure 2 summarizes the variance explained by significant covariates for the 16 subcategories of phenotype.

TABLE 6.

Summary of main effects

	Physiological phenotypes				Behavioral phenotypes
Covariate	Median log P	Mean % variance	SD	No. observed (significant/all)	Median log P	Mean % variance	SD	No. observed (significant/all)
Age	0.82	0.98	0.40	6/65	0.73	0.86	0.17	3/18
Apparatus	—	—	—	—	31.59	7.80	3.47	4/5
Cage density	1.01	0.68	0.34	9/70	0.84	—	—	0/18
Experimenter	2.04	3.30	2.44	7/25	2.50	1.80	0.56	6/20
Hour	1.55	1.16	—	1/29	1.51	1.41	—	1/20
Litter	0.97	0.90	0.31	9/70	0.88	—	—	0/18
Month	8.96	3.56	2.24	51/65	2.14	1.75	—	1/18
Season	5.47	1.90	1.25	38/65	1.57	—	—	0/18
Sex	12.41	9.47	11.62	48/70	2.06	2.19	1.79	5/18
Study day	1.00	2.03	1.60	15/65	1.27	0.73	—	1/18
Test order	0.37	—	—	0/25	0.72	—	—	0/16
Weight	2.92	3.06	3.89	27/65	2.06	0.90	0.23	6/18
Year	1.87	1.30	0.71	19/65	1.61	0.85	—	1/18

Variances (means and standard deviations) refer only to effects that were significant at log P > 4.55.

Figure 2.—

Main and interaction effects of covariates on 88 phenotypes from 16 experimental tests. The y-axis gives the percentage variance explained by significant covariates; the x-axis lists the test performed with the number of phenotypes measured from that test in parentheses. Physiological tests are listed first and behavioral tests second. Boxes show the median (central line) and interquartile range (IQR; box perimeter), whiskers indicate the furthest data point <1.58 IQRs from the median, and circles show outliers.

We then extended our model to test for gene-by-covariate interactions, taking the main-effects models reported above and then assessing how much adding interaction terms improved the fit. We found 389 significant interaction effects. Figure 3 illustrates the interaction between sex and family on the percentage of B-cells (%B220⁺) among white blood cells. It shows that the effect of sex is often marked within families but its direction can vary between families. Similarly, Figure 4 illustrates the interaction between family and season on mean adrenal weight measured at 10 weeks. It shows seasonal means (spring in green, summer in red, autumn in brown, and winter in blue) for 28 families. In 11 families, adrenal glands are heaviest when harvested in winter, whereas in 9 families they are heaviest in summer. The seasonal effects are strong within but inconsistent across families, reflecting the greater importance of interaction over main effects.

Figure 3.—

Interaction between sex and family for the immunological phenotype percentage of B-cells among lymphocytes in 2056 mice. For each of 69 families (x-axis) we plot means (solid circles) and standard errors (bars) of the phenotype value for males (blue) and females (pink). The y-axis gives the phenotype as the square root of the percentage of white blood cells presenting B220. The graph shows that sex can have a strong effect within families but that the direction of the effect varies between families (interaction log P = 10.7). For example, in families plotted on the left, males are enriched in the B-cell compared with females, whereas for families on the right this sex effect is reversed. The graph also illustrates the marginal effects on the trait of family (differing overall heights; heritability = 59.9%) and sex (females higher overall; main effect log P = 13.0).

Figure 4.—

Interaction between season and family for the physiological phenotype mean adrenal weight in 696 mice. For each of 28 families (x-axis) we plot the seasonal means (solid circles) and standard errors (bars) of the phenotype for animals phenotyped in winter (blue), spring (green), summer (red), and autumn (brown). The y-axis gives the phenotype as the logarithm to the base 10 of the mean weight in grams of adrenal glands at 10 weeks old. The graph shows that the effect of season is consistent within family but can vary between families. For example, for the rightmost family adrenal glands are lightest in animals tested in summer and heaviest in autumn. Yet the rank order of seasons varies considerably through the graph.

The distribution of the 389 significant interaction effects differed from that of the main effects (Figure 1 and appendix). Remarkably, half of the effects could explain >20% of the variance. In nine cases the interaction could explain >50% of the variance. The largest numbers of interactions were with month (65 significant effects), season (55), sex (53), litter (51), and cage density (40). There were only 13 significant interactions with experimenter.

Physiological phenotypes showed the largest number of interactions with covariates (56% of interactions tested were significant; Table 7). Largest effects were found on mean cellular hemoglobin concentration, serum sodium and serum chloride concentrations, and plethysmography measures. There were fewer interactions with behavioral phenotypes (5% of interactions tested were significant, amounting to 11 in total), although the effect sizes were much the same on average (mean of 18.1% for behavior compared with a mean of 18.6% for physiology; see Figure 2).

TABLE 7.

Summary of interaction effects between covariates and family

	Physiological phenotypes				Behavioral phenotypes
Covariate	Median log P	Mean % variance	SD	No. observed (significant/all)	Median log P	Mean % variance	SD	No. observed (significant/all)
Age	2.39	1.22	0.59	26/65	0.25	—	—	0/18
Apparatus	—	—	—	—	0.00	—	—	0/5
Cage density	5.05	10.80	4.45	40/70	0.37	—	—	0/18
Experimenter	4.28	26.41	6.89	11/25	2.35	16.65	1.62	2/20
Hour	6.17	23.69	7.78	21/29	1.96	—	—	0/20
Litter	9.17	13.58	7.21	51/70	0.53	—	—	0/18
Month	11.84	29.94	11.63	60/65	3.87	18.49	3.50	5/18
Season	8.04	29.24	11.66	52/65	2.25	18.94	3.92	3/18
Sex	6.82	22.33	6.66	52/70	2.21	16.38	—	1/18
Study day	2.86	0.03	0.02	22/65	0.39	—	—	0/18
Test order	0.21	—	—	0/25	0.00	—	—	0/16
Weight	3.88	0.59	0.14	28/65	1.39	—	—	0/18
Year	2.09	39.77	15.72	15/65	0.69	—	—	0/18

Variances (means and standard deviations) refer only to effects that were significant at log P > 4.55.

DISCUSSION

We have carried out the first systematic analysis of a range of covariates across multiple phenotypes (see appendix). We have estimated the heritability of 88 phenotypes, assessed the impact of a number of environmental factors, and measured the size of gene-by-environment interactions. Our large data set provides the most robust assessments to date of these measures in both behavioral and physiological domains.

We found large interactions between gene and environment and report that the effects are not restricted to behavioral phenotypes (see appendix). We do not believe this is an artifact of our analysis. Our calculations of percentage variance for random interaction effects and for fixed main effects are only roughly comparable with each other (see methods) and the interaction effects are subject to a slight upward bias. However, that is not sufficient to account for the substantially higher effect of significant interactions (18.6%) compared with significant main effects (3.7%). Second, inhomogeneity of phenotype variance across families is also unlikely to account for our findings since in many cases the rank order of covariate effects differs between families (Ungerer et al. 2003) as illustrated in Figures 3 and 4.

We report the effects of covariates as the percentage of phenotypic variance they explain and in doing so provide one assessment of how environmental covariates influence a phenotype. But the true nature of this interaction is more complex. For example, the concentration of alanine transaminase is subject to gene-by-environment interactions of month, accounting for 48.49% of the phenotypic variance, of season, accounting for 45.51%, and of litter, accounting for 18.17%. Yet these effects combine, with further covariates, to produce 100%. How is this possible?

The correlational structure of our data complicates an assessment of the relative importance of different covariates and interactions. The observed phenotypic variance is the sum of the variances of the covariates minus twice the covariances between the covariates. This means that two covariates could have individual effects of 50% but a summed effect of 60% if they are positively correlated (or one of <50% if they are negatively correlated). An observed covariate effect, just like an observed QTL effect, therefore includes a portion of the effect of any element that correlates with it; an actual month effect will partly manifest as observed litter and season effects and vice versa. A more comprehensive analysis would build a complete picture of each phenotype in the context of a path diagram or structural equation model that enumerated all relationships, both raw effects and correlations, between actors (e.g., Lynch and Walsh 1998).

The importance of gene-by-environment interactions has been emphasized in the analysis of mouse behavior and largely ignored in studies of mouse physiology. In the light of this, we designed our phenotyping protocol to minimize the effects of covariates on behavioral measures. All such tests were automated, so that the experimenter's intervention was limited to placing animals in the apparatus. This may explain why some covariates, previously suspected to influence behavioral phenotypes, were found to make a small contribution to the variance: time of day (hour) was a nonsignificant (or hardly significant with negligible effect) contributor to all measures including those that utilize exploration as a measure of anxiety (elevated plus maze, which had observations from 9 different hours of the day, and open field, which had observations from 10), despite the fact that exploratory activity has been reported to vary throughout the day (Aschoff 1981). The order in which animals are tested is also considered to have an important effect on behavior (Harro 1997), but we found no evidence for this: its effect was nonsignificant on all phenotypes measured.

Physiological phenotypes were not so controlled. There are no automated ways of administering an intraperitoneal glucose tolerance test, for example, and we observed large experimenter effects on these tests. This raises the question as to whether some phenotypes are more susceptible to interaction effects than others. Differences in the assessment protocols cannot be the only factor that accounts for the smaller number of interactions in behavioral tests. There are a number of covariates common to all phenotypes whose effects we could not ameliorate: month, season, year, sex, and weight. All of these covariates impinge more on physiological than on behavioral phenotypes (Tables 6 and 7).

Importantly, we observed many significant and large gene-by-environment interactions in our analysis of physiological phenotypes. Biochemical measures showed strong (>10% effect) gene-by-environment interactions with month (in 14 of 16 biochemical phenotypes), sex (12), season (9), and litter (8). We saw a similar pattern of strong seasonal and sex effects for hematology, immunology, plethysmography (which also had a strong hour interaction), and the glucose tolerance test (which also had a strong experimenter interaction). This has profound implications for QTL studies.

QTL detection experiments suffer when covariates are not adequately accommodated in the experimental design and subsequent analysis. First, a QTL may owe some, or indeed all, of its significance to an environmental effect confounded with the allelic variant. When a phenotype is strongly affected by who performed the experiment, any nonfunctional variant that correlates with the experimenter will manifest as a significant, but spurious, effect. The random nature of recombination means that in any experimental cross a fully balanced design is impossible and so confounds of this type are ineluctable. While the impact of covariates can be minimized by regressing out their effects prior to mapping (e.g., Valdar et al. 2006), this is highly conservative, since in the converse scenario, where experimenter acts as a surrogate variable for an actual QTL effect, the QTL will be missed.

Second, an interaction between a QTL and an environmental covariate may conceal the effect of both, even when covariate and QTL are in the model. For instance, if mice with allele a fear experimenter John more than experimenter Alice, but mice with allele A fear Alice more than John and all four conditions occur in about equal proportion, then neither experimenter nor QTL will have an observed effect. To recover the genetic effect in this case it is necessary to model the interaction in the mapping procedure (e.g., Wang et al. 2006).

Our analyses are limited by the relatively small number of covariates that we collected. We have no information on temperature fluctuation and humidity levels [shown to be important for behavioral tests of nociception (Chesler et al. 2002a,b)], which might explain month and seasonal effects. We have no information on noise levels that are significantly increased during working hours (Milligan et al. 1993). The predominance of significant temporal covariates reflects the importance of many other unknown environmental factors whose effect is moderated through the animals' genotypes. Thus the dissection of complex phenotypes in the mouse will require far more sophisticated observation and analysis of these interactions than has hitherto been attempted.