Abstract
Dominance (intralocus allelic interactions) plays often an important role in quantitative trait variation. However, few studies about dominance in QTL mapping have been reported in outbred animal or human populations. This is because common dominance effects can be predicted mainly for many full sibs, which do not often occur in outbred or natural populations with a general pedigree. Moreover, incomplete genotypes for such a pedigree make it infeasible to estimate dominance relationship coefficients between individuals. In this study, identity-by-descent (IBD) coefficients are estimated on the basis of populationwide linkage disequilibrium (LD), which makes it possible to track dominance relationships between unrelated founders. Therefore, it is possible to use dominance effects in QTL mapping without full sibs. Incomplete genotypes with a complex pedigree and many markers can be efficiently dealt with by a Markov chain Monte Carlo method for estimating IBD and dominance relationship matrices (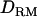 ). It is shown by simulation that the use of
). It is shown by simulation that the use of 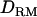 increases the likelihood ratio at the true QTL position and the mapping accuracy and power with complete dominance, overdominance, and recessive inheritance modes when using 200 genotyped and phenotyped individuals.
increases the likelihood ratio at the true QTL position and the mapping accuracy and power with complete dominance, overdominance, and recessive inheritance modes when using 200 genotyped and phenotyped individuals.
A variance component approach is an efficient and powerful tool for dissecting the variation due to quantitative trait loci (QTL) because of its generality and flexibility (Goldgar 1990; Amos 1994; Grignola et al. 1996; Almasy and Blangero 1998; Van Arendonk et al. 1998; Blangero et al. 2000; George et al. 2000). In the approach, QTL are treated as random effects, which makes it possible to apply complex covariance structures on the basis of general and complex pedigree. It is also feasible to simultaneously consider additional effects in the statistical model, e.g., those of other QTL and their interactions (Blangero et al. 2000).
Quantitative trait variation associated with causal mutations in the loci can be decomposed into additive genetic effects, dominance (intralocus interactions), and epistasis (interlocus interactions). Additive genetic effects due to QTL and their interlocus interactions have been explicitly considered in several QTL mapping studies (Jansen 1993; Zeng 1993, 1994; Mitchell et al. 1997; Blangero et al. 2000; Carlborg et al. 2000). However, few studies about dominance in QTL mapping have been reported for outbred populations although a part of variation due to QTL may be caused by dominance. The reason for dominance not having been explicitly considered may be because common dominance effects can be predicted mainly for full sibs that do not frequently occur in outbred or natural populations with a general pedigree. Moreover, such a general pedigree structure spans several generations with complex relationships, and ancestors' genotypes are often unavailable (Haley 1999).
Identity-by-descent (IBD) coefficients between haplotypes of unrelated founders in a recorded pedigree can be estimated on the basis of linkage disequilibrium (LD) using coalescence methods (Meuwissen and Goddard 2001; Perez-Enciso 2003; Morris et al. 2004). This makes it possible to estimate the covariance between unrelated animals due to additive gene effects and intralocus allelic interactions. Additive genetic and dominance relationship coefficients based on LD and pedigree information give much more information about covariance between individuals for a targeted QTL region. Therefore, this approach allows estimation of additive genetic and dominance effects in an outbred or natural population without a particular designed family structure.
The aim of this study is to investigate the use of LD-based 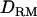 in mapping of QTL with a general complex pedigree. The mapping accuracy with and without
in mapping of QTL with a general complex pedigree. The mapping accuracy with and without 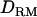 is investigated with various levels of LD and inheritance modes. In estimating IBD coefficients and
is investigated with various levels of LD and inheritance modes. In estimating IBD coefficients and 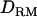 , a Markov chain Monte Carlo approach is used as it is a flexible and efficient tool to deal with the case of complex pedigree with incomplete genotypic data and many markers (Lee et al. 2005).
, a Markov chain Monte Carlo approach is used as it is a flexible and efficient tool to deal with the case of complex pedigree with incomplete genotypic data and many markers (Lee et al. 2005).
MATERIALS AND METHODS
Mixed linear model:
A vector of phenotypic observations can be modeled as
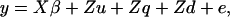 |
(1) |
where y is a vector of phenotypic observations on the trait of interest, 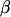 is a vector of fixed effects,
is a vector of fixed effects, 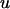 is a vector with a random polygenic effect for each of n individuals, q is a vector of n random additive genetic effects due to QTL, d is a vector of n random effects due to intralocus allelic interaction at the QTL, and e are residuals. The random effects u, q, d, and e are assumed uncorrelated with each other and normally distributed with mean zero and variance
is a vector with a random polygenic effect for each of n individuals, q is a vector of n random additive genetic effects due to QTL, d is a vector of n random effects due to intralocus allelic interaction at the QTL, and e are residuals. The random effects u, q, d, and e are assumed uncorrelated with each other and normally distributed with mean zero and variance 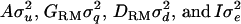 . A is the numerator relationship matrix based on additive genetic relationships predicted from pedigree,
. A is the numerator relationship matrix based on additive genetic relationships predicted from pedigree, 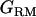 is the additive genotype relationship matrix at QTL whose elements are IBD probabilities between individuals computed for a putative QTL position and conditional on marker information,
is the additive genotype relationship matrix at QTL whose elements are IBD probabilities between individuals computed for a putative QTL position and conditional on marker information, 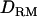 is the dominance relationship matrix at QTL based on IBD probabilities, and I is an identity matrix. X and Z are incidence matrices for the effects in
is the dominance relationship matrix at QTL based on IBD probabilities, and I is an identity matrix. X and Z are incidence matrices for the effects in 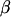 , and u, q, and d, respectively. From (1), the associated variance covariance matrix of all observations (V) for a given pedigree and marker genotype set is modeled as
, and u, q, and d, respectively. From (1), the associated variance covariance matrix of all observations (V) for a given pedigree and marker genotype set is modeled as
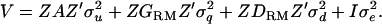 |
(2) |
It is noted that the IBD coefficients between all haplotypes (2n) are transformed to a covariance between individual genotypes without loss of information, which is 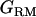 (n × n) (Tier and Solkner 1993; Pong-Wong et al. 2001; Lee and van der Werf 2006). Therefore, the number of terms corresponding to q reduces to n × n, which is the same for u. The number of terms corresponding to d is originally the same as that for u (Liu et al. 2002). Therefore, a single incidence matrix, Z, can be used for u, q, and d.
(n × n) (Tier and Solkner 1993; Pong-Wong et al. 2001; Lee and van der Werf 2006). Therefore, the number of terms corresponding to q reduces to n × n, which is the same for u. The number of terms corresponding to d is originally the same as that for u (Liu et al. 2002). Therefore, a single incidence matrix, Z, can be used for u, q, and d.
Estimation of GRM and DRM:
Probabilities of segregation states given marker data and pedigree:
Each configuration of segregation states has its own probability that is estimated on the basis of observed marker and pedigree. The probability for one configuration (S) is
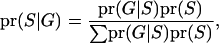 |
(3) |
where 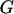 represents the observed marker data, pr(
represents the observed marker data, pr(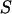 ) is prior probability of the segregation state, Pr(
) is prior probability of the segregation state, Pr(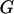 |
| 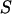 ) is the probability of the observed marker data given
) is the probability of the observed marker data given 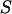 , and the denominator is summed over the probabilities of all possible segregation states. Since the computation of the denominator is not generally feasible, a Markov chain Monte Carlo approach is required to obtain the posterior distribution of the segregation state.
, and the denominator is summed over the probabilities of all possible segregation states. Since the computation of the denominator is not generally feasible, a Markov chain Monte Carlo approach is required to obtain the posterior distribution of the segregation state.
Sampling segregation state using Markov chain Monte Carlo approaches:
The meiosis Gibbs sampler makes joint updates for the inheritance at linked loci for one individual at a time. For example, for the ith individual, segregation indicators at all loci can be sampled using a forward–backward algorithm (Thompson and Heath 1999), according to all possible segregation states for the ith individual, conditional on the segregation indicators for other individuals (see Lee et al. 2005). Joint updates for each individual result in better mixing properties and the process is much more reliable than that of a single-site Gibbs sampler (Thompson and Heath 1999). To increase mixing properties, the random walk approach (Sobel and Lange 1996) is used for the potential reducible sites in the meiosis sampler (Lee et al. 2005).
Haplotype reconstruction:
In the process of the Markov chain Monte Carlo (MCMC) sampling, marker genotypes are sampled for paternal and maternal gametes for all animals conditioned on observable variables (e.g., observed marker data and pedigree information), taking into account the linkage across the chromosome. This is known as haplotype reconstruction. This procedure is performed in each sampling round.
QTL allelic identity-by-descent coefficients based on LD and linkage:
Given the sampled segregation state and haplotypes, it is possible to estimate QTL allelic IBD coefficients on the basis of LD and linkage. Sampled haplotypes for base animals are used to estimate LD-based IBD probabilities between unrelated base animals, using the method of Meuwissen and Goddard (2000, 2001). Sampled segregation indicators at multiple marker loci for descendants are used to estimate linkage-based IBD probabilities between relatives. There are four IBD probabilities between any pair of individuals i and j in the pedigree that are the probabilities of the paternal or maternal QTL allele of individual i being IBD to the paternal or maternal allele of individual j, given marker genotypes (Liu et al. 2002); i.e., 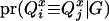 , where x is the paternal (P) or maternal (M) QTL allele for each individual. From the probabilities, the additive genotype coefficient between animals i and j at the QTL is
, where x is the paternal (P) or maternal (M) QTL allele for each individual. From the probabilities, the additive genotype coefficient between animals i and j at the QTL is
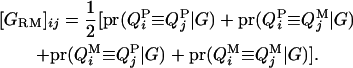 |
The dominance relationship coefficient between animals i and j at the QTL is
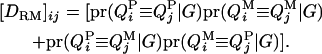 |
Restricted maximum likelihood:
By assuming multivariate normality of the data with vector 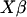 and a variance–covariance matrix of all observations, the resulting likelihood and variance components can be estimated. An efficient algorithm to obtain restricted maximum-likelihood (REML) estimates is one that uses the average of the information from the observed derived Hessian coefficients and the expected derived Fisher information coefficients (see Gilmour et al. 1995; Johnson and Thompson 1995). We solved the average information (AI) REML equation, directly using the variance–covariance matrix rather than using the mixed model equations (see Lee and van der Werf 2006).
and a variance–covariance matrix of all observations, the resulting likelihood and variance components can be estimated. An efficient algorithm to obtain restricted maximum-likelihood (REML) estimates is one that uses the average of the information from the observed derived Hessian coefficients and the expected derived Fisher information coefficients (see Gilmour et al. 1995; Johnson and Thompson 1995). We solved the average information (AI) REML equation, directly using the variance–covariance matrix rather than using the mixed model equations (see Lee and van der Werf 2006).
Simulation study:
One hundred generations with a population size of 100 were simulated for 10 marker loci at 1-cM intervals and a QTL to generate LD between QTL and flanking markers beyond the recorded pedigree. In each generation, the number of male and female parents was 50 and their alleles were transmitted to descendants on the basis of Mendelian segregation using the genedropping method (MacCluer et al. 1986). Parents were randomly mated with a total of two offspring for each of 50 mating pairs. Note that no pedigree information was recorded for these 100 generations.
The number of base alleles in each marker locus was four and starting allele frequencies were all at 0.25. The marker alleles were mutated at a rate of 4 × 10−4/generation (Dallas 1992; Weber and Wong 1993; Ellegren 1995). A QTL was located at the middle of the fourth and fifth markers, and unique numbers were assigned to the base population alleles. In generation 100 and afterward, phenotypic values for individuals were simulated as
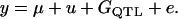 |
(4) |
The population mean (μ) was 100, values for polygenic effects (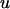 ) were drawn from
) were drawn from 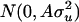 with
with 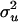 = 25 (A is numerator relationships among individuals calculated since generation t + 1), and values for residuals (
= 25 (A is numerator relationships among individuals calculated since generation t + 1), and values for residuals ( ) were from
) were from 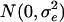 with
with 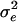 = 50. The value due to QTL genotypes (
= 50. The value due to QTL genotypes (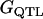 ) for each individual was decomposed as additive effects of paternal and maternal QTL alleles and their nonadditive allelic interaction; that is,
) for each individual was decomposed as additive effects of paternal and maternal QTL alleles and their nonadditive allelic interaction; that is,
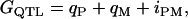 |
(5) |
where 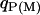 is the paternal (maternal) QTL allele and
is the paternal (maternal) QTL allele and 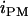 is interaction between the two alleles. Three cases were considered for intralocus allelic interaction for the QTL. The favorable QTL allele (
is interaction between the two alleles. Three cases were considered for intralocus allelic interaction for the QTL. The favorable QTL allele (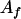 ) had an additive value of 7 (a = 7) and allelic interaction with a particular allele (say
) had an additive value of 7 (a = 7) and allelic interaction with a particular allele (say 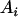 ) gave a value of 14 (d = 7) for case 1 or 21 (d = 14) for case 2. The last one (case 3) was that homozygous recessive alleles (any pair of
) gave a value of 14 (d = 7) for case 1 or 21 (d = 14) for case 2. The last one (case 3) was that homozygous recessive alleles (any pair of 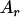 ) gave a value of 14 and otherwise no effects (Table 1). The allele
) gave a value of 14 and otherwise no effects (Table 1). The allele 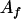 ,
, 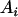 , or
, or 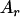 was randomly chosen from the base alleles with a frequency of >0.1 and <0.9. Since the number of alleles and their frequencies were stochastically simulated, the ratio of additive and dominance QTL variance over phenotypic variance (i.e.,
was randomly chosen from the base alleles with a frequency of >0.1 and <0.9. Since the number of alleles and their frequencies were stochastically simulated, the ratio of additive and dominance QTL variance over phenotypic variance (i.e., 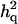 and
and 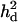 ) varied for each case (Table 1).
) varied for each case (Table 1).
TABLE 1.
No-interaction model and three cases of intralocus allelic interaction models considered in the simulation study
| No interaction
|
Case 1: complete dominance
|
Case 2: overdominance
|
Case 3: recessive
|
||||
|---|---|---|---|---|---|---|---|
| Genotype | Value | Genotype | Value | Genotype | Value | Genotype | Value |
 , , 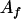
|
14 |
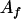 , , 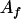 a a
|
14 |
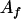 , , 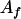
|
14 |
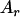 , , 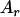 d d
|
14 |
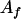 , , 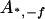
|
7 |
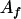 , , 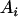 b b
|
14 |
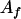 , , 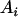
|
21 |
 , , 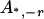 e e
|
0 |
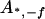 , , 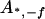
|
0 |
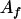 , , 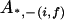 c c
|
7 |
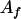 , , 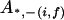
|
7 |
 , , 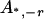
|
0 |
 , , 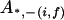
|
0 |
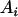 , , 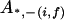
|
0 | ||||
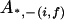 , , 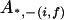
|
0 |
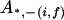 , , 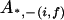
|
0 | ||||
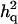 = 0.189 (0.006) = 0.189 (0.006) |
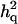 = 0.234 (0.009) = 0.234 (0.009) |
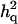 = 0.28 (0.011) = 0.28 (0.011) |
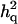 = 0.087 (0.012) = 0.087 (0.012) |
||||
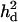 = 0 (0) = 0 (0) |
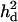 = 0.039 (0.003) = 0.039 (0.003) |
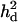 = 0.125 (0.008) = 0.125 (0.008) |
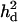 = 0.073 (0.029) = 0.073 (0.029) |
||||
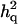 is the ratio of additive QTL variance over phenotypic variance, and
is the ratio of additive QTL variance over phenotypic variance, and 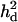 is QTL dominance variance over phenotypic variance. Empirical standard error over replicates is in parentheses.
is QTL dominance variance over phenotypic variance. Empirical standard error over replicates is in parentheses.
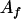 , an allele f in the QTL.
, an allele f in the QTL.
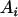 , an allele i in the QTL.
, an allele i in the QTL.
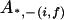 , all the other alleles except f and i.
, all the other alleles except f and i.
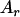 , an allele r.
, an allele r.
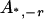 , all the other alleles except r.
, all the other alleles except r.
The likelihood ratio [LR = 2(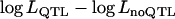 )] over 50 replicates was estimated in LD and linkage (LDL) mapping with or without fitting nonadditive intralocus allelic interaction (i.e., with or without using
)] over 50 replicates was estimated in LD and linkage (LDL) mapping with or without fitting nonadditive intralocus allelic interaction (i.e., with or without using 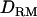 ). Both LR and proportion of replicates positioning QTL for each marker bracket are plotted against genomic region as an indication of the mapping accuracy. The power was calculated as the proportion of replicates detecting QTL with LR value that was >6.6 (=
). Both LR and proportion of replicates positioning QTL for each marker bracket are plotted against genomic region as an indication of the mapping accuracy. The power was calculated as the proportion of replicates detecting QTL with LR value that was >6.6 (= 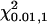 ). Analyses were carried out for a general pedigree of 2 generations (generation 100–∼101), varying marker density or past effective size with changing levels of LD. In addition, results from LDL mapping and linkage-only mapping are compared using a pedigree of 5 generations (generation 100–∼104). It is noted that a pedigree of 2 generations does not have enough linkage information to estimate
). Analyses were carried out for a general pedigree of 2 generations (generation 100–∼101), varying marker density or past effective size with changing levels of LD. In addition, results from LDL mapping and linkage-only mapping are compared using a pedigree of 5 generations (generation 100–∼104). It is noted that a pedigree of 2 generations does not have enough linkage information to estimate 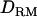 in linkage mapping alone. In all cases, marker genotypes and phenotypes were available for the last 2 generations (200 animals) for a fair comparison. For the pedigree of 5 generations, ancestral genotypes from generation 100–102 were totally missing.
in linkage mapping alone. In all cases, marker genotypes and phenotypes were available for the last 2 generations (200 animals) for a fair comparison. For the pedigree of 5 generations, ancestral genotypes from generation 100–102 were totally missing.
The middle point of each marker bracket is tested for QTL signal. Therefore, nine 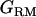 and
and 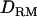 matrices were generated. Variance components for model parameters (
matrices were generated. Variance components for model parameters (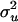 ,
, 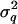 ,
, 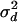 , and
, and 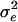 ) were estimated with each set of
) were estimated with each set of 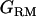 and
and 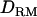 , using REML.
, using REML.
RESULTS
Increased accuracy of estimated position:
The averaged value of LR and the proportion of replicates positioning the QTL with or without  for each putative QTL position is plotted against the genomic region. When using a no-interaction model, the LR curve with
for each putative QTL position is plotted against the genomic region. When using a no-interaction model, the LR curve with 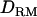 is almost identical to that without
is almost identical to that without 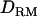 ; e.g., at the true QTL position, the LR is 20.7 with
; e.g., at the true QTL position, the LR is 20.7 with 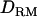 and 20.2 without
and 20.2 without 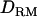 (Figure 1A). The density curve for the proportion of replicates positioning the QTL for each position is also very similar for both models with and without
(Figure 1A). The density curve for the proportion of replicates positioning the QTL for each position is also very similar for both models with and without 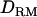 (Figure 1A). Whether
(Figure 1A). Whether 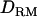 is used or not, the QTL is significantly detected for all replicates (the power is 1). This shows that the use of
is used or not, the QTL is significantly detected for all replicates (the power is 1). This shows that the use of 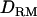 has no effect on the mapping performance when dominance effects are absent.
has no effect on the mapping performance when dominance effects are absent.
Figure 1.—
Likelihood ratio averaged over replicates (LR) and proportion of replicates positioning the QTL (density) across the genomic region when using a no-interaction model with 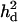 = 0 (A), complete dominance with
= 0 (A), complete dominance with 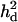 = 0.039 (case 1, B), overdominance with
= 0.039 (case 1, B), overdominance with 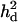 = 0.125 (case 2, C), and a recessive model with
= 0.125 (case 2, C), and a recessive model with 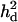 = 0.073 (case 3, D). Solid diamonds, analysis without
= 0.073 (case 3, D). Solid diamonds, analysis without 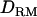 ; shaded boxes, analysis with
; shaded boxes, analysis with 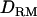 .
.
In case 1, the LR at the correct QTL position is much higher with 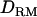 used to fit the effects of allelic interaction (31.1) than without
used to fit the effects of allelic interaction (31.1) than without 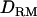 (26.8) (Figure 1B). The proportion of replicates positioning the QTL at the correct location is 0.62 with
(26.8) (Figure 1B). The proportion of replicates positioning the QTL at the correct location is 0.62 with 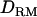 , whereas the proportion is 0.46 without
, whereas the proportion is 0.46 without 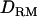 (Figure 1B) although the power is 0.96 for both models with and without
(Figure 1B) although the power is 0.96 for both models with and without 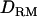 .
.
In case 2 (i.e., overdominance model), the LR value at the correct QTL position is substantially higher with 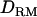 (49.5) than without
(49.5) than without 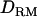 (34.4) (Figure 1C). The proportion positioning the QTL on the correct location is 0.74 with
(34.4) (Figure 1C). The proportion positioning the QTL on the correct location is 0.74 with 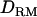 and 0.54 without
and 0.54 without 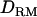 (Figure 1C). The power is 0.98 for both models. Compared to the result in case 1 (Figure 1B), the averaged LR value and the accuracy are higher and the difference between the models with and without
(Figure 1C). The power is 0.98 for both models. Compared to the result in case 1 (Figure 1B), the averaged LR value and the accuracy are higher and the difference between the models with and without 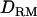 is much bigger.
is much bigger.
In case 3 (i.e., recessive model), the LR curve without 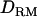 is relatively flat and low even at the correct QTL position (LR = 2.7) (Figure 1D). However, the LR curve with
is relatively flat and low even at the correct QTL position (LR = 2.7) (Figure 1D). However, the LR curve with 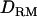 is highly peaked on the correct QTL position (LR = 7.7). The proportion positioning the QTL at the correct location is 0.32 with
is highly peaked on the correct QTL position (LR = 7.7). The proportion positioning the QTL at the correct location is 0.32 with 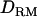 and 0.22 without
and 0.22 without 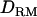 (Figure 1D). The power is much higher with
(Figure 1D). The power is much higher with 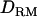 (0.5) than without
(0.5) than without 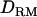 (0.14).
(0.14).
Effect of marker density and past effective size:
Since the IBD and dominance relationship coefficients are based on LD information, the performance of the proposed method may depend on the levels of LD. Lower LD could arise from using either a lower marker density or a higher past effective size. Figure 2 shows the patterns of LR values averaged over replicates when using two different marker densities (1 and 5 cM). The difference between the LR values at the correct QTL position with and without 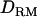 is significant (31.09 and 26.76) with a 1-cM marker spacing. However, the difference is negligible (9.16 and 8.79) in the case of a 5-cM marker spacing. The overall LR values across the genome region are much lower with the lower marker density.
is significant (31.09 and 26.76) with a 1-cM marker spacing. However, the difference is negligible (9.16 and 8.79) in the case of a 5-cM marker spacing. The overall LR values across the genome region are much lower with the lower marker density.
Figure 2.—
Likelihood ratio averaged over replicates with or without 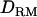 when using 1 cM of marker spacing (solid diamonds, LR without
when using 1 cM of marker spacing (solid diamonds, LR without 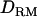 ; shaded boxes, LR with
; shaded boxes, LR with 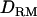 ) and 5 cM of marker spacing (solid triangles, LR without
) and 5 cM of marker spacing (solid triangles, LR without 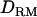 ; shaded dashed line, LR with
; shaded dashed line, LR with 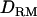 ) with the complete dominance model (case 1).
) with the complete dominance model (case 1).
Figure 3 shows LR values when using two different past effective sizes (100 and 400). The difference between the performances with and without 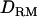 is much bigger when using an effective size of 100 (31.09 and 26.76) than when using an effective size of 400 (11.38 and 10.73). The overall LR value substantially decreases with the higher value of past effective size.
is much bigger when using an effective size of 100 (31.09 and 26.76) than when using an effective size of 400 (11.38 and 10.73). The overall LR value substantially decreases with the higher value of past effective size.
Figure 3.—
Likelihood ratio averaged over replicates with or without 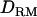 when using past effective size of 100 (solid diamonds, LR without
when using past effective size of 100 (solid diamonds, LR without 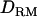 ; shaded boxes, LR with
; shaded boxes, LR with 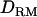 ) and past effective size of 400 (solid triangles, LR without
) and past effective size of 400 (solid triangles, LR without  ; shaded bars, LR with
; shaded bars, LR with 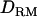 ) with the complete dominance model (case 1).
) with the complete dominance model (case 1).
The level of LD can be predicted given the length of a chromosomal region and the value of past effective size,
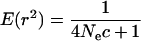 |
(6) |
(Sved 1971), where 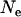 is past effective size and c is the recombination rate of the chromosomal region. E(r2) is defined here as the expected probability of the chromosomal region being IBD when two random haplotypes are taken from the population (Hayes et al. 2003). For the parameters used in the simulated data, the expected r2 is 0.2 with 1 cM of marker spacing and effective size of 100, 0.05 with 5 cM of marker spacing and effective size of 100, and 0.06 with 1 cM of marker spacing and effective size of 400.
is past effective size and c is the recombination rate of the chromosomal region. E(r2) is defined here as the expected probability of the chromosomal region being IBD when two random haplotypes are taken from the population (Hayes et al. 2003). For the parameters used in the simulated data, the expected r2 is 0.2 with 1 cM of marker spacing and effective size of 100, 0.05 with 5 cM of marker spacing and effective size of 100, and 0.06 with 1 cM of marker spacing and effective size of 400.
This shows that when the levels of LD are low (∼0.05), the use of 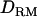 does not improve the value of the LR. It is also noted that the efficiency of LDL mapping decreases with lower LD. This is because IBD and dominance relationship coefficients are based on LD information.
does not improve the value of the LR. It is also noted that the efficiency of LDL mapping decreases with lower LD. This is because IBD and dominance relationship coefficients are based on LD information.
Comparison between LDL mapping and linkage mapping alone:
The accuracy of estimated QTL position with LDL mapping or linkage mapping is estimated and compared when using a five-generation pedigree where only the last two generations are genotyped (incomplete genotypes). The LR values with or without 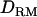 are estimated with a complete dominance model.
are estimated with a complete dominance model.
The accuracy of estimated QTL position with LDL mapping is much higher than that with linkage mapping (Figure 4). The LR value with LDL mapping is fairly peaked at the true QTL position and high (19.23 with 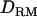 and 17.47 without
and 17.47 without 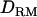 ). However, the LR curve with linkage mapping alone is flat and low (∼4 on the true QTL with or without
). However, the LR curve with linkage mapping alone is flat and low (∼4 on the true QTL with or without 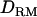 ) and gives little useful information about QTL position. It should be noted that analysis with
) and gives little useful information about QTL position. It should be noted that analysis with 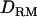 is clearly better than that without
is clearly better than that without 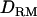 in LDL mapping. However, there is no difference in linkage mapping (Figure 4). This shows that dominance effects are not captured by linkage information in a general pedigree.
in LDL mapping. However, there is no difference in linkage mapping (Figure 4). This shows that dominance effects are not captured by linkage information in a general pedigree.
Figure 4.—
LR averaged over replicates with and without 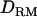 in LDL mapping (solid diamonds, LR without
in LDL mapping (solid diamonds, LR without 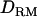 ; shaded boxes, LR with
; shaded boxes, LR with 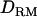 ) and linkage mapping only (solid triangles, LR without
) and linkage mapping only (solid triangles, LR without 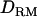 ; shaded bars, LR with
; shaded bars, LR with 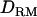 ) when using a pedigree of five generations.
) when using a pedigree of five generations.
Estimated variance components:
Table 2 shows estimated parameters with or without 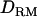 when a complete dominance model is considered. The ratio of polygenic variances over phenotypic variance (
when a complete dominance model is considered. The ratio of polygenic variances over phenotypic variance (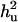 ) is not much biased for analyses both with and without using
) is not much biased for analyses both with and without using 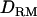 . The ratio of additive QTL variance over phenotypic variance is relatively accurate with using
. The ratio of additive QTL variance over phenotypic variance is relatively accurate with using 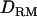 whereas it is overestimated without using
whereas it is overestimated without using 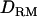 . The ratio of nonadditive QTL dominance variance over phenotypic variance is overestimated with using
. The ratio of nonadditive QTL dominance variance over phenotypic variance is overestimated with using 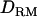 . This is probably due to the fact that the number of records is small with insufficient information to accurately estimate dominance variances, even though the power of QTL detection is increased due to
. This is probably due to the fact that the number of records is small with insufficient information to accurately estimate dominance variances, even though the power of QTL detection is increased due to 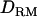 (see discussion).
(see discussion).
TABLE 2.
Parameters estimated with or without 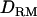 when using the complete dominance model
when using the complete dominance model
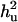 |
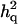 |
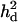 |
|
|---|---|---|---|
| True parameters | 0.242 (0.004) | 0.234 (0.009) | 0.039 (0.003) |
Estimated with 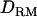
|
0.225 (0.015) | 0.237 (0.019) | 0.106 (0.016) |
Estimated without 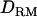
|
0.214 (0.014) | 0.308 (0.015) | NA |
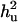 is ratio of polygenic variance over phenotypic variance. Empirical standard error over replicates is in parentheses. Two hundred individuals with known phenotypes and genotypes were used.
is ratio of polygenic variance over phenotypic variance. Empirical standard error over replicates is in parentheses. Two hundred individuals with known phenotypes and genotypes were used.
DISCUSSION
The use of 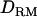 in variance component QTL mapping (in both linkage mapping and LDL mapping) has not been tested before for outbred populations. This is because lack of full sibs would give little or no information to estimate the (co)variance due to dominance effects (Goddard and Meuwissen 2005). This is true for the case that
in variance component QTL mapping (in both linkage mapping and LDL mapping) has not been tested before for outbred populations. This is because lack of full sibs would give little or no information to estimate the (co)variance due to dominance effects (Goddard and Meuwissen 2005). This is true for the case that 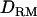 is based on linkage information alone (as illustrated in Figure 4), but IBD coefficients and
is based on linkage information alone (as illustrated in Figure 4), but IBD coefficients and 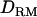 based on LD provide much more information. Our study investigated the usefulness of
based on LD provide much more information. Our study investigated the usefulness of 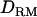 based on combined LD and linkage in QTL mapping. It was shown that the mapping resolution was higher with using
based on combined LD and linkage in QTL mapping. It was shown that the mapping resolution was higher with using 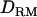 when
when 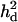 was higher.
was higher.
Previous reports on LD variance component mapping (Meuwissen and Goddard 2000, 2001; Meuwissen et al. 2002; Blott et al. 2003) have ignored intralocus interaction. We constructed 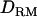 based on combined LD and linkage information with a general complex pedigree of two generations using a MCMC method (Lee et al. 2005) and investigated whether power and accuracy of mapping increases with the
based on combined LD and linkage information with a general complex pedigree of two generations using a MCMC method (Lee et al. 2005) and investigated whether power and accuracy of mapping increases with the 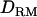 . Moreover, we showed that the MCMC method made it possible to construct IBD matrices and
. Moreover, we showed that the MCMC method made it possible to construct IBD matrices and 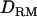 with a complex pedigree of several generations (approximately five generations) having a large proportion of missing genotypes. The recursive method described in Liu et al. (2002) could not deal with missing genotypes.
with a complex pedigree of several generations (approximately five generations) having a large proportion of missing genotypes. The recursive method described in Liu et al. (2002) could not deal with missing genotypes.
In cases 1 and 2, the power was high (>0.95) and the same for both models with and without 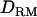 . This was probably due to the fact that additive QTL effects were already large enough to provide significant QTL signals (
. This was probably due to the fact that additive QTL effects were already large enough to provide significant QTL signals (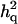 = 0.23–∼0.28) whether
= 0.23–∼0.28) whether  was used or not. However, the proportion of replicates positioning the QTL on the correct location was significantly increased with
was used or not. However, the proportion of replicates positioning the QTL on the correct location was significantly increased with 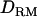 , which probably gave more information about the QTL position. When additive QTL effects were small as in case 3, it was clearly shown that the power as well as the accuracy was much higher with
, which probably gave more information about the QTL position. When additive QTL effects were small as in case 3, it was clearly shown that the power as well as the accuracy was much higher with 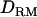 than without
than without 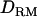 .
.
The LR values with a five-generation pedigree were lower than those with a two-generation pedigree. This was probably because haplotype reconstruction for the founders was based on descendants' genotypes, and this was less accurate compared to using their own genotypes as in the two-generation pedigree. In addition to, a high proportion of missing genotypes and complex relationships may often cause noncommunicating classes in the Markov chain (i.e., a reducibility problem). However, the LR values were still fairly peaked on the true QTL position with a five-generation pedigree using LDL mapping.
Our dominance model in case 1 assumed interaction only between 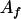 and
and 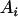 . An alternative interaction model was considered where
. An alternative interaction model was considered where 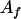 showed an allelic interaction with any other allele (
showed an allelic interaction with any other allele (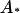 ), giving a value of 14. The results from this alternative were very similar to case 1 in that the LR values with
), giving a value of 14. The results from this alternative were very similar to case 1 in that the LR values with 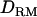 were significantly higher than those without
were significantly higher than those without 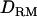 (Figure 5). This indicates that the proposed method performs well for different intraallelic interaction models.
(Figure 5). This indicates that the proposed method performs well for different intraallelic interaction models.
Figure 5.—
Likelihood ratio with or without 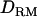 when using the alternative mode of allelic interaction. Solid diamonds, LR without
when using the alternative mode of allelic interaction. Solid diamonds, LR without 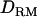 ; shaded boxes, LR with
; shaded boxes, LR with  .
.
In all cases, only a single QTL was involved with polygenic effects and residuals. The question is whether  still performs well when multiple dominance QTL are linked in a chromosome. We simultaneously simulated three QTL across a 100-cM genomic region, each with a different inheritance mode. The first QTL at 13.5 cM was additive (a = 7), the second QTL at 46.5 cM showed complete dominance (a = 5 and d = 5), and the third QTL at 76.5 cM was recessive (a = 7 and d = −7). The values for polygenic effects and residuals were the same as before. Thirty-eight markers were spanned across the region such that markers were basically positioned at 10-cM intervals, and 9 markers were added and positioned at 1-cM intervals for each region from 10 to 20 cM, from 40 to 50 cM, and from 70 to 80 cM. Twenty-five replicates were carried out. The average ratios of additive and dominance variance are
still performs well when multiple dominance QTL are linked in a chromosome. We simultaneously simulated three QTL across a 100-cM genomic region, each with a different inheritance mode. The first QTL at 13.5 cM was additive (a = 7), the second QTL at 46.5 cM showed complete dominance (a = 5 and d = 5), and the third QTL at 76.5 cM was recessive (a = 7 and d = −7). The values for polygenic effects and residuals were the same as before. Thirty-eight markers were spanned across the region such that markers were basically positioned at 10-cM intervals, and 9 markers were added and positioned at 1-cM intervals for each region from 10 to 20 cM, from 40 to 50 cM, and from 70 to 80 cM. Twenty-five replicates were carried out. The average ratios of additive and dominance variance are 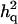 = 0.14, 0.13, and 0.089 and
= 0.14, 0.13, and 0.089 and 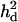 =0, 0.031, and 0.056 for the first, second, and third QTL, respectively. As shown in Figure 6, the pattern of LR curves clearly showed that the use of
=0, 0.031, and 0.056 for the first, second, and third QTL, respectively. As shown in Figure 6, the pattern of LR curves clearly showed that the use of 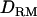 improved the mapping resolution more with higher
improved the mapping resolution more with higher 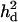 even when mapping simultaneously with other QTL. The LR value for the first QTL was the same for both models with and without
even when mapping simultaneously with other QTL. The LR value for the first QTL was the same for both models with and without 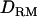 . However, the LR value with
. However, the LR value with 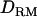 is higher for the second QTL and much higher for the third QTL.
is higher for the second QTL and much higher for the third QTL.
Figure 6.—
Likelihood ratio with or without 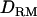 when simulating simultaneously with other multiple QTL with various
when simulating simultaneously with other multiple QTL with various 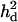 . Solid diamonds, LR without
. Solid diamonds, LR without 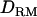 ; shaded boxes, LR with
; shaded boxes, LR with 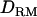 ; triangles, three true QTL positions.
; triangles, three true QTL positions.
The distribution of the estimated 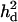 in replicates was upwardly skewed (Figure 7A), which caused overestimated
in replicates was upwardly skewed (Figure 7A), which caused overestimated 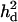 (Table 2). When the number of genotyped and phenotyped individuals used in the analysis increased to 1000, the upward bias was much reduced (Figure 7B). The mode of the distribution coincided with the true observed value for
(Table 2). When the number of genotyped and phenotyped individuals used in the analysis increased to 1000, the upward bias was much reduced (Figure 7B). The mode of the distribution coincided with the true observed value for 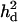 . Although the power to map the QTL on the correct position was high with a few hundred records, accurate estimation of variance parameters may require more numbers of records.
. Although the power to map the QTL on the correct position was high with a few hundred records, accurate estimation of variance parameters may require more numbers of records.
Figure 7.—
Distribution of estimated dominance ratio (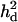 ) when using 200 individuals (A) or 1000 individuals (B) genotyped and phenotyped.
) when using 200 individuals (A) or 1000 individuals (B) genotyped and phenotyped.
Another reason for upward bias was probably because the dominance variances were estimated and averaged over for replicates where it was significant, which resulted in a truncated distribution of the estimation (Beavis 1994, 1998; Xu 2003). Bayesian model averaging (see Ball 2001; Sillanpaa and Corander 2002) could be used for this problem, which could reduce the upward bias of QTL effect estimates.
Inbreeding may produce a correlation between additive and dominance effects that was ignored in constructing the variance–covariance matrix (2). De Boer and Hoeschele (1993) reported that unbiased predictions of additive and dominance effects were obtained with only slightly reduced accuracies without considering the correlation between additive and dominance values even with highly inbred populations.
In this study, it was shown that LR values and mapping accuracy with using 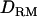 were significantly higher than those without using
were significantly higher than those without using 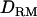 although the dominance variance was relatively small (
although the dominance variance was relatively small (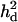 = 0.03–∼0.13). This implies that the proposed approach can be useful for economical traits in livestock populations where a significant proportion of genetic variation is caused by dominance effects (Gengler et al. 1997; Misztal et al. 1998). For mapping single-gene characteristics, e.g., a recessive disease gene, the proposed approach can also be an alternative to homozygosity mapping (Lander and Botstein 1987; Miano et al. 2000).
= 0.03–∼0.13). This implies that the proposed approach can be useful for economical traits in livestock populations where a significant proportion of genetic variation is caused by dominance effects (Gengler et al. 1997; Misztal et al. 1998). For mapping single-gene characteristics, e.g., a recessive disease gene, the proposed approach can also be an alternative to homozygosity mapping (Lander and Botstein 1987; Miano et al. 2000).
Acknowledgments
We are grateful for the comments from anonymous reviewers. This study was supported by Australian Wool Innovation, Sygen, and Sheep Genomics Australia.
References
- Almasy, L., and J. Blangero, 1998. Multipoint quantitative-trait linkage analysis in general pedigrees. Am. J. Hum. Genet. 62: 1198–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos, C. I., 1994. Robust variance components approach for assessing genetic linkage in pedigrees. Am. J. Hum. Genet. 54: 535–543. [PMC free article] [PubMed] [Google Scholar]
- Ball, R. D., 2001. Bayesian methods for quantitative trait loci mapping based on model selection: approximate analysis using the Bayesian information criterion. Genetics 159: 1351–1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beavis, W. D., 1994. The power and deceit of QTL experiments: lessons from comparative QTL studies. The Forty-Ninth Annual Corn & Sorghum Industry Research, Washington, DC, pp. 250–266.
- Beavis, W. D., 1998. QTL analyses: power, precision, and accuracy, pp. 145–162 in Molecular Dissection of Complex Traits, edited by A. H. Paterson. CRC Press, New York.
- Blangero, J., J. T. Williams and L. Almasy, 2000. Quantitative trait locus mapping using human pedigrees. Hum. Biol. 72: 35–62. [PubMed] [Google Scholar]
- Blott, S., J. J. Kim, S. Moisio, A. Schmidt-Kuntzel, A. Cornet et al., 2003. Molecular dissection of a quantitative trait locus: a phenylalanine-to-tyrosine substitution in the transmembrane domain of the bovine growth hormone receptor is associated with a major effect on milk yield and composition. Genetics 163: 253–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlborg, Ö., L. Andersson and B. P. Kinghorn, 2000. The use of a genetic algorithm for simultaneous mapping of multiple interacting quantitative trait loci. Genetics 155: 2003–2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dallas, J. F., 1992. Estimation of microsatellite mutation rates in recombinant inbred strains of mouse. Mamm. Genome 3: 452–456. [DOI] [PubMed] [Google Scholar]
- De Boer, I. J. M., and I. Hoeschele, 1993. Genetic evaluation methods for populations with dominance and inbreeding. Theor. Appl. Genet. 86: 245–258. [DOI] [PubMed] [Google Scholar]
- Ellegren, H., 1995. Mutation rates at porcine microsatellite loci. Mamm. Genome 6: 376–377. [DOI] [PubMed] [Google Scholar]
- Gengler, N., L. D. Van Vleck, M. D. MacNeil, I. Misztal and F. A. Pariacote, 1997. Influence of dominance relationships on the estimation of dominance variance with sire-dam subclass effects. J. Anim. Sci. 75: 2885–2891. [DOI] [PubMed] [Google Scholar]
- George, A. W., P. M. Visscher and C. S. Haley, 2000. Mapping quantitative trait loci in complex pedigrees: a two-step variance component approach. Genetics 156: 2081–2092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour, A. R., R. Thompson and B. R. Cullis, 1995. Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51: 1440–1450. [Google Scholar]
- Goddard, M. E., and T. H. E. Meuwissen, 2005. The use of linkage disequilibrium to map quantitative trait loci. Aust. J. Exp. Agric. 45: 837–845. [Google Scholar]
- Goldgar, D. E., 1990. Multipoint analysis of human quantitative genetic variation. Am. J. Hum. Genet. 47: 957–967. [PMC free article] [PubMed] [Google Scholar]
- Grignola, F. E., I. Hoeschele and B. Tier, 1996. Mapping quantitative trait loci in outcross populations via residual maximum likelihood. I. Methodology. Genet. Sel. Evol. 28: 479–490. [Google Scholar]
- Haley, C. S., 1999. Advances in quantitative trait locus mapping, pp. 47–59 in From J. L. Lush to Genomics: Visons For Animal Breeding and Genetics, edited by J. C. M. Dekkers, S. J. Lamont and M. F. Rothschild. Iowa State University, Ames, IA.
- Hayes, B. J., P. M. Visscher, H. C. McPartlan and M. E. Goddard, 2003. Novel multilocus measure of linkage disequilibrium to estimate past effective population size. Genome Res. 13: 635–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen, R. C., 1993. Interval mapping of multiple quantitative trait loci. Genetics 135: 205–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, D. L., and R. Thompson, 1995. Restricted maximum likelihood estimation of variance components for univariate animal models using sparse matrix techniques and average information. J. Dairy Sci. 78: 449–456. [Google Scholar]
- Lander, E. S., and D. Botstein, 1987. Homozygosity mapping: a way to map human recessive traits with the DNA of inbred children. Science 236: 1567–1570. [DOI] [PubMed] [Google Scholar]
- Lee, S. H., and J. H. J. van der Werf, 2006. An efficient variance component approach implementing an average information REML suitable for combined LD and linkage mapping with a general complex pedigree. Genet. Sel. Evol. 38: 25–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, S. H., J. H. van der Werf and B. Tier, 2005. Combining the meiosis Gibbs sampler with the random walk approach for linkage and association studies with a general complex pedigree and multimarker loci. Genetics 171: 2063–2072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Y., G. B. Jansen and C. Y. Lin, 2002. The covariance between relatives conditional on genetic markers. Genet. Sel. Evol. 34: 657–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacCluer, J. W., J. L. VanderBerg, B. Raed and O. A. Ryder, 1986. Pedigree analysis by computer simulation. Zoo Biol. 5: 147–160. [Google Scholar]
- Meuwissen, T. H. E., and M. E. Goddard, 2000. Fine mapping of quantitative trait loci using linkage disequilibria with closely linked marker loci. Genetics 155: 421–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., and M. E. Goddard, 2001. Prediction of identity by descent probabilities from marker-haplotypes. Genet. Sel. Evol. 33: 605–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., A. Karlsen, S. Lien, I. Olsaker and M. E. Goddard, 2002. Fine mapping of a quantitative trait locus for twinning rate using combined linkage and linkage disequilibrium mapping. Genetics 161: 373–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miano, M. G., S. G. Jacobson, A. Carothers, I. Hanson, P. Teague et al., 2000. Pitfalls in homozygosity mapping. Am. J. Hum. Genet. 67: 1348–1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misztal, I., L. Varona, M. Culbertson, J. K. Bertrand, J. Mabry et al., 1998. Studies on the value of incorporating the effect of dominance in genetic evaluations of dairy cattle, beef cattle and swine. Biotechnol. Agron. Soc. Environ. 2: 227–233. [Google Scholar]
- Mitchell, B. D., S. Ghosh, J. L. Schneider, G. Birznieks and J. Blangero, 1997. Power of variance component linkage analysis to detect epistasis. Genet. Epidemiol. 14: 1017–1022. [DOI] [PubMed] [Google Scholar]
- Morris, A. P., J. C. Whittaker and D. J. Balding, 2004. Little loss of information due to unknown phase for fine-scale linkage disequilibrium mapping with single-nucleotide-polymorphism genotype data. Am. J. Hum. Genet. 74: 945–953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Enciso, M., 2003. Fine mapping of complex trait genes combining pedigree and linkage disequilibrium information: a Bayesian unified framework. Genetics 163: 1497–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pong-Wong, R., A. W. George, J. A. Woolliams and C. S. Haley, 2001. A simple and rapid method for calculating identity-by-descent matrices using multiple markers. Genet. Sel. Evol. 33: 453–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SillanpÄÄ, M. J., and J. Corander, 2002. Model choice in gene mapping: what and why. Trends Genet. 18: 301–307. [DOI] [PubMed] [Google Scholar]
- Sobel, E., and K. Lange, 1996. Descent graphs in pedigree analysis: applications to haplotyping, location scores, and marker-sharing statistics. Am. J. Hum. Genet. 58: 1323–1337. [PMC free article] [PubMed] [Google Scholar]
- Sved, J. A., 1971. Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor. Popul. Biol. 2: 125–141. [DOI] [PubMed] [Google Scholar]
- Thompson, E. A., and S. C. Heath, 1999. Estimation of conditional multilocus gene identity among relatives, pp. 95–113 in Statistics in Molecular Biology and Genetics (IMS Lecture Notes), edited by F. Seillier-Moiseiwitsch. Institute of Mathematical Statistics, American Mathematical Society, Providence, RI.
- Tier, B., and J. Solkner, 1993. Analysing gametic variation with an animal model. Theor. Appl. Genet. 85: 868–872. [DOI] [PubMed] [Google Scholar]
- Van Arendonk, J. A., B. Tier, M. C. Bink and H. Bovenhuis, 1998. Restricted maximum likelihood analysis of linkage between genetic markers and quantitative trait loci for a granddaughter design. J. Dairy Sci. 81(Suppl. 2): 76–84. [DOI] [PubMed] [Google Scholar]
- Weber, J. L., and C. Wong, 1993. Mutation of human short tandem repeats. Hum. Mol. Genet. 2: 1123–1128. [DOI] [PubMed] [Google Scholar]
- Xu, S., 2003. Theoretical basis of the Beavis effect. Genetics 165: 2259–2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng, Z. B., 1993. Theoretical basis for separation of multiple linked gene effects in mapping quantitative trait loci. Proc. Natl. Acad. Sci. USA 90: 10972–10976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng, Z.-B., 1994. Precision mapping of quantitative trait loci. Genetics 136: 1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]









