Free-energy profiles for catalysis by dual-specificity phosphatases

Abstract

PTPs (protein tyrosine phosphatases) are fundamental enzymes for cell signalling and have been linked to the pathogenesis of several diseases, including cancer. Hence, PTPs are potential drug targets and inhibitors have been designed as possible therapeutic agents for Type II diabetes and obesity. However, a complete understanding of the detailed catalytic mechanism in PTPs is still lacking. Free-energy profiles, obtained by computer simulations of catalysis by a dual-specificity PTP, are shown in the present study and are used to shed light on the catalytic mechanism. A highly accurate hybrid potential of quantum mechanics/molecular mechanics calibrated specifically for PTP reactions was used. Reactions of alkyl and aryl substrates, with different protonation states and PTP active-site mutations, were simulated. Calculated reaction barriers agree well with experimental rate measurements. Results show the PTP substrate reacts as a bi-anion, with an ionized nucleophile. This protonation state has been a matter of debate in the literature. The inactivity of Cys→Ser active-site mutants is also not fully understood. It is shown that mutants are inactive because the serine nucleophile is protonated. Results also clarify the interpretation of experimental data, particularly kinetic isotope effects. The simulated mechanisms presented here are better examples of the catalysis carried out by PTPs.

INTRODUCTION

Protein phosphorylation plays a fundamental role in many cellular processes, such as signalling, growth, migration, proliferation, differentiation and death. PTPs (protein tyrosine phosphatases) counterbalance the effect of protein kinases by hydrolysing phosphotyrosine on other proteins, and hence, modulate the level of enzyme phosphorylation [1]. Perturbation of this balance is involved in the pathogenesis of cancer [2] and other diseases.

For example, binding of insulin to its membrane receptor activates the intrinsic tyrosine kinase activity, leading to phosphorylation of tyrosine residues on the insulin receptor and the insulin receptor substrate proteins. This signal is transduced by a cascade that stimulates glucose uptake in muscle and adipocytes. The insulin signal is negatively regulated by several PTPs. PTP1B is a key regulator of this cascade and dephosphorylates phosphotyrosine on the insulin receptor and the insulin receptor substrate proteins [3]. Hence, PTP1B has been extensively studied as a possible therapeutic target for the treatment of Type II diabetes and insulin resistance [4].

The PTP family includes tyrosine-specific or main group PTPs (such as PTP1B), LM-PTPs (low-molecular-mass PTPs) and DS-PTP (dual-specificity PTPs), which can also hydrolyse phosphoserine and phosphothreonine [5]. The first human DS-PTP identified, VHR (vaccinia VH1-related) phosphatase [6], regulates the action of MAPKs (mitogen-activated protein kinases) which mediate intracellular signalling events triggered by mitogens, growth factors and stress [7].

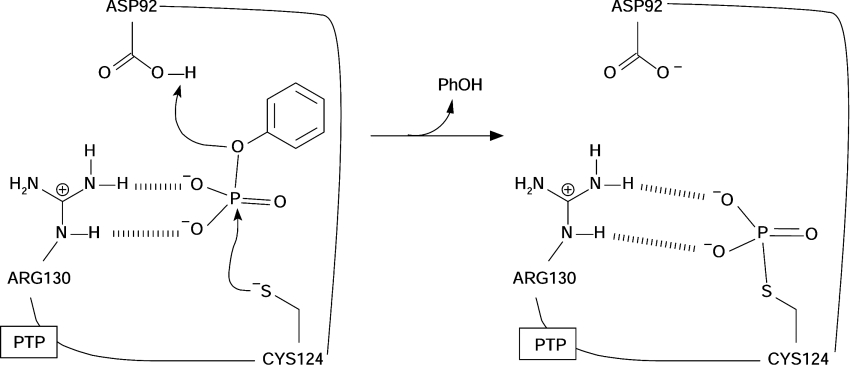
Although there is little similarity in their primary sequences, all PTPs share the same active site motif: Cys-Xaa₅-Arg-(Ser/Thr). Cys and Arg residues are strictly conserved and essential for catalysis, as is the presence of five unspecified residues in between (Xaa) [8,9]. This sequence is called the P-loop and corresponds to the binding site of the phosphorylated substrate. Main-chain hydrogens and the guanidinium group from the conserved Arg co-ordinate the substrate equatorial oxygens (Figure 1).

Figure 1. First reaction step of PTP catalysis.

The phenyl phosphate bi-anion represents the substrate. Residue numbering corresponds to the VHR PTP.

Tyrosine-specific PTPs and DS-PTPs have a similar tertiary structure [10]. The major structural difference is the active-site pocket, which is 3 Å (1 Å=0.1 nm) shallower in DS-PTPs. This is the suggested reason for selectivity in tyrosine-specific PTPs [11]. LM-PTPs, on the other hand, have different tertiary structure and lack a His residue in the P-loop [10].

Catalysis by PTPs proceeds via two uncoupled reactions [12,13]. First, the P-loop Cys side chain performs a nucleophilic attack toward the phosphorylated substrate, with a H⁺ transfer from a general acid (Asp) to the leaving group. A thiophosphorylated PTP intermediate is formed and substrate is dephosphorylated (Figure 1). The PTP intermediate is hydrolysed and free enzyme is regenerated in the second reaction [10]. Although a substantial body of experiments support this reaction mechanism [5,10], questions still remian with regards to the first step.

The usual interpretation of pH versus k_cat/K_m (or k_cat) [14,15] profiles, enzyme inactivation with iodoacetate [10], linear free-energy relationships [13] and KIEs (kinetic isotope effects) [16] assigns a bi-anionic state to the substrate, an ionized (Cys) nucleophile and a protonated (Asp) general acid, as shown in Figure 1. However, this interpretation has been challenged by Kolmodin and Åqvist [17,18]. On the basis of results from computer simulations with a LM-PTP, these authors [17,18] proposed that the reagent substrate is a mono-anion (mono-protonated).

The inactivity of PTP active-site Cys→Ser mutants [9,19] is also not clearly understood. This mutation corresponds to a simple sulfur-to-oxygen substitution in the nucleophile, and inactivates the enzyme. This strongly contrasts with the reactivity of phosphate esters in solution, where reaction with nucleophiles, centred by oxygen (as in the mutant), is 10⁷-fold faster than with nucleophiles centred with sulfur [as in the WT (wild-type enzyme)] [20]. Different explanations for mutant inactivity have been suggested, including structural alterations in the mutant [21–23], increased distance between nucleophile and substrate [22] and nucleophile protonation [23].

Given their importance in cellular signalling and potential as drug targets [4,5], understanding the details about the species and mechanisms involved in catalysis by PTPs is invaluable. In the present study, free-energy profiles obtained from computer simulation of reactions catalysed by the DS-PTP VHR are used to determine the protonation state of reagent groups and to investigate the inactivity in Cys→Ser mutants. An accurate hybrid potential, with specific parameters to simulate reactions in PTPs [24], was used in the computations.

The remainder of the present study is organized as follows. Procedures to set up enzyme models and obtain free-energy profiles are presented in the Experimental section. In the Results section, free-energy profiles for catalysis by DS-PTPs are shown for the first time. The reactions of phenyl phosphate with VHR WT and C124S mutant in different protonation states were simulated. Profiles for reactions of phenyl phosphate bi-anion with a PTP lacking the general acid, and dephosphorylation of an alkyl phosphate catalysed by WT PTP, are also shown. In the Discussion, the calculated results are compared with experimental measurements and the catalytic mechanism is analysed, and then answers to the two questions presented above are given. Previous computational studies are also discussed.

EXPERIMENTAL

The development and performance of the calibrated hybrid potential used here have been discussed in detail previously [24]. The procedures to set up simulations and to obtain free-energy profiles used here are standard ones, and details of references are given below.

Preparation of macromolecular models

Coordinates of the complex between VHR and Hepes were retrieved from the Protein DataBank (accession code 1VHR) [6] by Dillet et al. [25]. These authors [25] deleted all crystallographic water molecules and ions, built hydrogen atoms and substituted Hepes with phenyl phosphate bi-anion in the VHR structure chain A. Arg, Lys and His side chains were modelled in protonated form, in accordance with other PTP simulations [17,26,27]. Glu and Asp side chains were deprotonated, except for Asp⁹². Coordinates of this complex between VHR and phenyl phosphate are available for use (see [25]) and were used in the present study.

The protein complex was superimposed on to a pre-equilibrated cubic water box with dimensions of 55.92 Å, and 5832 water molecules. The complex was centralized in the solvent box and all water molecules located less than 2.8 Å from a non-hydrogen atom of the complex were deleted. Unfavourable contacts were relaxed in a short (2 ps) molecular dynamics run. This superposition and relaxation process was repeated until no more water molecules could be inserted [28,29]. The final macromolecular complex contained 17197 atoms, with 178 protein residues, one substrate and 4804 water molecules. This solvated complex was equilibrated to 300 K by Langevin molecular dynamics runs (40 ps in total) following standard procedures [28,29].

The OPLS-AA [30] force field was used to describe the protein, and the TIP3P [31] model was used for water. Atomic charges, Lennard–Jones and covalent parameters for phosphate phosphorus and oxygen were taken from the AMBER [32] force field, as discussed previously [24,33].

Positions of atoms located at more than 14 Å from the phenyl phosphate phosphorus atom were stationary and did not move in the calculation of free-energy profiles. However, all interactions between movable and frozen atoms were normally included. This procedure was also used in simulations of PTPs [17,18,26] and other enzymes [28,29], because it reduces computational costs.

The final solvated protein complex was used in the simulation of PhOPO₃²⁻ (where Ph indicates phenyl) reaction catalysed by WT VHR. The simulations with the C124S mutant used this starting structure, with oxygen substituted only in place of sulfur in Cys¹²⁴. The reactions of PhOPO₃H⁻ or the protonated nucleophile also used this structure, with a hydrogen attached to one of the phosphate oxygens or the nucleophile respectively. Reactions with the D92A mutant and the CH₃OPO₃²⁻ substrate were additionally equilibrated by molecular dynamics (3 ps), after the mutation or the alkyl substrate respectively were introduced.

Hybrid potential and free-energy profiles

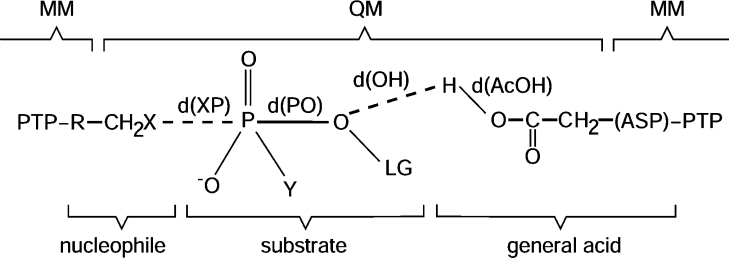
The hybrid QM/MM (quantum mechanical/molecular mechanical) potential used here employs a semi-empirical description of the QM region and a link-atom approach to cope with the covalent frontier between the QM and MM regions [34,35]. This approach has been used successfully in many studies of enzymatic reactivity [36]. The QM semi-empirical Hamiltonian, called MNDO+G/CHOPS [24], was calibrated specifically to thiolysis and alcoholysis of phosphate esters and for H⁺-transfer model reactions relevant to the chemistry of PTPs and their mutants. In comparison with high-level ab initio electronic structure calculations [MP2/6-311+G(2df,2p)] [37], the MNDO+G/CHOPS Hamiltonian has an accuracy of 2 kcal/mol (1 cal≈4.184 J) for reactions involving phosphate monoesters and of 3 kcal/mol for H⁺ transfers [24]. This is an excellent accuracy for studies of enzyme reactivity. QM and MM regions were defined according to Figure 2. The nucleophile (Cys¹²⁴ or Ser¹²⁴ in the mutant) side chain, substrate (modelled as PhOPO₃²⁻, PhOPO₃H⁻ or CH₃OPO₃²⁻), and general acid (Asp⁹²) side chain were represented in the QM region (Ala was in the MM region in the D92A mutant simulation). The rest of the protein and solvent were represented in the MM region. The covalent frontier between the QM and MM regions was defined as the C_α–C_β bond in the nucleophile and in the general acid (Figure 2). Hydrogen link atoms were used to saturate the valency in the QM region [34,35]. The OPLS-AA force field was used for the protein, and the TIP3P potential was used for water. Lennard–Jones parameters for the QM atoms were taken from the OPLS-AA and AMBER (for phosphate oxygens and phosphorus) force fields [24]. All molecular dynamics followed a velocity Verlet–Langevin algorithm [38]. A time step τ=1 fs and a friction coefficient γ=10 ps⁻¹ were used. An atom-based force-switching truncation scheme was used in the non-bonding interactions with r_on=10 Å and r_off=13 Å for both MM and QM/MM interactions [35]. Tests in other systems indicated that results obtained within this scheme are equivalent to results obtained without truncation [28,29]. The free-energy profiles are the potentials of mean force calculated along a reaction coordinate, ξ. Sampling along the reaction coordinate was enhanced with a harmonic umbrella potential [39]. Reference values ξ_i were equally spaced at 0.10 Å and a constant k_umb(=1500 kJ·mol⁻¹·Å⁻²), was used. The reaction coordinate was defined as the difference between the breaking and the forming bonds to phosphorus, ξ=d(PO)−d(XP) (Figure 2). This choice does not alter the associative or dissociative character of the mechanism [26]. Molecular dynamics runs with 4 ps of equilibration and 10 ps of data collection for each reference window ξ_i started from the protein complex described above. The reaction coordinate from reagents to products was covered by varying ξ_i. Potentials of mean force were finally calculated by the WHAM method [39] from the ξ occurrence collected during the molecular dynamic simulations. This procedure has been described in more detail previously [28,29]. All simulations, molecular dynamics and free-energy determinations in the present study were obtained with the DYNAMO library [35].

Figure 2. QM and MM regions used in the simulations.

See Table 1 for a list of the groups used in each simulation. Ac, acetyl.

RESULTS

There is considerable experimental evidence (e.g. steady-state kinetic measurements [10], ³¹P-NMR [13]) suggesting the two catalytic reactions in PTPs are uncoupled. Hence, only the first step of catalysis was simulated in the present study, as it is sufficient to answer the two questions asked in the Introduction.

In the following, MCs (Michaelis complexes) or reagents correspond to free-energy minima located in the left-hand region of the profiles, with ξ<0. MC also represent the zero values for relative free energy. Product complexes are located in the right-hand region (ξ>0) of the profiles (not shown for all profiles). TS (transition state) values are the maxima in the profiles between MC and product. Distances between centres are referred to as d(ZW), according to Figure 2.

WT VHR

PhOPO₃²⁻ as substrate

For the reaction of PhOPO₃²⁻ catalysed by WT VHR, equatorial phosphate oxygens form hydrogen bonds with the Arg¹³⁰ side chain and the protein backbone along all the reaction coordinate. The leaving group is protonated by Asp⁹² in the TS region, and the reaction product is the thiophosphorylated VHR, with Asp⁹² deprotonated and phenol complexed to the active site. Mean distances between relevant atoms in the MC, product complex and TS calculated from the molecular dynamic trajectories are shown in Table 2.

Table 2. Calculated mean distances for the reaction of PhOPO²⁻₃ catalysed by WT VHR.

Distances and S.D. are in Å. HN is a protein backbone hydrogen bonded to the amino acid shown in parentheses, and HO is the hydrogen bonded to a side-chain oxygen. See Figure 3 for the other definitions. Values were calculated by analysis of the trajectories accumulated over 10 ps. Distances were evaluated in intervals of 20 fs (i.e. 500 distance values were accumulated). Trajectories corresponded to the window with ξ_i=−1.8 Å for the MC and ξ_i=2.25 Å for the products. For the TS, windows with ξ_i=−0.3 and ξ_i=−0.4 Å were evaluated (therefore 1000 values of distance were accumulated).

Centres		MC	TS	Products
S (Cys124)	P (PhOP2−)	3.58±0.05	2.74±0.10	2.20±0.05
S (Cys124)	HN (SER131)	2.26±0.16	2.50±0.21	2.69±0.24
S (Cys124)	HO (SER131)	1.95±0.09	2.02±0.11	2.14±0.14
O1 (PhOP2−)	P (PhOP2−)	1.77±0.04	2.40±0.14	4.45±0.06
O2 (PhOP2−)	P (PhOP2−)	1.54±0.02	1.52±0.02	1.54±0.02
O3 (PhOP2−)	P (PhOP2−)	1.53±0.02	1.51±0.02	1.53±0.02
O4 (PhOP2−)	P (PhOP2−)	1.55±0.02	1.52±0.02	1.53±0.02
OH (Asp92)	HO (Asp92)	0.99±0.02	1.57±0.62	4.34±0.33
O1 (PhOP2−)	HO (Asp92)	4.09±0.05	2.46±1.48	0.98±0.02
O2 (PhOP2−)	HN2 (Arg130)	3.18±0.13	1.75±0.24	1.63±0.10
O2 (PhOP2−)	HN (Glu126)	2.16±0.21	2.21±0.22	2.67±0.21
O2 (PhOP2−)	HN (Arg125)	1.90±0.13	1.79±0.13	1.89±0.15
O3 (PhOP2−)	HN (Arg130)	2.47±0.22	1.98±0.16	1.84±0.13
O3 (PhOP2−)	HN1 (Arg130)	1.67±0.11	1.65±0.10	1.65±0.10
O4 (PhOP2−)	HN (Ser129)	1.95±0.17	1.88±0.16	1.77±0.12
O4 (PhOP2−)	HN (Tyr128)	2.28±0.23	2.12±0.24	1.91±0.16

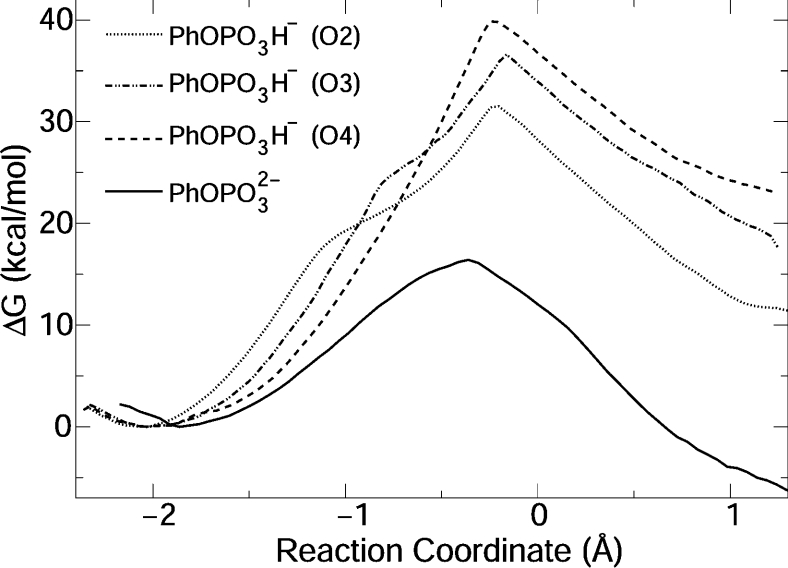
The free-energy profile for the reaction is shown in Figure 4. The calculated barrier, 16.4 kcal/mol, is remarkably similar to the experimental value, 15.5 kcal/mol, obtained by applying transition-state theory [6,40] to the measured rate constant (k₂) [24,41]. The reaction free energy is negative, indicating a thermodynamically favourable process. Unfortunately, no experimental measurements of reaction free energy are available for this reaction.

Figure 4. Free-energy profiles for catalysis by WT VHR.

O2, O3 and O4 indicate which phosphate oxygen was protonated. See Figure 3 for atom numbering.

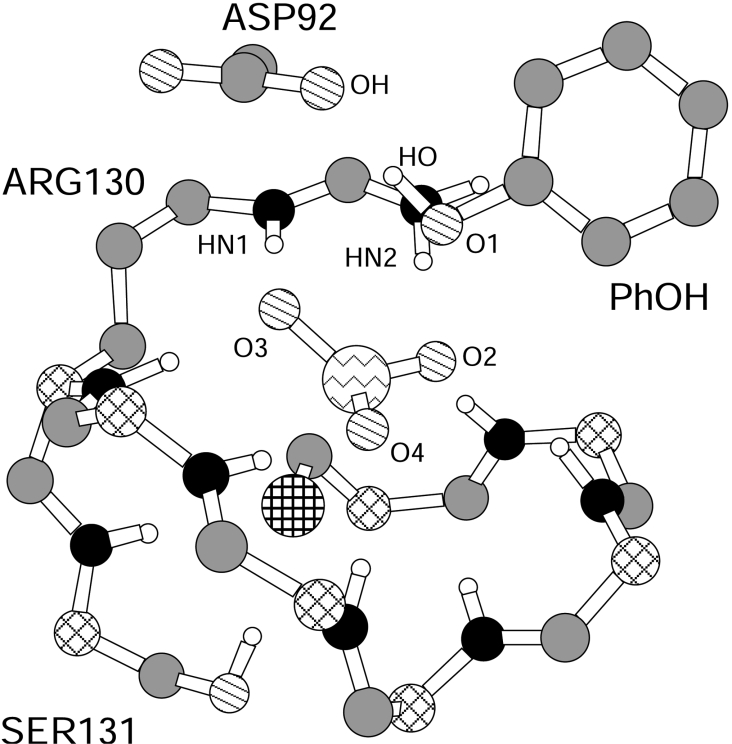
The simulated mechanism is A_nD_n that has a dissociative TS, with a metaphosphate-like character. The TS structure is a trigonal bi-pyramid with the sulfur of Cys¹²⁴ and leaving-group oxygen (O1) in axial positions (the S–P–O1 angle is 168.3±4.4°). The P–O bond is largely broken and little S–P bond is formed. Non-ligand phosphate oxygens (O2, O3 and O4, Figure 3) are equatorial and approximately co-planar with phosphorus. Mean±S.D. values of d(OH) and d(AcOH) (Figure 2) indicate that the H⁺ of Asp⁹² is transferred on to the leaving group in the TS region (Table 2). The H⁺ transfer occurs spontaneously during the molecular dynamics, without the addition of Asp⁹² H⁺ coordinates to the reaction coordinate. A configuration snapshot from the molecular dynamics simulation in the TS region after H⁺ is transferred on to the leaving group is shown in Figure 3.

Figure 3. Molecular dynamics snapshot of the VHR active site in the TS region for reaction of PhOPO₃²⁻.

Part of the protein and substrate were deleted for ease of visualization. H, white; C, grey; C_α, diagonal crossed lines; N, black; O, diagonal lines; P, jagged lines; S, horizontal and vertical crossed lines.

PhOPO₃H⁻ as substrate

Three free-energy profiles were obtained for reaction of mono-anionic substrate by protonating each of the three equatorial phosphate oxygens (Figure 4). These oxygens are non-equivalent, because they have different coordinations to the P-loop.

Reaction of PhOPO₃²⁻ with protonated Cys¹²⁴ was also simulated. However, during equilibration of the initial configuration (MC region), H⁺ is spontaneously transferred from the Cys¹²⁴ to O2 phosphate oxygen, and the free-energy profile obtained is equivalent to PhOPO₃H⁻ reaction with O2 initially protonated (Figure 4).

Hydrogen bonds are formed between the phosphate oxygens and the protein backbone and Arg¹³⁰ side chain in the MCs. For the reaction of PhOPO₃H⁻ with protonated O2 and O3, the phosphate acidic hydrogen is initially coordinated to the sulfur of Cys¹²⁴. For −1.1<ξ<−0.8 Å, this acidic hydrogen rotates towards the leaving group, resulting in the profile inflexion observed around these reaction coordinates (Figure 4). Product complexes for PhOPO₃H⁻ also differ; for the reaction of PhOPO₃H⁻ with protonated O2 or O3, VHR is thiophosphorylated, Asp⁹² is protonated and phenol is complexed to the active site. H⁺ was transferred on to phenol from the protonated phosphate oxygen. For PhOPO₃H⁻ with O4 protonated, H⁺ is transferred from Asp⁹² on to phenoxide, the thiophosphorylated VHR is protonated and Asp⁹² is ionized.

For the TS region in the three reactions, the P–O bond distances are 2.1–2.3 Å, and the S–P bond distances are 2.3–2.6 Å. These distances still characterize a very loose TS, but slightly less dissociative than the bi-anion TS. The simulated mechanisms are A_nD_n. Free-energy barriers are 15 to 25 kcal/mol higher than the barrier observed experimentally (see above).

CH₃OPO₃²⁻ as substrate

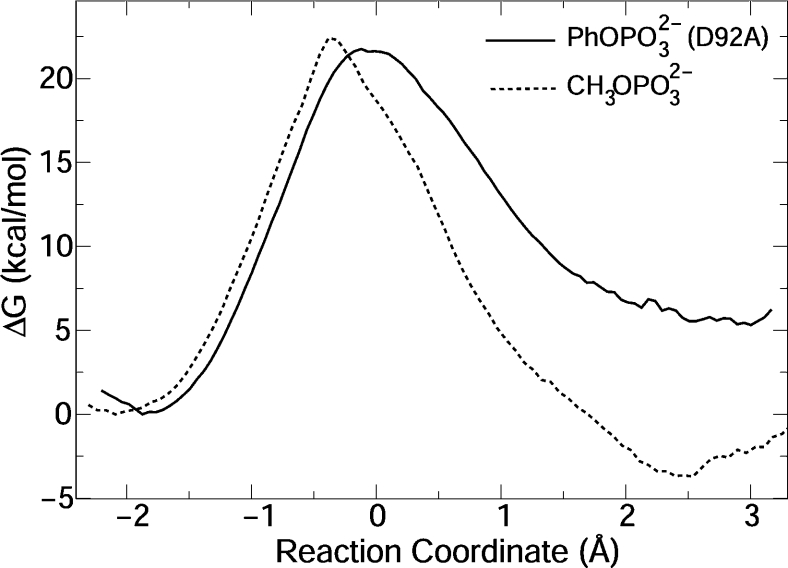
The structures of the MC, product complex and TS for the reaction of the methylphosphate bi-anion are similar to the structures observed for the reaction of PhOPO₃²⁻ (see above). The reaction mechanism is A_nD_n. The TS is dissociative with large P–O and S–P distances. H⁺ is transferred spontaneously from Asp⁹² to the methoxy leaving group in the TS region.

The free-energy profile is shown in Figure 5, with a calculated barrier height of 22.4 kcal/mol. The profile shape is also similar to the one obtained for the PhOPO₃²⁻ reaction (Figure 4). Experimental data for reaction of methyl phosphate catalysed by PTPs are not available. However, a rate constant of k₂=0.16 s⁻¹ is obtained from the measured k_cat (k_cat=k₂·k₃/k₂+k₃) for the dephosphorylation of phosphoserine catalysed by VHR [41]. This rate constant corresponds to a barrier of 18.7 kcal/mol.

Figure 5. Free-energy profiles for reaction of PhOPO²⁻₃ catalysed by VHR D92A mutant, and for CH₃OPO²⁻₃ catalysed by WT VHR.

D92A mutant

Only small structural alterations are observed for the MC in the reaction of PhOPO₃²⁻ catalysed by the VHR D92A mutant. The main difference to the WT reaction is the product complex comprises phenoxide complexed with a water molecule and the Arg¹³⁰ side chain. In the TS, distances between phosphorus and equatorial oxygens are 1.52±0.03 Å, d(SP)=2.53±0.09 Å and d(PO)=2.41±0.10 Å. The reaction free energy is positive and 15 kcal/mol higher than the one observed for catalysis by the WT enzyme. The reaction mechanism is A_nD_n, with slightly more bond formation to the nucleophile in the TS.

The calculated reaction barrier is 21.8 kcal/mol. Catalysis by the VHR D92N mutant (where general acid catalysis is not operating) has been measured as k_cat=2×10⁻³ s⁻¹ [13]. The absence of general acid catalysis in various PTPs results in a decrease of 10⁴-fold and 40-fold in k₂ and k₃ respectively [42]. Hence, k₂≪k₃ and k_cat≈k₂, thus the experimental barrier, 21.3 kcal/mol, can be obtained from the above k_cat.

C124S mutant

Catalysis by VHR C124S mutant was studied in different protonation states of substrate and serine nucleophile.

The MC for reaction of PhOPO₃²⁻ with ionized or protonated serine is similar to the WT complex, with the same hydrogen-bond pattern.

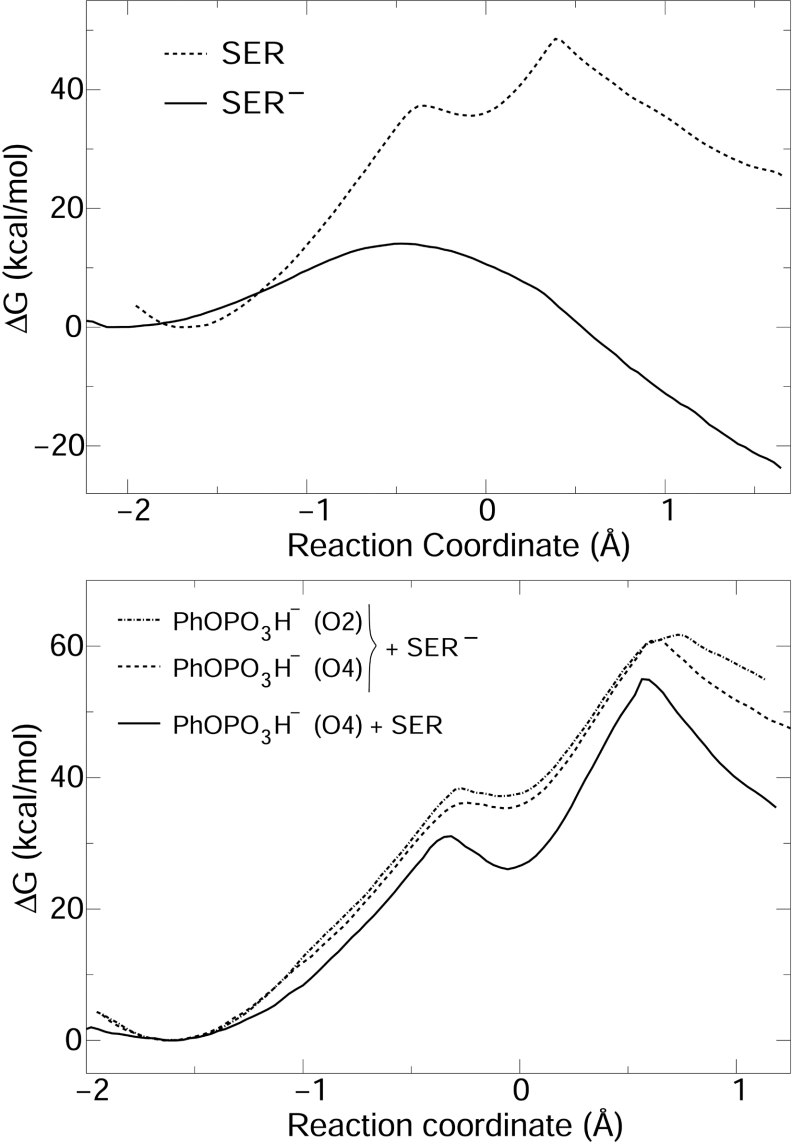
For ionized serine (Ser⁻, Figure 6), phenoxide is not protonated in the product. Asp⁹² is neutral and Ser¹²⁴ is phosphorylated. Hence, no H⁺ transfer was observed. A relatively associative TS is obtained, with d(OP)=2.37±0.07 Å for the nucleophile and d(PO)=1.90±0.06 Å for the leaving group. The reaction mechanism is A_nD_n and the free-energy profile is flat in the TS region. The reaction barrier is 14.1 kcal/mol, indicating the mutant would be active if Ser¹²⁴ is ionized and substrate is a bi-anion.

Figure 6. Free-energy profiles for reaction of PhOPO₃²⁻ (upper panel) and PhOPO₃H⁻ (lower panel) catalysed by VHR C124S mutant with the serine protonated (SER) or ionized (SER⁻).

For protonated serine (Ser, Figure 6), the hydrogen (Hδ) bound to Ser¹²⁴ O_γ is close to the equatorial phosphate oxygen O2 in the MC. At ξ∼−0.1, a pentacoordinated phosphorane is formed. This species is unstable, since decomposition in the reagent direction has a barrier smaller than 2 kcal/mol. The high energy TS is observed in ξ=0.4, with d(PO)=1.96±0.05 Å for the leaving group and d(OP)=1.69±0.03 Å for the nucleophile. Phenoxide is protonated by a H⁺ transferred from Ser¹²⁴ via phosphate oxygen O2. The mechanism is A_n*D_n with a late and associative TS. Bonding between serine nucleophile and phosphate substrate is largely complete in the TS and little bond fission is observed for the leaving group. The barrier height is 48 kcal/mol, indicating that no catalysis would be seen if Ser¹²⁴ is protonated.

Catalysis of PhOPO₃H⁻ reaction with either ionized or protonated serine presents barriers higher than 40 kcal/mol (Figure 6). The reaction mechanism is more associative, but the penta-coordinate intermediate is not stable for reactions with the ionized serine. For the protonated nucleophile, a trigonal bipyramidal intermediate is stable, but the barrier for its formation is higher than 30 kcal/mol.

DISCUSSION

Accordingly to titration experiments for various PTPs, the Cys nucleophile has a pK_a ranging from 4.7 in tyrosine-specific (Yersinia) PTPs, 5.5 in VHR to 6.75 in LM-PTP [10,18]. The MC at neutral pH corresponds to a state with deprotonated Cys nucleophile, protonated side chain for Asp general acid (Asp⁹² in VHR) and bi-anionic substrate [10]. This is exactly the protonation state found for the MC in the simulation which starts from PhOPO₃²⁻ and ionized Cys¹²⁴ (see above). Note that no constraints were imposed in the coordinates of the acidic hydrogen in our simulations. Hence, H⁺ rearrangements would be seen spontaneously if another protonation state were more stable.

KIE has been used to probe the TS structure of phosphate ester reactions [16,43]. KIEs are usually measured with p-nitrophenyl phosphate as a substrate model. The effect relative to the nitrogen position [¹⁵(V/K)] is unity for reaction catalysed by WT VHR [16], and is taken as evidence for leaving group protonation in the TS region of the rate-limiting step. This is indeed what is obtained for simulation of PhOPO₃²⁻ dephosphorylation by WT VHR. The effect relative to the ligand phosphate oxygen [¹⁸(V/K)_bridge=1.0118−1.0152 for reaction catalysed by different PTPs, including VHR] [16] is evidence for the substantial fission of the P–O bond and complete protonation of the leaving group in the TS. In the TS region for the PhOPO₃²⁻ simulation, H⁺ is transferred on to the leaving group and the P–O bond is 0.6 Å larger than the reagent P–O bond distance (Table 2), consistent with both experimental inferences. The effect relative to the equatorial phosphate oxygen [¹⁸(V/K)_non-bridge] measured for VHR catalysis is also unity [16]. The interpretation agrees with simulation results that show a dissociative, metaphosphate character to the TS for the reaction of PhOPO₃²⁻.

Values for ¹⁵(V/K) and ¹⁸(V/K)_bridge are higher than unity for catalysis by the VHR mutant lacking the general acid. This was credited to the non-existence of H⁺ transfer to the leaving group and to a possible alteration of the leaving group P–O bond order in the TS [16]. The P–O bond distance in the simulated TS is similar for dephosphorylation of PhOPO₃²⁻ by the D92A mutant and WT VHR, indicating the lack of protonation does not change the bond order. Two different interpretations were given to ¹⁸(V/K)_non-bridge>1 measured for catalysis by D92N VHR mutants. Initially, the increase in KIE was attributed to electrostatic interactions between the equatorial phosphate oxygens and the P-loop, particularly the Arg¹³⁰ side chain [43]. Later, the increase was attributed to ‘the TS assuming a somewhat larger degree of nucleophilic participation’ [16]. Comparison of S–P bond distances in the TS region for dephosphorylation of PhOPO₃²⁻ by VHR D92A and WT shows the P–S bond is 0.2 Å smaller in the mutant, corresponding to a more participative nucleophile in the TS.

Previous computational studies have addressed catalysis by PTPs. Based on energy minimizations with a QM/MM hybrid potential employing the PM3 semi-empirical Hamiltonian [44], Hart et al. [45] suggested H⁺ would be transferred from the general acid Asp on to the substrate phosphate in the MC of a PTP. Unfortunately, the PM3 Hamiltonian describes reaction energies for a series of model H⁺ transfers relevant to PTPs with an RMSD (root mean squared deviation) and a maximum error of 17 kcal/mol and 29 kcal/mol respectively in comparison with an initial reference [24].

Free-energy barriers calculated by Alhambra et al. [26] with a QM/MM hybrid potential for PhOPO₃²⁻ and PhOPO₃H⁻ dephosphorylation catalysed by a LM-PTP were 14 and 16 kcal/mol respectively. These numbers are within 2 kcal/mol of the experimental value (14.3 kcal/mol) [26], and suggest the mono-anion reaction would be competitive with the bi-anion. In comparison with the same ab initio reference [24], model H⁺-transfer energies obtained with the QM Hamiltonian employed by Gao et al. [26] (a mixture of MNDO and AM1 parameters) have a RMSD and maximum error of 10 and 14 kcal/mol respectively. Reaction energies and barriers for various model thiolysis of phosphate esters have an RMSD and maximum error of 15 and 28 kcal/mol [24]. In disagreement with the present understanding of PTP reaction mechanisms, H⁺ transfer on to the leaving group was not observed and an associative mechanism was obtained [26].

The main computational evidence supporting the fact that the substrate reacts as a mono-anion was presented by Kolmodin and Åqvist [17,18]. Calculated free-energy barriers for dephosphorylation of PhOPO₃²⁻ and PhOPO₃H⁻ catalysed by the same LM-PTP used by Gao et al. [26] were 14 kcal/mol for both substrates. However, the estimated binding energy for mono-anion was 16 kcal/mol lower than the binding energy of the bi-anion. Hence, only the mono-anion reaction was suggested to be observed [17]. The performance of the empirical valence bond method [46] used by the authors to calculate the free energies [17] depends heavily on a parameterization that uses experimental reaction free energies and barriers for non-catalysed reactions in water as models for enzyme reaction. However, there are no kinetic or thermodynamic measurements for thiolysis of phosphate monoesters in aqueous solution. Thus several approximations and data from other reactions were used to indirectly estimate free energies in aqueous solution. For instance, a barrier of 22 kcal/mol was given for thiolysis of phenyl phosphate in water [17]. This is clearly a large underestimation, because this reaction is not observed in solution and other studies indicate this barrier should be higher than 35 kcal/mol [37,47].

Density functional calculations by Bashford et al. [27] gave barriers of 9 and 22 kcal/mol for dephosphorylation of PhOPO₃²⁻ and PhOPO₃H⁻ respectively catalysed by the same LM-PTP. Inclusion of vibrational effects (neglected in their calculations) would lower both barriers by 1.5 kcal/mol [27]. Hence, the calculated barriers for both substrates disagree by approx. 6.5 kcal/mol of the experimental value and no solid conclusion can be obtained about the substrate protonation state.

In summary, previous computational studies of catalysis by PTPs were either obtained with inaccurate hybrid potentials or present large deviations from experimental observations. Thus these computational results should be taken with caution.

The mean barrier obtained in the present study for the three reactions of PhOPO₃H⁻ catalysed by the WT VHR (Figure 4) is 36.0±3.7 kcal/mol. The uncertainty is the standard deviation from the three barriers obtained. This barrier is 20 kcal/mol higher than the experimental value, indicating that VHR does not dephosphorylate mono-anions of phosphate monoesters.

Barriers calculated in the present study for PhOPO²⁻₃ dephosphorylation by WT and D92A VHR, and dephosphorylation of CH₃OPO₃²⁻ by WT VHR agree within 0.9, 0.5 and 3.7 kcal/mol respectively with the experimental measurements. Simulated reaction mechanisms and structures of the TS also agree with usual interpretations of KIE and pH-versus-rate profiles. Thus the PTP substrate is a bi-anion and the enzyme nucleophile is ionized.

Inspection of the TS structure and of relevant distances in the VHR active site (Table 2) suggests how the substrate dephosphorylation is catalysed. The equatorial oxygens O3 and O4 form two hydrogen bonds each and O2 forms three H-bonds with backbone hydrogens (HN) and Arg¹³⁰ side chain hydrogens. H-bond distances in the TS region approach equilibrium distances seen in model complexes [24], suggesting that stabilization provided by such interactions is maximum in the TS. Electrostatic interaction between substrate bi-anion and Arg¹³⁰ cationic side chain is also very important for TS stabilization [10]. The general acid catalysis contribution to TS stabilization is approx. 5 kcal/mol, because an increase in reaction barriers of the same magnitude is observed in experiments and simulations lacking the general acid.

Zhang [5] stated that ‘PTPs do not alter the TS to phosphate ester hydrolysis and their catalytic efficiency is achieved by stabilization of the TS for the reaction in solution’ and the following comments can be made about this statement. Catalysis by PTPs proceeds in two uncoupled reactions: thiolysis of phosphate ester (Figure 1), and hydrolysis of thiophosphate ester. Comparisons between TSs attained in solution and in PTP active sites should be done by an appropriate thermodynamic cycle, with the TS of thiolysis, and not hydrolysis, in solution. However, thiolysis of phosphate monoesters is not observed in solution [37].

Free-energy profiles calculated for the VHR C124S mutant in different protonation states (see above) indicate that reaction would be observed if Ser¹²⁴ side chain and substrate (PhOPO₃²⁻) were ionized. No activity is observed experimentally for PTP Cys→Ser mutants [9,19], hence, this is not the protonation state observed. Profiles obtained with protonated substrate (PhOPO₃H⁻), with Ser¹²⁴ protonated, or with both species protonated, show barriers higher than 40 kcal/mol. Thus the mutant is inactive, because at least one H⁺ is in excess. The C124S mutation should not alter the substrate protonation state, because mutants retain the capacity to bind substrates with binding energies very close to those observed for WT PTPs [48]. Therefore, Cys→Ser PTP mutants are inactive, because the nucleophile Ser is protonated in the mutant and reactions with the protonated nucleophile have very high activation barriers.

Based on fluorescence [22] and X-ray [21] measurements, it was argued that structural alterations observed in PTP Cys→Ser mutants would inactivate the enzyme. Zhang and Wu [22] also argue that fluorescence in the WT enzyme maybe selectively extinguished by the active site Cys, and such effect would not be seen in the mutant. The simulations presented here show very small structural alterations in the active site between the WT and the C124S VHR mutant. Comparison of hydrogen bond distances between phosphate oxygens and P-loop backbone hydrogens (data shown only for reaction of PhOPO₃²⁻ with WT VHR, Table 2) indicates that hydrogen bonds present in MC and TS regions are the same for mutant and WT VHR.

Although the C–O and O–P bond lengths in the C124S mutant are shorter than the corresponding C–S and S–P bond lengths in the WT VHR, dephosphorylation would occur if Ser¹²⁴ were ionized. Hence, the phosphate group has enough mobility in the P-loop to be attacked by an ionized Ser¹²⁴ nucleophile, even if O_γ is not optimally located [22,23].

Mutant inactivity is not related to a possible change in nucleophilicity [43], because reaction proceeds with comparable barriers (independent of substrate protonation) if the nucleophile is ionized for both WT and C124S VHR forms.

CONCLUSIONS

Computer simulations of the first catalytic step by DS-PTPs (Figure 1) obtained with a calibrated hybrid potential were presented.

In the WT VHR, the reaction mechanism is A_nD_n with a dissociative TS. Free-energy barriers calculated for reaction of phenyl phosphate catalysed by WT and D92A VHR mutant are within 1 kcal/mol of the experimental value. The barrier for methyl phosphate reaction catalysed by WT VHR is within 4 kcal/mol of the experimental value. This is a very good precision for different substrates, enzyme forms and catalytic mechanisms, and reflects the accuracy of the calibrated hybrid potential used [24].

The results of the present study clarify the interpretation of KIE measurements and pH versus rate profiles, agree with a large body of experimental evidence and support the fact that the substrate reacts as a bi-anion, the nucleophile (Cys¹²⁴ in VHR) is ionized, and the general acid (Asp⁹² in VHR) is protonated.

Free-energy profiles for the inactive VHR C124S mutant were also obtained. The mutant would catalyse substrate dephosphorylation only if the Ser¹²⁴ nucleophile were ionized and the substrate were a bi-anion. PTP Cys→Ser mutants are inactive because the Ser nucleophile is protonated.

Table 1. Definition of groups used in the evaluated free-energy profiles accordingly to Figure 2.

LG, leaving group.

Simulation	X	Y	LG
1	S−	O−	Ph
2	S−	OH	Ph
3	SH	O−	Ph
4	S−	O−	CH3
5	O−	O−	Ph
6	O−	OH	Ph
7	OH	O−	Ph
8	OH	OH	Ph