Abstract
Molecular surveys suggest that communities of microbial eukaryotes are remarkably rich, because even large clone libraries seem to capture only a minority of species. This provides a qualitative picture of protistan richness but does not measure its real extent either locally or globally. Statistical analysis can estimate a community's richness, but the specific methods used to date are not always well grounded in statistical theory. Here we study a large protistan molecular survey from an anoxic water column in the Cariaco Basin (Caribbean Sea). We group individual 18S rRNA gene sequences into operational taxonomic units (OTUs) using different cutoff values for sequence similarity (99 to 50%) and systematically apply parametric models and nonparametric estimators to the OTU frequency data to estimate the total protistan diversity. The parametric models provided statistically sound estimates of protistan richness, with biologically meaningful standard errors, maximal data usage, and extensive model diagnostics and were preferable to the available nonparametric tools. Our clone library exceeded 700 clones but still covered only a minority of species and less than half of the larger protistan clades. Our estimates of total protistan richness portray the target community as very rich at all OTU levels, with hundreds of different populations apparently co-occurring in the small (3-liter) volume of our sample, as well as dozens of clades of the highest taxonomic order. These estimates are among the first for microbial eukaryotes that are obtained using state-of-the-art statistical methods and can serve as benchmark numbers for the local diversity of protists.
Current knowledge of microeukaryotic species richness is emphatically deficient (2). Estimates of the total number of species are based on inductive reasoning rather than solid data and vary widely. While some argue that the global richness of free-living protozoa is less than 20,000 species (15), others maintain that a single phylum of ciliates comprises more than 30,000 species (16). Divergent views on the nature of protistan species exacerbate the discrepancies (10) but cannot fully account for the lack of agreement on the extent of protistan species diversity. We argue that even if a consensus were reached on a particular species definition, it would still be difficult to answer this basic question: what is the total protistan richness in the simplest possible case—within a given sample? When the extent of local richness is unknown, it is natural that global richness remains elusive.
Why is it so difficult to determine the local number of species (however defined)? There seem to be two principal reasons. First, the number of species, or operational taxonomic units (OTUs), appears very large even in environments that are supposed to be “simple,” such as extreme environments (1). Second, the observed species frequency distribution (that is, the number of OTUs observed once, twice, three times, etc.) is almost universally characterized by a large number of rare species and a small number of very abundant species (7, 12) (see Fig. 1). These factors make a complete inventory a daunting task. To our knowledge such completeness has never been claimed for any community or environment. The real challenge, however, is not the undersampling itself but how to estimate its extent: this is central to assessing total protistan richness, first locally and eventually globally.
FIG. 1.
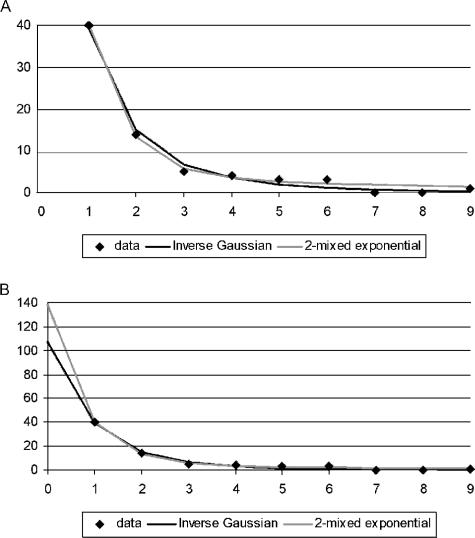
Inverse Gaussian-mixed Poisson and mixture-of-two-geometrics frequency count distributions fitted to 97% OTU data. The inverse Gaussian-mixed Poisson distribution was calculated as follows:
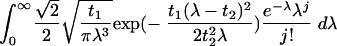 |
(1) |
where j = 0, 1, and so forth, t1 = 0.3431, and t2 = 0.7959. The mixture-of-two-geometrics distribution was calculated as follows:
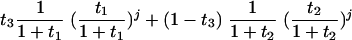 |
(2) |
where j = 0, 1, and so forth, t1 = 0.3672, t2 = 7.2341, and t3 = 0.8220. (A) Frequency count distribution fitted to frequency data. (B) Fitted frequency count distribution extended to zero.
There are two main families of statistical methods for estimating how much of the sample's richness is captured in a survey. Parametric methods are historically older, but computational difficulties have hindered their application until recently (3, 8, 17). Nonparametric methods, which are more recent, have been used extensively in prokaryotic diversity research (19, 20, 30) and are beginning to be employed in protistan biodiversity studies (12, 24). Both are undergoing rapid theoretical development (3, 8, 23, 38). We applied a new synthetic or comparative statistical approach, based on comparison of parametric and nonparametric tools, to 16S gene libraries (17). Here we extend the analyses to microbial eukaryotes, using as a test site an anoxic water column in the Cariaco Basin off the coast of Venezuela. Focusing on a single sample from this environment, we constructed four independent 18S rRNA gene libraries with four different primer sets, in order to minimize primer biases (7). Significant sequencing efforts brought us the single largest sequence data set on protistan rRNA diversity to date (32). Here we use these data set to estimate local protistan species richness; in particular we argue that for microbial communities with a high degree of richness, parametric modeling appears to be preferable to currently available nonparametric procedures.
MATERIALS AND METHODS
This research utilizes the results of two previous 18S rRNA surveys (32, 33), and we refer the reader to those papers for a detailed treatment of the sampling and molecular biological methods used.
Study site and sampling.
The Cariaco Basin is the world's largest truly marine body of anoxic water and represents a large natural sediment trap, collecting sinking debris and biota from surface waters. A description of this environment can be found elsewhere (27, 28, 35). For this study we sampled the area at a depth of 340 m, corresponding to the lower boundary of the redox interface.
DNA isolation, PCR amplification, cloning, and sequencing.
DNA was extracted from a single 3-liter water column sample as described previously (33), followed by PCR-aided amplification of ≈1,000- to 1,300-bp fragments of the 18S rRNA gene using four different primer sets: (i) E528F-Univ1391RE, (ii) E528F-Univ1492RE, (iii) Euk A-Euk B followed by a nested reaction with E528F-Univ1517, and (iv) Euk A-Euk B followed by a nested reaction with 360FE-U1492R (Table 1). The PCR protocol employed HotStart Taq DNA polymerase (QIAGEN, Valencia, CA) in all cases. The PCR products were cloned, separately for each primer set, using the TA cloning kit (Invitrogen, Carlsbad, CA) according to the manufacturer's instructions. Plasmids were either isolated from overnight cultures by using the Macherey-Nagel (Easton, PA) NucleoSpin Robot-96 plasmid kit or amplified from plate colonies by using the Templiphi 100 amplification kit (Amersham Biosciences, Piscataway, NJ) according to the manufacturer's instructions. The presence of the target insert was confirmed by PCR reamplification as described above. After sequencing, we applied the Check_Chimera command of the Ribosomal Database Project (RDP) (22), as well as neighbor-joining trees with partial sequences (partial treeing analyses [18]), to eliminate chimeric sequences (29).
TABLE 1.
Primer sets used in this study to amplify fragments of the eukaryotic small-subunit ribosomal DNA
Sequence clustering.
The 18S rRNA gene sequences were grouped into OTUs based on 99, 98, 97, 96, 95, 90, 80, 70, 60, and 50% sequence similarity cutoff values. This was achieved by first making all possible pairwise sequence alignments using ClustalW at default settings (36) and calculating percent sequence similarities, followed by clustering of the sequences into OTUs using the mean unweighted-pair group method using average linkages as implemented in the OC clustering program (http://www.compbio.dundee.ac.uk/Software/OC/oc.html). The OTU grouping was checked manually to verify that all OTUs were assembled at the cutoff level desired. The gene sequences from this study were previously deposited in the GenBank database as part of two earlier publications (32, 33) under accession numbers AY256203 to AY256336 and AY882442 to AY882540.
Statistical analysis.
The basic sampling model asserts that each species independently contributes a random number of representatives, which may be zero, to the sample. This number is a Poisson-distributed random variable, and its mean for a given species (that is, the expected number of representatives of a given species in the final sample) is known as the “sampling intensity” of that species (8, 38). The sampling intensities are typically roughly proportional to the species' abundances in nature, but this relationship may not be exact, due to the intervening stages required to obtain the final species frequency counts.
The parametric and nonparametric methods differ mainly in their treatment of the sampling intensities (8, 38). The parametric approach dates (at least) to the 1940s, and its main theoretical results were obtained in the 1970s (8), although significant work remains to be done (3). Essentially, the sampling intensities are assumed to follow a parametric probability distribution, which in turn generates a (mixed Poisson) parametric model for the observed frequency counts. This model is fitted to the data by maximum likelihood (ML), which yields an estimate of species richness and (asymptotic) standard error (SE), goodness-of-fit (GOF) assessments, and related statistics. Various distributional models have been proposed (3, 8), but until recently applications have been inconsistent or imprecise due to computational impediments. Using techniques from modern statistical computing theory, we obtained algorithms that compute the ML estimates to any desired precision (3). We have applied this method to several microbial richness data sets (4, 17, 40).
The nonparametric approach dates (at least) to the 1950s, but its main theoretical development began in the 1980s. One class of methods is based on nonparametric estimation of the sample coverage, i.e., the proportion of the population represented by the species appearing in the sample (8). These procedures are computationally simple and have been implemented in several software packages (11, 30) and used extensively in microbial richness estimation (19, 20, 30). A more recent class of methods employs nonparametric maximum-likelihood estimation of the distribution of sampling intensities; these methods are computationally intensive, and software has not yet become generally available. Recently, a mathematical framework has emerged to unify the nonparametric procedures (23, 38).
At present, computationally tractable parametric models often do not fit complete OTU frequency data sets, and nonparametric procedures are typically sensitive to the maximum observed frequency in the data. Both approaches thus require that the data be split into two parts: the set of “rare” species, which has lower counts in the sample, and the set of “abundant” species, which has higher counts. The splitting point or frequency, designated τ, is called the “tuning parameter” in recent statistical literature (38). We apply the desired statistical procedure only to the set of lower frequency counts (≤τ) or rare species, and we add the observed number of “abundant” species (frequencies of >τ) to obtain the final estimate. In parametric modeling, the choice of τ for a given model and a given data set is based on goodness of fit as measured by a (properly adjusted) chi-square statistic and by visual inspection. We initially fit every model at every possible τ, and we look for the largest acceptable τ, since this means using the maximum amount of the available data in the estimate (8, 38). For the coverage-based nonparametric procedures, a default τ of 10 has been recommended based on expert opinion and empirical experience (38), but it is advisable to examine the results at several τ values. A major goal of theoretical research is to find procedures that will allow the maximum value for τ, or that are insensitive to the choice of τ, or that do not require splitting of the data (3, 8, 38).
The advantages of the parametric models versus the coverage-based nonparametric methods include (i) control of the distribution of sampling intensities, leading to asymptotic normality of the parametric ML richness estimator, centered at the true richness (given the model), versus potentially unlimited bias in the nonparametric case (owing to the possible presence of arbitrarily many infinitesimally rare species [8, 38]); (ii) quantitative and graphical assessment of parametric model fit, versus limited diagnostic criteria for nonparametric estimators; (iii) use of the maximum amount of frequency data (maximum τ) by selection of an optimal parametric distribution, versus unclear or default selection of τ in the nonparametric case. The countervailing disadvantage is that a particular parametric model must be selected. There are currently no convincing theoretical arguments to inform this choice, because arguments to justify, e.g., the lognormal abundance distribution are readily refuted (39), and in any case the distribution of actual abundances may not be that of the operative sampling intensities. Hence, the choice of a model must at present be empirical. A general statistical methodology exists for this (6), but those methods, such as, e.g., the Akaike information criterion (AIC), typically apply to evaluation of different models on the same data set, whereas here we have the simultaneous problem of different models and different data sets, due to different values of τ. We evaluate all available models at all values of τ using relatively simple criteria (described below). While this in principle allows the possibility of overfitting, we find that overall the advantages of the parametric approach outweigh the disadvantage of the requirement of model selection.
We currently use seven candidate distributions, which we list below according to the sampling intensity/frequency count distribution (see http://www.stat.cornell.edu/∼bunge/).
(i) The single point mass/ordinary Poisson distribution (one parameter) assumes equal proportions of species, which is unrealistic, and indeed we have never found it to fit real data. However, it is computationally simple and fast and serves as a useful lower-bound benchmark.
(ii) The gamma/gamma-mixed Poisson or negative binomial distribution (two parameters) appears to admit only relatively low diversity and rarely fits real data; it has been used for comparison with coverage-based nonparametric analyses (8).
(iii) The inverse Gaussian/inverse Gaussian-mixed Poisson distribution (two parameters) is a special case of the generalized inverse Gaussian distribution, which has long been regarded as a potential “universal” abundance model (5, 8). The generalized inverse Gaussian distribution remains computationally intractable (although we are currently working on approximations), but the inverse Gaussian distribution sometimes fits real data well.
(iv) The lognormal/lognormal-mixed Poisson distribution (two parameters) has been the subject of considerable interest in biology and other fields (8, 39) and does fit some data sets but should not be regarded as an a priori choice (39).
(v) The Pareto or power law/Pareto or power law-mixed Poisson distribution (two parameters) is a “heavy-tailed” distribution, well known in a variety of statistical applications, but appears to be new to the species problem. It does provide a good fit in some cases but is technically intractable at certain parameter values (at which moments do not exist).
(vi) The mixture of two exponentials/mixture of two geometrics (three parameters) is a model that we have recently introduced and studied, along with its three-exponential (or three-geometric) extension (see below) (3). It represents the abundances or frequency counts as a mixture (convex combination) of two groups, with one rate of decrease prevailing toward the left-hand side of the curve and another, lower rate to the right. The resulting flexibility typically permits a higher value of τ than the previous models and often fits real data well.
(vii) The mixture of three exponentials/mixture of three geometrics (five parameters) is an extension of the previous model, allowing a left, a middle, and a right-hand rate of decrease. Because of the need to estimate a larger number of parameters, this model typically yields unusably high SEs in smaller data sets, although it can perform exceptionally well in large data sets. We note that in general, mixtures of exponentials can approximate a wide class of distributions (14).
We fit each model by ML at each τ. We then select a model and a value of τ by considering several criteria. First, we assess goodness of fit, using a chi-square statistic computed across all cells (frequency counts) as a simple measure of discrepancy, and also using a chi-square statistic computed after concatenating cells for a minimum expected cell count of 5 in order to obtain an asymptotically correct goodness-of-fit test. (Currently we are implementing a computationally intensive goodness-of-fit assessment that avoids the necessity of concatenating cells [37], and we are adding the AIC to our computations for comparison of several models at a fixed value of τ, which is sometimes of interest.) We augment this numeric analysis with careful point-by-point examination of model fit, especially to the rare frequency counts. Second, we require a reasonable SE [<(estimate/2)], since inadequate precision renders the estimate useless. Third, we seek the largest possible τ. Finally, we arrive at a preferred model and value of τ, along with its associated estimate of species richness and SE, and related statistics. We note that while it would be desirable to give confidence intervals (CIs) for the species richness, no CI procedure has yet been verified as mathematically valid for small samples in this problem. Asymptotically the usual Gaussian 95% CI (i.e., estimate ± 1.96 · SE) is valid, but we do not generally report it here.
We then calculate the coverage-based nonparametric estimates using SPADE software (http://chao.stat.nthu.edu.tw/). We consider the estimators ACE (abundance-based coverage estimator) and ACE1. ACE1 is a high-diversity modification of ACE and is recommended if the observed coefficient of variation of the frequency data is >0.8 (9) (http://chao.stat.nthu.edu.tw/). We computed these estimators at the default τ of 10 and also at τ values selected by the parametric analyses. Since this procedure does not postulate a specific underlying model for the frequency data, model selection and goodness of fit do not apply.
We note that the multiple-primer procedure falls under the purview of the basic sampling model, as follows. To minimize the biases of the rRNA approach, such as the primer bias (34), we used four different PCR primer sets and constructed four different clone libraries (as described above), all originating from a single DNA extract from a single water column sample. We then pooled the resulting sequence data to obtain OTU frequency counts. The total sampling intensity of a given species (relative to the pooled data) is assumed to be the sum of its four separate sampling intensities (relative to each primer set). (This is statistically valid because the sum of Poisson random variables is again Poisson.) This model does not use the separate frequency counts from each primer set; it is doubtful that introducing the further statistical complexity necessary to model the primer set effects separately would improve the total richness estimates, but this is a topic for future research.
RESULTS AND DISCUSSION
Using the multiple-primer approach, we obtained and sequenced a substantial number of clones, 725 in total (32, 33). The overall diversity was larger than could be obtained with a single primer set (see reference 32), and the overlap between OTU lists from four individual clone libraries was minimal. For example, when OTUs were defined on the basis of 99% sequence similarity, no single OTU was shared between all four lists (data not shown). This suggests that the multiple-primer approach may recover more species than a simple increase in the sequencing efforts (40); if so, our approach represents the natural protistan diversity better than a more standard practice of using a single primer set. (We are currently preparing a study to quantify the differences between the primer sets' effects, as well as the relationship between the multiple-primer approach and increased sampling effort.) This gave us arguably the largest and least biased 18S rRNA inventory collected to date for any single sample from any environment, including the target environment (anoxic water column).
We grouped the unique 18S rRNA sequences into OTUs, defining clusters by various degrees of sequence similarity, from 50 to 99%. The number of unique OTUs ranged from 1 to 107, respectively. We calculated the frequencies of each OTU at each level of similarity and subjected the resulting frequency counts to statistical analyses; the results are summarized in Table 2. As expected, the single point mass (ordinary Poisson), gamma (negative binomial), and mixture-of-three-exponentials distributions produced no usable estimates of protistan richness from these data. The single point mass unrealistically assumes equal OTU sizes, the gamma appears to be insufficiently flexible to accommodate the level of diversity encountered here (both gave goodness-of-fit test P values of <0.05 at all OTU cutoff levels and all τ values), and the mixture of three exponentials gave unusably high SEs despite an acceptable fit (results not shown). We observed similar results in a prokaryotic richness analysis (17). The inverse Gaussian, lognormal, Pareto, and mixture-of-two-exponentials distributions produced comparable estimates with acceptable goodness of fit, SEs, and values for the tuning parameter τ (Table 2). The inverse Gaussian and mixture of two exponentials appeared to be the best overall models in this study: Fig. 1 shows the corresponding frequency count distributions, i.e., the inverse Gaussian-mixed Poisson and the mixture of two geometrics, as fitted to the 97% similarity data. These give similar fits to the data observed but diverge somewhat when the fitted frequency count curves are projected to zero, to estimate the number of unobserved species. As noted above, without (at present) a convincing theoretical justification for a particular model, our choice of distribution remains empirical. The results in Table 2 show that different parametric distributions can give comparable results (when the SE is taken into account), which in turn suggests that they constitute different approximations to the true, unknown distribution.
TABLE 2.
Microbial richness of the samplea
| OTU boundary (%)b | Statistic | Detected richness of the sample | Estimate of the total sample's richness
|
|||||
|---|---|---|---|---|---|---|---|---|
| Parametric model
|
Nonparametric estimator
|
|||||||
| Inverse Gaussian | Lognormal | Pareto | 2-mixed exponential | ACE1c | ACE1d | |||
| 99 | No. of OTUs | 107 | 509 | 340 | 290 | 398 | 311 | 499 |
| SE | 244 | 170 | 74 | 156 | 84 | 394 | ||
| Naïve GOF | 0.30 | 0.17 | 0.10 | 0.11 | NP | |||
| Asymp. GOF | 0.27 | 0.16 | 0.11 | 0.17 | ||||
| τ | 10 | 10 | 10 | 31 | 10 | 31 | ||
| 98 | No. of OTUs | 99 | 285 | 223 | 191 | 263 | 228 | 370 |
| SE | 95 | 74 | 19 | 74 | 54 | 253 | ||
| Naïve GOF | 0.19 | 0.26 | 0.12 | 0.29 | NP | |||
| Asymp. GOF | 0.71 | 0.33 | 0.15 | 0.38 | ||||
| τ | 12 | 10 | 10 | 31 | 10 | 31 | ||
| 97 | No. of OTUs | 91 | 198 | 182 | 176 | 230 | 186 | 297 |
| SE | 48 | 53 | 19 | 65 | 43 | 181 | ||
| Naïve GOF | 0.39 | 0.30 | 0.21 | 0.12 | NP | |||
| Asymp. GOF | 0.59 | 0.49 | 0.28 | 0.49 | ||||
| τ | 9 | 9 | 9 | 31 | 9 | 31 | ||
| 96 | No. of OTUs | 85 | 190 | 173 | 160 | 244 | 173 | 244 |
| SE | 52 | 56 | 17 | 100 | 40 | 123 | ||
| Naïve GOF | 0.13 | 0.09 | 0.07 | 0.11 | NP | |||
| Asymp. GOF | 0.21 | 0.16 | 0.04 | 0.32 | ||||
| τ | 9 | 9 | 9 | 31 | 9 | 31 | ||
| 95 | No. of OTUs | 81 | 164 | 153 | 140 | 215 | 156 | 212 |
| SE | 40 | 46 | 16 | 84 | 35 | 104 | ||
| Naïve GOF | 0.26 | 0.19 | 0.15 | 0.15 | NP | |||
| Asymp. GOF | 0.23 | 0.19 | 0.06 | 0.32 | ||||
| τ | 9 | 9 | 9 | 31 | 9 | 31 | ||
| 90 | No. of OTUs | 50 | 99 | 92 | 76 | 178 | 98 | 106 |
| SE | 34 | 27 | 10 | 185 | 31 | 34 | ||
| Naïve GOF | 0.06 | 0.05 | 0.04 | 0.12 | NP | |||
| Asymp. GOF | 0.43 | 0.36 | 0.13 | 0.15 | ||||
| τ | 11 | 11 | 11 | 32 | 11 | 32 | ||
| 80 | No. of OTUs | 21 | 56,976 | 83 | 45 | 221 | 60 | 203 |
| SE | 131,990 | 123 | 10 | 467 | 35 | 181 | ||
| Naïve GOF | 0.02 | 0.01 | 0.02 | 0.00 | NP | |||
| Asymp. GOF | NA | NA | NA | NA | ||||
| τ | 5 | 5 | 5 | 32 | 5 | 32 | ||
Boldfaced values represent selected estimates. τ, maximum frequency used in statistical procedure. Naïve GOF, uncorrected chi-square GOF P value; Asymp. GOF, asymptotically correct chi-square GOF P value; NA, not available; NP, computation not possible.
Cutoff value for percent sequence similarity.
For default τ.
For maximum τ allowed by parametric model fit.
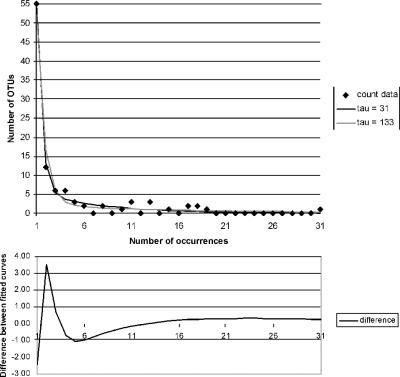
In fact, we typically find an acceptable (P > 0.05) fit of the mixture-of-two-exponentials model (see reference 25) to the entire data set (τ = maximum observed frequency), which would seem to be ideal. However, when the model is fitted to the full data set, the (typically) long right-hand tail (a few very abundant species) “weighs down” the left-hand side of the curve, so as to underfit the numbers of rare species. For example, in the 99% OTU data, the observed counts extend up to a maximum frequency of 133. Figure 2 shows the fitted mixture-of-two-exponentials curves using τ values of 133 (i.e., the full data set) and 31 (selected for best fit); the plot is truncated on the right at 31. The curves appear quite close, but the fitted curve with a τ of 133 has a shallower slope to the left and hence in particular underfits the number of singletons; it predicts 52 singletons, while the fitted curve with a τ of 31 predicts 54.5 (the observed number is 55). The difference (fitted curve with a τ of 133 − fitted curve with a τ of 31) is shown below the main plot. The effect of the underfit is that the model based on the full data set returns a species richness estimate and SE that are both probably unrealistically low (279 [SE, 59] versus 398 [SE, 156] using a τ of 31). In summary, at present we are not prepared to recommend fitting the mixture-of-two-exponentials model to the full data set in every case; model selection considerations (as discussed above) still apply.
FIG. 2.
Mixture-of-two-exponentials (geometrics) model fitted to full (τ = 133) and partial (τ = 31) OTU data, with difference between curves (OTU defined as rRNA gene sequence clusters at a cutoff level of 99% sequence similarity). The abscissa is truncated at 31.
When OTUs are defined narrowly, i.e., with 98 to 99% sequence similarity as the cutoff level, the OTU frequency distribution is extremely steep near the origin and equally shallow toward high frequency counts (Fig. 2). In such cases the bipartite nature of the mixture of two exponentials gives it an advantage, allowing a higher value of τ (and hence greater use of the observed data) than the other models. When the OTUs are more inclusive and the frequency distribution less extreme, this advantage seems to diminish. At 97% sequence similarity, the frequency distribution can be modeled equally well by the mixture-of-two-exponentials and inverse Gaussian models, and thereafter the latter appears to be preferable (except in cases of very inclusive OTUs that combined the rRNA species with >80% sequence similarity, where the potentially plausible analyses involve only 5 data points [Table 2]).
The models selected here also proved useful in estimating bacterial richness (17); they had not previously been used in microbial diversity research. On those few occasions when parametric models were used to estimate microbial richness, researchers relied predominantly on the lognormal distribution. Our data show that, even if a convincing a priori argument for a particular model such as the lognormal were available, it need not carry through to the empirical frequency data (17, 39). We therefore argue that a variety of models should be fitted to any given data set.
The coverage-based nonparametric statistics are also given in Table 2. For these data sets, ACE1 (the higher-diversity estimator) was preferred to ACE at every level of OTU definition, and in fact the value with ACE was on average 31% lower than that with ACE1 in this study. Selection of τ in this case is not straightforward, since ACE1 and its SE vary considerably with τ (Table 2); further diagnostic criteria are needed, and this is a topic for future research. As the level of OTU definition decreases and the data sets become less diverse, the parametric and nonparametric results converge. This empirical evidence, in addition to the theoretical and heuristic considerations discussed above, lead us to conclude that for estimation of species richness (99 or 98% sequence similarity), parametric models have a clear edge over nonparametric estimators. The advantage seems to diminish as the OTUs become more inclusive.
Finally, it is of considerable interest to obtain abundance estimates for individual OTUs. The total protistan abundance at the depth of our sample's origin has been reported to be around 3 × 106 cells liter−1. We do not know the frequency distribution of OTUs in the environment, but as a first approximation we may assume that it is similar to the distribution of OTUs in the clone libraries (e.g., mixture of two exponentials in Table 2). Using the relative abundance of OTUs given by this model and the total number of cells in the sample, we estimated the abundances of OTUs in this sample (for OTUs defined as clusters of clones with >99% similarity). The protists in the sample can be provisionally divided into three groups based on their abundances. The group of most abundant protists consists of nine OTUs whose abundance exceeds 100 cells ml−1; this group accounts for 51% of the total protistan community. Moderately abundant OTUs constitute 26% of the community and are represented by 28 OTUs with individual abundances ranging from 10 to 100 cells ml−1. Rare OTUs (<10 cells ml−1) represent the bulk of the protistan community (361 OTUs, or 91% of the entire richness) but contribute disproportionately little (23%) to the overall abundance. Among those, 118 OTUs seem exceedingly rare (<1 cell ml−1). Therefore, the protistan diversity of the sample may be residing in species present in very small numbers.
In summary, the degree of richness of microbial eukaryotes in anoxic waters of the Cariaco Basin appears to be very high (Table 2). For OTUs defined as groups of clones similar at ≥99%, the estimated total richness per single 3-liter sample was 398 ± 156 (SE) OTUs (Table 2). Our clone libraries contained 107 OTUs, and thus we estimate that these libraries captured approximately one-fourth of all the species in the sample. This is probably the highest such fraction among published 18S rRNA gene libraries. Parametric models such as the inverse Gaussian and the mixture of two exponentials currently appear to be preferable tools for estimating microbial richness. It is useful to examine as many models as is practical; the best model may be different for different surveys, as well as for differently defined OTUs within one data set.
Our synthetic approach estimates that a single water column sample from anoxic waters in the Cariaco Basin contains hundreds of different protistan populations. It also suggests that even our multiple-primer approach and extensive sequencing failed to register up to 75% of species, as well as up to 50% of clades of the highest taxonomic position. Collectively, these findings point to a high degree of richness of protists in the target environment.
Acknowledgments
We are grateful to Chesley Leslin and Valya Ilyin (Northeastern University) for outstanding help in performing thousands of pairwise sequence comparisons needed to correctly cluster sequences into OTUs. We are indebted to the captain and crew of the B/O Hermano Gines and the staff of the Estación de Investigaciones Marinas (EDIMAR) de Margarita (Fundación la Salle de Ciencias Naturales, Punta de Piedras, Isla de Margarita, Venezuela) for field assistance in this study and to the scientists of the CARIACO time series program, particularly F. Muller-Karger, R. Varela, and Y. Astor, for logistical field support and ancillary data. Constructive criticisms by three anonymous reviewers improved the manuscript.
This work was funded in part by U.S. National Science Foundation Microbial Observatory grant MCB-0348341 to S.S.E. and by Deutsche Forschungsgemeinschaft grant STO414/2-1 to T.S. The research was conducted using the resources of the Cornell Theory Center, which receives funding from Cornell University, New York State, federal agencies, foundations, and corporate partners.
Footnotes
Contribution 254 of the Marine Science Center of Northeastern University, Boston, Mass.
REFERENCES
- 1.Amaral Zettler, L. A., F. Gomez, E. Zettler, B. G. Keenan, R. Amils, and M. L. Sogin. 2002. Microbiology: eukaryotic diversity in Spain's River of Fire. Nature 417:137. [DOI] [PubMed] [Google Scholar]
- 2.Baldauf, S. L. 2003. The deep roots of eukaryotes. Science 300:1703-1706. [DOI] [PubMed] [Google Scholar]
- 3.Barger, K. J.-A. 2006. Mixtures of exponential distributions to describe the distribution of Poisson means in estimating the number of unobserved classes. M.S. thesis. Cornell University, Ithaca, N.Y. [Online.] http://hdl.handle.net/1813/2953.
- 4.Behnke, A., J. Bunge, K. Barger, H.-W. Breiner, V. Alla, and T. Stoeck. 2006. Microeukaryote community patterns along an O2/H2S gradient in a supersulfidic anoxic fjord (Framvaren, Norway). Appl. Environ. Microbiol. 72:3626-3636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bunge, J., M. Fitzpatrick, and J. Handley. 1995. Comparison of 3 estimators of the number of species. J. Appl. Stat. 22:45-59. [Google Scholar]
- 6.Burnham, K. P., and D. R. Anderson. 1998. Model selection and inference: a practical information-theoretic approach. Springer-Verlag Inc., New York, N.Y.
- 7.Caron, D. A., P. D. Countway, and M. V. Brown. 2004. The growing contributions of molecular biology and immunology to protistan ecology: molecular signatures as ecological tools. J. Eukaryot. Microbiol. 51:38-48. [DOI] [PubMed] [Google Scholar]
- 8.Chao, A., and J. Bunge. 2002. Estimating the number of species in a stochastic abundance model. Biometrics 58:531-539. [DOI] [PubMed] [Google Scholar]
- 9.Chao, A., and S.-M. Lee. 1992. Estimating the number of classes via sample coverage. J. Am. Stat. Assoc. 87:210-217. [Google Scholar]
- 10.Coleman, A. W. 2002. Microbial eukaryote species. Science 297:337. [DOI] [PubMed] [Google Scholar]
- 11.Colwell, R. K. 2005, posting date. EstimateS: statistical estimation of species richness and shared species from samples, version 7.5. [Online.] http://purl.oclc.org/estimates.
- 12.Countway, P. D., R. J. Gast, P. Savai, and D. A. Caron. 2005. Protistan diversity estimates based on 18S rDNA from seawater incubations in the Western North Atlantic. J. Eukaryot. Microbiol. 52:95-106. [DOI] [PubMed] [Google Scholar]
- 13.Edgcomb, V. P., D. T. Kysela, A. Teske, A. de Vera Gomez, and M. L. Sogin. 2002. Benthic eukaryotic diversity in the Guaymas Basin hydrothermal vent environment. Proc. Natl. Acad. Sci. USA 99:7658-7662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Feldmann, A., and W. Whitt. 1998. Fitting mixtures of exponentials to long-tail distributions to analyze network performance models. Perform. Eval. 31:245-279. [Google Scholar]
- 15.Finlay, B. J., and T. Fenchel. 1999. Divergent perspectives on protist species richness. Protist 150:229-233. [DOI] [PubMed] [Google Scholar]
- 16.Foissner, W. 1999. Protist diversity: estimates of the near-imponderable. Protist 150:363-368. [DOI] [PubMed] [Google Scholar]
- 17.Hong, S.-H., J. Bunge, S.-O. Jeon, and S. Epstein. 2006. Predicting microbial species richness. Proc. Natl. Acad. Sci. USA 103:117-122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hugenholtz, P., B. M. Goebel, and N. R. Pace. 1998. Impact of culture-independent studies on the emerging phylogenetic view of bacterial diversity. J. Bacteriol. 180:4765-4774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hughes, J. B., J. J. Hellmann, T. H. Ricketts, and B. J. Bohannan. 2001. Counting the uncountable: statistical approaches to estimating microbial diversity. Appl. Environ. Microbiol. 67:4399-4406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kemp, P. F., and J. Y. Aller. 2004. Bacterial diversity in aquatic and other environments: what 16S rDNA libraries can tell us. FEMS Microbiol. Ecol. 47:161-177. [DOI] [PubMed] [Google Scholar]
- 21.Lane, D. J. 1991. 16S/23S sequencing, p. 115-175. In E. Stackebrandt and M. Goodfellow (ed.), Nucleic acid technologies in bacterial systematics. John Wiley and Sons, Chichester, United Kingdom.
- 22.Maidak, B. L., J. R. Cole, T. G. Lilburn, C. T. Parker, Jr., P. R. Saxman, R. J. Farris, G. M. Garrity, G. J. Olsen, T. M. Schmidt, and J. M. Tiedje. 2001. The RDP-II (Ribosomal Database Project). Nucleic Acids Res. 29:173-174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mao, C. X., and R. K. Colwell. 2005. Estimation of species richness: mixture models, the role of rare species, and inferential challenges. Ecology 86:1143-1153. [Google Scholar]
- 24.Massana, R., V. Balagué, L. Guillou, and C. Pedros-Alió. 2004. Picoeukaryotic diversity in an oligotrophic coastal site studied by molecular and culturing approaches. FEMS Microbiol. Ecol. 50:231-243. [DOI] [PubMed] [Google Scholar]
- 25.McLachlan, G. J., and D. Peel. 2000. Finite mixture models. Wiley, New York, N.Y.
- 26.Medlin, L., H. J. Elwood, S. Stickel, and M. L. Sogin. 1988. The characterization of enzymatically amplified eukaryotic 16S-like rRNA-coding regions. Gene 71:491-499. [DOI] [PubMed] [Google Scholar]
- 27.Muller-Karger, F., R. Varela, R. Thunell, M. Scranton, R. Bohrer, G. T. Taylor, J. Capelo, Y. Asto, E. Tappa, T.-Y. Ho, and J. J. Walsh. 2001. Annual cycle of primary production in the Cariaco Basin: response to upwelling and implications for vertical export. J. Geophys. Res. 106:4527-4542. [Google Scholar]
- 28.Richards, F. A., and R. F. Vaccaro. 1956. The Cariaco Trench, an anaerobic basin in the Caribbean. Deep Sea Res. 3:214-228. [Google Scholar]
- 29.Robison-Cox, J. F., M. M. Bateson, and D. M. Ward. 1995. Evaluation of nearest-neighbor methods for detection of chimeric small-subunit rRNA sequences. Appl. Environ. Microbiol. 61:1240-1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schloss, P. D., and J. Handelsman. 2005. Introducing DOTUR, a computer program for defining operational taxonomic units and estimating species richness. Appl. Environ. Microbiol. 71:1501-1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shopsin, B., M. Gomez, S. O. Montgomery, D. H. Smith, M. Waddington, D. E. Dodge, D. A. Bost, M. Riehman, S. Naidich, and B. N. Kreiswirth. 1999. Evaluation of protein A gene polymorphic region DNA sequencing for typing of Staphylococcus aureus strains. J. Clin. Microbiol. 37:3556-3563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stoeck, T., B. Hayward, G. T. Taylor, R. Varela, and S. S. Epstein. 2006. A multiple PCR-primer approach to access the microeukaryotic diversity in the anoxic Cariaco Basin (Caribbean Sea). Protist 157:31-43. [DOI] [PubMed] [Google Scholar]
- 33.Stoeck, T., G. Taylor, and S. S. Epstein. 2003. Novel eukaryotes from the permanently anoxic Cariaco Basin (Caribbean Sea). Appl. Environ. Microbiol. 69:5656-5663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Suzuki, M. T., and S. J. Giovannoni. 1996. Bias caused by template annealing in the amplification of mixtures of 16S rRNA genes by PCR. Appl. Environ. Microbiol. 62:625-630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Taylor, G. T., M. I. Scranton, M. Iabichella, T.-Y. Ho, R. C. Thunell, F. Muller-Karger, and R. Varela. 2001. Chemoautotrophy in the redox transition zone of the Cariaco Basin: a significant midwater source of organic carbon production. Limnol. Oceanogr. 46:148-163. [Google Scholar]
- 36.Thompson, J. D., D. G. Higgins, and T. J. Gibson. 1994. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22:4673-4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tollenaar, N., and A. Mooijaart. 2003. Type I errors and power of the parametric bootstrap goodness-of-fit test: full and limited information. Br. J. Math. Stat. Psychol. 56:271-288. [DOI] [PubMed] [Google Scholar]
- 38.Wang, J.-P. Z., and B. G. Lindsay. 2005. A penalized nonparametric maximum likelihood approach to species richness estimation. J. Am. Stat. Assoc. 100:942-959. [Google Scholar]
- 39.Williamson, M., and K. J. Gaston. 2005. The lognormal distribution is not an appropriate null hypothesis for the species-abundance distribution. J. Anim. Ecol. 74:409-422. [Google Scholar]
- 40.Zuendorf, A., A. Behnke, J. A. Bunge, K. J. Barger, and T. Stoeck. Diversity estimates of microeukaryotes below the chemocline of the anoxic Mariager Fjord. FEMS Microbiol. Ecol., in press. [DOI] [PubMed]