Application of the Poisson-Nernst-Planck Theory with Space-Dependent Diffusion Coefficients to KcsA

Abstract

The Poisson-Nernst-Planck electrodiffusion theory serves to compute charge fluxes and is here applied to the ion current through a protein channel. KcsA was selected as an example because of the abundance of experimental and theoretical data. The potassium channels MthK and KvAP were used as templates to define two open channel models for KcsA. Channel boundary surfaces and protein charge distributions were defined according to atomic radii and partial atomic charges. To establish the sensitivity of the results to these parameters, two different sets were used. Assigning the potassium diffusion coefficients equal to the value for free-diffusion in water (1.96 × 10⁻⁹ m²/s), the computed currents overestimated the experimental data. Ion distributions inside the channel suggest that the overestimate is not due to an excess of charge shielding. A good agreement with the experimental data was achieved by reducing the potassium diffusion coefficient inside the channel to 1.96 × 10⁻¹⁰ m²/s, a value of substantial motility but nonetheless in accord with the intuitive notion that the channel has a high affinity for the ions and therefore slows them down. These results are independent of the open channel model and the parameterization adopted for atomic radii and partial atomic charges. The method offers a reliable estimate of the channel current with low computational effort.

INTRODUCTION

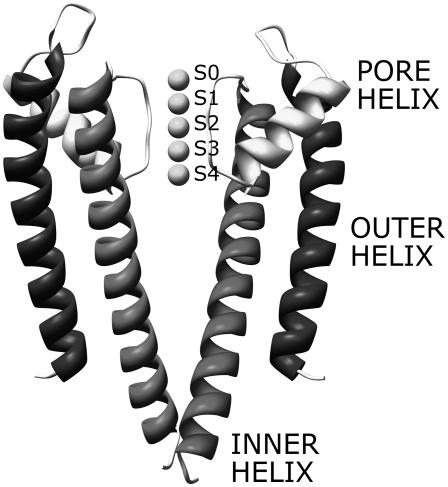
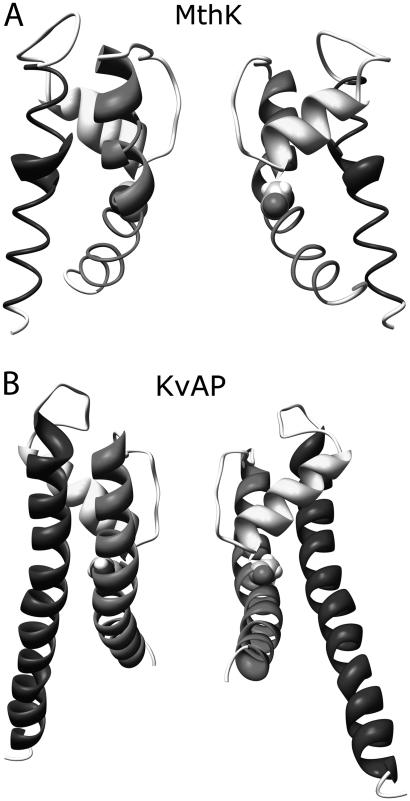
Ion channels are proteins embedded in the cell membrane that allow the flow of chemical species through the hydrophobic lipid bilayer. Ion channels play a central role in several cellular functions, such as excitability and secretion (1). The atomic structure of bacterial channels selectively permeable to potassium ions—KcsA, MthK, and KvAP—was recently characterized (2–4). The structure of the ion conduction pathway is remarkably conserved in these channels and consists of four subunits symmetrically placed around the channel axis. Each subunit is made up of three α-helix structures—the outer helix, the pore helix, and the inner helix—placed as shown in Fig. 1. The conduction pathway on the extracellular side is lined by the carbonyl oxygens of the amino acid sequence TVGYG, one from each subunit (see Fig. 1). This region, called selectivity filter (SF), is 16-Å long with a mean radius of 1.4 Å. Below the SF the channels open into a wide chamber connected to the intracellular space by a hydrophobic pore. Both the chamber and the hydrophobic pore are lined by the four inner helices. In KcsA, a bundle among these helices close to the intracellular mouth reduces the hydrophobic pore diameter to 4 Å, preventing ion fluxes through the channel; this configuration corresponds to a functionally closed state. In MthK and KvAP an outward movement of the inner helices, accomplished by bending around a hinge glycine, opens the intracellular mouth (Fig. 2). The structures of MthK and KvAP are representative of open states for potassium channels (5).

FIGURE 1.

Side view of the KcsA channel. For clarity, only two subunits are shown. Five potassium ions are included in the SF at the binding sites S0–S4; numbering starts from the top (extracellular side).

FIGURE 2.

Side views of MthK and KvAP channels. A rotation around the hinge glycines (highlighted in the Corey-Pauling-Kultin mode) opens the intracellular channel mouths to different extents in the two channels.

The two hallmarks of potassium channels are i), the rate of conduction (10⁸ ions/s) close to the diffusion limit, and ii), the high selectivity (K⁺ is 10⁴ times more permeant than Na⁺) (1). High fluxes need conduction mechanisms without energetic barriers, whereas selectivity needs a close interaction between ions and channel. Knowledge of the KcsA atomic structure has disclosed the mechanisms underlying these complex functionalities. Five ion-binding sites in the SF, called S0, S1, S2, S3, and S4, were revealed by x-ray crystallography (6) and molecular dynamics (MD) (7). The selectivity of these binding sites for K⁺ over Na⁺ was proved by MD simulations (8,9). In physiological conditions the SF is mostly occupied by two potassium ions separated by a water molecule (10,11). The configuration with ions in S1 and S3 can rapidly switch to that with ions in S2 and S4 because of the low energetic barrier (7). Conduction takes place when a third ion enters the SF from one side, causing the concerted motion of all the ions in the filter, and finally pushing an ion out from the opposite side. In agreement with the high throughput rate of potassium channels, no significant energetic barrier hampers any of the steps of the transport mechanism of potassium. To explain the lower conductance of rubidium, an ion slightly bigger than potassium, it is enough to introduce an energetic barrier between the configurations with two ions in the SF (S1–S3 and S2–S4) (10).

MD has disclosed the atomic details of conduction and selectivity (8,9,12–14), but it cannot routinely predict the ion current through the channels (15) because of the timescale of ion transport. The complexity of the system, due to the large number of atoms, limits MD simulations to the nanosecond scale. This temporal scale is adequate to observe single conduction events (transit time in a potassium channel is in the nanosecond scale) but not to estimate channel current, whose computation requires the mean temporal proprieties of conduction to be known. Since ion current is an important functional characteristic of ion channels and can be determined experimentally (16), it should be predicted starting from the channel atomic structure. Several simplified approaches have been adopted to reduce the computational effort required by MD (11,17,18). Since most of the complexity lies in the large number of water molecules in the extracellular and intracellular compartments, the computational load is strongly reduced in models based on a continuum picture of the solvent.

Brownian dynamics (BD) and Poisson-Nernst-Planck (PNP) electrodiffusion theory are possible approaches based on this idea. BD preserves the discrete nature of ions, and PNP handles the whole system as a continuum. BD has already been used to predict ion fluxes through potassium channels (11,19,20). A conductivity estimate of KcsA in good agreement with the experimental data was obtained by BD simulations based on a potential of mean force computed by MD (11). Applications of the PNP theory to membrane ion channels are more controversial (21). In wide channels this approach reproduces the experimental data quite well (22,23). On the other hand, the applicability of the PNP theory to narrow channels, with radii lower than 2 Deybe lengths, has been challenged (24). An overestimate of charge shielding inside the channel was indicated as the main cause of the PNP quantitative failure in these channels (25). To date, testing the PNP theory in narrow channels is limited to simplified channel models: simple cylindrical channels or models shaped on KcsA without explicitly including the protein charge distribution (24).

This work uses the PNP theory on the KcsA potassium channel. Two different open channel models are used for open KcsA. One is based on MthK, the other on KvAP. In PNP, channel boundary surfaces and protein charge distributions are defined according to atomic radii and partial atomic charges. Two different sets of parameters are used to assess the sensitivity of the results to these parameters. Independently of the parameterization and the open channel model adopted, the same results are reached: i), inside the SF anion concentration is several orders of magnitude lower than cation concentration; ii), the PNP theory overrates experimental data when diffusion coefficients are set at the experimental values for free diffusion in water, but a reasonable decrease of ion motility inside the channel makes experiments and theory coincide; and iii), cation distribution in the SF is characterized by four peaks corresponding to the potassium binding sites S1–S4.

METHODS

PNP theory

The PNP electrodiffusion theory describes a steady-state condition for a system of mobile charges. The mobile charges in membrane channels are the different ion species in solution whose space distributions are described by the concentrations C_s(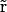) (subscript s marks the sth ion species; is the position in space). Assuming the electric field as the only driving force acting on ions, the steady-state flux of the sth ion species has the form

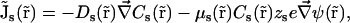(1)

where D_s(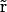), μ_s(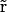), and z_s are diffusion coefficient, mobility, and valence of the sth ion species, respectively; e is the elementary charge; and ψ is the electrostatic potential. The first term, which is proportional to the concentration gradient, is due to diffusion processes, whereas the last is produced by the electric field. Since the PNP theory describes a steady-state condition, all quantities in Eq. 1 are time independent. Because of the mass conservation law, the divergence of 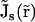is zero, which gives the set of differential equations

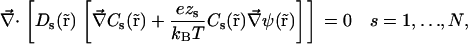(2)

where N is the number of ion species, k_B is Boltzmann's constant, and T is the absolute temperature. Equation 2 uses Einstein's relation between diffusion coefficient and ion mobility, D/μ = k_BT. PNP theory formulation is completed by the relationship between electrostatic potential and ion concentrations. This relation is defined by Poisson's equation

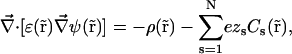(3)

where ɛ() is the dielectric constant and ρ() the charge distribution of the protein atoms, which unlike ion charge distribution is assumed fixed in space.

This study includes in the water solution only two monovalent ion species: one positive (s = +) and one negative (s = −). The PNP differential equation set is thus reduced to

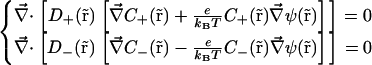(4)

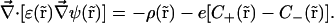(5)

Once these equations are solved, ion concentrations and electrostatic potential are computed (see Computational Algorithm section), then Eq. 1 is used to calculate the ion flux in the channel.

COMPUTATIONAL ALGORITHM

Equations 4 and 5 were solved numerically considering a cubic volume divided into three distinct subvolumes: the ion channel, the membrane, and the water solution. The channel was placed with its geometric center at the center of the cube and with the pore axis orthogonal to the upper and lower faces. The extracellular side of the channel pointed to the upper face. The height of the cube was twice the channel length along the pore axis (z axis). The position, radius, and partial charge of all the atoms define the ion channel subvolume. To separate extracellular and intracellular spaces, a subvolume surrounding the channel and extending between two planes orthogonal to the pore axis was included. This volume corresponds to the lipid bilayer of the cell membrane. The water solution spreads throughout the volume not occupied by channel and membrane. A mesh of 200 × 200 × 200 cubic grid elements was used to discretize the whole volume. The channel was meshed on the grid using the discretization algorithm implemented in DELPHI, a well-known Poisson-Boltzmann equation solver (26).

Equation 5 was solved in the whole volume, whereas Eq. 4 was solved for the water solution only. As boundary condition for Poisson's equation, the electrostatic potential on the six faces of the cube was assigned. The potential was set to zero on the upper face, and the membrane potential was applied at the lower face. For the potential of the side faces, a linear interpolation between zero and the membrane potential was used. Two different boundary conditions were assigned for the mass conservation equations. On the upper and lower faces, the boundary conditions were the ion concentrations to simulate. To have electrically neutral boundaries on both faces, anion and cation concentrations were set equal. Boundary conditions on the side faces and at the separation surfaces with channel and membrane were

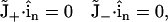(6)

where 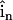is the surface normal vector. In this way, no ion flux was allowed through these surfaces.

The differential equation set was solved by an iterative scheme. At the first step, the electrostatic potential was computed solving Poisson's equation with ion concentrations set to zero. This potential was used to compute ion concentrations by the solution of mass conservation equations, and then the new concentrations were used to update the electrostatic potential. This procedure was repeated until a self-consistent solution was found. The convergence was tested by the root mean-square deviation (RMSD) between two successive iterations. All the differential equations were numerically solved by an algorithm based on the successive overrelaxation technique (27).

KcsA models

The three-dimensional atomic coordinates of the KcsA channel were taken from the crystallographic structure determined at 2 Å resolution by Y. Zhou et al. (6) (File 1K4C.pdb in the Protein Data Bank). The atomic coordinates of the first 21 amino acids at the N-terminal and of the last 36 at the C-terminal are not determined experimentally. Since both C- and N-terminals are located in the cytoplasm, far from the conduction pathway, these amino acids are not crucial for this study and therefore were not included in the channel model. Side chains with missing atoms were completed using ideal internal coordinates from the AMBER99 force field (28); the same procedure was used to add the hydrogen atoms. All the ionizable residues were assumed in the default protonation state except GLU-71, assumed protonated (29). An acetyl and an N-methylamine group were added to the C- and N-terminals, respectively.

The experimental structure of KcsA corresponds to a closed state of the channel. To compute ion fluxes, it is necessary to use an open channel structure. Closure of KcsA is due to a bundle of the four inner helices at the intracellular channel mouth (2). A connection between channel opening and outward movements of the transmembrane helices was first proved by electronic paramagnetic resonance experiments (30). These movements were further characterized by the x-ray crystallographic structure of MthK (1LNQ.pdb), a potassium channel from the Methanobacterium thermoautotrophicum that, unlike KcsA, was crystallized in an open state (3). MthK and KcsA structures are very similar, except in the inner helices. These helices are bent at the amino acid GLY-83 in MthK, and, as a consequence, the SF is connected to the intracellular space by a wide pore (minimum radius 6 Å). High conservation of this hinge glycine among different potassium channels suggests a common mechanism for channel gating. Despite this common mechanism, the inner helix bending can differ in different channels. In the crystallographic structure of KvAP (1ORQ.pdb) (4), a potassium channel from Aeropyrum pernix, the inner helices bending, hence the pore opening, is lower than in MthK (Fig. 2). It is not currently known if the KcsA open state is more similar to KvAP or to MthK or if an intermediate configuration is adopted. Consequently, two different open channel models were used to test the PNP theory: one based on MthK (Model I) and one based on KvAP (Model II).

To define these models, MthK and KvAP were superimposed on KcsA, minimizing the RMSD among the SF atoms. Channel structures differ mainly in the C-terminal of the inner helix after the hinge glycine (GLY-83 in MthK, GLY-99 in KcsA, and GLY-220 in KvAP). Smaller structural differences are localized in the outer helices. KcsA backbone angles (ϕ and ψ) in the inner and outer helices were modified to minimize the RMSD with backbone atoms of MthK (Model I) or KvAP (Model II). In detail, Model I was defined superimposing the amino acids 22–45 and 99–114 of KcsA with the amino acids 19–42 and 83–98 of MthK; Model II was defined superimposing the amino acids 22–60 and 99–119 of KcsA with the amino acids 134–172 and 220–240 of KvAP. Open channels structures were refined by 500 steps of energy minimization using the SANDER module of AMBER. During minimization backbone atoms were restrained by a harmonic potential, with a force constant of 40 Kcal mol Å⁻² to avoid large backbone displacements. A similar procedure to define open channel structures was recently used to perform Poisson-Boltzmann calculations in KcsA (31).

Channel models are completed by atomic radii and partial atomic charges, needed to define channel boundaries and protein charge distribution. These parameters were taken from the AMBER99 force field. To test the effects of the parameterization on the results, a second set of channel models was defined using the atomic radii and partial atomic charges proposed by Nina et al. (32).

Parameter assignment

The relative dielectric constant was set at 80 for the water solution and 2 for the channel and the membrane. To define membrane thickness, the position of the aromatic residues TRP-113 (z = −16 Å) and TRP-87 (z = 14 Å) of the inner helices was used. The water-relative dielectric constant is probably below 80 in the channel interior due to the small volume and to the consequently reduced mobility of water molecules. At the same time, because of the mobile charges, the channel dielectric constant can locally differ from 2. To assess the sensitivity of the results to the assignment of this parameter, we tested the effects of small changes in the relative dielectric constant with respect to reference values (relative dielectric constant set at 60 for water solution and 4 for the channel).

The diffusion coefficients were assigned considering three distinct regions: the channel outside (CO) corresponding to z > 15.5 Å and z < −15.5 Å, the SF spanning from z = −0.5 Å to z = 15.5 Å, and the intracellular chamber (IC) from the intracellular channel mouth, z = −15.5 Å, to the intracellular end of the SF, z = −0.5 Å. Outside the channel the diffusion coefficients were set at D₊ = 1.96 × 10⁻⁹ m²/s and D₋ = 2.03 × 10⁻⁹ m²/s, according to the experimental values of free diffusion in water solution for potassium (D₊) and chloride (D₋) (33). Since the mean radii of SF and IC are 1.4 Å and 5–7 Å, depending on the channel model, ions and water molecules in these areas interact with the channel, requiring a different value of the diffusion coefficients. MD simulations predicted a potassium diffusion coefficient one order of magnitude lower in SF and roughly half in IC (8,34). To assess the effects of space-dependent diffusion coefficients on the computed currents, we tested four diffusion coefficient profiles within the channel: i), equal to the free diffusion values, both in SF and IC; ii), reduced to 10% in SF; iii), reduced to 10% in SF and 50% in IC; and iv), reduced to 10% both in SF and IC. Computed currents were compared with KcsA experimental single channel currents measured in a planar bilayer system (35).

RESULTS

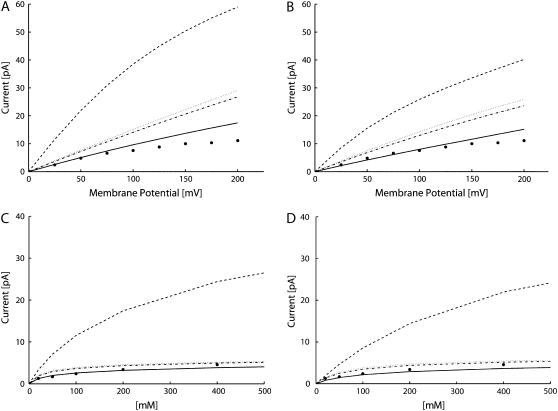
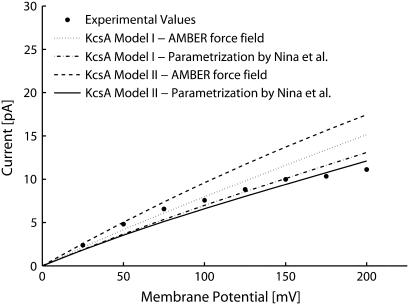
The currents predicted by the PNP theory (Fig. 3) overestimated the experimental data when the diffusion coefficients were assigned to the typical values for free diffusion in water in the whole system (SF, IC, and OC). For the current-voltage characteristics (see Fig. 3, A and B, dashed line), the percentage relative inaccuracy was large, independently of the membrane potential (at 25 mV 360% for Model I and 220% for Model II; at 200 mV 430% for Model I and 260% for Model II). By contrast, boundary ion concentrations strongly affected the percentage deviation as shown by the current-concentration characteristics in Fig. 3, C and D, dashed line (at 20 mM 160% for Model I and 50% for Model II; at 400 mM 440% for Model I and 380% for Model II). The conclusion is that the PNP theory, with constant diffusion coefficients, cannot reproduce the currents properly, especially at high ion concentrations.

FIGURE 3.

Computed currents varying the diffusion coefficients, D: D was set at the bulk value in the whole system (dashed line); D was reduced to 10% of bulk in SF (dotted line); D was reduced to 10% in SF and to 50% in IC (dot-dashed line); and D was reduced to 10% both in SF and IC (continuous line). Experimental data by LeMasurier et al. (35) (•). (A) Current-voltage characteristic with ion concentrations set at 100 mM in Model I. (B) Current-voltage characteristic with ion concentrations set at 100 mM in Model II. (C) Current-concentration characteristic with membrane potential set at 25 mV in Model I. (D) Current-concentration characteristic with membrane potential set at 25 mV in Model II.

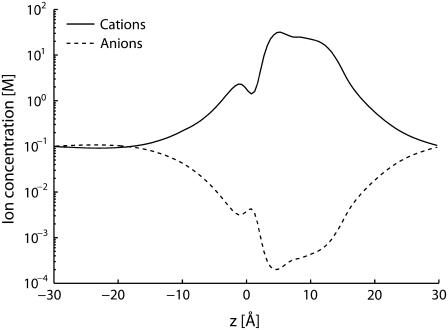
To establish whether the quantitative failure of the PNP theory is connected with charge-shielding overestimate, the ion concentrations inside the channel were analyzed. The amount of positive charge inside the SF (with boundary ion concentrations set at 100 mM and membrane potential at 25 mV) was ∼2 e for both channel models. Under the same conditions, the negative charge was <10⁻¹ e. Thus the positive charge is almost unshielded in the narrowest region of the channel, and consequently charge-shielding overrate cannot really be the main cause of the PNP failure. Ion concentrations along the channel pore further confirmed this conclusion (Fig. 4). The ratio between positive and negative charge inside the SF decreased when boundary ion concentrations were increased, and consequently charge shielding rose. Ion concentrations as high as 800 mM were tested and even in this case the ratio was higher than 10. Thus, even if the problem of shielding overrate at high concentration exists, it does not introduce quantitative deviations in the physiological range. Anion exclusion from the channel inside entails a channel current made up mainly of the positive charge flux. The ratio between positive and negative ion fluxes was higher than 3000 for both channel models (membrane potential set at 25 mV and ion concentrations at 100 mM). This ratio, just like the ratio between ion charges in the SF, decreased by increasing ion concentrations, but even at 800 mM it was higher than 200.

FIGURE 4.

Ion concentrations along the channel axis (Model I; Boundary ion concentrations set at 100 mM; Membrane potential at 25 mV).

The agreement between computed and experimental data improved using lower values of diffusion coefficients in SF and IC (see Fig. 3). All the data shown were obtained reducing both diffusion coefficients. Since most of the current is due to positive ion fluxes, similar results would have been reached by reducing just the positive ion diffusion coefficient. A reduction to 10% of diffusion coefficients in the SF greatly improved the agreement with the experimental currents, especially at high ion concentrations. In fact, current overrate does not increase when boundary ion concentrations are increased (see Fig. 3, C and D, dotted line). Thus, the reduction of diffusion coefficients, even restricted to a specific region of the pore, is enough to reproduce the current saturation at high ion concentrations. This result was confirmed for both channel models. Better agreement with the experimental data was reached (see Fig. 3) by reducing the diffusion coefficients also in the IC. Among the different diffusion coefficient profiles tested, the best agreement was reached by a reduction to 10% both in SF and IC, independently of the channel model. The agreement was particularly satisfactory for physiological conditions (membrane potential up to 100 mV; ion concentrations in the range 50–200 mM), where the mean relative deviation was 13% and 8% for Models I and II, respectively.

Similar results were obtained using the parameterization proposed by Nina et al. (32) for atomic radii and partial atomic charges (Fig. 5). Also with this parameterization the best agreement with the experimental data was reached by a reduction of diffusion to 10% in SF and IC, with a mean relative deviation of 15% and 20% for Models I and II, respectively.

FIGURE 5.

Current-voltage characteristics in 100-mM symmetric ion concentrations.

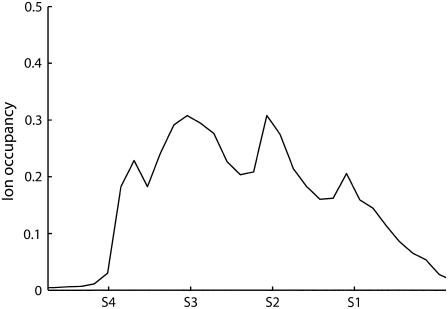
As a further test of the PNP theory in potassium channels, the positive ion distribution in the SF was analyzed. The channel inside was divided into slices orthogonal to the pore axis, and an ion occupancy index was defined in each slice according to

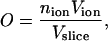(7)

where V_slice is the slice volume, n_ion the number of ions in the slice (computed by ion concentration), and V_ion the ion volume (defined according to standard Pauling radii). Independently of the channel model and the parameterization adopted, the cation occupancy profile shows four peaks in the SF, corresponding to the potassium binding sites S1–S4 (Fig. 6). The occupancy values in these peaks ranged from 0.2 to 0.5, depending on boundary ion concentrations. These results agree with the data obtained by x-ray crystallography (36). A dielectric constant change to 60 for water solution and 4 for membrane and protein did not significantly alter the previous results.

FIGURE 6.

Cation occupancy index inside the SF. The positions of the binding sites S1–S4 are marked on the ordinate axis. (Model I; boundary ion concentrations set at 100 mM; membrane potential at 25 mV).

DISCUSSION

The applicability of the PNP electrodiffusion theory to narrow ion channels (with internal radius lower than 2 Deybe lengths) has been challenged (21). The PNP theory describes the charge distribution by continuum functions, thus neglecting the discrete nature of ion charge. The consequence of this assumption is an overestimate of charge shielding near dielectric boundary surfaces. Overestimate of the shielding effect can lead to overestimate of both ion concentrations in the channel and ion fluxes. This inaccuracy was quantified by comparing the PNP theory with BD and dynamic lattice Monte Carlo simulations (DLMC) (24,37). The discrete nature of ion charges is preserved by BD and DLMC. The overestimate of the shielding effect introduced by PNP is reduced in the presence of fixed charges at the boundary surfaces. If the fixed charges are negative, as in the SF of potassium channels, many more positive than negative ions enter. The partial exclusion of negative charges from the channel inside limits the positive charge shielding.

The improvement of the PNP theory prediction in the presence of fixed charges was confirmed by comparison with BD using a simplified channel model (24), but to our knowledge no previous study was based on the experimental atomic structure of an ion channel. This study implemented a finite differences numerical algorithm to solve the PNP equations in three dimensions. The algorithm was applied to compute ion fluxes through the KcsA channel, described by its experimental atomic structure, partial atomic charges, and radii. KcsA was chosen for the wide availability of experimental functional data (fluxes and ion concentrations in the SF). The current predicted by the PNP theory overestimated the experimental data when diffusion coefficients were set at the bulk experimental values, but the overestimate was not due to wrong charge shielding. When the experimental atomic structure of the channel is used, the concentration of negative ions in the narrowest part of the channel is negligible, due to the presence of negative fixed charges in the channel protein. Thus in this region no shielding is introduced by the PNP theory.

PNP theory predictions were improved by using space-dependent diffusion coefficients. Four different diffusion coefficient profiles were tested. The best fit of the experimental data was achieved by a reduction of diffusion to 10% both in SF and IC. This result was independent of i), the specific model adopted for the open channel structure, ii), the atomic radii and partial atomic charges parameterization, and iii), small changes in the relative dielectric constants. The fit could be further improved for a specific parameterization and channel model by minor adjustments of the diffusion coefficients. However, the aim of this study was not to find this optimal fitting but to test the PNP theory in a channel model based on the protein atomic structure and to investigate the possibility to predict the experimental currents by adopting a reasonable reduction of diffusion coefficients inside the channel. According to these results we conclude that when the PNP theory is applied to a channel model based on the protein atomic structure, the experimental currents can be fitted by reducing ion motility inside the channel. Indeed, a reduction to 10% of the potassium diffusion coefficient in the SF agrees with MD simulations (8) and in further MD simulations, the potassium diffusion coefficient reduction in IC was gauged at ∼50% (34). The focus on the potassium diffusion coefficient is justified since the cation fluxes are far higher than anion fluxes. Application of the PNP theory to gramicidin, another narrow ion channel, required a similar reduction of diffusion coefficients to reproduce the experimental data (27,38). The agreement between our procedure and that used for gramicidin strengthens the case for a systematic reduction of diffusion coefficients in narrow ion channels when the PNP model is used.

The K⁺ fluxes are not only due to the shear transport within the channel but are also determined by association and dissociation processes with the local atomic charges of the filter (39). The latent periods due to these processes are not included in the PNP theory, and so a reduced diffusion coefficient of potassium compensates for this theory limitation. In practice, the value of the diffusion coefficients used to reproduce the experimental currents can be considered an effective parameter that is ultimately determined by the approximations used to obtain the PNP approach. The main approximations are i), the discrete nature of ions is neglected and aspects such as the exclusion of an ion from an already occupied binding site are not taken into account; and ii), the channel is modeled as a static structure, whereas the protein conformation changes are almost instantaneous with respect to the time involved in the conduction process (40).

Aside from these limitations, the simple method proposed reproduces the experimental current and the position of the ion binding sites quite well. Compared to an approach based on BDs, the PNP approach needs far fewer computational resources. PNP can therefore be a useful preliminary method to analyze the effects of protein structural changes on channel currents, providing a simple way to analyze channel dysfunctions.