Structure of Magainin and Alamethicin in Model Membranes Studied by X-Ray Reflectivity

Abstract

We have investigated the structure of lipid bilayers containing varied molar ratios of different lipids and the antimicrobial peptides magainin and alamethicin. For this structural study, we have used x-ray reflectivity on highly aligned solid-supported multilamellar lipid membranes. The reflectivity curves have been analyzed by semi-kinematical reflectivity theory modeling the bilayer density profile ρ(z). Model simulations of the reflectivity curves cover a large range of vertical momentum transfer q_z, and yield excellent agreement between data and theory. The structural changes observed as a function of the molar peptide/lipid concentration P/L are discussed in a comparative way.

INTRODUCTION

Antimicrobial peptides are membrane-active polypeptides with important functions in the innate host-defense system of many organisms. The structural mechanisms underlying their mode of action requires improved structural characterization on the molecular scale. Due to their relative structural simplicity, antimicrobial peptides may also serve as a testing ground for different experimental techniques addressing membrane polypeptides. Reviews on amphiphilic and antimicrobial peptides are given in the literature (1–8). Host-defense and cytolytic peptides are amphiphilic polypeptides of typically in between 20- and 40-amino-acid residues, with well-defined secondary structures formed by the interaction with the lipid bilayer. It has been shown that antimicrobial peptides interact directly with the microbial cell membranes rather than with specific membrane proteins, subsequently causing an increase in membrane permeability and cell lysis (see Fig. 1). Well-known examples are the cecropins expressed by insects. The first antimicrobial peptide discovered in vertebrates is magainin, expressed in the intestines and the skin of the frog Xenopus laevis. Antimicrobial peptides like magainin attack bacterial cell membrane but leave the plasma membranes of mammalian cells intact. Other examples of seemingly similar peptides are cytolytic also to mammalian cells, like the well-known alamethicin of the fungus Trichoderma viride. The interaction of phospholipid membranes with antimicrobial peptides is also pharmaceutically relevant (9). The understanding of peptide function in the natural organism should be accompanied by structural characterization of the peptides in model systems composed of only a few, controlled molecular components, e.g., hydrated phospholipid membranes consisting of controlled lipid and peptide components at varied molar peptide/lipid ratio, P/L.

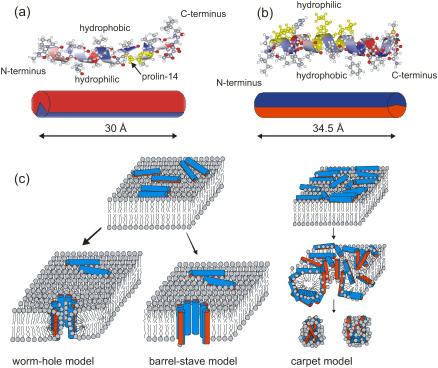
FIGURE 1.

(a) The α-helical conformation of alamethicin with its hydrophobic and hydrophilic sides of the helix (one of three crystal structures of alamethicin, the coordinate file 1AMT.PDB is taken from the Protein DataBank: http://www.rcsb.org/pdb), along with the representation as a amphiphilic cylinder, according to Fox and Richards (16) (bottom); the length of the molecule in this conformation is ∼30 Å. (b) The α-helical conformation of magainin with its hydrophilic and hydrophobic sides of the helix (one of 10 helical structures of magainin-2, the coordinate file 2MAG.PDB is taken from the Protein DataBank: http://www.rcsb.org/pdb), along with the representation as an amphiphilic cylinder, according to Gesell et al. (73) (bottom); the length of the molecule in this conformation is ∼34.5 Å. (c) Sketch of different models describing the functional mechanisms and underlying structure of antimicrobial peptides interacting with lipid bilayers, as discussed in the literature (74,2,4,75). (Left) The worm-hole model as proposed for magainin. (Top) Surface (S) state of antimicrobial peptides with the hydrophobic side groups anchored in the hydrophobic core of the bilayer. (Center) Barrel-stave model, as proposed for alamethicin. (Right) Carpet model: antimicrobial peptides crowding in the S state, and leading subsequently to micellation.

Despite recent advances stemming from a large number of different techniques, structural characterization of amphiphilic peptides in model lipid bilayers is a very difficult task. Secondary structure, including, e.g., the orientation and tilt of a helical axis, oligomerization of the peptides, and localization of individual residues, all need to be addressed. At the same time, the structural effects that the peptides cause on the lipid bilayers are important and need to be probed. While we are aware of the fact that no single technique can answer all these questions, we concentrate in this work on x-ray reflectivity carried out on highly oriented multilamellar stacks. This technique can give the average density profile ρ(z) of the bilayers along the membrane normal z after lateral averaging in x,y plane. For the x-ray reflectivity measurements, the incident beam with wave-vector k_i has to be collimated to less than a few 100ths of a degree and directed onto the sample at a glancing incidence angle α_i. The reflected intensity is then measured as a function of α_i under specular conditions, i.e., at an exit angle α_f = α_i with the wave-vector of the exit beam denoted by k_f. Thus, the momentum transfer of the elastic scattering q = k_f–k_i is always along q_z, with the z axis parallel to the sample normal. Reflectivity measurements at relatively small angles are sensitive to ρ(z) and respective changes upon peptide insertion, but cannot give any information on secondary structure. To this end, we have recently investigated aligned membranes of different alamethicin concentration P/L, mapping the wide-angle scattering distribution as a function of momentum transfer parallel q_‖ and perpendicular q_z to the oriented lipid bilayers (10). In the study, a surprisingly strong scattering distinctly different from the simulated scattering distribution of an ideal helix in the transmembrane state was observed for high P/L ≥ 0.05. It was explained by a transmembrane helical state with a compressed helical pitch with a broad distribution of transmembrane tilt angles. The helical peak was much less pronounced in magainin 2 (11). For both peptides, a strong effect on lipid acyl chain ordering was observed, reducing the short-range order of the chains by the perturbations of local packing induced by the peptides. From the analysis of peak intensity, the perturbation (strain) fields around a peptide were found to be medium-range.

Alamethicin is a 20-amino-acid peptide from the fungus Trichoderma viride, reviewed in the literature (1,2,12–14). Together with hypelcins, trichorzianins, and zervamicins it belongs to a class called peptaibols (14,15), which have similar structure and are also known to exhibit channel activity. Alamethicin is rich in hydrophobic amino acids, in particular α-methylalanine (Ala) and in the amino-acid α-aminoisobutyric acid (Aib), which supports the helical conformation. The sequence of alamethicin is Ac-Aib-Pro-Aib-Ala-Aib-Ala-Gln-Aib-Val-Aib-Gly-Leu-Aib-Pro-Val-Aib-Aib-Glu-Gln-Phl-OH. The crystal structure of alamethicin was solved more than 20 years ago by Fox and Richards by x-ray crystallography (16). In helical conformation, the length of the molecule is ∼30 Å; the Pro-14 residue acts as a bend in the helix (see Fig. 1). Alamethicin binds strongly to lipid bilayers and forms voltage-dependent, mildly cation-selective channels (17–21), which act as rectifiers (22). The channel activity occurs in discrete, multilevel conductances, suggesting a barrel-stave model (see Fig. 1) for the channel structure in which the discrete conductance steps result from a varying number of pore-forming peptides (18,23–25). The open alamethicin pore has been suggested to consist of 3–11 parallel helical molecules arranged around a water-filled pore, depending on the hydration and the lipid (26,27). The detailed structure of the channel is still under debate (28,29). The response to external voltage could be transmitted by the peptide dipole moment of ∼75 Debye = 16 e/Å (20) corresponding to a net +1/2 charge at the N- and a −1/2 charge at the C-terminus of the helix. A common structural model for alamethicin is based on a transmembrane orientation, with its N-terminus partially buried in the hydrophobic region of the lipid chains, while the C-terminus is supposed to be hydrogen-bonded to the water or the lipid headgroups (30–35). The ratio of peptides forming oligomeric channels as well as the conformational state of the majority population may strongly depend on the lipid type, voltage difference across the bilayer, temperature, humidity, and above all, the peptide/lipid concentration (P/L). NMR studies showed that the degree of helicity in the presence of lipid bilayers depends on the physical state of the lipid, the concentration P/L, and the presence of transmembrane potentials (1). By oriented circular dichroism and x-ray diffraction experiments, He et al. (36) demonstrated that up to a critical lipid/peptide ratio which is lipid dependent, alamethicin adsorbs on the membrane surface, resulting in a thinning of the membrane. At a concentration of P/L = 1:L15 or higher, all peptides adopt the transmembrane state. Circular dichroism spectroscopy experiments on alamethicin in DOPC membranes have shown that, at lower temperatures, alamethicin forms membrane-spanning channels while monomeric states are favored at higher temperatures (37). With increasing temperature the helix starts to partially unfold. Since the Ala residues stabilize the helical structure, the N-terminus is more stable than the C-terminus (38). Alamethicin in lipid bilayers has also been extensively studied by MD simulations (35,39–41). Tieleman et al. (42,43) studied alamethicin pores by MD simulation, in which the most stable model was found to be the hexamer. In DLPC the size of the pores corresponds to ∼8–9 monomers with a water pore of ∼18 Å in diameter, as inferred from a pore-pore correlation peak in small-angle neutron scattering (44). NMR studies showed that, in DMPC membranes, alamethicin in the transmembrane configuration is tilted by 10–20° to match the hydrophobic thickness of the bilayer (45).

The second amphiphilic peptide investigated in this study is the 23-residue peptide magainin from the granular gland of the skin of the African clawed frog Xenopus laevis, discovered by Zasloff (46). Its broad bacteriocidal, fungicidal, and virucidal activities helps to protect the host organism from infection. Similar amphiphatic and antimicrobial peptides were discovered subsequently in many vertebrate species. In the case of magainin, several studies conducted earlier have led to the following picture: Magainins interact directly with the microbial cell membrane rather than with specific membrane proteins (47), subsequently causing an increase in membrane permeability and leading to cell lysis. The mode of interaction depends strongly on the physicochemical properties (48), not only of the peptide, but also of the target membrane. By NMR spectroscopy, magainins were shown to be random-coiled in aqueous solution and to assume right-handed α-helical conformations in the presence of negatively charged phospholipid bilayers or organic solvents (reviewed in (1)). Helical wheel analysis of the 23-residue sequence GIGKFLHSAKKFGKAFVGEIMNS shows one side of the helix to be hydrophobic while the other is hydrophilic and cationic (4–5 positive net charges per molecule at neutral pH). The helical length of magainin is ∼34.5 Å (see Fig. 1). Therefore, a parallel binding state with the hydrophobic side groups indented into the lipid chain region seems plausible. More recently, Ludtke et al. (49) have found a transition from a parallel state of the helical axis at low and medium peptide concentration to a normal orientation interpreted as part of an oligomeric channel-forming process. Furthermore, the authors report a phase of highly correlated, hard-disk-like oligomeric channels in the binary-lipid system DMPC/DMPG, as deduced from a sharp interference maximum observed by in-plane neutron scattering (50,51).

In this work we use x-ray reflectivity to monitor the changes in the bilayer structure upon interaction with alamethicin and magainin. We use a wide range of phospholipid model membranes, to elucidate the role of initial bilayer thickness and of bilayer charge. This introduction is followed by Experimental Information, describing the model systems and sample preparation, as well as experimental details. The x-ray reflectivity model and data analysis is described in X-Ray Reflectivity: Modeling Building. The next section gives results for alamethicin and magainin-2, respectively, reconstituted in different lipid model systems. The article closes with a short summary and discussion in Summary and Conclusions.

EXPERIMENTAL INFORMATION

Materials

1,2-Dilauroyl-sn-glycero-3-phosphocholine (DLPC), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), 1,2-dimyristoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (DMPG), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-oleoyl-palmitoyl-sn-glycero-3-phosphatidylcholine (OPPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoserine (POPS) were purchased from Avanti (Avanti Polar Lipids, Alabaster, AL). Purity was claimed to be 99%, therefore these lipids were used without further purifications. Chloroform and 2-2-2-trifluoroethanol (TFE) (purity: 99.8%) were purchased from Sigma-Aldrich (Munich, Germany). The peptide magainin 2 (GIGKFLHSAKKFGK AFVGEIMNS) (product No. M7402) and alamethicin (XXPXAXAQXVXGLXPVXXEQ) (product No. A4665) were bought from Sigma-Aldrich (purity claimed >99%).

Preparation of lipid-protein multilamellar stacks

Multilamellar bilayers were prepared on cleaned silicon or glass wafers by spreading from organic solution, similar to the procedure first described by Seul and Sammon (52). The challenge is to simultaneously meet the solvation and wettability requirements. For sample deposition the substrates were cleaned by two 15-min cycles of ultrasonic cleaning in methanol, followed by two 15-min cycles in ultra pure water (specific resistivity ≥18 MΩ cm, Millipore, Bedford, MA), and drying under Nitrogen stream. The glass wafers were rendered hydrophilic by plasma etching in a plasma cleaner (Harrick Scientific, Ossining, NY) for 30 s. The lipid and peptide components were codissolved in the desired proportions (molar ratio P/L) in Chloroform/TFE (1:1) mixtures, at total concentrations between 4 and 20 mg/ml, depending on the total mass to be deposited. A drop of 0.1 ml was then carefully spread onto well-leveled and cleaned Si (100) or glass substrates of typically 15 × 25 mm² yielding average film thicknesses of ∼D ≃ 5–10 μm. The spreaded solution was allowed to dry only very slowly to prevent film rupture and dewetting. The films were then exposed to high vacuum over 24 h to remove all traces of solvent and subsequently rehydrated in a hydration chamber. The mosaicity in these samples was typically >0.02°. Oligo-membrane bilayers formed of stacks with a smaller number of bilayers N ≃ 10–20 were deposited by the spin-coating technique as detailed in Mennicke and Salditt (53). Typically, 0.1–0.2 ml stock solutions were spreaded on a wafer (a slow rotation was used to distribute the droplet), which was then subsequently rotated at 3000 rpm (Delta 10 spin-coater, BLE Laboratory Equipment, Singen, Germany) to achieve a thinner liquid film for bilayer nucleation, corresponding to a much reduced total mass, compared to the thick multilamellar stacks.

Sample environment

Sample environment for the control of temperature, humidity, and possibly other parameters can generally be made compatible with the x-ray experiments. Here, the sample chamber consisted of two stainless steel cylinders with kapton windows. The chamber was cooled or heated by a flow of 1:2 glycol/water mixtures from a temperature-controlled reservoir (Julabo, Seelbach, Germany). The samples were mounted in an inner chamber with a water reservoir to keep the relative humidity close to 100%. The temperature was measured in most cases in the inner chamber by a Pt-100 sensor, showing a stability of >0.03 K over several hours (54). A sensor for relative humidity (HIH2610-003, Honeywell, Freeport, IL) was additionally installed, but in most cases failed to give reproducible results near 100% relative humidity. In most of our measurements, uncharged membranes could not be swollen to their equilibrium periodicity in water vapor, even if the vapor was (nominally) at 100% relative humidity. This phenomenon, long known as the vapor pressure paradox, results from small temperature gradients in the sample chamber (55). In practice, we took the lamellar periodicity d of pure DMPC as a control of the humidity at a given temperature and chamber mounting. It is also possible to study solid-supported lipid films immersed in excess water (56,57). This is of interest for two reasons: Firstly, excess water warrants the physiologically relevant condition of full hydration. Secondly, membrane-active molecules can be adsorbed directly from the solution. However, films in excess water are unstable in the absence of osmotic agents (stressors). A thermal unbinding transition was observed (57,58), from a substrate-bound, multilamellar state at low temperatures to a state of freely dispersed bilayers in water at high temperatures. Unbinding can be suppressed (and the films thus stabilized) by adding an osmotic stressor to the excess water. The control of periodicity d can be achieved by the use of excess polymer solutions as osmotic stressors, and the equation of state can be determined (53,59). For charged systems, mixing of the bilayers and stressor polymers can be avoided by using polyelectrolytes of the same charge as the lipids. In this work, we used samples immersed in water for a DMPC/alamethicin series at only one osmotic pressure, using the solution of 14.2% polyethylene-glycol (PEG) as an osmotic stressor.

X-ray reflectivity experiment

Before x-ray reflectivity measurements, the resulting multilamellar stacks were inserted in a closed temperature and humidity-controlled chamber. The chamber consists of two concentric stainless steel cylinders, with kapton windows as mentioned above. The average temperature of the samples were kept at T = 45°C, well above the chain melting transition. The samples were mounted in the inner cylinder of the chamber facing a humid atmosphere set by a water reservoir placed at the bottom of the cylinder (59,60). The reflectivity experiments were carried out on the bending magnet beamline D4 of the DORIS storage ring at the synchrotron radiation laboratory HASYLAB/DESY (Hamburg, Germany) using a photon energy of 20 keV (i.e., λ = 0.62 Å), set by a Si⁽¹¹¹⁾ monochromator. The chamber was mounted on the z-axis diffractometer with the samples oriented vertically. To probe different P/L samples under exactly identical conditions, the series of up to five samples was placed on a multi-sample holder in the hydration chamber, stacking the samples in an array with the membrane-normals pointing perpendicular to the beam. Each sample could be translated into the beam and aligned separately. The reflectivity curves were measured with a fast scintillation counter (Cyberstar, Oxford instruments, Witney, Oxfordshire, United Kingdom), using motorized collimating slits on both incident- and reflected-beam paths. The reflectivity curves were corrected for ring current, sample illumination, and diffuse background (offset-scan). No radiation damage of the samples was observed from the instruments used, even after prolonged illumination.

X-RAY REFLECTIVITY: MODEL BUILDING AND DATA ANALYSIS

To evaluate the data, we have used full q_z-range fitting, since more structural information is exploited in this case than by the more empirical Fourier synthesis method, which uses solely the integrated peak intensities to compute the electron density profile, rather than full q_z range fits of the curves (61). Full q_z range fitting yields density profiles in absolute units, but is also time-consuming. As discussed above, a suitable model function must take into account effects of absorption, thermal fluctuations, static defects, and instrumental resolution, and yet keep the number of parameters manageable.

In semi-kinematic approximation, the x-ray reflectivity from an interface characterized by the electron density profile ρ(z) between a medium 1 with electron density ρ₁ and a medium 2 with density ρ₂ is given by (62)

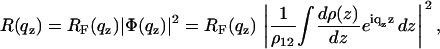(1)

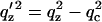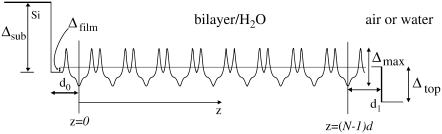
where R_F(q_z) is the Fresnel reflectivity of the ideal (sharp) interface between the two media, and ρ₁₂ is the density contrast. In this representation the interface normal is along the z axis and ρ(z) is the laterally (x,y plane) averaged density profile. R_F(q_z) can be conveniently written as |(q_z − q′_z)/(q_z + q′_z)|² with and the critical momentum transfer q_c as the only parameter. The critical momentum transfer or the critical angle is directly related to the density contrast by 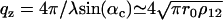with r₀ denoting the classical electron radius. The density increment ρ₁₂ is experimentally fixed by the measured q_c value, and is the natural unit for the density profile. Consider now a film of lipid membranes in a humidity environment with lamellar periodicity d. There are two interfaces, namely, the substrate-film and the film-air interfaces. More precisely, for hydrophilic substrates we expect a thin water layer with layer thickness d₀ (including a half-bilayer thickness; see Fig. 2). Similarly, we expect a thin water layer on top of the outermost bilayer with layer thickness d₁ (including a half-bilayer thickness, see Fig. 2). Hence the periodic water/bilayer density profile is bordered by two steps down in electron density from substrate to water and from water to air.

FIGURE 2.

A sketch of the electron density profile across the multilamellar film with the respective parameters used in text.

The electron density profile of the entire system consisting of N bilayers on a Si-substrate can thus be written as

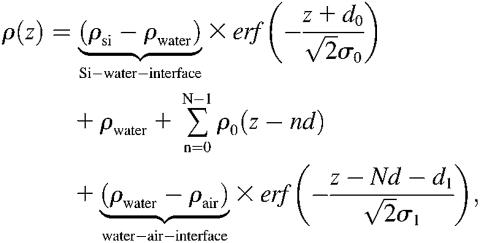(2)

where the electron density steps corresponding to the Si-water and water-air interface are smeared out by roughness parameters σ₀ and σ₁. This is accomplished by error functions 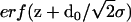and 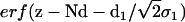. Here ρ₀ denotes the average bilayer electron density. After inserting Eq. 2 into Eq. 1, the model function can be written as

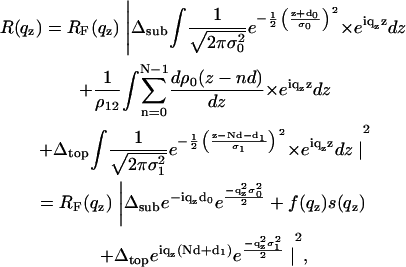(3)

where

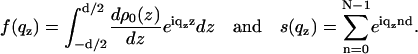(4)

Here, f(q_z) is the form factor of the bilayer and s(q_z) is the structure factor of the lipid bilayer stack. Some of the parameters needed to describe the film profile are defined in Fig. 2. The value Δ_sub denotes the density contrast between the substrate and a microscopic layer of water between film and substrate (e.g., silicon or glass). The value Δ_film denotes the contrast between water and the film, i.e., the water/lipid mixture; this quantity is typically very small and its influence on the reflectivity can be neglected for many lipids. Finally, the value Δ_top is the contrast between the film and medium 2 (air). All values are given in units of the net contrast rho₁₂, so that Δ_sub + Δ_film + Δ_top = 1. If the x-ray beam impinges from air (vacuum) onto the film on a silicon substrate, ρ₁₂ corresponds to the contrast of the air/silicon interface, and in the case of full hydration (bulk water) to the water/silicon interface (61). A less obvious situation is encountered, when the film/air interface is so spread out on a macroscopic scale due to thickness fluctuations (distribution of N, see below), that the beam enters the film with negligible reflection at its top. In this case, the observed critical angle corresponds to that of an interface between the average film medium (lipid/water mixture) and the silicon substrate, and correspondingly we have Δ_sub + Δ_film = 1. The value d₀ denotes the thickness of a thin water layer between the hydrophilized substrate and the first bilayer and d₁ the thickness of a water layer between (N – 1)^th bilayer and air. In the tables showing the results, we further use the parameter Δ_max, which is the prefactor of the bilayer form factor (amplitude of the density profile) in units of Δρ₁₂.

More generally, the structure factor for lipid membranes should also take into effect the thermal fluctuations, which are much more prominent for bilayers immersed in water than for the films hydrated from vapor phase at partial hydration. In the first case we used the structure factor

(5)

where u_m denotes the amplitude of thermal fluctuations for the m^th bilayer, calculated according to Constantin et al. (63). Finally, for multilamellar stacks the absorption of the x-ray beam in the sample has to be considered. This could be accounted for by imaginary wave vectors or as an approximation by an angle-dependent absorption term a(q_z), taking into account the path length of the beam in the sample (both incident and exit beams) with the total sample thickness D according to

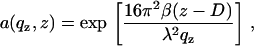(6)

where β is the imaginary component of the index of refraction which can be calculated from the molecular composition. The prefactors in the exponent arise simply from the relationship between angles α_i and q_z. In this case it did not play a significant (noticeable) role except at the Bragg peak position, in particular regarding the Bragg peak width. Since, however, the width is also influenced by finite domain size, instrumental resolution, extinction, and absorption, it was described by one parameter only in the simulation (the effective domain size L; see below) to avoid redundant parameterization. The structural parameters of the bilayer enter the reflectivity form factor of the bilayer s(q_z), defined as

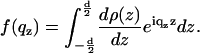(7)

To avoid the high number of parameters necessary in a box model to describe the bilayer density profile ρ_bl(z), we choose a parameterization of the bilayer in terms of its first No Fourier coefficients f_n,

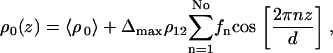(8)

where Δ_max is again an amplitude prefactor introduced for convenience to scale the f_n to f₁ = 1. The average bilayer density 〈ρ₀〉 is related to the substrate density ρ_sub by ρ₀ = ρ_sub – (Δ_sub – Δ_film) × ρ₁₂. The integral of the form factor can be solved analytically after inserting Eq. 8 into Eq. 7, yielding

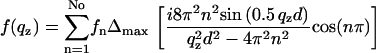(9)

The films prepared by spreading were in most cases inhomogeneous on the scale of a few tens of microns. Furthermore, a small fraction of the wafer exposed to the x-ray beam was not always covered with lipid. In these cases, the reflectivity of the blank substrate (fraction 1 – x) was discernible, particularly in the regime of total external reflection. This contribution, where present, was taken into account by superposition according to R(q_z) = (1 – x)R_blank(q_z) + xR_film, where R_blank and R_film denote the reflectivity of the wafer without and with the lipid film, respectively. Taking into account the roughness σ of the substrate, the additional component of the blank wafer is R_blank = R_Fblank(q_z) exp(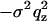). However, full coverage x ≃ 1 was reached for almost all samples after an iterative optimization of sample preparation avoiding dewetting and defects by choice of proper cleaning and solvent (mixtures). Of course, these lamellar defects might have an influence on the peptide lipid interaction. Firstly, we assume that the defects facilitate diffusion and distribution of peptides and water in the model membranes. Secondly, it is likely that peptides preferentially locate in the defect sites. Indeed optical microscopy shows that the borders of the lamellar domains change in morphology with P/L, pointing to the fact that the peptides change the line tension. However, at higher P/L values these effects are probably negligible in the sense that concentration of peptides in the membranes is not changed by enhanced partitioning at the domain boundaries. More important to the analysis is the fact that the films always consisted of different domains with a varying number of bilayers N. The domain size distribution resulted in a smearing of total thickness fringes (kissing fringes). Note that despite this lateral domain structure, all the domains were perfectly aligned with respect to the substrate, i.e., the mosaicity was in all cases below 0.02°. To account for the domain size variation, an exponential factor was included in s(q_z), according to

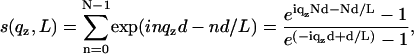(10)

where L is the effective (mean) domain size. Since the instrument resolution was typically >0.015°, mean domain sizes up to 2000 Å could be resolved. Of course, the exponential form of the cutoff or domain distribution factor in the sum is at this point a somewhat arbitrary choice, and a Gaussian distribution exp [−(nd/D)²] or other functional forms can also be chosen. However, we found that this form followed by a numerical convolution with the instrumental resolution gave quantitative agreement between the model and experimental lineshapes for thin films at partial hydration. Finally, combining the above equations, the expression

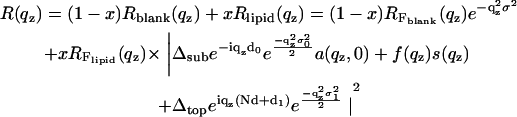(11)

is obtained and was used for the simulation and least-square fitting routines. The model reflectivity can now be studied with respect to all the parameters involved (61,64), in particular the parameters of the bilayer density profile. It is important to note that most of the parameters entering the model are either not free (but kept fixed) or are quite uncorrelated and linked to specific features in the reflectivity curve. Fixed are, for example, the substrate and water electron densities ρ_sub and ρ_H2O. Within a small range of variation, the substrate roughness σ is known from blank substrates after application of the same etching procedure. Together with the fixed values of ρ_sub and ρ_H2O the average film density ρ_film determines the density contrasts Δ_film and Δ_top. Lamellar periodicity d is immediately evident from the peak positions. The layer thicknesses d₀ and d₁ mainly influence the reflectivity below and around the first Bragg peak.

The instrumental resolution, in particular the x-ray divergence, causes a widening of the Bragg peaks, which is observable since the intrinsic width of multilamellar Bragg peaks is very small, given the high number of bilayers N. We therefore convolved the above model reflectivity with a normalized Gaussian

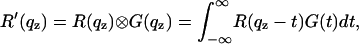(12)

where

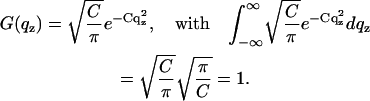(13)

The curve after convolution exhibits Bragg peaks with a characteristic width 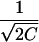. The convolution was carried out numerically as described in Li (64).

RESULTS

Alamethicin in model membranes

Aligned multilamellar membrane stacks of alamethicin/lipid bilayers have been deposited by the method described above for the following lipids: DLPC, DMPC, DPPC, DOPC, and POPC as well as a DMPC/DMPG (1:1) mixture. In all cases, a series of different concentrations (P/L values) was prepared and investigated, consisting of a minimum of three up to five different P/L values. The experiments have been carried out at the D4 bending magnet station, at a photon energy of E = 20keV. The sample temperature was set to T = 45°C to ensure that the bilayers were in the fluid L_α phase. However, this temperature is, for example, only 4°C above the chain melting of DPPC but >50°C above the one of DOPC, and the vicinity of a phase transition may have to be taken into account in the interpretation of results. Partial hydration was imposed by a water reservoir placed beneath the samples, and was monitored by a humidity sensor as well as indirectly by the multilamellar spacing d. To probe different P/L samples under exactly identical conditions, the series was placed on the multi-sample holder in the hydration chamber.

A total of 26 samples have been measured in the final setting of instrument and preparation conditions, after a cycle of iterative improvements. All curves have been treated with a full q_z fitting analysis. Here we can show only selected reflectivity curves and fits for illustration. The complete results are presented in Li (64). Let us first address a systematic variation of chain length of the saturated phosphatidylcholines DLPC, DMPC, and DPPC, with acyl chains of 12:12, 14:14, and 16:16 carbon groups, respectively.

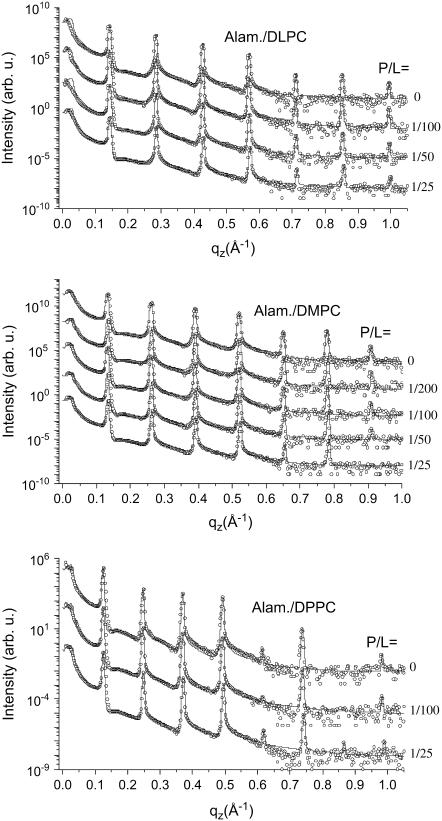
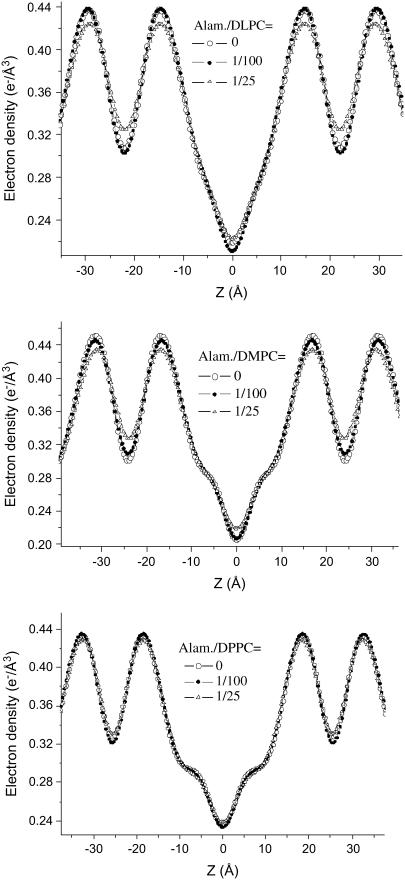
Fig. 3 shows the three corresponding P/L series of (top) alamethicin/DLPC, (middle) alamethicin/DMPC, and (bottom) alamethicin/DPPC, along with the fits shown as solid lines. For each series, the curves are shifted vertically for clarity. The reflectivity curves are plotted as a function of the vertical momentum transfer q_z after subtraction of the diffuse scattering (offset scan), and after illumination correction. The curves show the typical features of highly oriented multilamellar films: the plateau of total reflection at small q_z, and a set of sharp and intense, equidistant Bragg peaks. The parameters of the fits are given in Table 1. The hydration conditions in the chamber resulted in d ≃ 44.2, 48.4, and 51.1 Å, for DLPC, DMPC, and DPPC, respectively. This is an ideal condition for structural analysis, since the water layer is thick enough to warrant that the bilayer structure is not significantly changed by hydration. At the same time it is small enough to quench thermal fluctuations, leading up to seven lamellar Bragg peaks, and a measurable signal up to q_z ≃ 1 Å⁻¹. Fig. 4 shows the density profiles ρ(z) corresponding to the fits of the three P/L series shown in Fig. 3, again with (top) alamethicin/DLPC, (middle) alamethicin/DMPC, and (bottom) alamethicin/DPPC. The well-known interpretation of the profiles is the following: the two mean peaks of ρ (z) on either sides of the figure correspond to phospholipid headgroups, the two sides' minima to the water layer, and the central minimum is associated with terminal methyl moiety of the hydrocarbon chains. As usual we define the bilayer thickness as the distance between the two headgroup maxima (more precisely the maxima associated with the phosphorous group) d_pp. For completeness, the Fourier parameters defining the density profiles have been tabulated for all sample series in Tables 1 and 2.

FIGURE 3.

Reflectivity of multilamellar samples of DLPC, DMPC, and DPPC for increasing concentration P/L of alamethicin along with simulations (solid lines), shifted for clarity.

TABLE 1.

The parameters of sample series of alamethicin/lipid

Lipid	P/L	d	dpp	E	f1	f2	f3	f4	f5	f6	f7	Δmax
DLPC	0	44.23	29.66	0.5947	−1	−0.8	0.42	−0.18	−0.02	−0.025	−0.0115	0.2
DLPC	1/100	44.28	29.49	0.5959	−1	−0.87	0.4	−0.19	−0.024	−0.029	−0.011	0.2
DLPC	1/50	44.18	29.57	0.5548	−1	−0.76	0.38	−0.15	−0.017	−0.028	−0.0098	0.2
DLPC	1/25	44.01	29.59	0.4953	−1	−0.7	0.32	−0.13	−0.013	−0.025	−0.0077	0.2
DMPC	0	48.4	33.74	0.6126	−1	−0.65	0.45	−0.33	−0.038	−0.053	−0.0085	0.22
DMPC	1/200	48.2	33.59	0.6183	−1	−0.6	0.48	−0.3	−0.035	−0.042	−0.0085	0.22
DMPC	1/100	48.33	33.54	0.5716	−1	−0.65	0.4	−0.28	−0.032	−0.04	−0.006	0.22
DMPC	1/50	48.14	33.49	0.5722	−1	−0.62	0.41	−0.27	−0.028	−0.04	−0.0055	0.22
DMPC	1/25	48.01	33.8	0.4964	−1	−0.52	0.34	−0.23	−0.018	−0.034	0.0	0.22
DMPC/DMPG (1:1)	0	48.56	33.9	0.4509	−1	−0.475	0.33	−0.19	−0.033	−0.018	−0.0078	0.22
DMPC/DMPG (1:1)	1/100	48.34	33.53	0.5466	−1	−0.56	0.41	−0.24	−0.035	−0.024	−0.0076	0.22
DMPC/DMPG (1:1)	1/25	48.19	33.57	0.5223	−1	−0.54	0.38	−0.23	−0.028	−0.024	−0.0055	0.22
DOPC	0	50.75	35.49	0.6553	−1	−0.52	0.52	−0.32	−0.014	−0.011	0.006	0.2
DOPC	1/100	50.66	35.4	0.605	−1	−0.51	0.47	−0.27	−0.0125	−0.008	0.0028	0.2
DOPC	1/25	50.38	33.54	0.4989	−1	−0.41	0.39	−0.19	−0.0055	−0.0068	0.0	0.2
DPPC	0	51.12	37.24	0.5336	−1	−0.35	0.37	−0.36	−0.0065	−0.04	0.0	0.2
DPPC	1/100	51.12	36.91	0.5649	−1	−0.41	0.4	−0.35	−0.003	−0.038	0.0	0.2
DPPC	1/25	50.84	36.75	0.5131	−1	−0.37	0.37	−0.29	−0.0085	−0.036	0.0038	0.2
POPC	0	52.24	36.26	0.5698	−1	−0.52	0.45	−0.27	−0.045	−0.004	−0.006	0.22
POPC	1/100	51.07	35.89	0.5764	−1	−0.47	0.45	−0.25	−0.0105	−0.0121	0.0	0.22
POPC	1/25	50.89	35.9	0.5237	−1	−0.44	0.4	−0.22	−0.0082	−0.012	0.0	0.22
DMPC under 14.2% PEG solution	0	57.12	35.31	0.419	−1	−0.86	0.19	−0.0087	−0.038	0.0	0.0	0.22
DMPC under 14.2% PEG solution	1/200	57.3	36.3	0.4094	−1	−0.8	0.175	−0.0065	0.035	0.0	0.0	0.22
DMPC under 14.2% PEG solution	1/100	57.24	35.3	0.441	−1	−0.88	0.22	−0.0051	−0.056	0.0035	0.0	0.22
DMPC under 14.2% PEG solution	1/50	57.19	35.25	0.4518	−1	−0.89	0.23	0.0	−0.045	0.0	0.0	0.22
DMPC under 14.2% PEG solution	1/25	57.4	35.43	0.426	−1	−0.88	0.19	−0.011	−0.039	0.0	0.0	0.22

FIGURE 4.

Deduced electron density profiles ρ₀(z) of DLPC, DMPC, and DPPC, corresponding to the data of Fig. 3.

TABLE 2.

The parameters of sample series of magainin-2/lipid

Lipid	P/L	d	dpp	E	f1	f2	f3	f4	f5	f6	f7	Δmax
DMPC	0	49.63	34.36	0.4208	−1	−0.56	0.26	−0.1	0.026	−0.0057	0.0	0.22
DMPC	1/2000	49.86	35.27	0.3803	−1	−0.48	0.24	−0.095	0.033	−0.01	0.0	0.22
DMPC	1/1000	50.09	34.89	0.3038	−1	−0.45	0.2	−0.063	0.009	0.0	0.0	0.22
DMPC	1/500	48.64	33.65	0.545	−1	−0.64	0.36	−0.165	0.03	−0.015	0.0	0.22
DMPC	1/200	48.93	34.71	0.3147	−1	−0.42	0.21	−0.08	0.016	−0.007	0.0	0.22
DMPC	1/100	48.71	33.88	0.3667	−1	−0.49	0.24	−0.08	0.017	−0.0045	0.0	0.22
DMPC	1/50	48.37	33.14	0.4581	−1	−0.59	0.3	−0.095	0.022	−0.008	0.0	0.22
DMPC/DMPG (3:1)	0	51.66	33.29	0.4778	−1	−0.78	0.31	−0.069	−0.055	−0.00275	−0.0077	0.22
DMPC/DMPG (3:1)	1/200	51.94	32.88	0.4757	−1	−0.83	0.295	−0.04	−0.06	−0.0016	−0.0053	0.22
DMPC/DMPG (3:1)	1/50	54.23	34.03	0.2824	−1	−0.77	0.18	−0.011	−0.027	−0.002	−0.0016	0.22
DMPC/DMPG (3:1)	1/20	56.46	35.44	0.2836	−1	−0.72	0.065	−0.014	−0.008	−0.002	−0.002	0.22
OPPC	0	51.7	37.96	0.2715	−1	−0.26	0.21	−0.12	0.005	−0.006	0.0	0.22
OPPC	1/1000	51.67	37.45	0.4005	−1	−0.32	0.29	−0.19	0.0055	−0.0115	0.0	0.22
OPPC	1/200	51.31	36.97	0.2789	−1	−0.31	0.22	−0.09	0.005	−0.0018	0.0	0.22
OPPC	1/50	50.32	36.42	0.2184	−1	−0.26	0.2	−0.072	−0.0073	0.0	0.0	0.22
DMPC (oligo)	0	53.0	33.18	0.4678	−1	−0.82	0.32	0.012	−0.08	−0.00001	−0.014	0.17
DMPC (oligo)	1/200	54.0	33.6	0.4549	−1	−0.864	0.278	0.0052	−0.08	0.0	−0.014	0.1
DMPC (oligo)	1/50	56.4	31.52	0.352	−1	−1.1475	−0.08	0.06	−0.07	0.0	0.0	0.1
DMPC (oligo))	1/20	55.5	33.58	0.5317	−1	−1.07	0.3	0.025	−0.08	0.0	0.0	0.14
POPC (oligo)	0	53.26	35.92	0.5	−1	−0.53	0.4	−0.135	−0.047	0.0042	0.0077	0.13
POPC (oligo)	1/200	53.5	35.57	0.53	−1	−0.6	0.4078	−0.15	−0.053	0.0095	0.015	0.146
POPC (oligo)	1/50	54.1	34.26	0.476	−1	−0.67	0.39	0.019	−0.079	−0.004	−0.0012	0.155
POPC (oligo)	1/20	54.4	34.76	0.4507	−1	−0.67	0.33	−0.0015	−0.045	0.003	0.003	0.16
DMPC/DMPG (3:1) (oligo)	0	60.37	33.44	0.4346	−1	−1.3	0.0028	0.149	−0.07	0.003	−0.001	0.11
DMPC/DMPG (3:1) (oligo)	1/200	75.78	34.28	0.4722	−1	−2.9	−1.4	0.17	−0.1	−0.005	0.09	0.07
DMPC/DMPG (3:1) (oligo)	1/50	63.48	33.78	0.584	−1	−1.9	0.0	0.15	−0.04	−0.05	0.0	0.09
DMPC/DMPG (3:1) (oligo)	1/20	69.7	35.8	0.5125	−1	−2.0	−0.462	0.39	−0.2	0.0	0.0	0.05
POPC/POPS (3:1) (oligo)	0	63.67	34.76	0.5965	−1	−1.3	0.21	0.28	0.1	0.02	0.02	0.12
POPC/POPS (3:1) (oligo)	1/200	66.3	34.22	0.5152	−1	−1.5	−0.08	0.33	0.03	−0.1	0.02	0.1
POPC/POPS (3:1) (oligo)	1/50	67.0	37.8	0.5107	−1	−1.6	0.03	−0.238	−0.246	−0.2	−0.0213	0.08
POPC/POPS (3:1) (oligo)	1/20	72.5	35.82	0.4525	−1	−1.5	−0.27	0.25	0.076	−0.096	−0.01	0.09

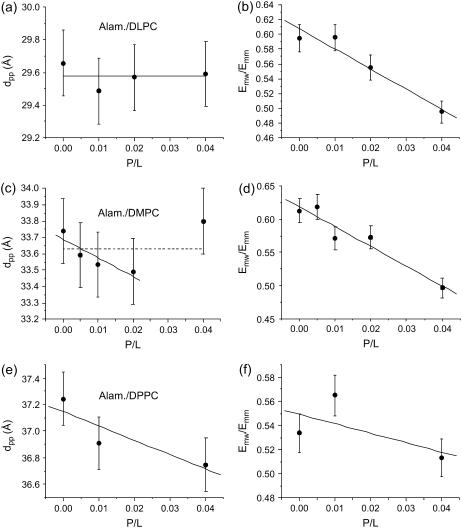
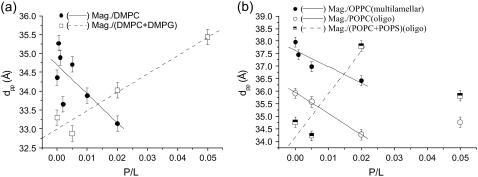
At the same time we display two parameters graphically to capture the most important changes in ρ(z): 1), the distance d_pp between the density maxima associated with the phosphorous groups; and 2), a shape parameter E, which we define as the ratio between the electron density contrast of the side to the main minima in ρ(z), i.e., E = E_mw/E_mm = (ρ_maximum – ρ_H2O)/(ρ_maximum – ρ_chain). Fig. 5 shows the variations of d_pp and E as a function of P/L for all three lipids: Fig. 5, a and b, for DLPC; Fig. 5, c and d for DMPC; and finally Fig. 5, e and f, for DPPC, respectively. For DMPC and DPPC, the linear fit to the bilayer thickness shows a slight decrease with P/L, while it stays approximately constant for DLPC. More precisely, for DMPC the bilayer thickness is first found to decrease, and then jumps up at P/L = 0.04. If, however, all data points are treated by a linear fit, the slope of the latter is close to zero within errors. Thus the data is consistent with no thinning effect. Note that a membrane thinning effect was reported by Huey Huang and co-workers for a number of antimicrobial peptides, including alamethicin (27). It was explained on the basis of bilayer thickness perturbations and elasticity theory (65,66). According to this theory, stress induced by adsorption of peptides at the surface is relaxed at a critical concentration P/L, when the peptides indent into the bilayer. The transition is thus denoted as a transition between the surface (S) and indented (I) states. In the I state, no thinning effect is observed (67). Therefore, the present data points to the fact that the alamethicin is already in the inserted state above the critical transition, in agreement with the previous finding that the critical concentration is rather low for alamethicin in DMPC and DLPC (68). For all three lipids, a pronounced decrease in the shape parameter E with P/L is observed, as in most peptide/lipid systems. The decrease can be explained by increasing disorder which washes-out the density profile, by increased density in the water layer, and/or an increase of the area per headgroup.

FIGURE 5.

Bilayer thickness d_pp and shape parameter E as a function of P/L, for (a,b) alamethicin/DLPC; (c,d) alamethicin/DMPC; and (e,f) alamethicin/DPPC, as a function of P/L.

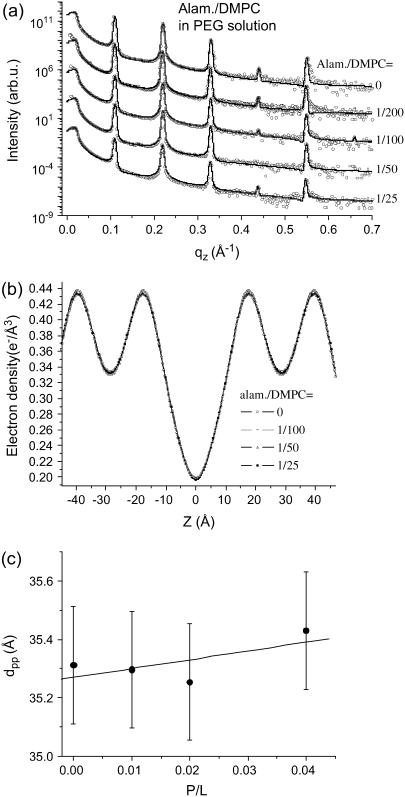
The decrease of the shape parameter as well as the bilayer thinning effect depends also on the swelling state. For comparison, one series of Alamethicin/DMPC membranes was measured while immersed in excess water solution with controlled osmotic stress. The osmotic stress was exerted by a solution of 14.2% PEG, corresponding to an osmotic pressure of 1.95 bar. Note that already gentle osmotic pressures prevent the membranes from unbinding and suppresses the strong thermal fluctuations typical for full hydration. The osmotic pressure corresponds to a lamellar periodicity d ≃ 57 Å (pure DMPC). Interestingly, this series did not show a thinning effect with P/L. The corresponding reflectivity curves are shown in Fig. 6 a, the resulting profiles in Fig. 6 b, and finally the extracted bilayer thickness in Fig. 6 c, all as a function of P/L. Obviously, the changes in the profiles ρ(z) are much smaller under these conditions. A fit of the data points in Fig. 6 c to a straight line (solid line in Fig. 6 c) gives a slope close to zero. Thus, similar to the sample series measured in vapor pressure (humidity chamber), bilayer thinning is not observed for these swollen samples immersed in solution. Note that besides the swelling state, the temperatures were also different for the two cases. The series in the humidity chamber was measured at T = 45°C, to keep the samples well above the main phase transition, even if the latter increases due to partial hydration conditions. Contrarily, the sample series in solution was measured at T = 30°C, since this temperature is already safely above from the phase transition at this higher swelling state. The difference in T also accounts for the higher d_pp values for the pure DMPC curve (P/L = 0).

FIGURE 6.

(a) Reflectivity of multilamellar samples of alamethicin/DMPC immersed in PEG solution along with simulation (solid line), shifted for clarity, and (b) the corresponding electron density profiles ρ(z), and (c) the bilayer thickness d_pp as a function of P/L.

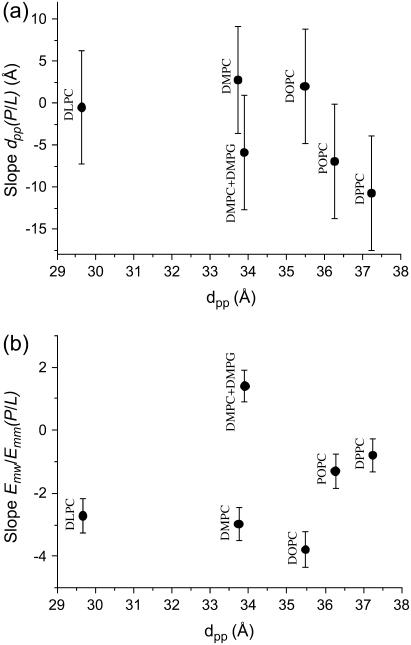
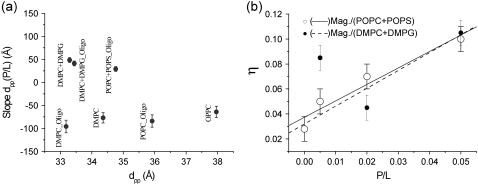
On the next level of data analysis, we now compare the fitted slopes of d_pp(P/L) and the fitted slope of the shape parameter E = E_mw/E_mm(P/L) for alamethicin in all measured lipid compositions (at identical conditions of partial hydration and T = 45°C in the humidity chamber). For this comparison, all P/L points have been included in the linear fits. Fig. 7 shows the results with the corresponding errors. The different lipids are ordered according to membrane thickness. What we see is that DLPC, DMPC (all points included), and DOPC do not exhibit a clear thinning effect, e.g., the error bars extend to the positive and negative axis, while DMPC/DMPG, POPC, and DPPC clearly show a bilayer thinning. The anionic DMPC/DMPG systems further also presents an exception to the trend in the shape parameter E. While all lipid compositions show the decreasing E, i.e., an increasingly washed-out profile, the anionic mixture shows an increase in the modulation of the electronic density profile, as described by the E parameter.

FIGURE 7.

(a) Bilayer thickness changes for alamethicin. The fitted linear slope of the d_pp(P/L) curves for alamethicin in various lipids and lipid mixtures, sequenced as a function of initial bilayer thickness. (b) Evolution of the shape parameter E as defined in the text for alamethicin in various lipids and lipid mixture. The fitted linear slope of the E(P/L) reflects the flattening of the profile which is observed for all lipids except the anionic DMPC/DMPG mixture.

Magainin in model membranes

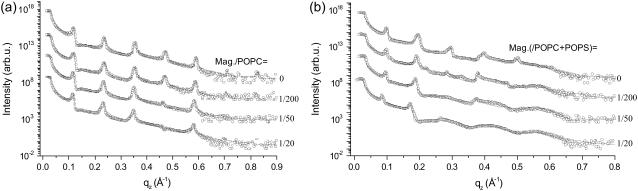
Aligned multilamellar samples of magainin/lipid model systems have been prepared by the method described above for the following lipids: DMPC, OPPC, and POPC, as well as for the mixtures DMPC/DMPG (3:1) and POPC/POPS (3:1). In all cases, a series of different concentrations (P/L values) has been prepared and investigated, consisting of a minimum of three, up to seven, different P/L values. The experiments have been carried out under identical conditions to the alamethicin series discussed above, except that in addition to thick multilamellar samples, thinner stacks, called oligo-bilayer systems, were also prepared by spin-coating (see Experimental Information). A total of 31 samples have been included in the analysis, which constrains us again to show selected data curves only.

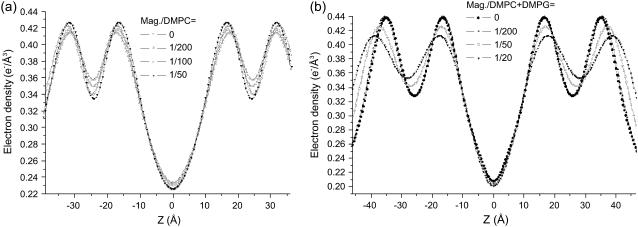
Fig. 8 shows the P/L series of (a) magainin/DMPC, and (b) magainin/(DMPC/DMPG) with a 3:1 molecular ratio of DMPC and DMPG. Since magainin carries 4–5 positive charges at neutral pH, the interaction of magainin with neutral and anionic lipids is very different. While most studies in solution are mainly sensitive to the changes following from the corresponding binding constants, the present sample preparation imposes a fixed peptide concentration at the bilayer. Thus, any changes can be directly attributed to a difference in the interaction, independent of changes in the binding constant. For the DMPC/DMPG mixtures, seven lamellar reflection orders are observed for the peptide-free bilayers, while only five orders persist in the presence of peptide sequence. This phenomenon is typical for the charged systems and even more pronounced in the oligo membranes (not shown). The effect leads to a smoothing of the deduced bilayer profile. Of course the local profile is not necessarily flatter for high P/L. Instead, this effect results from the increased lamellar disorder, since the determined profiles have to be regarded not as the intrinsic profile, but rather as a convolution of the intrinsic profile with the distribution function of the bilayer position, which broadens with increasing lamellar disorder. Fig. 9 shows the density profiles ρ(z) corresponding to the fits of the two P/L series shown in Fig. 8, again with (a) magainin/DMPC, and (b) magainin/(DMPC/DMPG) with a 3:1 molecular ratio of DMPC and DMPG. Fig. 10 shows the oligo-membrane P/L series of (a) magainin/POPC, and (b) magainin/(POPC/POPS) with a (3:1) molecular ratio of POPC and POPS. Fig. 11 shows the distance d_pp between the density maxima associated with the phosphorous groups for (a) multilamellar membranes of magainin/DMPC, multilamellar membranes of magainin/(DMPC/DMPG) (3:1) and (b) multilamellar membranes of magainin/OPPC, oligo-membranes of magainin/POPC, and oligo-membranes of magainin/(POPC/POPS) (3:1).

FIGURE 8.

Reflectivity of multilamellar samples of (a) magainin/DMPC and (b) magainin/(DMPC/DMPG) for increasing concentration P/L along with simulation (solid line), shifted for clarity.

FIGURE 9.

The electron density profiles ρ(z) corresponding to the data of Fig. 8.

FIGURE 10.

Reflectivity of oligo-membrane samples of (a) magainin2/POPC and (b) magainin/(POPC/POPS) (3:1 molecular ratio) for increasing concentration P/L along with simulations (solid lines), shifted for clarity. The interaction between magainin and anionic POPS leads to a particularly strong disordering effect.

FIGURE 11.

(a) The bilayer thickness d_pp corresponding to data of Fig. 8, and (b) the corresponding bilayer thickness d_pp of the oligo-membrane samples shown in Fig. 10 with additional data points of multilamellar OPPC (measurements not shown) included.

An increase in d_pp with P/L is observed for all sample series of anionic lipids. The effect of bilayer thickening with P/L is in striking contrast to the bilayer thinning observed for the zwitterionic phosphatidylcholines. In the case of bilayer thinning, elastic energy of the thinning is believed to drive the transmembrane insertion. Correspondingly, above a critical concentration (P/L)*, a transition from a parallel to a perpendicular (transmembrane) conformation has been reported for the model systems (50,67). In our experiments this scenario could account for the PC series, but not for the PC/PG and PC/PS mixtures. In these samples a strong increase in lamellar fluctuations is observed. Fig. 12 shows the (a) slope of d_pp for all magainin/lipids samples and (b) the Caillé parameter η for magainin/(POPC/POPS) (3:1) and magainin/(DMPC/DMPG) (3:1). Note that the disordering effect in the anionic membrane systems is so strong, that the reflectivity curves cannot be fitted without including the Caillé structure factor. For details of the structure factor used, we refer to the article by Constantin et al. (63), where the discrete Caillé model has been calculated for a stack with one interface fixed by the boundary condition of a flat substrate. Note that for the other sample series such a generalized structure factor was not necessary, since the conditions of partial hydration and the flat substrate quench long-range thermal fluctuations, and the peak lineshape was quite close to that of a perfect one-dimensional lattice. Obviously, this was no longer true of magainin on anionic membranes. For completeness, the Fourier parameters defining the density profiles have been tabulated again for all sample series in Table 2.

FIGURE 12.

(a) Bilayer thickness changes for magainin. The fitted linear slope of the d_pp(P/L) curves for various lipids and lipid mixtures, sequenced as a function of initial (pure lipid) bilayer thickness. (b) Caillé-parameter for magainin in anionic lipids. The increasing of the Caillé parameter reflects the disordering effect between magainin-2 and anionic DMPG and POPS.

SUMMARY AND CONCLUSIONS

In summary, for most lipids, interaction with magainin and alamethicin leads to a decrease in the amplitude of the averaged density profile with P/L, quantified by a decreasing shape parameter E. This flattening of the density profile with concentration seems to be a characteristic feature of many membrane-active peptides. It can be explained by a lateral variation of bilayer thickness and position arising from strain fields around absorbed peptides. Averaging in the x,y plane, these variations lead to a flattening or washing-out of ρ₀(z). For some combinations of lipid and peptides, e.g., alamethicin in DMPC/DMPG mixtures, this flattening is not observed, pointing to a particular interaction.

A second important result concerns the variation of bilayer thickness with P/L, often encountered in the form of a thinning effect. This thinning effect in alamethicin samples is weak, but observable for DMPC/DMPG, POPC, and DPPC, while the error bars are too high to determine a clear trend in DLPC, DMPC, and DOPC. Note that the thinning was in many samples <1 Å, thus smaller than a single C-C bond, underlining the fact that this is really an average effect on the bilayer thickness which originates from averaging over a laterally inhomogeneous thickness when peptides are present. In many cases the variations in the lamellar spacing d are stronger, in particular for charged lipids and for charged peptides (magainin) (see Tables 1 and 2). The distance d results from a subtle equilibrium of attractive and repulsive forces, which may change with P/L mainly due to different charging and screening effects as well as steric effects. We do not analyze this aspect of the data in the present work.

A pronounced decrease in the shape parameter E with P/L is also observed in most alamethicin samples systems, with the exception of the (DMPC/DMPG) mixtures. In contrast to alamethicin, the changes in d_pp(P/L) are much more pronounced for magainin. The modulus of the fitted slopes is approximately tenfold higher. Thinning is observed for all zwitterionic PC headgroup lipids, while the mixtures containing anionic PS or PG headgroups exhibit a clear thickening of the bilayer with increasing P/L. This effect may be explained by the interaction of the highly positively charged magainin (Z ≃ 4–5 at neutral pH) to the anionic headgroups. In a simple picture, the interaction may lead to a decrease of the area per headgroup by screening of repulsive forces between adjacent headgroups and hence to a thickening of the bilayer. Finally, the increasing lamellar fluctuations for magainin in anionic bilayers were quantified by the unitless Caillé parameter η. Thermal fluctuations are typically weak for solid supported membranes, since the wafer surface imposes a flat boundary condition. Therefore, at partial hydration levels, e.g., of 1.5 nm water in between PC bilayers, the effect of thermal fluctuations can be neglected for solid supported films. However, fluctuations and/or lamellar disorder become important in solid supported bilayers under conditions of full hydration (see (63,69)). Magainin in anionic membranes presents an exception to this rule, since it induces strong fluctuations or disorder even at partial hydration. Note that many studies report a strong interaction of magainin with anionic membranes, e.g., due to enhanced binding constants. In this study, the P/L ratios are fixed by the preparation for all lipids alike, and the differences between zwitterionic and charged headgroups can therefore be directly attributed to different interactions in the bound state. The interaction between magainin and anionic bilayers is particularly strong. With respect to the classical models described in the Introduction and shown in Fig. 1, the present data shows that magainin in anionic membranes does indeed lead to a more disordered state of the bilayer, but not really a strong destabilization as predicted by the carpet model. Contrarily, most model membranes show only a moderate increase in fluctuations and small changes in the density profile, consistent with the inserted pore-forming state at high concentration.

Concluding on the use of x-ray reflectivity, the direct changes in the density profile ρ₀ due to the peptides themselves must be distinguished from the indirect changes which the peptides impose on the lipid bilayers. Therefore, it is important to always measure a series of different P/L ratios. Secondly, ρ₀(z) must be determined on an absolute scale and with highest possible resolution. In this work the bilayer reflectivity curves were analyzed by semi-kinematical reflectivity theory (61,63,64). The absolute scaling of the intensity to the total external reflection and the critical angle α_c provided two extra parameters which make it possible to determine the electron density profile on an absolute scale (e/ų). Moreover, since the full q_z-range can be used for data analysis by fitting the reflectivity curve to a parameterized model ρ(z), a reasonable resolution in ρ(z) can also be reached for fully hydrated systems, in particular if the thermal fluctuations are taken into account. In most studies of oriented bilayers, only the integrated Bragg peaks of the multilamellar samples are exploited for data analysis, using a discrete set of Fourier coefficients f_n as described in the literature (70–72). This approach is easier and quicker, but somewhat restricted. A detailed comparison of the Fourier synthesis and the full q-range simulations is found in Li (64). The aim must be to reduce systematic and statistical errors as much as possible, since the expected direct effects in ρ(z) are small, in particular at medium P/L, since the density profile ρ(z) is averaged over the plane of the membrane (x,y plane). Still we see that despite a large effort and exhaustive data harvest by P/L series, the resulting ρ(z) curves cannot be readily interpreted in terms of peptide conformation and position. However, the results quantify different structural effects of lipid-peptide interaction in a comparative approach, and underline the different responsiveness of lipid model bilayers even to moderate peptide concentrations P/L, similar to those expected in the physiological context.

Important challenges in the structural biology of antibiotic peptides are linked to the question: How does the conformation and interaction of an antibiotic peptide depend on the type of membrane? To answer this, the reflectivity methods used in this work should be applied to an even wider range of different lipid compositions. Mixtures representing the eukaryotic membrane (in particular the mammalian cytoplasmic membrane rich in PC, SM, PS, and cholesterol) should be compared to models representative of bacterial membranes rich in PG and PE. In this work, we have concentrated on the two important antimicrobial peptides alamethicin and magainin, interacting mainly with single and two-component lipid membranes. The emphasis was on the membrane-thinning effect, as a function of the two parameters of chain length and surface charge. Further technical advancement should focus on 1), standardization of reflectivity analysis, and the development of dedicated software including the effects of thermal and static defects; 2), use of anomalous reflectivity for contrast variation on heavy atom labels; and 3), the helix scattering and direct detection of the molecular form factors by two-dimensional reciprocal space mapping. Finally, synergies between interface-sensitive scattering methods and spectroscopic techniques should be exploited.