Analysis of Transient Behavior in Complex Trajectories: Application to Secretory Vesicle Dynamics

Abstract

Analysis of trajectories of dynamical biological objects, such as breeding ants or cell organelles, is essential to reveal the interactions they develop with their environments. Many previous works used a global characterization based on parameters calculated for entire trajectories. In cases where transient behavior was detected, this usually concerned only a particular type, such as confinement or directed motion. However, these approaches are not appropriate in situations in which the tracked objects may display many different types of transient motion. We have developed a method to exhaustively analyze different kinds of transient behavior that the tracked objects may exhibit. The method discriminates stalled periods, constrained and directed motions from random dynamics by evaluating the diffusion coefficient, the mean-square displacement curvature, and the trajectory asymmetry along individual trajectories. To detect transient motions of various durations, these parameters are calculated along trajectories using a rolling analysis window whose width is variable. The method was applied to the study of secretory vesicle dynamics in the subplasmalemmal region of human carcinoid BON cells. Analysis of transitions between transient motion periods, combined with plausible assumptions about the origin of each motion type, leads to a model of dynamical subplasmalemmal organization.

INTRODUCTION

Complex trajectories are present at all scales in biology. Migrating birds travel thousands of kilometers every year (1). On a smaller scale, ants describe circuitous paths of tens of meters when looking for food (2). Neurons can move hundreds of micrometers in the developing cerebral cortex (3), whereas organelle traffic in the cytoplasm occurs on the micron scale (4). Finally, diffusion of proteins in the plasma membrane can occur on the nanometer scale (5). These trajectories are often characterized by transient behaviors such as temporary confinement in a particular zone followed by periods of random diffusion or directed movement. Scrutinizing these multifaceted trajectories is essential in revealing the biophysical processes that generate them and the interactions of the tracked objects with their environment.

Study of complex trajectories requires an appropriate analysis method to extract and characterize the transient behaviors they contain. This characterization should allow both the classification of the transient motion (diffusive, constrained, directed…) and the evaluation of associated parameters (diffusion coefficient, velocity…). Some efforts in dissecting such complex trajectories have been made to study various biological processes such as fibroblast migration (6), microtubule dependent transport of pigment granules in melanophores (7), or protein motions in the cell membrane (8,9). However, the methods developed to analyze these trajectories are usually designed to highlight only a particular behavior such as confinement or directed motion. In consequence, these methods are rather specific and can hardly be applied to other biological systems.

In this article, we describe an efficient motion analysis method allowing detection and characterization of the different kinds of transient movement a single particle may exhibit. This method overcomes the two main difficulties associated with the analysis of complex trajectories: i), detection of transient periods whose durations are highly variable and not known a priori, and ii), discrimination between true nondiffusive behavior and temporary apparent directed or confined periods originating from pure Brownian dynamics.

We have applied our analysis method to the study of secretory vesicle dynamics near the plasma membrane of endocrine BON cells. The BON cell line, which secretes serotonin, is derived from a human carcinoid tumor (10). Secretory products of these tumors are responsible for symptoms such as flush, diarrhea, and vasoconstriction. Individual secretory vesicles were imaged using total internal reflection fluorescence microscopy (TIRFM), also called evanescent wave microscopy. This technique exploits evanescent wave properties to selectively image fluorophores in an aqueous or cellular medium very near a glass surface (11,12). Thus, movements and fusion of individual labeled vesicles located near the plasma membrane can be observed with low background due to the absence of out-of-focus fluorescence (13,14). Using typical penetration decay constants of 100–300 nm for the evanescent wave, the observed region corresponds to a 200–600 nm deep layer of cytoplasm located just beneath the plasma membrane.

In various cell types, previous TIRFM studies have shown that vesicle behavior near the plasma membrane is far from simple: the mobility of a vesicle seems to depend on its distance from the plasma membrane (15,16) and some vesicles exhibit non-Brownian dynamics such as constrained or directed motion (14,17). This diversity of motion behavior is perhaps not surprising, given the complexity of the vesicle environment in this region of the cell: subplasmalemmal vesicles are immersed in a dense cytoskeleton of actin filaments and microtubules (18) and can also interact with the plasma membrane. This brings up the important question of whether vesicle dynamics can reveal interactions between the vesicles and their surroundings. In this context, the analysis method presented here should give precise information on the relationship between secretory vesicles, cytoskeleton, and cellular membrane.

MATERIALS AND METHODS

TIRFM setup

An upright microscope (BX50WI, Olympus, Tokyo, Japan) was adapted to TIRFM by the prism approach (12) (see Fig. 1 for a schematic view of the setup). To generate the evanescent wave, light from a 488 nm argon laser (177-G02, Spectra Physics, Newport, Irvine, CA) radially entered a BK7 glass hemisphere and was reflected from its planar face at a supercritical angle. The hemisphere was optically coupled to the glass coverslip on which cells were cultured, using immersion oil (518 C, Carl Zeiss MicroImaging, Oberkochen, Germany). The hemisphere also played the role of a light condenser for bright-field observations.

FIGURE 1.

Schematic setup of the TIRF microscope. A translation of the mirror modifies the evanescence depth without changing the illuminated area at the glass/cell interface.

The intensity of the evanescent wave decays exponentially in the direction normal to the interface. The penetration depth δ is defined as the distance over which the intensity falls off to 1/e of its value at the surface, and is given by

(1)

where λ = 488 nm is the wavelength of the laser beam, θ its incidence angle, and n_g and n_c are the refractive indices of the glass coverslip and the cell medium, respectively (see Calibration of the evanescence depth). According to Eq. 1, the penetration depth can be modified by varying the incidence angle of the laser beam (19). We used a telecentric system composed of a movable mirror and a lens, whose focal point coincided with the center of the hemisphere to tune the evanescence depth, without modifying the illuminated area on the cover slip (Fig. 1).

During time-lapse acquisition, the laser power was attenuated to ∼1 mW and illumination was restricted to image acquisition by a shutter coupled to the camera to minimize photobleaching. Cells were observed through a water immersion objective (60×, 0.9 NA, Olympus), and frames were captured with a charge-coupled device camera (CoolSnap HQ, Photometrics, Roper Scientific, Tucson, AZ) after choosing a region of interest typically encompassing a single cell. Under these conditions, one pixel corresponded to 107.5 nm. Unless stated otherwise, frames were acquired for 60 s at 10 Hz using Metamorph software (Universal Imaging, Molecular Devices, Downingtown, PA). These acquisition rates and durations compare quite favorably with what has been reported by other workers in similar systems (20–22).

Calibration of the evanescence depth

To know the thickness of the cell region illuminated using TIRFM, the penetration depth of the evanescent wave must be determined. However, this is a function of the refractive index of the cell medium (see Eq. 1), which is not well defined. Consequently, the evanescence depth had to be evaluated experimentally. To do so, intensities of fluorescent beads adsorbed onto living COS-7 cells were measured as functions of their vertical positions, as previously described by Steyer and Almers (14). These measurements were repeated for different incidence angles of the laser beam. The evanescent wave profiles thus obtained were well-fitted by simple exponential decays that corresponded to the theoretical profiles. From these fits, evanescence depths between 200 and 300 nm were obtained with a relative error of 15% (see supplemental Fig. 1 for an example). Using Eq. 1, we then deduced an average refractive index, n_c, for the cell medium of 1.37 ± 0.01, in agreement with previous estimations (23,24). It was assumed that the same refractive index was also valid for BON cells. Penetration depths used for time-lapse imaging and three-dimensional (3D) single-particle tracking were calculated with this cell medium refractive index.

Cell culture and vesicle labeling

COS-7 cells were routinely cultured in Dulbecco's modified Eagle's medium containing 4.5 g/L glucose and supplemented with 10% fetal bovine serum in 5% CO₂ at 37°C. The human carcinoid BON cell line was kindly provided by C. M. Townsend (University of Texas Medical Branch, Galveston, TX). BON cells were maintained in Dulbecco's modified Eagle's medium-nutrient mix F-12 (1:1), supplemented with 10% fetal bovine serum in 5% CO₂ at 37°C. Dense core secretory vesicles were labeled using the fluorescent chimera neuropeptide Y-green fluorescent protein (NPY-GFP), which is the fusion between the human proneuropeptide Y and the enhanced green fluorescent protein (25). This chimera specifically labels vesicles by accumulating inside these organelles. Expression of NPY-GFP in BON cells was obtained by transfection with a plasmid encoding this chimera (a gift of W. Almers, Oregon Health Sciences University, Portland, OR). In brief, cells (2 × 10⁶ in phosphate-buffered saline) were mixed with DNA vectors (2.5–10 μg) and transfected by electroporation using a PS10 electropulsator (Jouan, Thermo Electron, Woburn, MA). Stable transfectants were selected in the presence of 800 μg/ml G418 (Sigma-Aldrich, St. Louis, MO) and screened by fluorescence microscopy to detect NPY-GFP expression. All TIRF experiments were performed on a BON NPY-GFP clone, named BC6, which was selected and plated on uncoated glass-bottom dishes (P50G-1.5-14-F, MatTek Cultureware, Ashland, MA). Observations were performed at 31–33°C, between 48 and 72 h after plating. During TIRFM observations, cells were immersed in Locke solution (5.6 mM glucose, 3.6 mM HCO3⁻, 159.6 mM Cl⁻, 157.6 mM Na⁺, 5.6 mM K⁺, 5 mM Hepes-NaOH, 2.5 mM CaCl₂, 1.2 mM MgCl₂).

Cell stimulation by Ca²⁺ uncaging

To induce rapid elevation of intracellular free Ca²⁺ concentration, cells were incubated for 60 min in Locke buffer with 30 μM o-nitrophenyl-EGTA-acetoxymethyl ester (NP-EGTA-AM, Invitrogen, Carlsbad, CA) followed by 60 min incubation in the culture medium. Under the TIRF microscope, brief pulses of ultraviolet light were generated every 10 s using a xenon arc flash lamp (Rapp Optoelectronic, Hamburg, Germany) coupled to the epifluorescence port of the microscope using a liquid light guide. For these experiments only, BON cells transiently expressing NPY-GFP were used 48–72 h after transfection.

Three-dimensional single-particle tracking of secretory vesicles

Time-lapse sequences of BON cells, whose vesicles were labeled with NPY-GFP, were acquired to analyze vesicle movements. In these sequences, most vesicles appeared as diffraction limited fluorescent spots, since their sizes were similar to those obtained with 200 nm diameter fluorescent beads. However, a spot may appear artificially large due to the blooming effect in fluorescence detection, depending on the display settings chosen. Thus, in a collection of spots with different brightnesses such as the vesicles in video 1 of the Supplementary Material, the brightest spots appear larger than the diffraction limit. From the stacks of images, two-dimensional (2D) vesicle trajectories were obtained by single-particle tracking using the Metamorph software. We did single-particle tracking one vesicle at a time. The position of a given vesicle (x, y coordinate) on each frame was detected as the centroid of the fluorescent spot corresponding to that vesicle (26). To minimize positioning error, it was important to exclude as much of the image background as possible from the centroid calculation. This was achieved by setting a threshold brightness. Pixel values below the threshold were taken to be zero, whereas those above remained unchanged. Using this method, fluorescent spots were tracked along the sequence until the spot was lost from view or coalesced with another spot (corresponding to the encountering of two vesicles). A very small fraction of the fluorescent spots appeared as if composed of a few vesicles. Such spots were not tracked.

As the intensity of the evanescent wave decreases exponentially with a known penetration depth in the direction orthogonal to the cover slip (the z axis), displacements of a fluorescent vesicle along this axis can be obtained by measuring variations of its intensity (14–16). To evaluate the intensity of a vesicle in a given frame, its fluorescence profile was first plotted as a function of the distance from its center. Vesicle intensity (with the local background subtracted) was then defined by the area under a Gaussian fit to this profile. This was done using a method similar to that of Zenisek et al. (27). Concentric circles were drawn around the 2D vesicle position with radii, r, spaced in increments of 1 pixel unit. The intensity for r = 0 was the gray value of the pixel (16-bit images) which corresponded to the vesicle center. For , fluorescence at 100 equally spaced points on each circle was measured and averaged. Each of these averaged values corresponding to a given circle with a radius r contributed to the building of the vesicle fluorescence profile I_fluo. This procedure was continued for increasing r, until r reached a maximum value r_max for which the fluorescence intensity stopped decreasing. The intensity corresponding to r_max was taken as the local background intensity. The intensity profile was then fitted with a one-dimensional Gaussian function

(2)

with I₀ and σ the free parameters and I_bg = I_fluo(r_max) the local background intensity. Vesicle intensity corresponded to the area under the Gaussian fit given by 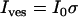. Intensity variations along a trajectory, I_ves(t), were obtained by repeating this procedure frame by frame. Vesicle coordinates orthogonal to the observation plane (relative to the initial position) were evaluated using the relation

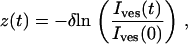(3)

where δ is the penetration depth of the evanescent wave.

To evaluate the precision of this approach, we first tracked fluorescent latex beads (200 nm diameter, labeled with fluorescein (Polysciences, Warrington, PA)) immobilized on a coverslip. The laser intensity was adapted to get signal/noise ratios for the beads similar to those typical for vesicles, and an evanescence depth of 200 nm was used. An important question is whether there is anisotropy between the normal and lateral precision in position detection. Fig. 2 shows the resolution anisotropy, 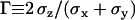, defined as the ratio of the root mean-squared error in the normal (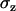) to the lateral direction 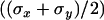, as a function of the signal/noise ratio (S/N) measured following Cheezum et al. (26). For the S/N values averaged over the beads (), a root mean-squared error of 16 (15) nm with a standard deviation of 3 (3) nm in particle position for the x, y (z) directions was found. Similar values were obtained for the vesicles in the stalled class. That is, at this evanescence depth, the precision was similar for the detection of lateral and normal movements. This lack of asymmetry in the detection precision considerably facilitates analysis and interpretation of 3D trajectories.

FIGURE 2.

Resolution anisotropy, 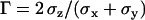, versus S/N for fluorescent beads and vesicles (see text).

To validate our 3D tracking algorithm, we applied it to follow the dynamics of fluorescent beads immersed in a medium of high viscosity to have diffusion coefficients as close as possible to those measured for the vesicles (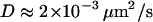 for diffusing vesicles; see Table 2). We used a glycerol-water mixture (75–80% of glycerol by volume), whose viscosity was ∼50–80 cP. At higher concentrations of glycerol, it is difficult to obtain an evanescent profile with the minimum incidence angle we can use in our setup (73–74°), since the refractive index of glycerol is close to that of BK7 glass (n_glycerol = 1.48). These viscosities were actually not high enough for vesicle-sized beads (200–300 nm diameter) to diffuse slowly enough. To obtain slower dynamics, we used larger beads (475 nm diameter), which appeared slightly larger than those corresponding to the vesicles, at a penetration depth of 200 nm. From the 3D trajectories, diffusion coefficients of the beads were calculated to be (see below) 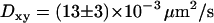and 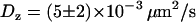. These values are in good agreement with the hydrodynamic theory for a particle in the vicinity of a solid boundary (28–30). For the same bead diameter and medium viscosity and considering that the mean distance between the bead and the wall is comparable to the evanescence depth, the theoretical values for the diffusion coefficients are and 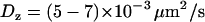, taking the viscosity of the medium to be 80 and 50 cP, respectively. We also used beads of 200 nm diameter, more closely matching the sizes of the vesicles in BON cells. For such small-sized beads, however, the hydrodynamic theory breaks down and the ratio 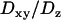becomes even larger for a particle undergoing Brownian dynamics. Thus, for 200 nm diameter beads 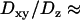5–6 was found in this work, whereas Banerjee et al. reported 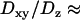3–4 (30). The difference between the two measurements on these small, highly mobile beads may be explained by a stronger “sectioning effect” in our case, i.e., that in the z direction, one is biased to detecting slower moving beads, since they remain longer in the evanescent zone. For the detection of vesicles, however, the sectioning effect is rather small, since the mobility of most of them is much smaller than the mobility of the 200 nm beads used here.

TABLE 2.

Characteristics of the four motion classes exhibited by secretory vesicles; values are given as mean ± SD

Motion class	Characteristics
Stalled	Mean duration	8.5 ± 0.3 s
Constrained	Mean duration	20 ± 2.1 s
	Cage “radius” R	69 ± 10 nm
	Vesicular diffusion coefficient	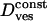(37 ± 14) × 10−4μm2/s
	Cage diffusion coefficient Dcage	(2.3 ± 0.8) × 10−4μm2/s
Directed	Mean duration	2 ± 0.2 s
	Transport velocity v	0.64 ± 0.18 μm/s
Diffusive	Mean duration	10.3 ± 0.6 s
	Diffusion coefficient D	(22 ± 8) × 10−4μm2/s

Three-dimensional trajectory simulations

For 3D random walk simulations, a method derived from that previously described by Simson et al. (8) was used. Brownian trajectories of 5–600 frames with 10 frames/s were simulated for a range of diffusion coefficients D (5 × 10⁻⁵ μm²/s < D < 5 × 10⁻² μm²/s). These characteristics matched the recording rates used for TIRFM time-lapse imaging and the diffusion coefficients measured for secretory vesicles. The number of frames matched the durations of the transient motion behaviors observed for the vesicles. To simulate 3D Brownian motion with a diffusion coefficient D, it was needed to generate trajectories composed of steps exhibiting a uniform probability distribution for step direction and a mean step length equal to (6 DΔt)^1/2, where Δt = 0.1 s is the step period. To achieve these characteristics, each step comprising the trajectory was obtained by the combination of 100 substeps. The size of each substep, l, was obtained for time δt = 0.001 s (such that Δt = 100 δt = 0.1 s), according to l = (6 Dδt)^1/2. For each substep, one direction among the six directions defined from Cartesian coordinates (x, −x, y, −y, z, −z) was randomly chosen based on the MATLAB random number generator rand.

For constrained motion simulations, trajectories exhibiting a diffusion coefficient D were generated with the same procedure, but the particle movements were restricted to a spherical cage of radius R and with a reflective surface. The center of the cage underwent Brownian motion with a diffusion coefficient 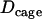. To simulate directed motion with a velocity v, trajectories exhibiting a diffusion coefficient D were generated using the method described above and for each step a displacement of Vδt was added along the x coordinate. For the simulation of noisy trajectories, an isotropic Gaussian noise with a standard deviation of 16 nm, corresponding to the precision of the tracking algorithm, was added along the three Cartesian directions for each point of the trajectory.

It was verified that grid and sampling artifacts were negligible by comparing simulations run on a mesh to those run in continuous space, using two approaches. In the first continuous method, each step in a simulated trajectory was chosen from a Gaussian step-length distribution with variance 6 DΔt, where Δt was the step period and D the simulated diffusion coefficient. The azimutal direction angle of the step θ was picked randomly from [0, π] and the polar direction angle ψ was chosen from a probability distribution proportional to sin(ψ), with ψ between 0 and π. In the second continuous method, each step was composed of projections along Cartesian coordinates which had Gaussian distributions with variance 6 DΔt. All methods gave nearly identical results, suggesting grid and sampling artifacts are negligible.

RESULTS

Principles of the transient motion analysis

To describe the different behaviors exhibited by a vesicle, four motion classes are considered (31): 1), stalled vesicles, whose mobility is close to the detection limit; 2), diffusive class, in which vesicles exhibit Brownian motion; 3), directed class, corresponding to vesicles undergoing Brownian motion superimposed with displacement in a particular direction; and 4), constrained class, in which vesicles experience Brownian motion impeded by obstacles or restricted to a limited area that itself can diffuse (vesicles moving inside a “cage” or held by a “leash”). Impeded and restricted diffusion are bracketed in the same class because they refer to quite similar motion characteristics.

The usual method to classify a given subtrajectory into one of the four categories above is the analysis of the mean-squared displacement (MSD). Let δt be the time between two consecutive vesicle positions and L the distance that a vesicle travels in the time interval Δt = nδt, where n is an integer (in our experiments, frames were acquired at 10 Hz so that δt = 0.1s). The MSD is defined as

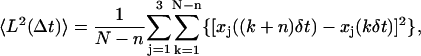(4)

where the vesicle position (x, y, z) is written as (x_j) with j = 1,…,3 and N is the total number of vesicle positions. For Brownian motion, the MSD increases linearly with time interval Δt, whereas for constrained or directed motion, it is curved downward or upward, respectively (32). Consequently, the MSD curvature can be used to classify subtrajectories. However, for experimental, finite-length trajectories, analysis of MSD curves is somewhat difficult. The accuracy of MSD values decreases with increasing time interval Δt, due to averaging over smaller number of positions. More precisely, for a particle experiencing random motion with a diffusion coefficient D, the variance of the MSD value for a given time lag Δt = nδt is equal to (32):

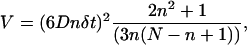(5)

where N is the total number of particle position measurements. Analyses of the MSD curves are thus valid only for small ratios n/N, i.e., for the initial portions of these curves. As a consequence, classification using the MSD analysis requires vesicle subtrajectories of at least several tens of points. This condition is not restrictive to classify periods of immobilization, diffusive, or constrained motion, whose typical durations are longer (see Table 2). However, the use of MSD analysis is not appropriate to detect directed periods, which, at least in our application, typically last <30 points. A particularity of these directed trajectories is that they are highly asymmetric due to the existence of a preferred direction for vesicle displacements. Consequently, we use the trajectory asymmetry rather than the MSD curvature to detect directed periods (see below).

In summary, then, three parameters are used to make the classification: the diffusion coefficient, D, the MSD curvature, and the trajectory asymmetry. The first parameter is used to detect stalled periods. The second and third parameters are used in deciding whether a portion of a trajectory corresponds to constrained or directed motion, respectively. Because these parameters measure deviations from Brownian motion, parts of a trajectory that are classified into none of the three previously detected classes belong to the Brownian class. The definition of these three parameters will be presented first, in the following subsection. To detect transient behavior, the three classification parameters are calculated along trajectories using a rolling analysis window. A challenge of the method was to choose the width of this rolling window. A width too long reduces the ability to detect brief specific motion due to averaging vesicle behavior, whereas a width too short does not allow a reliable classification of the analyzed subtrajectory. In addition, the duration of these temporary events is not known a priori. To overcome these problems, we use a rolling window, whose width is optimized to fit the duration of the transient behavior under investigation. The method employed for the calculation of the three parameters along a trajectory using this variable width window will be presented in the subsection Calculation of the classification parameters along trajectories. Another difficulty is the fact that pure Brownian motion can temporarily mimic directed or confined periods (33), which would result in MSD curves showing upward or downward curvature. In consequence, the parameter quantifying MSD curvature has to be thresholded to distinguish real non-Brownian behavior from statistical fluctuations of random motion. For the same reason, the asymmetry parameter has also to be thresholded. In the subsection Optimizing detection sensitivity: setting thresholds and minimum crossing times, we will show how the detection sensitivity of the method is optimized by choosing appropriate thresholds for each parameter. Application of the method to the study of secretory vesicle trajectories in endocrine BON cells is described in the subsection Transient motions of secretory vesicles, and in the final subsection, Critical evaluation of the motion analysis method as applied to secretory vesicle dynamics, a number of tests are presented, validating the algorithm.

Definition of the motion-type classification parameters

Diffusion coefficient to detect stalled vesicles

Some periods of vesicle trajectories exhibited very limited mobility (displacement <1 pixel ≈ 100 nm during 10 s). These periods of immobilization or stalling of the vesicles are defined by a diffusion coefficient lower than a value D_min, which is close to the detection limit of our single-particle tracking method, evaluated by measuring diffusion coefficients of fluorescent latex beads (200 nm diameter, labeled with fluorescein) immobilized on a coverslip. The laser intensity in these measurements was adapted to get a signal/noise ratio for the beads similar to that typically obtained for vesicles. Under these conditions, the MSD fit (see below) yielded an average diffusion coefficient of 0.1 × 10⁻⁴ μm²/s. D_min was set to 10 times this detection limit, i.e., D_min = 1×10⁻⁴ μm²/s.

Thus, the diffusion coefficient, D, is calculated along a trajectory using a rolling analysis window, and periods for which D drops below D_min are classified as stalled periods. To evaluate the diffusion coefficient for a given trajectory window, a regression line is fitted through the first N_f points of the MSD curve with each point weighted by the reciprocal of its relative variance V_rel, obtained from Eq. 5:

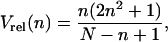(6)

where N is the total number of particle positions in the considered period of trajectory. The diffusion coefficient D is calculated as D = s/6, with s being the slope of the linear fit. The choice of the number of MSD points used for the linear fit N_f has to take into account two aspects: i), a precise measure of the diffusion coefficient requires a large N_f value, ii), as the choice of N_f is related to the length of the analyzed segment of trajectory (N_f ≪ N, see above the subsection Principles of the transient motion analysis), detection of brief immobilization periods requires a short N_f value. To satisfy these two opposite criteria, N_f was set to 5 (which corresponds to a linear fit for Δt < 0.5 s under the experimental conditions used). We will discuss later how this N_f value governs the length of the minimal period used to measure diffusion coefficients (see the subsection Calculation of the classification parameters along trajectories). As a comparison, previous works measured diffusion coefficients of tracked single particles by analyzing only the first point of the MSD (16,34) or fitting a straight line trough the first 2–20 points of the MSD curve (35,36).

MSD curvature to detect constrained motion

A downward curvature of the MSD is indicative of constrained motion. However, even for a particle undergoing pure Brownian motion, the MSD versus Δt can deviate from linearity. A quantitative analysis of the MSD shape is then required to distinguish between true constrained motion and simple diffusion. To quantify the MSD curvature, the relative deviation of the MSD curve from a linear fit of its first points is calculated as follows. A regression line is fitted through the first N_diff points of the MSD curve with each point weighted by the reciprocal of its relative variance V_rel(n) given by Eq. 6. This regression line is the expected average MSD for a particle undergoing simple diffusion. We introduce a parameter, Dev, which quantifies the difference between the MSD curve and the linear fit 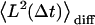, averaged over the first N_dev points in the MSD:

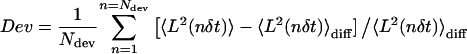(7)

Negative or positive values of Dev reveal downward or upward curvatures, respectively, for the MSD curve.

The choice of the number N_diff of MSD points used for the linear fit is governed by the same constraints as for the choice of N_f (see above Diffusion coefficient to detect stalled vesicles). Consequently, N_diff was also set to 5. The second parameter that had to be defined was the number of points N_dev employed to quantify the MSD deviation from a straight line. To obtain a precise evaluation of this deviation, the ratio N_dev/N_diff should be large. We set it to 10, i.e., N_dev = 50 (which corresponds to an averaging for Δt < 5 s under the experimental conditions used). Kusumi et al. (31) quantified the MSD curvature in a similar manner. However, in that work, the deviation of the MSD curve from a linear fit to its first points was only evaluated at a single point. For our parameter Dev, the deviation is averaged along N_dev points to minimize the effect of MSD fluctuations. As a consequence, we could use shorter MSD curves, yet quantify their curvatures satisfactorily.

An alternative approach to detect constrained motion entails plotting the MSD versus 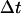on a log-log plot. A power law, 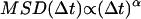, with α < 1, is indicative of constrained motion (37). Thus, on a logarithmic plot, the y-intercept yields the diffusion coefficient regardless of the value of the scaling exponent α,which is obtained from the slope of the fit. However, errors on particle position measurements artificially reduce the value of α measured with this method at short times and can thus lead to the detection of artifactual subdiffusion (38). More specifically, the quantity , where is the mean error in particle position detection, determines the timescale below which noise leads to artificial subdiffusion (38). For us, , with 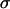calculated from beads immobilized on the coverslip (which provides only a lower bound on 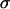). Under these conditions, Brownian motion will appear subdiffusive at least up to 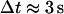(38). Since only the initial portion of the MSD can be used for analysis (a few seconds in our case), the use of this approach is not appropriate here. Moreover, it is especially difficult to determine an accurate scaling exponent for short tracks of ∼100 points (38).

To test whether the limited accuracy of the vesicle localization procedure could also be problematic in our approach, we evaluated the parameter Dev for simulated 3D Brownian trajectories with or without added noise. For positioning errors and diffusion coefficients similar to those measured for the vesicles (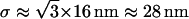, 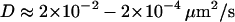), the Dev values were not significantly modified by the presence of noise (data not shown) indicating that the use of this parameter would not lead to detection of artificial subdiffusion.

The determination of a threshold value for the parameter Dev to distinguish between constrained and Brownian motion is not trivial and is discussed in the section Optimizing detection sensitivity: setting thresholds and minimum crossing times.

Asymmetry to detect directed motion

As discussed above, the analysis of the MSD curve is not well adapted for detection of directed motion because the typical duration of this type of motion is too short. Evaluation of trajectory asymmetry is a more efficient way to detect this kind of movement, which is highly asymmetric. However, even a pure Brownian trajectory is not perfectly symmetric (39). As a consequence, asymmetry must be properly quantified to allow discrimination between random walk and directed motion (as discussed similarly for the MSD curvature). For this, an asymmetry parameter, slightly different from that of Saxton (33), is introduced. First, the 3D radius of gyration tensor R_g is calculated:

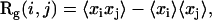(8)

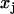where and are the three Cartesian axes and the average values are defined over all n steps of the analyzed subtrajectory, e.g., 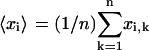. The gyration radii R₁, R₂, and R₃, which are the square roots of 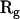eigenvalues, are obtained by diagonalizing this tensor. The asymmetry is then quantified by the parameter

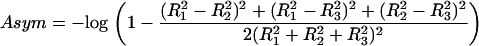(9)

High values of Asym indicate a greater tendency for a preferred direction. For example, for a perfectly symmetric trajectory, Asym = 0, whereas for a straight line, . For simulated 3D Brownian trajectories, Asym rapidly converges to ≈0.242 for large N. Higher transient Asym values may reveal periods of directed motion, but this behavior has to be distinguished from nonsymmetric Brownian motion using appropriate statistical considerations. This will be presented in the section Optimizing detection sensitivity: setting thresholds and minimum crossing times.

Calculation of the classification parameters along trajectories

Using the three parameters described above, it is possible to define the type of motion associated with a given part of a vesicle trajectory. To highlight the different kinds of movement experienced by a given vesicle, each of these three parameters is calculated along its trajectory using a rolling window. Let us consider the asymmetry parameter as an example. The analysis window is defined by its central point position, as shown in Fig. 3. For a given position of the window (i.e., a given point on the trajectory), the Asym parameter is calculated for window widths ranging from W_min to W_Max. For the sake of simplicity in the definition of the window center, only windows with an odd number of points are considered. Among these window widths, only the one maximizing Asym is retained, corresponding to the highest probability of nondiffusive motion. This procedure is repeated point by point along a trajectory to obtain an Asym versus time profile as the one shown in Fig. 4 B. The parameter Dev and the diffusion coefficient D are calculated in a similar manner and plotted against time as shown in Fig. 4, C and D, except that the retained window widths are those minimizing these parameters.

FIGURE 3.

Measurement of the asymmetry parameter Asym along a vesicle trajectory. To estimate Asym for a given point of the trajectory (indicated by the arrowhead), this parameter was calculated for various window widths (marked in bold) centered on the point of interest. Only the window width that maximized Asym value was retained (boxed). The asymmetry profile was obtained by repeating this procedure point by point along the trajectory (see Fig. 4).

FIGURE 4.

Profiles of the three motion classification parameters calculated for a sample vesicle trajectory. (A) Analyzed vesicle trajectory. The solid dot indicates the beginning of the trajectory. (B) Profile of the Asym parameter that quantifies the trajectory asymmetry. (C) Profile of the Dev parameter used to evaluate MSD curvature. (D) Profile of the diffusion coefficient D. (The tracked vesicle was from a BON cell expressing NPY-GFP; evanescence depth = 200 nm; acquisition rate = 10 Hz.)

How does one choose the minimum and maximum window widths, W_min and W_Max? To account for the specificities of each motion category, different values of W_min and W_Max were chosen for each parameter, although the same general considerations applied, as follows. The minimum width, W_min, has to be long enough for a reasonably accurate estimation of the parameter in question. Parameter estimation improves with increasing number of points used in the analysis window. However, the minimum window width must remain narrower than the minimum duration of the specific motion one is trying to detect. Thus W_min is chosen to provide an acceptable worst-case precision in parameter estimation. The requirement that W_min be shorter than the shortest specific motion under consideration can only be rigorously verified a posteriori to the analysis. However, for very characteristic motion, such as some of the directed motions seen in video 1 (Supplementary Material), one can have a rough idea on their minimum durations by manual detection of these. The choice of the maximum width, W_Max, on the other hand, is rather trivial: it can be made equal to the mean vesicle trajectory length so that it can match the longest possible duration of specific motions. However, if a given type of motion has lifetime much shorter than the observation time, W_Max can be set shorter to save computation time (this turns out to be the case for directed motions—see below). Thus, to choose the optimal minimum and maximum analysis window widths, one has to have some knowledge about the system under study. The best procedure to follow to optimize these parameters is then an iterative one. One takes a small pool of vesicle trajectories, and sets initial values for W_min and W_Max. Upon analysis of this “test” pool, one checks whether W_min is short enough to capture short specific motion, and whether a shorter W_Max can be used to save computation time.

Let us first consider the detection of stalled periods. This requires measurement of small diffusion coefficients along vesicle trajectories. The estimated relative error for the measured diffusion coefficient is given by the relation (32)

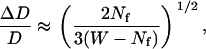(10)

where W is the window width and N_f is the number of MSD points used to evaluate the diffusion coefficient (see above Diffusion coefficient to detect stalled vesicles). To have a relative error <25% and with N_f = 5 chosen above, a minimal value of 51 points was obtained for W from Eq. 10, i.e., 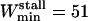(recall that the analysis window contains an odd number of points). We chose to match the mean duration of vesicle trajectories.

Secondly, constrained motion is detected using the parameter Dev (Eq. 7), calculated by averaging the deviation of the MSD curve from a straight line over its first points (see above MSD curvature to detect constrained motion). However, the variance of the points of the MSD curve increases with increasing time interval Δt, thus the minimum number of points to be used in the calculation of Dev should be larger than 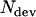. We consider that the fraction of the MSD curve on which the deviation from linearity is evaluated should not exceed the first 2N/3 points of this curve, that is 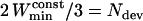, or 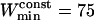points. For the maximum window width, 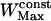, a value of 301 points was chosen, identical to that used for the detection of stalled periods. As a comparison, previous works restricted their analyses to the first N/3 (35) or N/2 (17) points of the MSD curve to detect constrained motion, where N is the number of vesicle positions in the considered subtrajectory (these would correspond to 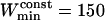and 100, respectively).

Finally, for the Asym parameter, we observed that simulated Brownian trajectories shorter than 10 points (see Fig. 6 C) gave artificially large asymmetry values. Therefore, it is assumed that the asymmetry estimation becomes relevant for window widths longer than 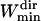= 11 points. As for the maximum window width, we noticed that a large majority of the directed periods lasted <7 s (i.e., 70 points with an acquisition rate of 10 Hz) and thus a maximum window width 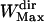of 71 points was chosen to save computation time. We checked a posteriori that the mean lifetime of directed periods, 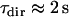(20 points), is much shorter than 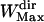, and sufficiently longer than .

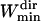FIGURE 6.

Statistical behavior of the parameters Dev and Asym that quantify MSD curvature and trajectory asymmetry, respectively, for simulated 3D Brownian trajectories. (A) Histograms of the number of simulated 3D Brownian trajectories for Dev for different lengths of trajectories N. Thresholds Dev_0.99 chosen such that Dev > Dev_0.99 for 99% of the simulated tracks are indicated as vertical dotted lines. Values of Dev_0.99 are shown above each histogram. (B) Dev_0.99 plotted as a function of N on semilogarithmic scale. (C) Thresholds Asym_0.99, chosen such that 99% of the simulated trajectories had Asym < Asym_0.99 (at fixed N) plotted as a function of N on semilogarithmic scale.

Using this procedure, asymmetry, MSD curvature, and diffusion coefficient profiles are calculated along a given trajectory (Fig. 4). By thresholding these profiles, periods exhibiting different motion types are highlighted. The choice of the thresholds is the subject of the next subsection.

Optimizing detection sensitivity: setting thresholds and minimum crossing times

Because random walks can temporarily mimic stalled, constrained, or directed periods, the diffusion coefficient, MSD curvature, and asymmetry profiles measured along a purely Brownian trajectory will exhibit peaks or troughs, as illustrated in Fig. 5. Amplitudes and durations of these fluctuations are usually smaller and shorter than the ones associated with real non-Brownian transient motion (cf. Fig. 4). In consequence, definition of a threshold value and a minimal duration above or below this threshold (i.e., a minimum crossing time) for each profile would suppress the detection of these apparent nonrandom behaviors without excluding real stalled, constrained, or directed periods.

FIGURE 5.

Profiles of the three motion classification parameters calculated for a simulated noisy Brownian trajectory with a diffusion coefficient of 20 × 10⁻⁴ μm²/s. (A) Analyzed trajectory. The solid dot indicates the beginning of the trajectory. (B) Profile of the Asym parameter that quantifies the trajectory asymmetry. (C) Profile of the Dev parameter used to evaluate the MSD curvature. (D) Profile of the diffusion coefficient D.

How does one choose the thresholds and the minimum crossing times? In general, the thresholds are chosen such that a purely Brownian trajectory would have negligible probability of crossing them for more than a few consecutive points. These probabilities, in turn, are obtained from analysis of a large number of computer-generated 3D Brownian trajectories. The only exception to this rule is the choice of a threshold, D_min, for detecting stalled periods, which is imposed by our detection limit. In fact, D_min = 1 × 10⁻⁴ μm²/s has already been set in the section Definition of the motion-type classification parameters. In addition, a minimum crossing time of three consecutive points (i.e., 0.3 s with a 10 Hz acquisition rate) was chosen for the detection of stalled vesicles. It was checked a posteriori that under these conditions, the probability of detecting a stalled period for a simulated Brownian trajectory with a diffusion coefficient equal to the mean diffusion coefficient of the vesicles in the diffusive class (i.e., ≈2 × 10⁻³ μm²/s, Table 2, section Transient motions of secretory vesicles) is <1%.

Concerning constrained and directed periods, it was first verified whether a unique threshold for each is sufficient to distinguish real non-Brownian behaviors from fluctuations of diffusive motion. Indeed, as the windows defined to evaluate each parameter along a given trajectory have variable widths, the use of a unique threshold supposes that the statistical properties of the asymmetry (Asym) and the MSD curvature (Dev) parameters do not depend on trajectory lengths, N. It turns out that for Asym, the use of an N-independent threshold is justified, provided 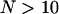. Setting an N-independent threshold on the Dev parameter, however, was not possible, and defining a new classification parameter was required.

To see the trajectory-length dependence of the thresholds set on Dev and Asym, a large number of 3D Brownian trajectories containing N points were simulated, and N was varied. Histograms of the number of simulated tracks versus Asym and Dev were obtained for various N values. Fig. 6 A shows some sample histograms for the Dev parameter. For each histogram, we evaluated (at fixed N) the threshold, Dev_0.99, defined such that 99% of the simulated trajectories exhibited higher Dev values (Fig. 6 A). A similar threshold was defined for the Asym parameter, Asym_0.99, for which 99% of the simulated trajectories had Asym values lower than Asym_0.99. The N-dependence of these thresholds, obtained from histograms for different N, are shown in Fig. 6, B and C. We verified that the plots of Asym_0.99 and Dev_0.99 as a function of N did not depend on the diffusion coefficient used for simulated trajectories over three orders of magnitude in D, for 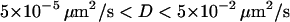(data not shown). Fig. 6 B shows that Dev_0.99 increases as a function of N. This increase is well described by

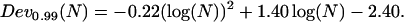(11)

Actually, the increase of Dev_0.99 with increasing N could have been anticipated from Eq. 5. Consequently, Dev_0.99 cannot be used as a unique threshold to detect constrained motion from the Dev profile. Thus, rather than analyzing Dev variations, we use the residual deviation of the MSD from linearity, Dev_r = Dev − Dev_0.99(W), with W the window width that minimizes Dev. By definition, statistical properties of Dev_r are independent of the window width, and thus a unique threshold can be used to detect constrained periods on the Dev_r profile. Regarding the asymmetry parameter, Asym_0.99 drops rapidly to a plateau for trajectories lasting more than 10–15 points (Fig. 6 C). As a consequence, directed motion periods can be detected from Asym profiles using a unique threshold, provided the analysis window is larger than ∼10 points (c.f. the minimum analysis window width is 11 points for the Asym profile calculation; see the previous subsection).

To define thresholds and minimum crossing times, the motion analysis method was applied to simulated 3D Brownian trajectories. The effect of different thresholds and minimal durations on the detection of confined and directed behaviors for simulated random motion was examined (Fig. 7). To select the most appropriate thresholds and minimal durations, we also took into account the fact that transient constrained vesicular motions tend to be quite long (∼200 points, i.e., 20 s with an acquisition rate of 10 Hz), whereas temporary directed motions are usually short (∼20 points). Under these conditions, the following settings were chosen:

1. Concerning the MSD curvature parameter, Dev_r, we chose a threshold level of −0.01 and a minimal duration of 20 consecutive points (2 s) below this threshold; 7% of the simulated random walks exhibited at least one period of constrained motion with this set of limit values.

2. Regarding the asymmetry parameter Asym, we chose a threshold level of 1.00 and a minimal duration of 10 points (1 s) above this threshold; 1% of the simulated random walks displayed at least one period of directed motion with this set of limit values.

FIGURE 7.

Percentages of 3D simulated Brownian trajectories exhibiting constrained (left) or directed (right) periods for different thresholds and minimal durations. Left panel shows the influence of the minimal duration below threshold for different Dev_r thresholds (0.05, −0.01, and −0.05); 7% of the simulated random walks exhibit at least one period of constrained motion with the chosen threshold (−0.01, heavy line) and minimal duration (20 points), indicated by a solid circle. Right panel shows the influence of the minimal duration above threshold for different Asym thresholds (0.95, 1.00, and 1.05); 1% of the simulated random walks exhibit at least one period of directed motion with the chosen threshold (1.00, heavy line) and minimal duration (10 points), indicated by a solid circle. The simulated random trajectories included 300 points, a value that matched the mean duration of experimental trajectories obtained from vesicle tracking.

Let us now see how one detects transient motion periods applying the above thresholds to Asym, Dev_r, and D profiles. Taking the example of the asymmetry parameter, the position of a directed motion period is located in the following manner. The first and the last points P_i and P_f of a segment of the asymmetry profile larger than the threshold are first determined. As previously described, each of these points is associated with a window, Win_i and Win_f, respectively. The beginning of window Win_i and the end of window Win_f together define the position of the directed motion period. Applying the same procedure to Dev_r and diffusion coefficient profiles, periods of constrained motion and of immobilization are detected. Periods of trajectory that remain unclassified correspond to simple diffusion. A sample vesicle trajectory is analyzed this way in Fig. 8.

FIGURE 8.

Motion analysis of a vesicle trajectory. (A) Analyzed vesicle trajectory. The segment marked in black corresponds to directed motion and the one in gray to constrained motion, as detected by the algorithm. The black dot indicates the beginning of the trajectory. (B) MSD plot for Δt < 5s calculated for the entire trajectory shown in A. The dashed line corresponds to the weighted linear fit of the 5 initial MSD points (see text). (C) Profile of the Asym parameter that quantifies the trajectory asymmetry as a function of time, calculated for the trajectory shown in A. The dashed line corresponds to the threshold used to distinguish directed and diffusive motions (Asym > 1.00). The black bar indicates the position of the detected directed period. (D) Profile of the Dev_r parameter that evaluates the MSD curvature as a function of time, calculated for the same trajectory. The dashed line corresponds to the threshold used to discriminate between constrained and diffusive motion (Dev_r < −0.01). The gray bar indicates the position of the detected constrained period. (Tracked vesicle from a BON cell expressing NPY-GFP; evanescence depth = 200 nm; acquisition rate = 10 Hz.)

To validate the set of thresholds and minimum crossing times chosen, the motion analysis method was applied to trajectories of 475 nm diameter fluorescent beads immersed in a glycerol-water mixture (see Materials and Methods); ∼7% of the diffusive bead trajectories exhibited at least one constrained and ∼7% at least one directed period, as detected using the settings above. The higher proportion of apparent directed motions in the case of bead trajectories as compared to simulated ones is probably due to the proximity of the glass coverslip, which induces an intrinsic asymmetry as evidenced by the significant differences observed between the lateral (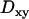) and the normal () diffusion coefficients.

The thresholds and minimal durations defined above imply that the study of transient directed or constrained movements exhibited by the vesicles will be relevant only if the proportion of trajectories exhibiting these kinds of behaviors is significantly higher than the false-positive percentage of 7%.

Transient motions of secretory vesicles

Characterization of 3-D vesicle trajectories

The motion analysis method was applied to the study of secretory vesicle dynamics in the subplasmalemmal region of endocrine BON cells. Individual vesicles were clearly visualized by TIRF microscopy in cells expressing a NPY-GFP chimera in a stable manner. Due to the large size of these vesicles (diameters of ∼250–300 nm have been deduced from electron micrographs by Parekh et al. (40)), TIRFM images exhibited a high signal/noise ratio under conditions minimizing photobleaching. Video 1 of the Supplementary Material shows that vesicles experience different motion types such as directed movement or nearly complete immobilization. In addition, the behavior of a significant fraction of the vesicles appears complex, that is vesicles switch from one motion type to another.

Using the techniques described here, 3D trajectories of 358 vesicles from four cells were obtained and analyzed (evanescence depth = 200 nm). Fig. 8 shows a sample trajectory that exhibited a directed motion period followed by a constrained motion one. The MSD curve calculated for the entire trajectory is almost linear, as shown in Fig. 8 B. As a consequence, this trajectory would have been considered as diffusive if it were analyzed globally. Complex trajectories were very common: ∼50% of the trajectories contained at least one motion-type transition, justifying the investment in the development of tools to detect and analyze them. In addition, we found that 30% and 50% of the vesicle trajectories exhibited at least one period of constrained or directed movement, respectively. These proportions are significantly higher than the false-positive percentage of 7% obtained for fluorescent beads undergoing Brownian motion. Consequently, the characterization of detected nonrandom transient behaviors is considered relevant. Table 1 shows the proportion of detected transient periods for each class. The proportions of time spent in each class are also displayed.

TABLE 1.

Proportions of detected transient periods for each of the four motion classes and proportions of time spent in each class for the secretory vesicle trajectories; values are given as mean ± SD

Motion class	Proportion of periods	Proportion of time
Stalled	9 ± 5%	8 ± 4%
Constrained	16 ± 4%	35 ± 8%
Directed	35 ± 6%	8 ± 2%
Diffusive	40 ± 2%	49 ± 9%
Total	794 periods	7162 s

Once the detection and classification of transient periods of motion is achieved, obtaining the characteristics of each motion class is rather simple. For example, if a subtrajectory is classified as diffusive, the associated diffusion coefficient D is derived from the linear fit of the MSD as described above. For directed motion, the MSD follows (37)

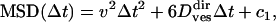(12)

where v is a transport velocity and c₁ is a numerical constant corresponding to the apparent displacement created by the limited accuracy of the vesicle localization procedure. Thus, fitting Eq. 12 to the MSD of a directed subtrajectory, one obtains the transport velocity v and the diffusion coefficient 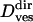(however, due to the limited time resolution, diffusion coefficients for directed motion periods obtained this way are not very accurate; 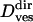= 60 ± 55 × 10⁻⁴ μm²/s). Finally, constrained motion is analyzed considering diffusion restricted to a limited area that itself can diffuse. The MSD for this case obeys (14)

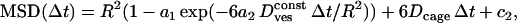(13)

where a₁ = 0.99 and a₂ = 0.85, R is the “radius” of the cage (this radius corresponds either to the size of the space remaining between a vesicle and its cage or to the length of the “leash” holding the vesicle), and D_cage and 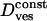are the diffusion coefficients of the cage and of the vesicle inside the cage, respectively. The numerical constant c₂ is due to the limited accuracy of the tracking technique. These characteristics are summarized in Table 2 along with the average duration of each class.

We took advantage of the method to study transitions between motion periods. For this analysis, the stalled and the constrained periods were gathered in the same category. This was motivated by two related considerations. First, the mean cage diffusion coefficient for constrained motion, 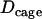, nearly matched the limit value used to define the stalled periods, 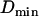. This observation suggests that a stalled period may actually correspond to constrained motion for which we can only measure the displacements of the cage and cannot resolve the motions of the vesicle inside. The “radii” of such cages should be smaller than the spatial resolution of our tracking technique i.e., smaller than 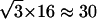nm. Second, sometimes conflicts arose in the classification of constrained and stalled periods, most often involving a stretch that could be classified either as stalled (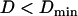) or constrained (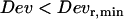) found in a constrained subtrajectory. Actually, such conflicts are not surprising given that cages move with a diffusion coefficient that is close to our detection limit (). Such subtrajectories were classified as constrained. Thus, given the resolution of the method, keeping the two categories separate is not justified. In addition, gathering the two classes into one simplifies the analysis. The proportion of time spent by vesicles in this combined class (class C, constrained/stalled) is 44% with mean duration s.

The first finding concerning the transitions was their reversibility. That is, the number of transitions from one class to another was similar in either direction. Secondly, we found that most of the transitions occurred between diffusive (class B, Brownian) and directed periods (class D) at a rate of s⁻¹ (53% of all transitions) or B and C at a rate of 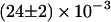s⁻¹ (41% of all transitions). Transitions between D and C were rare (rate 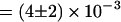s⁻¹, 6% of all transitions).

Origin of the different motion classes

What are the interactions that lead to the observed heterogeneity of vesicular motions? A first attempt has been made to obtain clues about the origins of different motion types.

For directed motion periods, data from the literature suggested that they may correspond to vesicular displacements along microtubules (17,41,42). Transport velocities measured for vesicles undergoing directed motion (∼0.6 μm/s, Table 2) are consistent with previously measured, microtubule-based vesicle displacements (17,42). To substantiate this hypothesis, BON cells were incubated for 10 min with 30 μM nocodazole, a drug that depolymerizes microtubules (43). Vesicle motions were analyzed and compared to those observed in the same cells before drug addition (3 cells, 251 and 191 vesicles before and after nocodazole treatment, respectively, using an evanescence depth of 200 nm). After microtubule depolymerization, the proportion of time spent by the vesicles in the directed class was reduced by 53 ± 4%. This reduction very closely matched the average reduction in the density of the cortical microtubule network, visualized by immunolabeling with anti-tubulin antibody and using TIRFM. This result strongly suggests that directed motions correspond mainly to vesicles moving along microtubule tracks.

The origin of the stalled/constrained periods was investigated next. A number of previous studies have suggested that the mobility of a vesicle may become restricted as it approaches or arrives at the cell membrane (15,16,44). Thus, the stalled/constrained class could correspond to vesicles in the vicinity of the membrane or attached to it. Testing this hypothesis would be trivial if vesicle positions in the z direction with respect to the cell membrane could be obtained in TIRFM. However, at least in resting cells, this is quite difficult to do: due to the dispersion of vesicle sizes and the number of fluorophores per vesicle, one cannot simply assign an intensity to a given distance from the cell membrane (16,45). Thus, generally the best that can be done in resting cells is to track individual vesicles and relate their fluorescence intensity variations (usually relative to the intensity in the first tracked frame) to relative z displacements (cf. Eq. 3). In cells stimulated for exocytosis, however, it can be safely assumed that a vesicle had to be at the cell membrane shortly before fusing with it. Taking the average intensity of a vesicle in the few frames preceding its fusion as reference, its z positions with respect to the cell membrane can be obtained. Thus, we have analyzed movements of vesicles responding to stimulation by fusing with the cell membrane. Exocytosis was elicited by ultraviolet flash photolysis of a “caged calcium” compound, NP-EGTA-AM. Fusion events were detected thanks to their characteristic signature on TIRFM images: when fusion occurs, disappearance of a vesicle is preceded by a transient brightening of the vesicle followed by a fluorescence spread corresponding to the diffusion of the fluorophores in the extracellular medium (12). The mean z position of a vesicle during the last second (10 points) preceding exocytosis was taken as reference (i.e., z set equal to 0). We studied specifically vesicles that remained within 50 nm of the cell membrane during their entire trajectory. The proportion of time spent by these vesicles in the constrained/stalled class was ∼85% (65 vesicles from 23 cells), whereas the remaining time was spent in the Brownian class. This result, which has to be compared to those of Table 1, is consistent with the idea that constrained/stalled periods can be associated with vesicles interacting with the plasma membrane.

Results obtained in stimulated cells may be criticized by arguing that vesicle motions may be altered by elevated cytosolic Ca²⁺ concentrations induced by stimulation. If constrained/stalled vesicles are attached to the cell membrane, then a withdrawal from the cell membrane is expected when a vesicle switches from this class of motion to another one, even in resting cells. A 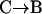transition in a resting cell is shown in Fig. 9. The transition clearly involves a net displacement of the vesicle toward the cytosol, away from the glass-solution interface (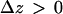). Similarly, transitions from Brownian to constrained/stalled periods (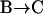) were often accompanied by an approach toward the cell membrane. On average, the approach/withdrawal amplitude was 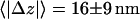(mean ± SD, calculated by comparing the mean z positions of vesicles during the 3 s before and after a transition, 44 transitions from 4 cells).

FIGURE 9.

Vesicles withdraw from the plasma membrane during transitions from constrained to diffusive motions. Shown is a representative vesicle trajectory in the (x, z) plane. The segment marked in gray corresponds to constrained motion and the one in black to diffusive motion, as detected by the algorithm. The solid dot indicates the beginning of the trajectory.

Finally, some initial attempts to find the origin of the Brownian class were made. Based on the findings above, the Brownian class was not expected to be associated either with vesicles interacting with microtubules or with the cell membrane. This led us to suspect that these motions may be driven by the remaining major structural element in the subplasmalemma, namely the actin cortex. This hypothesis was tested pharmacologically, by disrupting the F-actin cortical network. Treatment of BON cells with 25 μM latrunculin-B (46) for 5 min induced a nearly complete depolymerization of actin filaments as judged from TIRFM observation of fixed cells labeled by rhodamin-phalloidin (data not shown). We analyzed vesicle trajectories from three cells before (269 vesicles) and after (195 vesicles) latrunculin-B treatment (evanescence depth = 200 nm). Surprisingly, actin depolymerization did not inhibit Brownian motions. However, a significant increase (∼40%, p < 0.01, Kolmogorov-Smirnov test) of the mean diffusion coefficient associated with the Brownian class was observed, suggesting a link between the diffusive class and the actin network.

CRITICAL EVALUATION OF THE TRANSIENT MOTION ANALYSIS METHOD AS APPLIED TO SECRETORY VESICLE DYNAMICS

To validate the motion analysis method for the detection and characterization of different motion types exhibited by the vesicles, a number of tests were run. First, the ability of the method to detect transitions occurring in simulated trajectories was tested. For this, the algorithm was applied to simulated 3D Brownian trajectories into which a transient nondiffusive period (directed, constrained, or stalled) was inserted at a random position. Such transitions (between diffusive and nondiffusive motion) account for >90% of all the observed transitions for the vesicles. The characteristics of the different motion types used in these simulations were the same as those obtained for the vesicles (Table 2). At each position of a simulated trajectory, typical noise was added. Using the analysis method, first the probability of detecting a given transition was evaluated. A transition from a diffusive to a nondiffusive period was detected for >98% of the simulated trajectories. The precision and accuracy in locating a transition (Table 3) and the motion characteristics before and after transitions were also calculated (Table 4). Overall, the precision in detecting transitions and characterizing the transient motion parameters is satisfactory. A negative detection lag indicates that there is a tendency to include a short stretch of diffusive motion in the nondiffusive transient periods.

TABLE 3.

Time lags between actual (simulated) and detected transitions: a negative time lag indicates that detection preceded the actual transition; values are given as mean ± SD

Transition type	Detected lag
Diffusive→stalled	−0.5 ± 0.8 s
Diffusive→constrained	−1.2 ± 1.7 s
Diffusive→directed	−0.1 ± 0.2 s

TABLE 4.

Comparison between actual characteristics of motion (fed as input to simulated trajectories) and those evaluated with the motion analysis method, after detection of a simulated motion-type transition (Table 3); values are given as mean ± SD

Motion class	Characteristics	Simulated value	Measured value
Stalled	Mean duration	9 s	10 ± 1 s
Constrained	Mean duration	20 s	23 ± 3 s
	Cage “radius” R	70 nm	72 ± 9 nm
	Vesicular diffusion coefficient	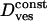35.10−4μm2/s	(34 ± 14) × 10−4μm2/s
	Cage diffusion coefficient Dcage	2.10−4μm2/s	(1.9 ± 1.1) × 10−4μm2/s
Directed	Mean duration	2 s	2.1 ± 0.3 s
	Transport velocity v	0.65 μm/s	0.62 ± 0.09 μm/s
Diffusive	Diffusion coefficient D	20.10−4μm2/s	(22 ± 8) × 10−4μm2/s

Using simulated transitions, we also estimated the maximum cage “radius” R and the minimum velocity v for which the detection of constrained and directed motions, respectively, becomes less efficient. Thus, keeping the period duration and the diffusion coefficient inside the cage, 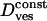, and that of the cage, 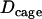, as fixed parameters (using the average values obtained for vesicles), and varying the cage radius, we have found that the probability of detecting a constrained period drops below 0.80 for R > 145 nm and below 0.50 for R >190 nm. Similarly, the probability of detecting a directed period is below 0.80 for v < 0.45 μm/s and below 0.50 for v < 0.35 μm/s (keeping the period duration and 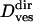fixed). The mean cage radius (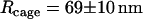) and the transport velocity () measured for the vesicles are well below and above these detection limits, respectively (Table 2).

Some minor difficulties discovered in the application of the method should be mentioned. Although the optimization of the rolling window width leads to efficient detection of constrained and directed periods, often short adjacent stretches of other motion types (typically Brownian) are counted in these periods, as well. Thus, a manual verification and correction on the durations of directed and constrained periods are often required. Another minor difficulty concerns short artifactual diffusive periods generated by default whenever a stretch cannot be classified into one of the nondiffusive categories. Two processes contribute to this. First, because window widths cannot be increased to W_Max at the beginnings and the ends of trajectories, parameter optimization and, consequently, detection of nondiffusive behavior is less efficient. This implies that trajectory extremities (typically <5 points for each) are sometimes erroneously classified as diffusive. Second, since the worst precision in locating a motion-type transition is ∼1.5 s (15 points, see Table 3), shorter periods may artifactually be classified as diffusive. To overcome both effects, diffusive periods lasting <1.5 s were discarded.

In addition, there are some specific issues related to the use of TIRFM as a detection method. The first question is the influence of the anisotropy inherent in the TIRFM detection. To answer it, the resolution anisotropy, , was studied as a function of S/N (see Materials and Methods). Fig. 2 shows that decreases slightly for increasing S/N, from ∼1.2 (for ) to ∼0.7 (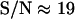). The effect of the resolution anisotropy is expected to be most critical in the detection of directed periods of motion, since this uses the Asym parameter. Thus, directed trajectories were simulated by taking into account resolution anisotropy at its extreme values. The detection of directed periods flanked by diffusive stretches was not significantly affected for 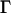= 0.7, 1, or 1.2.

Another issue related to the TIRFM method is the effect of the error (15%) in the determination of the evanescence depth, , on our measurements. To assess this, a pool of 30 vesicles chosen at random was analyzed using 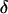= 170, 230, and 200 nm, corresponding to 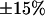error in 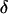, and its nominal value, respectively. The differences in the results in all cases were negligible compared to statistical variations measured at 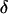= 200 nm (Table 2), the biggest variation being on the calculation of the diffusion coefficients of the constrained vesicles (±20% at 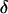= 170 and 230, compared to 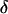= 200 nm).

Finally, one must be careful in using the asymmetry of a trajectory in making a motion-type classification using TIRFM, since the detection volume in this method is itself highly asymmetric. That is, for vesicles exploring a volume larger than the detection volume, only a “slice” of their trajectories would be detected. In this case, even an isotropic trajectory would appear asymmetrical. Fortunately however, the great majority (∼85%) of the vesicles moved less than about their own diameter and remained within the detection volume. Most of the exceptions were the vesicles that moved in a directed manner, usually traveling several vesicle diameters. Such vesicles were successfully classified into the directed class. However, for these vesicles we typically observed different motion characteristics in the x, y plane versus the z axis (data not shown). This may be due to the fact that the TIRFM is biased to detecting vesicles moving in the x, y plane. However, it is not clear how much our results are influenced by this artifact, because the subplasmalemmal region itself is inherently asymmetric.

DISCUSSION

3D transient motion detection algorithm and application to secretory vesicle dynamics near the cell membrane

Efficient methods have been developed for the description of complex movements such as those of membrane proteins (8,9), subchromosomal foci (47), or cells during morphogenesis (48). However, these methods were designed to identify only a particular transient behavior such as confinement or directed motion. More recently, 2D entire trajectories of individual virus-like particles on live cells and artificial membranes were analyzed in terms of modes of motion using a novel and promising approach based on the moment scaling spectrum (49). To analyze in an exhaustive way complex 3D trajectories, we have developed a method based on the determination of the profiles of three different classification parameters along these trajectories. Each parameter is used to distinguish a particular deviation from diffusive motion: the diffusion coefficient, the MSD curvature, and the trajectory asymmetry allow one to identify stalled periods, constrained and directed motions, respectively. To efficiently detect transients of various durations, these three parameters are calculated along the trajectory using a rolling analysis window with a variable width. Finally, thresholding of the parameter profiles allows discrimination of true nondiffusive transient behaviors from statistical fluctuations of Brownian motion. Although this method has been developed for analysis of secretory vesicle trajectories, it is quite general and should be applicable to many other trajectories encountered in biology with minor modifications.

The motion analysis method was applied to the study of secretory vesicle dynamics in the subplasmalemmal region of endocrine BON cells. Using TIRF microscopy, time-lapse sequences of BON cells whose secretory vesicles were labeled by NPY-GFP were obtained. From these sequences, we determined 3D vesicle trajectories by combining single-particle tracking to obtain displacements in the observation plane (x, y) and intensity measurements to quantify movements in the z direction. Many recent works in the area of vesicle dynamics restricted their analyses to lateral (x, y) vesicle displacements (50–53). However, several authors (15,16) showed that the characteristics of the movements changed when the vesicles approached the plasma membrane, probably due to the modification of the vesicle environment. Consequently, study of 3D trajectories should be important to understand the dynamic organization of the subplasmalemmal region.

Analysis of 3D trajectories using the method provided a detailed overview of secretory vesicle dynamics in BON cells. A first conclusion is that complex trajectories with motion transitions are frequent events: about half of the tracked vesicles exhibited such changes within their trajectories, typically lasting 20–30 s. This suggests that, at least in this cell line, secretory vesicles can switch from one local environment to another or modify the interactions they develop with their neighborhood quite frequently. If one could track vesicles over sufficiently long periods of time and with high enough temporal resolution, it is expected that such changes in motion type should be observed for any vesicle in any kind of cell.

Another interesting novel finding is that the proportion of directed motions is clearly not negligible in this work (∼50% of vesicle trajectories exhibited at least one period of directed motion), in contrast to many previous studies (14,16,35). Although this may be a specific feature of BON cells, directed periods generally tend to be short in other cell types, as well (a few seconds in chromaffin cells, (14,15)); hence short stretches of directed periods would easily be missed by global approaches characterizing vesicle dynamics over entire trajectories, or using slow acquisition rates.

A possibly serious drawback of the method concerns the analysis of the diffusive motion class. Periods not classified as constrained, stalled, or directed are classified as diffusive by default. The question arises then as to the efficiency of detecting constrained periods when the cage radius exceeds a critical size, or detecting directed periods when the velocity is below a critical value. Using simulated transitions, these critical values were obtained and compared to experimental data. The results suggested that a large majority of the constrained and directed periods of vesicle trajectories can be detected efficiently with our method in this system. In addition, except for the constrained and stalled classes, conflicts in the classification of motion periods were never observed. The fact that conflicting classifications do not arise between constrained and directed periods indicates that constrained vesicles explore space within cages of low asymmetry.

Perhaps the main usefulness of our approach is that it allows study of transition probabilities from one motion type to another that reflect dynamical interactions between the vesicles and their surroundings. For the analysis of transitions, we pooled the constrained and stalled periods together, since the cage diffusion coefficients that we could measure for the constrained class were close to our detection limit. Thus we have analyzed transitions between three classes of motion: Brownian (B), constrained or stalled (C), and directed (D). We have found that transitions between these classes are largely reversible, i.e., they occur at about the same rate in both directions between any two classes. Since we looked at cells at rest, it is expected that the number of vesicles in each category be roughly conserved, that is the cell is at some steady state. Obviously, reversible transitions can lead to a steady state. However, there are other ways a steady state can be sustained, for example involving only circular irreversible transitions (e.g., 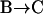, , 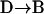), thus reversibility was not a priori expected and it is an important finding on its own.

Another important, and perhaps more surprising finding is that transition probabilities between pairs of classes are quite different. Thus, we have found that most transitions involve the Brownian and the directed classes (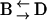, 53%), whereas transitions between the Brownian and the constrained/stalled class are also significant (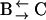, 41%). Most interestingly, transitions between the directed and the constrained/stalled class are virtually “prohibited” (, only 6%).

Transient secretory vesicle motions and the dynamic organization of the subplasmalemma

Combined with information on the origin of the different motion types, transition probabilities would immediately lead to a dynamic picture of the subplasmalemmal region. By observing effects of well-defined perturbations of the cell organization, some clues were obtained on the origins of the different motion types.

Concerning directed periods of motion, a number of previous works using TIRFM suggested that they may reflect displacements driven by molecular motors along microtubule tracks (17,41,42). Use of a microtubule depolymerizing drug, nocodazole, led to a 50% reduction in the proportion of time spent in the directed motion class by vesicles and a similar decrease in the microtubule density near the cell membrane, suggesting that the majority of directed motion most likely occurs on microtubule tracks. Furthermore, the average transport velocity measured for such movements (Table 2) is consistent with this picture (17,42).

As for constrained/stalled periods, several arguments indicated that they may correspond to vesicles that are tethered or docked onto the plasma membrane. A difficulty here is that in TIRFM it is quite difficult to know the distance of a vesicle from the cell membrane under usual circumstances. In stimulated cells, however, we assumed that a vesicle had to be at the cell membrane shortly before fusing with it. This provides a reference intensity for that vesicle, which can be tracked backward in time to see its movements as a function of distance from the cell membrane. In this way, we analyzed motions of vesicles that remained within 50 nm of the cell membrane during their entire trajectory (lasting 20–30 s) before their exocytosis. We hypothesized that these vesicles could be attached to the cell membrane. The overwhelming majority of these vesicles displayed constrained/stalled motions.

Stimulation causes a marked elevation of cytoplasmic Ca²⁺ concentration, which is known to modify the organization of the cortical cytoskeleton. Although potentially vesicle motions may be altered upon stimulation, one may expect that the nature of the motions would remain the same for a given vesicle-subplasmalemmal element interaction, i.e., only transition probabilities and lifetimes would be affected. Nevertheless, it was desirable to look at the origin of the constrained/stalled motions in cells at rest using an alternative approach. If constrained/stalled vesicles are attached to the cell membrane, one would expect an approach toward (withdrawal from) the cell membrane when a vesicle switches to (from) the constrained/stalled class from (to) another motion class. This is indeed what was observed.

Assigning the origin of the constrained/stalled periods of motion to an interaction of the vesicles with the cell membrane is consistent with direct observations of single-vesicle dynamics in chromaffin cells at rest or under stimulation (44,54), and in BON cells in our laboratory (S. Tran, E. Karatekin, S. Huet, I. Fanget, S. Cribier, and J.-P. Henry, unpublished results), which showed that the mobility of a vesicle may drop significantly upon arrival to the cell membrane, leading, in many cases, to nearly complete immobilization. It is also consistent with “unroofing” experiments in a number of cell types, which indicated that vesicles attached to the cell membrane are immobile or have very small mobility (for a review, see Lang (55)). In these experiments, the top portion of a cell is removed using sonication or shear flow. A cell membrane patch remains attached onto the surface, along with secretory vesicles. Addition of calcium caused some vesicles to fuse with the cell membrane patch, indicating that the fusion machinery remained intact, at least for some time after unroofing. In the few cases in which the mobility of the vesicles was quantified, vesicles remaining attached to the cell membrane patch after unroofing were immobile ((56), and S. Huet, E. Karatekin, S. Tran, I. Fanget, S. Cribier, and J.-P. Henry, unpublished results).

Finally, concerning the diffusive class, we expected it to be associated neither with the microtubule network nor attachment to the cell membrane, based on the findings above. The strongest remaining candidate for the origin of these motions is the cortical actin network. It has been demonstrated that vesicles can physically link actin filaments (50), and that a dramatic decrease in vesicle mobility can be induced by blocking the actin cortex remodeling (35). Lang et al. suggested that in PC12 cells, the seemingly random motion of vesicles could originate from the dynamics of the actin cortex (35). To test this hypothesis, we applied latrunculin-B, a drug that disrupts the cortical actin organization by sequestering actin monomers, to BON cells. Somewhat surprisingly, Brownian motion periods were not inhibited by this treatment, although immunofluorescence using rhodamine-phalloidin could hardly detect any actin filaments in the TIRFM zone. The only observable effect on vesicular motions was an increase (∼40%) of the mean diffusion coefficient associated with the Brownian class, suggesting a link between the Brownian class and the acting network. The fact that actin depolymerization induces an increase of the diffusion coefficient of vesicles undergoing seemingly random motion may be interpreted as the actin cytoskeleton hindering vesicle movements, consistent with some previous reports (16,17,57). However, other workers have reported conflicting results on the effect of actin network disruption on vesicle dynamics (15,35,58). Overall, these findings indicate that the role of the actin cortex may be quite sophisticated and it can restrict as well as mediate vesicle movements. It is also possible that latrunculin-B treatment may lead to a reorganization of the cortical actin network and not necessarily to a complete depolymerization (59). Clearly, more work and alternative approaches are needed to unambiguously determine the mechanisms responsible for the seemingly random motion of these vesicles. However, for the purposes of this article, the important point is that the origin of the Brownian motion class seems to be related, at least partially, to the dynamics of the actin cortex.

Given these—certainly oversimplified—assumptions on the origin of the different motion types, the transition probabilities suggest the following picture. Vesicles can explore large distances over short periods of time near the cell membrane via transport over microtubule tracks. Microtubules in BON cells seem to form a network that is dense (mesh size ∼1 μm) and that runs parallel to the cell membrane (S. Huet, unpublished observations). A vesicle running on a microtubule would move, on average, 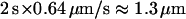(from Table 2) before moving off onto actin filaments. Within the actin cortex, a vesicle would move in a seemingly random manner with a mean diffusion coefficient of 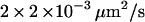and a duration of ∼10 s, exploring a region of ∼300 nm. During this time, if the vesicle encounters an attachment site on the cell membrane, it would anchor and become constrained/stalled for 16 s on average. If it cannot find an attachment site, then it is likely to get back onto the microtubules to go another ∼1 μm away and make another tethering/docking attempt.

Given that many vesicles are transported along microtubule tracks in the vicinity of the cell membrane, the question arises as to whether these organelles could use the microtubule network to reach the plasma membrane directly, without requiring assistance from the actin cortex. Such a direct delivery mechanism has been demonstrated for GLUT4 vesicles in adipose cells (60) or in the case of constitutive secretion (61). In contrast, we have found that in BON cells, secretory vesicles cannot attach onto the cell membrane directly from microtubule tracks: transitions between microtubule-bound and cell membrane-bound vesicles must be mediated by the actin network. The difference may be due to different targeting and attachment mechanisms that may operate in calcium-regulated secretion. Alternatively, the difference may have to do with the density and localization of attachment sites on the cell membrane, and the density of the microtubule tracks. If attachment sites are sparse, covering long distances rapidly (via microtubule based transport) and stopping occasionally to make a local search for membrane-attachment sites (based on actin cortical dynamics) should be quite an efficient search strategy. A similar strategy is employed by many species in nature when searching for prey, a sexual partner, or shelter (62,63, and references therein). The space explored during a diffusive period is also just about sufficient to cross the cortical actin cytoskeleton whose thickness is ∼200–400 nm (18,35). If correct, this model implies that there may be a spatial correlation between the microtubule network and the immobile tethering/docking sites on the plasma membrane, since the space explored by a vesicle in the actin meshwork (∼300 nm) is considerably smaller than the microtubule mesh size (∼1 μm).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.