Extracting Dwell Time Sequences from Processive Molecular Motor Data

Abstract

Processive molecular motors, such as kinesin, myosin, or dynein, convert chemical energy into mechanical energy by hydrolyzing ATP. The mechanical energy is used for moving in discrete steps along the cytoskeleton and carrying a molecular load. Single-molecule recordings of motor position along a substrate polymer appear as a stochastic staircase. Recordings of other single molecules, such as F1-ATPase, RNA polymerase, or topoisomerase, have the same appearance. We present a maximum likelihood algorithm that extracts the dwell time sequence from noisy data, and estimates state transition probabilities and the distribution of the motor step size. The algorithm can handle models with uniform or alternating step sizes, and reversible or irreversible kinetics. A periodic Markov model describes the repetitive chemistry of the motor, and a Kalman filter allows one to include models with variable step size and to correct for baseline drift. The data are optimized recursively and globally over single or multiple data sets, making the results objective over the full scale of the data. Local binary algorithms, such as the t-test, do not represent the behavior of the whole data set. Our method is model-based, and allows rapid testing of different models by comparing the likelihood scores. From data obtained with current technology, steps as small as 8 nm can be resolved and analyzed with our method. The kinetic consequences of the extracted dwell sequence can be further analyzed in detail. We show results from analyzing simulated and experimental kinesin and myosin motor data. The algorithm is implemented in the free QuB software.

INTRODUCTION

Kinetic analysis of data from individual biological molecules started in the 1970s, with the development of the patch clamp technique for ion channels (1). Motor proteins, such as kinesin (2,3), myosin (4), and dynein (5,6), are now studied at the single-molecule level. The motor protein converts chemical energy into mechanical energy by hydrolyzing ATP. The mechanical energy is used for transporting cargo in discrete steps along cytoskeletal filaments, such as microtubules for kinesin and dynein, and actin for myosin. Since motor function is independent of the length of the substrate, the process can be simplified to an infinite chain of identical reaction units (7), where a unit is the set of conformations assumed by the motor protein while it moves one step along the substrate. The location of individual motors as a function of time can be measured with nanometer precision using fluorescence microscopy (6,8,9). Typically, a fluorescent probe is attached to the motor, and a charge-coupled device camera on an optical microscope records the position of the probe. The motors—driven by ATP hydrolysis—track along cytoskeleton filaments immobilized on a glass substrate (8), and their location is traced from frame to frame. The frame rate determines the time resolution of the measurements. The data consist of a time series of the probe position projected along the filament axis. Since the motor proteins generally move forward in discrete steps, the data look like a staircase, although backward steps may occasionally occur, as predicted for all reversible reactions.

A staircase step, i.e., a segment in the data where the measured position of the probe is constant, is called a “dwell”. The duration of each step (the dwell time) is stochastic, with exponential distribution. There may be multiple conformational states associated with a single position of the probe—analogously to the multiple “closed” states of ion channels—and transitions between them are not distinguishable as individual events. Nevertheless, the existence of these unobservable states can be inferred statistically from the distribution of the observed events (10). We denote by “state” the combination of biochemical and positional states. Due to the finite sampling time and exponential distribution of event durations, there will always be missed events. The effect of missed events upon the interpretation of reaction kinetics has been extensively studied in the context of single ion channel kinetics (11–14). In the case of molecular motor data, the same considerations apply. This means that not only are the estimated rate constants in error, but the motor may take one or more steps during a single frame and some of the observed movements will reflect multiple steps.

In this article, we present a maximum likelihood algorithm that extracts the most likely (highest probability) dwell time sequence from the data and returns the global parameters that describe the step size distribution and the rate constants (10). The method relies upon the large knowledge base developed over the last 30 years for the analysis of single ion channel data (11–30). Our main objective is to realistically model the mechanochemistry of the motor in terms of the kinetics and step size distributions, and to take into account instrumental limitations, including various noise sources. The noise components can be described by a continuum of states. These include wideband noise arising from random photon statistics, digitizing errors, and the Brownian motion of the motor. There are also low frequency noise sources arising from drift of the microscope, and errors in correcting for the bending of the substrate filament. We have modified and combined algorithms for hidden Markov models (31) to describe the discrete states of the motor, and Kalman filters (32) for the continuous states of the noise. Thus, we model the mechanochemistry with a periodic Markov chain, as required by the identical chemistry of each step, whereas the Kalman filter models the variability of the motor step and of the baseline. A modified Baum-Welch algorithm (31) recursively extracts (i.e., “idealizes”) the most likely sequence of motor positions (the dwells), and subsequently calculates maximum likelihood estimates for the state transition probabilities, for the mean and standard deviation of the step size distribution, and for the measurement noise. We found that including the Kalman filter also made the algorithm less sensitive to initial parameter estimates.

The algorithm is general, capable of dealing with arbitrary kinetic models, with a wide set of available a priori constraints and step size distributions. The most common kinetic models in the literature have one or two states per reaction unit, irreversible kinetics and uniform steps. Our method is applicable to any staircase-style data, such as that generated by F1-ATPase, where the rotational angle of the rotary motor is traced from frame to frame (33,34), tracking RNA polymerase along the DNA template (35), or tracking topoisomerase activity (36). A distinct advantage of our method is that it fully utilizes the correlation between sequential dwell times that is a consequence of the topology of connections between states (37,38). Since the algorithm is fast, it allows the user to easily compare different models—quantitatively—by computing the likelihoods. Our method is global, in that the model is fitted to all the data at once, whether in a single or in a collection of data files. In comparison, the t-test (39) is a local extraction method, with the generally implicit assumption of a model with only two states and with uniform steps.

We take advantage of the periodic structure of the Markov model (10) to make the algorithm efficient and fast. Staircase data can be fitted to a traditional finite state Markov model (40), but—with the assumption that the minimum number of states is the number of discrete positions of the motor—large data sets would generate huge transition matrices. For example, if there were 100 steps in the data set, one would have to use a matrix of at least 10⁴ elements. Our algorithm is implemented in Windows, and freely downloadable along with other tools, such as single molecule simulators (41). The user graphically inputs a state model of three consecutive reaction units, and a set of initial parameter values. The model can include constraints such as detailed balance or fixed rates, etc. The program internally creates a list of the most likely state at each data point, and uses it to create a sequential list of the dwell times at each position of the motor. This idealized list is an abbreviated data set (there are fewer dwells than there are data points) that can be used to further explore different kinetic models (10).

Our results show that, as with all fitting algorithms, confidence in the output depends upon the signal/noise ratio (SNR) and the length of the data set. We define the SNR as the ratio of the mean step size (allowing for multimodal distributions) to the standard deviation of the background noise. Ideally, the SNR should be >2. The noise level of current experiments is ∼1–3 nm (5,6,8,9), so that steps as small as 8 nm (e.g., kinesin or dynein) can be successfully analyzed. As shown further, the SNR has a strong effect upon the estimated kinetic parameters, and in many cases it is worth sacrificing the time resolution by reducing the bandwidth of the data with appropriate resampling to maintain the validity of the first order Markov assumption. Our studies show that, as expected, the variance of the step size (whether intrinsic to the mechanochemistry or caused by instrumental noise) has a significant effect on the step resolution, and in general we recommend selecting a unit model with only a few steps of fixed amplitude (a multimodal distribution of the step sizes), without intrinsic variance. This multimodal distribution may reflect, for example, the availability of multiple binding sites for the same motor step, or an asymmetrical positioning of the fluorescent probe on the motor.

MODEL AND ALGORITHM

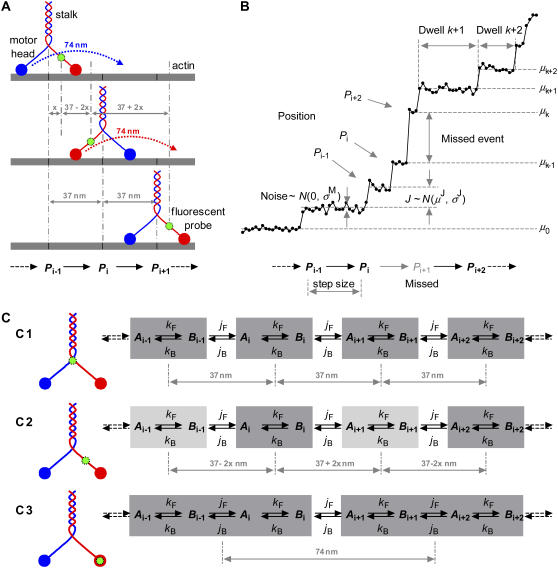
A cartoon representation of a typical molecular motor—myosin V—is depicted in Fig. 1 A. This dimeric protein has two chains twisted around each other, forming the “stalk”. One end of the stalk has the cargo-binding domain. The other end of the stalk splits into two, with each end terminating into a catalytic motor “head” (42,43). Myosin V walks with a hand-over-hand mechanism (8) along the actin filament, with the stalk taking 37 nm steps per ATP hydrolyzed. To walk, the motor alternately rotates its two heads about the stalk: the rear head moves 74 nm forward (twice the stalk movement) to become the leading head, and so on (Fig. 1 A). Kinesin has a similar mechanism (9).

FIGURE 1.

Modeling the mechanochemistry of a molecular motor. (A) Myosin walks hand-over-hand along the actin filament, with the stalk taking 37 nm steps per ATP. The motor alternately swings its heads to walk: the rear head moves 74 nm (twice the stalk movement) and becomes the leading head. (B) Staircase data from single molecule measurements. Each data point is the position of the fluorescent probe measured along the axis of the filament, as a function of time. The motor may take more than one step within the sampling interval (notice the missed event between positions P_i and P_i+2). (C) The position of the fluorescent probe within the motor protein results in different step patterns. The mechanochemistry is modeled as an infinite chain of identical reaction units. At least two kinetic states per unit are necessary to describe the ATP binding step and the position translocation.

STAIRCASE DATA

Fig. 1 B shows how the “staircase” position data are generated, and illustrates some of our definitions. “Positions” are the sites on the substrate where the motor binds during its walk. A “step” is the unitary translation of the motor between two consecutive positions, as would be seen with a perfect instrument. “Jump” refers to the observed amplitude of the riser in the staircase. With perfect data, an observed jump would be the same as a motor step. Note that the motor may take more than one step within the sampling interval, e.g., the missed event between positions P_i and P_i+2. We call the jumps between consecutive positions “first order”, and jumps between nonconsecutive positions “higher order”. For example, the jump P_i → P_i+2 in Fig. 1 B is “second order”. Inferring the jump order from the observed jump amplitude can only be done in a probabilistic way, as discussed below. We denote by μ^J and σ^J the mean and standard deviation of the jump size corresponding to a displacement between discrete positions of the motor.

A “dwell” is a horizontal segment in the staircase sequence. The observed position of the motor is constant during a dwell. We say observed because the motor may in fact undergo reversible transitions during this time that are too short to be observed. The dwell times have exponential distribution. The “amplitude” of a dwell is the mean vertical position (the y coordinate) of those data points within the dwell time. We denote by μ_k the mean amplitude of the kth dwell in the staircase sequence. By definition, two consecutive dwells are separated by a jump. However, two consecutive dwells do not necessarily correspond to consecutive positions because of the potential for missed events. We approximate the measurement noise of the probe position (primarily determined by the number of photons per pixel, per frame) as a δ-correlated Gaussian with zero mean and standard deviation σ^M.

STEP SIZE DISTRIBUTION

The motor protein has a certain degree of structural flexibility, so that in a single step it may reach over a variable distance, and hence it can potentially bind to several sites. Thus, the ideal distribution of the step size is discrete. However, the very flexibility of the motor (twisted polymers with allowable backbone rotations) and that of the substrate, together with other sources of variability, spread these discrete probabilities into a continuous, multimodal distribution. In the interest of simplicity in explaining the method, in the following we will discuss only the cases of uniform steps and of alternating small and large steps. In either case, each step has a unimodal Gaussian distribution. Nonetheless, extension to other models is straightforward.

The observed jump amplitude—noted “J” in Fig. 1 B—follows the distribution of the step size, but it is also affected by the location of the fluorescent probe within the motor molecule (9). Different jump patterns occur as follows:

1. A fluorophore positioned on the stalk produces uniform jumps (Fig. 1 C1) with 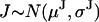, where N refers to the Gaussian distribution function.

2. A fluorophore attached to the lever arm connecting the stalk to the head results in alternating small and large jumps (Fig. 1 C2). In this case, J is distributed as the sum of two weighted Gaussians, reflecting the two possible step sizes of the probe: 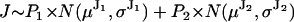. For the physical models under consideration, the two unequal steps must alternate, hence the weighting factors P₁ and P₂ are in fact conditional probabilities that alternate between 0 and 1. The sum of two such unequal jumps is equal to twice the jump of the stalk: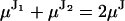. Regardless of fluorophore position, the molecular structure remains the same, and thus it seems reasonable to assume that the combined variance of a pair of unequal jumps is twice the variance of the uniform jump. Hence, we also assume that the relative variance of each jump in the pair is proportional to the relative jump amplitude: .

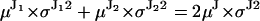3. Finally, a probe attached to a head results in uniform jumps, but twice larger than the jump of the stalk, and with slower apparent kinetics (Fig. 1 C3). In this case, the motor takes two single steps for each first order observed jump, and 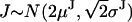. Note that, since the amplitude of first order jumps is modeled as a random Gaussian variable, the amplitude of a higher order jump is also a random Gaussian variable. As with any fitting program, the most rapid convergence and most reliable parameters come from the best starting guesses. If one knows a priori the location of the probe within the motor, the appropriately constrained model should be used in the analysis.

KINETIC MODEL

The mechanochemistry of molecular motors is a repetitive chain of identical reaction units (7), where each unit corresponds to a position on the substrate. A minimum kinetic model must include at least two distinct states per unit (Fig. 1 C): an ATP binding step and a position translocation step. Although the motor appears stationary, it actually undergoes conformational transitions between these two (or more) states. If N_S is the number of states per reaction unit and N_P is the number of all the substrate positions occupied by the motor within a given data set, then the process can be described by a Markov model with N_S × N_P states (10). The frequency of transition between kinetic states is quantified by rate constants, conventionally grouped into a rate matrix Q. For our idealization algorithm, we focus on the probability of observing a transition between any two states, within a sampling interval dt. These probabilities are grouped into a matrix noted A, which can be calculated as 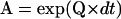. The properties of the Q and A matrices—notably the periodicity constraints—and their computational details are given in Milescu et al. (10). Transitions between states within the same reaction unit cannot be directly observed, but their statistical properties can be inferred from the distribution and cross correlations of dwell times.

LIKELIHOOD FUNCTION

The cost function of our algorithm is the likelihood, defined as the conditional probability of observing the data given a model M:

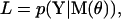(1)

where Y = {y₀,…y_t,…y_T} is the set of noisy position measurements, indexed by the discrete time variable t (i.e., from frame to frame), and M is a topological model with a set of parameters θ. “Topological” refers to the number of states and their connectivity, and the parameters θ describe the state transitions and the step size distribution. Note that the absolute value of the likelihood is only used to compare models. The likelihood function includes all possible states occupied by the motor at each time t. Its calculation must take into account all possible state sequences and their intrinsic probabilities

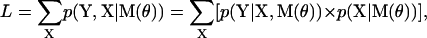(2)

where X = {x₀,…x_t,…x_T} is the sequence of Markov states occupied by the motor, indexed by the discrete time variable t, with x taking values between [0…(N_S × N_P)].

Of special interest is the sequence of states that maximizes the likelihood

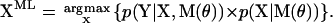(3)

Due to the memory-less character of a first order Markov process and the assumption of δ-correlated measurement noise, the argument in the above expression can be simplified to

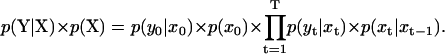(4)

Note that for simplicity we have excluded M(θ), but the dependency on model and parameter values is implicit. The probabilities in the above expression have been presented many times before, for ion channels (30,44,45). Briefly, the state conditional probabilities are the elements of the transition matrix A:

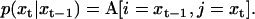(5)

The “hidden” character of the Markov process comes from the fact that one has to observe the state sequence in the presence of noise, so that neither the state nor the amplitude can be known unequivocally at any data point. The probability of picking the state of correct amplitude at any given data point generally comes assuming a Gaussian distribution of errors. Thus, the conditional probability of making a measurement y_t given a state x is the following Gaussian:

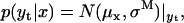(6)

where the mean μ_x is a function of the state x (see the Appendix). With processive motor data, the μ_x values represent the positions successively occupied by the motor on the substrate. These values are stochastic quantities, because the difference between two consecutive positions is equal to the step size, which is itself stochastic, as discussed above.

We cannot directly measure the size of the motor steps, due to finite temporal resolution and background noise. Hence, the step sizes must be inferred from the mean dwell amplitudes μ_k, discussed above. The result is that the model contains some parameters that are stochastic quantities—the μ_k values—and the likelihood function must be modified to include the probability of a particular set of mean dwell amplitudes, as follows:

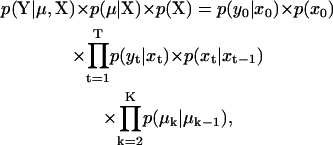(7)

where μ = {μ₀,… μ_k,… μ_K} is the sequence of mean dwell amplitudes (there are K dwells), and p(μ_k|μ_k−1) is the conditional probability that the kth dwell has mean amplitude μ_k, given that the previous dwell had mean amplitude μ_k−1. This probability is implicitly a function of the state(s) occupied by the motor during the respective dwells, and its form depends on how the step probability distribution is defined, as discussed above. Obtaining the X^ML sequence, while at the same time estimating the parameters θ, is the goal of the idealization algorithm presented next.

IDEALIZATION ALGORITHM

Each point must be assigned to a state in the reaction scheme, and implicitly to a discrete position along the substrate. The staircase data are then partitioned into a sequence of dwells, as defined above. Generally, the Forward-Backward procedure (31), or the Viterbi algorithm (46,47) is used to optimally idealize Markov data in the presence of noise when the parameters are known. The result is the most likely state sequence X^ML, out of all possible sequences. Given that the true parameters are unknown (except for simulations), the strategy is to run an optimizing algorithm based on the Expectation-Maximization framework (48), such as Baum-Welch (31), or segmental k-means (30,49). There are several reasons why we cannot directly apply these algorithms to molecular motor staircase data:

1. If the size of the motor step is variable, as previously discussed, then the magnitude of the observed jumps is also variable. Hence, the algorithm should be formulated for Markov models with stochastic parameters (such as the step size).

2. The data may be corrupted by low frequency noise such as microscope stage drift.

3. The number of steps taken by the motor during the recording—and thus the numbers of occupied positions and observed dwells—is not known a priori. Consequently, the number of states in the Markov model is unknown.

Fortunately, the periodic structure of the Markov model (10) permits a simple solution to the unknown number of states. We advance hierarchically in complexity, starting with a small number of unitary steps, and add more states as it becomes necessary. To gain efficiency, the state space is truncated to eliminate those transitions that are not likely to happen (10). To deal with the complications caused by step size variability and baseline drift, we take an approach based in part on our previous work idealizing single-channel data with nonstationary baseline (50). Thus, we use the hidden Markov model to describe the state transitions of the motor, and a continuous Gaussian model (51) to describe the baseline and—more importantly—the variability of the motor step size. Note that only the relatively small and continuous component of step variability is handled this way, whereas the larger and discrete step variability, such as that due to alternating small and large steps, is explicitly included in the Markov model. Thus, we regard all motor steps of the same kind (e.g., small or large, etc.) as having constant amplitude throughout the data, and account for variability in the observed jumps through the baseline noise distribution. In its simplest form (i.e., an unbiased random walk), the baseline model is given by the equation

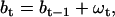(8)

where b_t is the baseline position at time t, and 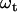is Gaussian noise modeled as 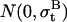that adds random changes to b_t. The standard deviation 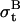is assumed small relative to the step size, as the baseline is expected to deviate little between two consecutive data points. To allow for step variability, 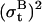is augmented at jump points by a quantity proportional to the step variance and the jump order. Note that, in addition to baseline drift and step variability, the Gaussian process implicitly includes the uncertainty in the initial step size estimate.

The Kalman filter (32,51) is commonly used to estimate the continuous state sequence generated by a noisy Gaussian process—the baseline position in our case. For each data point, the filter provides the most likely baseline from a Gaussian probability distribution, with mean b_t and variance V_t. Obviously, we cannot apply the Kalman filter directly to the staircase data, as the Markov data are summed with the baseline, and there is some cross talk between the Markov and Kalman estimators, since a variation in probe position could be attributed to either process. It is the job of the optimizing algorithm to best separate the two processes. Note that, even though the baseline drift is essentially deterministic, its direction is initially unknown. Hence, from an algorithmic point of view, the baseline can be conveniently modeled as a random process with small variance. Our tests showed that adding a deterministic bias is an unnecessary complication.

We implemented the idealization as an Expectation-Maximization (EM) optimizer, based on a modified Baum-Welch algorithm. The EM optimizer alternates two computational steps:

1. An “Expectation” step estimates the conditional probability that each data point came from a particular state, given the whole data sequence and the current parameters.

2. This is followed by a “Maximization” step, which is actually a prediction of a better set of parameters than the last one.

These two steps are iterated until satisfying a convergence criterion (e.g., only a small change in likelihood). The final Expectation step finds the most likely sequence of Markov states and calculates the likelihood, whereas the Maximization step obtains the maximum likelihood parameters. Next, we explain the two steps of the algorithm.

Expectation—state inference

The Expectation is divided into Forward and Backward steps (31). The Forward step recursively calculates the probability of observing the data points {y₀,…y_t} and ending up in state i. This probability is denoted 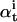. The Backward procedure does the complementary calculation: 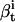is the probability of observing the data {y_t+1,…y_T}, having begun in state i. Additional quantities are also calculated: 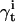is the probability that the state is i at time t, given the entire data sequence {y₀,…y_T}; 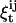is the probability that the state is i at time t and j at time t + 1, given the entire data sequence. All these probabilities are calculated from the current set of parameters, as presented in detail in the Appendix. The α, β, γ, and ξ calculated here are the dependent variables used in the Maximization step. Idealization is the specification of the most likely state for each data point, i.e., the state index i that maximizes γ_t:

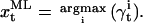(9)

Knowing the state, we also know the position, and from that we can calculate the expected amplitude μ_k of each dwell. Note that the sequence of most likely states 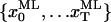so obtained is not necessarily equal to the most likely sequence of states X^ML (Eq. 3). Strictly speaking, to obtain X^ML, we should run Viterbi (46,47) as the final Expectation step, but our tests showed that for all practical purposes, the two state sequences are identical. Our tests also showed that replacing the Forward-Backward procedure with Viterbi throughout the computation, i.e., using a segmental k-means algorithm (30,49), results in significantly poorer performance.

Maximization—parameter reestimation

We want to estimate several parameters: the state transition probabilities stored in the A matrix (10) and the parameters controlling the amplitude distribution, i.e., the measurement noise σ^M, the mean μ^J and the standard deviation σ^J of the step size distribution, and the mean amplitude of each dwell μ_k. The transition probabilities a_ij are reestimated (updated) with the standard formula 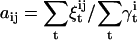, but adjusted to satisfy the periodicity constraints of the model (10). Reestimation of σ^M, μ^J, σ^J, and μ_k is more complicated. For a given dwell sequence, there are two independent sources of variance in the data: the variability of the step size, and the measurement noise. Thus, any parameter estimator should not only minimize the total data variance, in a sum of squares sense, but should also correctly partition this variance (SS) between the intrinsic step size variability (SS^J) and the measurement noise (SS^M). If we were to consider a model with zero step variability, then SS^J would be zero, and only SS^M would have to be minimized. Unfortunately, in the general case, SS^J and SS^M cannot be minimized independently, because they are both functions of μ_k, and because the amplitudes of consecutive dwells are correlated through the step size distribution. Minimizing SS with respect to σ^M, μ^J, σ^J, and μ_k simultaneously requires a nonlinear optimization with a large number of free parameters. As a compromise, we made a linear approximation: we first estimate μ_k and μ^J given the previous σ^M and σ^J, and then estimate σ^M and σ^J, given the new μ_k and μ^J.

The expression of SS^J may take different forms for different models. In the general case, the following issues must be considered:

1. The observed jump size may not be a simple measure of the true step size. A given amplitude jump may reflect a single motor step or multiple steps where the durations were too short to be resolved. If one can observe sufficiently long lasting dwells separated by different jump sizes, then one can make a good estimate of how to fit the data. But if the jump sizes are part of a continuum or happen to be discrete multiples of each other, e.g., 4, 8, and 12 nm, then a jump of 8 nm could represent a transition between any two states that differ in position by 8 nm, or two steps between states that differ in position by 4 nm. Even with perfect data, a finite time resolution will not permit separation of a large amplitude difference between two consecutive dwells as one large single step, or as two smaller steps. Since the actual data is contaminated by noise as well, discrimination of multiple amplitudes is very dependent on the SNR and the length of the data set.

2. Another consequence of step variability is that two dwells in the staircase data sequence that are separated by an equal number of forward and backward motor steps are not expected to have the same observed amplitude, unless the step variance is zero. Hence, their amplitudes must be estimated separately.

All these difficulties are handled by our algorithm, but to avoid confusion, we will illustrate the calculations only for two simple cases that apply to many types of experimental data. For irreversible models with uniform step size (i.e., unimodal step size distribution), SS^J takes the following form:

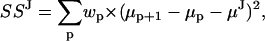(10)

where μ_p is the mean amplitude of the data when the motor is located at position p along the substrate, and w_p is a weighting factor. Note that the sum above is over all the positions—indexed by p—occupied by the motor during the recording. However, not all these occupancies are observed, as some will be missed events. Thus, the weighting factor w_p is proportional to the time that the motor was observed at positions p and p + 1. If the motor was not observed at either p or p + 1 position, then w_p = 0. Minimizing the SS^J above—simultaneously for all μ_p values and for μ^J—satisfies all the necessary constraints, i.e., Gaussian distribution of the step size (with mean μ^J) and correlation between the mean amplitudes of consecutive dwells. Estimates of the μ_p values are obtained for all positions, either occupied (from the actual data and from correlations), or unoccupied (from correlations only). The subset of positions with observed occupancy gives the mean dwell amplitudes μ_k. Similarly, for irreversible models with alternating small and large steps (i.e., bimodal step size distribution), we minimize

(11)

This formulation makes the calculation less sensitive to mistakes in classifying a jump as corresponding to either a small or a large step.

The minimization of SS^J with respect to μ_p values and μ^J (or μ^J1 and μ^J2) is done by imposing the conditions 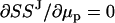and 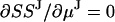, and solving the resulting matrix equation. Once μ_p and μ^J are determined, the step variance is calculated as 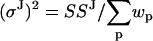. The measurement error SS^M can be calculated simply as 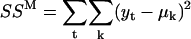, where the sum over all dwells (indexed by k) is in fact reduced to only one term, as only one dwell time interval includes the measurement y_t. From this, the measurement variance is obtained as 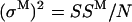, where N is the number of data points.

MATERIALS AND METHODS

Computer simulations

All simulations were done with QuB (41). The simulated data were sampled like the experimental data at 0.5 s intervals. For those experiments designed to test the idealization algorithm as a function of SNR and motor step variability, the random number generator was initialized with the same seed, resulting in identical dwell sequences.

Stage-stepping data

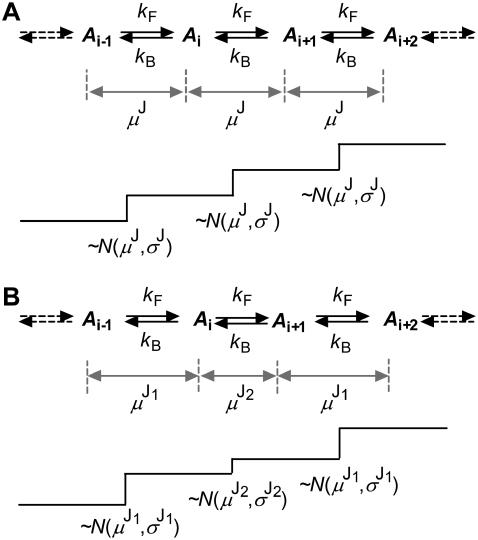
These control data were obtained by attaching a fluorescent probe to the substrate and programming the microscope stage to move in a prescribed pattern, thus characterizing the instrumental resolution. A single Cy3 molecule was attached to a 20-mer dsDNA segment immobilized on a glass coverslip. The stage was translated by a 0.7 nm-resolution piezoelectric stage (8), according to stochastic dwell time sequences created by simulation of the model shown in Fig. 2 A that describes stalk-attached probes (Fig. 1 C1). Specifically, the model had one kinetic state per reaction unit and irreversible kinetics with forward rate constant k_F = 0.25 s⁻¹. The SNR was varied by changing the step size to 8, 13, and 30 nm. Despite the desired precision of the stage, both visual inspection and the idealization program show somewhat higher variability in the actual jump amplitude, possibly a result of limited digital-to-analog resolution of the driver. No significant baseline drift is visible. The data sets were recorded with a sampling time of 0.5 s, and were between 46 and 176 s long.

FIGURE 2.

State models used to simulate and idealize data. (A) A kinetic model with one state per reaction unit, and motor steps of uniform size. A transition between consecutive states is observed as a jump in the staircase data representing the position of the motor. (B) A single state model, where the motor takes alternatively small and large steps. The discrete variability of the step size is explicitly included in the state model. For both of these models, the unitary step has additional variability of a continuous nature, modeled as a Gaussian. Both these models are simplifications and implicitly include an ATP-binding step.

Myosin V data

Chick brain myosin V lever arm was exchanged with bifunctional Rhodamine-labeled calmodulin (Br-CaM) (52). Biotinylated actin filaments were immobilized on a glass surface coated with biotin-BSA and streptavidin. Myosin V was added to the sample flow chamber after actin immobilization, excess was washed off, and the surface was excited by objective-type TIR and the emission was imaged with a charge-coupled device camera. Each fluorescent spot had full width at half maximum of ≈280 nm. Each spot contained 5,000–10,000 photons, so the two-dimensional Gaussian centroid could be fitted with 3 nm error in the peak position for typical spots, and 1.5 nm for brighter spots. The spots displayed quantal bleaching indicative of a single molecule. In the absence of ATP, the fluorescent spots were immobile. The addition of 300 nM ATP led to discernable steps, with the rate increasing with [ATP]. Only the steps of singly labeled myosins were analyzed.

Kinesin data

Human ubiquitous kinesin was labeled in the head region with a single Cy3 dye as described previously (9). Sea urchin axonemes (a microtubule rich structure) were immobilized onto the glass surface by flowing a suspension through a chamber. The chamber was then rinsed and perfused with kinesin. Positional stability measurements of labeled kinesin bound to axonemes in the absence of ATP showed that the axonemes were well attached to the glass and kinesins were strongly bound to the axonemes; 150 nM ATP caused the kinesins to walk along the axonemes.

RESULTS

We tested the algorithm in three different ways. The most comprehensive test was with simulated data, for which the kinetic and noise models were known. We tested basic properties of the algorithm: precision and accuracy of parameters, sensitivity to noise, sensitivity to initial parameter values, and convergence. We varied 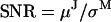by changing the measurement noise σ^M. As a convenient measure of motor step variability, we used the coefficient of variation 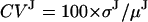, and varied it by changing the standard deviation of the motor step size σ^J. The next step was to analyze control stage-stepping data, where there was only instrumental noise, but the transition points were known. Finally, we analyzed the behavior of myosin and kinesin as a full test, although there are no a priori models with which to compare the results. This last analysis confirmed the adequacy of the various assumptions made about the kinetic and noise models of experimental data.

Computer simulated data sets

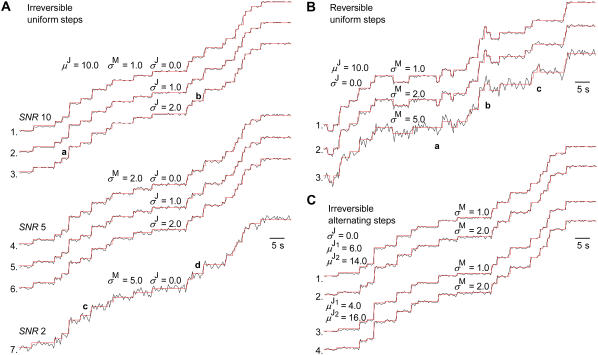
We generated staircase data with irreversible and reversible models having uniform or alternating small and large steps. We have tested kinetic models of increasing complexity, but since similar results were obtained, we discuss here only the simpler models shown in Fig. 2, having one state per reaction unit. In all cases, we used a forward rate constant k_F = 0.25 s⁻¹, and a backward rate constant k_B = 0.0 s⁻¹ for the irreversible and k_B = 0.05 s⁻¹ for the reversible models. The SNR of the simulated data was varied between 1and 10. Except for data with alternating steps, the jump amplitude was μ^J = 10 nm. For each SNR, CV^J was varied between 0% and 20%, by changing σ^J between 0 and 2 nm. Note that μ^J is not important in its absolute value, but only as relative to σ^J and σ^M. Idealization examples are presented in Fig. 3. Note that data generated with larger models (i.e., with two or more states per reaction unit) could be well idealized with a single state model, since the differences in kinetic complexity have only second order effects on idealization. The results obtained from irreversible models having uniform steps were further analyzed, since that is the default model used in the literature, and the results are presented in Figs. 5 and 6.

FIGURE 3.

Idealization of computer simulated data. The red traces are the idealized dwell sequences. All data were simulated and processed with the state models shown in Fig. 2, having one state per reaction unit. The data in A and C have irreversible kinetics (k_F = 0.25 s⁻¹, k_B = 0.0 s⁻¹), whereas the data in B have reversible kinetics (k_F = 0.25 s⁻¹, k_B = 0.05 s⁻¹). The data in A and B have uniform steps, whereas the data in C have alternating steps. The SNR (approximated as μ^J/σ^M) was varied between 10 and by changing σ^M between 1 and 5 nm; the step variance was varied by changing σ^J between 0.0 and 2.0 nm. (A) Irreversible kinetics with uniform steps, μ^J = 10.0 nm When the step variance is high (2.0), the jump order is occasionally mistaken, as marked in the figure by a and b. Thus, the true jump orders of a and b are 3 and 1 but are incorrectly estimated as 2 and 2, respectively. (B) Reversible kinetics with uniform steps, μ^J = 10.0 and σ^J = 0.0 nm. (C) Irreversible kinetics with alternating steps, σ^J = 0.0 nm with different SNR and step sizes μ^J1 and μ^J2. The constraint that the small and large steps must alternate allows a successful idealization even when the SNR of the small step is only 2 (trace 4).

FIGURE 5.

Effects of SNR, step variance, and missed events on idealization. Computer simulated data as in Fig. 3 A. Each estimate is the mean over 100 data sets, idealized individually. The true parameter values are marked by dotted lines. The rate constant k_F was calculated by dividing the data length by the number of detected dwells. (A) The effect of SNR (varied by changing σ^M) and of step variance (varied by changing σ^J). (B) The effect of missed events. Data with SNR 5 were downsampled (without changing the analog bandwidth) by factors of 2, 4, 8, and 16, increasing the fraction of higher order jumps f_H. For zero step variance, all parameters were accurately estimated, even when f_H ≈ 0.7. These results suggest the limits are SNR ≥ 2 and CV^J ≤ 10%.

FIGURE 6.

Statistical distribution of idealization estimates. Irreversible kinetics with uniform steps with SNR 5 and CV^J = 0 (A1 and B1) or 10% (A2 and B2); 1000 data sets were idealized individually. (A) The estimates of μ^J, σ^J, and σ^M have Gaussian distribution. (B) There is good correlation between the estimated and the true values, for μ^J and for k_F, but poor correlation for σ^J. Ideally, all estimates should fall on the diagonal line, as observed for zero step variability (B1).

Irreversible models with uniform steps

Data with uniform steps can be obtained with the fluorescent probe attached either to the stalk, or to the motor head. We focus here on the first case, but note that the only practical difference between the two types of data is that the SNR in the second case is twice as large. Thus, if idealization works for the stalk-attached probe, it works even better for the head-attached. Examples of idealization results are shown in Fig. 3 A. The data were idealized with the model shown in Fig. 2 A, without mistake for SNR ≥ 5, and only with a few mistakes at SNR as low as 2 (e.g., Fig. 3 A, trace 7, c and d). Note that since a model is fitted to an entire data set, a few errors in detection have little effect upon the final parameters.

This level of performance can be achieved only when the intrinsic step variance is zero (traces 1, 4, and 7). Increasing the step variance (CV^J > 5–10%; traces 2, 3, 5, and 6) causes two kinds of errors. First, small jumps are undetected in the presence of wideband noise. This leads to an overestimation of μ^J, since the next detected jump is two or more steps high, and the corresponding rate constants are smaller since transitions have been missed. Secondly, the visible jumps may be misclassified as jumps of order 1 when they were actually jumps of order 2 or higher, and vice versa. The question of jump order occurs regardless of SNR, but it can be treated by including all possible combinations in the reestimation procedure. Examples of this error are marked in trace 3, a and b, where the true jump orders are 3 and 1, but were incorrectly estimated as 2 and 2, respectively.

Note that since we knew these data were obtained with irreversible models, we imposed the constraint that all entries in the A matrix corresponding to backward steps were zero. This condition, when enforced at the start, propagates throughout the iterations. Without this constraint, especially at low SNR, noise artifacts are more likely to be misidentified as backward steps. We want to reiterate the value of a priori constraints: the more constraints, the more precise the results. The penalty is that the accuracy may suffer because the model is wrong. Modeling must be hierarchical and only expand in complexity when the likelihood indicates significant improvement in the fit.

Reversible models with uniform steps

Idealization results for simulated data are presented in Fig. 3 B, obtained using the model in Fig. 2 A. For the same SNR, reversible data are more difficult to idealize than irreversible data as they lack the constraint of no backward transitions. The result is that it is more likely to miss a transition (trace 3, a and b) or to mistake noise for a movement of the motor (trace 3, c). Missing transitions has the primary effect of underestimating rates, whereas mistaking noise spikes for motor transitions results in overestimated rates and possibly overestimated step variance. At SNR ≥ 5, reversible data were idealized without mistakes (traces 1 and 2).

Irreversible models with alternating small and large steps

Examples of idealization results for simulated data are presented in Fig. 3 C, obtained using the model in Fig. 2 B. The small steps are intrinsically more difficult to detect than the large steps. However, the constraint that the steps do not occur independently but must alternate allows reliable idealization of both small and large steps. The example traces shown in Fig. 3 C are idealized without mistake, even when the small step has a corresponding SNR = 2 (trace 4). Note that a simpler jump detector, such as the t-test, which uses only local data information (the means of two samples), may not be so successful at resolving small jumps.

Idealization of experimental data

Stage-stepping control data

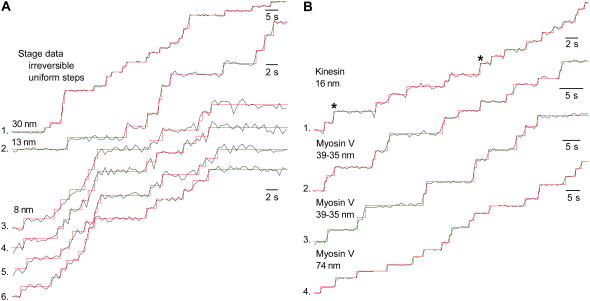
The stage-stepping data were idealized using the model in Fig. 2 A, with results similar to the computer simulations, as shown in Fig. 4 A. Although these data were generated with zero step variance (σ^J = 0.0 nm), we measured a finite jump variance illustrating the sensitivity of the method and the limitations of the instrument. The data with μ^J = 30.0 (trace 1) and 13 nm (trace 2), with SNR ≈ 10, were idealized without error. In contrast, the idealization of 8 nm steps data (traces 3–6), with SNR ≈ 4, had a few mistakes because of the lower SNR and the more prominent experimental artifacts. Note that true error rates can only be known with computer simulated data, where the properties of the input data are known to arbitrary precision.

FIGURE 4.

Idealization of experimental data. The red traces are the idealized sequence. (A) Stage stepping control data. The SNR was varied by changing μ^J: 30.0 nm (SNR ≈ 10; trace 1), 13.0 nm (SNR ≈ 10; trace 2), and 8 nm (SNR ≈ 3–4; traces 3–6). All traces were generated according to a model with σ^J = 0.0 nm, but we extracted a finite step variance. Using the model in Fig. 2 A, the following results were obtained for μ^J, σ^J, σ^M (in nm), and k_F (in s⁻¹): (30 nm) 28.51, 1.40, 3.10, 0.2557; (13 nm) 12.27, 1.28, 1.37, 0.2151; (8 nm, trace 1) 8.02, 0.57, 2.36, 0.2921; (8 nm, 2) 8.11, 0.52, 2.57, 0.2921; (8 nm, 3) 8.12, 0.77, 2.17, 0.2921; and (8 nm, 4) 8.12, 0.75, 1.58, 0.2921. (B) Kinesin (trace 1) and myosin (traces 2–4) data. The kinesin data (sampled at 0.333 s) have uniform steps (head-attached fluorophore), whereas the myosin data (sampled at 0.5 s) have alternating (traces 2 and 3) or uniform steps (trace 4). The optimized values for μ^J, σ^J, σ^M, and k_F: (kinesin, trace 1) 16.74, 2.16, 3.46, 0.4634; (myosin, trace 2) 38.57/34.50, 2.98, 4.54, 0.2807; (myosin, trace 3) 39.76/35.96, 3.70, 4.60, 0.1419; and (myosin, trace 4) 71.88, 3.15, 7.32, 0.1895. All these experimental data were idealized practically as well as the simulated data, suggesting that the assumptions hold (e.g., δ-correlated Gaussian measurement noise).

Kinesin motor data

An example of kinesin data is shown in Fig. 4 B, trace 1. Since the fluorophore was head-attached, we expected to see uniform 16 nm steps. We idealized with the model in Fig. 2 A, having irreversible kinetics with a single state per reaction unit and uniform step size. The algorithm correctly detects the same jump points that we hand-picked. However, the relatively large estimated step variance (CV^J > 10%) made estimating the order of jumps more problematic. All jumps were estimated to be first order, except two that were predicted to be double jumps (marked with asterisks in the figure), in agreement with our hand-picked solution. The algorithm predicted the step size distribution to be μ^J = 16.75 nm, and σ^J = 1.86 nm.

Myosin motor data

Examples of myosin data are shown in Fig. 4 B, for alternating steps (the dye attached near the motor midpoint, traces 2 and 3) and for uniform steps (the dye attached near the head region, trace 4). We idealized with irreversible, single-state models, with alternating steps (Fig. 2 B), or with uniform steps (Fig. 2 A). As myosin's step size is bigger than kinesin's, the SNR in this case is better and the CV^J is smaller. Hence, all these traces were idealized without difficulty. For these particular examples, we estimated ∼39/35 nm alternating steps, and ∼72 nm uniform steps, in good agreement with the literature (8).

Effects of SNR and step variance—simulated data

The effects that the SNR and the step variance have on the accuracy of estimates are quantified in Fig. 5 A. Clearly, for zero step variance, the estimates of μ^J, σ^J, σ^M and k_F are excellent, even at SNR = 2 (Fig. 5 A, red lines). Estimates are still accurate for CV^J = 10% (Fig. 5 A, blue lines) and SNR = 2, with the exception of σ^J. All parameters are significantly less accurate when the step variance is increased to 20% (Fig. 5 A, green lines), and the idealized dwell sequence has more mistakes. These results were obtained without accounting for all possible jump orders between consecutive dwells, as discussed, but even so, the errors were <2–3%. We advise that photon integration time should be reduced, despite an increase in measurement noise, as long as the SNR remains within the acceptable range. The increased time resolution reduces the number of missed events, whereas the global nature of the fit tends to remove the influence of the excess photon noise.

Effect of missed events

Amplitude discrimination improves with SNR. We recommend using an offline digital filter (e.g., the one in the QuB program), rather than increasing the photon integration time, since the software filter is reversible. The data should be resampled at the Nyquist limit after filtering (nominally two data points per cycle at the cutoff frequency) to satisfy the Markov assumption. Our algorithm is not designed to deal with higher order Markov processes, but extension is possible (25,53). The net effect of filtering is to improve the SNR at the expense of time resolution. The penalty is that there are more higher order jumps (missed events). Although higher order jumps are not a problem when the step variance CV^J = 0, they pose a serious challenge when CV^J > 10%.

We tested the effects of missed events on the idealization of staircase data with irreversible and uniform steps. Data simulated as in Fig. 3 A, with SNR 5 and CV^J = 0…20%, were downsampled by factors of 2, 4, 8, and 16, which progressively eliminated shorter dwells, and increased the fraction of higher order jumps, noted f_H. We intentionally left the bandwidth constant to separate the effects of SNR—determined by bandwidth—from the effects of missed events. The dwells averaged 8 points in duration for the original data, but only 0.5 points when downsampled by a factor of 16. The results are shown in Fig. 5 B. For zero jump variance, all parameters were estimated accurately, even when the fraction of higher order jumps f_H ≈ 0.7. For 10% jump variance, the estimates of μ^J and k_F are still good, but estimates of σ^J and σ^M are incorrect when f_H is high. For CV^J = 20%, the estimates are not usable.

Statistical distribution of estimates

The estimates of μ^J, σ^J, and σ^M have a Gaussian distribution, as illustrated in Fig. 6 A, for simulated irreversible staircase data with uniform steps, in this case with SNR 5 and 10, and CV^J = 10%. The width of the distribution depends on SNR and CV^J (results not shown for the latter). No outliers were observed for any of the estimated parameters. As previously discussed and shown in Fig. 5 A, the distributions of σ^J and σ^M are biased toward larger and smaller values, respectively, as the SNR decreases. The estimated parameters are well correlated with the true parameters used in simulation, as shown in Fig. 6 B for μ^J, σ^J, and k^F.

Convergence of the algorithm

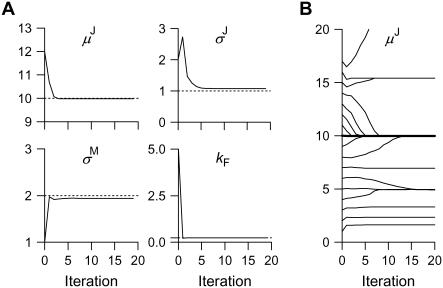
The algorithm is always started with an initial guess of the parameters, and it is desirable that different initial guesses lead to the same solution, i.e., there is a global optimum. We tested the influence of the starting values, as shown in Fig. 7. In the first experiment, all parameters were chosen from a random hypercube in parameter space whose range was ±20% of the true values. With SNR 5 and CV^J = 10%, the program converged to the correct answer in 5–10 iterations (Fig. 7 A). The rate of convergence increased with SNR, and decreased with CV^J. The algorithm did not converge at SNR 1. In general, the algorithm converged monotonically.

FIGURE 7.

Idealization algorithm converges to the true solution. Shown for data simulated with the model in Fig. 2 A with irreversible kinetics, and SNR 5 and CV^J = 10%. (A) μ^J, σ^J, σ^M, and k_F converged to the correct values, even when initialized over a wide range. (B) The idealization is sensitive to the initial value of μ^J, and may converge to incorrect values. For an initial estimate of μ^J within ≈20% of the true value, the idealization converged to the correct parameters.

In a second set of experiments, we determined the importance of each parameter, separately. All parameters were assigned their true values, except one parameter, which was assigned a range of initial values. Thus, any value of μ₀ (mean amplitude of the first dwell) within two σ^M of the first data point always resulted in convergence to the same solution. The measurement noise σ^M also had a wide range of convergence to the same optimal solution. For example, for data with SNR 10 and CV^J = 0…20%, any value of σ^M between 1 × 10⁻¹⁰ and 1 × 10² converged (true value was 0.1). The step size standard deviation σ^J showed good convergence as well. The jump amplitude μ^J was the most critical of all parameters. Its attraction basin is wide at high SNR but narrows as the SNR degrades, and especially as the step variance rises. An example is shown in Fig. 7 B, for SNR 5 and CV^J = 10%. Depending on the starting value of μ^J, the idealization converged to correct or incorrect μ^J, or did not converge at all. For initial estimates of μ^J within ≈20% from the true value, the idealization converged to the correct solution. In contrast, at SNR 2, the initial values had to be within ≈5%.

DISCUSSION

The algorithm presented here can rapidly extract the dwell time sequence from processive molecular motor staircase data, utilizing nearly all the information contained in the data. The algorithm can be used to compare different kinetic and stepping models, and to select the best model based on the likelihood score. Although it is impossible to test the algorithm under all combinations of data and model parameters, the program is freely available (41) so that investigators can test the models and the parameters that best suit their data. For example, the time resolution can be increased by collecting fewer photons per image, and the data set will be proportionally longer, but will the length of the data compensate for the increased measurement noise, for a particular model? Our tests suggest that the algorithm is applicable, in its generality, for most staircase data (see Fig. 4 for examples) (5,6,8,9,33–36). Being nearly maximally efficient (31), no other type of algorithm can make a significant improvement in performance. Convergence will always improve as the number of free parameters is reduced, and we remind the reader that the hierarchical approach to modeling is the most reliable: start with highly constrained, small models, and based upon the results of those fits, slowly relax the constraints.

Comparison with other dwell sequence extraction methods

There are two other published methods of staircase data idealization: the hand picking of events and the t-test (e.g., Carter and Cross (39)). The hand picking is not reproducible and not objective. Nevertheless, the hand picking is a powerful tool in the hands of the trained experimenter, who implicitly uses contextual and global information, as well as the prior experience of having looked at many different data sets. A simple, automated and reproducible method is the t-test, which detects events by comparing the means of two samples. Thus, a transition is detected if the averages of the previous m points and of the next m points are significantly different. However, the t-test is not objective either, because choosing m and the level of significance (e.g., 0.9, 0.95, or 0.99) is subjective and inherently assumes a two-state model of the step. The m points to be averaged may in fact contain multiple transitions that are not allowed in the two-state model. The appeal of the t-test—the apparent independence from a model—is also a critical disadvantage: the t-test does not permit more complex modeling studies. For example, one cannot test a model with alternating small and large steps versus a model with uniform but variable steps.

The maximum likelihood method presented here is model-based, and therefore allows model testing. The underlying model includes not only the step size distribution and the wideband noise, but also the step sequence (e.g., alternating small and large steps, or randomly small or large), and the kinetics. Despite the use of an explicit kinetic model in the idealization, the idealization depends primarily upon the amplitude distribution, and less upon the kinetics, as shown for single channel data (30). Once idealized, the data can be rapidly modeled (seconds) with different kinetic schemes (10). The resulting models can be recursively applied to the idealization, although that tends to have little effect due to the prevalence of the amplitude information. The kinetic modeling using likelihood permits models to be compared on an objective basis, although like any statistic, significance is ultimately judged by the investigator. Another maximum likelihood method is presented by Smith et al. (54), based on modeling the changes in the variance within a sliding window. That method does not explicitly model the processive nature of the molecular motor.

Idealization is limited mostly by step variability

From simulations (Fig. 3) and experimental data (Fig. 4), we found that the SNR should be ≥2 (see Figs. 3–6), and ideally ≥5, although those limits will change with the length of the data set and the average dwell time. This performance is comparable with that achieved by other algorithms (30,31,44,45,53), which can estimate step size (but not kinetics) from ion channel data even at SNR < 1. Note that idealization of processive motor data is a more difficult task than single channels, since the error in amplitude at any time is correlated with the errors at all previous times—there is no immediate baseline measurement available at each step.

Step variability (equivalent to ion channel “substates”) is a critical factor affecting idealization, especially at low SNR. For example, a step variance CV^J = 20% limits the useful SNR to >5 (see Figs. 3–6). We emphasize that we are referring here strictly to the small and continuous component of the step variability, handled by the Kalman filter. Larger and discrete variability, e.g., due to alternating small and large steps, or to multiple binding sites on the substrate, is handled explicitly by the Markov model. Furthermore, note that the jump detection procedure works well even when the step variance is large. What becomes problematic is the classification of jumps, as first, second, or higher orders. As previously discussed, an observed large jump in amplitude could be classified either as a large single step, or as a multiple of small single steps. Given this inherent uncertainty, our algorithm can still find a maximum likelihood state sequence.

Variance estimation is not always reliable

Co-estimation of step variance (σ^J) and measurement noise (σ^M) is difficult, and success is not guaranteed since they are strongly correlated (see Figs. 5 and 6). Thus, σ^J may be underestimated while σ^M is overestimated, or vice versa. The simplest solution may be to extract σ^M from control experiments and constrain it when fitting the biological data. Note that an independent estimation of the dwell amplitudes μ_k and of the jump amplitude μ^J, done by minimizing separately the two error terms SS^M and SS^J, proved to result in even less accurate estimates and in more idealization mistakes.

The idealization algorithm has good convergence

If the SNR is within the acceptable range, the idealization usually converges to the true solution (Fig. 7). The algorithm may have stable solutions (likelihood maxima) not only for the true value of the jump amplitude μ^J, but also for its submultiples: ½ μ^J, ⅓ μ^J, etc. This ambiguity can be avoided by inspecting the estimated A matrix: the transition probabilities for the correct μ^J should have a monotonic exponential decay, but for ½, ⅓, etc., they are interspersed with zeroes due to lack of evidence in the data for these transitions. For example, first, third, fifth… order jumps will be missing when the algorithm has converged to the ½ μ^J solution, a highly improbable event. When enough data are available, the exponential profile of transition probabilities might even be used as a visual indicator for convergence to the correct solution.

APPENDIX: THE FORWARD-BACKWARD PROCEDURE

We illustrate the concepts with an irreversible model having uniform motor step size and one state per reaction unit, in which case the state index and the position index are equal. Extension to more general models is conceptually straightforward, but description of the formalism is tedious.

Forward step

The Forward step recursively calculates α jointly with the baseline quantities b_t and V_t, and it is itself implemented as an Expectation-Maximization procedure. The Expectation step predicts the state occupancy probabilities from the previous , conditional on the current estimate of b_t+1. Then, the Maximization step obtains a posteriori estimates of b_t+1 and V_t+1, using b_t, V_t, and the current 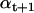estimate. The estimates of b_t+1 and V_t+1 are obtained with a Kalman filter. The Forward step can be summarized as follows:

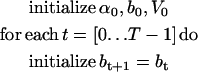repeat

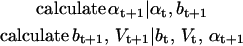until convergence

end.

The baseline and 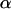can be initialized as follows:

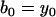(a1)

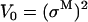(a2)

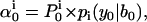(a3)

where 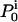is the starting probability for state i, and 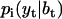is the conditional Gaussian probability density of data point y_t, given the state i, the state amplitude μ_i, and the baseline b_t, calculated as follows:

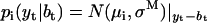(a4)

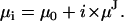(a5)

The amplitude μ₀ of the first dwell and the measurement noise σ^M are parameters of the idealization procedure, and can be initialized by manual data selection. For each iteration, 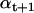is calculated conditional on b_t+1, as follows:

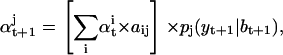(a6)

where a_ij is the conditional state transition probability, stored in the A matrix calculated as in (10). The standard Kalman filter formulae (e.g., (51)) compute b_t+1 and V_t+1 conditional on , as follows:

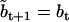(a7)

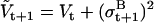(a8)

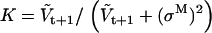(a9)

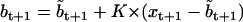(a10)

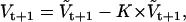(a11)

where x_t+1 and 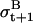are calculated as follows:

(a12)

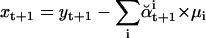(a13)

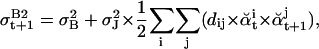(a14)

where d_ij = abs(j − i). In Eq. a14, if a jump of order k is detected between t and t + 1, the reference baseline variance (σ^B)² is augmented by k times the jump variance (σ^J)². The iteration of Expectation-Maximization steps is stopped when b_t+1 changes little from the previous iteration.

Backward step

The backward step calculates 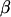recursively, as follows:

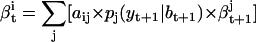(a15)

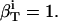(a16)

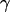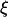The auxiliary quantities and are calculated as follows:

(a17)

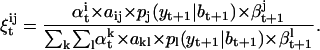(a18)

In all the above equations, we intentionally did not specify the range of the state index, as it refers to the theoretically infinite state space, but the computation is effectively done in a finite truncated state space (10).

Glossary of mathematical symbols

N, number of data points.

dt, sampling interval.

t, discrete time index, with values [0…T].

y_t, position measurement at time t.

Y, sequence of noisy position measurements {y₀,…y_t,…y_T}.

σ^M, standard deviation of the measurement noise.

N_S, number of states per reaction unit.

N_P, number of substrate positions occupied by the motor.

x_t, Markov state at time t, with values [0…(N_S × N_P)].

X, sequence of states {x₀,…x_t,…x_T}.

X^ML, most likely sequence of states.

Q, rate matrix, with elements q_ij.

A, transition probability matrix, with elements a_ij.

k_F, forward rate constant.

k_B, backward rate constant.

J, random variable describing the observed jump amplitude.

μ^J, mean of J.

σ^J, standard deviation of J.

μ_k, average data amplitude for the kth dwell in the staircase sequence.

μ₀, average data amplitude for the first dwell.

μ, sequence of dwell amplitudes {μ₀,… μ_k,… μ_K}.

μ_p, expected data amplitude when the motor is located at position p.

μ_i (or μ_x), expected data amplitude when the motor is in state i (or x).

b_t, mean of the baseline offset at time t.

V_t, variance of the baseline offset at time t.

ω_t, Gaussian noise adding random changes to b_t.

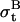, standard deviation of ω_t.

L, likelihood.

M(θ), topological model with parameters θ.

SS, total sum of square errors.

SS^J, sum of square errors due to intrinsic step size variability.

SS^M, sum of square errors due to measurement noise.

SNR, signal/noise ratio, defined as μ^J/σ^M.

CV^J, coefficient of variation of the step size, defined as 100 × σ^J/μ^J.

f_H, fraction of higher order jumps.

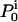, probability that the motor starts in state i at time 0.

p(y_t|x_t), probability density function (pdf) of measurement y_t given state x, at time t.

p_i(y_t|b_t), pdf of measurement y_t, given state i and baseline b_t, at time t.

p(x_t|x_t−1) probability of state x_t, given previous state x_t−1.

p(μ_k|μ_k−1) pdf of the kth dwell's μ_k, given the previous dwell's μ_k−1.

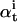, probability of measuring data {y₀,…y_t} and ending in state i.

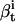, probability of measuring data {y_t+1,…y_T}, having begun in state i.

, probability that state is i at t, given data {y₀,…y_T}.

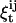, probability that state is i at t and j at t + 1, given data {y₀,…y_T}.