Universality of color names

Abstract

We analyzed the World Color Survey (WCS) color-naming data set by using k-means cluster and concordance analyses. Cluster analysis relied on a similarity metric based on pairwise Pearson correlation of the complete chromatic color-naming patterns obtained from individual WCS informants. When K, the number of k-means clusters, varied from 2 to 10, we found that (i) the average color-naming patterns of the clusters all glossed easily to single or composite English patterns, and (ii) the structures of the k-means clusters unfolded in a hierarchical way that was reminiscent of the Berlin and Kay sequence of color category evolution. Gap statistical analysis showed that 8 was the optimal number of WCS chromatic categories: RED, GREEN, YELLOW-OR-ORANGE, BLUE, PURPLE, BROWN, PINK, and GRUE (GREEN-OR-BLUE). Analysis of concordance in color naming within WCS languages revealed small regions in color space that exhibited statistically significantly high concordance across languages. These regions agreed well with five of six primary focal colors of English. Concordance analysis also revealed boundary regions of statistically significantly low concordance. These boundary regions coincided with the boundaries associated with English WARM and COOL. Our results provide compelling evidence for similarities in the mechanisms that guide the lexical partitioning of color space among WCS languages and English.

Languages differ greatly in how basic color terms are used to name colors. Until the late 1960s, the prevailing view was that differences in color naming occur as a result of cultural factors, which were thought to operate through language to influence strongly individuals' awareness of their chromatic environment (e.g., ref. 1). Then Berlin and Kay (2) advanced a very different view, based on their review of 98 world languages, 20 of which they studied empirically. Although Berlin, Kay, and their colleagues (3–5) have modified some details of their original proposals over the years, two central principles remain: (i) a universal set of processes constrains the lexical encoding of color, and (ii) nearly all languages partition color space lexically into a modest number of categories, which are drawn from a limited set of allowable color categories, including those categories found in English plus certain composite combinations of them. For the past 35 years, these “universalist” principles have shaped the debate regarding how the chromatic properties of the environment become part of the language and thought of a culture.

In the years that followed Berlin and Kay's landmark monograph, many scholars were critical of the small number of (mostly bilingual) subjects and the modest number of languages chosen for empirical study (for review, see ref. 6). Partly in response to this difficulty, Kay and his coworkers collected a massive database of color-naming data and focal color data known as the World Color Survey [WCS; (ref. 5)]. The test materials consisted of 330 achromatic and colored chips selected from the Munsell Color System, as shown in Fig. 1a. The WCS contains color names supplied by 2,616 informants of 110 mostly unwritten languages spoken by preindustrial societies. Color naming in WCS languages is thought to be relatively uncontaminated by contact with highly industrialized cultures whose color lexicons closely resemble that found in English. Thus, comparison of WCS and English patterns in color naming provides a strong test of the universalists' claims.

Fig. 1.

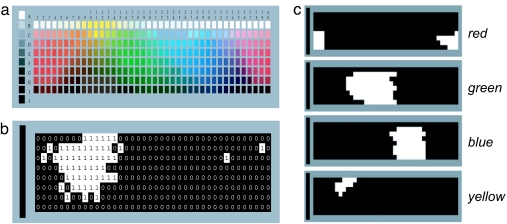
WCS stimuli and color name encoding. (a) The 330 Munsell chips in the WCS color chart. Of the chips, 320 consist of 40 hues spanning the color circle (arranged horizontally), each printed in 8 values (arranged vertically). An additional 10 chips are achromatic colors (sidebar). (b) Bitmap (black = 0; white = 1) illustrating encoding of a chromatic color-naming pattern into a binary-valued vector containing 320 elements, one for each chromatic chip in the WCS color chart. The pattern was obtained from a Yacuna-speaking (Columbia, South America) WCS informant (informant 22). (c) Example bitmaps illustrating colors called red, green, blue, and yellow, respectively, by an English-speaking informant.

Kay and his coworkers have used the WCS to revisit the question of universal constraints on color naming. However, rather than analyzing the full distributions of chips given a particular name by informants, they confined their studies to single-color surrogates for these distributions. The surrogates studied by Kay and his associates were either (i) the color naming “Lab-centroids,” the averaged CIE L*a*b* coordinates of each color-naming pattern (6), or (ii) the “focal colors” selected by informants as the best examples of each color-naming pattern (7). In each case, Kay and his associates found evidence for clustering of the surrogates in regions of color space that approximate the locations of English Lab-centroids or focal colors.

As compelling as these results are, there remain issues regarding the universalist claims that have not been resolved by previous analyses of the WCS database. Among these relationships is that between the surrogates (the Lab-centroids and the focal colors) and the color-naming patterns on which they are based. The surrogates discard much of the information contained in the full color-naming patterns, information that could conceivably challenge the universalist view. Another issue is the precise number of color categories. Do WCS informants reveal as many clusters of color names as exist in English? Do they reveal fewer? Do they reveal more?

For the present study, we conducted two analyses of the WCS color-naming data set to test the universalist claims summarized above. In our first analysis, we examined the clustering of color-naming patterns, treating each pattern obtained from each informant as a separate observation. We were particularly interested in how cluster membership varied as we manipulated the number of clusters, K, into which the color-naming patterns of the WCS were partitioned.

We restricted our analysis to those color-naming patterns that were wholly contained within the 320 chromatic chips of the WCS chart, excluding all patterns that included any of the 10 achromatic chips (see Fig. 1a). We did so because an achromatic pattern, by definition, may differ from a chromatic pattern by only a single chip (black, white, or gray) drawn from a region of color space disjoint from those regions containing the chromatic chips. We were concerned that our clustering methods would be insensitive to these small but possibly (from a theoretical point of view) important differences in color naming.

Each name deployed by each WCS informant produced a corresponding color-naming pattern, which we encoded as a 320-element binary vector (see Fig. 1 b and c). These vectors were then subjected to k-means cluster analysis, in which color-naming vectors were assigned to a predetermined number of clusters, K, using a similarity metric based on Pearson correlation. The aims of the cluster analysis were to see whether the patterns, like their surrogates, tend to group together and to assess objectively how many groupings there are.

In the second analysis, we tested for universal constraints on color naming by exploiting a well known aspect of color-naming data: informants who speak the same language often disagree on what to name a particular WCS chip. We hypothesized that if there are universal constraints on the lexical partitioning of color space, then some colors might be universally more (or less) salient than others, and we should therefore observe regularities in concordance across the WCS color chart, regardless of the language spoken.

Results

Cluster Analysis.

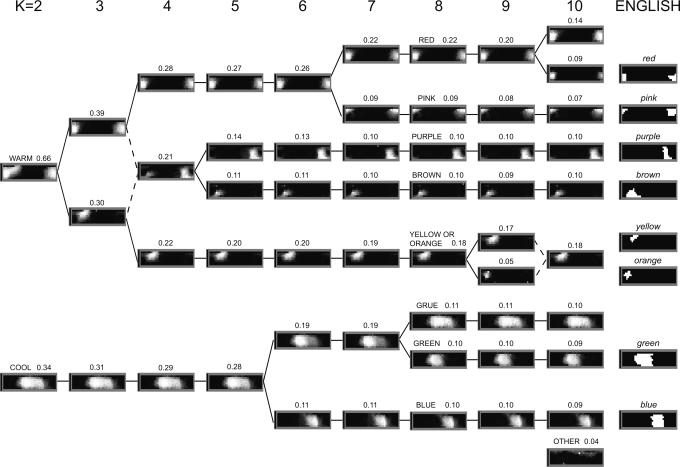
Fig. 2 shows grayscale images of average WCS color-naming vectors derived from our cluster analysis for 2 ≤ K ≤ 10. The vector elements of each average are arranged in the two-dimensional coordinate system of the WCS color chart. The grayscale value of each vector element is related to the frequency with which the corresponding WCS color sample is included in the set of color-naming patterns assigned to a particular cluster by our k-means analysis. The grayscale images in Fig. 2 have been normalized for clarity so that each average color-naming pattern has a maximum grayscale value of 1.0 (white). The original data (e.g., Fig. 1b) had values of either 0 or 1 on each of the 320 dimensions, based on our binary encoding of color naming. In contrast, the averages shown in Fig. 2 are the average locations in 320-space of all of the color-naming patterns included in each cluster. Therefore, they generally have values other than 0 and 1, and in many cases, individual chips are associated with more than one cluster. The number above each grayscale image representing a k-means cluster corresponds to the fraction of patterns (of a total of 14,236 patterns) assigned to that cluster. Therefore, the sum of all fractions in a particular column in Fig. 2 is 1.0.

Fig. 2.

Results of the k-means cluster analysis. The panels in each column indicate the average color-naming patterns associated with each of K clusters (K = 2–10) compared with English (far right). Cluster labels in are uppercase letters; English labels are in italics. The number above each grayscale image indicates the fraction of 14,236 color-naming patterns that fell into the indicated k-means cluster.

Two features of these results stand out. First, regardless of the value of K, the patterns generally correspond to readily identifiable English categories (right column in Fig. 2) or their composites; and second, the changes in the average patterns as K varied are generally well characterized by a binary tree structure.

Let us compare the average color-naming patterns with the corresponding English color categories. The categories obtained for K = 2 are readily described as WARM (including red, yellow, orange, and pink) and COOL (including blue and green). For K = 3, we see COOL, red-plus-pink, and yellow-plus-orange patterns. As K is increased to 6, BLUE and then GREEN emerge. At the level of 8 clusters, we see aggregate color-naming patterns that approximate all of the English color-naming patterns, with two exceptions: patterns corresponding to the English terms orange and yellow are not resolved but are represented as a composite YELLOW-OR-ORANGE category, and, in addition to GREEN and BLUE, the WCS also shows the composite category GRUE (GREEN-OR-BLUE). It is also worth noting that the English red and purple, for example, are more localized than are their WCS counterparts. At K = 10, RED splits into a broad, composite category encompassing red and pink plus a more localized, English-like red. At K = 10, we also see an amorphous cluster (labeled OTHER in Fig. 2) that cannot be described as a composite of English chromatic color-naming patterns. The average pattern associated with this amorphous cluster is composed of chips consisting mainly of high reflectance, desaturated colors, so it might seem reasonable to label this average pattern as achromatic. Recall, however, that we specifically excluded achromatic color-naming patterns from analysis. Increasing K from 10 to 12 further increased the number of these amorphous patterns (not shown in Fig. 2).

The second feature of the diagram in Fig. 2 is its diverging binary tree structure: as K increases from 2 to 10, we see an unfolding of successively more subordinate categories. The only violations of this binary tree structure occurred when K changed from 3 to 4 and from 9 to 10 (shown by dashed diagonal lines in Fig. 2), where the graphs converge rather than diverge. Notice also that the color-naming patterns observed at a given level of the tree tend to persist as K is increased, which shows that our classification algorithm is robust. The general conclusions we draw from our k-means analysis will not depend critically on the precise value of K; we find evidence for English-like categorical structure across a wide range of values of K.

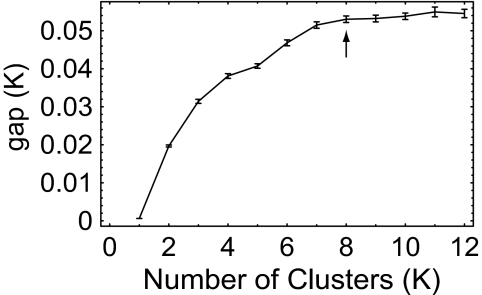
The k-means cluster analysis will generate a solution for any prespecified number of clusters, K, ranging in value from 1 to the total number of observations. Can we estimate an optimal value for K? We did so by using the gap statistic of Tibshirani et al. (8), which measures, as a function of K, the log(ratio) (the “gap”) of the degree of clustering of the WCS data to that obtained from a simulated uniform (cluster-free) reference distribution. The results of our gap analysis shown in Fig. 3 indicate an optimal value for the WCS data of K = 8. It is optimal in the sense that increasing the number of clusters beyond 8 does not reduce gap(K) by a statistically significant amount (see Methods).

Fig. 3.

Graph of gap statistic (±1 S.E.) as a function of the number of k-means clusters. The arrow points to the optimal solution. For details, see Methods.

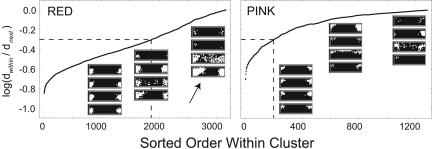
Although the gap statistic indicates that 8 is the optimum cluster number, the gap statistic values are modest (≈0.06 log unit or less), indicating that the color-naming patterns do not all cluster tightly around their respective cluster means. This feature of the WCS color naming is illustrated in Fig. 4, which shows color-naming patterns classified as RED by our cluster analysis. The left column shows individual color-naming patterns with dissimilarities calculated by Pearson correlation that fell close to the RED cluster average. Those patterns in the middle and right columns had, respectively, intermediate and large dissimilarities with respect to the RED cluster average.

Fig. 4.

Sorted order of relative within-cluster dissimilarities, κ, for all patterns assigned to RED or PINK clusters. κ is defined as the logarithm of the ratio of d_within (dissimilarity of a pattern from its within-cluster mean) to d_next (dissimilarity of that pattern from mean of next-nearest cluster). For points to the left of the vertical dashed line, κ < −0.3 (factor of 2.0). (Insets) Examples of color-naming patterns. (Insets Left) Close matches to cluster mean (red, −0.85 ≤ κ ≤ −0.8; pink, −0.6 ≤ κ ≤ −0.55). (Insets Center) Intermediate matches (−0.35 ≤ κ ≤ −0.3). (Insets Right) Poor matches (−0.15 ≤ κ ≤ −0.1). The arrow points to a diffuse warm color-naming pattern, which was part of the red cluster for K = 8.

The reader may be tempted to extend the analysis for cluster numbers beyond K = 8 in hopes of finding additional clusters; for example, one might wish to find a superordinate WARM cluster that would include the larger RED color-naming pattern occasionally seen in the WCS (arrow in Fig. 4). That temptation must be resisted. The gap analysis shows that one would not be accounting for significantly more of the variance than in the K = 8 analysis. Furthermore, expanding the analysis beyond 8 clusters reveals increasingly many unanticipated categories, including the amorphous OTHER categories (lower right corner of Fig. 2) that would also have to be explained somehow, along with the well defined composite categories that might emerge.

Concordance Analysis.

In this analysis, we were interested in color-naming concordance, the extent to which informants of a language agree on how each of the WCS color chips should be named (see Methods). We calculated the concordance within each language in the naming of each chip, and then we looked at the average concordance for all 110 WCS languages. Unlike the cluster analysis described above, we did not restrict our analysis to the chromatic chips but also included color-naming patterns that contained any or all of the ten achromatic chips on the far left side of Fig. 1a.

Fig. 5a shows the mean concordances for each of the chips, coded as grayscale values relative to the grand mean of 0.67 (SD = 0.05). Concordance is clearly nonuniform across the color chart, showing areas of relatively high and low concordance.

Fig. 5.

Concordance analysis results. (a) Grayscale diagram of the concordance for each of 330 chips in the WCS color chart, averaged across the 110 WCS languages. Arrows divide warm and cool colors. (b) Statistical significance compared with the global mean (0.67 ± 0.06) by t tests corrected for multiple comparisons (df = 419, P < 0.01) (21). Concordance: gray, not different from the global mean; white, significantly above the mean; or black, significantly below the mean. Focal colors in English: circles, ref. 2; asterisks, ref. 22.

We compared each mean shown in Fig. 5a with a lower bound on the mean concordance calculated by assuming that the color names available to WCS informants are assigned by them at random to each of the chips. If informants of a language use available words indiscriminately, then, by chance alone, some words are more likely than others to be used to name a particular chip in the WCS color chart. These maxima in word usage will occur randomly across the WCS color chart. Simulation of this process produced a grand mean concordance of 0.178 (n = 110 languages; SD = 0.004) for all 330 chips. We used a t test, corrected for multiple comparisons, to compare the 330 mean concordances with the lower bound grand mean and found that all individual means were statistically significantly above the lower bound (df = 419; P < 0.0001).

We also used a t test, corrected for multiple comparisons, to compare the 330 mean concordances with the observed grand mean. Fig. 5b shows the chips that are significantly above (white) or below (black) the grand mean concordance level at the P < 0.01 confidence level. The narrow black regions of below-average concordance divide the color chart coarsely into two broad regions of average or above-average concordance that correspond roughly to warm and cool colors. The white islands of high concordance correspond closely to five of the six English focal colors related to five of the six Hering primaries: black, white, red, green, and yellow (dots and asterisks). An interesting exception to this rule is the blue region of the WCS chart, which did not reach statistically significant concordance (P > 0.05). We have argued elsewhere that this occurrence may be the result of heavy exposure to UV-B solar radiation in regions where these languages are spoken. UV-B can have phototoxic effects on the ocular lens and/or short-wavelength-sensitive cones that reduce the blueness of nominally blue chips (9, 10). For a contrary view, see refs. 11 and 12.

The reader may be puzzled by apparent discrepancies between the results of the k-means and concordance analyses. Recall that the k-means analysis excluded the achromatic chips, so the k-means analysis cannot reveal BLACK, WHITE, or GRAY. Concordance is low in some regions of color chart (e.g., pink, brown, purple) around which color-naming patterns tend to cluster because the concordance analysis is at the level of the language, and it explicitly considers what color name each informant uses. In contrast, the k-means analysis is at the level of the individual color-naming pattern, and it explicitly does not consider color names at all. The concordance results suggest that certain colors (e.g., red, green, and yellow) are particularly salient to WCS informants, regardless of what language they speak, and they are named in a consistent way. Names for secondary colors (e.g., pink, brown, and purple) are apparently used in a less consistent way, on average, even though the patterns of color naming associated with these colors tend to be similar across languages.

Discussion

We have used cluster and concordance analyses to show that the statistical properties of color naming by WCS informants reveal universal constraints on how cultures lexically partition color space. In our cluster analysis, we introduced the technique of Pearson correlation as a similarity metric so that we could analyze each informant's patterns of color naming rather than surrogates for these patterns. We restricted our cluster analysis to chromatic colors (excluding black, white, and gray), and we showed that WCS clusters correspond to recognizable English color categories or combinations of English categories over a wide range of cluster numbers. Our analysis also showed that the optimum number of WCS chromatic color categories is 8: RED, PINK, BLUE, GREEN, BROWN, PURPLE, YELLOW-or-ORANGE, and GRUE (GREEN-OR-BLUE). Our concordance analysis showed the greatest average concordance in regions corresponding to five of the six Hering color-opponent primaries: red, yellow, and green, black and white. Concordance analysis also showed two major fault lines of low concordance in the WCS color chart, indicating the existence, among WCS informants, of a fundamental psychological distinction between the English composite color categories WARM and COOL.

Central-Color Analyses vs. Color-Naming Patterns.

Previous work by Kay and his colleagues relied on analyses in which each color-naming pattern was reduced to a single central color: either the focal color (2, 7) or the Lab-centroid (6). In contrast, Roberson et al. (13) have argued that color-naming patterns emerge from particularly salient color distinctions drawn at the boundaries between colors rather than from focal examples. Previous work by Regier et al. (7) rejects this hypothesis by showing greater clustering for WCS focal colors (which do not explicitly depend on category boundaries) than for the Lab-centroids derived from the corresponding color-naming patterns (which do depend on boundary locations). WCS focal colors also tended to cluster around Hering primary colors. Our concordance study showed high concordance in regions of the color chart that are associated with five of six Hering primaries. We infer that high concordance across WCS languages indicates that colors in these areas of the color chart may be universally highly salient. Furthermore, we also find boundary regions of statistically significant low concordance, and hence, low salience, which can occur only if (i) individual languages have consistently low concordance at some boundary regions, and (ii) these boundary regions are in approximately the same location in most languages. These two findings are in agreement with the general results of Kay and his colleagues, and they challenge the boundary-salience hypothesis of Roberson et al.

Evolutionary Sequence.

Berlin and Kay (2) speculated that color terminology within each language might have evolved over human history from primitive color lexicons that had only two basic color terms (for light/warm and dark/cool) to color lexicons of technologically advanced cultures that have 11 basic color terms. Can our results address the principle of an evolutionary sequence? This problem is complex because the WCS is a snapshot of the color terms used at the end of the 20th century by these particular 110 world languages. If we were lucky, we might find the color-naming patterns associated with each step of the sequence. But if color terms from the earliest steps along the way have become extinct, we would only see suggestive evidence of their previous existence.

At the optimum level of 8 categories, our k-means analysis did not show statistically significant evidence of all of the composite categories predicted by the evolutionary sequence. On the positive side, there was a significant GRUE cluster along with GREEN and BLUE, and we found a YELLOW-OR-ORANGE category that is not divided (yet?) into YELLOW and ORANGE. But on the negative side, there was no COOL cluster that included GRUE and PURPLE, and no WARM cluster that included RED, PINK, and YELLOW-OR-ORANGE, nor do we find the composite RED-OR-PINK.

It is tempting to view the cluster analysis tree shown in Fig. 2 as a recapitulation of color term evolution from ancient color-naming systems because it exhibits a hierarchical structure similar to that required by most versions of the evolutionary sequence hypothesis, and the tree closely mirrors the associations observed subjectively by Berlin, Kay, and coworkers (e.g., ref. 14). However, the WCS cannot reveal time-dependent processes without certain additional assumptions because it reflects the statistics of color-naming patterns at only one point in history. What the cluster analysis tree does clearly show is that the statistics of WCS color naming favor certain, English-like associations (e.g., red, pink, yellow, and orange) over others (e.g., red, brown, and green) when we restrict the number of clusters that the k-means procedure has to work with. The existence of English-like favored associations provides additional support for universal constraints on color naming. We do not, however, believe that our analysis can be used to deduce a particular evolutionary sequence or to deduce whether the same sequence should be applied to all languages.

How does color space come to be partitioned lexically according to the set of universal constraints we have observed? Certain color distinctions are apparently innate because they can be demonstrated in infants who are too young to speak any language (15, 16). Presumably, at least some color categories are the result of the evolutionary interaction between the visual nervous system and the natural environment, without any significant contribution of culture. However, we are far from any full understanding of how this interaction occurs. Color theorists have developed color-opponent theory as a possible physiological basis of the Hering primaries. However, even if color-opponent theory were a correct model of color appearance (but see ref. 17), we still have no physiological theory explaining why some secondary basic color terms do exist (gray, pink, orange, and purple) whereas others do not (light green, for example). However, the absence of a physiological explanation for these colors at this time does not mean that none will ever be found. We believe that our analyses sharpen the questions that need to be addressed by future theories of color naming.

Methods

Cluster Analysis.

The 320 vector elements corresponding to the chips assigned a given name by an informant were assigned a value of 1; otherwise, they were assigned a value of 0 (see Fig. 1b). Thus, each chromatic chip was treated as an independent color-naming dimension in a 320-dimension naming space, and each color-naming pattern corresponded to a point in this space. We encoded 14,236 chromatic color-naming patterns from the 2,616 informants included in the WCS. The resulting vectors were transformed so that the elements of each vector had zero mean and unit variance. These vectors were contained in the matrix S_i,j, where i (i = 1… 14,236) corresponded to a particular color-naming vector, and j (j = 1… 320) corresponded to a chromatic chip in the WCS color chart.

Color-naming vectors were assigned to clusters by using k-means cluster analysis [Matlab 7.0; The MathWorks, Inc., Natick, MA (refs. 18–20)]. This analysis is an iterative technique that partitioned the color-naming patterns, S_i,* (rows in the matrix S_i,j), according to their “nearness” to K cluster means, C_k,*, where nearness was specified by the dissimilarity, d(x, y), calculated as 1 − the Pearson correlation between vectors x and y:

The cluster means, C_k,*, were the means of all vectors assigned to each cluster, k, normalized to zero-mean, unit variance.

Initially, the C_k,* were randomly assigned vectors in color-naming space. Thereafter, the k-means procedure iteratively partitioned the color-naming vectors among the K clusters, assigning each vector to the nearest C_k,* (Eq. 1), then recalculating cluster means if cluster membership changed from the previous iteration. Eventually, no change in any cluster membership occurred, and the k-means algorithm terminated. In this way, the k-means algorithm minimized the total within-cluster dissimilarity among all 14,236 color-naming vectors. K-means techniques do not guarantee a global minimum in the total within-cluster dissimilarity. We are confident, however, that we achieved or were close to a global minimum because we repeated each analysis in two blocks of 100 iterations using randomly initialized C_k,* in each iteration, and we found no statistically significant differences in minima obtained from the two blocks.

Gap Analysis.

We calculated the gap values plotted on the ordinate of Fig. 3 as follows:

where W is proportional to the total, across all clusters, of the sums of within-cluster, pairwise dissimilarities between cluster members. W and W* refer, respectively, to actual and reference distributions, and E_n [log(W*_k)] indicates expected value. We created reference distributions by rotating the color-naming patterns of each WCS informant by a random integral number of chips in the hue/chroma plane of the Munsell system and then by projecting them back into the coordinate frame of the WCS color chart (for a similar approach, see ref. 6). We calculated gap(K) for 11 different numbers of clusters (K = 2… 12). In each case, log(W*) (see Eq. 2) was obtained from 20 reference distributions obtained by sampling, with replacement, from our database of uniformly distributed color-naming vectors. We used the variation of gap(K) obtained from these 20 samples to calculate se_k, the standard error of gap(K). The optimal number of clusters, K_best, is defined as the minimum number of clusters such that gap(k) ≥ gap(K + 1) − se_k+1.

Concordance Analysis.

We defined “concordance” in the following way. Let n_l,i,j represent the number of times that term j is used among s informants of language l to name the ith chip in the WCS color chart. Then, concordance c_l,i is expressed as:

As an example of this calculation, suppose that of 25 English speakers, 15 name a particular WCS chip red, whereas 5 call the same chip scarlet, and another 5 say crimson. The concordance value for this chip is arg max({15,5,5})/25 = 15/25 = 0.6. Mean concordance for chip i was calculated by averaging c_l,i across l, the 110 WCS languages. The grand mean concordance was the average concordance across all chips.

Abbreviation

WCS

World Color Survey.