Abstract
Multistep carcinogenesis through sequential cycles of mutation and clonal succession is usually described as tumor progression, or the clonal evolution of tumor cell populations. However, many mutations found in cancers are also compatible with normal appearing phenotypes and therefore genetic progression may precede tumor progression. To better characterize such pretumor progression (mutations in the absence of visible phenotypic changes), a quantitative model was developed that postulates most oncogenic cancer mutations first accumulate in normal appearing colon crypt niche stem cells. Each crypt contains multiple stem cells, and random niche stem cell loss with replacement eventually leads to the loss of all stem cell lineages except one. This niche succession or crypt clonal evolution is similar to the clonal succession of tumor progression except it does not require selection or change visible phenotype. Mutations may sequentially accumulate during stem cell clonal evolution either through drift (passenger mutations) or selection. To determine the feasibility of pretumor progression, mutation rates sufficient to recreate the epidemiology of colorectal cancer were estimated. Pretumor progression may completely substitute for visible tumor progression because it is theoretically possible for all cancer mutations to first accumulate in normal appearing colon with normal replication fidelity. Elevated mutation rates or tumorigenesis may be unnecessary for early progression.
Cancer is thought to progress through sequential clonal expansions or clonal evolution.1 An adenoma-cancer sequence describes colorectal tumor progression2 but is limited to events relatively late in life because adenomas usually appear after the age of 50 years. Does anything important happen before visible tumorigenesis? Potentially many of the mutations found in cancers may first accumulate earlier in life because many oncogenic mutations are also compatible with normal phenotypes.3,4 For example, individuals with heterozygous APC and mismatch repair germline mutations are born with normal appearing colons.2 Most mutations fail to expose a gatekeeper defect2 and could accumulate before tumor formation. Therefore, genetic progression (the accumulation of mutations eventually important to a cancer phenotype) may precede tumor progression.
The phenotype of a cancer cell progenitor for the majority of its lifetime is a stem cell because mutations in nonstem cells will not accumulate.5 For example, a cancer cell in a 70-year-old may have 1 year with a cancer phenotype, 10 years with an adenoma phenotype, and 59 years with a stem cell phenotype. Despite this lengthy stem cell prelude, stem cell biology is irrelevant to tumor progression because most mutations presumably accumulate in tumor cells and not stem cells. A description of tumorigenesis such as the adenoma-cancer sequence does not require knowledge of stem cell properties, which is fortunate because very little is currently known about human stem cell biology. However, incorporation of stem cell biology into progression could potentially improve the understanding of how cancers eventually arise. Events that occur in stem cells before tumor progression are defined as pretumor progression.
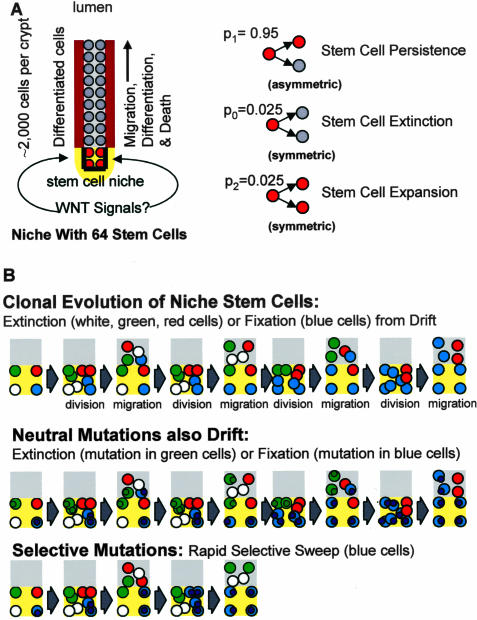
Human colon crypt stem cells cannot be directly identified or isolated. Each crypt appears to contain multiple stem cells, but there are no visible markers or traits that distinguish nonstem cells from stem cells.6,7 Stem cells are not intrinsically immortal but instead appear to be extrinsically defined by signals from a niche.8,9 Cells within a niche are stem cells whereas nonstem cells are outside of a niche (Figure 1). Little is known about human stem cell niches because niche biology is typically studied in model systems that allow fate mapping. Recent studies using methylation changes as stem cell fate markers reveal human colon crypts also maintained by niches. A baseline human scenario suggested 64 stem cells (with ∼2000 total crypt cells) per crypt that divide every day.10 Approximately 95% of the time a stem cell divides asymmetrically to yield one stem cell daughter and one daughter that leaves the niche and differentiates. Sometimes a stem cell will become extinct (2.5% of the time) when both daughter cells leave the niche, balanced by another stem cell that produces (2.5% of the time) two stem cell daughters.10 This population type mechanism (random loss with replacement) normally occurs in all niches and does not require mutation or selection. Eventually this drift results in the periodic loss of all stem cell lineages except one, or niche succession (Figure 1).
Figure 1.
A: Human crypts contain ∼2000 cells. Most crypt cells differentiate, migrate, and die, replenished by a smaller number of stem cells present near crypt bases. There are 64 stem cells per crypt in our baseline model. Only four stem cells per crypt are illustrated. Stem cells are not immortal but rather are extrinsically defined by niches (yellow). Most of the time (p1 = 0.95) stem cell division is asymmetrical. Sometimes (p0 = 0.025) a stem cell lineage will produce two differentiated daughter cells and become extinct, balanced by another lineage that produces (p2 = 0.025) two stem cell daughters and expands. B: Random stem cell loss with replacement or drift eventually results in the loss of all current stem cell lineages except one. This bottleneck resembles the clonal evolution of tumor progression except the clonal evolution of stem cell populations is visibly occult and inherent, requiring neither mutation nor selection. Stem cell somatic mutations (small circles) have uncertain fates because their stem cells (colored circles represent different lineages) have variable fates. Neutral or passenger mutations are usually lost because only one current stem cell lineage will survive niche succession. A neutral mutation may also be fixed when it occurs in the stem cell that eventually drifts to niche dominance. Stem cells with selective mutations may be fixed faster and more frequently.
Inherent niche turnover potentially imposes a Darwinian challenge because stem cells differentiate and die all of the time, and the majority of stem cell lineages become extinct. Therefore, clonal evolution occurs throughout life and not just during tumor progression. In clonal evolution, populations periodically experience bottlenecks whenever replaced by progeny derived from single cells. The clonal evolution of tumor populations1 involves visible sequential selection cycles by individual tumor cells with more fit phenotypes. Occult clonal evolution also occurs in crypts whenever progeny from a single stem cell displace all other competing stem cell lineages and attain crypt dominance (Figure 1). Crypt niche succession is repetitive and in one scenario10 recurs with a median interval of 8.2 years (95% intervals between 2.7 and 19 years). A stem cell destined to transform must survive multiple potential crypt extinction cycles or bottlenecks.
If pretumor progression eventually contributes to carcinogenesis, at least some mutations must accumulate in stem cells and progeny of these stem cells must persist. Most pretumor oncogenic mutations are likely initially neutral because they cannot visibly alter stem cell phenotype. Whereas neutral mutations have no formal roles in tumor progression, stem cells with initially neutral pretumor mutations may attain dominance or fixation simply through drift because niche populations are small relative to visible tumors. For example, although TP53 mutations are common in colorectal cancers, TP53 mutations are also consistent with normal phenotypes.2 Even without a change in visible phenotype, a stem cell with a new TP53 mutation may eventually dominate its niche through drift, which increases the chance for another sequential mutation. However, most neutral or passenger mutations will be lost during pretumor progression because most stem cells lineages (63 of 64) normally become extinct.
Some mutations may also enhance niche survival in the absence of visible changes because stem cell turnover is normally invisible. For example, a mutation may confer a selective advantage and relative immortality to its stem cell by decreasing its chance of leaving the niche. Stem cells with such mutations would tend to persist and have a greater potential for subsequent progression. Intestinal stem cell properties appear to be controlled genetically because mutations in Tcf-4 deplete crypt stem cells in mice.11 Therefore, mutations altering the TCF/β-catenin pathway might be more common in cancers if they confer niche survival advantages during pretumor progression.
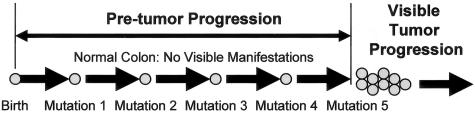
Conceivably most of the oncogenic mutations found in cancers may accumulate during pretumor progression by clonal evolution analogous to tumor progression—sequential cycles of mutations in stem cells followed by crypt niche dominance by the mutant stem cells. Pretumor progression (Figure 2) is fundamentally different from tumor progression (Table 1). Pretumor progression is not merely early tumor progression because mutations accumulate in tumor cells during tumor progression and confer visible phenotypic changes. In contrast, mutations confer no visible changes during pretumor progression and accumulate in stem cells. A visible clonal expansion marks the change from a stem cell to a tumor cell, or the transition between pretumor and tumor progression (Figure 2).
Figure 2.
The mutations and events that precede visible tumorigenesis are defined as pretumor progression. Pretumor progression starts from birth and oncogenic mutations accumulate in stem cells but initially fail to confer visible changes in phenotype. Stem cell niches allow for clonal evolution during pretumor progression because multiple niche stem cells compete for dominance (see Figure 1). Eventually mutation combinations convert a stem cell into a tumor cell, which ends pretumor progression and starts tumor progression. The current analysis suggests pretumor progression can directly progress to cancer without evoking elevated mutation rates.
Table 1.
Pretumor versus Tumor Progression
| Feature | Pretumor progression | Tumor progression |
|---|---|---|
| Clonal evolution | Yes | Yes |
| Start | Birth | Adenoma |
| Interval | Birth to tumor formation | Adenoma to tumor removal |
| Target cell | Stem cell | Tumor cell |
| Multiple mutations needed for cancer | Yes, accumulate throughout life | Yes, most accumulate in adenomas |
| Clonal expansion | Limited to niche | Yes |
| Visible manifestations | No | Tumors |
| Precancerous lesion | Entire colon | Adenoma |
| Selection | Yes | Yes |
| Drift | Yes | Unlikely |
Pretumor progression must be modeled and inferred because it occurs in the absence of visible changes. A number of other investigators have described how early mutations may accumulate.2,12–17 Similarly, we take a multistep approach in which oncogenic mutations sequentially accumulate from birth but fail to confer visible changes in phenotype until transformation. Our model incorporates niche biology, recognizing that neutral pretumor mutations are subject to underlying stem cell turnover and selective mutations may change stem cell turnover. In this article we describe the model and test it for feasibility against the epidemiology of colorectal cancer. Can stem cells accumulate all of the mutations necessary for transformation without evoking increased mutation rates or tumorigenesis?
Materials and Methods
The Model
Our model for progression to cancer is that when a single cell accumulates k-specific mutations, a cancer quickly develops. These mutations may be acquired in any order. Unlike clonal growth models (eg, Armitage and Doll17), before the first stem cell accumulates these k mutations there is no growth, and indeed the tissue appears normal and healthy.
The human colon is lined with ∼15 million crypts (C Potten, personal communication).18 These crypts are believed to evolve independently. Each crypt contains on the order of four to several hundred stem cells.10 It is believed that there is a balance between the stem cells dying and producing new stem cells so that the number of stem cells in each crypt remains approximately constant. The relevance to cancer modeling is that when a new stem cell is produced it inherits the same mutations as its parent, and possibly acquires more.
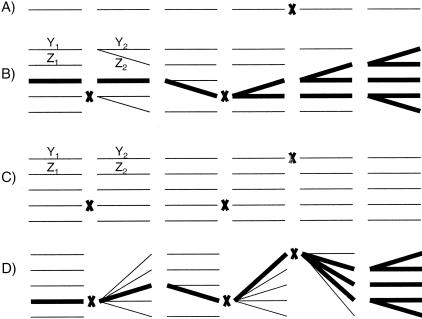
We consider two models for crypt dynamics. The first model is a neutral model and is described in Yatabe and colleagues;10 it is illustrated in Figure 3, scenario B. This model is called neutral because the genealogy of the stem cells is independent of their mutations. Each crypt contains a constant number n of stem cells. In every generation, all of the stem cells simultaneously die and produce two new cells. From these 2n new cells, n become the next generation of stem cells (and the other n become nonstem cells that do not further concern this model). Conditional on the number of stem cells remaining constant, each deceased stem cell produces one new stem cell with probability p1, zero new stem cells with probability p0 = (1 − p1)/2, and two new stem cells with probability p2 = (1 − p1)/2. Previously p1 has been estimated to be 0.95.10 The time until the first stem cell accumulates k mutations in this general model is less than for the case n = 1 (only one stem cell per crypt, scenario A in Figure 3). Below we argue that this time is also greater than for the case p1 = 1 (each of the n stem cells has independent lineages, scenario C in Figure 3).
Figure 3.
The crypt dynamics models. Scenarios A to D each illustrate the time evolution of one crypt. Scenarios A to C are different cases of the neutral model, and scenario D is the sweep model. Time increases from left to right. The figure depicts six generations. The lines represent a single stem cell’s life. The left ends of the lines point to the stem cell’s ancestor (so when all of the lines are parallel as in scenario C the lineages are independent, and when the lines branch as in scenarios B and D the lineages are dependent). The X’s indicate that a mutation has occurred. In the Time to Cancer section, we argue that these four scenarios are in decreasing order of the time until the first cell accumulates k mutations. In scenarios B and C, Y1, Y2, Z1, and Z2 are the number of mutations acquired in the indicated lineages and generations; they are used in a technical argument at the end of the “Time to Cancer” section. A: The case of the neutral model in which there is one stem cell per crypt (n = 1). B: The general neutral model (n > 1, p1 < 1). A stem cell leaves either zero, one, or two descendent stem cells. In this realization, there are five stem cells per crypt (n = 5). The thicker lines highlight the lineage that has survived to the present. In this model, the mutations and the stem cells’ ancestry are independent. C: The case of the neutral model in which each deceased stem cell produces exactly one new stem cell (p1 = 1). In this realization, there are five stem cells per crypt (n = 5). D: The sweep model. Every time there is a mutation, this mutation quickly sweeps to fixation in the crypt. Unlike the neutral model, the mutations and the stem cells’ ancestry are dependent. The thicker lines highlight the lineage that has survived to the present. In this realization, there are five stem cells per crypt (n = 5).
The second model is a sweep model: once a stem cell acquires a mutation this mutation quickly sweeps to fixation in the crypt. This model is illustrated as scenario D in Figure 3. The motivation is that stem cells possessing the mutation have more stem cell descendents than those stem cells not possessing it.
The Time to Cancer
Let μi be the probability a new stem cell acquires the ith mutation (the units are per cell per generation). For the neutral model and the case n = 1, the probability one stem cell lineage acquires the ith mutation in d or less generations is
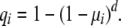 |
This is one minus the probability the lineage has not acquired the mutation in d generations. Let m be the number of crypts. Because we assume the crypts evolve independently and the mutations are acquired independently and in any order, the probability at least one stem cell in any of the crypts accumulates the k mutations in d or less generations is
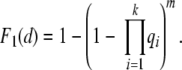 |
For the case n = 1, equation 2 is the cumulative probability that a patient aged d stem cell generations has developed cancer. For the case n >1 and p1 = 1, the analysis is the same except there are n times more independent lineages. Therefore the probability that at least one stem cell in any of the crypts accumulates k mutations in d or less generations is
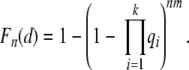 |
For the sweep model, assuming nμi ≪ 1, the mutation rate is n times as large, implying the probability one crypt acquires the ith mutation in d or less generations is,
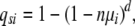 |
and the probability at least one stem cell in any of the crypts accumulates k mutations in d or less generations is
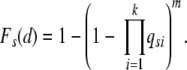 |
We are interested in the time the first cell in any of the crypts accumulates k mutations. If we view the time the first cell in a single crypt accumulates k mutations as a random variable, then we are interested in the minimum of m random variables, where m is the number of crypts. Because we have assumed the different crypts evolve independently, and there are a large number of crypts, this problem is an application of extreme value theory (eg, Ferguson19). It follows from this theory that the distributions in equations 2, 3, and 5 approximately follow the Weibull distribution. The Weibull distribution has two parameters γ and k, and the following distribution function
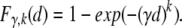 |
Consider the geometric mean of the k mutation rates
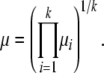 |
Then for the neutral model, case n = 1, the parameter γ is related to the model parameters by the following equation
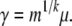 |
We see this by comparing equation 2 to its limit equation 6. For the second case of the neutral model, the case n > 1 and p1 = 1, we use equations 2 and 3 to see that
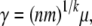 |
whereas for the sweep model, we use equations 1 and 4 to see that
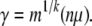 |
Consistent with the observation of Armitage and Doll,14 for both models the hazard rate is log-log linear. Although the model allows different mutations to have different rates, for the type of data we consider in this study it is only possible to infer their geometric mean.
In this paragraph, we argue that for the general neutral model (n > 1, p1 < 1) the time until the first stem cell accumulates k mutations is bounded by the two cases of one stem cell per crypt (n = 1) and each stem leaving exactly one stem cell descendent (p1 = 1). For each crypt in the neutral model, there is one stem cell lineage that is the ancestor for all future generations. The case n = 1 is equivalent to considering only this lineage. Then for any time, the probability one stem cell has accumulated k mutations is less for the case n = 1 than for n > 1. Next we show that the case p1 = 1 provides the opposite bound for the general neutral model. In Figure 3, Y1 and Z1 are the number of mutations the two stem cells acquired in the indicated generation; and Y2 and Z2 are the number of new mutations acquired by the two new stem cells in the next generation. Y1, Z1, Y2, and Z2 are independent and identically distributed random variables. In scenario B, the lineages are dependent (one stem cell leaves two new stem cell descendents, whereas the other stem cell leaves no stem cell descendents); in scenario C the lineages are independent. For the dependent case,the probability that both stem cells have less than k mutations is
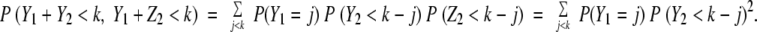 |
For the independent case, the probability is
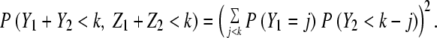 |
By Jensen’s inequality,20 equation 11 is more than equation 12. This argument extends to an arbitrary number of stem cells and generations. Therefore for any time, the probability one stem cell has accumulated k mutations is greater for the case p1 = 1 than for p1 < 1. Exactly where between the two bounds the inferred mutation rate lies is a function of the parameter p1. But as we see from equations 8 and 9 for relevant n and k, the two bounds are close (eg, if n = 100 and k = 5, the two bounds differ by a multiplicative factor of ∼2.5). In the Results section, the two bounds we give for μ for the neutral model are obtained from equations 8 and 9 using the 95% credibility region for γ. For the sweep model, we use equation 10 and the 95% credibility region for γ.
Ascertainment Bias
The data set we consider lists the age of patients when they are diagnosed with colon cancer.21 Because all these patients eventually develop cancer there is an ascertainment bias. Let S(t) be the probability a person is still alive after age t. We approximate this function by using values from a table (National Center for Health Statistics. GMWK 310 1999 for white males in the United States. http://www.cdc.gov/nchs/datawh/statab/unpubd/mortabs/gmwk310_10.htm. May 2003). This table incorporates deaths from all causes. The probability a patient is diagnosed with cancer in the time interval (t1,t2) conditioned on this happening before he dies, is the probability a stem cell accumulates k mutations for the first time in the interval (t1,t2) and the patient is still alive when this happens, divided by the probability this event happens in any time period. In mathematical terms, the conditional probability is
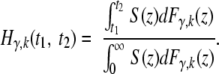 |
To derive this equation we consider two independent random variables: the first drawn from the death table distribution and the second from our pretumor progression model distribution. If the second random variable is less than the first then the patient develops cancer. Because colon cancer is a relatively minor cause of death, the assumption of independence is appropriate. Because we only know the age of diagnosis in resolution of years t, the probability a patient develops cancer at age t is Hγ,k (t,t + 1), which we abbreviate Hγ,k (t). By the same logic, the cumulative probability someone has developed cancer before age t (without any conditioning) is
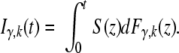 |
We use equation 14 in Figure 4. The difference between equation 14 and equation 6 (which is the limit of equations 2, 3, and 5) is that equation 6 assumes the person has lived for d stem cell generations.
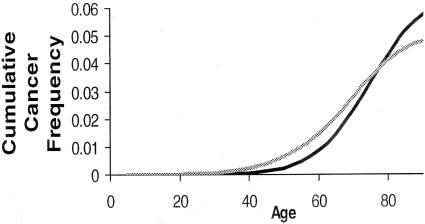
Figure 4.
Cumulative cancer frequency age plots of colorectal cancer comparing epidemiology (black line21) with predictions of our pretumor progression model (gray line).
Bayesian Inference
We take a Bayesian approach. Given the data, we want to infer the parameters k and γ. The data Δ = {t1, t2,… , tn} are the ages of patients when they are diagnosed with cancer.21 Using Bayes’ rule
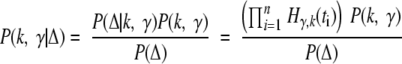 |
We assume a uniform prior P(k,γ) on the number of mutations k = {2,3,… ,9} and γ = [0.001,0.1] per year. The uniform prior on γ translates to a uniform prior on μ; however, the values depend on k, which model we are considering, the parameters m and n, and the stem cell division rate. For all values of k the mode of the posterior appears to be contained in the prior for γ, giving us confidence we have chosen this prior appropriately. We then use equation 15 to compute numerically the posterior P(k, γ Δ). Finally we use a range of estimates for m, n, and the stem cell division rate to infer a range for μ for the two models.
Results
A common criticism of both multistage and multihit models is that they require unrealistically high mutation rates. Paraphrasing Stein,16 if the mutation rate is 10−5 to 10−6 per cell generation, then a five-hit event will require on the order of 1025 to 1030 generations; and based on the number of cells in the human body, predicted cancer incidence rates are many orders of magnitude lower than observed. However, this calculation assumes that all mutations occur in one cell generation. Instead let us consider our neutral model for the case of a single stem cell per crypt (n = 1). Equation 2 is the cumulative probability a person aged d stem cell generations has developed cancer. We will assume the person has lived this long and consider the following parameters: 15 million crypts (m), five mutations required for cancer (k), and 3120 stem cell divisions (d, for each stem cell lineage one generation per week for a 60 year old). If the mutation rate per division is 10−6 then the cumulative probability a 60 year old has developed cancer is 4.4 × 10−6; and if the mutation rate is increased to 10−5 then the cumulative probability is 0.34. If we increase the number of stem cell divisions to 21,840 (so for each stem cell lineage, one generation per day for a 60 year old) then for the above range of mutation rates the cumulative probability range increases to 0.068 to 0.99. For both the case n > 1, p1 = 1 of the neutral model and the sweep model, the cumulative probabilities will be higher. This example shows our model can produce reasonable cancer incidence rates with normal replication fidelity.
We use equation 15 to infer model parameters from colorectal cancer epidemiology.21 For this data set the posterior is completely concentrated on five mutations required for cancer (k). The 95% credibility region for γ = [0.0072, 0.0074] per year. Table 2 shows how these γ values translate to estimates of the mutation rate per division (μ) as a function of the two models and the different model parameters. A higher stem cell division rate naturally translates to a lower mutation rate per division. Other than this, the inferred rates are relatively robust to model parameters except for the sweep model that is sensitive to the number of stem cells per crypt (n). With on the order of 100 stem cells per crypt, the inferred mutation rates for the sweep model are two orders of magnitude lower than for the neutral model. Assuming a baseline model10 with 15 million crypts (m), 64 stem cells in each crypt (n), and one stem cell division per day, for the neutral model the inferred mutation rate is 3.2 × 10−7 to 7.4 × 10−7. For the sweep model and the same parameters, the mutation rate decreases to 1.1 × 10−8 to 1.2 × 10−8. If some of the mutations are neutral and others are positively selected for, then the inferred mutation rate would be between these two models’ estimates. Using these parameters, Figure 4 shows the predicted (equation 14) cumulative probability of cancer as a function of age. Comparisons with the SEER data21 indicate that our model can produce reasonable cancer incidence rates with normal replication fidelity.
Table 2.
Estimates for Mutation Rates (μ)
| One stem cell division per week | One stem cell division per day | |
|---|---|---|
| Neutral model | ||
| n = 1, m = 10 × 106 | 5.5–5.7 × 10−6 | 7.9–8.1 × 10−7 |
| n = 1, m = 20 × 106 | 4.8–4.9 × 10−6 | 6.8–7.0 × 10−7 |
| n = 4, m = 10 × 106 | 4.2–5.7 × 10−6 | 6.0–8.1 × 10−7 |
| n = 4, m = 20 × 106 | 3.6–4.9 × 10−6 | 5.2–7.0 × 10−7 |
| n = 100, m = 10 × 106 | 2.2–5.7 × 10−6 | 3.1–8.1 × 10−7 |
| n = 100, m = 20 × 106 | 1.9–4.9 × 10−6 | 2.7–7.0 × 10−7 |
| Sweep model | ||
| n = 1, m = 10 × 106 | 5.5–5.7 × 10−6 | 7.9–8.1 × 10−7 |
| n = 1, m = 20 × 106 | 4.8–4.9 × 10−6 | 6.8–7.0 × 10−7 |
| n = 4, m = 10 × 106 | 1.4–1.4 × 10−6 | 2.0–2.0 × 10−7 |
| n = 4, m = 20 × 106 | 1.2–1.2 × 10−6 | 1.7–1.8 × 10−7 |
| n = 100, m = 10 × 106 | 5.5–5.7 × 10−8 | 7.9–8.1 × 10−9 |
| n = 100, m = 20 × 106 | 4.8–4.9 × 10−8 | 6.4–7.0 × 10−9 |
n = number of stem cells per crypt; m = number of crypts per colon.
Discussion
A pretumor progression model specifies that stem cells accumulate mutations stochastically and sequentially from birth in normal appearing colon (Figure 2). Pretumor progression has similarities and differences with tumor progression (Table 1). Mutations accumulate in stem cells during pretumor progression whereas mutations accumulate in tumor cells during tumor progression. Pretumor progression ends with visible tumor formation. Although the adenoma-cancer sequence implies that most mutations accumulate during tumor progression, a tumor progenitor spends the majority of its lifetime as a stem cell because adenomas and cancers usually appear after the age of 50 years.2,22 Calculations illustrate potentially all oncogenic mutations found in cancers may first accumulate with normal replication fidelity in normal appearing colon.
Our pretumor progression model uncouples genetic from phenotypic progression and implies tumorigenesis requires the accumulation of multiple interacting mutations. Instead of incremental changes in tumor size and phenotype with each mutation during tumor progression, individual oncogenic mutations initially fail to confer visible changes during pretumor progression. Consistent with pretumor progression, engineering a tumor phenotype from a normal human cell requires multiple changes.23 Moreover, correction of cancer defects often suppresses tumorigenicity rather than causing an incremental decrease in tumorigenicity.24–26 Many alterations may be found even in small adenomas, suggesting genetic instability early in tumor progression.27 An alternative explanation is pretumor progression because an occult series of mutations could precede any tumor. The potential to accumulate many cancer mutations during pretumor progression may help explain some cancers that appear shortly after negative clinical examinations.28,29
Lottery-Like Accumulation of Stochastic Mutations
Pretumor progression mutation rates are likely to be close to normal and therefore ∼10−6 to 10−8 per gene per division.12,30 It may be difficult to accumulate multiple oncogenic mutations with such low rates, suggesting progression involves development of a mutator phenotype that increases mutation rates30 or clonal expansions12 that increase numbers of cells at risk. However, instead of a focus on the acquired neoplastic potential of a few initiated cells, our model starts from birth and the entire colon is preneoplastic as all stem cells remain potential tumor progenitors. The probability that an average cell accumulates multiple mutations within a lifetime is low,30 but a more relevant question is when the first cell out of millions acquires a critical number of mutations. By chance, one cell may accumulate many more mutations than the average cell even when mutation rates are equal for all cells.
The process is analogous to number picking in a lottery. Although the odds of winning for any given player may be extremely low (say 1 in 120 million), the players that win the lottery play far fewer than 120 million attempts. Our pretumor progression model is similar to a lottery because a large number of stem cells are at risk. Although the probability any given stem cell accumulates a rare combination of mutations in a lifetime is incredibly small, the probability just one of the many stem cells accumulates these mutations is not nearly as small.
The lottery-like aspect of our model (a rare winner among millions of losers) implies cancer cells contain many mutations because of chance. One way to distinguish between chance and an increased mutation rate is to examine prospectively for an ability to pick new mutations. Consistent with chance, mismatch repair proficient cancer cell lines acquire new mutations at rates similar to normal cells.30 Another way to distinguish between chance and an increased mutation rate is to examine random cancer genome segments. With an elevated mutation rate, mutations should be common throughout a tumor genome but with a lottery-like process (a few lucky hits in the right places), mutations should be concentrated in critical oncogenes or tumor suppressor genes. Consistent with luck, recent sequencing studies did not detect widespread sequence changes in random portions of mismatch repair-proficient colorectal cancer cell lines.31 A lottery-like process can also account for the presence but relative rarity of somatic mutations in normal colon. Most lottery players pick zero or only a few correct numbers. Similarly TP53 mutations are detectable in normal colon but at extremely low frequencies.32
Clonal Evolution of Stem Cell Populations
Clonal evolution is predicated on competition and change, features inherent to stem cell niches. Stem cells compete because they are not immortal but rather multiple stem cells turnover in crypt niches.8–10 Stem cell populations and their mutations continuously change as individual lineages become extinct or dominant from random stem cell loss with replacement.10 A stem cell that does not persist cannot transform.
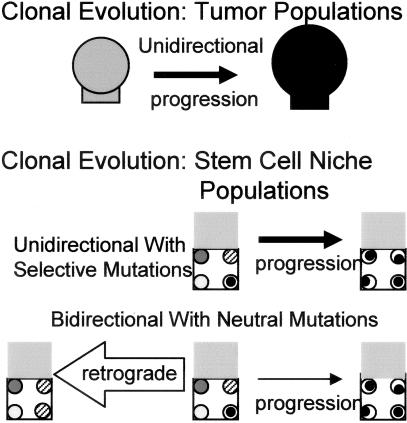
The clonal evolution of tumor populations is driven by mutations acquired in single tumor cells that confer selective advantages over surrounding cells, resulting in clonal dominance.1 Clonal evolution also occurs in crypts whenever progeny from a single stem cell completely populate a niche, but is inherent, visibly occult, and does not require mutation or selection. The small size of stem cell niche populations allows for drift, and passenger mutations (neutral mutations or mutations with minimal selective value) may increase in frequency and become fixed whenever they occur in the stem cell that attains dominance. Therefore, sequential cycles of clonal dominance by mutant stem cell populations may occur without selection, changes in phenotype, or tumorigenesis. Niche dominance because of drift is slow (median time, 8.2 years10) and most neutral mutations will be lost because only one current stem cell lineage attains future dominance.
Mutations may also influence survival if they confer an increased ability for their stem cells to remain within a niche, which may increase the probability and decrease the time of fixation. Any niche advantage is constrained during pretumor progression because by definition, a visible change in phenotype may not occur. However, selective sweeps would be allowed because stem cell turnover is normally occult to morphological examination. Interestingly, mutations in the WNT signaling pathway are frequent in colorectal cancers33 and change stem cell survival in model systems. Alteration of a β-catenin homologue changes stem cell survival probabilities in Drosophila niches.34 Tcf-4 is needed for intestinal stem cell survival11 and with β-catenin, mediates cell position and differentiation in murine crypts.35
Pretumor Progression Pathways to Cancer
Pretumor progression links stem cell turnover with stochastic mutations, with or without selection. Rates of progression can be calculated for a few defined scenarios (Figure 3). The slowest scenario involves a single stem cell per crypt. The fastest scenario involves multiple stem cells per crypt and selective mutations that are immediately fixed by clonal evolution. A realistic scenario likely involves multiple stem cells per crypt and clonal evolution with combinations of neutral and selective mutations. Mutation rates for all scenarios (Table 2) are within the range of normal replication fidelity,12,30 indicating all cancer mutations may first accumulate during pretumor progression.
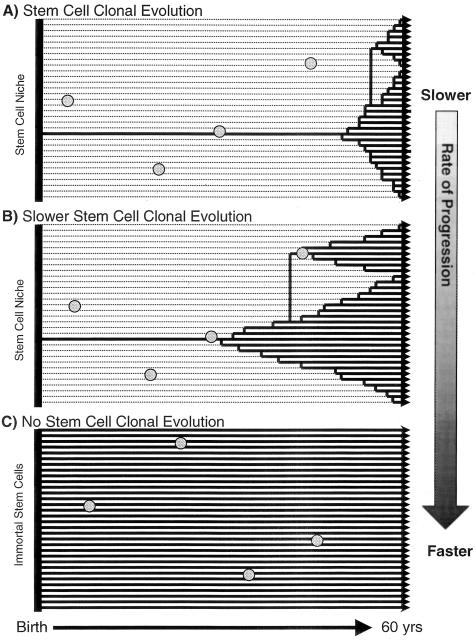
Of note, with multiple stem cells per crypt and neutral mutations, both total numbers of stem cell divisions (or age) and how long stem cell lineages persist influence progression (Figure 5). For example, progression is faster if stem cell lineages are immortal (never become extinct) and all mutations persist. Progression is slower with crypt clonal evolution as most niche stem cell lineages and their mutations become extinct. Differences in clonal evolution intervals allow crypt mutations to accumulate at different frequencies even though they arise at the same rates (Figure 5). Unlike the inevitably forward selection for more aggressive phenotypes during the clonal evolution of tumor progression, pretumor clonal evolution can be a protective or anti-tumorigenic mechanism because mutant stem cells may be lost (Figure 6). Pretumor progression to cancer is faster with longer intervals between niche bottlenecks (slower clonal evolution), which more resemble immortal stem cells, as initially neutral mutations persist longer (Figure 5). Niche clonal evolution rates appear to be genetically modulated and influence progression because stem cell clonal evolution intervals (but not division rates) are longer in some familial adenomatous polyposis crypts compared to nonfamilial adenomatous polyposis crypts.36
Figure 5.
Clonal evolution influences pretumor progression in crypts with multiple stem cells (32 stem cells are illustrated) and neutral mutations. Trees represent 60-year-old stem cell lineages under different scenarios. Time moves from left to right. Solid horizontal lines represent surviving stem cell lineages. Dotted horizontal lines represent past but now extinct stem cell lineages. Circles represent mutations that do not persist if they occur in stem cell lineages that become extinct. Essentially, with initially neutral mutations, pretumor progression to cancer is faster with longer-lived stem cell lineages (crypts with more black lines than dotted lines). A: Clonal evolution is inherent to stem cell niches as stem cell lineages both expand (black lines) and become extinct (dotted lines). Pretumor progression to cancer is slower relative to immortal stem cells (C) because many neutral mutations are lost during niche stem cell turnover. Illustrated is an example of niche stem cell clonal evolution with a bottleneck interval of 8 years (all current stem cells are descendants arising from a single stem cell that existed 8 years ago). B: Pretumor progression is faster with slower stem cell niche clonal evolution (longer intervals between bottlenecks). Illustrated is a bottleneck interval of ∼30 years. Slower stem cell niche clonal evolution more resembles immortal stem cells (C). C: Pretumor progression with neutral mutations is fastest with multiple immortal stem cells. Without clonal evolution or bottlenecks, all crypt stem cell lineages and their mutations persist.
Figure 6.
Unlike the unidirectional clonal evolution of tumor populations, niche stem cell clonal evolution may be anti-tumorigenic because most initially neutral mutations are lost.
Other investigators also incorporate crypt niche biology into progression models,15,37,38 noting that small niche populations influence progression because drift rather than selection may be more important for mutation fixation. They conclude mutations leading to chromosomal instability may also precede tumorigenesis. Our model describes essentially the same niche biology but concludes most oncogenic mutations, including some leading to genomic instability,39 may precede tumorigenesis by assuming early mutations do not immediately confer tumor phenotypes. Furthermore, we analyze the theoretical implications of our model with experimental data in two subsequent articles.36,39
Summary
A number of colorectal cancer models1,2,12–15,40 are consistent with its biology but propose other progression pathways. Distinguishing between models is problematic and no single model may describe all cancers. For example, pretumor progression may be followed by an adenoma-cancer sequence. Pretumor progression follows the logic of clonal evolution1 without evoking tumorigenesis, increased mutation rates, or selection at every stage. Although challenging to analyze, pretumor progression imposes relatively few biological conditions on mutation rates or effects. Mutations start to accumulate from birth at normal rates in stem cells. Mutation combinations eventually confer tumor phenotypes, but individual mutations may initially hitchhike along with the inherent clonal evolution of stem cell niches. Selective pretumor mutations merely eliminate other stem cells during niche turnover.
Modeling pretumor progression may be fundamentally easier than tumor progression because normal appearing crypts intrinsically limit possible changes and parameters. Whatever happens during pretumor progression cannot change visible phenotype. In contrast, tumor progression models must account for greater variations in clone sizes, division or mutation rates, and physiology.41 Many mammalian tissues appear to be maintained by niches9 and better knowledge of how stem cells compete and turnover may help explain pretumor progression for different cancer types.
A major problem with pretumor progression is the absence of tangible evidence for its existence. Pretumor progression must be inferred because it lacks visible changes. Although it is feasible to accumulate all cancer mutations during pretumor progression, the model is dependent on a number of assumptions. Unconfirmed are numbers of stem cells, how often they divide and exit a niche, stem cell mutation rates, numbers of rate-limiting cancer mutations, and the very existence of crypt niches. Our model is dependent on these assumptions and therefore its calculations and conclusions remain unconfirmed.
Yet a major strength of our approach is its assumptions because they construct a very specific pretumor progression model. Instead of a nebulous period before tumor progression, our model defines an active but otherwise occult prelude of mutation and clonal evolution (Figure 2). If stem cell niches exist, pretumor mutations would be captive to their inherent rhythms of extinction and dominance. Application of the model with the same assumptions to a variety of data sets should provide a clearer understanding of what may or may not occur during pretumor progression. In the following articles36,39 we analyze our model with two familial cancer syndromes, hereditary nonpolyposis colorectal cancer and familial adenomatous polyposis. We demonstrate mismatch repair loss likely occurs late during hereditary nonpolyposis colorectal cancer pretumor progression. Some heterozygous APC mutations appear to confer selection and enhanced stem cell survival in normal appearing familial adenomatous polyposis crypts.
Footnotes
Address reprint requests to Darryl Shibata, Department of Pathology, 1200 North State St., Unit I, Room 2428, University of Southern California Keck School of Medicine, Los Angeles, CA 90033. E-mail: dshibata@hsc.usc.edu.
Supported by the National Institutes of Health (grants DK61140 to D.S., and GM58897 and GM67243 to S.T.) and the National Science Foundation (grant DMS-0102008 to P.C.).
References
- Nowell PC. The clonal evolution of tumor cell populations. Science. 1976;194:23–28. doi: 10.1126/science.959840. [DOI] [PubMed] [Google Scholar]
- Kinzler KW, Vogelstein B. Lessons from hereditary colorectal cancer. Cell. 1996;87:159–170. doi: 10.1016/s0092-8674(00)81333-1. [DOI] [PubMed] [Google Scholar]
- Pearson H. Surviving a knockout blow. Nature. 2002;415:8–9. doi: 10.1038/415008a. [DOI] [PubMed] [Google Scholar]
- Kim KM, Shibata D. Methylation reveals a niche: stem cell succession in human colon crypts. Oncogene. 2002;21:5441–5449. doi: 10.1038/sj.onc.1205604. [DOI] [PubMed] [Google Scholar]
- Cairns J. Mutation selection and the natural history of cancer. Nature. 1975;255:197–200. doi: 10.1038/255197a0. [DOI] [PubMed] [Google Scholar]
- Potten CS, Loeffler M. Stem cells: attributes, cycles, spirals, pitfalls, and uncertainties. Lessons for and from the crypt. Development. 1990;110:1001–1020. doi: 10.1242/dev.110.4.1001. [DOI] [PubMed] [Google Scholar]
- Bach SP, Renehan AG, Potten CS. Stem cells: the intestinal stem cell as a paradigm. Carcinogenesis. 2000;21:469–476. doi: 10.1093/carcin/21.3.469. [DOI] [PubMed] [Google Scholar]
- Spradling A, Drummond-Barbosa D, Kai T. Stem cells find their niche. Nature. 2001;414:98–104. doi: 10.1038/35102160. [DOI] [PubMed] [Google Scholar]
- Watt FM, Hogan BL. Out of Eden: stem cells and their niches. Science. 2000;287:1427–1430. doi: 10.1126/science.287.5457.1427. [DOI] [PubMed] [Google Scholar]
- Yatabe Y, Tavaré S, Shibata D. Investigating stem cells in human colon by using methylation patterns. Proc Natl Acad Sci USA. 2001;98:10839–10844. doi: 10.1073/pnas.191225998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korinek V, Barker N, Moerer P, van Donselaar E, Huls G, Peters PJ, Clevers H. Depletion of epithelial stem-cell compartments in the small intestine of mice lacking Tcf-4. Nat Genet. 1998;19:379–383. doi: 10.1038/1270. [DOI] [PubMed] [Google Scholar]
- Tomlinson IP, Novelli MR, Bodmer WF. The mutation rate and cancer. Proc Natl Acad Sci USA. 1996;93:14800–14803. doi: 10.1073/pnas.93.25.14800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luebeck EG, Moolgavkar SH. Multistage carcinogenesis and the incidence of colorectal cancer. Proc Natl Acad Sci USA. 2002;99:15095–15100. doi: 10.1073/pnas.222118199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armitage P, Doll R. The age distribution of cancer and multistage theory of carcinogenesis. Br J Cancer. 1954;1:1–12. doi: 10.1038/bjc.1954.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak MA, Komarova NL, Sengupta A, Jallepalli PV, Shih IEM, Vogelstein B, Lengauer C. The role of chromosomal instability in tumor initiation. Proc Natl Acad Sci USA. 2002;99:16226–16231. doi: 10.1073/pnas.202617399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein WD. Analysis of cancer incidence data on the basis of multistage and clonal growth models. Adv Cancer Res. 1991;56:161–213. doi: 10.1016/s0065-230x(08)60481-9. [DOI] [PubMed] [Google Scholar]
- Armitage P, Doll R. A two-stage theory of carcinogenesis in relation to the age distribution of human cancer. Br J Cancer. 1957;11:161–169. doi: 10.1038/bjc.1957.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng H, Bjerknes M, Amar J. Methods for the determination of epithelial cell kinetic parameters of human colonic epithelium isolated from surgical and biopsy specimens. Gastroenterology. 1984;86:78–85. [PubMed] [Google Scholar]
- Ferguson TS. New York: Chapman and Hall,; A Course in Large Sample Theory. 1991:p 95. [Google Scholar]
- Durrett R. New York: Duxbury Press,; ProbabilityTheory and Examples, (ed 2) 1996:p 14. [Google Scholar]
- Ries LAG, Eisner MP, Kosary CL, Hankey BF, Miller BA, Clegg L, Edwards BK, editors. Bethesda: National Cancer Institute.; SEER Cancer Statistics Review, 1973–1999, 2002 [Google Scholar]
- Fearon ER, Vogelstein B. A genetic model for colorectal tumorigenesis. Cell. 1990;61:759–767. doi: 10.1016/0092-8674(90)90186-i. [DOI] [PubMed] [Google Scholar]
- Hahn WC, Counter CM, Lundberg AS, Beijersbergen RL, Brooks MW, Weinberg RA. Creation of human tumour cells with defined genetic elements. Nature. 1999;400:464–468. doi: 10.1038/22780. [DOI] [PubMed] [Google Scholar]
- Goyette MC, Cho K, Fasching CL, Levy DB, Kinzler KW, Paraskeva C, Vogelstein B, Stanbridge EJ. Progression of colorectal cancer is associated with multiple tumor suppressor gene defects but inhibition of tumorigenicity is accomplished by correction of any single defect via chromosome transfer. Mol Cell Biol. 1992;12:1387–1395. doi: 10.1128/mcb.12.3.1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SJ, Markowitz S, Fearon ER, Willson JK, Vogelstein B. Suppression of human colorectal carcinoma cell growth by wild-type p53. Science. 1990;249:912–915. doi: 10.1126/science.2144057. [DOI] [PubMed] [Google Scholar]
- Tanaka K, Oshimura M, Kikuchi R, Seki M, Hayashi T, Miyaki M. Suppression of tumorigenicity in human colon carcinoma cells by introduction of normal chromosome 5 or 18. Nature. 1991;349:340–342. doi: 10.1038/349340a0. [DOI] [PubMed] [Google Scholar]
- Shih IM, Zhou W, Goodman SN, Lengauer C, Kinzler KW, Vogelstein B. Evidence that genetic instability occurs at an early stage of colorectal tumorigenesis. Cancer Res. 2001;61:818–22. [PubMed] [Google Scholar]
- Winawer SJ, Zauber AG, O’Brien MJ, Ho MN, Gottlieb L, Sternberg SS, Waye JD, Bond J, Schapiro M, Stewart ET, Panish J, Ackroyd F, Kurtz RC, Shike M, The National Polyp Study Workgroup Randomized comparison of surveillance intervals after colonoscopic removal of newly diagnosed adenomatous polyps. The National Polyp Study Workgroup. N Engl J Med. 1993;328:901–906. doi: 10.1056/NEJM199304013281301. [DOI] [PubMed] [Google Scholar]
- Gorski TF, Rosen L, Riether R, Stasik J, Khubchandani I. Colorectal cancer after surveillance colonoscopy: false-negative examination or fast growth? Dis Colon Rectum. 1999;42:877–880. doi: 10.1007/BF02237093. [DOI] [PubMed] [Google Scholar]
- Loeb LA. Mutator phenotype may be required for multistage carcinogenesis. Cancer Res. 1991;51:3075–3079. [PubMed] [Google Scholar]
- Wang TL, Rago C, Silliman N, Ptak J, Markowitz S, Willson JK, Parmigiani G, Kinzler KW, Vogelstein B, Velculescu VE. Prevalence of somatic alterations in the colorectal cancer cell genome. Proc Natl Acad Sci USA. 2002;99:3076–3080. doi: 10.1073/pnas.261714699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussain SP, Amstad P, Raja K, Ambs S, Nagashima M, Bennett WP, Shields PG, Ham AJ, Swenberg JA, Marrogi AJ, Harris CC. Increased p53 mutation load in noncancerous colon tissue from ulcerative colitis: a cancer-prone chronic inflammatory disease. Cancer Res. 2000;60:3333–3337. [PubMed] [Google Scholar]
- Fodde R, Smits R, Clevers H. APC, signal transduction and genetic instability in colorectal cancer. Nat Rev Cancer. 2001;1:55–67. doi: 10.1038/35094067. [DOI] [PubMed] [Google Scholar]
- Song X, Zhu CH, Doan C, Xie T. Germline stem cells anchored by adherens junctions in the Drosophila ovary niches. Science. 2002;296:1855–1857. doi: 10.1126/science.1069871. [DOI] [PubMed] [Google Scholar]
- Batlle E, Henderson JT, Beghtel H, van den Born MM, Sancho E, Huls G, Meeldijk J, Robertson J, van de Wetering M, Pawson T, Clevers H. Beta-catenin and TCF mediate cell positioning in the intestinal epithelium by controlling the expression of EphB/ephrinB. Cell. 2002;111:251–263. doi: 10.1016/s0092-8674(02)01015-2. [DOI] [PubMed] [Google Scholar]
- Kim KM, Calabrese P, Tavaré S, Shibata D. Enhanced stem cell survival in familial adenomatous polyposis. Am J Pathol. 2004;164:1369–1377. doi: 10.1016/S0002-9440(10)63223-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova NL, Lengauer C, Vogelstein B, Nowak MA. Dynamics of genetic instability in sporadic and familial colorectal cancer. Cancer Biol Ther. 2002;1:685–692. doi: 10.4161/cbt.321. [DOI] [PubMed] [Google Scholar]
- Michor F, Iwasa Y, Komarova NL, Nowak MA. Local regulation of homeostasis favors chromosomal instability. Curr Biol. 2003;13:581–584. doi: 10.1016/s0960-9822(03)00172-6. [DOI] [PubMed] [Google Scholar]
- Calabrese P, Tsao JL, Yatabe Y, Salovaara R, Mecklin JP, Järvinen HJ, Aaltonen LA, Tavaré S, Shibata D. Colorectal pretumor progression before and after loss of DNA mismatch repair. Am J Pathol. 2004;164:1447–1453. doi: 10.1016/S0002-9440(10)63231-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moolgavkar SH, Luebeck EG. Multistage carcinogenesis: population-based model for colon cancer. J Natl Cancer Inst. 1992;84:610–618. doi: 10.1093/jnci/84.8.610. [DOI] [PubMed] [Google Scholar]
- Knudson AG. Two genetic hits (more or less) to cancer. Nat Rev Cancer. 2001;1:157–162. doi: 10.1038/35101031. [DOI] [PubMed] [Google Scholar]