Protonation of the β-lactam nitrogen is the trigger event in the catalytic action of class A β-lactamases

Abstract

The pH dependence of the pK_a values of all ionizable groups and of the electrostatic potential at grid points corresponding to catalytically important atoms in the active site of TEM-1 β-lactamase has been calculated by a mean-field approach for reaction intermediates modeled on the basis of energy minimized x-ray crystallographic coordinates. By estimating electrostatic contributions to the free energy changes accompanying the conversion of the free enzyme into the acylenzyme reaction intermediate, we found that acid-catalyzed protonation of the β-lactam nitrogen is energetically favored as the initiating event, followed by base-catalyzed nucleophilic attack on the carbonyl carbon of the β-lactam group. N-protonation is catalyzed through a hydrogen-bonded cluster involving the 2-carboxylate group of the substrate, the side chains of S130 and K234, and a solvent molecule. Nucleophilic attack on the carbonyl carbon is carried out by the side chain of S70 with proton abstraction catalyzed by a water molecule hydrogen-bonded to the side chain of E166. Stabilization of ion pairs in the active site through interactions with distant clusters of charged residues in the enzyme was concluded to be an important driving force of the catalytic mechanism.

Little is known about the structural basis for variability in the mechanisms of β-lactamases although they constitute the major source of β-lactam antibiotic resistance in pathogenic organisms. The most common β-lactamases are the class A and class C enzymes that function via an active site serine residue (1). The class B zinc metallo-enzymes have come into clinical prominence because they are not susceptible to inhibitors effective against the serine hydrolase enzymes (2). Although x-ray structures of class A and C enzymes are known (3), the chemical roles of active site residues are not resolved, except for that of the nucleophilic serine residue (4, 5). There is even less information to define the mechanism of action of class B metallo-enzymes (6, 7).

For class A enzymes a general base is presumed to participate in the active site by abstracting a proton from the nucleophilic S70 side chain to facilitate acylenzyme formation as in serine proteases. The pH profiles of the steady-state kinetic parameters k_cat/K_M and k_cat are approximately bell-shaped with rate-controlling ionization constants pK_a1 and pK_a2 centered on values of ≈ 4.4 and ≈ 8.2, respectively (8–12). It has been suggested that K73 is uncharged in TEM-1 β-lactamase and functions as the proton acceptor (4, 13). This suggestion implicitly assigns pK_a1 to K73 as the general base. In contrast, both K73 and K234 are thought to contribute to pK_a2 in the Bacillus licheniformis 749/C enzyme (12). NMR titration studies of TEM-1 β-lactamase biosynthetically enriched with [ɛ-¹³C]lysine show that the pK_a of K73 is ≥ 10, whereby the authors conclude that E166 is the only residue left to account for pK_a1 (14). No assignment of pK_a2 was made, however. Contradictory conclusions have been made through simulations of electrostatic interactions. Swarén et al. (15) calculate that the pK_a of K73 is 8.0 in the free TEM-1 enzyme and is increased by 6.4 pH units in the Michaelis complex. In contrast, Wade and coworkers (16, 17) conclude that the pK_a of K73 must be ≥10 in both the free enzyme and the Michaelis complex.

Our analysis of the conjectural aspects of the mechanism of class A β-lactamases is derived through a different route (11, 18). The x-ray structure of the acylenzyme of TEM-1 β-lactamase rendered deacylation impaired through an E166N mutation (19) shows that the S70 side chain approaches the C=O group from the convex or exo side of the penicillin molecule (4), opposite to expectation based on stereoelectronic rules (20, 21). Because solvolytic hydrolysis of free β-lactam antibiotics follows stereoelectronic rules, we have argued that the mechanism of class A β-lactamases must differ from the serine protease analogy. On this basis we suggested that protonation of the β-lactam N(1) by the enzyme before or concerted with nucleophilic attack would render the β-lactam group stereoelectronically equivalent with respect to exo or endo nucleophilic attack (11, 18).

Processes such as proton transfer and base catalyzed nucleophilic attack in enzymes are governed by electrostatic interactions (22, 23). Therefore, we have analyzed the pH dependence of calculated pK_as of all ionizable groups and the electrostatic potential Φ_el at grid points corresponding to functionally important atoms in the active site of TEM-1 β-lactamase, using a mean-field approach developed previously for other globular proteins (24–26). On the basis of energy minimized coordinates to model intermediates of the reaction cycle, we have extended this approach to quantify the influence of electrostatic interactions in directing the course of the enzyme catalyzed reaction. We describe here the important electrostatic interactions governing acylenzyme formation at pH 6.5 corresponding to maxima in the pH profiles of k_cat/K_M and k_cat. A more detailed analysis for the complete reaction cycle will be reported later.

Methods

Structural Optimization.

The atomic coordinates of TEM-1 β-lactamase of Escherichia coli (ref. 27; Brookhaven Protein Data Bank file 1BTL) and the benzyl penicilloyl-S70 acylenzyme of the E166N mutant form of TEM-1 β-lactamase (ref. 4; N.C.J. Strynadka and M.N.G. James, personal communication) were used to model all reaction species. Because the initial coordinate listing of the acylenzyme (4) contained a number of residues fitted with alanyl residues to fix the positions of C^β and backbone atoms in the electron density map, these positions were corrected according to sequence and side-chain conformation in the wild-type enzyme (27). The N166 residue was similarly replaced with a glutamate side chain.

The molecular model of the Michaelis complex (ES) was derived by docking the kinetically specific spin-labeled substrate 6-N-(2,2,5,5-tetramethyl-1-oxypyrrolinyl-3-carboxyl)penicillanic acid (18) into the active site of the free enzyme E (27) guided by simulating the hydrogen-bonding and electrostatic interactions of the benzyl penicilloyl moiety in the E166N mutant (4). For this substrate we have developed force-field parameters to account for its spectroscopically (18) defined structure in solution (C.J. Van Zele, M.A. Cunningham, P.A. Bash, and M.W.M., unpublished work). Modeling of the acylenzyme (EY) was similarly guided by the x-ray-defined benzyl penicilloyl-S70 reaction intermediate (4). Electron nuclear double resonance studies of the spin-labeled acylenzyme show that the penicilloyl moiety is precisely superpositioned onto that defined by x-ray in the E166N mutant (D. Mustafi, A. Sosa-Peinado, and M.W.M., unpublished work). The enzyme–product complex (EP) was obtained by docking the corresponding spin-labeled penicilloic acid (11) into the active site of EY (4). Attention was paid to modeling of hydrogen-bonding and electrostatic interactions in the oxyanion hole (28, 29) and the anion binding site with R244 and K234. The E, ES, EY, and EP reaction species, each enclosed within a solvent shell, were subjected to energy minimization and structural optimization consisting of 10–20 steps of molecular dynamics simulations with charmm (30) to remove sterically strained interatomic contacts. Polar hydrogens were added according to the hbuild script in the program. Comparison of the optimized EY structure to the refined coordinates of the benzyl penicilloyl-S70 TEM-1 β-lactamase provided at a later date (N.C.J. Strynadka, personal communication) showed them to be completely overlapping.

Electrostatic Calculations.

The pH-dependence of the electrostatic potential Φ_el,i(pH) at the i^th proton binding site was evaluated by a mean-field approach (24) according to Eq. 1.

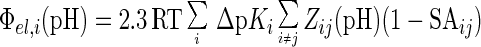1

The term ΔpK_i(pH) is the change in the intrinsic pK_a of the i^th site (pK_int,i) as described below; Z_ij(pH) is the pH-dependent net charge of the i^th group resulting from interactions with all partial and discrete charges (j) in the system; and SA_ij is the normalized, average static solvent accessibility (31) of group i interacting with group j. The pK_a for the i^th group [pK_i(pH)] is calculated iteratively by Eq. 2:

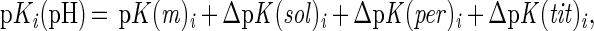2

where pK(m)_i is the pK_a of the i^th site according to model compounds (cf., lists in refs. 24–26), ΔpK(sol)_i is the Born self-energy of the i^th site defined previously (24), and ΔpK(per)_i is the contribution of the i^th site interacting with the set (j) of (permanent) partial charges as assigned in amber (32). The term pK(tit)_i is the pK_a shift of the i^th site caused by interactions with all other charged groups and is evaluated according to a self-consistent iterative procedure (24). Active-site water molecules were defined according to the tip3p model (33). For bulk solvent a local grid of water molecules was modeled as point dipoles covering the active site up to a thickness of 10 Å from the protein surface.

If the first three pH-independent terms of Eq. 2 are collected under the term pK_int,i, then

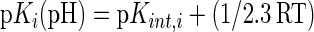3

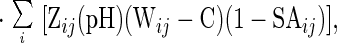where C is the Debye-Hückel term for ionic strength, W_ij is an empirically determined potential function for pairwise interactions given by Eq. 4:

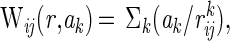4

in which r_ij is the separation between groups i and j and k = 1 for long-range (Coulombic) interactions, 2 for mid-range charge-dipole interactions, and 3 for short-range dipole-dipole interactions. The a_k estimated by a nonlinear procedure is found to be relatively constant for a test set of globular proteins (24–26). As a test of the parameters for class A β-lactamases, simulated pH titration curves were compared with experimentally determined pH titration curves of buried and surface tyrosinyl residues in E. coli TEM-1 β-lactamase and Bacillus cereus β-lactamase I. There was good agreement for both enzyme species (B.P.A., A. Shosheva, B. Villoutreix, A. Sosa-Peinado, and M.W.M., unpublished work). Also, the pK_a values of the catalytically involved residues E35 and D52 in hen egg white lysozyme calculated according to this approach (25) are in good agreement with experiment and are equivalent to results recently reported by others with use of a screened Coulombic potential approximation (34).

The atomic coordinates were mapped onto a 65 × 65 × 65 three-dimensional grid in 1-Å units. The resultant three-dimensional maps of Φ_el were analyzed on a Gateway 2000 PC with use of surfer (Golden Software, Golden, CO). The three-dimensional distribution of Φ_el in E also was calculated by the finite difference method to solve the Poisson-Boltzmann equation (35) as used in delphi (Biosym Technologies, San Diego). An additional calculation was performed with delphi at an ionic strength of 0.1 M with values of the dielectric constant assigned as 4–10 for protein and 80 for water. The results were in essential agreement with those presented here at pH 6.5. The total electrostatic energy ΔG_el(pH) for each species was calculated as described by Sharp and Honig (36) to evaluate electrostatic contributions to the free energy changes associated with conversion of E to EY. The following energy conversion units were used: 1 kcal = 4.186 kJ = 1.68 RT units (at 298 K) = 0.735 pK_a units. The units of Φ_el,i(pH) are kcal/mol⋅e equal to 43.176 mV or 30.24 mC/m².

Results and Discussion

Modeling the Reaction Cycle.

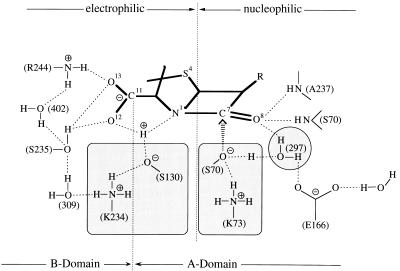
Fig. 1 illustrates important hydrogen-bonding and electrostatic interactions of a penicillin substrate with active-site residues that underlie the catalytic reactivity of TEM-1 β-lactamase identified through x-ray studies (3–5, 13, 27). The two mechanisms for substrate hydrolysis for which we have compared the influence of electrostatic interactions are depicted in Fig. 2. The only constraint in our calculations was that S70 serves as a nucleophile in accord with x-ray studies (4, 5). Solvent molecules identified in the active site (4, 27) facilitated the reaction energetically and therefore were retained in the coordinate listings. Wolfe (37) also showed earlier in simulation studies that strategically positioned water molecules lower the activation barrier for methanolysis of penicillins.

Figure 1.

Hydrogen-bonding and electrostatic interactions in the active site of TEM-1 β-lactamase. The hydrogen-bonded serine-lysine side chains (S70·K73) and (S130·K234) are highlighted because of their functional importance. The numbered designations of active-site water molecules are taken from x-ray studies of the free enzyme (27).

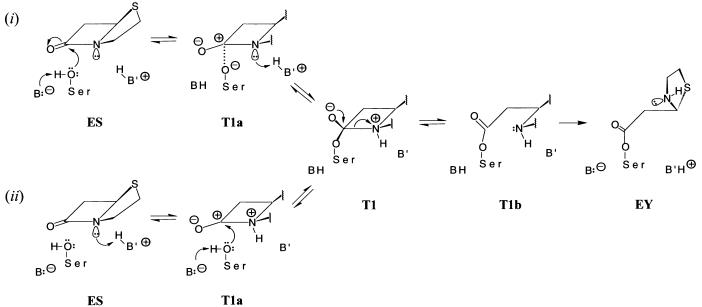
Figure 2.

Comparison of mechanisms for hydrolysis of β-lactam antibiotics catalyzed by TEM-1 β-lactamase to illustrate as the initiating event (i) general-base catalyzed nucleophilic attack by S70 and (ii) general-acid catalyzed protonation of the β-lactam N(1). The two schemes differ mechanistically up to formation of the first tetrahedral adduct of the reaction T1. Structural formulae are, therefore, illustrated only for the acylation portion of each reaction cycle. Formation of the T2 tetrahedral adduct (not shown) occurs through nucleophilic attack on the penicilloyl moiety in EY by a water molecule sequestered in the active site. The structures of the tetrahedral adducts T1 and T2 were deduced by close examination of sterically allowed interactions that an incoming nucleophilic S70 side chain, correspondingly, water molecule, may experience in the ES and EY intermediates, respectively. We discuss results for only sequential reaction mechanisms. The corresponding concerted reaction mechanisms were found to be less favorable energetically. T1a and T1b represent transient species in formation and breakdown of T1. T1a was modeled by applying the electronic configurations of active-site atoms in T1 to nuclear positions in ES. T1b was modeled by applying the electronic configurations of EY to the nuclear coordinates of T1. This sequence of changes in electronic structure and nuclear coordinates follows from first-principle considerations of the Born-Oppenheimer approximation and the Franck-Condon rule. A similar procedure was applied to evaluate electrostatic interactions governing deacylation.

In the acylenzyme of TEM-1 β-lactamase (4), the [N(1)–C (5)–C(6)–C(7)] torsion angle of the β-lactam ring has a value of ca. −33° compared with ≈ 0° in the intact substrate. Because N(1)–C(7) bond scission must occur during transformation of T1 into EY, this is modeled in Fig. 2 as a two-step process involving scission of the bond, followed by a torsional change about C(5)–C(6). Samama and coworkers (29) have pointed out that structural relationships of active site residues differ with respect to the acyl moiety according to whether they resemble acylation or deacylation transition-state species. It is probable that this step leads to the change in conformation of active-site residues from acylation to deacylation species.

Analysis of electrostatic interactions was based on two sets of coordinates studied in parallel: (i) structurally optimized coordinates of E, ES, EY, and EP species each within a solvent environment, as described in Methods and (ii) reaction species modeled only on the basis of x-ray defined coordinates of E and EY. By comparison of results calculated in parallel, we separated out effects of structural differences due to energy minimization of the protein in two different crystal environments from structural changes intrinsic to the simulated reaction species. Crystal packing effects were associated primarily with the “histidine-rich” regions of the protein surface. Effects intrinsic to the reaction species were distributed over multiple regions of the protein.

As a result of structural optimization, E was found to be similar but not identical to the EY intermediate. Correspondingly, energy minimization of EY without the acyl moiety led to a slightly different model of E than obtained by structural optimization of the x-ray enzyme (27). Although the differences were small, we believe that they reflect structural variations of functional importance. The free enzyme E determines the structures of ES and T1. Correspondingly, EY determines the structure of T2, the second tetrahedral adduct, leading to EP complex formation and product release. Molecular modeling shows that the nucleophile must sterically approach the carbonyl group from different sides of the β-lactam ring in formation of T1 and T2 adducts. Also, as pointed out above, there are structural differences of active site residues in acylation and deacylation steps of the reaction (29).

Analyzing Electrostatic Interactions.

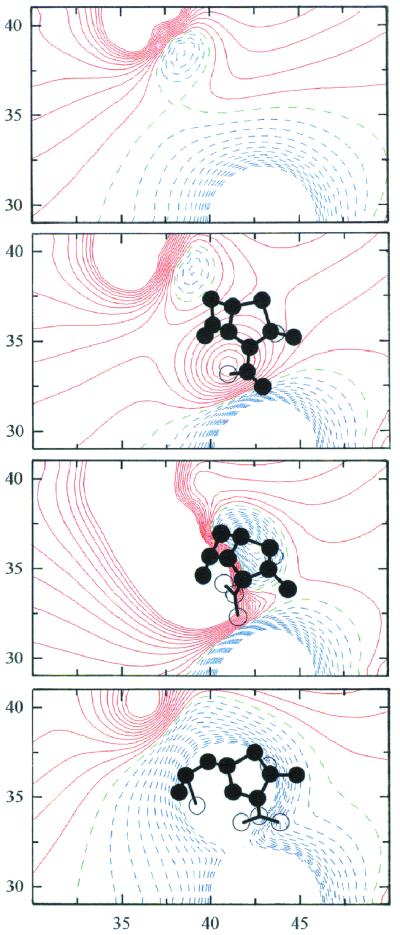
Fig. 3 shows contour maps of Φ_el in the active site of the E, ES, T1, and EY species of TEM-1 β-lactamase. The maps of these species are derived from coordinates of E and EY and are independent of the electronic configurations through which the pathways differ in Fig. 2. By analysis of contour maps generated for each of the species in Fig. 2, we estimated electrostatic contributions to the free energy changes accompanying the transformation of E into EY for (i) general-base catalyzed proton abstraction from S70 as the initiating event followed by nucleophilic attack on the β-lactam C=O group and for (ii) general-acid (electrophilic) catalyzed protonation of the β-lactam N(1) as the initial step followed by general-base catalyzed nucleophilic attack by S70.

Figure 3.

Contour maps of the electrostatic potential in the active site of TEM-1 β-lactamase for E, ES, T1, and EY (top to bottom). The contour levels are calculated at intervals of 0.5 kcal/mol⋅e (≈0.83 RT/e). Solid red contours indicate negative isopotential curves; broken blue contours show positive isopotential curves while broken green contours represent curves of 0 potential. The contours are deleted at distances less than 2.5 Å from hydrogen-bound atoms. The maps are drawn for x = 30–50 Å and y = 28–42 Å with respect to the crystal axis system of the E166N acylenzyme (4). The contour maps are projected along the z axis from z = 29.5 Å to z = 32.5 Å. [The level of z = 31 Å corresponds to the position of N^ɛ(K73).] The circles represent substrate or acyl atoms viewed in projection within (filled) and outside (unfilled) of the 3-Å slab projected here and identify catalytically important regions where steep gradients are visible.

Comparing the energetics of the initiating step in the ES complex for each mechanism, we found that formation of the (S130)O⁻⋅ ⋅ ⋅⁺HN(1) ion pair in reaction ii is significantly more favorable (δΔG_el = −8.8 kcal/mol) than formation of the (S70)O⁻⋅ ⋅ ⋅⁺H₃O(WAT297) ion pair (δΔG_el = −2.4 kcal/mol) assumed by others (cf., e.g., refs. 38 and 39) or of the (S70)O⁻⋅ ⋅ ⋅⁺NH₃(K73) ion pair (δΔG = −3.7 kcal/mol) postulated by Strynadka et al. (4, 13) for reaction i. Moreover, the S130·N(1) ion pair energetically promotes more strongly polarization of the β-lactam carbonyl group and formation of the (S130)O⁻⋅ ⋅ ⋅⁺HN(1)⋅ ⋅ ⋅C(7)⁺⋅ ⋅ ⋅⁻O(8) quadupole in the T1a species from which the T1 tetrahedral adduct is formed (compare Fig. 2). This step is accompanied by an energetic change of δΔG_el = −17.5 kcal/mol compared with −11.4 kcal/mol for formation of the (S70)O⁻⋅ ⋅ ⋅⁺OH₃(WAT297)⋅ ⋅ ⋅C(7)⁺⋅ ⋅ ⋅⁻O(8) quadrupole. This difference alone underscores the energetic preference of N-protonation to facilitate polarization of the carbonyl bond. In reaction ii, the polarized carbonyl bond then readily promotes (S70)OH⋅ ⋅ ⋅OH₂(WAT297) → (S70)O⁻⋅ ⋅ ⋅⁺OH₃(WAT297) proton transfer, activating S70 for nucleophilic attack. We thus conclude that general-acid catalyzed protonation of the β-lactam N(1) is energetically favored as the initiating trigger event over general-base catalyzed nucleophilic attack by S70.

With respect to Fig. 1 electrostatic and hydrogen-bonding interactions involving the chain of donor and acceptor atom pairs (S70)OH⋅ ⋅ ⋅OH₂(WAT297)⋅ ⋅ ⋅O^ɛ1,2(E166) are catalytically important. The proton transfer event (S70)OH⋅ ⋅ ⋅OH₂(WAT297) → (S70)O⁻⋅ ⋅ ⋅⁺H₃O(WAT297) is favored because it results in two ion pairs, NH₃⁺(K73)⋅ ⋅ ⋅⁻O^γ(S70) and H₃O⁺(WAT 297)⋅ ⋅ ⋅⁻O^ɛ1,2(E166), as well as increased (S70)O⁻⋅ ⋅ ⋅⁺C (7) interactions. With complete polarization of the carbonyl bond in T1 (compare Fig. 2), the C(7)⁺–O(8)⁻ ion pair strengthens these interactions further because sp² → sp³ hybridization of C(7) places O(8)⁻ into the oxyanion hole so as to interact more strongly with NH(S70) and NH(A237). The transient formation of three ion pairs (K73)NH₃⁺⋅ ⋅ ⋅⁻O^γ(S70), C(7)⁺–O(8)⁻, and (WAT297)H₃O⁺⋅ ⋅ ⋅⁻O^ɛ1,2(E166) is stabilized by (K234)NH₃⁺⋅ ⋅ ⋅⁻O^γ(S130) and O(12)⁻⋅ ⋅ ⋅⁺HN(1) from one side of the substrate, and by O(8)⁻⋅ ⋅ ⋅HN(S70), HN(A237) interactions on the other. These dipolar interactions further stabilize O(8)⁻ in the oxyanion hole upon annihilation of the C(7)⁺⋅ ⋅ ⋅⁻O^γ(S70) ion pair through covalent bond formation. In contrast to other proposals for the mechanism of hydrolysis (4, 13, 15, 27), residues K73 and K234 are calculated to remain protonated throughout the reaction cycle and to stabilize ion-pair formation. Recent corroboration of this conclusion is given by the continuum electrostatic calculations of Wade and coworkers (17), indicating that the pK_a values for K73 and K234 are ≥ 10.0 in both E and ES species.

Hydrogen-bonding interactions of the substrate's carboxylate group with its immediate neighbors shown in Fig. 1 are catalytically essential. Because the β-lactam N(1) is trigonal, its lone pair orbital is directed toward one of the lone pairs of O(12) where there is a high negative potential, providing a preferred site for proton binding. Within the E form of the enzyme, two groups, HO^γ(S130) and ⁺H₃N^ɛ(K234), were identified as possible proton donors. On the basis of dipolar interactions, a three-center, bifurcated hydrogen bond (40) with N(1), O(12), and HO^γ(S130) is favored by 9.6 kcal because of the resultant interactions with other nearby dipoles and HO^γ(S235) and ⁺H₂N^ζ(R244) and because, after proton transfer to N(1), two ion pairs are formed for which the interaction is more stabilizing than formation of a neutral (K234)NH₂⋅ ⋅ ⋅HOOC complex. Similar bifurcated hydrogen-bonding interactions have been proposed in the HIV-protease reaction (41). Analysis of electrostatic interactions in TEM-1 β-lactamase showed that interaction of HO^γ(S130) and ⁻O(12) with ⁺HN(1) was more stabilizing, thereby incorporating the substrate's 2-carboxylate group into the mechanism of action. Ishiguro and Imajo (42) also have postulated participation of the carboxylate group in proton transfer to N(1). In their model, however, proton transfer occurs after nucleophilic attack by O^γ(S70). Our results show that proton transfer to N(1) is energetically favored as the trigger event before nucleophilic attack.

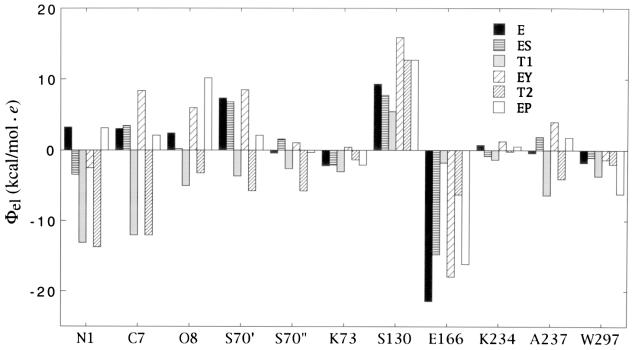
Values of the electrostatic potential Φ_el at grid points corresponding to functionally important atoms are illustrated in Fig. 4 for reaction species in the N-protonation mechanism (compare Fig. 2). These results are derived from analysis of contour maps of the type shown in Fig. 3. We point out further insights that can be made on the basis of Fig. 4 consistent with N-protonation as the favored reaction. In ES, the sign of Φ_el changes from negative on N(1) to positive on C(7), indicating bond polarization that facilitates protonation of N(1). On the other hand, the sign of Φ_el at N(1) becomes positive in EP, aiding product release through its repulsive interaction with R244. Also, Φ_el at NH(S70) and NH(A237) alternates in value in T1 and T2 adducts, supporting the suggestion (29) that these residues forming the oxyanion hole are differentially involved in acylation and deacylation processes.

Figure 4.

Histogram comparison of the electrostatic potential Φ_el,i at the positions of catalytically important atoms for N-protonation. The value of Φ_el,i was calculated in each case at grid points coinciding with the position of the catalytically important atom of the residue, i.e., N(1), C(7), O(8), O^γ(S70) (=S70′), N(S70) (=S70′′), N^ɛ(K73), O^γ(S130), O^ɛ1,2(E166), N^ɛ(K234), N(A237), and O(WAT297). The value for O^ɛ1,2(E166) is given at the grid point midway between the two carboxylate oxygens. Although the N(1), C(7), and O(8) atoms do not occur in the free enzyme E, the values of Φ_el,i are given at the grid points that are occupied by these atoms in the ES complex.

Contrary to more usual formulations of the mechanism of the serine hydrolase β-lactamases (cf., refs. 38 and 39), we find that the catalytic action of class A β-lactamases is not analogous to that of serine proteases. The fused thiazolidine ring of penicillin exhibits an approximate “butterfly” conformation with N(1) occupying a position, because of its trigonal bonding structure, so as to direct the lone pair orbital away from the β-lactam carbonyl group, positioning N(1) optimally for protonation from the convex or exo side of the molecule (compare Fig. 1). In this respect, the stereochemistry around the β-lactam N(1) can be considered to mimic a transition-state species to facilitate proton addition. In peptide hydrolysis nucleophilic attack at the carbonyl carbon is required to facilitate C–N bond rotation for proton donation because of the π-electron structure of the C–N bond. In contrast, the β-lactam group is structured so as to facilitate proton donation, which leads directly to bond cleavage without bond rotation. The structural, electrostatic, and protonation requirements leading to acylation in the two types of enzyme-catalyzed reactions are thus distinguishably different. On the other hand, the deacylation step catalyzed by class A β-lactamases finds a direct counterpart in the deacylation step in serine proteases. Electrostatic interactions controlling substrate hydrolysis including the deacylation step of serine proteases have been discussed in detail by Warshel and coworkers (22, 23, 43). For this reason we have emphasized here the electrostatic interactions governing formation of the EY intermediate of TEM-1 β-lactamase because of its different mechanistic pathway.

As pointed out above, the proton transfer event (S70)OH⋅ ⋅ ⋅OH₂(WAT297) → (S70)O⁻⋅ ⋅ ⋅⁺H₃O(WAT297) is energetically favored in the wild-type enzyme in which H₂O(WAT297) is hydrogen-bonded to ⁻O^ɛ1,2(E166). However, the important step that must drive N(1)–C(7) bond scission is protonation of the β-lactam N(1) because the E166N mutant is capable of forming an acylenzyme (4, 19). The rate constant for acylation is decreased in the E166N mutant from that in the wild-type enzyme by only ≈10⁻³ compared with the decrease for deacylation by ≈10⁻⁸ (44). The decreased acylation rate constant is consistent entropically with proton abstraction from (S70)OH by a water molecule that is not optimally positioned as in the wild-type enzyme. On the other hand, E166 is required in the EY intermediate not only to promote ionization of a hydrogen-bonded water molecule for deacylation but also to position the water molecule for nucleophilic attack.

Assigning Ionizing Groups.

The assignment of ionizations governing the pH dependence of k_cat and k_cat/K_M remains an important objective in β-lactamase studies. The pH profile of k_cat/K_M, in general, reflects ionizations in the free substrate or free enzyme while the pH profile of k_cat refers to a catalytically competent enzyme-substrate species formed before the rate-limiting step of the reaction. There is no requirement that pK_as governing k_cat must arise from the same groups governing k_cat/K_M. Evaluating the gradient of Φ_el between donor-acceptor atom pairs for a constant hydrogen-bond length of 2.8 Å, we found that the pH dependence of Φ_el,i was essentially the same in E for both S70·K73 and S130·K234 with an inflection point near pH 8.2. Also, predicted pK_a values of the β-lactam N(1) and the carboxylic acid group of the substrate were markedly altered, effects that have not been previously evaluated in the catalytic mechanism of TEM-1 β-lactamase. The highly positively charged environment of the active site results in a complex behavior of Φ_el over the atomic positions of the substrate, yielding a pH dependence with inflection points at 4.4 and 8.2. An inflection point near pH 4.4 also is seen in the ES for the hydrogen-bonded E166·WAT297 couple.

The pH dependence of Φ_el for the E166:WAT297 couple in ES supports the suggestion of Damblon and coworkers (14) that the ionization with pK_a1 ≈ 4.4 governing k_cat is due to E166. Because the pK_a of N(1) in the free substrate is likely to be <4.0 (45), pK_a1 governing k_cat/K_M is also best attributed to E166. The pH dependence of Φ_el in the active site for E and ES provides no unambiguous suggestion for the origin of pK_a2. Because the pK_a of N(1) is calculated to increase by about 5 units in the ES, ⁺HN(1) in the active site could account for pK_a2 governing k_cat. On the other hand, in addition to the inflection points calculated for the pH dependence of Φ_el for the two active site Ser:Lys dyads in E, the pH dependence of Φ_el also suggests an inflection at pH ≈ 8.2 for S130·K234 in the ES. These results suggest that the most reasonable assignment for pK_a2 governing k_cat/K_M in the free enzyme and k_cat in the ES is the hydrogen-bonded pair S130·K234.

In summary we conclude that the catalytic action of TEM-1 β-lactamase results from a trigger effect of N-protonation through electrophilic general-acid catalysis to facilitate general-base catalyzed nucleophilic attack by S70 to form EY. Wolfe (37) was the first to identify the energetic favoring of N-protonation in methanolysis of β-lactams. His computational modeling, however, was restricted to a four-center approach of a methanol OH group to the C(7)–N(1) atom pair in the β-lactam ring. Our results indicate that N-protonation involves the substrate's 2-carboxylate group in the active site of the enzyme in addition to the side chain of S130 hydrogen-bonded to K234. The focus of the electrostatic interactions is directed to the N(1)–C(7)=O(8) part of the substrate, which is reinforced through the charged multipole nature of the protein. Details of these interactions with distant clusters of charged and ionized residues will be described more fully elsewhere.

Abbreviations

ES

Michaelis complex

EP

enzyme–product complex

EY

acylenzyme