Auditory sensitivity provided by self-tuned critical oscillations of hair cells

Abstract

We introduce the concept of self-tuned criticality as a general mechanism for signal detection in sensory systems. In the case of hearing, we argue that active amplification of faint sounds is provided by a dynamical system that is maintained at the threshold of an oscillatory instability. This concept can account for the exquisite sensitivity of the auditory system and its wide dynamic range as well as its capacity to respond selectively to different frequencies. A specific model of sound detection by the hair cells of the inner ear is discussed. We show that a collection of motor proteins within a hair bundle can generate oscillations at a frequency that depends on the elastic properties of the bundle. Simple variation of bundle geometry gives rise to hair cells with characteristic frequencies that span the range of audibility. Tension-gated transduction channels, which primarily serve to detect the motion of a hair bundle, also tune each cell by admitting ions that regulate the motor protein activity. By controlling the bundle's propensity to oscillate, this feedback automatically maintains the system in the operating regime where it is most sensitive to sinusoidal stimuli. The model explains how hair cells can detect sounds that carry less energy than the background noise.

Detecting the sounds of the outside world imposes stringent demands on the design of the inner ear, where the transduction of acoustic stimuli to electrical signals takes place (1). Each of the hair cells within the cochlea, which act as mechanosensors, must be responsive to a particular frequency component of the auditory input. Moreover, these sensors need the utmost sensitivity, because the weakest audible sounds impart an energy, per cycle of oscillation, which is no greater than that of thermal noise (2). At the same time, they must operate over a wide range of volumes, responding and adapting to intensities that vary by many orders of magnitude. Clearly, some form of nonlinear amplification is necessary in sound detection. The familiar resonant gain of a passive elastic system is far from sufficient for the required demands because of the heavy viscous damping at microscopic scales (3). Instead, the cochlea has developed active amplificatory processes, whose precise nature remains to be discovered.

There is strong evidence that the cochlea contains force-generating dynamical systems that are capable of executing oscillations of a characteristic frequency (4–10). In general, such a system exhibits a Hopf bifurcation (11): as the value of a control parameter is varied, the behavior abruptly changes from a quiescent state to self-sustained oscillations. When the system is in the immediate vicinity of the bifurcation, it can act as a nonlinear amplifier for sinusoidal stimuli close to the characteristic frequency. That such a phenomenon might occur in hearing was first proposed by Gold (3) more than 50 years ago. The idea was recently revived by Choe, Magnasco, and Hudspeth (12) in the context of a specific model of the hair cell. No general analysis of the amplification afforded by a Hopf bifurcation has been provided, however, and no theory has been advanced to explain how proximity to the bifurcation point might be ensured.

In this paper, we provide both a generic framework that describes the known features of acoustic detection and a detailed discussion of the specific elements that could be involved in this detection. We first derive the general resonance and amplification behavior of a dynamical system operating close to a Hopf bifurcation and emphasize that such a system is well suited to the ear's needs. For active amplification to work reliably, tuning to the bifurcation point is crucial. We introduce the concept of a self-tuned Hopf bifurcation, which permits the favorable amplificatory properties of a dynamical instability to be obtained in a robust way. Self-tuning maintains the system in the proximity of the critical point and is achieved by an appropriate feedback mechanism that couples the output signal to the control parameter that triggers the bifurcation. The concept can explain several important features of the auditory sensor, such as the frequency selectivity, high sensitivity, and the ability to respond to a wide range of amplitudes. It can also explain the intrinsic nonlinear nature of sound detection (13, 14) and the occurrence of spontaneous sound emission by the inner ear (9, 10). Furthermore, self-tuned criticality provides a framework for understanding the role of noise in the detection mechanism. The amplificatory process, which involves a limited number of active elements, introduces stochastic fluctuations, which adds to those caused by Brownian motion. We show that the response to weak stimuli can take advantage of this background activity.

The proposed existence of a self-tuned Hopf bifurcation raises questions about the specific mechanisms involved: What is the physical basis of the dynamical system? How is the self-tuning realized? It might be expected that different organisms have evolved different apparatus to implement the same general strategy. In the mammalian cochlea, outer hair cells are probably responsible for amplification (5). In this paper, we restrict our specific discussion to the simpler case of nonmammalian vertebrates whose cochlea contain only inner hair cells. We propose a model of the hair cell of the inner ear that accords with data from a wide variety of physiological experiments. The model incorporates a physical mechanism that allows motor proteins to generate spontaneous oscillations (15). We find that molecular motors, such as dyneins in the kinocilium or myosins in the stereocilia, are natural candidates for the force generators involved in the amplification of hair-bundle motion. Tension-gated transduction channels in the stereocilia serve primarily to detect this motion, but also have a second function: by admitting ions that regulate the motor protein activity, they provide the self-tuning mechanism.

Generic Aspects

Amplification and Frequency Filtering of a Hopf Bifurcation.

We discuss the behavior of a dynamical system that is controlled by a parameter C. Above a critical value, C > C_c, the system is stable; for C < C_c, it oscillates spontaneously. At the critical point (or Hopf bifurcation), C = C_c, the system shows remarkable generic response and amplification properties. These generic properties can be described as follows. Because we are interested in the response to a periodic stimulus with frequency ν = ω/2π, we express the hair-bundle deflection x(t) by a Fourier series x(t) = ∑x_ne^inωt with complex amplitudes x_n = x^*_−n. In the vicinity of the bifurcation, the mode n = ±1 is dominant, and the response to an externally applied sinusoidal stimulus force f(t) = f₁e^iωt + f₋₁e^−iωt can be expressed in terms of a systematic expansion in x₁. Symmetry arguments (see supplementary material at www.pnas.org) imply that the first nonlinear term is cubic:

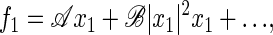1

where 𝒜(ω,C) and ℬ(ω,C) are two complex functions. The bifurcation point is characterized by the fact that 𝒜 vanishes for the critical frequency, 𝒜(ω_c,C_c) = 0. For C < C_c and no external force, the system oscillates with  |x₁| ²≃Δ²(C_c − C)/C_c, where Δ is a characteristic amplitude. For C = C_c, the response to a stimulus at the critical frequency has amplitude

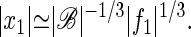2

This represents an amplified response at the critical frequency with a gain

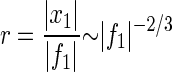3

that becomes arbitrarily large for small forces.

If the stimulus frequency differs from the critical frequency, the linear term in Eq. 1 is nonzero and can be expressed to first order as 𝒜(ω,C_c) ≃ A₁(ω − ω_c). The dramatic amplification of weak signals, implied by Eq. 3, is maintained as long as this term does not exceed the cubic term in Eq. 1. If the frequency mismatch increases such that |ω − ω_c|≫|f₁|^2/3|ℬ|^1/3/|A₁|, the response becomes linear

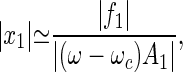4

i.e., the gain is independent of the strength of the stimulus.

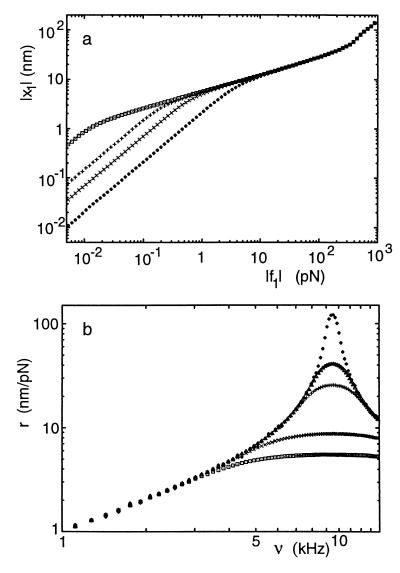
Thus the Hopf resonance acts as a sharply tuned high-gain amplifier for weak stimuli and as a low-gain filter for strong stimuli. This generic behavior is illustrated in Fig. 1 with data obtained by numerical simulation. Laser interferometry measurements of the motion of the basilar membrane, when the live cochlea is stimulated by pure tones, display strikingly similar features (16, 17). In particular, the peak response as a function of force amplitude has been demonstrated to obey a power law |x₁|∼|f₁|^0.4±0.2 (17). This strongly suggests that the membrane is being driven by a dynamical system that is poised at a Hopf bifurcation.

Figure 1.

Response to external forces near a Hopf bifurcation (a) Amplitude  x₁  as a function of force  f₁  at various driving frequencies ν (⋄ 2 kHz, × 5 kHz, □ 10 kHz, + 13 kHz). (b) Gain r as a function of frequency ν for different amplitudes  f₁  (⋄ 0.01 pN, ▵ 0.05 pN, + 0.1 pN, × 0.5 pN, □ 1 pN). Although the form of these curves is generic, the numerical values of force, amplitude, and frequency depend on the physical nature of the dynamical system. The values given here correspond to the specific model of a hair cell discussed in the text, with parameters chosen to give a critical frequency of approximately 10 kHz.

Self-Tuned Critical Oscillations.

How does the system come to be so precisely balanced at the critical point? [Self-tuning to a coexistence point has been discussed previously in certain dynamic first-order transitions (18)]. The control parameter must be tuned to C ≃ C_c, otherwise the nonlinear amplification is lost. Moreover, the value of C_c differs for hair cells with different characteristic frequency. We propose a feedback mechanism that allows the dynamical system to operate automatically close to the bifurcation point, whatever its characteristic frequency. Without loss of generality, we assume that the control parameter decreases as long as the system does not oscillate. After some time, critical conditions are reached, and spontaneous oscillations ensue. The onset of oscillations triggers an increase of the control parameter, which tends to restore stability. Hence the system converges to an operating point close to the bifurcation point. To illustrate this general idea, we consider the following simple feedback which changes C in response to deflections x:

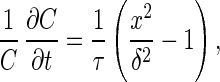5

where δ is a typical amplitude. If no external force is applied, this feedback, after a relaxation time τ, tunes the control parameter to a value C_δ for which spontaneous oscillations with |x₁| ≃ δ occur. If δ is small compared with the characteristic amplitude Δ, this is on the oscillating side close to the bifurcation, |C_δ − C_c|/C_c ≃ (δ/Δ)². Two modes of signal detection are possible: (i) For transient stimuli short compared with τ, the system operates at C_δ. The amplitude |x₁| shows the characteristic nonlinear response discussed above. (ii) For stimuli sustained over longer times, self-tuning maintains |x₁| ≃ δ constant for different stimulus amplitudes. This effect of the feedback represents a perfect adaptation mechanism. In the presence of noise, phase locking of the response (to be discussed later) occurs as soon as an external stimulus is applied, and this can be detected.

Model

Mechanosensitivity and Self-Tuning Mechanism Provided by Transduction Channels.

We demonstrate the general principles introduced above by devising a specific model for the amplification of acoustic stimuli by hair bundles in nonmammalian vertebrates. A schematic representation of a hair bundle is shown in Fig. 2. It consists of several stereocilia and a single kinocilium (19, 20). Transduction of hair-bundle deflection to a chemical signal occurs via channels located near the tip of each stereocilium. Tip links that connect neighboring stereocilia are believed to be the gating springs of the transduction channels. If the hair bundle is deflected, tension in the tip links triggers the opening of the channels. The subsequent influx of ions (principally K⁺, but also Ca²⁺) causes a corresponding change of the membrane potential of the hair cell which, in turn, generates a nervous signal.

Figure 2.

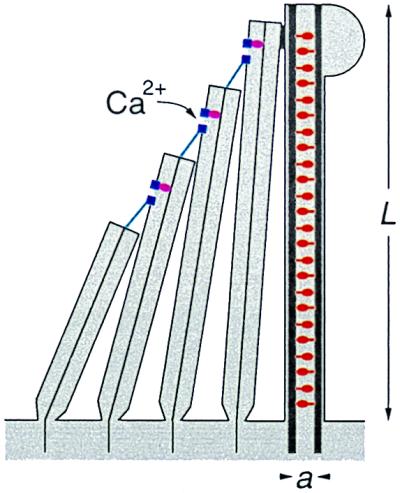
A hair bundle consists of a single kinocilium and tens to hundreds of stereocilia. The kinocilium contains dynein motors (red). The stereocilia contain transduction channels (blue) that are gated by the tension in the tip links (cyan); the steady-state tension is maintained constant by adaptation motors (magenta). In our model, the kinocilium is the active part of the mechanoreceptor and the stereocilia act as the detection apparatus. Feedback control of the active amplificatory process involves the influx of Ca²⁺ ions through the transduction channels; the ions diffuse into the kinocilium and regulate the generation of force by the motor proteins.

The mechanosensor can be used for self-tuning as well as signal detection. Many physiological processes are regulated by ionic concentrations, so it is natural to identify the Ca²⁺ concentration with the control parameter C. We assume that C decreases if the transduction channels are closed because of the action of pumps in the cell membrane. When the hair bundle is deflected by x, the transduction channels open with probability P_o(x). We therefore characterize the mechanosensor by the equation

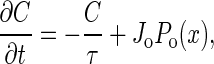6

where J_o is the Ca²⁺ flux through open transduction channels. Note that this equation provides self-tuning. In this case, it replaces the more simple but less realistic Eq. 5. For our numerical examples, we use a two-state model for the channels with

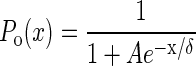7

where (1 + A)⁻¹ ≪ 1 is the probability that a channel is open when the hair cell is quiescent, and δ is the characteristic amplitude of motion to which the system is sensitive. For a sufficiently long relaxation time τ, the slow variation C₀ of C ≃ C₀(t) + C₁e^iωt can be separated from the small-amplitude oscillations, giving

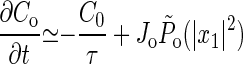8

where P̃_o = ∫₀^1/ν dt P_o(x₁e^iωt + x₋₁e^−iωt) is the averaged probability of channel opening in the presence of oscillations, which increases monotonically with their amplitude x₁. For physically relevant parameter values, the system reaches a steady state close to the bifurcation point, independent of the initial value of C.

Oscillations Generated by Molecular Motors.

It has been suggested that the transduction channels (7, 12) or molecular motors in the hair bundle (21, 22) might be the active elements responsible for amplification. Recently, a simple physical mechanism has been proposed that allows motor proteins operating in collections to generate spontaneous oscillations by traversing a Hopf bifurcation (15, 23). Typically, motors move along cytoskeletal filaments, and elastic elements oppose this motion. In this case, two possibilities exist: the system either reaches a stable balance between opposing forces, or it oscillates around the balanced state. Three time scales characterize this behavior: the relaxation time λ/K of passive relaxation, where λ is the total friction and K is the elastic modulus; and the times ω₁⁻¹ and ω₂⁻¹, where ω₁ is the kinetic rate at which a motor detaches from a filament and ω₂ is the attachment rate. An explicit solution of a simple model is derived in the supplementary material. We find that for an appropriate value of a control parameter C, which is related to the ratio ω₁/ω₂, a Hopf bifurcation occurs with critical frequency

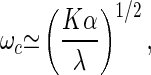9

which is the geometric mean of the passive relaxation rate K/λ and the typical ATP hydrolysis rate α = ω₁ + ω₂. The above identification of C with the Ca²⁺ concentration is consistent with the fact that Ca²⁺ regulates motor protein activity (24). The system oscillates if the elastic modulus does not exceed a maximal value K_max ≃ k₀N, where k₀ is the crossbridge elasticity of a motor and N is the total number of motors. The maximal frequency, obtained when K = K_max, can be significantly higher than the ATP hydrolysis rate α.

Characteristic Frequency of a Vibrating Kinocilium.

The kinocilium is a true cilium containing a cylindrical arrangement of microtubule doublets and dynein motors. Because cilia have the well-established tendency to beat and vibrate with frequencies from tens of Hz up to at least 1 kHz (25, 26), the kinocilium is a natural candidate to be responsible for the Hopf bifurcation. A simple two-dimensional model can be used to discuss the main physical properties of a vibrating cilium near a Hopf bifurcation (27). In this model, motors induce the bending of a pair of elastic filaments separated by a distance a (corresponding to the distance between neighboring microtubule doublets in the axoneme). An isolated kinocilium of length L and bending rigidity κ, fixed at the basal end but free at its tip, will vibrate in a wave-like mode with wavelength Λ ≃ 4L. A typical displacement z of the motors along the filaments leads to bending of the filament pair and a deflection of the tip by a distance x ≃ zL/a. The elastic bending energy is of order (κ/L³)x² ≃ (κ/a²L)z². Therefore, the total elastic modulus experienced by the motors is given by

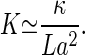10

The viscous energy dissipation per unit time because of motion of the kinocilium is of order ηL(∂_tx)² ≃ (ηL³/a²)(∂_tz)². Therefore, the total friction experienced by the motors can be written as

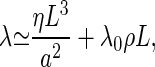11

where λ₀ describes the dissipation within the kinocilium per motor and ρ = N/L denotes the number of dynein motors per unit length along the axoneme. If internal friction can be neglected, i.e., if L ≫ L₀ = (λ₀a²ρ/η)^1/2, the frequency of a vibrating cilium at the bifurcation point is given by

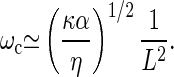12

Using typical values λ₀≃10⁻⁹ kg/s, a≃20 nm, ρ≃5 10⁸ m⁻¹ and η≃10⁻³ kg/ms, we find L₀≃200 nm, shorter than typical kinocilia. Using α≃10³ s⁻¹, k₀≃10⁻³ N/m and κ≃4 10⁻²² Nm² (the bending rigidity of 20 microtubules), the frequency range between 100 Hz and 10 kHz can naturally be spanned by changing the length of the kinocilium between 1 μm and 10 μm.

The above argument neglects the contribution of the stereocilia to elasticity and motion. The elastic response of stereocilia to hair-bundle deflections has been measured (6, 28). It can be well described by an angular spring at the base of each stereocilium, which contributes an elastic energy per stereocilium of the order of k_s(x/L)², where k_s is an angular elastic modulus. The kinocilium length L in a hair bundle is approximately inversely proportional to the number N_s of stereocilia (19), and we write N_s≃l_s/L, where l_s≃10⁻⁴ m is the total length of stereocilia. With this assumption, we find an additional elastic modulus

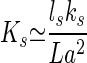13

contributed by the stereocilia to K. The contribution of stereocilia to the friction coefficient λ can be estimated as

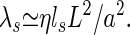14

The measured value of k_s (28) indicates that K_s dominates the contribution to K given by Eq. 10. Similarly, because l_s>L, λ_s should dominate friction. In this case, we expect

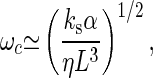15

and the range of frequencies is somewhat reduced.

If the stiffness of the ensemble of stereocilia greatly exceeds that of the kinocilium, a new situation arises. Because the kinocilium is attached to the stereocilia at its tip (20), movement of the tip is strongly reduced, and the kinocilium preferentially vibrates in a mode with wavelength Λ≃2L for which the relation given by Eq. 12 is again valid.

Adaptation Motors.

Finally, we note that to obtain a robust self-tuning, the feedback mechanism must be sensitive only to the oscillation amplitude x₁ and not to a stationary displacement x₀; we assumed in Eq. 8 that P̃_o is independent of x₀. The transduction mechanism of stereocilia and their tension-gated channels does indeed have this property: it is well known that an ATP-dependent adaptation mechanism (29) exists that removes the dependence of the channel current on a constant displacement x₀. It is widely believed that this adaptation involves the motion of myosin motors, which maintains constant the steady-state tension in the tip links that control the transduction channels (30). Therefore, the stereociliar transduction mechanism has precisely the required properties to be used as a feedback signal for self-tuning the bifurcation.

Simulation

The above analysis does not include the effects of noise. Brownian motion is one source of fluctuations in the movement of the hair bundle (31). Another source of noise is stochastic fluctuations of force-generating elements in the hair bundle (32). To investigate the consequences of this randomness, we performed a Monte Carlo simulation of the two-state model described in ref. 15 by using a realistic number of motor proteins. The motors, when attached, experienced a potential of amplitude U and period l (the corresponding crossbridge elasticity is k₀ = U/l²). The attachment rate was constant and independent of position, ω₂ = α. Detachment was localized to a region of width 0.1 l, centered on the potential minimum, and the detachment rate ω₁ was regulated by the Ca²⁺ concentration C. We chose ω₁/ω₂ = (C_q/C)³, where C_q is the steady-state Ca²⁺ concentration in a quiescent hair cell; the precise functional dependence is unimportant as long as ω₁/ω₂ decreases monotonically with increasing C in a fairly sensitive way. We simulated systems with n = 1,000–4,000 motors, representing hair cells with different kinocilium length and stereociliary number.

Self Tuning and the Characteristic Frequency of Spontaneous Oscillations.

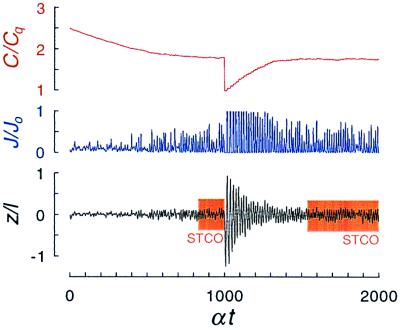
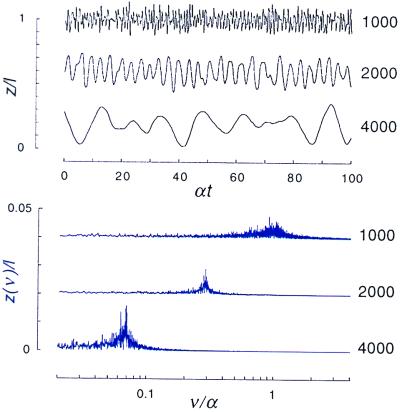
The self-tuning of a hair cell to the vicinity of the bifurcation, where small-amplitude spontaneous oscillations occur, is demonstrated in Fig. 3. When a change of the internal Ca²⁺ concentration is imposed, the system is transiently perturbed, but after an interval of time of order τ, it returns to the same steady state. Hair cells with different numbers of motors acquire different internal concentrations of Ca²⁺ to adjust the motor detachment rate in such a way that the system approaches the critical point. The spontaneous oscillations of three different hair bundles are shown in Fig. 4. Note that the characteristic frequency is approximately proportional to the inverse-square of the number of motors, as expected from Eq. 12, and that it can exceed the typical ATP cycle rate α when the total number of motors is small (short kinocilium). All three hair cells execute spontaneous oscillations with a similar amplitude, as expected from our arguments above. However, the noise introduces a significant new effect: the oscillations are irregular. The incoherence of the phase of the oscillation is evident in the Fourier transform of the displacement, which exhibits a broad peak centered on the characteristic frequency.

Figure 3.

Self-tuning of a hair bundle. If the Ca²⁺ concentration C within the cell is artificially high, the hair bundle is initially quiescent, but as Ca²⁺ ions are pumped from the cell, it gradually begins to oscillate with small amplitude. If C is suddenly artificially lowered, the hair bundle becomes unstable and executes high-amplitude spontaneous oscillations. Because these movements open the transduction channels, the influx J of Ca²⁺ ions increases; the consequent change in C regulates the motors and diminishes the amplitude of the oscillation until it almost disappears. In the steady state, the bundle executes self-tuned critical oscillations. For this simulation, we assumed that the probability of transduction channels opening was P_o(z) = (1 + 10 exp(−20 z/l)⁻¹, where z is the motor displacement, and that the time constant for equilibration of the Ca²⁺ concentration was τ = 1,000/α.

Figure 4.

Self-tuned critical oscillations of systems comprising n = 1,000, 2,000, and 4,000 motors. In each case, the oscillation has small amplitude z≃0.1 l and is irregular, as can be seen from the broadness of the Fourier spectrum. For these simulations, we chose parameters k₀/λα = 4 10⁷N⁻³ and K/λα = 4 10¹³N⁻⁴, which correspond with the scaling dependence of the spring constant and friction coefficient on kinocilium length in Eqs. 10 and 11 and also with the order of magnitude estimates of the physical parameters, given in the text.

Dynamic Response to a Tone at the Characteristic Frequency.

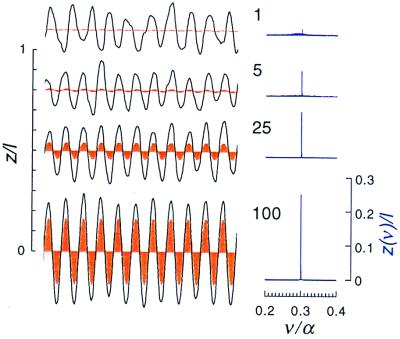
The response of a self-tuned hair bundle to a sinusoidal force with a frequency approximately equal to the bundle's characteristic frequency is illustrated in Fig. 5. For weak stimuli, the amplitude of the oscillation does not increase with the amplitude |f₁| of the applied force; this is because the small response to the stimulus is masked by the noisy spontaneous motion. Instead, the phase of the hair-bundle oscillation becomes more regular; as it does so, a peak emerges from the Fourier spectrum at the driving frequency. The height of the peak grows approximately as |f₁|^1/3 for intermediate values of |f₁|, and approximately linearly for very weak stimuli, and also for very strong stimuli (for which the response is essentially passive). Thus the Fourier component of the hair-bundle displacement at the driving frequency responds to the stimulus in the generic manner discussed above.

Figure 5.

Response of a system with n = 2,000 motors to a sinusoidal force at frequency ν = 0.3α, close to the hair bundle's characteristic frequency. Curves are marked by the dimensionless amplitude of the force,  f₁ /f_mot, where f_mot = U/l is the force produced by a motor molecule. Note that a force equal to that of a single motor is sufficient to elicit a response in the Fourier spectrum. Curves shaded red are the responses of an equivalent passive hair bundle (i.e., a bundle with identical mechanical properties but no force generators).

Phase Locking of the Nervous Signal.

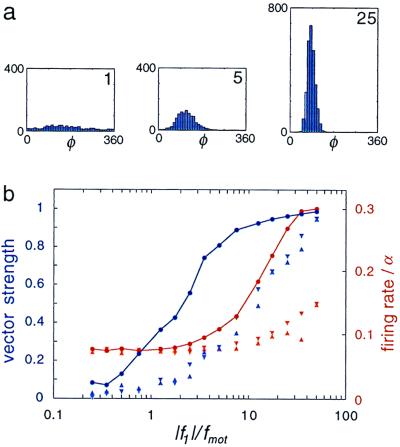
The flow of ions through the transduction channels depolarizes the cell membrane which, in turn, opens voltage-gated channels at the base of the hair cell and generates a synaptic current (1). This sequence of events happens fast enough for variations at the synapse faithfully to reflect the hair-bundle motion at frequencies below 1 kHz. Information about the auditory stimulus is subsequently passed along the auditory nerve in the form of a spike train. Simplifying this transduction process, we assume that a spike is elicited whenever the transduction channel current J passes a threshold value of 0.5J_o. The resulting nervous response is shown in Fig. 6. In the absence of a stimulus, the self-tuned critical oscillations of the bundle cause the nerve to fire stochastically, at a low rate. When a weak sinusoidal stimulus is applied at the characteristic frequency, the firing rate does not increase above the spontaneous rate, but the spike train becomes detectably phase-locked to the stimulus. The degree of phase-locking increases rapidly as the amplitude of the stimulus increases, reflecting the growing regularity of the hair-bundle motion. It is only when the neural response is almost completely phase-locked that the firing rate begins to rise. Eventually, for strong stimuli, the spike rate saturates at the stimulus frequency. This behavior is strikingly similar to that which is observed experimentally. In particular, it is well known that the threshold for phase-locking in the auditory nerve fiber is 10–20 dB lower than the threshold at which the firing rate begins to rise (33, 34).

Figure 6.

(a) Histogram of the phase φ of the driving force at the instants when nervous spikes are generated, for various values of the force amplitude (marked by the value of  f₁ /f_mot). (b) Degree of phase locking (blue; expressed as the vector strength ∫dφ p(φ)e^iφ) and firing rate (red), as a function of the driving force. The frequency selectivity of the bundle can be appreciated by comparing the neural response to a stimulus with frequency close to the characteristic frequency, ν = 0.3α (●), with the response to other frequencies, ν = 0.15α (▿) and ν = 0.6α (▵).

Discussion

The self-tuned critical oscillator that we have introduced as a system for signal detection has characteristic amplification properties and a response in the presence of noise that are generic and do not depend on the choice of a specific model. In our specific model for nonmammalian hair cells, the oscillation frequency depends on the rate constants associated with attachment and detachment of motors, the passive stiffness, the damping, and thus on the geometry of the hair bundle. A simple morphological gradient along the basilar membrane would endow the ear with the ability to analyze a wide range of frequencies. Experimentally, it is well established that the height of hair bundles progressively increases along the cochlea, and that concurrently the characteristic frequency of the hair cells declines (19, 35). Our proposition that the kinocilium might play an active role in nonmammalian vertebrate hair cells suggests experiments that study the motility of the kinocilium and its potential for generating oscillations. If the self-tuning mechanism is removed (by cutting the tip links, for example), our model predicts that the hair bundle should exhibit stronger spontaneous oscillations. Careful control of the extracellular ion concentrations, such as Ca²⁺, would be essential in such experiments.

The simulations of our model reveal how a hair bundle can achieve its remarkable sensitivity to weak stimuli. By profiting from the periodicity of a sinusoidal input and measuring phase-locking rather than the amplitude of response, the mechanosensor can detect forces considerably weaker than those exerted by a single molecular motor. (If the bundle were a simple passive structure, its response to such forces would be smaller than its Brownian motion). An important implication of this detection mechanism is that even though the hair cell selects a certain frequency, the signal must still be encoded by the interval between spikes elicited in the auditory nerve. Paradoxically, the stochastic noise caused by the motor proteins serves a useful purpose. It ensures that the self-tuned critical oscillations of the hair bundle are incoherent, so that the pattern of spontaneous firing in the nerve is irregular. Against this background, the regular response to a periodic stimulus can easily be detected. [The benefits of noise have been discussed in a variety of situations, such as those involving stochastic resonance (38)].

Another beneficial feature of noise arises from the fact that weak stimuli do not increase the amplitude of oscillation above the spontaneous amplitude. Thus the Ca²⁺ concentration remains constant, the hair bundle stays in the critical regime, and active amplification can be sustained indefinitely. Stronger stimuli cause the system to drift away from the critical point, so that the degree of amplification diminishes over time. It is well known that both the perception of loudness (36) and the firing rate of the auditory nerve (37) decrease over a period of a few seconds, when a stimulus of moderate intensity is maintained. This phenomenon, which is usually referred to as “adaptation,” is consistent with our self-tuning mechanism. After the sustained presentation of a loud stimulus, the spontaneous firing rate diminishes, and the threshold to weak stimuli is augmented (37). Such “fatigue” is also accounted for by our self-tuning mechanism.

Because self-tuning positions the system slightly on the oscillating side of the critical point, self-tuned criticality provides a natural explanation for otoacoustic emissions (9, 10). In its normal working state, the inner ear would generate faint sounds with a broad range of frequencies. If the feedback mechanism were to fail in certain cells, the spontaneous oscillations could become large enough for distinct tones to be emitted.

A self-tuned Hopf bifurcation is ideal for sound detection, because it provides sharp frequency selectivity and a nonlinear gain that compresses a wide range of stimulus intensities into a narrow range of response. We therefore believe that the concept applies to all vertebrate hearing systems and potentially to other mechanoreceptor systems. Kinocilia are absent in mature mammalian cochlea, and we suggest that their force-generating role has been assumed by the outer hair cells. Self-tuning of these motile cells might be realized by a mechanism similar to that presented here, by using transduction channels in their hair bundles. It could, however, work very differently; for example, it might involve feedback from the inner hair cells, via the efferent nervous system.

Tuning to the proximity of a critical point is likely to be a general strategy adopted by sensory systems. Simple molecular receptors (39), as well as the physiological sensors of higher organisms, can enhance their response to weak stimuli in this way. We propose that the physics of self-tuned criticality is the “central science of transducer physiology” spoken of by Delbrück (40).