SURVEY AND SUMMARY: Difference in conformational diversity between nucleic acids with a six-membered ‘sugar’ unit and natural ‘furanose’ nucleic acids

Abstract

Natural nucleic acids duplexes formed by Watson–Crick base pairing fold into right-handed helices that are classified in two families of secondary structures, i.e. the A- and B-form. For a long time, these A and B allomorphic nucleic acids have been considered as the ‘non plus ultra’ of double-stranded nucleic acids geometries with the only exception of Z-DNA, a left-handed helix that can be adopted by some DNA sequences. The five-membered furanose ring in the sugar–phosphate backbone of DNA and RNA is the underlying cause of this restriction in conformational diversity. A collection of new Watson–Crick duplexes have joined the ‘original’ nucleic acid double helixes at the moment the furanose sugar was replaced by different types of six-membered ring systems. The increase in this structural and conformational diversity originates from the rigid chair conformation of a saturated six-membered ring that determines the orientation of the ring substituents with respect to each other. The original A- and B-form oligonucleotide duplexes have expanded into a whole family of new structures with the potential for selective cross-communication in a parallel or antiparallel orientation, opening up a new world for information storage and for molecular recognition-directed self-organization.

The conformation of natural nucleic acids duplexes

Nucleic acids can fold in a wide variety of complex structures that may involve extensive non-Watson–Crick base pairing. However, nucleic acid conformational diversity is much more constrained when exclusively Watson–Crick base pairing systems are considered. The majority of available nuclear magnetic resonance (NMR) and crystal structures from such double-stranded oligonucleotides belong to one of the two major groups of right-handed helixes, i.e. the A and B nucleic acids. Very few are classified into a third allomorphic group, i.e. the left-handed Z-helixes, which can be formed by some polynucleotides that contain alternating pyrimidine and purine nucleotides. The observation that the nucleic acid polymorphism is reduced to three classes (A, B and Z) is rather surprising since each single nucleoside has six variable backbone angles, its furanose ring can adopt a wide variety of conformations (from C3′-endo via O4′-endo to C2′-endo) with two variable regions available for the glycosidic torsion angle (1). The self-assembly process to which these natural polymeric supramolecules are destined finds its origin in the formation of interstrand hydrogen bonds and the stacking of the hydrophobic bases that stabilizes the duplex by interactions of π-electron clouds of neighboring base pairs. This typical base-paring pattern greatly restricts the conformational diversity of nucleic acid duplexes, with nucleobases in the center and sugar–phosphate backbones at the periphery. Within the framework of the available chemistry that nature uses to construct its DNA, the spectrum of potential duplex structures is narrowed further by the sugar–phosphate backbone that imposes restraints on the nucleotide conformation of the natural nucleic acids. Questions have risen what structures would be obtained when the nature of the backbone does not allow the interactions that are required to form the classical double helices and, alternatively, what structures would be obtained if a rigid sugar–phosphate backbone (fixing the orientation of the nucleobases relative to the backbone) were to dictate the potential geometries of the duplex. Attempts to find some answers have led to the discovery of new nucleic acids geometries.

Characterization of helices

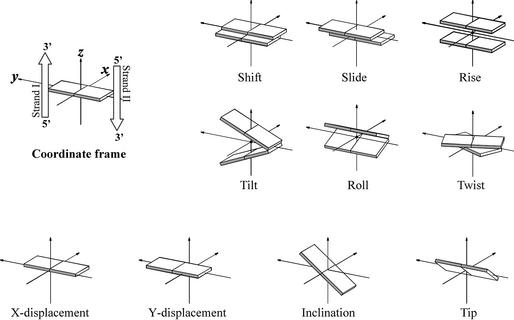
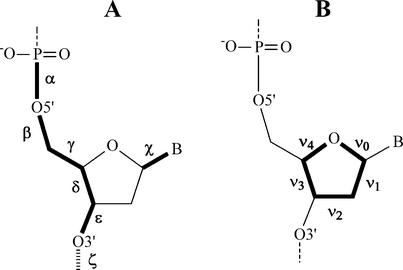
DNA and RNA duplexes are known to be dynamic helical structures, and their local geometry and plasticity are determined by the base sequence that is important for the biological function as a carrier of the genetic code. To describe the local geometry of a duplex, inter-base pair parameters are used (2). Reviewing the nucleic acid duplexes, the influence of base sequence on the local geometry is neglected and only the overall conformation is considered. Using global parameters, the different families of helical conformations from nature can be readily distinguished. This approach describes the double helix in terms of the position of the base pairs relative to each other and with respect to the helical axis. The most important parameters to describe a regular double helix are the rise and twist between the successive base pairs (leading to the pitch of the helix and the number of base pairs per turn), combined with the distance from the base pair center to the central helix axis (x- and y-displacement) and the inclination of the base pairs with respect to that axis (Fig. 1). Most of these parameters are interrelated to each other (e.g. x-displacement and inclination) (3). The range of conformations accessible to oligonucleotides is also correlated to backbone torsion angles and sugar puckering (Fig. 2).

Figure 1.

Calladine–Drew representation of parameters describing the position of two successive base pairs relative to each other (shift, slide, rise, tilt, roll, twist) and parameters that characterize the location of a base pair relative to the helix axis (x/y-displacement, inclination, tip). Figures depict positive values of designated parameters as defined in Blackburn and Gait (2).

Figure 2.

(A) The main torsion angles that describe the nucleic acid backbone structure (α, β, γ, δ, ε and ζ) and torsion angle χ that describes the orientation of the nucleobase relative to the sugar. (B) Endocyclic torsion angles of the sugar denoted by ν0 to ν4.

‘Standard’ A- and B-type helices

The distinctive morphologies of the A and B structures originate from the C3′-endo furanose ring, with a mean δ value of +80° and a ζ value of –80° in the former versus the C2′-endo ring, with a δ value of 130° and a ζ value of – 120° in the latter helical type (1). Distortions from this regular backbone conformation in A-DNA occur primarily on the 5′ side of the sugar ring (α, γ), while they are more common on the 3′ side of the sugar ring in B-DNA (ε, δ) (3). The different sugar pucker results in longitudinal phosphate–phosphate separa tion of 5.9 Å for A-DNA and 7.0 Å for B-DNA. In the A-form, puckering is closely clustered around the C3′-endo center, while the puckering distribution in the B-form is more diffuse in the C2′-endo region; therefore, sugar puckering is considered less flexible in A-DNA compared with B-DNA (1).

Despite the different sugar puckering, both A- and B-type duplexes adopt a right-handed helical structure because stacking interactions together with hydrogen bonding and solvation are driving forces to stabilize those helices. In furanose nucleic acids, this helix formation is favored due to the five-memberedness of the sugar rings, which implies that the δ torsion angle has to be >60° (4) regardless of the sugar conformation.

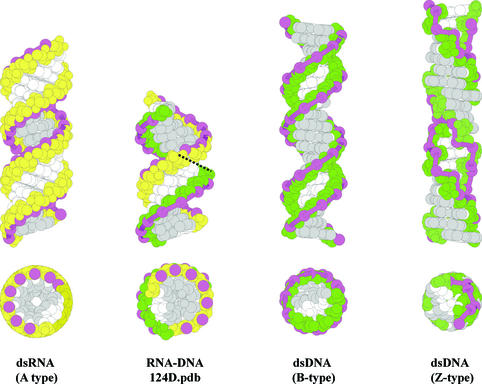
The diagnostic parameters to distinguish the A- and B-antiparallel duplexes are their rise per residue and helical twist (base step parameters) and the position of the base pairs along the helix axis described by x (y)-displacement and inclination (base pair parameters) (Table 1). The mean value for helical twist of A structures is 31° and for B structures 36° (1). This corresponds to a helix with 11–12 nucleosides in each winding for A-DNA and with 10 residues for B-DNA. The mean axial rise from one base pair to another along the helix axis is 2.90 Å in A-DNA and 3.37 Å in B-DNA. Base pairs in A-DNA are laterally displaced from the helix axis towards the periphery of the duplex over a distance of 4 Å, while in B-DNA they are placed astride the helix axis. This x-displacement results in a different depth of the grooves (Fig. 3). In A-DNA, the minor groove is shallow and the major groove is deep; whereas in B-DNA, major and minor grooves are of equal depth (3). Another typical helical feature is the large inclination (12°) of the base pairs in A-DNA compared with B-DNA, where they are almost perpendicular to the helix axis (inclination = 2.4°). The B to A transition in DNA can then be visualized as moving the base pairs away from the axis towards the minor groove, increasing the positive inclination and reducing the helical twist and rise (5). During this process, the successive base pairs are sliding over each other (increasing the interstrand base stacking) and a roll wedge is created between them. The observation that DNA sequences can exist in both conformations depending on circumstances suggests that the A- and B-forms are the energy-minimized forms of a right-handed structural continuum of the double helix. When analyzing local variations in structural parameters, both A-type and B-type DNA indeed represent a large conformational spectrum. This diversity in fine structures arises from changes in nucleotide conformation and stacking pattern. It is, however, still an open question whether A-DNA exists in the cell, although it has been suggested that the cell nucleus might contain tightly compacted A-DNA in a paracrystalline aggregate state (3). In certain water-deficient crystalline environments and at high ionic strength, A-DNA with its hydrophobic shallow minor groove is favored over B-DNA, while in solution DNA adopts the B-form that is more suitable for involvement in molecular recognition by proteins due to its higher malleability. However, when a hydrophilic group (e.g. hydroxyl) is introduced in the minor groove at the 2′ position of DNA, the B-form converts to an A-form (3). The right-handed A-form is the natural conformation of RNA helixes. The shallow minor groove becomes more hydrophilic and the stabilization of the A-form may be partially explained by direct and water-mediated hydrogen bonding within the sugar–phosphate backbone and between sugar and base units (1). The hydration of the 2′-OH group may contribute to the increased rigidity of A-RNA duplexes compared with A-DNA. The RNA–DNA hybrid with its minor groove width of 7.5–9 Å and with an average sugar puckering in the O4′-endo conformation may be considered as an intermediate between the A and B allomorphic nucleic acids (6,7), further supporting the hypothesis that the conformation of natural double-stranded nucleic acids may oscillate between both extremes (Table 2). This motion of nucleic acids should be well coordinated, avoiding impending clashes at specific base pair steps.

Table 1. Global helical parameters of duplexes with five-membered sugars.

DNA type	Average helical twist (°)	Average helical rise per residue (Å)	No. of nucleotides per helix	Base pair inclination (°)	x-displacement (Å)
Right-handed helix
Da	45.0	3.02	8.0	–15.9	1.05
Cb	39.5	3.31	8.5	–17.0	3.45
α-DNA:β-DNAc	39.8	3.37	10.1	–3.1	–1.16
Bd	36.1	3.37	10.0	2.4	0.80
RNA:DNA duplexe	32.7	2.62	11.0	11.7	–4.46
Ad	31.1	2.90	11.5	12.0	4.10
Left-handed helix
Zd	–30.0	3.8	12.0	–6.2	3.3

^aValues from Curves (10) on the D-DNA model from Eschenmoser and Dobler (4).

^bCurves calculation on C-DNA model (BII_9_1_model.pdb from http://www.fos.su.se/physical/lorens/) (9).

^cα-/β-DNA: Curves calculation on the reconstructed model (11).

^dValues from Eschenmoser and Dobler (4).

^eCurves calculation on the structure of the RNA:DNA duplex, pdb entry 124D (6).

Figure 3.

Side and top view of space-filling models of double helices formed by Watson–Crick base pairing between complementary DNA and RNA. Ribose sugars are depicted in yellow and deoxyriboses in green. A ribbon is drawn through the P atoms in the sugar–phosphate backbone and highlights the zigzag pattern in Z-type dsDNA. Base atoms exposed in the major groove of the helix are gray-colored; other atoms of the nucleobase are in white. A-, B- and Z-type helices are constructed in InsightII (Accelrys Inc.) and each have 20 bp. RNA–DNA duplex is an 8mer determined by Federoff et al. [pdb: 124D (6)] and is depicted twice in the side view: both figures are separated by a dashed line.

Table 2. Groove widths and depths in A- and B-helical structures (dimensions in Å).

	Minor Width	Depth	Major Width	Depth
Aa	11.0	2.8	2.7	13.5
Ba	5.7	7.5	11.7	8.5
RNA–DNA	8.5b	2.0b	–	–
	7.5→9.0c

^aFrom Saenger (8).

^bCalculated using Curves (10) on pdb entry 124D (6).

^cFrom Gonzales et al. (7).

Alternative helical structures

The previously described C- and D-DNA are B-like structures with reduced rise per residue (3.31 and 3.02 Å) and increased helical twists (39.5 and 45°, respectively) (1,9,10). Although the discovery of these structures might not have been considered as important at that time, they do indicate that the conformational monopoly of the right-handed A- and B-forms could be broken.

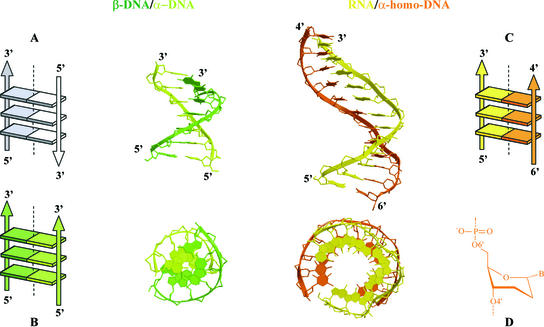
When the stereochemistry at the 1′ position is inverted, α-oligonucleotides (11) are obtained, which represent a new type of Watson–Crick base pairing families. The inversion of configuration at the anomeric center diminishes the steric hindrance associated with a syn orientation of the nucleobases. A solution structure of the α-DNA–β-DNA duplex shows that a right-handed helical structure is obtained with Watson–Crick base pairing (11); see Figure 4. The average helical twist is 39.8° (∼9 bp per turn). The backbone torsion angles for the β-strand are typical of a B-DNA conformation, and the glycosyl linkage on the β-strand is in the anti conformation. On the α-strand, the bases are in the syn conformation, the α, β and γ torsion angles occur in two distinct states: respectively gauche– (∼300°), gauche+ (∼60°) and gauche+ in the majority of the nucleotides, and gauche+, gauche– and trans (∼180°) at two nucleotide positions. The δ torsion angle fluctuates around 150°. The deoxyriboses of both anomeric sugars are in the C3′-exo conformation. The right-handed helix geometry is conserved when both strands are oriented parallel as in the α-DNA–β-DNA duplex.

Figure 4.

Side and top views of the β-DNA–α-DNA duplex reconstructed from Lancelot et al. (11) and the modeled β-RNA–α-homo-DNA (13). Both have parallel-oriented strands as depicted in the Calladine–Drew representations: (A) Antiparallel orientation in natural nucleic acid duplexes, (B) β-DNA–α-DNA, (C) β-RNA–α-homo-DNA. The conformation of the sugar in α-homo-DNA is depicted in (D).

The most unusual allomorph of A- and B-DNA is the left-handed Z-form (12) (Fig. 3), with its characteristic zigzag pattern of the backbone. The conformational repetitive unit in this helical family is a dinucleotide instead of a mononucleotide, and its backbone pattern is a reflection of the alternating conformation in each GC dinucleotide step. Nucleobases are in the anti conformation for cytosine nucleotides with sugars in the C2′-endo conformation (χ= 208°) and in the syn conformation for guanine nucleotides with sugars in the C3′-endo conformation (χ = 67°). The average rise is 3.8 Å and the average helical twist per base pair is –30° [the helical twist angle alternates between –50.6° and –9.4° which reflects the difference between d(GpC) and d(CpG) dinucleotide steps]. The helix axis lies in the minor groove (x-displacement of 3.3 Å and y-displacement of 2.3 Å). As a result of this, Z-DNA appears as a long and narrow double helix having base pairs almost perpendicular to the helix axis (inclination of –6.2°).

Expanding the structural diversity of nucleic acid duplexes by increasing the ring size of the sugar–phosphate backbone

The conformational flexibility of the five-membered furanose ring is represented by its pseudorotation cycle (Fig. 5). In (oligo)nucleotides, the furanose ring fluctuates between the C3′-endo conformation and the C2′-endo conformation, crossing an intermediate low energy barrier. In a saturated six-membered ring, the chair forms are the most stable conformations (Fig. 6) and a chair flip (⁴C₁↔¹C₄) requires considerable energy since a high-energy barrier separates both low-energy states. Substituents on a cyclohexane ring in each of the two low-energy states are positioned either axially or equatorially, which means that the torsion angles in the ideal chair conformation are either ±60° (axial–equatorial or equatorial–equatorial) or ± 180° (axial–axial). Figure 7 summarizes the nucleosides commented on with six-membered ‘sugar’ rings.

Figure 5.

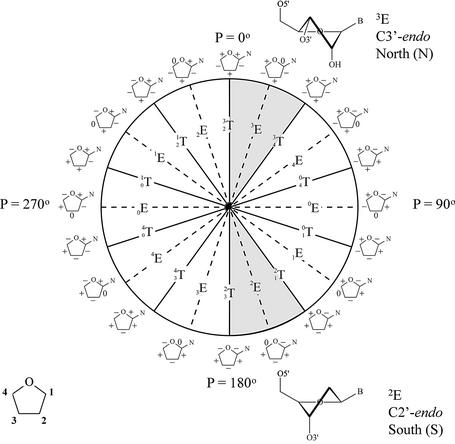
Pseudorotation wheel of the furanose ring and preferred conformation of ribose (top) and deoxyribose nucleotides (bottom). Each point on the circle represents a specific value of the pseudorotation angle P (8). Shaded regions indicate conformations found in A- and B-type helices. On the periphery of the cycle, riboses with signs of the endocyclic torsion angles (ν0 to ν4) are indicated (+) positive, (–) negative and (0) torsion angle at 0°.

Figure 6.

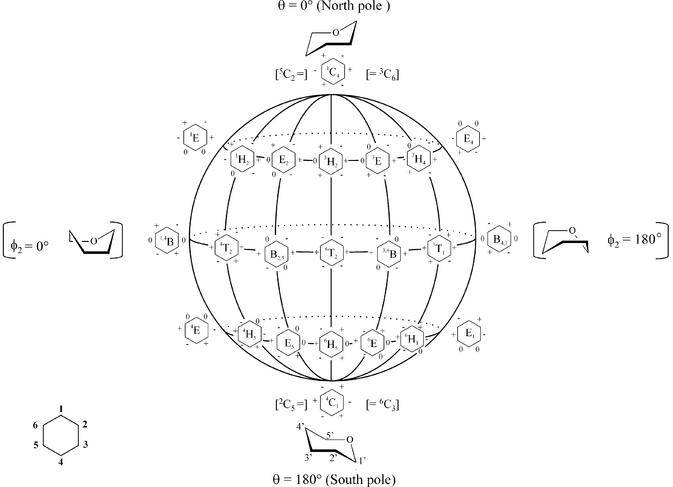
Pseudorotation globe of the cyclohexane ring and preferred conformation of pyranose (top and bottom). On the front surface of the globe, six-membered rings with signs of the endocyclic torsion angles (ν0 to ν6) are indicated (+) positive, (–) negative and (0) dihedral angle at 0°.

Figure 7.

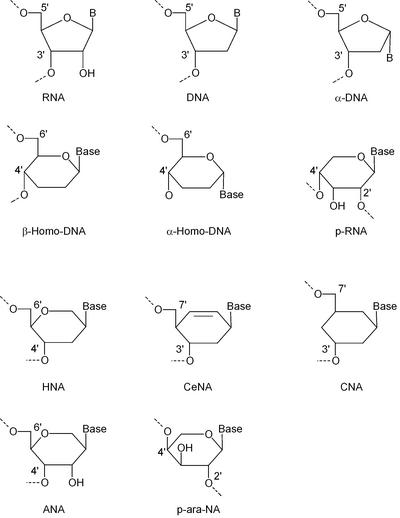
Structures of nucleotides with a five-membered and a six- membered ‘glycon’ moiety that were used for oligonucleotide synthesis.

In comparison with a furanose ring, with four carbon atoms and a ring oxygen, the pyranose and hexitol rings have an extra carbon atom in their ‘sugar’ ring, which provides two more substitution sites. A cyclohexane ring lacks the ring oxygen but has two carbon atoms more in the ring, representing four extra substitution sites compared with the furanose ring. Those additional substitution sites in a ‘six-membered’ nucleoside allow for more isomers than a ‘five-membered’ nucleoside because they increase the possible locations of a nucleobase relative to the hydroxyl groups involved in phosphodiester bonding. This results in a much larger structural diversity of ‘six-membered’ versus ‘five-membered’ oligonucleotide duplexes.

The potential for cross-talking between ‘six and six’ and between ‘six and five’ oligonucleotides further increases the available duplex structures. It is beyond the scope of this review to hypothesize about all possible structures and combinations. We will restrict ourselves to an overview of those duplexes for which experimental structural data are available, mainly using NMR spectroscopy.

Homo-DNA (α and β)

The first two DNA relatives with a six-membered sugar ring that should be envisaged are α-homo-DNA (13) and β-homo-DNA (4). In both constructs, the nucleobase is positioned at the anomeric carbon atom of a pyranose, while the hydroxyl group and the hydroxymethyl group are situated at position 4 and 5, respectively. The β-homo-DNA monomer is an all-equatorial system in the ⁴C₁ conformation, while the α-homo-DNA monomer is an equatorial (base), axial (hydroxyl group), axial (hydroxymethyl group) system in the ¹C₄ chair conformation. Consequently, the rigid six-membered ring restrains the δ backbone angle to ∼60° in β-homo-DNA and to ∼180° in α-homo-DNA. β-Homo-DNA does not hybridize with natural nucleic acids, in contrast to α-homo-DNA.

Using a qualitative conformational analysis of the single-stranded backbone structure, the conformation of double-stranded β-homo-DNA was predicted by Eschenmoser to be linear in the idealized form (and not helical) (Fig. 8) (4). β-Homo-DNA forms antiparallel (Watson–Crick type) purine– pyrimidine duplexes with a higher thermal stability than double-stranded (ds) DNA duplexes (14). Regardless of the ambiguity of base pairing, the disadvantage of a highly stable duplex is that it is less capable of presenting its base sequences to the outside world by local melting, and hence less apt to transfer the genetic information that it carries. The structure of β-homo-DNA duplexes was studied by NMR spectroscopy (14). They appear as a dynamic equilibrium between two quasi-linear conformational types that differ in the α and γ backbone angle. Both models are interconvertible by a counter-rotation of 120° around these axes (model I, α = –60 and γ = +60°, model II, α = –180° and γ = +180°) (13). Due to the positioning of the base moieties in the 1′ position in an all-equatorial system, the average rise in the β-homo-DNA duplexes is 4.5 Å, which is too large to allow for optimal stacking interaction between adjacent base pairs. Theoretically, helix formation will bring bases closer to each other. Changing χ and the backbone torsion angles of β-homo-DNA may induce helicity in their duplexes, but the two hydrophobic methylene groups at the 2′ and 3′ position sterically prevent bases from consecutive residues in a chain from approaching each other to optimal stacking distance (∼3.4 Å). Hence, the driving force for helix formation is abolished and β-homo-DNA stays in a linear form. Nevertheless, helical structures were observed during a free molecular dynamics simulation in vacuo (Fig. 8, left). The exact helical parameters of double-stranded β-homo-DNA are difficult to be determined on the described structures since the studied duplex does not contain a full helical winding. Roughly, they correspond to a maximal right-handed helical twist of 10°, which means at least >36 bp for a complete helix turn (up to 120 nucleotides per helix turn has been reported) (Table 3). Depending on the model, the base pair axes are ‘inclined’ relative to the strand axis by ∼60° (model I) and 45° (model II), corresponding to 30° and 45° inclination of the base pairs relative to the helix axis, respectively. This strong ‘inclination’ relative to the strand axis is reflected in a high preference for antiparallel strand orientation (15). This backbone axis versus base pair inclination has been stressed as being an important parameter controlling the capability of cross-pairing between different nucleic acids (16) (in these presentations, the backbone/base pair inclination is defined in a two-dimensional model). However, this rule should be carefully interpreted since its validity in systems with a more pronounced helical twist is not clear.

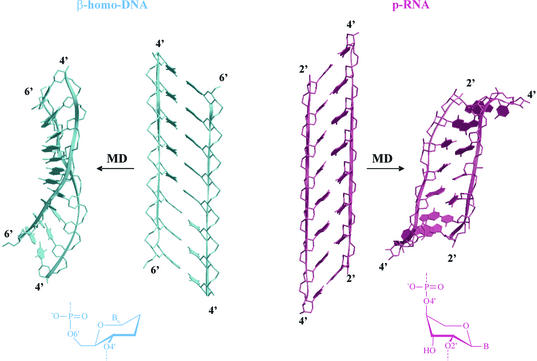
Figure 8.

Comparison between β-homo-DNA and p-RNA duplexes, reconstructed from parameters described in the literature (14,23) and after a molecular dynamics simulation. The scheme of the sugar ring conformation in duplexes is represented at the bottom.

Table 3. Global helical parameters of duplexes with six-membered sugars calculated using Curves 5.1^a.

Type	Average helical twist (°)	Average helical rise per residue (Å)	No. of nucleotides per helix	Base pair inclination (°)	x-displacement (Å)
Right-handed helix
HNA:RNAb	34.4	3.0	11.0	11.3	-3.5
dsHNA type 1 (trig)c	33.2	2.2	11.0	24.2	-6.2
dsHNA type 2 (hex)c	24.2	3.3	15.0	13.4	-6.5
α-homo-DNA:RNAd	24.0	3.6	15.0	–0.2	5.7
ds β-homo-DNAe	10.0	5.8→6.1	36.0	130.0 (45.0)
f	1.9	9.2	189.5	137.3	19.4
g	18.3	5.2	19.7	156.2	–3.5
Left-handed helix
ds p-RNAh	18.9→20	5.8→6.1	18.0→19.0	145.0→55.0
i	–0.5	6.9	750.0	–47.9	–0.6
j	0.8	4.2	456.0	–52.0	0.3

^aCurves 5.1 (10).

^bpdb entry 1EJZ (18).

^cNucleic Acid Database (ndb) entries HD0001.pdbs and HD0002.pdbs (coordinates with symmetry-related strands) corresponding to pdb entries 481D (trig) and 1D7Z (hex), respectively (20).

^dModel from Wippo et al. (16).

^eValues from Otting et al. (14).

^fLinear model reconstructed from Otting et al. (14).

^gCurled model of double-stranded β-homo-DNA after 100 ps of molecular dynamics simulation.

^hValues reported in Schlonvogt et al. (23).

ⁱQuasi-linear model reconstructed from Schlonvogt et al. (23).

^jCurled model of double-stranded p-RNA after 100 ps of molecular dynamics simulation.

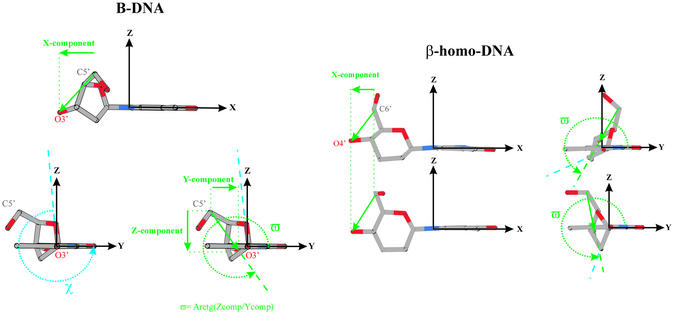
A more accurate model should be defined in a three-dimensional frame. A suggestion might be to use the orientation of the vector, defined by the outer atoms of the δ dihedral angle relative to the planar nucleobase (Fig. 9). The orientation of this vector is determined by the conformation of the sugar, the position of substituents on the sugar moiety and the orientation of the base relative to the sugar (χ). The origin of this right-handed Cartesian reference frame is located at N1 in pyrimidine and N9 in purine nucleosides. The x-axis is oriented along the glycosidic bond between the sugar and base towards the base, the y-axis points in the direction of base atoms involved in Watson–Crick base pairing and is located in the average plane formed by the atoms of the nucleobase, and the z-axis is perpendicular to this plane. In this reference frame, the considered vector can be characterized by its x-component and the angle ϖ determined by its z- and y-components. The ϖ angle is related to the orientation of the base relative to the sugar, since χ changes by rotation around the defined x-axis, which does not alter the x-component. Cross-talk between two systems is considered possible if both the x-component and ϖ of those systems adopt comparable values. This requirement can be checked using the monomer in its energy-minimized conformation (Table 4).

Figure 9.

Vectorization of the positioning of the sugar moiety with respect to the nucleobase, which generates parameters (x-component in Å, ϖ and χ in °) for the prediction of hybridization between oligonucleotides. The ‘special’ case of β-homo-DNA is represented.

Table 4. x-component (in Å), ϖ and χ (in °) angle of the denoted vector for different nucleic acid analogs as depicted in Figure 9.

	Vector	x-component	ϖ	χ
B-DNA	C5′–O3′	–2.2	309	262
A-RNA	C5′–O3′	–0.8	318	194
HNA	C6′–O4′	–0.6 (-0.7)a	307 (316)a	215 (223)a
p-RNA	C4′–O2′	2.7 (3.0)b	312 (296)b	241 (230)b
	O4′–O3′	0.2	350	241
α-Lyxo	C4′–O2′	2.2	18	212
	O4′–O3′	–0.6	344	212
α-DNA	C5′–O3′	3.0	111	140
	Parallel: O3′–C5′	–3.0	291	140
α-Homo-DNA	C6′–O4′	0.3	116	136
	Parallel: O4′–C6′	–0.3 (–0.3)c	296 (326)c	136 (158)c
β-Homo-DNA	C6′–O4′	–1.6 (–1.6)d	281 (233)d	230 (278)d

Values are listed for energy-minimized monomers and as measured in a duplex structure if available. For comparison, values in an A-RNA and B-DNA canonical duplex are mentioned.

^a pdb entry 1EJZ (18).

^bQuasi-linear model reconstructed from Schlonvogt et al. (23).

^cModel from Froeyen et al. (13).

^dLinear model reconstructed from Otting et al. (14).

For a β-homo-DNA monomer, the proposed requirement to base pair with DNA is fulfilled. However, in the β-homo-DNA duplex, the methylene groups at the 2′ and 3′ position in the preceding residue of the considered dinucleotide sterically prevent bases from approaching each other to stacking distance when ϖ ∼300° (χ ∼270°). In the quasi-linear duplex structure determined by NMR, all residues have their nucleobases in a χ ∼200° orientation, which brings their ϖ in a region (∼281°) completely different from other nucleic acids (Table 4). The β-homo-DNA demonstrates that cross-hybridization should be investigated in every particular case, considering not only the high capacity of nucleic acids to accommodate to other systems by a combination of adjustments in χ, backbone torsion angles and sugar conformation (especially DNA and RNA) (17), but also possible differences in conformational freedom of monomeric nucleosides and those incorporated in oligomers. However, this information is not available when trying to predict hybridization between modified nucleic acids since, so far, it is impossible accurately to predict the structure and dynamics of an oligomer by computational methods. Thus the requirement for ‘cross-talk’ mentioned above could be used as a first selection procedure for a project on the molecular design of new synthetic nucleic acids to eliminate constructs that have no chance to form duplexes with a selected target system (but it is no guarantee for success on those monomers that fulfill the requirement). The potential of newly designed nucleic acids to ‘cross-talk’ with RNA and DNA is required in antisense and antigene strategies, respectively. In the search for how nature developed the nucleic acids it uses nowadays, ‘evolutionary chemistry’ has to consider the potential self- and cross-hybridization of nucleic acid analogs as a starting point in the selection of constructs that should be investigated.

The orientation of the C6′–O4′ vector is determined by the substitution pattern, and changing the configuration at the C1′ from β-homo-DNA to α-homo-DNA (Fig. 7) (13) alters the x-component as well as ϖ. It was observed experimentally that the pyranose nucleotides of α-homo-DNA appear in the thermodynamically more stable ¹C₄ conformation (Fig. 4), both in the monomers and in a α-homo-DNA–RNA duplex. It is an axial (hydroxymethyl), axial (hydroxyl), equatorial (base) system with a δ angle of ∼180°. This chair inversion from ⁴C₁ in β-homo-DNA to ¹C₄ in α-homo-DNA does dramatically alter the x-component and ϖ in a minimized monomer. Their values become significantly different from those observed in natural A-RNA- and B-DNA-type helices (Table 4). However, if the O4′–C6′ vector is considered as a measure for cross-pairing with parallel strand orientation, values of the x-component and ϖ come close to those in A-RNA-type helices. Changes in the remaining torsion angles of the phosphodiester linkages in the backbone are expected to enable accommodation of both RNA and α-homo-DNA strands to each other and allow cross-talk between these systems. It is indeed shown that α-homo-DNA is able to cross-pair with RNA, and both strands are oriented parallel.

Initial helix parameters of an α-homo-DNA:RNA duplex were obtained using molecular modeling. According to the modeled structure, base pairs in this duplex are displaced over 5.7 Å into the minor groove and are located almost perpendicular to the helix axis (inclination –0.2°), resulting in a much deeper major groove than in ‘standard’ nucleic acid duplexes described above. The average rise in the base pair steps is 3.6 Å and the mean helical twist is 24°, which means that there are ∼15 bp per helical turn (Table 3). The major groove width is much larger than in regular A- and B-type nucleic acids duplexes. The ribose sugars in the RNA strand of the duplex have a C3′-endo puckering. Overall, the right-handed duplex structure containing α-homo-DNA differs significantly from the A- and B-type duplexes. In the series of structures from D-DNA to β-homo-DNA, the α-homo-DNA:RNA duplex helix can be situated geometrically as intermediary between the right-handed A-DNA and β-homo-DNA. In this order, the duplex becomes more and more unwound and the number of base pairs per turn increases from 8 to near 120.

Hexitol nucleic acids (HNAs)

An alternative strategy to change the orientation of the C6′–O4′ vector in β-homo-DNA duplexes and to allow cross-pairing with natural nucleic acids is to put the nucleobase at the C2′ axial position instead of the regular C1′ anomeric (equatorial) site. This brings the extra methylene group of the six-membered ring in the minor groove site where it should not influence the conformational freedom of nucleobases in neighboring residues. The energy-minimized monomers have a C6′–O4′ vector with an x-component of –0.6 Å and ϖ ∼306° (Table 4). This feature is expected to favor an antiparallel orientation of the strands in the duplex especially with A-type RNA (x-component = –0.8 Å, ϖ ∼318°). Based on this strategy, the β-HNAs were obtained.

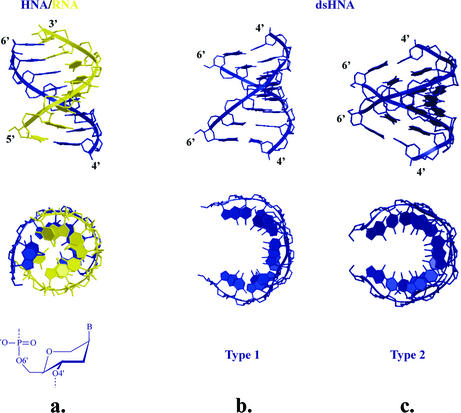
β-HNAs have a ⁴C₁ conformation of the sugar moiety and a 2,4,5 substitution pattern. The substituents are oriented equatorial (hydroxymethyl), equatorial (hydroxyl group), axial (base moiety). The backbone torsion angles of the HNA strand in the HNA:RNA duplex (18) are close to the A-form, and the cooperative adjustment of the backbone angles away from the ideal values of 60° and 180° allows base stacking and helicity (Fig. 10a). The α, β, γ, ε and ζ torsion angles are about the same in the HNA strand and the RNA strand. The average δ and χ torsion angles show somewhat larger differences, i.e. χ is 12° larger in the HNA strand, while the δ angle is 18° smaller as it is constrained by the conformation of a six-membered ring system instead of a five-membered furanose. This observation demonstrates that the ring size is not determinative for the helicality of nucleic acids duplexes. Both furanose oligomers and their relatives with six-membered sugars can adopt helical conformations. The helical parameters show a negative base displacement (–3.5 Å), an axial rise of 3.0 Å and a mean twist angle of 34.4°. With its minor groove width of 10.0 Å and an inclination of 11.28°, this HNA:RNA structure has a very similar conformation to the A-form dsRNA. The d-altritol nucleic acids (ANAs) have the same properties as HNAs, with increased duplex stability due to better hydration of the groove and increased pre-organization (19).

Figure 10.

Comparison between HNA–RNA duplex determined by NMR (a) and both helical types of dsHNA as found by crystallography (b, type 1; and c, type 2). Structures have 8 bp each and all hexitol rings adopt a ring conformation as represented below the HNA–RNA duplex.

The analysis of dsHNA crystal structures (20) allowed us to identify the existence of a family of helical conformations attainable by 1,5-anhydrohexitol nucleic acids. Although the local polymorphism of ‘six-membered’ DNA is expected to be lower than that of furanose-DNA, also in the ‘six-membered’ field, there is a place for considerable conformational diversity. Crystallography on a self-complementary HNA sequence revealed the existence of two antiparallel, right-handed, Watson–Crick base pairing, double helixes (type 1 and 2 in Fig. 10b and c) (20). Both show a difference in backbone conformation of the α to γ torsion angle [–synclinal (sc), +antiperiplanar (ap), +sc in type 1 and +ap, +ap, +ap in type 2]. The δ torsion angle of HNA structures is generally lower (69–77°) than for typical A-type structures due to the (slightly flattened) chair conformation of the hexitol ring. The global helical parameters between both helix structures vary considerably. Both structures have a similar high x-displacement of the base pairs (–6.5 Å). The base pairs are highly inclined with respect to the helix axis in type 1 (24.3°), while in the other structure the inclination is very small (3.4°). The rise per base pair is 2.2 and 3.3 Å, respectively, and the twist angles are 33.2 and 24.2°, reflecting that the second duplex (type 2) is seriously underwound (11 and 15 bp per helical turn, respectively). The increased inclination (24.3°) and the lower rise (2.2 Å) of the type 1 HNA structure versus the typical A-DNA structure is due to the higher x-displacement of the bases relative to the helix axis while maintaining appropriately the same twist angle (number of base pairs per turn). The major groove becomes very narrow (4.1 Å) when the helical twist is reduced, the helical rise increases and the inclination decreases, giving rise to the type-2 HNA structure. The major groove widens considerably (12.9 Å). In both structures, the nucleobases approach an approximate stacking distance of 3.4 Å.

The fourth HNA structure which has been determined by NMR is the dsHNA with four consecutive T:T wobble pairs flanked by G:C Watson–Crick base pairs (21). Although we did not intend to describe here non-canonical base pair systems, it is worthwhile to mention this duplex structure briefly. A cooperative effect of all backbone torsion angles results in the formation of a helical structure with an x-displacement of –4.3 Å and an average twist angle of 10°, which is very near to the value found for β-homo-DNA.

The strong sequence selectivity of HNA, the high stability of HNA against enzymatic degradation and the high thermal stability of HNA:RNA and dsHNA duplexes combined with its ability to function as a template in non-enzymatic polymerase reactions renders HNA an excellent candidate for various applications (e.g. molecular assembly, modulation of gene expression by antisense strategy, diagnostic tool, molecular computing, etc.).

Ribopyranosyl oligonucleotides (p-RNA)

Ribopyranosyl(4′→2′)oligonucleotides (Fig. 7) were designed as constitutional isomers to natural RNA. p-RNA shows Watson—Crick pairing which is stronger and more selective (Watson–Crick type) than in natural nucleic acids (22). However, p-RNA does not hybridize with DNA, which can be explained by the positive x-component of its C5′–O2′ vector in the reference frame we defined previously. The structure of double-stranded p-RNA was determined using NMR and molecular modeling (Fig. 8) (23). Both strands are antiparallel oriented with a predominance of interstrand base stacking that is induced by the pronounced inclination of the base pairs with respect to the helix axis (∼45°) (24). The duplex forms a weak left-handed helix with a helical pitch of ∼110 Å and a twist angle of ∼20° (18 nucleotides per helical turn). p-RNA is expected to be a more rigid structure than other nucleic acids because not only δ but also γ is determined by the six-membered sugar ring, which reduces the number of flexible bonds between adjacent phosphates to four (25). The backbone angles allow better interstrand stacking and decrease unfavorable 1,5 interactions (23). The inclination in p-RNA is of opposite orientation compared with β-homo-DNA (24). A similar negative inclination is observed in other pentopyranose systems: α-l-lyxo-(4′→2′)-pyranose and β-d-xylo-(4′→2′)-pyranoses (26,27). Recently, a new self-pairing duplex of (4′→2′)-l-α-arabino-pyranosyl-(CGAATTCG) (p-ara-NA, Fig. 7) was studied by NMR (28). The essential features of the resulting structures are an antiparallel, Watson–Crick paired duplex with a band-like overall shape, having a strong ‘inclination’ (±–50°) of the base pairs relative to the strand axis and, therefore, predominant interstrand base stacking.

The conformational continuum of double-stranded nucleic acids

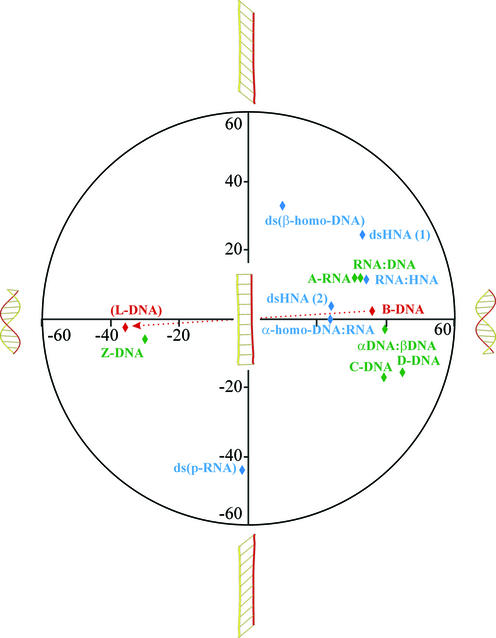
With the appearance of the ‘six-membered’ nucleic acids, the beautiful double helix structure of Watson and Crick has lost its monopoly position and, most probably, the complexity of nucleic acid duplex structures will continue to increase. Besides the sequence-induced deformations of the helix, the local variability in helical parameters can be increased by mispairing, by introduction of base modifications with altered hydrogen bonding pattern or, more generally, by slight modifications in the nucleotide conformation. These local adjustments will have an influence on the large-scale deformations and, thus, on the global parameters. However, the most profound deviations from the classical Watson–Crick, right-handed B-DNA helix are obtained when the pentofuranose sugar is replaced by a ‘six-membered’ ring. The theoretically developed β-homo-DNA was the first example of a new secondary DNA motif. The right-handed D-form of DNA (B-like structure) with its average helical twist of 45°, its rise per residue of 3.02 Å and only eight nucleotides per helical turn can be considered as the most compact double-helical nucleic acid which is situated at one end of the structural hemisphere [previously, the A- and B-forms were denoted as the hemispheres of a right-handed structural continuum (3)]. As an intellectual exercise (the structure of these nucleic acids has not yet been determined), it is not unrealistic to propose that the mirror-imaged l-dsDNA is able to adopt the extreme form on the other side of the structural hemisphere, being a left hand compact helix. By slowly unwinding the right-handed B-DNA (4), the helical twist decreases and the number of nucleotides per turn increases from eight to ∞ and, upon rewinding in the other direction, back to eight, as found in the theoretical model of the left-handed l-DNA (Fig. 11). The transition can be described as a continuum from which half of the helical structures are described by the right-handed models of D-DNA, HNA, α-homo-DNA and β-homo-DNA, and half by the left-handed models of p-RNA, Z-DNA and l-DNA. New examples will be added to this conformational continuum of nucleic acids once the structures of new synthetic nucleic acids have been determined. This conformational continuum is, only to a limited extent, accessible for interaction with natural nucleic acids (because of the five-memberedness of the furanose ring). It is clear that nature decided to work with only a small window of potential duplex structures, which is driven by thermodynamic considerations. Synthetic nucleic acids whose geometries fall beyond this accessible region are not suitable for control of gene expression (antisense and antigene strategies). However, they could be used as alternatives for DNA in other applications that require a carrier of the genetic information and when stability against enzymatic degradation is preferred (e.g. molecular computing).

Figure 11.

Illustration of the conformational continuum of nucleic acid duplexes based on helicity and inclination. The definitions of inclination used are those described in the original literature for the individual duplexes. Helical twists are given on the x-axis and inclination on the y-axis.

Double-stranded nucleic acid structures are stabilized by stacking interactions of their nucleobases. The strategy of stacking can be realized by inclining and twisting (25) (Fig. 11). Both phenomena increase this typical interaction between neighboring base pairs and compact the duplex structure. If stabilization by stacking cannot be obtained in a duplex through helicalization by twisting the successive base pairs (e.g. β-homo-DNA), it could be obtained through inclination (or perhaps bending). Examples of both strategies are available. For instance, the B-DNA helix shows only twist and almost no inclination, while the base pairs in β-homo-DNA have almost no twist but a large inclination of ∼50°. In most double-stranded nucleic acids, twist as well as inclination deviate from zero (Fig. 11). Both parameters (and also additional helix parameters such as propeller twist) may alter when modified nucleotides are incorporated into regular DNA or RNA, indicating the strong influence that modified nucleotides can have on duplex stability.

Nature has selected the 1-β-d-ribofuranose nucleotides as building blocks for the genetic system, most probably based on their flexibility (29). As a consequence, it preferred systems that use the principle of helicalization (instead of increasing the inclination) to condense and stabilize nucleic acid duplexes. Formation of helical structure has the advantage that more compact molecules are obtained and less energy is needed for unwinding and (further) processing DNA. RNA is more suited as a template for non-enzymatic replication compared with DNA (30), which basically needs enzymes to assist in its replication process. This could be caused, partially, by the larger inclination of RNA (versus DNA), providing incoming residues with a better accommodation for incorporation and, partially, by the lower acidity of the 3′-OH of deoxynucleotides.

Transitions between B- and A-forms of DNA through the influence of external agents such as proteins, water and counter-ions represent the common structural movement of a natural DNA duplex. This apparent structural continuum of natural nucleic acid conformations is reflected by the observation that it is often difficult to assign a DNA to a pure structural class when it is in complex with a protein. On the other hand, the breadth of variation for helical parameters in each specific type of DNA double helix (A- or B-type) is very limited due to restrictions imposed by the continuous sugar– phosphate backbone and the stacking preferences of the base pairs.

However, we should also consider the concept of the existence of equilibria between different helical structures in the ‘six-membered DNA’ field, which might have the same or different geometries as in natural nucleic acids. An interesting example, in this respect, is cyclohexanyl nucleic acid (CNA) (31). Solution phase analysis reveals that cyclohexanyl nucleosides adopt a conformation with equatorial base moieties (opposite to the conformation of hexitol nucleosides due to the increased 1,3-diaxial interactions when an oxygen atom is replaced by a methylene group). In this conformation, oligonucleotides constructed of cyclohexanyl nucleosides and phosphodiester internucleoside linkages should adopt a quasi-linear structure, and no stacking interactions are expected. Chair inversion of the nucleosides, however, allows base stacking and hybridization with natural nucleic acids (the base pair inclination is reduced to near 0°). Generally, the preferred conformation of the six-membered ring in nucleotides is unchanged when they are incorporated into a polynucleotide. However, in this case, the preferred conformation of a single nucleotide analog is different from its conformation in an oligomer. The energy difference between both chair conformations is low. Although it could be stressed that CNA might represent an example of oligonucleotides that can exist in two extreme forms, i.e. an equilibrium between an A-type right-handed helix and a linear structure with an unlimited number of nucleotides per turn, the latter form has not been observed experimentally yet. A structural study of a CNA:α-HNA hybrid will probably reveal this, since the rigid α-HNA strand is expected to be linear because it is an all-equatorial system (17). Circular dichroism (CD) spectra of a CNA:RNA hybrid show a pattern similar to A-type dsRNA. Nucleic acids that appear in different conformations are useful to create dynamic constructs such as molecular switches or oscillating molecular machines.

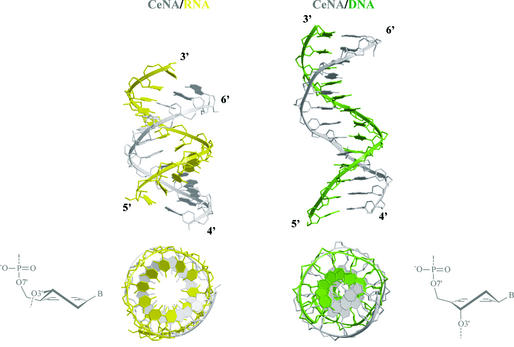
A more realistic model describing conformational equilibria between helical structures in the ‘six-membered DNA’ field is that of cyclohexenyl nucleic acids (CeNAs) (32). CeNAs consist of cyclohexenyl nucleotides with a half-chair as global minimum. The cyclohexene ring is more flexible than a cyclohexane ring and approaches the conformational mobility of a furanose ring. When the two extreme half-chair forms are considered (³H₂ and ²H₃), it may be concluded that the cyclohexene ring in its ³H₂ form is a good mimic of a furanose ring in its C3′-endo conformation, while its ²H₃ conformation may be considered as a good mimic of a C2′-endo puckered furanose. The former conformation with the base moiety in a pseudoaxial position is the most stable. Model building of a CeNA:RNA and a CeNA:DNA duplex suggests that both helical structures may exist (Fig. 12). The CeNA:RNA hybrid appears as an A-form duplex, while the CeNA:DNA duplex is of the B-type. Overall, the CeNA model might represent an example of conformational mobility in the series of ‘six-membered’ nucleic acids, which is similar to the natural nucleic acids situation. The existence of a ³H₂ cyclohexenyl nucleotide in dsDNA helix with two CeNA residues in neighboring base pairs has been observed experimentally. It remains to be demonstrated under which external conditions a transfer to the B-form might occur. Nevertheless, the CeNA system is the best fit of the natural DNA/RNA in the domain of ‘six-membered’ nucleic acids and therefore it is a promising candidate for the control of gene expression using an antisense strategy that is further explored.

Figure 12.

Duplexes obtained by docking CeNA onto an A-RNA and B-DNA template (13 bp).

Conclusions

It remains very difficult to predict accurately the three-dimensional structure of a macromolecule based on the constitutional and conformational properties of its repeating monomers, even in the case when some rules need to be respected (such as helicity and Watson–Crick base pairing). It is the destiny of all existing theories that, once the rules have been formulated, a never-ending list of exceptions starts to emerge and this is no different in the field of helical DNA. Expanding the sugar ring size of nucleic acids and keeping the potential for communication via base pairing has increased the structural diversity of nucleic acids beyond the classical A-, B- and Z-forms of DNA. Two complementary oligonucleotide strands can be sewn into a double helix with an architecture that depends on the nature of the constituents. This dynamic chemistry of spontaneous supramolecular assembly generates structural and functional diversity. The modified oligonucleotides behave as a programmed system from which many of the properties and potential applications still have to be discovered.

The duplex formation is driven by molecular recognition based on hydrogen bonding between adenine and thymine (or uracil) and between guanine and cytosine. Using these nucleotide building blocks, nucleic acids allow storage of all information needed for every form of life on this planet. The complexity of this language of information can be increased by including other base pair systems such as isoC:isoG (33). Non-canonical base pairing may also influence the structure of nucleic acid duplexes and their potential as an information system, especially in the non-helical complexes. Furthermore, the kind of helix structure adopted is dependent on conditions, which means that a double-stranded nucleic acid represents a dynamic material. The assembly/disassembly process as well as the reversible switch between two helical conformations depends on the presence of the appropriate outside trigger.

The birth of molecular biology was dependent on chemical discoveries such as the understanding of the structure of the DNA double helix and the development of an efficient method for DNA synthesis. The generation of information-directed organized functional structures (34) (a series of water-soluble nucleic acid helices are part of this family of supramolecular associations) will have a major impact on material and computer sciences (nanotechnology) and on medicine (diagnostics and therapeutics), and it will give a better insight into the origin of life on this planet.

Model building

For those duplexes described in the literature that are not deposited in the PDB or NDB databases, models were reconstructed based on structural parameters mentioned in published papers. All energy refinement and molecular dynamics calculations were done using the Amber 7.0 programs (35) and using the 1999 parameter database (36).

The model of α-d(5′-TCTAAAC-3′):β-d(5′-AGATTTG-3′) (11) was reconstructed starting from a normal antiparallel B-DNA double helix which was generated using the Amber program nucgen. The chirality of C1′ atoms in one chain was reversed to obtain an α-DNA strand. The bases in the α-chain were kept in their positions while the sugar rings were moved and remodeled to obtain a parallel stranded duplex. The sander classic module in the Amber software was used for optimization (energy minimization and molecular dynamics in vacuum conditions) of the model. The NMR restraints from Lancelot et al. (11) and Watson–Crick hydrogen bond restraints were applied during the calculations. After a while, the NMR restraints were removed and the molecular dynamics calculations were continued until a stable structure was obtained. This structure is depicted in Figure 4 and was also used in the Curves v5.1 calculation (10).

For the reconstruction of the β-homo-DNA and p-RNA duplexes, first the atomic charges of the β-homo-DNA and p-RNA nucleotides were calculated using Gamess (37) at the 6–31G** level, followed by a RESP calculation (38). The Amber parameter database used was again the 1999 data set.

A single-stranded β-homo-DNA (14) was constructed from a poly-ethene chain mimicking the backbone and setting the backbone torsion angles using the program EDPDB (39) to α = –60°, β = 180°, γ = 60°, δ = 60°, ε = 180° and ζ = –60° corresponding to the first conformation in Otting et al. (14). Then β-homo-DNA nucleotides (csd entry PAKWIH) (40) were fit onto this backbone (41) with χ = –120°. The second complementary chain was added by fitting Watson–Crick base pairs to construct the antiparallel duplex.

The energy of the duplex was optimized (energy minimization and molecular dynamics in vacuo) while restraining the Watson–Crick hydrogen bonds and some NMR distances from the original reference (14). This structure was used in the Curves calculation and is depicted in Figure 8. When the NMR restraints were removed, a curled structure was obtained, on continuing the molecular dynamics simulation (Fig. 8, right).

The same procedure was used in the construction of the p-RNA model (23). The backbone angles were set initially to α = +60°, β = 180°, γ = 180°, δ = 60°, ε = –60° and ζ = –180°, with χ = –125° corresponding to the structure in Schlonvogt et al. (23). Again, initially, a quasi-linear double-stranded duplex was obtained (Fig. 12, left). When continuing the molecuar dynamics simulation without NMR restraints, the duplex became left handed (Fig. 12, right).

Top and side view pictures of oligonucleotides were generated by Molscript (42) and Bobscript (43).