Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity

Abstract

The probability of choosing an alternative in a long sequence of repeated choices is proportional to the total reward derived from that alternative, a phenomenon known as Herrnstein's matching law. This behavior is remarkably conserved across species and experimental conditions, but its underlying neural mechanisms still are unknown. Here, we propose a neural explanation of this empirical law of behavior. We hypothesize that there are forms of synaptic plasticity driven by the covariance between reward and neural activity and prove mathematically that matching is a generic outcome of such plasticity. Two hypothetical types of synaptic plasticity, embedded in decision-making neural network models, are shown to yield matching behavior in numerical simulations, in accord with our general theorem. We show how this class of models can be tested experimentally by making reward not only contingent on the choices of the subject but also directly contingent on fluctuations in neural activity. Maximization is shown to be a generic outcome of synaptic plasticity driven by the sum of the covariances between reward and all past neural activities.

There is a long tradition of experiments on decision making in which a subject chooses repeatedly between alternative options and is rewarded according to her choices. In many such experiments, choosing an alternative makes it less likely to yield a reward in the future, corresponding to the economically relevant case of diminishing return. The aggregate behavior in these experiments can phenomenologically be described by the “matching law.” This empirical law states that choices are allocated such that the accumulated rewards harvested from an alternative, divided by the number of times it has been chosen, is equal for all alternatives. For each alternative, we will define income as the accumulated rewards harvested from it, investment as the number of times it has been chosen, and return as income divided by investment. According to the matching law, the return is equal for all alternatives.^† Rational choice theory predicts that behavior should maximize reward, but in many contexts, matching behavior is not equivalent to maximization. Indeed, the matching law has been invoked to explain seemingly irrational behaviors such as addiction (4).

In an experiment where a subject, animal, or human is placed on a reinforcement schedule, it takes some time before its choice frequencies converge to those predicted by the matching law (5, 6). The dynamics of this convergence has been modeled mathematically by a number of researchers. In these models, the subject makes choices stochastically, as if by tossing a biased coin.^‡ The choice probabilities evolve in time based on the rewards received, in a process of learning or adaptation. Over long time scales, the choice probabilities converge to values satisfying the matching law (4, 5, 10).

Although the present work is another attempt at a theory of how matching behavior is learned, its goals are very different from those of previous theories. We seek to describe matching not simply at the behavioral level, but to explain it in terms of hypothetical events taking place at synapses. It is widely believed that some forms of learning are due, at least in part, to long-lasting modifications of the strengths of synapses. Here, we hypothesize that such synaptic plasticity is responsible for the behavioral changes that are observed as animals learn to match.

What properties of synaptic plasticity are likely to lead to matching behavior? Addressing this question seems like a formidable task, in particular because little is known regarding the neural circuit underlying decision making. Remarkably, it is possible to prove a mathematical theorem that gives a broad answer to this question. According to the theorem, matching is a generic outcome of synaptic plasticity that is driven by the covariance between reward and neural activity. In statistics, the covariance between two random variables is the mean value of their product, provided that one or both has zero mean. Accordingly, covariance-based plasticity arises naturally when synaptic change is driven by the product of reward and neural activity, provided that one or both have zero mean. Either signal can be made to have zero mean by measuring it relative to its mean value.

An important implication of the theorem is that the details of the neural circuit for decision making are not important for matching behavior. This statement holds provided that it is truly the covariance that drives synaptic plasticity. This assumption is violated, for example, if plasticity is based on the product of reward and activity without subtracting mean values. In this case, matching behavior may hold for specific neural circuits satisfying quite restrictive assumptions, but the generality of the phenomenon is lost.

If matching indeed is driven by the covariance between reward and neuronal activity, then making reward contingent directly on neural activity is expected to lead to significant deviations from matching behavior. We demonstrate this prediction in a specific decision-making neural circuit.

Above we contrasted matching with maximizing. Can maximizing behavior also be produced by a synaptic plasticity rule driven by the covariance of reward and neural activity? The answer is yes, provided that the rule includes not only the covariances of reward with neural activity in the immediate past, but also with neural activities that accompanied choices further in the past.

Models for learning that are based on the covariance between reward and choice are common in economics and are used phenomenologically to explain human behavior in strategic environments (7, 11, 12). In computer science, such learning algorithms are often used for adaptive control (13). These models are formulated at the behavioral level of choices and rewards. Our hypothesis can be viewed as the extrapolation of these models to the neural level.

Results

Synaptic Plasticity and Reward.

In the introduction, it was hypothesized that animals learn matching behavior because reward influences plasticity at synapses in their brains. The precise nature of this influence is not well understood. Reward may be encoded in the overall level of a neuromodulator. For example, some studies suggest that the neuromodulator dopamine signals the mismatch between actual reward and expected reward (14, 15). According to other studies, dopamine codes only for the positive mismatch between the actual and expected rewards (16–18), and it has been speculated that other neuromodulators, such as serotonin, report the negative mismatch between actual and expected rewards (19). The effects of dopamine are spatially diffuse for a number of reasons. First, midbrain dopamine neurons send long axons that arborize widely over almost the entire brain. Second, dopamine can “spill” out of the synapses where it is secreted and affect extrasynaptic targets. Third, the dopamine neurons are thought to be a fairly homogeneous population in their response properties (20). Thus, dopamine may be considered as a global signal shared by many synapses.

It is well known that neural activity changes the strength of synapses in the brain. For example, in Hebbian plasticity, the covariation in the firing rates of coupled neurons leads to potentiation of the synapse that connects them. In other cases, the activation of the presynaptic neuron or postsynaptic neuron is sufficient to induce synaptic changes (21). However, it is not well understood how global neuromodulatory signals that encode reward interact with the local neural activity signals to modulate synaptic efficacies. According to one popular idea, dopamine gates local plasticity rules (22). One can imagine a number of specific implementations of this general idea. For example, the change ΔW in synaptic strength W could be given by

where η is the plasticity rate, R is the reward harvested in that trial, E[R] is the average of the previously harvested reward, and N is some measure of neural activity. For example, N could correspond to the presynaptic activity, the postsynaptic activity or the product of presynaptic and postsynaptic activities. In the latter case, the plasticity rule of Eq. 1a can be called Hebbian, because this synaptic learning rule depends on the product of the activities of the presynaptic and postsynaptic neurons. The sign of the synaptic change depends on whether the reward R is greater or less than its expected value E[R].

Other biologically plausible implementations of reward-modulated plasticity are as follows:

The next section will show that the plasticity rules of Eqs. 1 a–c share the common feature that they are driven by the covariance between reward and neural activity.

Covariance Between Reward and Neural Activity.

In general, the dynamics of Eqs. 1 a–c are difficult to analyze, in part because they are stochastic. If the right-hand side of these equations is replaced by their expectation value, then a deterministic “mean field” approximation is obtained. In general, a stochastic dynamics often resembles its mean field approximation, although there can be differences (23). Typically the mean field approximation is better as the plasticity rate η becomes small.^§

Our theoretical analysis will focus on the mean field approximations to Eqs. 1 a–c. For all these plasticity rules, the expectation value of the right-hand side is proportional to Cov[R, N], the covariance between R and N. Therefore, the mean field approximation to Eqs. 1 a–c takes the form

For this reason, we say that the plasticity rules of Eqs. 1 a–c are driven by the covariance between reward and neural activity. At a steady state of Eq. 2, the covariance vanishes, Cov[R, N] = 0. In the next sections, we show that vanishing covariance is equivalent to the matching law under quite general conditions. It follows that the steady state of the mean field dynamics Eq. 2 obeys the matching law.

What Matching Implies About Neural Activity.

A fundamental assumption of our theory is that neural activity is a stochastic hidden variable for the reward schedule. Ordinarily, reward depends on choice behavior but has no direct dependence on neural activity:

Assumption 1.

Reward R is independent of neural activity N, when conditioned on the choice A.^¶

To understand the meaning of this assumption, it is helpful to imagine a situation in which it is violated. For example, suppose that a neurophysiologist records neural activity N in an animal and makes reward contingent not only on the animal's behavior, but also on N. This reward schedule would invalidate Assumption 1 (as discussed in Experimental Predictions). More typically, R has no direct dependence on N and Assumption 1 is valid. If the neural activities at different trials are correlated, then under some conditions, Assumption 1 also will be violated. However, it is possible for R to have an indirect dependence on N through A. Such a dependence would typically cause Cov[R, N] to be nonzero, because the covariance is a measure of dependence between two random variables.

But the following theorem shows that this covariance vanishes, provided that the animal behaves in a special way according to the matching law. To see this result, recall that the matching law corresponds to equality of returns from the two choices. The return from choice 1 can be written as the conditional expectation E[R|A = 1] and, similarly, for the return from choice 2. Therefore, the matching law can be written as E[R|A = 1] = E[R|A = 2], which is how it appears in the following theorem.

Theorem 1.

Suppose that Assumption 1 is satisfied. If E[R|A = 1] = E[R|A = 2], then Cov[R, N] = 0.

Proof:

If E[R|A = 1] = E[R|A = 2] = E[R], then E[R|N = n] = E[R] for all n. It follows that E[δR|N = n] = 0, where δR = R − E[R]. Thus, E[δR·N] = 0 or, equivalently, Cov[R, N] = 0.

A more intuitive proof is possible in the special case where R is binary, taking on the values 0 and 1. Then the matching law E[R|A = 1] = E[R|A = 2] is equivalent to independence of R and A and, therefore, implies that R and N are independent, in which case their covariance must vanish.

What Neural Activity Implies About Matching.

According to Theorem 1, for any animal behaving according to the matching law, the covariance between reward and the activity of any neuron in its brain is equal to zero. Now consider the converse of Theorem 1. Suppose that Cov[R, N] vanishes. Can we conclude that behavior satisfies the matching law? Theorem 2 shows that this conclusion is valid, provided that we make a further assumption.

Assumption 2.

E[N|A = 1] and E[N|A = 2] are different from E[N].

This assumption is reasonable if N is the activity of a neuron in a brain area that is involved in making the choice. Because N is one of the causes of A, we expect its average value to be different in trials when the animal chooses A = 1, and trials when it chooses A = 2.^‖ Given both Assumptions 1 and 2, matching behavior becomes a necessary and sufficient condition for the vanishing of the covariance of reward and neural activity.

Theorem 2.

Suppose that Assumptions 1 and 2 are satisfied. Then Cov[R, N] = 0 if and only if E[R|A = 1] = E[R|A = 2].

Proof:

Define the deviation δN = N − E[N]. Then E[δN] = 0 by construction, so that

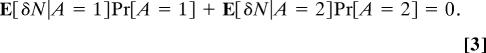Using Assumption 1, we also can write

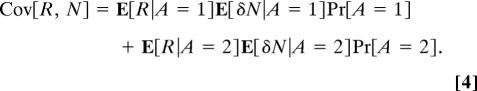Combining Eqs. 3 and 4 yields,

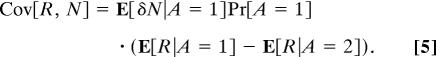By Assumption 2, E[δN|A = 1] and E[δN|A = 2] are nonzero. Because the choice probabilities Pr[A = 1] and Pr[A = 2] must sum to one, it follows that they are nonzero from Eq. 3 and, hence, E[δN|A = 1]Pr[A = 1] is nonzero. Then Eq. 5 implies that Cov[R, N] = 0 if and only if E[R|A = 1] = E[R|A = 2].

For a more intuitive argument, consider the special case where R, N, and A are binary variables, taking on the values 0 and 1. Then the theorem states that R and N are independent if and only if R and A are independent. In other words, the only way to break the chain of dependences N → A → R is to break the second link, because the first link cannot be broken by Assumption 2.

Decision making is often studied in situations in which choosing an alternative makes it less likely to yield a reward in the future, corresponding to the economically relevant case of diminishing return. This principle is commonly implemented by using the concurrent variable-interval (VI) reward schedule (25) (see Supporting Text, which is published as supporting information on the PNAS web site). In Theorems 1 and 2, the conditional expectations E[R|A = 1] and E[R|A = 2] played an important role. It may not be obvious how to define these quantities for reward schedules such as the concurrent VI, in which reward depends not only on the current choice but also on past choices. For example, if we assume that a subject makes decisions by tossing a biased coin, to define E[R|A = a] we assume that the subject already has made an infinite number of choices by tossing a biased coin with probabilities Pr[A = 1] and Pr[A = 2]. Now the subject chooses A = 1, and the expected value of reward is E[R|A = 1].** Because of the history dependence, E[R|A = 1] and E[R|A = 2] are not fixed but are actually functions of the choice probabilities Pr[A = 1] and Pr[A = 2]. This dependence allows the animal to achieve matching behavior by allocating its choices appropriately. If the returns were fixed and independent of the animal's choices, as in the two-armed bandit schedule, and also different from each other, then it would be impossible to achieve matching behavior.

According to Theorem 2, under quite general conditions, matching behavior emerges if and only if the covariance of reward and neural activity vanishes. Consequently, the steady state of the mean field approximation of the synaptic plasticity rules of Eqs. 1 a–c corresponds to matching behavior. This result suggests that matching is a generic outcome of the plasticity rules, although there is no formal mathematical guarantee. Whereas matching is a steady state of the mean field approximation, it might not be a stable steady state. Furthermore, the stochastic dynamics might deviate significantly from its mean field approximation. Because of these mathematical uncertainties, it is helpful to study numerical simulations of particular examples of decision-making networks, as is done below.

Example: Matching Behavior in a Neural Network Model

In this section, we study choice behavior in a particular example of a decision-making network. We demonstrate matching behavior when the plasticity rule is driven by the covariance of reward and neural activity. We show that substantial changes to the properties of the network and the plasticity rule have no observable effect on matching behavior, as long as the plasticity rule is driven by the covariance of reward and neural activity. In contrast, a change to the plasticity rule that violates the covariance rule leads to substantial deviations from matching behavior.

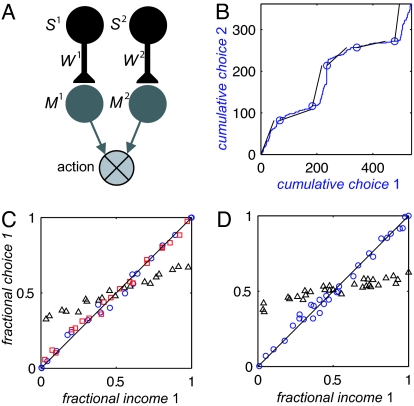
Decision making is commonly studied in experiments, in which the subject repeatedly chooses between two actions, each corresponding to a sensory alternative. For example, in recent experiments with primates, the stimuli are two visual targets, and the actions are saccadic eye movements to the targets (5, 26). We demonstrate matching behavior with a minimal model in which the two stimuli are represented by two populations of sensory neurons, S¹ and S², and the two actions are represented by two populations of premotor neurons, M¹ and M² (Fig. 1A). Input from the sensory neurons determines the activity of the premotor neurons via M^a = W^a·S^a, where W^a is the efficacy of the synaptic connection from the sensory to the premotor population that correspond to alternative a. Alternative 1 is chosen in trials in which M¹ > M². Otherwise, alternative 2 is chosen. The comparison could be performed by a winner-take-all network with lateral inhibition (27, 28) but is not explicitly modeled here. The source of stochasticity in this model is Gaussian trial to trial fluctuations in S¹ and S². After each action, the synapses are changed according to the plasticity rule of Eq. 1b with N = S^a, ΔW^a = η R (S^a − E[S^a]).

Fig. 1.

Matching behavior in a reinforcement learning model. (A) A decision-making network consisting of two populations of sensory neurons S^a, corresponding to the two targets, and two populations of premotor neurons M^a, corresponding to the two actions. Alternative 1 is chosen in trials in which M¹ > M². Otherwise, alternative 2 is chosen (see Example in Results). (B and C) Matching behavior in a concurrent VI schedule. (B) Cumulative choice of alternative 1 versus cumulative choice of alternative 2 (blue). The baiting probabilities switched every 150 trials (blue circles). Black lines show the average ratio of incomes within each block (ratio of baiting probabilities here: 1:1, 1:6, 3:1, 1:1, 1:8, and 6:1). (C) The probability of choice as a function of fractional income. Each point corresponds to one experiment with fixed baiting probabilities. The diagonal is the expected behavior from the matching law. Blue circles, population model with a covariance plasticity rule. Black triangles, population model with a noncovariance plasticity rule. Red squares, Poisson model. (D) Deviations from matching behavior by making reward directly contingent on neural activity. The probability of choice as a function of fractional income in a concurrent VI schedule with a covariance plasticity rule, Eq. 1b. Circles, matching behavior emerges if reward is contingent on action only. Triangles, the concurrent VI schedule is modified so that harvesting reward also requires that S^los > T (see Experimental Predictions). Simulation parameters: Reward was delivered according to a concurrent VI schedule with a fixed sum of baiting probabilities, 0.3. Every symbol in C and D corresponds to 2,000 trials of fixed baiting probabilities, and results are the average over the last 1,000 trials. Population model: Synaptic plasticity rate η = 0.2; activity of the S^a neurons is drawn from a Gaussian distribution with mean 1 and a coefficient of variation σ = 0.1. Threshold T in D is T = 1.1. Initial conditions in all simulations W^a(t = 1) = 1. Poisson model: Sensory populations 1 and 2 contain 25 and 50 neurons, respectively; premotor populations 1 and 2 contain 10 and 25 neurons, respectively. Spike count is drawn from a Poisson distribution with a mean of 10 for the sensory neurons and I_k^a (see text) for the premotor neurons. Synaptic plasticity rate η = 10⁻⁴; average return is calculated with an exponential filter of width 50 trials. Initial conditions, W_kj^a (t = 1) = 0.01.

The two-alternative concurrent VI schedule is controlled by two parameters, which are called baiting probabilities. We simulated the model with the concurrent VI schedule, where the baiting probabilities switch every 150 trials. Fig. 1B depicts the cumulative choice of alternative 2 as a function of the cumulative choice of alternative 1 (blue line). Two feature of this simulation are notable. First, the model appears to adjust its behavior to changes in the rates of the reward (blue circles). Second, the blue line generally parallels the black lines that indicate the ratio of rewards in the corresponding block of trials with fixed baiting probabilities, in agreement with the matching law. Matching behavior is quantified further in Fig. 1C (blue circles) when we study choice behavior in concurrent VI schedule with fixed baiting probabilities. Each blue circle corresponds to one simulation in which the baiting probabilities of the two targets were kept fixed. The fraction of trials in which alternative 1 was chosen is plotted versus the fractional income earned from action 1 (the ratio of the income from action 1, divided by the sum of incomes from both actions). The model obeys the matching law essentially perfectly, as demonstrated in the correspondence between the simulation results and the diagonal (solid line).

If the emergence of matching behavior in the model is a consequence of the covariance-based synaptic plasticity rule, then, in general, other plasticity rules are not expected to lead to matching behavior. For example, we replaced the plasticity rule of Eq. 1b with the plasticity rule ΔW^a = η R S^a. With this plasticity rule, the change in synaptic efficacy is proportional to the product of reward and neural activity. However, because neither the reward R nor the neural activity S^a has zero mean, this plasticity rule cannot be considered as a covariance rule. Simulating the network of Fig. 1A with this plasticity rule in the same conditions leads to large deviations from matching behavior (Fig. 1C, black triangles).

In contrast, as long as the plasticity rule is driven by the covariance of reward and neural activity, other changes in the properties of the decision-making network are not expected to have an effect on matching behavior. We replaced the population model of Fig. 1A with a more biophysical model of the same architecture, where we explicitly modeled the neurons in each population and the synapses between them. More formally, let S_j^a be the activity of neuron j in the sensory population a, measured as the number of spikes in a relevant time window. Each spike count S_j^a is assumed to be drawn from a Poisson distribution with a constant mean. The synaptic input to premotor neuron M_k^a is given by the weighted sum I_k^a = Σ_jW_kj^aS_j^a,where W_kj^a is the efficacy of the synaptic connection from neuron j in sensory population a to neuron k in premotor population a. The spike count M_k^a of premotor neuron k in population a also is assumed to be drawn from a Poisson distribution with mean I_k^a. In general, we do not assume symmetry between the two alternatives and the number of neurons in the different populations may be different. The action is chosen by comparing the activities of the two premotor populations. If the average number of spikes per neuron in premotor population 1 is larger than that of population 2, alternative 1 is chosen. Otherwise alternative 2 is chosen. After each action, the synapses are changed according to the plasticity rule of Eq. 1a, where N is the product of the activities of the presynaptic sensory neuron, and the postsynaptic premotor neuron in a Hebbian-like fashion, ΔW_kj^a = η(R − E[R])·S_j^a·M_i^a. E[R] is computed as the running average of the past few rewards. Simulating this model in the same concurrent VI schedule leads to matching behavior that is indistinguishable from that seen in the more abstract model (Fig. 1C, red squares).

The success of the covariance-based models in generating matching behavior in numeric simulations substantiates our hypothesis that matching behavior results from synaptic plasticity that is driven by the covariance of reward and neural activity.

Experimental Predictions

Our theorem states that matching behavior occurs if and only if Cov[R, N] = 0. We hypothesize that matching behavior results from a synaptic plasticity rule that is driven by the covariance of reward and neural activity. According to this perspective, behavior adapts because synapses in the brain perform statistical computations. However, a very different class of matching models has been proposed in which the brain performs computations that are “financial.” A common conceptual explanation for operant matching is known as melioration (4). The basic idea is that subjects keep track of the return of each alternative and stochastically shift their behavior to alternatives that provide a higher return. Thus, in a diminishing-return experiment, this behavior would equalize the returns of the different alternatives. According to one implementation of this idea, the decision maker explicitly measures the incomes from each of the two targets, calculates the ratio of the incomes, and chooses by tossing a biased coin with odds given by this ratio (5, 12). By construction, the choice probabilities are in the same ratio as the incomes, so the matching law is satisfied. This model is similar to the linear reward-inaction algorithm (13) that has been proposed by economists to explain human behavior (11) and is commonly used in machine learning. An alternative phenomenological model for matching has been proposed in which the difference of the two incomes, rather than the ratio, determines the bias of the stochastic choice (29). Because the mathematical form of the matching law is divisive, this dynamics leads to approximate matching behavior only in a restricted range of parameters. An explicit neuronal model for decision making that calculates returns by using synaptic plasticity recently has been proposed (30).

A common feature of these models is the implicit assumption that there exists a learning mechanism that is driven by choices and rewards, which calculates financial quantities, and a source of stochastic neural activity that translates the financial quantities into a probability of choice. Because these models generate matching behavior, by our theorem, the covariance of reward and the stochastic neural activity vanishes in the brain of such a decision maker. However, learning is not driven by this covariance, as it is in our model.

How Can a Covariance-Based Plasticity Model Be Distinguished Experimentally from the Financial Models?

Consider a reward schedule in which reward is made directly contingent on fluctuations in the stochastic neural activity. This experiment could be done by measuring neural activity in a brain area involved in decision making by using microelectrodes or brain imaging and making reward contingent on these measurements and on actions. This sort of contingency has been used by neurophysiologists, although not in the context of operant matching (31, 32). In our model, such a contingency would lead to violation of the matching law. This violation is because our theorem depends on Assumption 1, that reward depends on neural activity only through actions. Violation of Assumption 1 typically will break the equivalence of vanishing covariance and matching behavior, because our theorems are no longer valid.

To illustrate this point, we have performed numerical simulations of the decision-making network of Fig. 1A with the plasticity rule of Eq. 1b, while making reward contingent also on neural activity. We assume that S¹ and S² are recorded in the decision-making circuit. Let S^los be the activity of the “losing” sensory neuron (the neuron corresponding to the nonchosen action). The concurrent VI schedule is modified so that harvesting reward also requires that S^los > T, where T is a predefined threshold. The result of such a contingency on neural activity is a shift to “undermatching” behavior (black triangles), which means that the ratio of choice probabilities is closer to one than the ratio of incomes (compare with the control case where reward is contingent only on action, blue circles). The larger the threshold is, the larger the deviation from matching behavior (data not shown). The nature of deviation from matching depends not only on the characteristics of the contingency of reward on neural activity in the reward schedule but also on the properties of the decision-making network.

Consider now a financial model in which financial computations and probabilistic choice are implemented in two separate brain modules. One brain module records past reward and choices to calculate quantities such as income and return, and the other brain module utilizes these quantities to generate stochastic choice in accordance with the matching law. In that case, if reward is contingent on neural fluctuations in the choice module, the financial module still should operate properly. The contingency on neural fluctuations effectively may change the reward schedule and, hence, change the allocation of choices, but because the computation of the financial quantities is not compromised, matching behavior would be retained.

The assertion that matching behavior in financial models is robust to making the reward contingent on neural activity relies on the assumption that the computation of financial quantities are not affected by neural fluctuations. One subtlety concerning this prediction should be mentioned. Any plausible learning process in the brain is likely to be affected by some stochastic neural activity. However, if the stochasticity in the learning process is uncorrelated with the stochasticity of the decision-making process, as is likely to be the case if the financial computations and probabilistic choice are implemented in two separate brain modules, then it is possible, in principle, to distinguish between our covariance-based model and financial models, but such experiments require recording the choice-related fluctuations in neural activity.

Matching and Gradient Learning.

In this paper, we have hypothesized that matching is the result of a plasticity rule that is driven by the covariance of reward and choice-related neural activity. More precisely, we have assumed that the change in synaptic efficacy in a trial is driven by the covariance between the reward harvested in that trial and the neural activity that generated the choice in that trial. However, in reward schedules such as concurrent VI, reward depends not only on the immediate past, but also on choices further in the past. This dependence leads to the problem of temporal credit assignment in reinforcement learning (33). The problem can be solved by a covariance-based plasticity rule that includes neural activities associated with past choices. In this section, we show that under certain assumptions, maximization is equivalent to vanishing of the sum of covariances of reward and past neural activities.

In addition to Assumption 2, our theorem requires the following assumptions.

Assumption 3.

The joint probability distribution of neural activity and choice is identical in each trial, that is, from trial to trial, each draw of (N_t, A_t) is independent.

From this assumption, it immediately follows that choices at different trials are independent and, therefore, choice behavior is characterized by a single parameter p, the probability of choice.

Assumption 4.

Reward R_t is independent of neural activity N_t-τ, when conditioned on the choice A_t-t.

Note the similarity between this assumption and Assumption 1.

Assumption 5.

There is a unique stationary distribution of the sequence of rewards if alternatives are chosen by tossing a biased coin (see footnote **).

Theorem 3.

Suppose that Assumptions 2–5 are satisfied and define the expected reward U(p) = E[R_t]. Then U′(p) = 0 if and only if Σ_{τ = 0}^∞Cov[R_t, N_t−τ] = 0.

The proof of Theorem 3 follows the same route as the proof of Theorem 2 and appears in Supporting Text.

Thus, under these assumptions, maximizing takes place if and only if the infinite sum of the covariances of past neural activities and current reward vanishes. These results raise the intriguing possibility that matching behavior is a form of bounded rationality. A plasticity rule that is driven by the covariance between rewards and the sum of past neural activities is expected to lead to maximizing, but requires a long memory of past activities, whereas a plasticity rule that is driven by the covariance between rewards and recent neural activities is expected to lead to matching behavior but does not require long memory.

Discussion

In this paper, we have explored the hypothesis that matching is the result of a plasticity rule that is driven by the covariance of reward and choice-related neural activity. We hypothesized that the locus of this plasticity is the synaptic efficacies between neurons.

An experimental test of the hypothesis was proposed: making reward directly contingent on neural activity and choices. We predict that such neural contingency could lead to significant deviations from matching. A plasticity rule that is driven by the covariance between reward and the sum of past neural activities may maximize reward.

Robustness and Fine-Tuning in Covariance Computation.

Theorem 2 implies that matching behavior should emerge in very different decision-making networks, as long as their synaptic plasticity is driven by the covariance of reward and neural activity. This conjecture is supported by our numerical simulations demonstrating matching behavior in networks with different properties. Therefore, we believe that a plasticity rule based on covariance is robust in its ability to generate matching behavior independent of the details of the network in which the synapses are embedded.

Whether plasticity rules like Eqs. 1 a–c indeed exist in the brain remains to be explored by neurobiological experiments. Even if synaptic plasticity turns out to be well approximated by Eqs. 1 a–c, these equations are not expected to be perfectly accurate. Therefore, it is important to test the effects of small deviations from these plasticity rules. In particular, if the subtractions of Eqs. 1 a–c are not completely accurate, then there will be error in the covariance computation. Although a full exploration of this issue is outside the scope of this paper, two points that arise from numerical simulations should be mentioned. First, inaccuracies of mean subtraction lead to a drift in the magnitude of the synapses. This drift can be prevented by adding a decay term to the synaptic weight or by normalizing the synaptic efficacies. Second, small inaccuracies of subtraction produce only small deviations from matching behavior. This result suggests that small errors in the calculation of the covariance do not result in catastrophic effects.

It is interesting to note that the issue of covariance computation also has been important for models of associative memory based on Hebbian plasticity. In the Hopfield model, synaptic strengths are set by the covariance of activity in the patterns to be memorized. The Hopfield model can store a number of memories that scales linearly with the number of neurons (34). When the mean neural activity is not properly subtracted, the synaptic efficacies drift and the storage capacity is significantly reduced. Therefore, proper subtraction of mean activity levels also is important for the computational function of Hebbian plasticity.

Potentiation and Depression in Covariance-Based Plasticity.

According to our covariance hypothesis, the same neural activity will lead to either potentiation or depression, depending on whether a reward was associated with that trial. There is some experimental evidence suggesting that the neuromodulator dopamine, a plausible reward signal, may reverse the sign of Hebbian plasticity (for review, see ref. 22).

Transient Dynamics.

In this paper, we have concentrated on the steady-state matching behavior of a decision-making model whose synaptic plasticity is driven by reward and neural activity. The dynamics of the transient convergence to matching behavior is an area of active research. In an experiment in which the reward schedule unexpectedly changes, it takes some time before its choice frequencies converge to those predicted by the matching law (5, 6, 26). This adjustment happens remarkably rapidly. In one study, it has been estimated that the time scale associated with an adjustment to new baiting probabilities is ≈10 trials, in which only ≈3 rewards are delivered (5). Our numeric simulations demonstrated adaptation in a covariance-based model (Fig. 1B). The time scale of the adaptation of the model is determined by the properties of the decision making network, and the plasticity rule, the plasticity rate η, and the time scale of estimation of E[R] (in Eqs. 1a and 1c). Importantly, if synaptic weights are purely driven by covariance-based rules, then the synapses do not have a characteristic efficacy, and their efficacy is expected to drift in a random-walk fashion. The time scale of adjustment of the model at any point in time depends on the current magnitudes of the synapses. Therefore, to make a quantitative comparison of the time scale of a covariance-based model with that observed in experiments, a more concrete synaptic plasticity rule with boundaries on synaptic efficacies is needed.

Gradient Learning.

The present work has some mathematical connections to the REINFORCE class of learning algorithms used in computer science, which are based on the correlation between reward and an eligibility trace (35, 36). When REINFORCE algorithms are applied to neural networks, the correlation between reward and the eligibility trace may become a covariance between reward and neural activity. For example, a REINFORCE algorithm for neural networks with stochastic synaptic transmission is basically a plasticity rule of the form Eq. 1b, where the variable N indicates whether a synapse has released neurotransmitter in response to stimulation. It was shown that this plasticity rule leads to matching behavior in numerical simulations of a decision-making network (37). The theorems of the present paper help to explain why.

In the theory of REINFORCE algorithms, it is shown that the correlation between reward and the eligibility trace is equal to the gradient of the expected reward. In contrast, our mathematical analysis does not use the idea of gradient-following. Instead, we only analyze the steady state of learning (or at least its mean field approximation), and make no statement regarding convergence. In general, plasticity rules like Eqs. 1 a–c do not follow the gradient of expected reward. Under certain assumption, a plasticity rule that is driven by the covariance of reward and sum of neural activities approximates a gradient learning rule. In that case, the sum of neural activities is similar to the eligibility trace in REINFORCE.

Abbreviation

VI

variable-interval.