Phylogeny can make the mid-domain effect an inappropriate null model

Abstract

The mid-domain effect (MDE), a bias in species richness towards the midpoint of a given geographical dimension, has been used as a null model in macro-ecological studies. Departures from a MDE are often thought of as interesting. The MDE is a product of the interaction between geometric boundaries and range locations, with species being forced to occupy more central positions in proportion to their range size. We criticize this mechanism for assuming species' locations to be wholly independent from their evolutionary past. We present a simple simulation model that shows how range locations arising as part of a phylogenetic process depart from a MDE. The amount of departure is positively correlated with phylogenetic imbalance (tree shape), but a deviation from an equal-rates Markov speciation model is not necessary to negate a MDE. We suggest that the MDE is an appropriate ecological null model only when phylogenetic influence on range location is demonstrably low or non-existent.

1. Introduction

Understanding the spatial distribution of species richness is a primary goal of macro-ecological studies. In one recent model (Colwell & Hurtt 1994), species richness gradients may be simply a product of geometric constraints on species range boundaries. This model has been gaining attention in the recent literature (e.g. Colwell et al. 2004; Pimm & Brown 2004), although not always uncritically (Hawkins & Diniz-Filho 2002; Laurie & Silander 2002).

Colwell & Hurtt (1994) suggest that the random placement of species’ ranges within a bounded domain results in a peak in species richness near the centre—the mid-domain effect (MDE). They suggest that species with large distributions, approaching the size of a bounded domain, are constrained to have their centre point near the centre of the domain. As the size of a species' range decreases, this constraint becomes more relaxed and range midpoints progressively closer to the boundary of the domain become more feasible. As a consequence, there is probably greater overlap of species' ranges towards the centre of a domain producing a central peak in species richness. This expectation might be useful as a null model of patterns of species richness (Colwell & Hurtt 1994; Colwell & Lees 2000; Jetz & Rahbek 2001; Colwell et al. 2004), and deviation from the MDE has been used explicitly to assess environmental and historical influences on patterns of species richness (Jetz & Rahbek 2002; Connolly et al. 2003). The adoption of null models in evaluating ecological hypotheses is widely accepted (Harvey et al. 1983), but the utility of a null model such as the MDE is entirely conditional upon the realism of the underlying assumptions.

In the MDE, the placement of ranges within a domain is solely a product of their geographical extent, i.e. species' locations in space are independent. We use a simulation approach to investigate the possible consequence of a violation of this assumption based upon empirical estimates of phylogenetic tree shape.

To date, the majority of ecological biogeographical studies have treated species' distributions as independent (e.g. Gaston & Williams 1996; Brown & Lomolino 1998). Like any species attribute, location in space is inherited, with modification, from the ancestor, and therefore can be expected to covary with phylogeny. Our rationale is that phylogeny and, in particular, phylogenetic imbalance (the unequal distribution of species between sister clades) may influence the location and density of species’ distributions. If so, imbalanced trees might be expected to show clustering of species in spatial locations incompatible with the central peak of mid-domain models.

2. Methods

A C++ computer program was written to emulate the processes of speciation and range expansion/contraction from a single central point of origin to a ‘fauna’ of 500 species within a 100×100 rectangular matrix (see Electronic Appendix for detailed description of the algorithm and source code). Per-cell expansion and contraction probabilities were held constant. Phylogenetic trees were evolved using a pure birth process, although lineages could become extinct if their geographical range became zero. Per-iteration speciation probabilities (Z) were evolved under a punctuated log-Brownian process (log Z_new=log Z_old+ϵ, where ϵ is a random variate drawn from a normal distribution with a mean of zero and a standard deviation σ). At speciation, the ancestral range was divided allopatrically, with a random proportion allocated to each descendant such that the outline and location of the ancestral range was identical to the union of the descendants. Each evolution to 500 species (replicate) generated a phylogeny and a 100×100 richness map.

For each of three combinations of per-cell expansion/contraction probabilities, 1000 replicates were simulated for σ=0 and σ=0.3 (this latter set of parameters generates tree imbalances closely approximating empirical studies; Heard & Mooers 2000). In addition, for both σ=0 and σ=0.3, another 1000 replicates were simulated with the spatial linkage between ancestral and descendant ranges being broken: at speciation, one descendant species' range was placed randomly on the grid with the shape being held constant. We refer to these as ‘randomized’ cases, and to the former as ‘inherited’. We regard the randomized cases as showing the phylogenetic independence of range location that is implicit within current MDE models. We therefore regard the inherited cases as preserving phylogenetic signal in range location. Large post-speciation range movements may distort this pattern. We therefore assessed the behaviour of the model across a range of per-cell expansion/contraction probabilities (see Electronic Appendix A).

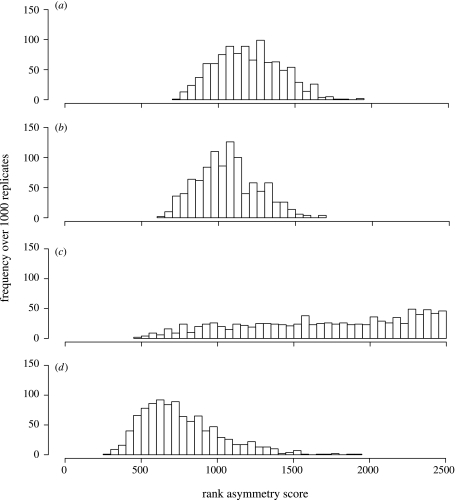
The MDE is taken here to describe a richness distribution with a maximum at the midpoint of all dimensions that declines symmetrically towards the dimension endpoints. For each case, a frequency map for the 1000 replicates was made, giving the number of times a given cell contained the maximum richness values for a replicate. Symmetry about the midpoint of the latitudinal richness gradient of each replicate was assessed. Each row in the map was ranked by maximum richness, and the summed difference in rank between rows equidistant from the midpoint was obtained. Perfectly symmetrical distributions obtain a summed difference of zero, with asymmetrical distributions gaining higher sums. The significance of all pairwise differences in median asymmetry was assessed by a jackknife randomization test.

3. Results

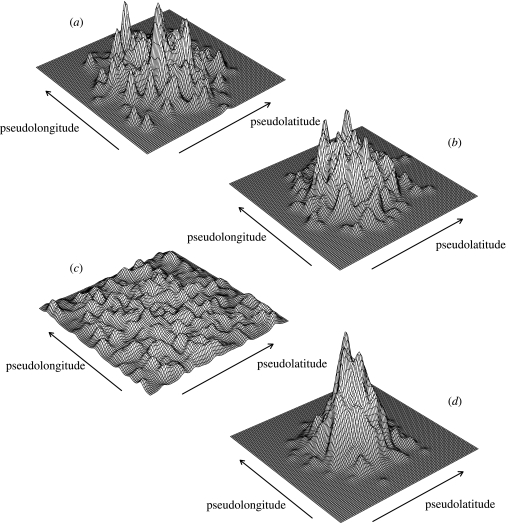
The inherited models produced distributions that were significantly (all pairwise randomization tests: p<0.001) less symmetrical than the randomized models (figure 1a–). This was most obvious when speciation probability (Z) was allowed to vary across lineages (figure 1c), indicating that as phylogenetic imbalance increases so does asymmetry. As predicted by the MDE, the randomized models tend to peak in richness close to the centre of the domain (figure 2b,d). By contrast, the peaks in richness among the inherited models have a wider spatial distribution (figure 2a,c). Again, this was more apparent when Z was allowed to vary, producing an almost even distribution of richness peaks across the domain (contrast figure 2a with 2c). All results presented are for per-iteration expansion and contraction probabilities of 0.7 and 0.2, respectively. Results for other combinations are congruent (see Electronic Appendix A).

Figure 1.

Frequency histograms of richness map asymmetry scores for 1000 replicates each of (a) equal-rates phylogenies, (b) equal-rates phylogeny with range randomization, (c) variable-rates phylogenies (σ=0.3) and (d) variable-rates phylogenies with range randomization.

Figure 2.

Frequency surfaces of the location of the cell with maximum species richness for 1000 replicates each of the cases in figure 1. Frequency is on the z-axis (range in plot 0–4), latitude on the y-axis and longitude on the x-axis. The frequency values have been smoothed via a two-dimensional kernel smoother of constant bandwidth.

4. Discussion

Patterns of species richness generated by our model are solely a consequence of the random expansion and contraction of ranges and the division of ranges upon speciation events. Density dependence is not explicitly included, although the likelihood of any unoccupied cell subsequently becoming occupied is a function of the number of occupied adjacent cells. An artefact of this is that cells surrounding the edge of the matrix will tend to be species-poor as the number of possible occupied adjacent cells is limited (e.g. Bokma et al. 2001). These ‘edge effects’ are an unavoidable corollary of a bounded space.

We find that when the location of ranges is randomized with respect to phylogeny, richness maps resemble the predicted distribution of species richness of the MDE, both in symmetry and the distance of the maximum peak in richness from the centre of the domain. The evolution of species' geographical extents within our model therefore produces a range-size frequency distribution that is susceptible to the MDE, i.e. random range placement tends to increase range-overlap towards the centre of the domain. If sister species are constrained to have adjacent ranges at the time of divergence then the resulting richness maps depart from the expectations of the MDE. This tendency increases when speciation rates are allowed to evolve across the phylogenetic tree, hence increasing phylogenetic imbalance.

Variation in tree shape, taxon age and biological traits associated with range dynamics may explain why the power of mid-domain models in explaining empirical patterns of species richness tends to vary among taxa, as reported by Colwell et al. (2004), without the need to ascribe ecological explanations. Although Colwell & Lees (2000) recognize that neither range shape nor placement are likely to be truly random with respect to ecological and evolutionary history, they argue that either multiple deterministic factors influencing species distributions will result in a distribution of range extents equivalent to those produced by chance, or that post-speciation range movement would break the tie between phylogenetic relatedness and geographical location.

The existence of such spatial patterning, however, is a fundamental premise of historical biogeography. Phylogenetic signal in range location may remain, even within clades of highly mobile taxa, such as mammals (B. M. Fitzpatrick and M. Turelli, unpublished data). Closely related species are also likely to share many biological and ecological traits, which may result in correlated range movement over time (e.g. Jablonski 1987; Peterson et al. 1999; Qian & Ricklefs 2004), rather than independent drift.

Our analysis indicates that the assumptions of the MDE should be examined before adopting it as a null model in ecological hypotheses testing. Critically, even phylogenetic trees generated by equal-rates Markov processes may depart from the MDE, so a hypothesis of differential selection between clades is unnecessary. We advocate that phylogenetic signal in the location of species ranges be examined routinely: if more closely related species are found to be in closer geographical proximity than expected by chance alone it is an indication that the assumptions of the MDE are violated. Potential bias may be most pronounced within recently diverged clades (see Pimm & Brown 2004) and among species with limited dispersal.

5. Conclusion

Our model generates evolutionary trees mirroring imbalance among empirical studies and investigates a range of parameters influencing species range movements. We demonstrate that under the assumption of phylogenetic non-independence in the geographical location of related species (closely related species tend to be closer geographically than expected by chance), patterns of species richness can depart significantly from the MDE. Consequently, care should be taken in its selection as a null model. In ecological studies the effect of phylogenetic non-independence could confound attempts to identify causal mechanisms. For example, species richness hotspots may be a product of one or a few geographically local but species‐rich lineages. By extension, a departure from the MDE may offer insights into differential speciation and extinction rates within clades—a uniquely ecological approach to assessing variation in evolutionary rates.