Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions

Abstract

We have used fluorescence correlation spectroscopy measurements to quantify the hydrodynamic sizes of monomeric polyglutamine as a function of chain length (N) by measuring the scaling of translational diffusion times (τ_D) for the peptide series (Gly)-(Gln)_N-Cys-Lys₂ in aqueous solution. We find that τ_D scales with N as τ_oN^ν and therefore ln(τ_D) = ln(τ_o) + νln(N). The values for ν and ln(τ_o) are 0.32 ± 0.02 and 3.04 ± 0.08, respectively. Based on these observations, we conclude that water is a polymeric poor solvent for polyglutamine. Previous studies have shown that monomeric polyglutamine is intrinsically disordered. These observations combined with our fluorescence correlation spectroscopy data suggest that the ensemble for monomeric polyglutamine is made up of a heterogeneous collection of collapsed structures. This result is striking because the preference for collapsed structures arises despite the absence of residues deemed to be hydrophobic in the sequence constructs studied. Working under the assumption that the driving forces for collapse are similar to those for aggregation, we discuss the implications of our results for the thermodynamics and kinetics of polyglutamine aggregation, a process that has been implicated in the molecular mechanism of Huntington's disease.

The accumulation of ordered intracellular and extracellular protein aggregates are visible molecular characteristics of a variety of neurodegenerative and systemic diseases (1–6). Nine neurodegenerative diseases, including Huntington's disease, are associated with the aggregation of proteins that contain genetic expansions of polyglutamine tracts above a normal threshold length of 35 glutamine residues (7–10). Ages of onset of disease show nonlinear, inverse correlation with the length of polyglutamine expansions (11). Different hypotheses have been put forth to explain both the toxicity associated with polyglutamine expansions and what it is about the expansion above a normal length range that confers toxicity. A majority of proposed mechanisms center on the aggressive, length-dependent, ability of polyglutamine to form ordered intermolecular aggregates (12).

CD and NMR data indicate that monomeric polyglutamine sequences prefer the random coil state under physiological conditions (12–15). As chain length increases, there is no obvious change in the ensemble averaged solution “structure” of polyglutamine peptides (14) although data from different in vitro experiments indicate that rates of aggregation increase with polyglutamine length (14, 16). Mechanistically, polyglutamine aggregation is a nucleation-dependent process (16), and analysis of kinetic data using a thermodynamic nucleus model (17) suggests that an energetically unfavorable conformation of the monomer, i.e., a single polyglutamine chain, acts as the critical nucleus for aggregation (16, 18).

It is important to recognize that one can invoke a range of mechanisms to explain kinetic data for polypeptide aggregation (5, 16, 17) and the dominant mechanism will vary with solution conditions and polypeptide concentration. Characterization of the average properties and fluctuations in the monomeric ensemble provides constraints on mechanistic models used to interpret kinetic data. Accordingly, our focus is on a complete description of the aqueous solution structure of monomeric polyglutamine. This description is not possible with CD or NMR measurements alone because these probes do not provide information about the global sizes and shapes preferred by monomeric polyglutamine. In recent studies based on molecular dynamics simulations of monomeric polyglutamine it was shown that as chain lengths increase there ought to be an increased probability for sampling compact, roughly spherical geometries (19). These predictions needed to be tested experimentally. Hence, we have carried out systematic measurement of hydrodynamic properties for monomeric polyglutamine as a function of chain length.

Monomeric polyglutamine is analogous to linear, flexible polymers that have access to conformationally heterogeneous ensembles. In such systems, quantities such as chain size, measured by radius of gyration (R_g), hydrodynamic radius (R_h), or translation diffusion time (τ_D, which is directly proportional to R_h), scale with chain length (N) according to power laws of the form N^ν (20). R_g and R_h are equivalent, but not identical, measures of chain size. If the polymers are sufficiently long and flexible, ν assumes one of three values: ν = 0.59 for a chain in a good solvent; ν = 0.5 in a theta or indifferent solvent; and ν = 0.33 in a poor solvent.

Solvent quality, as measured by the value of ν, provides quantitative assessment of the balance between chain–solvent and chain–chain interactions for a polymer in a specific environment (21). It also provides information regarding the preferred sizes and shapes of molecules in solution. In a good solvent (ν = 0.59), there is a marked preference for conformations that promote favorable interactions with the surrounding solvent (21). Therefore, the ensemble is characterized by large fluctuations, and chains form loosely packed structures with an average preference for prolate ellipsoidal shapes (22). This is the case for polypeptides in high concentrations of denaturants such as 8 M urea or 6 M GdnCl (23). In a theta solvent (ν = 0.5), chain–chain and chain–solvent interactions counterbalance exactly and statistical properties of polymers follow those of classical ideal chain models formulated by Flory (24). Finally, in a poor solvent (ν = 0.33), chain–chain interactions are favored over chain–solvent interactions, and collapsed, roughly spherical conformations dominate the ensemble (20).

CD spectra for monomeric polyglutamine in PBS at 37°C resemble those of proteins in strong denaturants (12–14). Does this mean that the ensemble for monomeric polyglutamine in aqueous solutions is akin to those of denatured proteins? This question can be answered by quantifying the scaling of chain size as a function of chain length, which we have done by using fluorescence correlation spectroscopy (FCS). This technique is ideally suited for quantitative studies of systems that are prone to aggregation mainly because we need only nanomolar concentrations of peptide samples to carry out the experiments (25, 26). At such small concentrations the signal from the monomer is not compromised by the possible presence of small amounts of aggregates. Using data collected from an FCS experiment, one can determine the translational diffusion time, τ_D, which is directly proportional to the hydrodynamic radius, R_h.

Results

Variation of τ_D with Chain Length N.

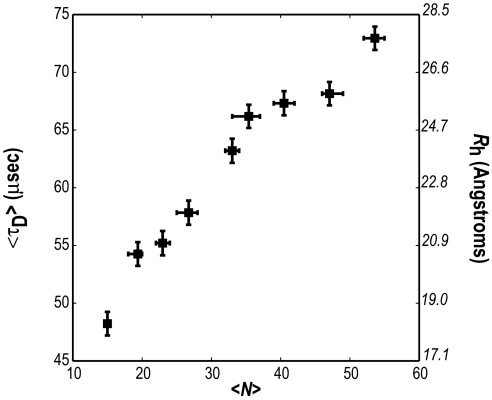
Fig. 1 shows FCS data for the average translational diffusion time 〈τ_D〉 (measured in microseconds) as a function of the average chain length 〈N〉 for the peptide series Gly-(Gln)_〈N〉-Cys*-Lys₂. A fluorophore is attached to the cysteine residue as described in Methods. It can be seen that 〈τ_D〉 increases monotonically with chain length, which means that there is no abrupt change in the ensemble averaged structure of polyglutamine as the chain length crosses the pathological length threshold (N > 35). This observation is consistent with the conclusions of Chen et al. (14) who showed that CD spectra of monomeric polyglutamine peptides are insensitive to variations in chain length.

Fig. 1.

Variation of 〈τ_D〉 with 〈N〉, the average number of glutamine residues in the peptide series Gly-(Gln)_〈N〉-Cys*-(Lys)₂. Horizontal error bars are asymmetric because they are not true error bars. Instead, they are meant to convey the range of chain lengths within each peptide sample. The ordinate labels shown in italics are estimates for the hydrodynamic radius (〈R_h〉) in Å, which were calculated from measured values for 〈τ_D〉 by using the prescription described in Methods.

Linear Regression Analysis.

If 〈τ_D〉 = τ_o〈N〉^ν, then ln(〈τ_D〉) = ln(τ_o) + νln(〈N〉). The computed linear correlation coefficient between ln(〈τ_D〉) and ln(〈N〉) is 0.961 with a P value of 8 × 10⁻⁵. This finding indicates that our data support the hypothesis for the existence of statistically significant linear correlation between ln(〈τ_D〉) and ln(〈N〉).

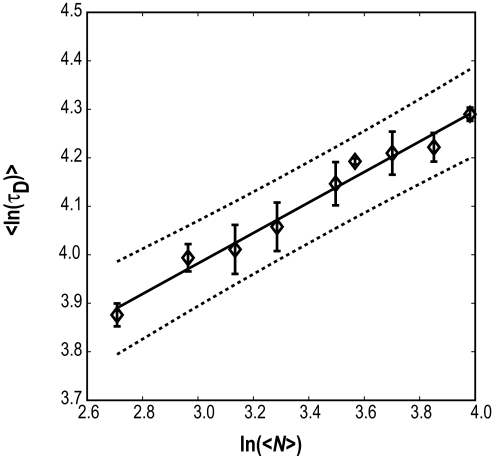
Fig. 2 shows results from linear regression analysis. Here, we plot FCS data for ln(〈τ_D〉) versus ln(〈N〉), the line of best fit to the data based on values for ν and ln(τ_o) obtained from linear least-squares fits to FCS data and the 95% confidence intervals. The parameters for the line of best fit to the data for ln(τ_D) versus ln(N) are a slope ν and intercept ln(τ_o) of 0.32 ± 0.02 and 3.04 ± 0.08, respectively. Goodness of fit is assessed by the observation that all points lie within the 95% confidence interval. The norm of the residuals from the line of best fit is 0.02.

Fig. 2.

Plot of ln〈τ_D〉 as a function of ln(〈N〉). The solid line is the line of best fit to FCS data shown as open diamonds, and the dotted lines represent the 95% confidence intervals. Error bars are standard errors in our estimate for the mean value of ln〈τ_D〉, which is obtained from Monte Carlo bootstrap analysis (see Methods).

Based on the value obtained for ν, we conclude that in aqueous solvents individual polyglutamine molecules behave like chains in a poor solvent. The implication is that these systems prefer collapsed, roughly spherical geometries in aqueous environments. Both CD and NMR data suggest that polyglutamine in PBS is intrinsically disordered (12–15). Taken together with these data and results from molecular dynamics simulations (19), the value of ν ≈ 0.33 is consistent with the interpretation that, in water, polyglutamine has access to an ensemble of distinct collapsed structures, and no single collapsed structure dominates the equilibrium distribution. The demonstration that monomeric forms of polyglutamine polypeptides (i) form collapsed structures in water and (ii) do not show evidence of abrupt changes in average solution structure as chain lengths cross the pathological threshold region has important implications for both the thermodynamics and kinetics of aggregation.

Discussion

General Implications of FCS Results.

The conclusion that aqueous environments are polymeric poor solvents for polyglutamine is striking because it is generally assumed that scaling of sizes with chain length follow theoretical predictions only if chains are sufficiently long (N > 100) (20). The implication of our result is that even relatively short polyglutamine peptides are akin to generic, flexible, linear polymers.

Our result for the value of ν contradicts expectations based on hydrophobicity scales (27–30). According to these scales, glutamine, which is a polar amino acid, is hydrophilic. If we were to follow these hydrophobicity scales, the prediction would be that polyglutamine prefers relatively extended conformations (5, 12) because polar tracts are unlikely to favor collapsed structures in water. Accordingly, one might expect the value for ν to be either 0.5 or 0.59. The former would be based on the expectation that intrachain interactions exactly counterbalance chain–solvent interactions, and the latter would suggest that chain–solvent interactions are preferred to chain–chain interactions. Our results clearly show that both of these expectations are incorrect.

Although the free energy of hydration for primary and secondary amides is highly favorable (31), we find that even short polyglutamine chains (about N = 15) prefer collapsed structures that minimize interactions with aqueous solvents. This may be explained as being the result of a “tug-of-war” between the self-association versus solvation of polar components within the chain (32). For polyglutamine in water, self-association is favored.

FCS Results Are Consistent with the Phase Behavior of Polyglutamine.

In a poor solvent, polymers either form collapsed globules or intermolecular aggregates (20, 21). The former occurs in dilute solutions, and the latter are realized as chain concentration is increased. This two-phase behavior is available only to polymers in poor as opposed to good or theta solvents (20). Therefore, the observation that water acts as a poor solvent for polyglutamine is not surprising given its tendency to aggregate in aqueous solvents (12, 33).

Perutz et al. (34) proposed that phase separation and aggregation of polyglutamine may be driven by the special hydrogen bonding characteristics of the glutamine side chain. Conversely, Dobson and coworkers (4, 35–37) have argued that the ability to form ordered aggregates is a generic attribute of polypeptide chains. If water is a poor solvent for polar polyglutamine, it must be a poor solvent for generic polypeptides. If so, the driving force for aggregation for all polypeptides may be attributed to commonalities in the balance of chain–chain and chain–solvent interactions in water. Clearly, we have much to learn about the details of polypeptide hydration and how these details influence coil-globule transitions (38–40) and phase behaviors of polypeptides, especially for sequences that are deficient in residues that are deemed to be hydrophobic (40–42).

Reconciling FCS Results with CD and NMR Data.

The value of ν = 0.32 ± 0.02 obtained from analysis of our FCS data is similar to the value for ν calculated by Dima and Thirumalai (43) for a collection of 403 folded, globular, monomeric proteins. They showed that for these systems, R_g, the radius of gyration, scales with chain length as N^0.33. In light of these observations and expectations from polymer theories, we interpret our FCS results to mean that polyglutamine prefers collapsed structures in aqueous solvents. As noted earlier, CD and NMR data suggest that there is marked heterogeneity in local conformational preferences for monomeric polyglutamine. Are the FCS and CD/NMR results compatible with each other? Results from computational studies on conformational equilibria of monomeric polyglutamine peptides in water are consistent with both sets of observations (19). Monomeric polyglutamine is shown to prefer a wide range of collapsed structures. Additionally, the ensemble is characterized by an absence of marked preference for distinct secondary structures (19). For a homopolymer such as polyglutamine, it is unlikely that there will be a strong preference for a unique collapsed conformation, because there is no unique way to partition glutamine residues in the chain between the interior and the surface of a globule (44, 45). Consequently, sterically allowed conformations that are consistent with the requirement of being compact are likely to be of equivalent stability.

Implications for Nucleation of Aggregation.

The behavior of monomeric polyglutamine has direct relevance for aggregation in poor solvents because the boundaries between the soluble and insoluble phases are of importance in dilute or semidilute solutions. Theories that take into account both the structural preferences of individual chains in poor solvents and the driving forces for aggregation have identified two important characteristics for the mechanism of aggregation (46–49). First, anisotropic expansion of the chain from the globular state is required to promote intermolecular associations (49). Second, the number of molecules in the critical nucleus for aggregation could be as small as one (a single chain or a portion of a single chain) (49), a proposal consistent with the observations of Hurshman et al. (50).

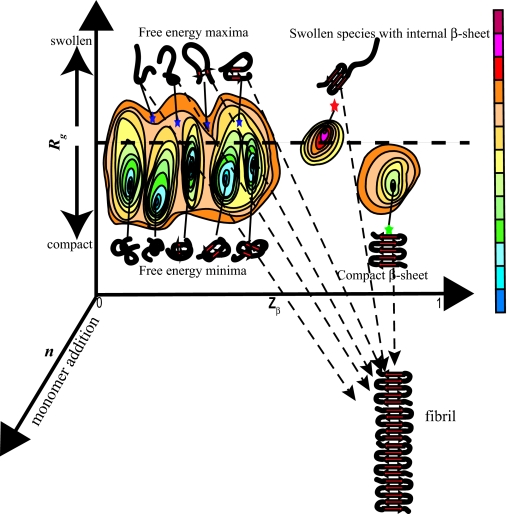
We speculate about the mechanism of nucleation for polyglutamine aggregation. This speculation is based on theoretical predictions (19, 46–49) and the assumption that forces that drive intermolecular association are similar, if not identical, to the forces that drive chain collapse. By definition, the critical nucleus ensemble is the species of highest free energy along an appropriate reaction coordinate (51). If R_g is one of the reaction coordinates, then in a poor solvent collapsed structures correspond to free energy minima, whereas partially or fully extended conformations are free energy maxima because of the increased interface with the surrounding solvent. Minima are metastable species, whereas maxima are unstable. Fig. 3 shows a schematic free energy surface, G(R_g, Z_β), for a single polyglutamine chain. The two reaction coordinates are R_g and Z_β, and they monitor chain size and the overall β-strand content within a chain. These reaction coordinates were chosen because our FCS result places constraints on the size and shape of individual molecules in solution and increased β content is expected as polyglutamine becomes incorporated into a growing aggregate. We stipulate that for a β-strand, Z_β ≈ 1 and Z_β ≈ 0 if none of the backbone (φ, ψ)-angles assume β-strand values. For both free energy minima and maxima the first derivatives are zero, i.e.,

Conversely,

is positive for free energy minima and negative for maxima. Based on the schematic shown in Fig. 3 for the free energy surface, there are three distinct models for how a single chain can act as a critical nucleus for aggregation. Models for larger nucleus sizes are possible, but they are not discussed here.

Fig. 3.

Schematic of the free energy surface G(R_g, Z_β) for a single polyglutamine chain. The radius of gyration (R_g) and overall β-content (Z_β) are the two reaction coordinates. The horizontal dashed line is meant to denote the distinction between collapsed and extended structures. The third reaction coordinate, n, denotes monomer addition. If a single chain acts as the critical nucleus, then monomer addition is a downhill process and conformational changes within the monomer are either rate-limiting or thermodynamically unfavorable. Accordingly, the dominant free energy minima are shown as being compact with very few internal β-sheet contacts. The blue stars denote free energy maxima, which are putative nuclei for model 1. The red star shows the critical nucleus for model 2. This is a free energy maximum on account of being partially swollen and is different from other partially swollen conformations because of the extent of internal β-sheet formation. Finally, the compact β-sheet, which is the model proposed by Chen et al. (16) is shown as a green star. In the color bar, as intramolecular free energies increase, the colors change from blue to red. The dashed arrows from the different putative nuclei to the fibril are meant to depict the proposal that if the critical nucleus is a single chain, monomer addition is downhill in free energy.

Model 1: Heterogeneous Nucleation.

For intrinsically disordered polyglutamine in a poor solvent, transitions between distinct free energy minima of equivalent stability, which should occur via spontaneous fluctuations, will require passage through free energy maxima. At a free energy maximum, the chain has two options for overcoming the instability associated with sampling partial or fully extended conformations. The free energy can be lowered either through intermolecular association or chain collapse. In this scenario, irrespective of conformation, intermolecular associations are possible between extended or semiextended species. On account of conformational heterogeneity, we refer to this model as the heterogeneous nucleation model for aggregation (52). The increased rate of aggregation with chain length may be attributed to the increased nucleation potential associated with partial or fully extended conformations.

Model 2: Homogeneous Nucleation.

It is possible that only one or a small number of free energy maxima characterized by a critical number of internal β-sheet contacts are competent nuclei for ordered aggregation of polyglutamine (53). In this scenario, nucleation is rate-limiting because of the height of the barrier between a single free energy maximum and the disordered free energy minima. Accordingly, increase in the overall rate of aggregation with chain length may be attributed to a decrease in the free energy barrier with chain length.

Model 3: Thermodynamic Nucleus Model for Homogeneous Nucleation.

The nucleus, in addition to possessing a critical number of internal β-sheet contacts, is defined as a metastable species (free energy minimum) rather than an unstable species. In a poor solvent, the nucleus is metastable if it is compact. According to this model (17), the stability of the nucleus is the main determinant of the chain-length dependence of aggregation.

Whereas the instability associated with partial or fully extended species provides a driving force for aggregation in models 1 and 2, the driving force in model 3 is likely to derive from the need to satisfy uncompensated edges in a compact β-sheet (54). Models 1–3 focus on ways for a single chain to act as a critical nucleus for aggregation. Monomer addition, which can lead to both elongation and conformational rearrangement of the nucleus, is viewed as a thermodynamically downhill process. The extent of conformational rearrangement would be large if the β-content within the nucleus is low as proposed in model 1 and small for the ordered nucleus proposed in model 3. Also, if the nucleus is as depicted in models 1 and 2, there will be a finite likelihood of populating off-pathway oligomers and disordered aggregates.

The main distinction between the proposals in models 2 and 3 can be inferred by drawing an analogy to two-state proteins (55, 56). In these systems, there are two metastable states, namely, folded and unfolded states, separated by a single barrier, i.e., the transition-state ensemble, which acts as the nucleus for folding (51, 56). Accordingly, the nucleus in model 2 is viewed as being analogous to the transition-state ensemble, whereas the nucleus in model 3 is analogous to the folded state, albeit a folded state that is thermodynamically unfavorable (18).

Implications for Toxicity Mechanisms.

Our hypothesis is that toxicity is linked to the mechanism of polyglutamine aggregation (12). An alternative hypothesis is that monomeric polyglutamine with repeat lengths above the pathological threshold populate a distinct conformation that possesses a toxic activity such as the ability to undergo deleterious associations with other macromolecules. The main evidence to support this hypothesis comes from the existence of antibodies that appear to bind preferentially to expanded forms of polyglutamine (57). However, this preferential binding can be explained on the basis of the “linear lattice” effect according to which expanded polyglutamine molecules present an increased number of binding sites when compared with “normal” length polyglutamine (58). We raise this issue because we find that τ_D increases monotonically with chain length as shown in Fig. 1 and interpret this as a lack of evidence for dramatic changes in solution structure as N crosses the pathological threshold of 35 aa. Furthermore, two separate linear regression analyses, one using data for N > 35 and the other using data for N > 35 yield similar values for ν, i.e., the differences are not statistically significant.

Summary.

Using FCS we have quantified the scaling of hydrodynamic size as a function of chain length for monomeric polyglutamine and demonstrated that water acts a poor solvent for polyglutamine. Attractions between chain residues are preferred to interactions with the surrounding solvent. Therefore, chains either collapse to form globular structures or, as concentration increases, they form intermolecular aggregates (20, 21). Our observation that water is a poor solvent for monomeric polyglutamine implies that there is a generic driving force for polyglutamine aggregation. Additionally, if monomeric polyglutamine does not show a clear preference for a specific globular conformation (a proposal supported by CD and NMR data and results from molecular dynamics simulations), at equilibrium a heterogeneous ensemble of globular conformations is preferred. This preference for conformational heterogeneity, i.e., disorder, provides an additional driving force for folding via aggregation.

Although structural and thermodynamic studies place necessary constraints on models for nucleation of aggregation, they cannot be used to adjudicate between different mechanisms. It is important to reiterate that a range of nucleation mechanisms are possible, especially if one views aggregation as being analogous to polymer aggregation/crystallization. Evidence of different mechanisms can be inferred from the presence of on- or off-pathway intermediates (59–61), the absence of intermediates under certain conditions (12), variations in morphologies with solution conditions (62), and the fact that nucleus size can depend on chain concentration (63, 64). The dominant mechanism will depend crucially on solution conditions, and it is important to uncover the family of possible mechanisms rather than focusing on any one mechanism.

Further developments in FCS technologies are relevant for mechanistic studies of aggregation-prone systems (65) because they will require only small (10–50 nM) concentrations of labeled species. Application of improved FCS methods for analysis of kinetic data at low peptide concentrations, as opposed to supersaturating conditions, might provide us with the ability to choose between different proposals for nucleation.

Methods

Preparation of Peptide Samples.

All peptides were purchased in crude form from Yale University's Keck Biotechnology Center (New Haven, CT). The peptides were synthesized by using solid-phase synthesis according to the general design Gly-(Gln)_〈N〉-Cys*-Lys₂. The C-terminal lysine residues were included to increase peptide solubility, and a cysteine residue was incorporated to label the peptides with fluorophores. The crude peptides were disaggregated (12, 66) and purified by using RP-HPLC on a preparative C₃ reverse-phase column (Agilent, Palo Alta, CA) to yield peptides of average length 〈N〉 = 15, 20, 24, 27, 33, 36, 40, 47, and 53. Identities of the peptides were confirmed by using electrospray mass spectrometric analysis. Peptide synthesis yields a narrow distribution of chain lengths around the desired value and purification further narrows this distribution. Nevertheless, purified peptides are mixtures of repeat lengths and 〈N〉 is therefore a weighted average of these mixtures. The asymmetric horizontal error bars in Fig. 1 are not true standard deviations. Instead they are meant to denote the range of chain lengths present in each peptide sample.

Upon purification, each peptide sequence was chemically modified via a through-cysteine covalent attachment of the fluorescent dye, AlexaFluor-488-C₅-maleimide (Molecular Probes, Portland, OR). Freshly disaggregated peptides were reacted overnight with four-fold excess dye at room temperature in 20 mM Hepes buffer [(N-(2-hydroxy ethyl)piperazine–N-(2-ethanesulfonic acid)], pH 8.0 with 10 mM Tris-(2-carboxyethyl)phosphine and 5 mM EDTA. After the labeling reaction, the reaction mixture was lyophilized and subjected to disaggregation (12, 66). All unreacted dye was removed by using a size exclusion column with a cutoff of 1,400 Da (Pierce, Rockford, IL). The unreacted peptide molecules were removed and the desired product was further purified by using RP-HPLC (C₃ chromatography column; Agilent). The identities of labeled peptides were confirmed by using electrospray mass spectrometry. Purified, labeled, and properly disaggregated peptides were dissolved in a pH 3.0 trifluoroacetic acid–water mixture. Aliquots of 50-μl vials of 1 μM concentrations were made, immediately flash-frozen in liquid nitrogen, and stored at −80°C.

Before carrying out the FCS measurements, peptide samples were thawed at room temperature. Each sample was diluted to a concentration of 50 nM in Dulbecco's PBS at pH 7.4 (8.0 g NaCl, 0.2 g KCl, 1.15 g Na₂PO₄, 0.2 g KH₂PO₄, dissolved in pure H₂O, 25°C). Four hundred microliters of this solution was placed in a single well of an eight-chamber Nunc/Lab-Tek (Rochester, NY) 1.0 Borosilicate Coverglass System. One of the wells always contained a 20-nM solution of free Alexa488-maleimide for reference purposes.

FCS.

All measurements were performed on a Confocor II LSM system (Carl Zeiss-Evotec, Jena, Germany) with a ×40 water-immersion objective. Data for fluorescence intensity autocorrelation functions were analyzed with Zeiss Confocor II FCS software. The samples were excited at 488 nm with an argon laser, and emissions were collected in the 505– to 550-nm range. In all experiments, the laser power was allowed to stabilize for at least 30 min before beginning data collection. This was done to minimize any nonlinearity during startups, which were monitored by keeping track of photon counts from the free dye. Once the photon counts from the free dye stabilized, the counts from each sample were monitored to account for nonspecific adsorption of the peptide to the chamber walls. Typically, photon counts reached a steady state at peptide concentrations of 10 nM, and this was the peptide concentration used in all FCS measurements.

For a given peptide sample in a well, an independent measurement refers to a single 25 × 25 scan, which corresponds to the collection of FCS data 25 times where the duration for each data collection run was 25 s. Each scan yielded a distinct estimate for the diffusion time wherein the autocorrelation curves from all 25 experiments were averaged and the resultant curve was fit by using the model shown in Eq. 1. We carried out eight different 25 × 25 scans and obtained eight independent estimates of τ_D for each of the nine peptide samples.

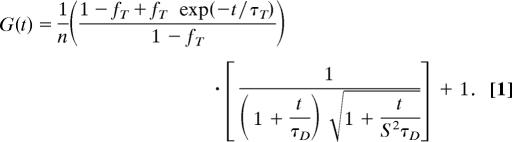In Eq. 1, n is the average number of fluorescent molecules in the beam volume, f_T is the fraction of the triplet state formed per dye molecule, τ_T is the decay constant of the triplet, S is a structure factor that describes the shape of the beam volume, and τ_D is the translational diffusion time. S is a fixed parameter for an independent experiment, i.e., for a 25 × 25 scan. All other parameters in Eq. 1 were estimated by using a Levenberg-Marquardt nonlinear least-squares fit of the model to observed data. The parameters f_T and τ_T are determined primarily by the photo-physics of the fluorescent dye. As a result, the fitting procedure is deemed to be robust if f_T and τ_T are essentially invariant with chain length.

We are confident that for all chain lengths the diffusing species is monomeric polyglutamine, rather than a distribution of monomers and small oligomers. This assertion is based on four criteria. First, the concentrations used are well below the estimated critical concentrations for aggregation (14). Second, MALDI-TOF mass spectrometry analysis of labeled peptide samples at concentrations higher than those used in the FCS experiments do not show evidence for species other than the monomeric form. Third, if we assume the presence of a second diffusing component, the diffusion times we obtain for this component are considerably smaller than that of the free dye. Fourth, the brightness per molecule in all our measurements is similar to that of the free dye. If labeled molecules formed dimers, then they would appear twice as bright if dimers were the dominant species or brightness fluctuations would be considerably larger than what we observe and there would be statistically significant outliers from the line of best fit shown in Fig. 2, but this is not the case.

Data Analysis.

Data collection yielded eight independent estimates of τ_D for each of the nine peptide samples. The goals for data analysis were 3-fold: first, to compute the correlation coefficient between ln(τ_D) and ln(N); second, to estimate values for the parameters ln(τ_o) and ν using the method of least squares; and third, to assess the goodness of the line of best fit obtained with linear regression analysis.

We used a global analysis based on Monte Carlo bootstrap methods (67) to analyze the data for scaling of 〈τ_D〉 as a function of 〈N〉. Each Monte Carlo trial proceeded as follows: A measured value of τ_D was drawn at random for each of the nine chain lengths, which leads to the generation of a random data set. Linear regression analysis was carried out on the data set to estimate ln(τ_o), ν, the residuals from the line of best fit, estimates for standard deviations in prediction errors, and the correlation coefficient between ln(τ_D) and ln(N). The procedure of randomly drawing measured data points to create a data set for linear regression analysis was repeated 5 × 10⁵ times. The results from multiple, independent linear regression analyses were used to compute averages and standard deviations for τ_D as shown in Figs. 1 and 2 and to assess error bounds on our estimates for ln(τ_o) and ν.

The hydrodynamic radius R_h is directly proportional to the translational diffusion time τ_D, and we calculated R_h from the measured values for τ_D by using the following prescription. The radial (ω₁) and axial (ω₂) dimensions of the laser beam were identical for each FCS experiment. The former was quantified by measuring the diffusion of the free Alexa dye by using the formula ${\omega }_1=\sqrt{4D\langle {\tau }_D\rangle }$. The diffusion constant for the Alexa dye (D = 2.24 × 10⁻¹⁰ ms⁻²) is known and allowed us to compute the value for ω₁. For each peptide sample, we used the known value for ω₁ (which is fixed) and the measured value of 〈τ_D〉 and first calculated the diffusion coefficient D (as shown above) and then used this value to determine 〈R_h〉 by using the Stokes-Einstein relationship, namely,

Here, k = 1.38 × 10⁻²³ JK⁻¹, T = 294.5 K, and η is the viscosity of water, which is 9.67 × 10⁻³ poise at 21.5°C (68). In using this prescription for computing R_h, we implicitly assume the “nondraining” limit, i.e., we are stipulating that there is minimal solvent penetration. This assumption must be regarded with extreme caution and therefore, while the estimated values of R_h are shown in Fig. 1, we use only the directly measured quantity namely, τ_D, to assess solvent quality.

Abbreviation

FCS

fluorescence correlation spectroscopy