Resolving the nanoscale adhesion of individual gecko spatulae by atomic force microscopy

Abstract

Animals that cling to walls and walk on ceilings owe this ability to micrometre and nanoscale attachment elements. The highest adhesion forces are encountered in geckoes, which have developed intricate hierarchical structures consisting of toes (millimetre dimensions), lamella (400–600 μm size), setae (micrometre dimensions) and spatulae (∼200 nm size). Adhesion forces of setae on different substrates have previously been measured by a micro-electromechanical system technique. Here we report the first successful experiments in which the force–displacement curves were determined for individual spatulae by atomic force microscopy. The adhesion force for these smallest elements of the gecko's attachment system is reproducibly found to be about 10 nN. This method sheds new light on the nanomechanisms of attachment and will help in the rational design of artificial attachment systems.

1. Introduction

Understanding the mechanisms of biological adhesion is an essential prerequisite for the bioinspired design of dry adhesive systems. The gecko, in particular, whose attachment system (Ruibal & Ernst 1965; Russel 1975) is the most elaborate in nature so far discovered (Autumn & Peattie 2002; Irschick et al. 1996), is of great scientific interest. The ventral side of its toes bears so-called lamellae, with arrays of 3–5 μm thick setae, which in turn are subdivided at their tips into 100–1000 spatulae of 200 nm dimensions (figure 1a–e). So far several measurements at varying hierarchical levels, corresponding to adhesive forces between micronewtons and newtons, have been reported for the gecko (Autumn et al. 2000; Hiller 1968; Irschick et al. 1996). Recently, the adhesion force of a single seta has been measured using a micro-electromechanical system (Autumn et al. 2000). The spatula level has, however, remained inaccessible so far. For the first time it has become possible to determine the adhesion force of single spatulae by applying advanced methods of specimen preparation and force measurement.

Figure 1.

Hierarchical organization of the gecko attachment system: (a) longitudinal section of the gecko toe with three lamellae (lm) covered with setae (st) on the ventral side (scale bar, 200 μm); (b) setae (scale bar, 10 μm); (c,d) setae branching into spatulae (sp; scale bar, 2 μm); (e) spatulae (scale bar, 300 nm; a–d SEM images; e TEM image); (f) single seta with four single spatulae attached to the AFM cantilever (SEM image; 0.5 kV accelerating voltage); (g) experimental procedure: first, the spatula was brought into contact with a defined compressive preload perpendicular to the surface. Then the specimen was sheared over a distance of 7 μm while maintaining the preload. Finally, the force–distance curve was measured during retraction, from which the adhesion force was extracted.

2. Materials and methods

(a) Preparation of individual spatulae

We cut off a foot of a non-moulting gecko (Gekko gecko) just after dying and froze it immediately at −20 °C. The frozen foot was then dipped into liquid nitrogen, and the setae were sheared with a needle tip. With the aid of a binocular microscope, one dry, isolated seta was then glued to the end of a commercially available contact mode cantilever for an atomic force microscope (AFM; MikroMasch, Tallinn, Estonia). We used UV curing glue (Henkel Loctite Deutschland GmbH, München, Germany) to allow time for the correct alignment of the seta, which had to be perpendicular to the cantilever to ensure correct force measurements (figure 1f). When the seta was perfectly positioned, we immediately performed the curing with a UV lamp (wavelength: 366 nm, exposure time: 10 min). The specimen was then processed in a focused ion beam microscope (FIB; 200×P, FEI Company, OR, USA). Working with low currents and starting at the glue dot we moved along the stalk of the seta cutting off one spatula after another at each emerging branch connection. Imaging of the spatulae was avoided in order to prevent radiation damage by the Ga⁺ ions. We also verified in the FIB that the glue did not creep up the stalk of the seta, which could have changed the mechanical properties of the specimen. Finally, we obtained a seta with less than five spatulae at the end of the cantilever, which was then installed in the AFM.

(b) Adhesion measurement for individual spatulae

To measure the pull-off force we calibrated the contact silicon cantilever CSC12/Cr–Au/50 using the well established thermal noise method (Butt & Jaschke 1995; Hutter & Bechhoefer 1993) just before the gluing procedure. The force resolution of the AFM (JPK Instruments AG NanoWizard, Berlin, Germany) amounts to a few piconewtons. As described in the literature (Autumn et al. 2000; Stork 1980), a minimum compressive preload was necessary to maximize the pull-off force of a single seta. A preload of 90 nN seemed to assure an ideal contact formation at the spatular level, while increasing the preload beyond this value did not lead to higher adhesion forces. The contact formation was achieved by automatically approaching the cantilever towards the glass while simultaneously measuring the compressive force. In order to mimic the gecko's toe uncurling motion, an indispensable shearing movement parallel to the substrate surface preceded each adhesion measurement. After a successful approach we controlled the piezoelectric actuator of the AFM by means of a Java script developed by the AFM manufacturer. This made it possible to shear the spatula parallel to the surface in any direction. The direction of shear was defined by the alignment of the spatula relative to the cantilever beam, which was known from the manipulation in the FIB. After shearing the cantilever was vertically withdrawn, while simultaneously measuring the forces (1024 points per cycle). A closed loop scanner assured accurate force measurements during retraction. The detachment force was defined as the minimum of the compressive force–distance curve equivalent to the maximum tensile force a spatula could exert perpendicularly to the surface immediately before detachment. In this way, measurements for two different setae were made in air (temperature=25 °C, relative humidity=35%). Ten force–distance curves were determined at 13 different locations of the glass cover slip (peak to peak roughness <10 nm) for each seta, resulting in 260 data points. By this overall procedure (figure 1g) we achieved a high consistency in our results.

3. Results and discussion

For a seta with four spatulae, we observed three typical force–distance curves (types 1, 2 and 3), as shown in figure 2a. Frequently, type 1 was encountered, which displays a maximum pull-off force of ∼10 nN. Type 2 exhibits almost exactly twice this value. Finally, in type 3 (which occurred in about 5% of the measurements) two pull-off force maxima are seen. From these force–distance curves, we infer the following sequence of events: in type 1, exactly one spatula was in contact with the substrate before detachment; whereas in type 2, two spatulae detached simultaneously. Type 3, the most interesting case, can be explained by assuming that two of the four spatulae were initially in contact; and that on retraction, one of the spatulae detached first at a force of ∼8 nN, whereas the second spatula exhibited the usual pull-off force (∼10 nN). The reason for this difference may be a load shedding process caused by variability in spatula length.

Figure 2.

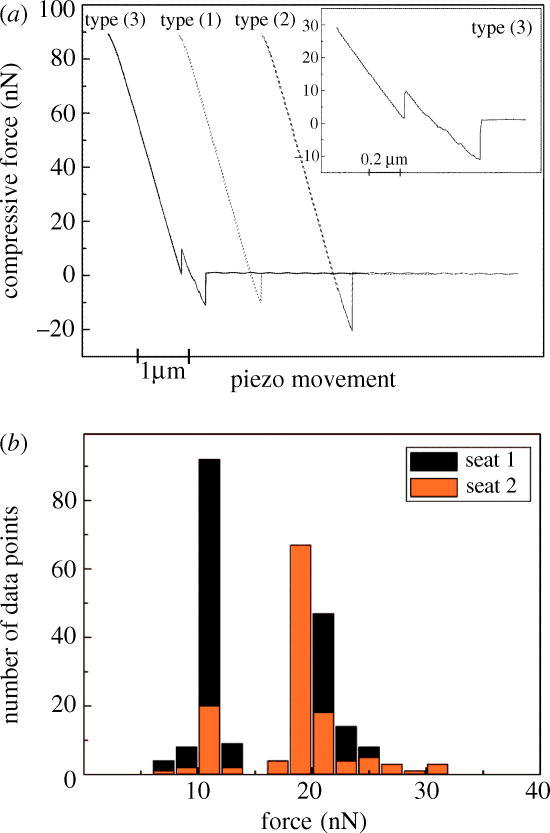
(a) Typically observed force–distance curves (during the retraction phase) for a seta with an array of four spatulae at its tip. Three different types of curve were observed: type 1, a pull-off force of approximately 10 nN suggesting contact of only one spatula; type 2, pull-off force of roughly 20 nN, corresponding to joint detachment of two spatulae; type 3, two pull-off force maxima, suggesting sequential detachment of two spatulae. The inset renders this curve in more detail. All curves (except inset) are the result of two measurements, which superimpose exactly in these plots. (b) Frequency histogram of all 260 measurements showing two strong peaks at 10.8±1.0 nN and 20.4±1.9 nN. A weak peak is seen at ∼30 nN. The peaks are attributed to the detachment of one, two (and three) spatulae (e) from the glass substrate.

Figure 2b presents a histogram of the measured adhesion forces. It clearly shows two peaks, which can be attributed to the discrete number of spatulae adhering to the substrate. The first peak, which occurred in 43.5% of our experiments, lies at a mean value of 10.8 nN (with a standard deviation of 1.0 nN); it is assumed to correspond to single-spatula detachment. In 53.8% of cases the second peak at 20.4±1.9 nN appeared, and is ascribed to two-spatula detachment. A weak third peak can be identified at ∼30 nN, which may be the result of three spatulae detaching simultaneously. As higher pull-off forces were not measured, the case of four spatulae in contact does not seem to have occurred in the experiments.

The measured adhesion force of ∼10 nN per spatula is in agreement with theoretical estimates and earlier results. Since Hertz (Hertz 1882) several groups (Chaudhury et al. 1996; Derjaguin et al. 1975; Greenwood 1997; Maugis 1999; Persson 2003; Tabor 1977) have significantly advanced the field of contact mechanics. We use the model by Johnson, Kendall and Roberts (Johnson et al. 1971) for the adhesive contact of a sphere with a semi-infinite half space to obtain a rough estimate for the work of adhesion γ. If we approximate the tip of the spatula by a sphere of radius R=100 nm and set the pull-off force F=10 nN, we obtain:

$$\gamma =\frac{2F}{3\text{p}R}\approx 21\text{mJ}{\text{m}}^{-2}.$$ (1)

A similar estimate results from Kendall's considerations (Kendall 1975), which describe the force required to peel a thin band with width w (assumption w=200 nm) from a rigid substrate in perpendicular direction:

$$\gamma \approx \frac{F}{w}\approx 50\text{mJ}{\text{m}}^{-2}.$$ (2)

Both calculated values lie well in the range expected for adhesion by intermolecular forces (10–100 mJ m⁻²; Israelachvili 1992). In addition, our results are in agreement with the earlier measurements by Autumn et al. (2000). Dividing their setal adhesion forces, which range from 1 to 20 μN, by the number of spatulae per seta (100–1000), leads to an expected force value of the magnitude found in our experiments. While these estimates show that van der Waals forces can account for the measured adhesion, we cannot unambiguously exclude contributions from capillary forces. The method described here is currently employed to separate their contribution. The adhesion force of a whole gecko foot (with about 10⁹ spatulae) can be estimated as 10 N. Considering a typical body weight of 50–100 g, this would result in a ‘safety factor’ of not less than 10. This large value supports the contention that only a fraction of the spatulae are in contact with the substrate at a given moment.

Finally, we note that technological contact systems may profit from a better understanding of gecko adhesion. Recent modelling has shown that the adhesive force of a fibrillar system can be increased by splitting up the contact into progressively smaller fibres (Arzt et al. 2002, 2003; Autumn et al. 2002). This effect has also been theoretically studied as a function of contact shape (Gao & Yao 2004; Spolenak et al. 2005b), with the result that at the nanoscale the shape loses importance. The question remains whether the adhesion forces could be further increased for fibres considerably finer than gecko spatulae. The interplay between fibre radius, fibre aspect ratio, material and shape to find an optimal solution has been described in a recent paper (Spolenak et al. 2005a). One finds that while contact mechanics imposes limits on contact refinement, there seems to remain scope for improving the contact strength over that of the gecko. First prototypes exhibit promising adhesive properties that partly substantiate the effect of contact splitting (Geim et al. 2003; Peressadko & Gorb 2004).