High dispersal in a frog species suggests that it is vulnerable to habitat fragmentation

Abstract

Global losses of amphibian populations are a major conservation concern and their causes have generated substantial debate. Habitat fragmentation is considered one important cause of amphibian decline. However, if fragmentation is to be invoked as a mechanism of amphibian decline, it must first be established that dispersal is prevalent among contiguous amphibian populations using formal movement estimators. In contrast, if dispersal is naturally low in amphibians, fragmentation can be disregarded as a cause of amphibian declines and conservation efforts can be focused elsewhere. We examined dispersal rates in Columbia spotted frogs (Rana luteiventris) using capture–recapture analysis of over 10 000 frogs in combination with genetic analysis of microsatellite loci in replicate basins. We found that frogs had exceptionally high juvenile dispersal rates (up to 62% annually) over long distances (>5 km), large elevation gains (>750 m) and steep inclines (36° incline over 2 km) that were corroborated by genetic data showing high gene flow. These findings show that dispersal is an important life-history feature of some amphibians and suggest that habitat fragmentation is a serious threat to amphibian persistence.

1. Introduction

Dispersal among populations is expected to increase population persistence through the ‘rescue effect’ whereby immigrants reduce local extinction rates (Brown & Kodric-Brown 1977). Immigrants may reduce extinction rates directly by reproducing in the populations to which they disperse, and indirectly by boosting genetic diversity, which can reduce negative inbreeding effects on reproductive and survival rates (Tallmon et al. 2004). Because rescue effects may be important for the persistence of populations naturally connected by dispersal, the isolation of populations with high dispersal rates through habitat fragmentation is expected to increase extinction rates. On the other hand, if dispersal rates are low and populations are naturally isolated, then fragmentation is unlikely to isolate populations further and fragmentation will not increase extinction rates.

Despite recognition of the importance of dispersal in population dynamics, few studies have attempted to quantify dispersal in amphibians (Trenham et al. 2001; Lowe 2003). Amphibians are thought to have low dispersal rates (Blaustein et al. 1994), although this may not apply to all species (Alford & Richards 1999; Marsh & Trenham 2001). Advances in capture–recapture analysis and highly variable molecular genetic markers greatly improve the potential to understand dispersal patterns. In particular, multistate capture–recapture analysis allows statistically rigorous estimation of current movement rates among populations (Nichols & Kendall 1995). Moreover, microsatellite loci are sufficiently variable to uncover patterns of gene flow over small geographical scales in order to infer historic dispersal. In this study, we used capture–recapture analysis in combination with microsatellite analysis to investigate dispersal in the Columbia spotted frog (Rana luteiventris), a pond frog distributed throughout the northwestern United States, western Canada and southeastern Alaska.

2. Materials and methods

(a) Capture–recapture analysis

We uniquely marked and recaptured juvenile and adult Rana luteiventris from 21 ponds in two replicate basins, Keeler Creek (9 ponds) and Marten Creek (12 ponds), in northwestern Montana, USA (figure 1a). Ponds were separated by a maximum straight-line distance of approximately 7 km in each of these basins, which are sixth code hydrologic units (Seaber et al. 1984). Most of the ponds used by R. luteiventris in Keeler Creek and Marten Creek are beaver ponds adjacent to the creeks and connected to them by small inlet and outlet streams. Frogs were caught using dip-nets during capture sessions of approximately three weeks in July and August of each year for four consecutive years starting in 2000. We made a total of 15 008 captures of 10 443 uniquely marked frogs during these 4 years.

Figure 1.

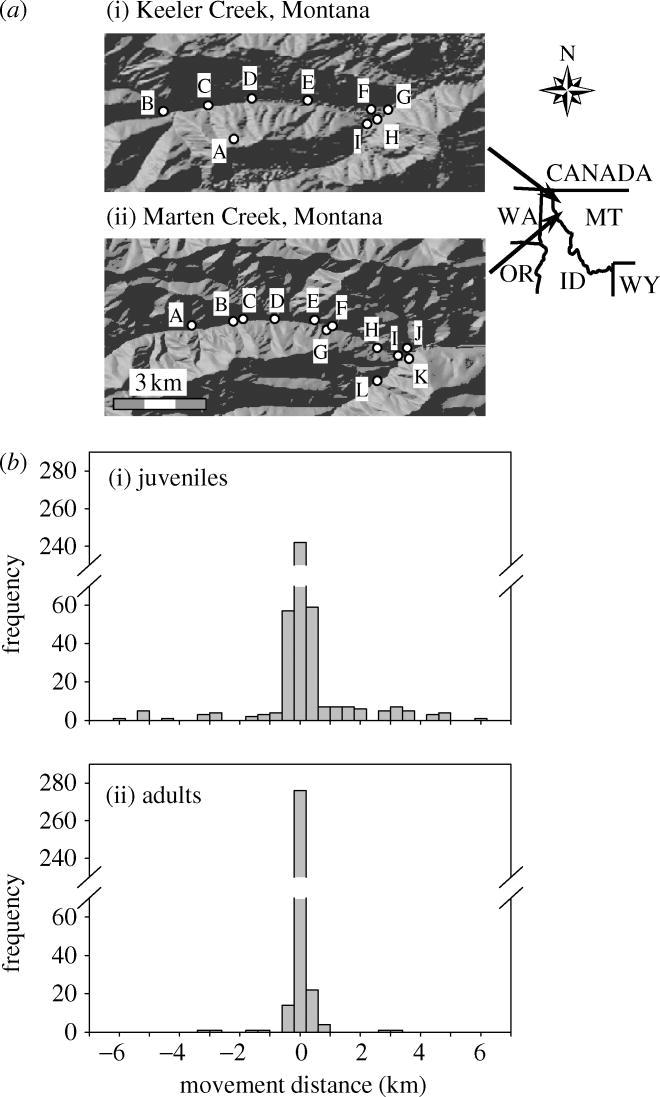
(a) Location of Columbia spotted frog breeding ponds in (i) Keeler and (ii) Marten Creeks, Montana, sampled for capture–recapture and genetic analyses. (b) Movement distributions of (i) juvenile and (ii) adult Columbia spotted frogs from Keeler and Marten Creeks, Montana. Negative values represent downstream movements and positive values upstream movements.

We marked frogs by clipping a unique combination of 3–7 toes using an alphanumeric coding system (Waichman 1992; Donnelly et al. 1994). Thumbs were not cut because they are used by males for clasping females during breeding. We tested whether there was an effect of toe-clipping on return rate using logistic regression with the number of toes clipped and the year first marked as independent variables (Parris & McCarthy 2001). The regression coefficient for the number of toes clipped was not significant for Keeler Creek (b=−0.075, n=2563, p=0.407), but was significant for Marten Creek (b=−0.206, n=7879, p<0.001). The regression coefficient of −0.206 in Marten Creek is equivalent to a reduction in return rate of 0.009–0.019 for each additional toe removed after three toes.

Movement distributions were compared among stages, sexes and basins using Kolmogorov–Smirnov tests (Sokal & Rohlf 1981). Upstream or downstream bias in movement was examined by testing whether movement distributions were significantly skewed (Zar 1984). Site-specific capture histories were then used to estimate annual stage-specific movement probabilities between the lower and upper group of ponds in each basin using multistate capture–recapture analysis. Basins were divided into lower and upper groups of ponds at the elevational midpoint between the lowest and highest pond in each basin. In Keeler Creek, the upper group was pond A and the lower group comprised ponds B–I (figure 1a(i)). In Marten Creek, the upper group included ponds A–D and ponds E–L were considered the lower group (figure 1a(ii)).

We analysed capture–recapture models with stage-, annual- and site-specific variation in movement, survival and capture probabilities in the program Mark (White & Burnham 1999). A step-down modelling approach (Lebreton et al. 1992) was used to reduce sources of variation in survival and capture probabilities and then test hypotheses about variation in movement probabilities. Sixty-four models were analysed to examine variation in survival and capture probabilities, and 16 were used to analyse variation in movement probabilities in each basin. Akaike's information criterion adjusted for sample size (AICc) was used to identify the best models in terms of a trade-off between parsimony and fit to the data. Because no generally agreed upon method exists for independently testing the fit of multistate models, we followed the recommendation of Cooch & White (2001) to increase the variance inflation factor $(\hat{c})$ from one to assess confidence in the best model. Increasing $\hat{c}$ favoured models with fewer parameters, as expected, but did not qualitatively change our finding that juvenile dispersal rates are high in both Keeler and Marten Creeks. (The best-supported capture–recapture models are found in tables 1 and 2 in Electronic Appendix A.)

(b) Microsatellite analysis

We also analysed genetic variation in five ponds from Keeler Creek (ponds A, D, F, H and I) and six ponds from Marten Creek (ponds B, C, E, G, H and K) at six microsatellite loci to estimate gene flow (figure 1a). These ponds were chosen because they supported the largest numbers of breeding adults. We genotyped a total of 312 adult frogs (mean=28 frogs per pond) sampled during spring breeding seasons. Primer sequences, DNA extraction methods, microsatellite DNA amplification conditions and Hardy–Weinberg proportion and gametic disequilibrium analyses are found in Funk et al. (2005). F_st averaged over loci was estimated using Fstat v. 1.2 (Goudet 1995). The five ponds sampled in Keeler Creek are equivalent to ponds 1–5, and the six ponds sampled in Marten Creek are equivalent to ponds 7–12 in Funk et al. (2005), respectively.

3. Results

Marked Columbia spotted frogs showed high dispersal rates over long distances in both basins. Juveniles moved significantly more than adults (p<0.001; figure 1b). Twenty-five per cent of recaptured juveniles moved 200 m (n=108) or further, 14% moved 1000 m (n=60) or further, 9% moved 2000 m (n=39) or further, and 2% moved 5000 m (n=7) or further. In contrast, only 4% of adults moved 200 m (n=13) or further, 2% moved 1000 m (n=6) or further, and 1% moved 2000 m (n=4) or further. The maximum distance moved was 5750 m, the maximum elevation gain was 770 m and the greatest incline traversed was 36° (700 m elevation gain over 1930 m horizontal distance), all by juveniles (figure 2).

Figure 2.

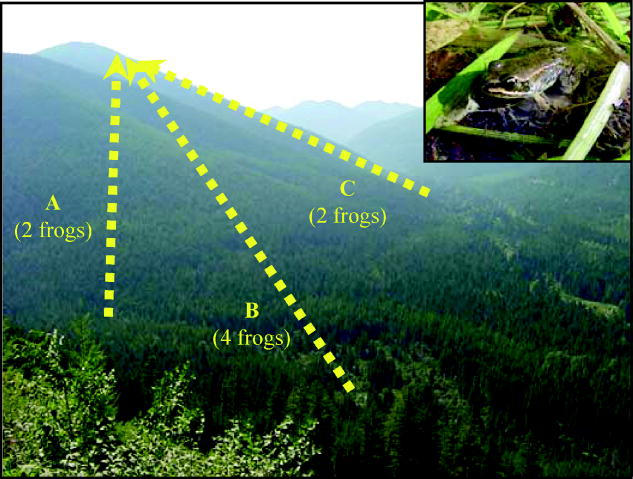
Movements of juvenile Columbia spotted frogs from low elevation ponds to a high elevation lake in Keeler Creek, Montana. The inset shows a juvenile Columbia spotted frog (approximately 25 mm in total length). Vector A represents an elevation gain of 770 m over a horizontal distance of 4240 m (18° mean incline); vector B an elevation gain of 760 m over 4620 m (16° incline); and vector C an elevation gain of 700 m over 1930 m (36° incline). The numbers of frogs observed moving from each low elevation pond to the high elevation lake are shown in parentheses.

Annual juvenile movement probabilities between the lower and upper groups of ponds were exceptionally high in some years. In Keeler Creek, juvenile movement probabilities were 0.29±0.12 (s.e), 0.00±0.00 and 0.49±0.19 in 2000, 2001 and 2002, respectively. In Marten Creek, juvenile movement probabilities were 0.12±0.11, 0.09±0.04 and 0.02±0.01 from the lower to the upper group of ponds and 0.62±0.31, 0.03±0.04 and 0.26±0.16 from the upper to the lower group in 2000, 2001 and 2002, respectively. Annual adult movement probabilities between the lower and upper groups of ponds approximated to zero for all years in both basins. (Movement, survival and capture probability estimates are found in tables 3 and 4 in Electronic Appendix A.)

Ninety-five per cent of frogs (21 out of 22) that were marked, recorded in a new location in a subsequent year and then caught again in another year remained in the site to which they immigrated. This indicates that almost all movement represents permanent dispersal rather than temporary migration. Moreover, annual juvenile survival rates were fairly high in both basins (mean=0.33), suggesting that juveniles often survive long enough to reproduce in the sites to which they immigrate. We found no difference in movement distributions between basins (p=0.59 for juveniles and p=0.29 for adults) or sexes (p=1.00), nor any bias towards upstream or downstream movement (0.10<p<0.20).

F_st was low in Keeler Creek (0.064±0.011) and in Marten Creek (0.016±0.002), as expected if historical dispersal rates and gene flow are high. This degree of subdivision is expected if there are on average 2.5 and 10.5 dispersers (genetic ‘migrants’) entering each population during each generation in Keeler and Marten Creeks, respectively, assuming an island model of migration corrected for a finite number of populations (Wright 1969; Slatkin 1995). Moreover, the island model estimate of the number of dispersers is probably biased low for Keeler Creek because of decreasing gene flow with increasing geographical distance in this basin (p=0.01). Distance does not predict gene flow in Marten Creek (p=0.21).

4. Discussion

Our study shows that current and historical rates of dispersal are exceptionally high in Rana luteiventris. Other studies have also shown high dispersal rates in some amphibians (Alford & Richards 1999; Marsh & Trenham 2001), but this is the first study, to our knowledge, to quantify amphibian dispersal using formal capture–recapture analysis in replicate basins and to confirm that current dispersal patterns are representative of historic patterns with genetic analysis. Moreover, this is the first study, to our knowledge, to document high dispersal rates between low and high elevation populations of amphibians, suggesting that populations in these different habitats are connected demographically. The negative relationship between return rate and the number of toes clipped in Marten Creek indicates that capture, survival, and/or movement probabilities are negatively affected by toe-clipping in this basin, and we are currently investigating the effects of toe-clipping on each of these parameters in more detail. The general agreement between the capture–recapture and microsatellite data, however, suggests that any effects of toe-clipping on movement rates are subtle.

High dispersal rates in R. luteiventris and other amphibians suggest that dispersal plays an important role in the population dynamics of some amphibians and that isolation of these populations through habitat fragmentation may increase extinction rates. Dispersal of amphibians can be impeded by roads, urbanization and clear-cutting of forests (Hitchings & Beebee 1997; Johnston & Frid 2002) and several studies indicate that dispersal is important for amphibian population persistence. For example, extinction probability is correlated with population isolation in pool frogs (Sjögren 1991) and the dispersal of stream salamanders from downstream to upstream sections increases population growth rates of upstream sections (Lowe 2003). The maintenance of habitat connectivity should therefore be a high priority for amphibian conservation. It seems likely that other amphibian species also have high dispersal rates, but this can only be verified by studies designed to quantify dispersal over large distances. We feel that capture–recapture and genetic analyses should be applied more widely for estimating amphibian movement rates to determine whether high dispersal rates are more common in amphibians than was previously recognized.