Abstract
Conformational changes in oat phytochrome A (phy) in solution after photoexcitation of the red-absorbing form (Pr) were studied in time-domain by the pulsed laser-induced transient grating technique. It was found that the diffusion coefficient (D) of far-red-absorbing form (Pfr) of large phy (1.3 × 10−11 m2 s−1) is markedly reduced compared with that of Pr (5.8 × 10−11 m2 s−1). This large reduction indicates that the conformation of Pfr is significantly changed from that of Pr, so that the intermolecular interaction with water molecules increases. This change completes within 1 ms after the photoexcitation. On the other hand, D of Pr of intact phy (4.1 × 10−11 m2 s−1) first decreases upon photoexcitation to 0.89 × 10−11 m2 s−1 within 1 ms and then gradually increases with a time constant of 100 ms to the value of Pfr, 1.7 × 10−11 m2 s−1. This slower phase suggests that the conformation of the N-terminal region changes with 100 ms to decrease the intermolecular interaction with water after a global change in the large phy region. The increase of D was interpreted in terms of α-helix formation in the Pfr form from the random coil structure in the Pr form.
INTRODUCTION
Phytochrome (phy) is a light sensor protein that controls a variety of light-driven adaptations of green plants including seed germination and flowering (1–3). Phy exists in one of the two stable photochromic forms; one absorbing preferentially in the red region of the visible spectrum with an absorption maximum at λmax = 666 nm (Pr), and the other absorbing in the far-red with λmax = 730 nm (Pfr). Phy consists of the N-terminal domain including the amino-terminal extension sequence (∼6 kDa), the photosensory domain containing chromophore (∼64 kDa), and the C-terminal domain that contains two Per-Arnt-Sim related domains and one histidine kinase-related domain (4). Although intact phy regulates the photoresponse in plants, large phy lacking the N-terminal extension sequence is biologically inactive (5). Recently, by using a C-terminal-truncated phyB sample fused to the nuclear localization signal domain, it was shown that the C-terminal part is not directly involved in phy signal transduction (6). These facts suggest that the conformation of the N-terminal domain is physiologically important. Revealing the photoinduced conformational change upon excitation has been a target of extensive researches in chemistry, biophysics, and photobiology of phy.
The ternary and quaternary structures have been studied by the quasi-elastic light scattering (7), electron micrography (8–10), size exclusion column chromatography (11), circular dichroism (CD) (12–14), and small angle x-ray scattering (SAXS) techniques (15,16). CD spectra of Pr and Pfr states showed that the α-helix content of these states is nearly identical for large phy (12), but it increased by ∼5% upon the transformation from Pr to Pfr for intact phy (13). Recently, a SAXS measurement combined with a simulation method revealed a global structural change upon the Pr→Pfr transformation (16). Besides these steady-state measurements, the dynamics of the photoresponse should be essential to understand the reaction. By monitoring the absorption changes upon photoexcitation of Pr, for example, several intermediates have been detected during the Pr→Pfr phototransformation process, and several reaction schemes have been proposed (17–19). Although such information is valuable, we should always be careful with the fact that absorption changes reflect a conformational change only around the chromophore. Most of the conformational changes in the N-terminal or C-terminal regions should be spectrally silent and they are very difficult to be detected spectroscopically. One of the unique techniques is the time-resolved CD method. Indeed, the time-dependence of the CD intensity, which reflects the content of the secondary structure, was observed upon the photoexcitation of Pr (20,21).
Another useful physical property reflecting the conformation of a protein is the diffusion coefficient (D), which is a physical quantity indicating the speed of the diffusion. According to the Stokes-Einstein relationship, under a given environment (temperature and viscosity), D of a molecule reflects the molecular size (22,23). More importantly, however, not only the size, but also the intermolecular interaction, affects the magnitude of D. If the friction between the diffusing solute and the solvent molecules increases, D should decrease. Therefore, measurements of D in time domain would be a powerful technique to study the time development of the intermolecular interaction, which is spectrally silent. For example, it has been recently revealed that formation or unfolding of α-helices change the diffusion of a protein significantly (24,25). Hence, if D can be detected in time domain, it provides us with the information on the dynamics of protein conformational changes. Although D has been considered to be a static physical property for a long time, the pulsed laser-induced transient grating (TG) method was recently proven to be a powerful technique to monitor the time-dependence of D. (24) It enables us to monitor the time-course of the D-changes after photoexcitation (25).
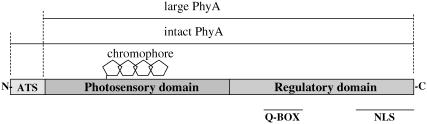
In this work we adopted TG method to study D-changes in large phy and intact phy (Fig. 1) upon photoexcitation of the Pr state. We found that D of the large Pfr-phy species is markedly reduced (by approximately one-quarter) compared with the Pr form. This large reduction was interpreted in terms of significant conformation changes, which increase the intermolecular hydrogen-bonding and changes in the surface roughness. This change completes within 1 ms after the photoexcitation. Very interestingly, we found that D of intact phy first decreases upon the photoexcitation within 1 ms and then gradually increases with a time constant of 100 ms. This result is interpreted in terms of the α-helix formation in the N-terminal domain.
FIGURE 1.
Schematic illustration of the intact phy and large phy we used. Some domains are described: ED, N-terminal extended domain; NLS domain, nuclear localization signal domain; and Q-BOX, quail box domain.
PRINCIPLE
The time-resolved measurement of D was performed by the TG technique. In the TG method, a sample is photoexcited by an optical interference pattern that is created by the interference of two laser beams (24–29). When the photoexcitation induces a chemical reaction to produce a product from a reactant, the spatial modulations of the concentrations of the reactant and product species leads to a modulation of the refractive index (δn) and the absorption sinusoidally. This modulation can be monitored by a diffraction of a continuous wave probe beam (TG signal). In this study, we used a wavelength of the probe light such that the change in absorption can be ignored and only the refractive index change is considered.
There are several origins of the refractive index change. Under a weak excitation condition with a nanosecond excitation pulse, the refractive index change comes mainly from the thermal energy releasing (thermal grating: δnth) and created (or depleted) chemical species by the photoreaction (species grating). Under a weak diffraction condition, the grating intensity (ITG) is proportional to the square of the variation in the refractive index. Since the photoexcitation depletes a reactant and produces a reaction product, the phase of the spatial modulation of the product concentration is shifted 180° from that of the reactant. The grating intensity can then be written as
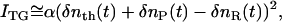 |
(1) |
where α is a constant. The terms of δnR(>0) and δnP(>0) are, respectively, the refractive index changes due to the changes of the reactant and the product concentrations.
When a product (P) is created from a reactant (R) upon photoirradiation within a time-resolution of an experimental system, 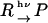 , the temporal development and the spatial distribution of the concentrations of the reactant and the product can be calculated by solving diffusion equations. In this case, one may find that the time development of the species grating signal is expressed by a biexponential function as (25–27)
, the temporal development and the spatial distribution of the concentrations of the reactant and the product can be calculated by solving diffusion equations. In this case, one may find that the time development of the species grating signal is expressed by a biexponential function as (25–27)
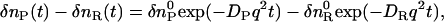 |
(2) |
where q is the grating wavenumber, and DR and DP are the diffusion coefficients of the reactant and the product, respectively. Similarly, the thermal grating signal decays exponentially with a rate constant of Dthq2 (Dth; thermal diffusivity of the solution). Since the grating wavenumber can be varied by varying the crossing angle of the excitation beams (26,27), one can determine these diffusion coefficients from the decay rates of the TG signals measured at different crossing angles.
When a reactant (R) is converted to an intermediate species (I) suddenly upon the photoexcitation and this intermediate is transformed to a product (P) with a rate constant of k, 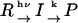 , and the diffusion coefficient of I (DI) and P (DP) are different, the averaged D (apparent D) of the photoinduced species should change with a rate constant of k. The time dependence is expressed by the following equations (24):
, and the diffusion coefficient of I (DI) and P (DP) are different, the averaged D (apparent D) of the photoinduced species should change with a rate constant of k. The time dependence is expressed by the following equations (24):
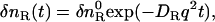 |
(3a) |
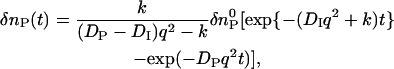 |
(3b) |
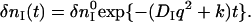 |
(3c) |
Using these equations, one may find that the temporal profile of species grating signal can be expressed by
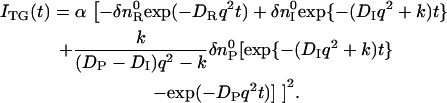 |
(4) |
EXPERIMENTAL
The experimental setup was similar to that reported previously (26–28). Briefly, a laser pulse (wavelength = 610 nm) from a dye laser (HyperDye 300, GSI Lumonics, Watertown, MA) pumped by an excimer laser (Lambda Physik, Ft. Lauderdale, FL; XeCl operation, 308 nm) was used as an excitation beam and a diode laser (835 nm) as a probe beam. The excitation beam was split into two by a beam splitter, and crossed inside a sample cell. The sample is photoexcited by the created interference pattern to induce the refractive index modulation in the sample. A part of the probe beam was diffracted by the modulation (TG signal). The signal was isolated from the excitation laser beam with a glass filter and a pinhole, detected by a photomultiplier tube (model No. R1477, Hamamatsu Photonics, Hamamatsu City, Japan), and recorded by a digital oscilloscope. The spacing of the fringe was measured by the decay rate constant of the thermal grating signal from a calorimetric standard sample (aqueous solution of malachite green), which releases all the photon energy of the excitation as the thermal energy within a time response of our system. All measurements were carried out at room temperature (∼20°C). At the intervals of the TG data collection, the infrared light from a diode laser (wavelength = 785 nm) was irradiated to convert the sample state from Pfr to Pr.
Native (124 kDa) oat phytochrome A (phyA) was obtained from etiolated oat seedlings (Avena sativa, L. cv. Garry) with a specific absorbance ratio (SAR = A660/A280 ratio) of over 1.0, as previously described (30). Large phytochrome lacking the N-terminal 65 amino-acid residues (114-kDa species) was obtained from the tryptic digests of Pr form of 124-kDa oat phyA (use 11). The digestion of phytochrome was performed at a trypsin/phytochrome ratio of 1:200 (w/w) in 10 mM Tris-HCl buffer (pH 8.0) containing 2 mM EDTA for 15 min reaction at 37°C under green safelight. Proteolysis was terminated with the addition of 4 mM PMSF. Then, we used the ammonium sulfate back-extraction procedure to separate the tryptic phytochrome species and the intact phytochrome as follows. The phytochrome digests were pelleted by 20 g/100 ml of ammonium sulfate. Using washing procedures with 100 mM phosphate buffer containing 5 mM EDTA, 5 mM 2-ME, and 2 mM PMSF (pH 7.8), we were able to separate the soluble 114-kDa species and insoluble native oat phyA. At the final step, size-exclusion chromatography on Superose 12 HR 10/30 column in 10 mM Tris-HCl, 150 mM NaCl, 2 mM DTT, and 1 mM EDTA (pH 7.8) at 4°C was performed to purify large phytochrome. The purity of 114-kDa large phytochrome was >95% as judged by Coomassie Brilliant Blue staining after SDS-PAGE. The specific absorption ratio A666 A280 was >1.0.
RESULTS AND DISCUSSION
Dynamics of large phy
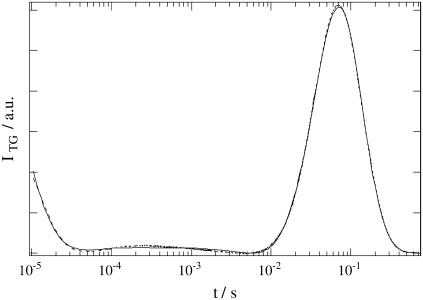
The TG signal of large phy in the Tris buffer solution was measured upon photoexcitation at 610 nm. A typical signal measured at q2 = 5.26 × 1011 m−2 is depicted in Fig. 2. The signal rose quickly with a time response of our system (∼20 ns), decayed, and showed a weak rising component. After this rise, it decayed to the baseline and finally a relatively strong growth-decay component appeared. We found that this signal could be analyzed well with a sum of five exponential functions. For the assignment of these components, we measured the signals under various grating wavenumbers (q2), and found that three rate constants depended on the q2-value, whereas two of them were independent.
FIGURE 2.
Observed TG signal (dashed line) after photoexcitation of large phy in the Tris buffer solution at q2 = 5.3 × 1011 m−2. The best fitted line with Eqs. 1 and 2 (i.e., Eq. 5) is shown by the solid line.
The q2-dependence indicates that this time-dependence represents a diffusion process. By comparing with the thermal grating signal from a calorimetric reference sample (aqueous solution of malachite green), we found that one of the rate constants agreed with Dthq2 under this experimental condition. This fact indicates that this component is the thermal grating component created by the thermal energy due to the nonradiative transition from the excited state. The temporal profile of the TG signal can be expressed by
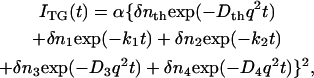 |
(5) |
where ki (i = 1 and 2) represents the q2-independent rate constants (k1 > k2), Di (i = 3 and 4) denotes the diffusion coefficient (D3 > D4).
From the fitting of the signals at various q2, the q2-independent rate constants were determined to be k1 = (40 μs)−1 and k2 = (10 ms)−1. This q2-independent dynamics reflect an intrinsic reaction of phy, not a diffusion process. There are two types of contributions in the species grating signal; the population grating, which is associated with an absorption spectrum change, and the volume grating, which comes from the density change due to a molecular volume change. The faster component with the 40-μs lifetime is close to that reported before by using the beam diffraction method (43.4 μs at 20°C) (31). This signal may originate mainly from the population grating but a possible volume grating contribution cannot be excluded. Indeed, a relatively large energetic relaxation and volume change associated with this process was reported (32).
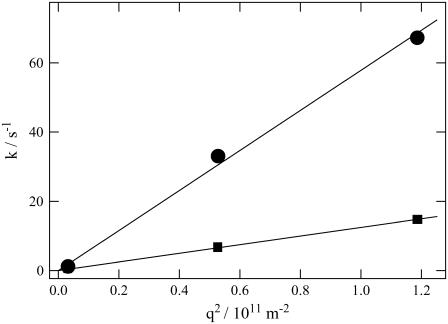
The slower q2-dependent components should represent the molecular diffusion processes. This last rise-decay curve (diffusion peak) was fitted by the last two exponential terms of Eq. 5. From the q2-plot of the rate constants (Fig. 3), D of the rise and decay components were determined to be D3 = (5.8 ± 0.2) × 10−11 m2/s, and D4= (1.3 ± 0.1) × 10−11 m2/s. Furthermore, the preexponential factors were determined to be δn3 <0, δn4> 0, and |δn3| < |δn4|. The signs of the preexponential factors were determined without ambiguity, using a fact that the sign of the thermal grating signal is negative (δnth < 0), and the diffusing species can be assigned from the signs of the preexponential factors and the theoretical equation (Eq. 2). On the basis of the signs, we can easily attribute the δn3 and δn4 terms of Eq. 5 to the δnR and δnP terms of Eq. 2, respectively. Hence, D3 and D4 should respectively correspond to the diffusion coefficients of the reactant ( 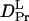 ) and that of the product (
) and that of the product ( 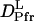 ) for large phy.
) for large phy.
FIGURE 3.
Plot of the rate constants (k) from the diffusion signal against q2 (circles, reactant, Pr; squares, product, Pfr) for large phy. The solid lines are the best fitted line with k = Dq2. The slopes of the fitted lines represent the diffusion coefficients.
It is significant that 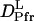 (1.3 × 10−11 m2/s) is drastically smaller than
(1.3 × 10−11 m2/s) is drastically smaller than 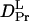 (5.8 × 10−11 m2/s). In general, D is determined by the size and shape of a solute, and varieties of intermolecular interactions. At first, we tried to explain the observed D from the viewpoint of a radius change of the proteins. According to the Stokes-Einstein relationship, D is inversely proportional to the radius of the molecule if the other solution properties (e.g., viscosity or temperature) are identical (22). We examined whether or not the reduction in D can be explained in terms of an increase in molecular radius. There have been attempts to establish the relation between the radius of gyration (Rg) and D. One of the recent successful attempts was reported by Hem and Niemeyer (33). They proposed an empirical equation that can reproduce D (in m2 s−1) of a variety of native proteins from Rg (in Å) and the molecular weight (M in g · mol−1) in a solution of temperature T (in K) and viscosity η (in Pa s),
(5.8 × 10−11 m2/s). In general, D is determined by the size and shape of a solute, and varieties of intermolecular interactions. At first, we tried to explain the observed D from the viewpoint of a radius change of the proteins. According to the Stokes-Einstein relationship, D is inversely proportional to the radius of the molecule if the other solution properties (e.g., viscosity or temperature) are identical (22). We examined whether or not the reduction in D can be explained in terms of an increase in molecular radius. There have been attempts to establish the relation between the radius of gyration (Rg) and D. One of the recent successful attempts was reported by Hem and Niemeyer (33). They proposed an empirical equation that can reproduce D (in m2 s−1) of a variety of native proteins from Rg (in Å) and the molecular weight (M in g · mol−1) in a solution of temperature T (in K) and viscosity η (in Pa s),
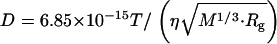 |
(6) |
Using the average value of the reported Rg for each state (5.71 nm for Pr and 6.26 nm for Pfr of Pea large phy) and the molecular weight of the dimer 236 kDa (phy exists as a dimer form) (16,33), one may calculate D of Pr and Pfr to be DPr = 3.4 × 10−11 m2 s−1, and DPfr= 3.2 × 10−11 m2 s−1. The difference in the calculated D between Pr and Pfr is much smaller than that of the experimentally observed value. Therefore, the large reduction in D upon photoexcitation is not due to the change in Rg.
A possible origin for the observed reduction in D may be the change in the protein-protein interaction to produce, e.g., a dimer of the reactant. This possibility was examined by measuring the concentration dependence of the TG signal. If the dimer or aggregates are formed by photoexcitation, the signal shape should be concentration-dependent, which was clearly displayed by other photosensitive proteins (34,35). However, in this phy case, the TG signal was independent of concentration in the range of 10 ∼ 70 μM. Therefore, we exclude the aggregation formation for explaining the D-reduction.
Previously, it was found that the enhanced intermolecular interaction between a protein (or a macromolecule) and water molecules reduced D significantly. For example, it was reported that D of the unfolded form of cytochrome c is nearly half of the native form (24). Similarly, D of poly-glutamic acid with the secondary structure of α-helices decreased upon unfolding of the α-helices (36). These changes were explained as follows. When an α-helix is unfolded, the intramolecular hydrogen bonding of the α-helix is rearranged to the intermolecular one between the protein and water molecules. The intermolecular hydrogen bonding acts as an additional friction for the diffusion to reduce D. Hence, if the α-helix content of Pr decreased upon Pfr formation, it could be a cause of the reduction of D. However, previously reported CD spectra of Pr and Pfr did not show significant differences in the α-helix content (12). Therefore, the change in the extent of the α-helix from Pr to Pfr may not be the cause of the D-change.
Finally, the other possible origin for the reduced D-value is the change in surface corrugation and roughness of proteins. When protein surface expands so that the solvent molecules interact, the protein molecule consequently feels more frictional drag in the solvent. Its dynamic flexibility is more restrained (37). The surface roughness of a protein molecule is related to D. Indeed, the larger the surface roughness, the smaller the diffusion coefficient. In this respect, the global structural changes calculated from the SAXS data showed that the Pfr state structure is more elongated and corrugated (16). Main reason for the corrugation is related to the exposure of the nuclear localization signal domain (6,38,39) and/or the structural change of the Quail box domain (40), both of which are thought to have major importance on the biological function of phy molecule.
Dynamical information on the conformation change in phy is important for studying the reaction mechanism of this transformation. How fast does this change occur after the photoexcitation? It should be noted that the observed signal at various q2 can be reproduced very well by Eq. 5, which indicates that  and
and 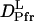 are time-independent within the observed time range; i.e., the D-change from Pr to Pfr has already completed before the diffusion signal appeared, which was ∼1 ms. This fast change in D after the photoexcitation can be further confirmed by the analysis described below.
are time-independent within the observed time range; i.e., the D-change from Pr to Pfr has already completed before the diffusion signal appeared, which was ∼1 ms. This fast change in D after the photoexcitation can be further confirmed by the analysis described below.
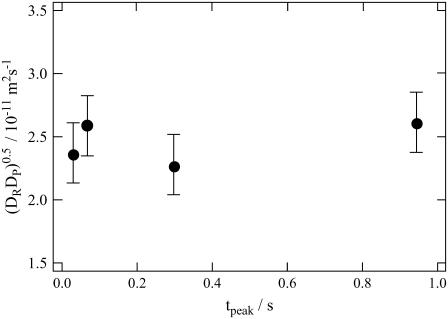
The curvature of a biexponential function at the maximum intensity provides a geometric mean of reactant DR and product DP at this peak time (tpeak) (41),
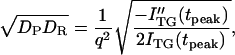 |
(7) |
where ITG(tpeak) is the signal intensity at the peak and ITG″(tpeak) is the second derivative at this time. It should be noted that DP in this equation does not necessarily mean D of the final product, but this D could be a species created from the reactant at this peak time. Hence, this value could be D of an intermediate species, if it exists. The value of (DPDR)1/2 calculated from Eq. 7 is plotted in Fig. 4 against the peak time. The plot shows that mean values are nearly constant during the observation time range indicating that DP is time-independent. Therefore, we conclude that the D-change has already completed before the diffusion signal appeared.
FIGURE 4.
Plot of the geometric means of the diffusion coefficients (DPDR)1/2 calculated from the curvature of the diffusion peak (Eq. 7) versus the peak time (tpeak).
Dynamics of intact phy
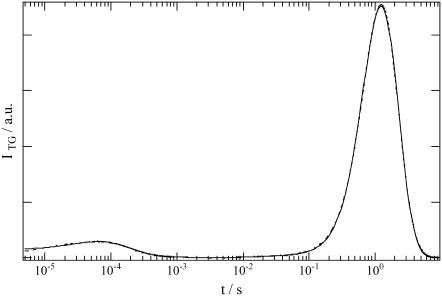
The TG signal of intact phy was similar to that of large phy. The observed signal at q2 = 4.87 × 1011 m−2 is shown in Fig. 5. The signal rose with the time-response of our system, decayed with a rate constant of Dthq2, and showed a weak rising. Finally it exhibited a strong rise-decay component. From the TG signals at various q2, the latest strong rise-decay curve was attributed to the signal representing molecular diffusion. The assignment of the signal component was similar to that of large phy. The rise and decay of the diffusion peak represent the diffusion of Pr and Pfr, respectively. Therefore, the diffusion of Pfr also is slower than that of Pr of the intact phy.
FIGURE 5.
Observed TG signal (dotted line) after photoexcitation of intact phy in the Tris buffer at q2 = 3.0 × 1010 m−2. The best fitted line with Eq. 4 is shown by the solid line.
Although these qualitative features of the signal are similar to those of large phy, we noted several differences. First, the diffusion peak intensity compared with the thermal grating or the species grating intensity of the 40-μs component is much stronger than that of large phy. Second, most interestingly, the diffusion signal cannot be reproduced by Eq. 5. The fact that the diffusion peak cannot be fitted by the biexponential function may be explained in two ways: there may be more than two species involved in the diffusion signal, or apparent D is changing during the observation time range.
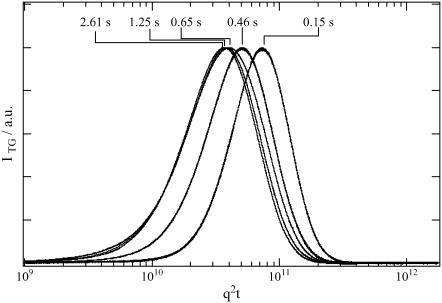
If the profile represents only the diffusion process, the time-dependence should be expressed by a combination of terms of exp(−Dq2t) (e.g., Eq. 2). In this case, if the signals measured at various q2 are plotted against q2t, the signals should be identical. However, Fig. 6 shows that the signals are totally different depending on q2-value. Therefore, the failure of the biexponential function cannot be explained by simply adding more diffusion terms; instead, it indicates that D is time-dependent.
FIGURE 6.
TG signals of intact phy measured at q2 of 4.9 × 1011, 1.1 × 1011, 6.2 × 1010, 3.0 × 1010, and 1.5 × 1010 m−2 (from right to left of the curves). The times of the peak after the photoexcitation are indicated in the figure. The signals are normalized at the peak intensity and plotted against q2t to show the temporal changes of D.
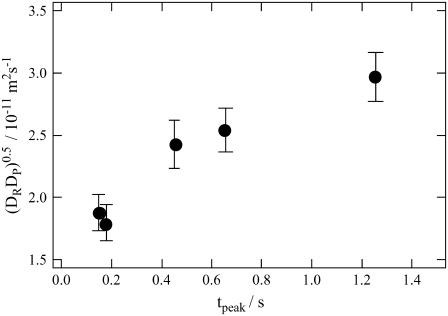
The time-dependent D was further confirmed by the curvature analysis of the diffusion peak (Eq. 7). Fig. 7 depicts the geometric mean of D ((DPDR)1/2) against the peak time. As mentioned above, this DP is D of the photoinduced species existing at this time. Interestingly, the mean value of D gradually increases with time. This feature strongly suggests that D first decreases upon photoexcitation and then gradually increases during the observation time range. This fact indicates that there is an intermediate species having different D-value.
FIGURE 7.
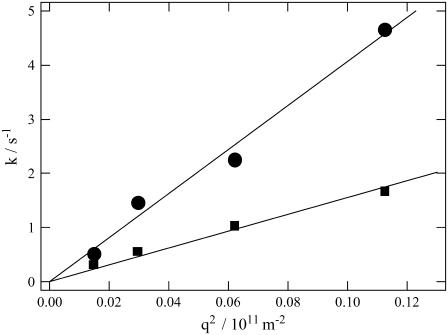
Plot of the rate constants (k) from the diffusion signal against q2 (circles, reactant, Pr; squares, product, Pfr) for intact phy. The solid lines are best fitted lines with k = Dq2. The slopes of the fitted lines represent the diffusion coefficients.
The observed signal should be analyzed based on the time-dependent D model such as Eq. 4. However, since there are many parameters in Eq. 4, the parameters cannot be determined uniquely by the fitting. Hence, we analyzed the signal by the following way. First, it should be noted that the signals plotted against q2t are relatively close to each other for the signals measured at relatively small q2. This fact indicates that D is almost time-independent in a longer time region. From this q2t plot, we first roughly estimated that the time dependence of D is almost negligible after 0.5 s from the photoexcitation. Hence, the diffusion signals after 0.5 s were analyzed by the time-independent equation, i.e., Eq. 3. From the slope of the q2 dependence of the rate constants from the biexponential fitting, D of the reactant (Intact Pr) and the final product (Pfr) are determined to be 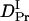 = (4.1 ± 0.2) × 10−11 m2/s, and
= (4.1 ± 0.2) × 10−11 m2/s, and 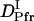 = (1.7 ± 0.1) × 10−11 m2/s (Fig. 7). Since the molecular size of intact phy is larger than that of large phy, this slightly smaller
= (1.7 ± 0.1) × 10−11 m2/s (Fig. 7). Since the molecular size of intact phy is larger than that of large phy, this slightly smaller 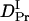 than
than 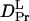 may be reasonable. Interestingly, on the other hand,
may be reasonable. Interestingly, on the other hand, 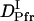 is larger than
is larger than 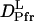 .This difference will be explained later.
.This difference will be explained later.
The time-dependence of D indicates that Pr does not convert to Pfr directly with respect to D, but an intermediate species is involved in the reaction path. If we refer this intermediate species as DI (diffusion detected intermediate), the reaction scheme is 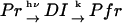 .
.
The peak profile analysis (Fig. 8) indicates that D of the DI intermediate ( 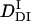 ) is smaller than D of Pfr. Hence, we analyzed the temporal profile of the TG signal based on the two-state model by assuming
) is smaller than D of Pfr. Hence, we analyzed the temporal profile of the TG signal based on the two-state model by assuming 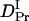 >
> 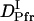 >
> 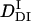 . The signal over a wide time range (10 ms–10 s) can be fitted consistently with this model and two adjustable parameters,
. The signal over a wide time range (10 ms–10 s) can be fitted consistently with this model and two adjustable parameters, 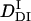 and k. The following parameters were determined:
and k. The following parameters were determined: 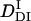 = (0.89 ± 0.09) × 10−11 m2/s, and the rate constant k = 10 ± 3 s−1. This time constant of 100 ms is sufficiently shorter than the time range used for the biexponential fitting to determine
= (0.89 ± 0.09) × 10−11 m2/s, and the rate constant k = 10 ± 3 s−1. This time constant of 100 ms is sufficiently shorter than the time range used for the biexponential fitting to determine 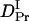 and
and 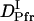 (longer than 0.5 s).
(longer than 0.5 s).
FIGURE 8.
Plot of the geometric means of the diffusion coefficients (DPDR)1/2 calculated from the curvature of the diffusion peak (Eq. 7) versus the peak time (tpeak).
It is interesting to note that the factor of the reduction in D from Pr to Pfr of large phy ( 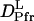 /
/ 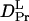 = 22%) is very close to that of intact phy (
= 22%) is very close to that of intact phy ( 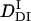 /
/ 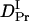 = 22%) (see Fig. 8). Furthermore, the time range, in which the reduction in D occurs for intact phy is faster than 1 ms, which agrees with the result of large phy. These facts suggest that the conformational change that causes the D-reduction is considered to be similar, probably localized in the large phy domain.
= 22%) (see Fig. 8). Furthermore, the time range, in which the reduction in D occurs for intact phy is faster than 1 ms, which agrees with the result of large phy. These facts suggest that the conformational change that causes the D-reduction is considered to be similar, probably localized in the large phy domain.
Previously, Nishida et al. demonstrated that D increases with the folding of the α-helices of cytochrome c (24). The increase in D for the DI→Pfr process suggests that the α-helix is forming during this process. In the case of intact phy, the time-resolved CD analysis showed the secondary structure change (α-helix generation) occurred at N-terminal domain and its time constant was 70∼160 ms. We suggest that the cause of the D-increase ( 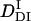 to
to 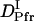 ) with time constant 100 ms is due to the generation of the secondary structure, e.g., α-helices of this protein.
) with time constant 100 ms is due to the generation of the secondary structure, e.g., α-helices of this protein.
Reaction dynamics of phy
The reaction scheme of phy has been investigated mainly by the transient absorption methods and a variety of schemes have been proposed. For example, Zhang et al. analyzed the data based on a sequential model with time constants of 7.4 μs, 89.5 μs, 7.6 ms, 42.4 ms, and >266 ms (18). Eilfeld et al. showed kinetics of 35.7 μs, 2.7 ms, and 50 ms (17). Losi and Braslavsky analyzed the absorption changes by a parallel model showing time constants of (10 μs, 7 ms, 400 ms), and (90 μs, 50 ms, 3000 ms) (19). In our TG signal, we observed 40-μs and 10-ms population grating kinetics at 20°C. Possible other dynamics could be masked by the strong diffusion signal of the TG method. Our unique observations here are the relatively fast conformational change of the large phy domain and 100-ms dynamics of the N-terminal region, both of which are spectrally silent. In particular, our observations such as the relatively fast (< 1 ms) conformational change and intermolecular interaction change in the large phy domain will be useful information for revealing the reaction dynamics of phy.
Previously, D-values of Pr and Pfr of large and intact phy were reported by using the quasi-elastic light scattering method at 14°C at relatively dilute condition (0.2 mg/ml = 1.6 μM) (7). The results showed that D-values of Pr and Pfr for large phy were almost identical (2.7 × 10−11 m2/s). The D-values of the intact phy-Pr and -Pfr species were also similar (1.76 × 10−11 m2/s and 1.82 × 10−11 m2/s). The reason for the discrepancy between the previous light-scattering data and our TG data is not clear at present. However, we may consider that the difference could be due to the different principle of the measurements. In the previous light-scattering experiment, D-values were measured under a steady-state condition with illumination of red or IR light to the sample. If there is a meta-stable intermediate state, phy could equilibrate among various conformational states by the steady-state light illumination. The D-values measured by the quasi-elastic light-scattering method could represent such a mixture state of several species. On the other hand, our TG measurement detects light-induced D change directly. Hence, this is a more straightforward detection method. This contradiction should be examined in future by the quasi-elastic light-scattering measurement with highly controlled intensity and the wavelength of the red/IR light. Comparison of D-values from different methods under well-controlled conditions could reveal more detailed reaction properties of phy.
CONCLUSION
Photoreactions of large and intact oat phytochrome A were investigated from a viewpoint of time-dependent diffusion coefficients. After the photoexcitation of large phy, D decreased quickly within 1 ms from 5.8 × 10−11 m2 s−1 (Pr) to 1.3 × 10−11 m2 s−1 (Pfr). This significant reduction in D was interpreted in terms of the change in the surface roughness of phy. This result indicates that the global conformation change from Pr to Pfr completes within 1 ms after the photoexcitation. The TG signal of intact phy was different from large phy in several points. Most significantly, D of intact phy (4.1 × 10−11 m2 s−1) initially decreased to 0.89 × 10−11 m2 s−1 within 1 ms and gradually increased (1.7 × 10−11 m2 s−1) with a time constant of 100 ms. It is interesting to note that the initial D change is similar to that observed for large phy and the second phase is characteristic of intact phy. Hence the conformational change of the large phy domain in intact phy completes quickly within 1 ms. After this change, the increase in D, which is interpreted in terms of the α-helix formation in the N-terminal region, takes place with the time constant of 100 ms.
Acknowledgments
This work is supported by Grants-in-Aid (Nos.13853002 and 15076204) from the Ministry of Education, Science, Sports and Culture in Japan. The work was also supported in part by the Korea Science and Engineering Foundation/Ministry of Science and Technology to the Environmental Biotechnology National Core Research Center (to J.-I. K. and P.-S.S.; grant No. R15-2003-012-01003-0).
References
- 1.Briggs, W. R., and H. V. Rice. 1972. Phytochrome: chemical and physical properties and mechanism of action. Annu. Rev. Plant Physiol. 23:293–334. [Google Scholar]
- 2.Furuya, M. 1987. Phytochrome and Photoregulation in Plants. Academic Press, New York.
- 3.Sineshchekov, V. A. 1995. Photobiophysics and photobiochemistry of the heterogeneous phytochrome system. Biochim. Biophys. Acta. 1228:125–164. [Google Scholar]
- 4.Song, P.-S. 1988. The molecular topography of phytochrome: chromophore and apoprotein. J. Photochem. Photobiol. B. 2:43–57. [DOI] [PubMed] [Google Scholar]
- 5.Jordan, E. T., J. R. Cherry, J. M. Walker, and R. D. Viestra. 1996. The amino-terminus of phytochrome A contains two distinct functional domains. Plant J. 9:243–257. [DOI] [PubMed] [Google Scholar]
- 6.Matsushita, T., N. Mochizuki, and A. Nagatani. 2003. Dimers of the N-terminal domain of phytochrome B are functional in the nucleus. Nature. 424:571–574. [DOI] [PubMed] [Google Scholar]
- 7.Sarkar, H. K., D. K. Moon, P.-S. Song, T. Chang, and H. Yu. 1984. Tertiary structure of phytochrome probed by quasi-elastic light scattering and rotational relaxation time measurements. Biochemistry. 23:1882–1888. [Google Scholar]
- 8.Jones, A. M., and H. P. Erickson. 1989. Domain structure of 124-kiloDalton phytochrome from Avena sativa visualized by electron micrography. Photochem. Photobiol. 49:479–483. [DOI] [PubMed] [Google Scholar]
- 9.Tokutomi, S., M. Nakasako, J. Sakai, M. Kataoka, K. T. Yamamoto, M. Wada, F. Tokunaga, and M. Furuya. 1989. A model for the dimeric molecular structure of phytochrome based on small-angle x-ray scattering. FEBS Lett. 247:139–142. [Google Scholar]
- 10.Nakasako, M., M. Wada, S. Tokutomi, K. T. Yamamoto, J. Sakai, M. Kataoka, F. Tokunaga, and M. Furuya. 1990. Quaternary structure of pea phytochrome I dimer studied with small-angle x-ray scattering and rotary-shadowing electron microscopy. Photochem. Photobiol. 52:3–12. [Google Scholar]
- 11.Lagarias, J. C., and F. M. Mercurio. 1985. Structure function studies on phytochrome. J. Biol. Chem. 260:2415–2423. [PubMed] [Google Scholar]
- 12.Hunt, R. E., and L. H. Pratt. 1981. Physicochemical difference between the red- and the far-red-absorbing forms of phytochrome. Biochemistry. 20:941–945. [DOI] [PubMed] [Google Scholar]
- 13.Deforce, L., S. Tokutomi, and P.-S. Song. 1994. Phototransformation of pea phytochrome A induces an increase in α-helical folding of the apoprotein: comparison with a Monocot phytochrome A and CD analysis by different methods. Biochemistry. 33:4918–4922. [DOI] [PubMed] [Google Scholar]
- 14.Chai, Y. G., P.-S. Song, M. M. Cordonnier, and L. H. Pratt. 1987. A photoreversible circular dichroism spectral change in oat phytochrome is suppressed by a monoclonal antibody that binds near its N-terminus and by chromophore modification. Biochemistry. 26:4947–4952. [DOI] [PubMed] [Google Scholar]
- 15.Tokutomi, S., M. Kataoka, J. Sakai, M. Nakasako, F. Tokunaga, M. Tasumi, and M. Furuya. 1988. Small-angle x-ray scattering studies on the macromolecular structure of the red-light-absorbing form of 121 kDa pea phytochrome and its 114 kDa chromopeptide. Biochim. Biophys. Acta. 953:297–305. [Google Scholar]
- 16.Nakasako, M., T. Iwata, K. Inoue, and S. Tokutomi. 2005. Light-induced global structural changes in phytochrome A regulating photomorphogenesis in plants. FEBS J. 272:603–612. [DOI] [PubMed] [Google Scholar]
- 17.Eilfeld, P., P. Eilfeld, J. Vogel, and R. Maurer. 1987. Evidence for a sequential pathway from Pr to Pfr of the phototransformation of 124-kDa oat phytochrome. Photochem. Photobiol. 45:825–830. [Google Scholar]
- 18.Zhang, C. F., D. L. Farrens, S. C. Bjorling, P.-S. Song, and D. S. Kliger. 1992. Time-resolved absorption studies of native etiolated oat phytochrome. J. Am. Chem. Soc. 114:4569–4580. [Google Scholar]
- 19.Losi, A., and S. E. Braslavsky. 2003. The time-resolved thermodynamics of the chromophore-protein interactions in biological photosensors as derived from photothermal measurements. Phys. Chem. Chem. Phys. 5:2739–2750. [Google Scholar]
- 20.Chen, E. F., W. Parker, J. W. Lewis, P.-S. Song, and D. S. Kliger. 1993. Time-resolved UV circular dichroism of phytochrome A: folding of the N-terminal region. J. Am. Chem. Soc. 115:9854–9855. [Google Scholar]
- 21.Chen, E. F., V. N. Lapko, P.-S. Song, and D. S. Kliger. 1997. Dynamics of the N-terminal α-helix unfolding in the photoreversion reaction of phytochrome A. Biochemistry. 36:4903–4908. [DOI] [PubMed] [Google Scholar]
- 22.Cussler, E. L., 1984. Diffusion, Mass Transfer in Fluid Systems. Cambridge University Press, Cambridge, MA.
- 23.Tyrrell, H. J. V., and K. R. Harris. 1984. Diffusion in Liquids: A Theoretical and Experimental Study. Butterworth, London, UK.
- 24.Nishida, S., T. Nada, and M. Terazima. 2004. Kinetics of intermolecular interaction during protein folding of reduced cytochrome c. Biophys. J. 87:2663–2675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eitoku, T., Y. Nakasone, D. Matsuoka, S. Tokutomi, and M. Terazima. 2005. Conformational dynamics of phototropin 2 LOV2 domain with the linker upon photoexcitation. J. Am. Chem. Soc. 127:13238–13244. [DOI] [PubMed] [Google Scholar]
- 26.Terazima, M., and N. Hirota. 1993. Translational diffusion of a transient radical studied by the transient grating method, pyrazinyl radical in 2-propanol. J. Chem. Phys. 98:6257–6262. [Google Scholar]
- 27.Terazima, M., K. Okamoto, and N. Hirota. 1995. Translational diffusion of transient radicals created by the photoinduced hydrogen abstraction reaction in solution—anomalous size dependence in the radical diffusion. J. Chem. Phys. 102:2506–2515. [Google Scholar]
- 28.Terazima, M. 2000. Is the translational diffusion of organic radicals different from that of closed-shell molecules? Acc. Chem. Res. 33:687–694. [DOI] [PubMed] [Google Scholar]
- 29.Nada, T., and M. Terazima. 2003. A novel methods for study of protein folding kinetics by monitoring diffusion coefficient in time domain. Biophys. J. 85:1876–1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lapko, V. N., and P.-S. Song. 1995. A simple and improved method of isolation and purification for native oat phytochrome. Photochem. Photobiol. 62:194–198. [DOI] [PubMed] [Google Scholar]
- 31.Lagarias, J. C., and F. M. Mercurio. 1985. Structure function studies on phytochrome. J. Biol. Chem. 260:2415–2423. [PubMed] [Google Scholar]
- 32.Michler, I., and S. E. Braslavsky. 2001. Time-resolved thermodynamic analysis of the oat phytochrome A phototransformation. A photothermal beam deflection study. Photochem. Photobiol. 74:624–635. [DOI] [PubMed] [Google Scholar]
- 33.Hem, L. H., and B. Niemeyer. 2003. A novel correlation for protein diffusion coefficients based on molecular weight and radius of gyration. Biotechnol. Prog. 19:544–548. [DOI] [PubMed] [Google Scholar]
- 34.Hazra, P., K. Inoue, W. Laan, J. Hellingwerf, and M. Terazima. 2006. Tetramer formation kinetics in the signaling state of AppA monitored by the time-resolved diffusion. Biophys. J. 91:654–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nakasone, Y., T. Eitoku, D. Matsuoka, S. Tokutomi, and M. Terazima. 2006. Kinetic measurement of transient dimerization and dissociation reactions of Arabidopsis phototropin 1 LOV2 domain. Biophys. J. 91:645–653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Inoue, K., N. Baden, and M. Terazima. 2005. Diffusion coefficient and the secondary structure of poly-L-glutamic acid in aqueous solution. J. Phys. Chem. B. 109:22623–22628. [DOI] [PubMed] [Google Scholar]
- 37.Choi, J. H., H. Kim, and S. Lee. 1998. Correlation dimension as a measure of surface roughness of protein molecules. J. Chem. Phys. 109:7001–7004. [Google Scholar]
- 38.Kircher, S., L. Kozma-Bognar, L. Kim, E. Adam, K. Harter, E. Schafer, and F. Nagy. 1999. Light quality-dependent nuclear import of the plant photoreceptors phytochrome A and B. Plant Cell. 11:1445–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sakamoto, K., and A. Nagatani. 1996. Nuclear localization activity of phytochrome B. Plant J. 10:859–868. [DOI] [PubMed] [Google Scholar]
- 40.Quail, P. H., M. T. Boylan, B. M. Parks, T. W. Short, Y. Xu, and D. Wagner. 1995. Phytochromes—photosensory perception and signal-transduction. Science. 268:675–680. [DOI] [PubMed] [Google Scholar]
- 41.Spiegel, D. R., A. H. Marshall, N. T. Jukam, H. S. Park, and T. Chang. 1998. Measurement of mass diffusion coefficients using nonexponential forced Rayleigh scattering signals. J. Chem. Phys. 109:267–274. [Google Scholar]