The Persistence Length of DNA Is Reached from the Persistence Length of Its Null Isomer through an Internal Electrostatic Stretching Force

Abstract

To understand better the effect of electrostatics on the rigidity of the DNA double helix, we define DNA*, the null isomer of DNA, as the hypothetical structure that would result from DNA if its phosphate groups were not ionized. For the purposes of theoretical analysis, we model DNA* as identical to ordinary DNA but supplemented by a longitudinal compression force equal in magnitude but oppositely directed to the stretching (tension) force on DNA caused by phosphate-phosphate repulsions. The null isomer DNA* then becomes an elastically buckled form of fully ionized DNA. On this basis, we derive a nonadditive relationship between the persistence length P of DNA and the persistence length P* of its null isomer. From the formula obtained we can predict the value of P* if P is known, and we can predict the ionic strength dependence of P under the assumption that P* does not depend on ionic strength. We predict a value of P* for null DNA drastically lower than the value of P for DNA in its ordinary state of fully ionized phosphates. The predicted dependence of P on salt concentration is log-c over most of the concentration range, with no tendency toward a salt-independent value in the range of validity of the theory. The predictions are consistent with much of the persistence-length data available for DNA. Alternate theories of the Odijk-Skolnik-Fixman type, including one by the author, are considered skeptically on the grounds that the underlying model may not be realistic. Specifically, we doubt the accuracy for real polyelectrolytes of the Odijk-Skolnik-Fixman assumption that the polymer structure is invariant to changes in electrostatic forces.

INTRODUCTION

The persistence length is a useful measure of the degree of structural rigidity of a polymer chain and the energy cost of deforming it (1–4). A continuing stream of persistence-length data for DNA (5–13) reflects the importance attached to an understanding of DNA bendability by proteins (14,15). DNA is among the stiffest of known polymers with a persistence length of ∼50 nm (150 bp) in 0.1 M aqueous NaCl. Despite that, we have calculated a mere 6% neutralization of phosphate groups as enough to reduce to zero the energy penalty of bending DNA to its nucleosomal radius of curvature (16). Further, it is known that neutralization of phosphate charge on one face of DNA causes bending toward the neutralized face (14,17,18). Even asymmetric fluctuations of the distribution of counterions condensed on DNA can generate bending angles of a few degrees (19), while bending away from a protein-shaped region of low dielectric constant maintains well-solvated DNA phosphates (20).

There is some impression that ∼50 nm is the smallest value to which the persistence length can be brought by weakening phosphate electrostatic repulsions. Nonetheless, there are data at salt concentrations >0.1 M indicating values as low as 30 nm (6,9,11). Adding trivalent cobalt hexamine at concentrations short of triggering condensation of the DNA, Pörschke found that the persistence-length drops to 20 nm (21). In conditions of more extensive phosphate-charge neutralization by this trivalent cation, Baumann et al. (13) get 15 nm for the persistence length.

DNA can be deposited as dispersed single molecules on mica surfaces coated with cationic polyamines of various species and molecular weights and then viewed as AFM images. Podestá et al. (22) have carried out a systematic study of the persistence length by this technique. Controls include observation of contour lengths typical of B-form DNA and an expected 56-nm persistence length value in the absence of the polyamine. The persistence lengths are determined as equilibrium values from segments of the DNA chains with contours described accurately as equilibrium wormlike chains. The authors report a DNA persistence length that decreases with increasing concentration of polyamine to values as low as 11 nm, or only 32 basepairs.

The observations just discussed are at variance with theories of the Odijk-Skolnick-Fixman (OSF) type (23–25). These theories calculate an electrostatic contribution to the persistence length that tends rapidly to zero with increasing ionic strength. At 0.1 M NaCl, for example, the maximum value of the OSF electrostatic persistence length (obtained from linear Debye-Hückel theory) is <6 nm. To compare with a measured overall persistence length, the electrostatic contribution is assumed additive onto a contribution of nonelectrostatic origin—which, although unspecified, may, at most, equal 11 nm, as suggested by the data discussed above. The OSF predicted persistence length is thus <17 nm at 0.1 M NaCl, whereas measurements yield values approximately equal to 50 nm. The large quantitative discrepancy between OSF theory and measurements suggests a more fundamental qualitative failing. The OSF model misses the full implications of an important source of electrostatic stiffening, namely, the internal electrostatic tension that must be present in any polyelectrolyte chain.

In this article, we base a theory of the persistence length of a polyelectrolyte on the electrostatic stretching force caused by repulsions among the charged groups on the polymer. We introduced the concept of polyelectrolyte tension in 1989 (17,26,27), and it has recently been utilized independently by Netz in a related but different context (28). A preliminary version of our theory has appeared (26). The arguments here have been sharpened and made more transparent, leading to an explicit formula for the polyelectrolyte persistence length.

We begin by assembling the required theoretical tools. From the theory of polyelectrolytes, we need the calculated electrostatic stretching force, derived here in a form applicable at higher salt concentrations than in our previous work (17,26). In an excursion closely related to the analysis by Netz (28), we find an application of the polyelectrolye tension to the plastic range of DNA structure (defined below). The critical length for buckling of a rod under compression was a seminal contribution of Leonhard Euler to the theory of elasticity (29,30). The buckling persistence length and its relation to the more familiar bending persistence length come from the statistical theory of polymers (4, 31). In connection with these two different kinds of persistence length, we use the notation P for the bending persistence length and the calligraphic symbol 𝒫 for the buckling persistence length. The term “persistence length” will mean the usual persistence length for bending fluctuations, whereas reference to the persistence length for buckling will always be made explicitly.

We then give the derivation of the primary result of this article, a formula that relates the persistence length of a polyelectrolyte to that of its “null isomer,” properly defined. We offer comparison of theory to experiment for the case of DNA, emphasizing the low values of persistence length observed under conditions of extensive neutralization of phosphate charge. We pay critical attention to recent single-molecule measurements of the salt concentration dependence of the persistence length (13), but we review as well the voluminous data for the salt dependence that preceded them (5–12). Finally, we come back to a discussion of OSF theory and its relation to the present one.

POLYELECTROLYTE TENSION AND DNA PLASTIC YIELD

We use our simplest model for a polyion, a linear array of N discrete univalent charged sites, where N is large enough to avoid end effects. This model has been explored in depth (32), and it has been recently reviewed (25,33). A single such polyion with counterions of unsigned valence Z is immersed in a salt solution, and the ions from the salt with charge opposite to the polyion charge also have unsigned valence Z. An example would be DNA with Mg²⁺ counterions immersed in MgCl₂ solution, Z = 2. The electrostatic free energy G_el of this model in the framework of counterion condensation theory is given by the expression

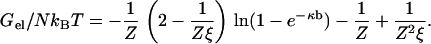(1)

Here, k_BT is the product of the Boltzmann constant and absolute temperature. The array of charge sites on the polyion is characterized by spacing b, assumed uniform. The free energy of interaction of the polyion with solvent in the absence of counterions and salt is determined by a dimensionless polyion charge density ξ = ℓ_B/b, where ℓ_B = q²/Dk_BT is the Bjerrum length for the pure solvent (the distance at which two unit charges ± q, where q is the protonic charge, have unsigned Coulomb energy equal to k_BT if the solvent has dielectric constant D). The salt solution is characterized by Debye length 1/κ, where in electrostatic (cgs) units, κ² = (8π) × 10⁻³N_Aℓ_BI, the ionic strength I having molarity units. A convenient numerical formula for the Debye length in aqueous uni·univalent salt solution of molarity c is 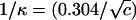nm, or 0.96 nm at 0.1 M aqueous NaCl. Equation 1 is valid above the charge density threshold for counterion condensation, ξ > 1/Z. For our primary application to DNA, ξ is >4.

There is a tension, or stretching force, within the line of charges representing the polyion due to electrostatic repulsions among the charge sites. It may be calculated as the negative derivative of G_el with respect to the length L = Nb of the polyion (for long lengths), holding the number of charge sites N constant. Designating the tension by F_el, we get

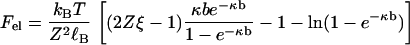(2)

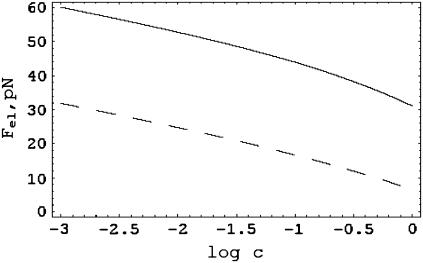
The electrostatic tension has expected properties. It becomes weaker at higher salt concentration and lower polyion charge density, as seen in Fig. 1. From direct inspection of the formula, one may also check that at constant ionic strength, the tension is weaker for counterions of higher valence, which neutralize more of the polyion charge by condensation. Equation 2 goes beyond the corresponding Debye-Hückel formula derived by Netz (28) in that it accounts fully for effects of the condensed layer of counterions, including its internal free energy as well as charge renormalization.

FIGURE 1.

The electrostatic tension in pN as a function of salt molarity with univalent counterions. Solid curve for DNA parameters, ξ = 4.2, b = 0.17 nm; dashed curve for a polyelectrolyte with half the DNA charge density, ξ = 2.1, b = 0.34 nm.

Equation 2 also has an unusual feature. At high salt, κb ≈ 1, the tension changes sign and becomes a stabilizing mutual attraction of the charges. This effect is caused by the entropy of the condensed counterions. There is a detailed discussion in Manning (33), where corroborating evidence from simulations for the existence of the attraction is highlighted. However, for the line charge model with DNA parameters, the crossover occurs at an impractically high salt concentration (over 10 M) and has no impact on the present analysis, at least not for DNA.

An interesting application of Eq. 2 is to the data of Baumann et al. (13) for the salt concentration dependence of the B-DNA → S-DNA, or “overstretch,” transition. The following analysis is closely related to a prior discussion of Netz (28), but the numbers are somewhat different because we have handled counterion condensation more completely by including effects from the internal free energy of the condensed layer. The quantitative difference allows us to extend his conclusions slightly.

When an externally applied stretching force is exerted on a single DNA molecule, the polymer responds with increasing applied force first by stretching out its entropic flexibility at low forces to the full length characteristic of ordinary B-DNA, then resisting further increases of force with almost no further extension. But then at a critical yield value of the applied force, the DNA begins to extend with little further increase of the applied force, ultimately to ∼1.7-times the B-DNA contour length.

The force-extension curve after configurational entropy has been pulled out would be recognized by a mechanical engineer as typical of macroscopic materials; see, for example, Fig. 1 of den Hartog (34). A metal bar pulled by an applied tension at first resists with very little elongation in an elastic response according to Hooke's Law with a strong Young's modulus. Then, at a critical applied tension, the rod becomes plastic and extends easily under relatively little increase of the tension. The B-DNA → S-DNA transition can thus be characterized as a nanoscale example of plastic yielding. The advantage of this phenomenological view, as emphasized by Netz (28), is that some analytical discussion then becomes possible without delving into the unique features of DNA molecular structure.

The value of the applied force at which DNA begins to yield depends significantly on the salt concentration. From Fig. 2 A of Baumann et al. (13) we read that the yield force for λ-DNA is approximately equal to 37 pN at 0.001 M NaCl, to 60 pN at 0.05 M, and to 65 pN at 0.5 M. These data by themselves demonstrate that there must preexist within the DNA an internal salt-dependent tension with magnitude on the scale of tens of pN. The internal tension diminishes with increasing salt concentration, so that, as observed, a larger applied tension must be used to bring about plastic yield.

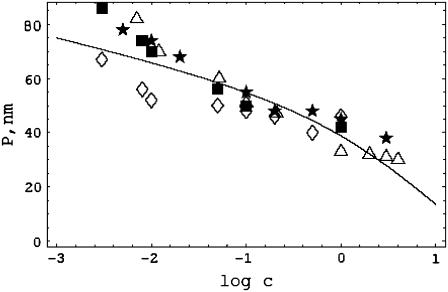
FIGURE 2.

The dependence of persistence length in nm on salt concentration in molarity for DNA. The solid curve is Eq. 25 with DNA structural parameters b = 0.17 nm, ξ = 4.2, R = 1 nm. P* = 7.4 nm then gives P = 55 nm at c = 0.1 M. The data are from Sobel and Harpst (11) (stars); Cairney and Harrington (9) (squares); Rizzo and Schellman (7) (diamonds); and Borochov et al. (6), as corrected for excluded volume by Manning (8) (triangles). For the latter, Post's excluded volume corrected data are nearly the same (10,11).

With Netz (28), we suggest that the electrostatic stretching force F_el of Eq. 2 is the obvious candidate for the tension pre-existing in DNA even in the absence of an externally applied tension. We calculate (see Fig. 1) that F_el equals 60 pN, 47 pN, and 36 pN, respectively, at salt concentrations 0.001 M, 0.05 M, and 0.5 M. If these values are added to the corresponding values measured for the yield force as listed in the previous paragraph for λ-DNA, we get a total tension (internal electrostatic plus applied tensions) equal to 97 pN, 107 pN, and 101 pN, respectively, for the three different salt concentrations. A reasonable interpretation would be that in this range of salt concentrations a total tension of ∼100 pN drives λ-DNA into its plastic phase.

ELASTIC RESILIENCE OF RODLIKE POLYMER SEGMENTS

The model of a polymer in solution as a long elastically rodlike object subject to thermal fluctuations has played a central effect in the development of the statistical theory of polymers (1,2). In this section we review some elements of elastic rod theory (29,30), and then we consider the flexibility bestowed on an otherwise stiff rod by thermal fluctuations.

When a thin cylindrical rod of unperturbed length L is uniformly stretched or contracted along its central axis by the relatively small amount ΔL, the elastic energy ΔU stored in the rod (free energy if the rod is in thermal equilibrium with its environment) is given by Hooke's Law in the form

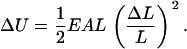(3)

Like any macroscopic energy, ΔU is extensive (proportional to rod length L), and like any linear elastic energy, it is proportional to the square of the deformation strain ΔL/L. The product EA is the Hooke's Law compression/extension stiffness. The coefficient E is Young's modulus and depends on the rod material (the atomic composition and structure of the polymer in this case), while A is the area of the cross section of the rod,

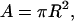(4)

where R is the radius of the rod.

There is also a Hooke's Law for uniform bending deformations of the rod (the central axis of the rod is bent to the arc of a circle, while its length L remains invariant),

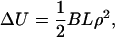(5)

where the measure of the bending strain is the curvature ρ of the axis (reciprocal of its radius of curvature), and the elastic modulus for stiffness against bending is called B.

Since bending involves compression on the inside of the bend and extension on the outside, there is a relation between B and Young's modulus E,

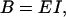(6)

where I is the moment of inertia of the cross section,

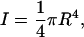(7)

so that the ratio B/EA of the two Hooke's Law moduli depends only on the radius R of the rod,

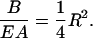(8)

When a small longitudinal compression force is applied to the ends of a rod, the rod merely becomes slightly shorter. But if the force is large enough, the rod responds by buckling radially outwards. Early on in the development of the theory of elasticity, Euler found that buckling of a rod of given length L and elastic bending stiffness B is a critical phenomenon,

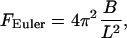(9)

where physically appropriate boundary conditions determine the numerical coefficient 4π² (see below). The meaning of Euler's formula is that an applied compression force F < F_Euler is met by simple longitudinal contraction, but forces ≥F_Euler buckle the rod.

If we solve Eq. 9 for the rod length L, it is the latter that becomes critical:

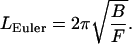(10)

Now the meaning is that for a given compression force F, only rods longer than the Euler length L_Euler will buckle.

We mentioned that the numerical coefficient in Euler's formulas depends on the boundary conditions applicable at the ends of the rod. In our application to polymers, the rod is an internal segment of the polymer, and the compression force originates from abutting segments of the polymer. In stating the formulas, we chose the boundary condition of “clamped ends,” which corresponds to smooth merging of the buckled segment into the polymer structure, avoiding invocation of kinks at the interfaces. (For pictures, see Fig. 19, in (30).)

To this point, we have not discussed the thermal fluctuations that occur in the shape of the rod when it is immersed in a temperature bath. Isolated from temperature, the rod is static. It remains straight with constant length unless acted upon, as in mechanical engineering applications, by applied forces and torques. At any non-zero temperature, however, an elastic rod undergoes a variety of conformational changes. Among them are contraction and extension fluctuations longitudinally along its central axis. We are interested in a uniform fluctuation of its length, and the corresponding thermal force that causes the length change by acting at its ends. The root mean-square (RMS) values of this fluctuating compression/extension force is given by

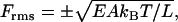(11)

where the plus sign corresponds to an extension force and the negative sign to a compression force. According to this formula, the thermal force transmitted along the length of the rod is greater for short rods of large stiffness modulus EA. This relation was stated but not derived in Manning (31). The derivation is a brief exercise in classical fluctuation theory and is given here in the Appendix. In the following, we make use only of the thermal compression force. Moreover, we have no need of the negative sign, so we drop it.

An attribute of thermally fluctuating rods more familiar in polymer theory is the persistence length P (1, 2). In the context of elasticity theory, it is best defined by

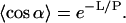(12)

On the left is the thermal average of the cosine of the fluctuating directional correlation of a rod of length L. The angle α is that between the directions at the two ends of the rod. The meaning of the definition is that a rod with persistence length P long in comparison with its physical length L is scarcely bent by thermal fluctuations; the average bending angle is close to zero. But if the persistence length is short relative to L, then the directions of the two ends are uncorrelated; the average bending angle is close to the orthogonal.

Given this definition and its physical meaning, there must be a close correlation between persistence length P and the Hooke's Law bending stiffness B of the rod. The well-known relationship from wormlike chain theory is (1,2)

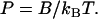(13)

The persistence length is long for a stiff rod (which bends only slightly), but it becomes shorter at higher temperatures when thermally fluctuating bending torques have greater energy.

We have introduced the idea of a persistence length for buckling fluctuations to supplement the more familiar persistence length P in Eqs. 12 and 13 for bending fluctuations (4,31). To understand it clearly requires a slight shift in our thinking. A polymer in solution is conceptualized as a fluctuating chain of rodlike segments, each of which retains elastic resilience in the face of thermal buffeting. There is a fluctuating compression/extension force acting at the ends of each segment and transmitted undiminished throughout the length of the segment. The physical origin of the force is the thermal energy of adjacent segments, and that is why it has the same effect as a force applied at the ends of an elastic rod.

The buckling persistence length 𝒫 of a polymer is defined to be the Euler length corresponding to an RMS compression force acting at the ends of a rodlike segment. In other words, polymer segments shorter than 𝒫 do not buckle in response to a typical (RMS) compression fluctuation, but segments longer than 𝒫 do.

Equation 10 indicates that the Euler length depends on the bending stiffness B, and according to Eq. 13, the bending persistence length P is also correlated with B. It is therefore reasonable to expect that the bending persistence length P and the buckling persistence length 𝒫 are related (31). Here we give an efficient derivation of the relationship.

The quantitative expression of the definition of 𝒫 is Eq. 10 with 𝒫 substituted for L_Euler and F_rms for F,

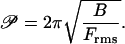(14)

The RMS compression force in this definition acts on a rod of length equal to the buckling persistence length. The formula for F_rms given by Eq. 11 is therefore substituted into Eq. 14 with rod length L replaced by buckling persistence length 𝒫:

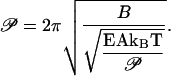(15)

Equation 15 may be solved for 𝒫 by squaring twice, whereupon

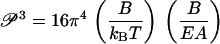(16)

The factoring in Eq. 16 is intentional, since each factor in parentheses is familiar, the first from Eq. 13 (it equals the bending persistence length), and the second from Eq. 8 (it depends only on the rod radius R). Immediately, then, we obtain the desired relation between buckling and bending persistence lengths,

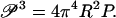(17)

As a numerical example, we calculate the buckling persistence length of DNA. With the accepted value 55 nm (160 bp) for the bending persistence length P at 0.1 M aqueous NaCl at room temperature, and with radius R = 1 nm for the double helix, 𝒫 comes out as equal to 28 nm, or 82 bp, approximately half as long as P. Thus, persistence length segments of DNA (P segments), being longer than the buckling persistence length, undergo significant buckling distortions as well as bending motions in solution.

THE CONNECTION BETWEEN THE PERSISTENCE LENGTHS OF A POLYELECTROLYE AND ITS NULL ISOMER

In the previous two sections we have gathered all the theoretical tools needed to derive the central result of this article, a formula that relates the persistence length of an electrostatically charged polyelectrolyte to the persistence length of its discharged null isomer. We recall our definition of “null isomer” (26). It is the hypothetical structure that would be adopted by the polyelectrolye chain if the electrostatic charge on it were set to zero (without affecting the solvation of the polymer). In this way we eliminate the effect on polyelectrolye structure of electrostatic repulsions among its ionized groups.

In the case of a weak polyacid such as polyacrylic acid, the null isomer has all carboxylate groups fully protonated. It can be approached in the laboratory by dissolving polyacrylic acid in water. Due to the weakly acidic nature of the monomers, a few of the carboxylate groups ionize, so the resulting polymer chain bears some electrostatic charge and is only an approximation to the null isomer, which remains, strictly speaking, hypothetical. For a strong acid like DNA, whose phosphate groups are not protonated in ordinary solution conditions, the hypothetical null isomer has been approached in the laboratory by other means to be discussed.

To proceed with our derivation of a formula with quantitative predictive capability, we require a mathematical yet physically compelling model for the null isomer. Our aim is to abolish the polyelectrolyte stretching force with the device of the null isomer. We therefore take as our model for the null isomer the fully charged polyelectrolyte supplemented by an applied compression force F* that is equal but oppositely directed to the electrostatic tension F_el that exists internally in the charged polyelectrolyte. The internal tension is given by Eq. 2. Therefore F* equals the right-hand side of Eq. 2 (a positive quantity):

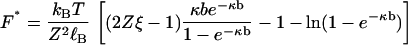(18)

For DNA, the null isomer, which we call DNA*, is represented by ordinary DNA with its fully ionized phosphate groups and bending modulus B but exposed to an externally applied compression force F* that exactly balances the tension in the DNA caused by phosphate-phosphate repulsions. As an elastic rod subject to compression, there is thus a critical Euler length L_Euler* associated with the null isomer DNA*. It is given by Eq. 10:

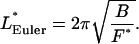(19)

DNA in the absence of thermal fluctuations is straight (if its basepair sequence is essentially random). But if the DNA molecule is longer than L_Euler*, then the central axis of its null isomer DNA* is not straight. It is buckled.

For DNA, every quantity in Eq. 19 is known numerically. In 0.1 M aqueous NaCl, B may be obtained from the known value 55 nm for DNA persistence length in Eq. 13. The quantities occurring in Eq. 18 for F* have been discussed in connection with Eq. 2. The value of L_Euler* works out to equal 14 nm, or 40 bp. We recall from the previous section that segments of DNA of length less than or equal to 82 bp do not undergo buckling fluctuations in solution. However, when the charge on DNA disappears to form the null isomer DNA*, then 82-bp segments of DNA*, being longer than 40 bp, are buckled.

We pause here to gain some physical intuition. DNA is under internal phosphate-phosphate repulsive tension. If the phosphate charge is abruptly eliminated with, initially, no structural change, then the tension is gone, but the internal forces that had kept the DNA structure in balance with the tension are still there. These restoring forces drive the DNA to a new structure. According to our model, the new structure will be a slightly contracted version of the original one for short DNA segments (<40 bp); but the restoring forces are strong enough to buckle DNA segments longer than 40 bp.

We proceed to consider the effect of thermal fluctuations on the null isomer. We begin with determination of its buckling persistence length 𝒫^*. We assert that it is equal to the null Euler length L_Euler*, i.e., the Euler length of the polyelectrolyte under the compression F* that balances the electrostatic tension:

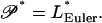(20)

The argument for this identification is that it cannot be otherwise. To understand why, recall first the definitions of these two lengths. Null segments of length shorter than 𝒫^* are not buckled by the relatively weak RMS thermal compression force F_rms. Longer segments are buckled by F_rms. Similarly, null segments of length shorter than L_Euler* are not buckled by the relatively strong compression force F* that is present in the null isomer. Longer segments of the null isomer are buckled—even in the absence of thermal fluctuations. Then 𝒫^* cannot be shorter than L_Euler*, since null segments shorter than L_Euler* are not buckled by the weak force F_rms, because they are not even buckled by the stronger force F*. But 𝒫^* also cannot be longer than L_Euler*, because null segments longer than L_Euler* are already buckled even in the absence of thermal fluctuations.

We return to Eq. 19, the right-hand side of which now provides a formula for the buckling persistence length of the null isomer:

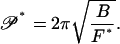(21)

But for any polymer, including the null isomer, Eq. 17 relates the buckling persistence length to the ordinary bending persistence length. We rewrite Eq. 17 as it applies to the null isomer,

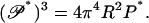(22)

We solve Eq. 22 for the persistence length P* of the null isomer, and then we use Eq. 21 to eliminate the buckling persistence length 𝒫^*:

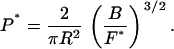(23)

In a final step, we express the bending modulus B in terms of the persistence length P of the original charged polyelectrolye by means of Eq. 13, and at the same time we substitute the right-hand side of Eq. 2 for F*:

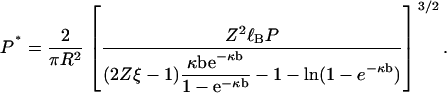(24)

We have arrived at our central result. In the form of Eq. 24 it expresses the persistence length of the null isomer, the polyelectrolyte without its electrostatic charge, in terms of the persistence length of the charged polyelectrolyte. We will also use it the other way around. Solving Eq. 24 for P, we get

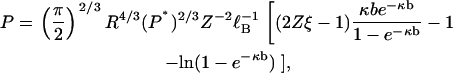(25)

thus providing a formula for the persistence length of a polyelectrolyte in terms of the persistence length of the polyelectrolyte without its electrostatic charge.

A qualitative remark to which we will return repeatedly is that Eq. 25 states that the relationship between the persistence lengths of a polyelectrolyte and its null isomer is multiplicative, not additive. In this theory, there is no additive electrostatic component to the persistence length of a polyelectrolyte. There is no “electrostatic persistence length.”

NUMERICAL CALCULATIONS AND COMPARISON WITH EXPERIMENTAL DATA

The null persistence length

We calculate the numerical value of the persistence length of the null isomer of DNA from Eq. 24. Except for the persistence length P of DNA, all the parameters on the right-hand side of this equation are characteristic either of the structure of B-DNA (b = 0.17 nm, R = 1 nm), or of water (ℓ_B = 0.71 nm at room temperature), or of both (ξ = ℓ_B/b=4.2), or of the counterion (Z = +1 for Na⁺), or of the salt concentration (κ =1/(0.96 nm) in 0.1 M aqueous NaCl). Moreover, a consensus measured value of P in these conditions is 55 nm. The numerical value of P* then works out to be 7 nm (∼20 basepairs of B-DNA).

The remarkably low predicted value for the persistence length of the null isomer, P* = 7 nm, is consistent with current knowledge from experiments. As discussed in the Introduction, increasingly efficient neutralization of phosphate charge by counterions yields increasingly smaller values of the persistence length, from 55 nm at moderate concentrations of NaCl, to 30 nm at high NaCl (6,9,11)), to 20 nm at concentrations of trivalent cobalt hexamine short of triggering DNA collapse (21), to 15 nm at cobalt hexamine concentrations above the collapse threshold (the latter measurement is under conditions of single-molecule stretching that prevent collapse) (13). Finally, deposition of DNA on mica surfaces coated with positive charge (in the form of poly-L-ornithine) yields images of DNA contours with persistence lengths decreasing with increasing concentrations of positively charged substrate down to P = 11 nm at the highest concentrations (22).

The value 55 nm of the persistence length of DNA is much larger than the 7 nm it would be if the phosphate charge were lacking. The enhancement of persistence length is due to the electrostatic tension within the DNA double helix generated by phosphate-phosphate repulsions. The difference between 55 and 7 is 48. There is no implication, however, that all polyelectrolytes of linear charge density equal to that of DNA would have a minimum electrostatic persistence length equal to 48 nm plus some nonelectrostatic contribution (the electrostatic tension according to Eq. 2 depends only on the linear charge density). The reason is that Eqs. 24 and 25 are not additive relationships. The persistence length P is not the sum of electrostatic and nonelectrostatic contributions.

For polyelectrolytes of the same linear charge density (equal values of axial charge spacing b and hence also of reduced charge spacing ξ = ℓ_B/b), the dependence of P on length quantities from Eq. 25 is

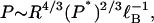(26)

where the Bjerrum length factor is independent of polyelectrolyte species and serves only to show explicitly that the units are correct. The two relevant lengths are the polymer radius R and the persistence length P* of the polyelectrolyte lacking its charge. Then a hypothetical polyelectrolyte with the same charge density and radius as DNA but with a null persistence length 10-times smaller than 7 nm (persistence lengths of typical single-chain polymers are only a few monomers long) would have a persistence length P = 12 nm. If, additionally, the hypothetical polymer had a radius three-times less than DNA (as would be typical of most single-chain synthetics), then P drops to 3 nm. Finally, if we return to the full Eq. 25 and use in it the charge density ξ = 2.8 typical of a polyphosphate chain or a vinylic chain with an ionized group on every monomer (instead of the DNA value 4.2), then P = 1.5 nm. The prediction thus would be that if fully protonated polyacrylic acid has a persistence length of approximately three monomers (0.7 nm), then the fully ionized polyacrylate chain would have a persistence length of approximately six monomers.

One may make the preceding numerical estimates without, however, gaining physical insight. Why do polyelectrolytes of the same charge density, hence with the same electrostatic tension in the chain, nevertheless not experience the same stiffening effect of the tension? The insight, as well as the numbers, must come from Eq. 26.

The radius R of the polymer cross section appears in Eq. 26 because of the radial dependence of the moment of inertia of the cross section from Eq. 7. It is the radial cross section that bears the bending torque generated by longitudinal buckling and extension forces. Thinner polymers are subject to smaller torques from the same longitudinal force than thicker ones, and are thus extended less than thicker ones from the buckled configuration of the null isomer by the same electrostatic tension.

The dependence of P on P* indicated by Eq. 26 is also susceptible to qualitative interpretation. A chargeless polymer with small persistence length P* has a higher configurational entropy than one with long persistence length P*. Equal electrostatic tensions in the two polymers do not have equal effects. The same tension force F_el experiences more entropic resistance in straightening the high entropy chain than the low entropy one.

As discussed, the persistence length of DNA is many times larger than the persistence length of its uncharged isomer, that is, the ratio P/P* is large for DNA. Rearranging Eq. 26 to form this ratio, we get

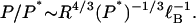(27)

This equation shows that for polymers of the same charge density, the slight dependence of P/P* on P* is dominated by the dependence on the radius of the polymer cross section. Polyelectrolytes thinner than DNA, even if of comparable charge density, will not have P/P* ratios as large as DNA.

Ionic strength dependence of the persistence length

The null persistence length P* is the persistence length of a polymer with no electrostatic charge. It is reasonable to assume that P* lacks a dependence on ionic strength. Therefore Eq. 25 becomes a formula for the persistence length P of the charged polyelectrolyte with an explicit dependence on ionic strength. The ionic strength appears only through the Debye screening parameter κ. At first glance the dependence looks complicated, but it is not. For dilute salt, κb < < 1 (for DNA with its small value of b, this condition covers nearly the entire salt range of interest). The first term in the bracketed factor in Eq. 25 becomes constant, and the third term yields a ln-c dependence, where c is the salt concentration.

The solid curve in Fig. 2 is a plot of P for DNA as given by Eq. 25. We used the value P* = 7.4 nm, as discussed in the previous section. Also shown in Fig. 2 are the combined data from four different laboratories (6,7,9,11). All of these data report true persistence lengths unaffected by, or corrected for (8,10), long-range excluded volume effects.

As mentioned in the Introduction, there is some impression that the measured ionic strength dependence of DNA persistence length is independent of salt concentration except at low salt. We will discuss the basis for this impression, but first we wish to note that it is not visually supported by the data shown in Fig. 2, which, again, are combined from four laboratories. Taken separately, the data of Sobel and Harpst (11) can be fit to a log c dependence with correlation coefficient 0.96 up to 3 M NaCl; the data of Borochov et al. (6) can be fit to a log c dependence with correlation coefficient 0.96 up to 4 M NaCl; the data of Cairney and Harrington (9) can be fit to a log c dependence with correlation coefficient 0.92 up to 1 M NaCl; and the data of Rizzo and Schellman (7) can be fit to a log c dependence with correlation coefficient 0.85 up to 0.5 M NaCl. In the analysis of the latter set of data, an outlier at 1 M NaCl is omitted (but included in Fig. 2).

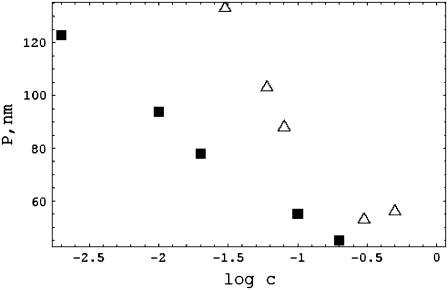
In Fig. 3, we exhibit two further sets of data that show strong dependence on salt concentration. Nordmeier's measurements (12) can be fit almost perfectly to a linear log c dependence (correlation coefficient 0.99) up to 0.2 M NaCl, the highest concentration he used. The data of Frontali et al. (5) fit a log c line with correlation 0.91. These two sets of data are not used in Fig. 2 because they exhibit a steeper ionic strength dependence than the data shown there. It may be noted that the Frontali group used NH₄Cl as the salt in their electron microscopic method. Because the Frontali and Nordmeier P-values are much higher at lower salt than the data in Fig. 2, they do not compare quantitatively to our theoretical prediction. However, their logarithmic dependence on salt concentration is in qualitative agreement with the theory.

FIGURE 3.

The persistence-length data of Frontali et al. (5) (triangles) and of Nordmeier (12) (squares). The latter are corrected for excluded-volume effects according to the procedure in Manning (8).

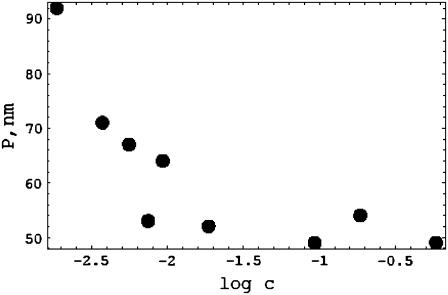
The impression of ionic strength independence appears to come from two well-publicized articles. One of these (35) reports persistence-length values inconsistent with all other data of which this author is aware, including the data of Baumann et al. (13). It has been commented upon elsewhere (11). The other more recent measurements of Baumann et al. (13) are exhibited in Fig. 4. The difference from the six data sets in Figs. 2 and 3 is evident. With increasing salt concentration, the values of Baumann et al. drop to ∼50 nm at ∼0.01 M NaCl, and remain more or less constant at 50 nm up to the highest ionic strength used by the authors, 0.6 M.

FIGURE 4.

The persistence length data of Baumann et al. (13). At each salt concentration, we show the average of the three values reported in Table 1 of Baumann et al.

It is worth contrasting the data of Baumann et al. with those of the others in more detail. From 0.01 M NaCl up to 0.6 M, Baumann et al. find that P remains invariant at ∼50 nm. The data from six other laboratories indicate the following: a decrease of P from 68 nm to 48 nm over the salt range 0.02–0.5 M (11); a decrease from 70 nm to 33 nm over the range 0.01–1 M (6); a decrease from 70 nm to 42 nm over the range 0.01–1 M (9); a decrease from 52 nm to 40 nm over the range 0.01–0.5 M (7); a decrease from 130 nm to 50 nm over the range 0.03–0.5 M (5); and a decrease from 78 nm to 45 nm over the range 0.02–0.2 M (12).

Based on their salt concentration data, Baumann et al. report observing a “nonelectrostatic contribution [that] dominates P” at salt concentrations >∼0.01 M. With reference to some of the same data that appear in Fig. 2, they state further that this observation is “in accord with previous experimental determinations….” The latter statement is certainly incorrect.

OSF theories

Polyelectrolyte persistence length theories of the Odijk-Skolnick-Fixman (OSF) type proceed from the assumption that electrostatic and nonelectrostatic interactions in a polymer contribute independently to the bending stiffness. The persistence length data in Figs. 2 and 3 cannot be fit to the shape of curves calculated from OSF theories, which flatten out to a constant nonelectrostatic value at higher salt. From a quantitative point of view, we have noted in the Introduction that at 0.1 M NaCl, the maximum value consistent with OSF theories for the total persistence length of DNA is 17 nm, whereas the actual measured value is ∼50 nm.

Baumann et al. (13) report that their data can be fit to an OSF theory given by their Eq. 3. They incorrectly characterize their Eq. 3 as the result of a nonlinear Poisson-Boltzmann theory, whereas it actually comes from a linear Poisson-Boltzmann calculation incorrectly corrected for counterion condensation (see Discussion in (25)). More importantly, we are unable to reproduce the solid curve in their Fig. 5, said to represent their Eq. 3. Instead, we can fit the data in their Fig. 5 only by assuming a numerical coefficient approximately three-times larger than the coefficient 0.324 from their Eq. 3. But there is no physical basis for this value that fits the data. It corresponds neither to the value 5.80 from uncorrected linear Poisson-Boltzmann, nor to the value 0.324 incorrectly corrected for counterion condensation as in their Eq. 3, nor to 2.42 from a more accurate counterion condensation calculation (25). (Note that the modified OSF Eq. 13 in (25) is correct, and the factor 2.42 quoted here corrects some errors that crept into the discussion of this formula.) More importantly still, as discussed in the previous section, the data of Baumann et al. (13) appear themselves to be problematic.

According to the model addressed in this article, OSF theories may suffer from an important omission. It seems obvious that the stretching force from charge-charge repulsions within a polyelectrolyte should play a significant effect in stiffening the polymer, yet the effect of longitudinal tension from electrostatic forces is not considered by OSF theory. The structural change from a buckled to a stretched conformation that occurs when functional groups on a polymer chain become ionized is missed. The strength of the internal electrostatic tension depends on salt concentration, and therefore the structure of a polyelectrolyte chain must change with salt concentration. The consequence is that the OSF nonelectrostatic persistence length is not a constant, but itself depends on salt concentration.

APPENDIX

Here we derive Eq. 11 for the RMS compression/extension force on an elastic rod in a temperature bath. We follow the classical treatment of fluctuations in Landau and Lifshitz (36). Let x be any small fluctuation and

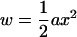(28)

be the work required to establish it to quadratic order, where a is some constant modulus. The mean-square value of x is calculated from

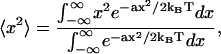(29)

since even though x is physically small the exponentials allow extension of the integration limits to infinity. Therefore the RMS values of x are given by

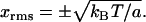(30)

For length fluctuations ΔL of an elastic rod of static length L, we take x = ΔL/L to be the longitudinal strain fluctuation. From Hooke's Law for the elastic energy, a is equal to EAL, where E is Young's modulus, and A is the cross-sectional area. The RMS strain fluctuation is then

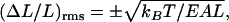(31)

where the plus sign corresponds to extension and the negative sign to compression. Hooke's Law also provides a linear stress-strain relation between the strain ΔL/L and the compression/extension force F that produces it:

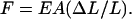(32)

Equation 11 of the text now follows from Eqs. 31 and 32.