The Role of F-Actin and Myosin in Epithelial Cell Rheology

Abstract

Although actin and myosin are important contributors to cell-force generation, shape change, and motility, their contributions to cell stiffness and frequency-dependent rheology have not been conclusively determined. We apply several pharmacological interventions to cultured epithelial cells to elucidate the roles of actin and myosin in the mechanical response of cells and intracellular fluctuations. A suite of different methods is used to separately examine the mechanics of the deep cell interior and cortex, in response to depletion of intracellular ATP, depolymerization of F-actin, and inhibition of myosin II. Comparison of these results shows that F-actin plays a significant role in the mechanics of the cortical region of epithelial cells, but its disruption has no discernable effect on the rheology of the deeper interior. Moreover, we find that myosins do not contribute significantly to the rheology or ATP-dependent, non-Brownian motion in the cell interior. Finally, we investigate the broad distribution of apparent stiffness values reported by some microrheology methods, which are not observed with two-point microrheology. Based on our findings and a simple model, we conclude that heterogeneity of the tracer-cytoskeleton contacts, rather than the network itself, can explain the broad distribution of apparent stiffnesses.

INTRODUCTION

The ability of cells to respond to external mechanical stimuli relies on the coordinated disassembly and assembly of cytoskeleton polymers. This ability to remodel itself is critical for various cell functions including adhesion, wound healing, division, and locomotion. In addition, cells can sense their local environment mechanically, as they spread more on, and migrate toward, stiffer substrates (1). In particular, networks of F-actin and its protein cross-linkers have been implicated as major contributors to the mechanical properties of the cell (2,3). This article investigates the role of the actin network and myosin in maintaining the mechanical properties of cultured TC7 epithelial cells through measurements of rheology under pharmacological interventions including an actin disruptor, a myosin II inhibitor, and ATP depletion agents.

Many techniques have been used to characterize cell rheology, and recently they have begun to report comparable results. Typically, cells' mechanical properties are quantified with a complex, frequency-dependent shear modulus, G*(ω) = G′(ω) + iG″(ω), where G′(ω) reports the elastic response and G″(ω) the viscous response. Dynamic rheometry performed on cells using magnetic twisting cytometry (MTC) (4), atomic force microrheology (AFM) (5), and a method we developed, two-point microrheology (TPM) (6–8), all report a low-frequency complex modulus that increases as a weak power-law with respect to frequency, G* ∼ Aω^β, with stiffness A ranging from tens to thousands of Pascals and exponent β in the range 0.1–0.25. Such power-law behavior implies that microscopic stress relaxation processes inside cells must have a very broad distribution of characteristic times or rate constants, but the nature of those processes remains unknown.

The effects of three interventions (latrunculin A, blebbistatin, and sodium azide/deoxyglucose) were studied using four different microrheology methods (Fig. 1). This approach allows us to probe the cellular response from the cell exterior and interior using either active or passive driving forces. To obtain an active measurement, an oscillatory torque (stress) is applied to a cell and the resulting deformation (strain) is measured. As used here in MTC, the relative amplitude and phase shift of the stress and the strain directly determine the shear modulus at the driving frequency. Passive techniques, such as laser tracking microrheology (LTM), report mechanical properties by tracking the Brownian motion of tracer particles embedded in a cell, which is converted to a mean-squared displacement from which G*(ω) is computed numerically. TPM cross-correlates the motion of pairs of tracers to infer the Brownian motion of large segments of the cytoskeleton spanning between them, allowing it to unambiguously determine the rheology independent of the tracer-network connection (6,9). Passive methods based on Brownian motion are generally confounded by any non-Brownian motion in the cell. We use passive methods to quantify the non-Brownian motion under conditions in which it is predominant, and to compute the rheology when it is negligible.

FIGURE 1.

Sketch of our four cell rheology techniques, side view. From top to bottom: MTC measures rocking motion of 4.5-μm-diameter tracers, adhered to the apical cell surface by integrins, in response to a sinusoidal magnetic torque; TPM measures the correlation of the random motions of pairs of endogenous traces to infer the Brownian fluctuations of the intervening network; and LTM measures the translational Brownian motion of the MTC tracers either phagocytosed in the cell interior or adhered to the apical surface.

A recent study in our laboratory used the same suite of techniques to study the frequency dependence of the cell mechanical response in detail (8). It was found that two rheology curves emerged, ultimately leading us to conclude that different techniques measure the differing responses of either the deep cell interior or a cortical region. This finding of two mechanical networks is compatible with a number of literature results (4,5,10–12).

This article investigates the role of both actin and myosins in cell mechanics and examines the sensitivity of some microrheology methods to tracer-cytoskeleton connections. As might be expected for a system composed of two distinct mechanical networks, we observe different responses to drug treatment depending on whether we are probing the cortex or the deep interior. Moreover, the use of multiple cell rheology techniques reveals discrepancies between different methods in response to ATP depletion, allowing us to distinguish actual changes to the cytoskeleton rheology from purely artifactual changes.

Finally, we examine the origin of the broad distributions of apparent stiffness reported by our measurements. We consider the possibility of cell heterogeneity as a cause for these variations, but find that this is unlikely given the narrow dispersion of cell stiffnesses reported by TPM. Instead, we suggest an alternative hypothesis: the broad distribution in apparent stiffness seen by LTM is due to a heterogeneous distribution of contacts between the tracer and the cytoskeleton. A simple computational model of a phagocytosed tracer reveals that a log-normal distribution of the number or size of contacts is required to generate the observed stiffness distribution.

METHODS

Cell culture and drug treatments

TC7 African green monkey kidney epithelial cells are grown at 37°C and 5% CO₂ in plastic culture flasks using Dulbecco's modified Eagle's medium (DMEM; Invitrogen, Carlsbad, CA) supplemented with 10% bovine calf serum (Hyclone, Logan, UT) and penicillin-streptomycin (75 IU/ml and 75 μg/ml, ATCC). Cells are plated on collagen I-coated coverslips (BD BioCoat; BD BioSciences, San Jose, CA) and are incubated over night before experimentation. Before any drug treatment, cells are incubated with serum-free medium for at least 2 h. Latrunculin A (0.1 μM), blebbistatin (50 μM), and the ATP-depletion cocktail (50 mM 2-D-deoxyglucose, 0.05% NaN₃, Alfa Aesar, Ward Hill, MA) are diluted in DMEM or minimal essential medium and applied to cells. For MTC and LTM experiments, 4.5 μm ferromagnetic tracer beads coated with RGD peptide are attached before drug treatment.

Immunofluorescence microsopy

To stain F-actin, cells are rinsed with PBS and fixed with 4% formaldehyde in PBS at 37°C for 8 min. Cells are then permeablized and blocked using an immunofluorescence wash (0.2% Triton-X, 0.01% Tween, 0.1% BSA; Sigma-Aldrich, St. Louis, MO). After fixing and permeabilizing, all cells are blocked using 3% normal goat serum (Jackson Pharmaceuticals, West Grove, PA). TRITC-Phalloidin (Sigma-Aldrich) is used to stain F-actin structures. Immunofluorescence is viewed using an inverted confocal microscope (Nikon Eclipse TE-300 (Nikon, Tokyo, Japan) and BioRad Radiance 2000-MP (BioRad, Hercules, CA) with a 60× objective.

Microscopy

Cells are imaged with shadow-cast DIC microscopy (DM-IRB, Leica, Deerfield, Il) using a 100×, NA 1.4, oil-immersion objective and illumination provided by a pulsed 2W multimode diode laser (SDL-2460, λ = 808 nm, Spectra Diode Labs, San Jose, CA). To use an oil-immersion condenser, a custom-top dish was constructed which supported an upper coverslip immersed in the medium ∼0.5 mm above the bottom coverslip. During data collection, the stage, condenser, and objective were heated to 37°C and the atmosphere above the cells was maintained at 5% CO₂. In these conditions, cell viability for up to 8 h on the microscope has been confirmed.

Multiple particle tracking

Cell chambers are focused 2–4 μm into the 6- to 10-μm-thick TC7 cells. For each cell, roughly 9 gigabytes of image data are recorded at rates of 50 and 1000 frames/s over a 35-min period with a high-speed digital CMOS camera (Phantom 4, Vision Research, Wayne, NJ). (Shorter acquisition periods show substantially similar data with larger statistical variance). The cell is illuminated with a 20–30 μs strobe and the image scale is 96 nm/pixel. Typically, a few hundred organelles (presumed by morphology to be primarily lipid granules and mitochondria) are found within each cell and ∼2 μm depth of focus, yielding ∼10⁷ positions per single cell dataset with 5–8 nm spatial resolution. Tracers in nuclei or lamella are omitted from the analyses. Methods for particle tracking (13) and computing two-point correlations (6) are described elsewhere. The measured correlation, D_rr(r,τ) is independent of the size of the tracers used to compute it. To render it directly comparable to the results for LTM, it can be scaled according to TPM mean-square displacement (MSD) = (2r/a_eff)D_rr(r,τ), with a_eff = 2.2 μm being the radius of the LTM tracers.

Magnetic twisting cytometry and laser tracking microrheology

Measurements are performed using ferromagnetic tracer beads (4.5-μm diameter, Spherotech, Libertyville, IL) coated with RGD-peptide (AC-G(dR)GDSPASSKG₄S(dR)-NH₂, Integra LS, Plainsboro, NJ), which specifically attach to the cell exterior via integrin receptors (14). Before attaching beads, the cells are incubated in serum-free medium for 45 min. For active measurements, beads are magnetized vertically after cell attachment using an ∼1000 Gauss magnetic-field pulse lasting ∼100 μs. Beads are then selected visually using the microscope described above; cells with multiple attached or phagocytosed beads are rejected. The bead is then illuminated with a CW red laser diode (λ = 638 nm), keeping absorbed laser power <1/3 mW to minimize heating effects (estimated to be ∼1°C/mW) and imaged onto a quadrant photodiode module (OSI Optoelectronics, Newbury Park, CA) with a 4.5× auxiliary magnification and dark-field Fourier filter. This system determines bead displacement with a resolution of ∼0.2 nm for lag times <100 μs (shot noise limited) and 1 nm for lag times >10 ms (vibration limited). In the active experiments, externally attached beads are rocked by a 10-Gauss (peak) oscillatory horizontal magnetic field. The magnet current and bead-position signals were simultaneously digitized at 50 kHz (National Instruments, Austin, TX). The amplitude and phase shift of the bead displacement are determined in real time using a LabView-based digital lock-in. The elastic and loss moduli, G′ and G″, are then deduced up to a multiplicative prefactor that depends on bead-cell contact area. To avoid errors due to time-dependent fluctuations of this prefactor, we drive the bead with a sum of two sinusoids, sweeping one in frequency while using the other as a reference. The ratio of these two amplitudes is nearly time-independent, allowing the precise determination of the frequency dependence of G′ and G″ of single cells. Relative changes in rocking amplitude, and thus cortical stiffness, can be measured by averaging the amplitudes of the reference frequency data. Absolute cortical stiffnesses are not estimated in this study.

In the passive experiments, no field is applied and the bead deflection signal is digitized at rates up to 50 kHz. The mean-square displacements, 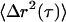, are computed from 30-s trajectories. At lag times dominated by Brownian motion (as confirmed by ATP depletion), G′ and G″ are extracted from the (LTM or TPM) MSDs, 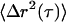, using the generalized Stokes-Einstein relation,

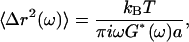(1)

and computation methods previously described (15,16).

Statistical and systematic error

In general, the MSD amplitude data in this study are better described by a log-normal distribution than a Gaussian one; that is, the logarithms of the MSD amplitudes at a given lag time are Gaussian distributed. For this reason, these data were log transformed before averaging, computation of standard deviations, and the use of significance testing.

Although the lag time (or frequency) dependence of our LTM data were quite reproducible, the mean amplitudes of both LTM methods vary slowly over long periods of time, due presumably to subtle, uncontrolled changes in the culture conditions, passage number, tracer chemistry, and RGD peptide. To mitigate this source of systematic uncertainty, when pooling data together to compare an intervention and control, all data were collected within a single campaign spanning no more than 2 weeks of time, using the same lot of reagent and media and interleaving the acquisition date of intervention and control data.

Computational model of tracer mobility with small, finite-sized contacts

To calculate the resistance to displacement of tracers having only small adhesive contacts with their surroundings, we must first know the force that results at each contact when the tracer is moved a given distance. Because the forces on different contacts are coupled by the external strain field, determining them is a nontrivial continuum mechanics problem. As we are only interested in the basic scaling of the full mechanics problem, we use an electrostatic analogy (9), computing the simpler problem of the total capacitance of a number of small spherical capacitors (radius r_c) whose centers lie on the surface of a much larger sphere (radius a). The force at each contact is analogous to the charge, q_i, on each capacitor and the displacement is represented by the potential, φ_i. Since the contact displacements in the mechanical problem are all the same (since they are assumed to be attached to a rigid tracer), the problem reduces to solving for the set of capacitor charges that causes all the capacitors to be at the same potential.

We begin by distributing N capacitors randomly on a spherical surface, assuring that they are separated by more than 2 r_c to avoid overlap. Each capacitor is initially assigned a unit charge and each capacitor's potential is determined by:

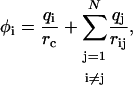(2)

where r_ij is the distance between the two capacitors. We then use an iterative, steepest-descent approach to adjust the capacitor charges until their potentials are equal. The algorithm is considered converged when the standard deviation of the potentials φ_i is <10⁻⁵. The total capacitance for the system is then calculated using

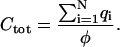(3)

The ratio of the force to the displacement in the mechanics problem corresponds to this total capacitance in the electrostatics problem. The corresponding force/displacement ratio for the Stokes-like, uniform no-slip boundary condition is the capacitance of a sphere, which in our units is simply its radius, a. Thus, the ratio of the forces required to identically displace tracers in the two cases is simply M = C_tot/a. For a given N and r_c/a, we compute an ensemble of different starting configurations, allowing us to assess both the mean value and the standard deviation of M due to the contacts' random locations. Note that the far-field electrostatic potential in this problem looks like that of a point charge, but for a given surface potential, it is a factor of M smaller (as is the total charge) than in the uniform spherical capacitor case.

Of course, both the electrostatic potential and the steady-state diffusion problem are described by Poisson's equation. For this reason, our computation is mathematically identical to the well-known biophysics problem of diffusive capture of molecules to small disk-like absorbers on a spherical surface (17).

RESULTS

Overview of cell rheology and fluctuations

We briefly summarize the findings of our recent study (8) regarding the frequency-dependent mechanical response of epithelial cells in both the cortical and deeper intracellular regions. Both regions display weak power-law rheology (Fig. 2) at low frequencies, crossing over to a steeper dependence at high frequencies that can be accurately fit using

(4)

FIGURE 2.

Normalized shear modulus for ATP-depleted cells collapses onto two master curves (offset by 2× for clarity). As discussed in the text, the upper curve is the TPM-like response and the lower is the MTC-like response. The small black points are from single-tracer external-bead LTM trajectories, which can correspond to either curve. The squares are cell-averaged internal (phagocytosed) LTM data (N = 41), triangles a typical single-cell MTC response, and open circles are cell-averaged TPM (N = 7). Dashed lines are best fits of Eq. 2 to the data (upper curve, β_int = 0.26, A_int = 0.51, B_int = 0.020; lower curve, β_cort = 0.17, A_cort = 0.66, B_cort = 0.009; both normalized by G₀ = |G*(ω = 10 rad/s)|. In an earlier TPM study (8), we found G₀ to be ∼40 Pa in the cell interior. The high-frequency line has slope 0.75.

The TPM and internal LTM methods measure the interior network and report β_int ∼0.26. The cortical region is measured by active MTC and reports a value of β_cort ∼0.16. External LTM reports either curve, depending on the tracer (presumably due to differences regarding the relative contacts of the tracer to both regions). Although these results were found under ATP depletion they are consistent with a number of literature studies on normal (i.e., not ATP-depleted) cells. We assume Eq. 4 describes the baseline rheology of the cortical and deep intracellular regions of normal cells.

Although the frequency dependence is robust, the apparent amplitudes A_int and A_cort vary significantly between individual tracers or cells in a given method, as well as systematically between methods. As seen in other studies (12,18), the A-values have a broad distribution (Fig. 3 A), which can be described by a log-normal distribution. For externally attached tracers, it has been suggested that this wide range of A-values is caused by geometric factors such as variation between bead-cell contact area (12,18,19), but it is not clear how this can explain the distribution in amplitudes seen for phagocytosed tracers. Our TPM studies provide additional insights into cellular heterogeneity. In a three-dimensional continuum, the degree of correlation between the random motion of two tracers of separation r should vary as 1/r. This has been confirmed, via TPM, in several cell types between 2 < r < 8 μm, and implies that the deep cytoskeleton deforms as a continuum on these length scales. This observation does not rule out microheterogeneity, cells' presumably heterogeneous and porous character on micron length scales. The continuum response of cells measured by TPM, however, does seem to rule out gross cytoskeletal heterogeneity as an explanation for the broad distribution of measured LTM amplitudes.

FIGURE 3.

Plot of typical data from two of our rheology techniques. (A) Internal LTM shows the wide range of amplitudes, with most curves having a similar shape. (B) Pooling internal LTM results from N = 31 cells produces an average curve that can be divided into three regimes where Brownian forces dominate, a regime where non-Brownian (such as molecular motor) forces dominate, and a crossover region between the two. Error bars are 95% confidence, log-transformed standard errors. (C) Typical single-cell MTC data normalized at 5 Hz.

Typical data for our LTM and MTC techniques are shown in Fig. 3. In LTM, random tracer displacements, 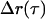, during a lag-time interval τ, are time-averaged to obtain an MSD 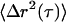. The MSD curves exhibit three separate responses as a function of lag time. At short times (Fig. 3 B), tracer motion is Brownian, and has an MSD amplitude at τ that is, roughly speaking, inversely proportional to the modulus at ω ∼1/τ . The short time, MSD ∼ τ^¾, corresponds to G* ∼ ω^¾ at high frequencies, and is characteristic of transverse Brownian fluctuations of single cytoskeletal filaments. For τ > 10⁻³, the MSD begins to roll over due to G* crossing over to its weak power-law form, ∼ω^β, at low frequencies (see Fig. 2). At lag times τ > 0.02 s, cells exhibit superdiffusive behavior, τ^α, α > 1, which is mathematically inconsistent with Brownian driving. This non-Brownian behavior has been seen previously (7,8) and is attributed to active, ATP-dependent processes. The superdiffusive results for LTM experiments (Fig. 3 B) show a non-Brownian motion with variable crossover times and exponents, α, causing the functional form of the average curve to look roughly diffusive at long lag times. On the other hand, for TPM experiments the cross over to non-Brownian motion is more reproducible in form with α ∼1.5. The non-Brownian motion likely has several molecular contributors, and our three passive techniques presumably have different sensitivities to those different contributors. Nevertheless, we will treat non-Brownian motion in this work as a single, aggregate quantity.

Interpretive approach

Interpreting cellular mechanics results from four techniques requires analysis of both the amplitude of the rheology (stiffness) and its frequency dependence, and must be done for two different cellular regions. Moreover, we must consider the non-Brownian motion, its confounding effects on the passive methods, and the potential contributions of tracer-cytoskeleton contacts (20).

To interpret this wealth of data in response to an intervention, we use the following three approaches to interpret our results. 1), If there is no change to the MSD amplitude at short lag times, we assume the stiffness has not changed. 2), MSD changes at long lag times will be interpreted as a change in either non-Brownian motion or the stiffness, depending on whether the short lag time response has changed. 3), Since TPM has been shown theoretically (9) and experimentally (6) to be independent of tracer-cytoskeleton contacts, when discrepancies between the internal LTM and TPM response occur (e.g., mean stiffness, stiffness distribution, or stiffness change under intervention), the discordant LTM result will be treated as artifactual.

ATP depletion

To examine the role of ATP-dependent molecular motors and non-Brownian fluctuations on cell rheology, an ATP depletion cocktail (50 mM 2-D-deoxyglucose, 0.05% NaN₃) is applied to the cells. Depletion is confirmed using a luciferase-based assay. In addition, there is a decrease in unidirectional trafficking of endogenous particles. Actin structure is affected by ATP depletion, but not as severely as with latrunculin A or blebbistatin treatment (Fig. 4). There is no significant effect on the mechanical response as measured by MTC (Fig. 5). At long lag times (τ > 0.1 s), all passive techniques find a significant decrease in the magnitude of the MSD (Fig. 6, A–C, arrow 1). As explained earlier, ATP depletion extends the frequency domain in which the rheology can be measured using passive methods revealing frequency dependence corresponding to literature studies, and suggesting that ATP does not change the frequency-dependent rheology of cells (8).

FIGURE 4.

Phalloidin F-actin staining (confocal, maximum-value projection) in (A) control; (B) ATP-depletion sample (50 mM 2-D-deoxyglucose, 0.05% NaN3, 2 h); (C) sample treated with 50 mM blebbistatin for 2 h;. and (D) sample treated with 100 nM latruncunlin A for 2 h. Disruption of stress fibers is seen in both C and D. Scale bar, 10 μm.

FIGURE 5.

Summary of MTC findings. (A) The cortical rheology exponent changed under latrunculin A treatment, β_cort = 0.06 (0.1 μM latrunculin A), β_cort = 0.16 (control). Other treatments did not change significantly. (B) MTC rocking amplitude due to a constant-intensity 5-Hz oscillating magnetic field is inversely proportional to cortical stiffness. No significant change in relative stiffness was found for any treatment. Error bars, 95% confidence mean ± SE (A) or log-transformed mean ± SE (B).

FIGURE 6.

Mechanical properties of TC7 cells treated with either ATP depletion (black) versus control (white) (A–C), or latrunculin A (black) versus control (white) (D–F). ATP depletion results in a loss of non-Brownian motion at long lag times (τ > 10⁻³), manifested through a reduction in the magnitude of the MSD (A–C). Internal LTM (B) shows a softening at short lag times (τ < 10⁻²), suggesting a change in bead-cytoskeleton contact. In contrast, treatment with latrunculin A (D–F) leads to no statistically significant change to the rheology or non-Brownian motion. All error bars are 95% confidence, log-transformed standard errors. Number of cells for interventions are: (A) N = 20; (B) N = 18; (C) N = 7; (D) N = 27; (E) N = 20; and (F) N = 6. For controls, N = 32 for external LTM; N = 20 for internal LTM; and N = 15 for TPM. Arrows are explained in the text.

Close comparison of MSD data from internal LTM and TPM (in ATP-depleted cells) shows that they have the same functional dependence on lag time, differing only by a multiplicative factor, as shown in Fig. 2. However, stiffnesses reported by the two methods differ systematically, with TPM reporting a mean stiffness of 38 Pa (at ω = 10 rad/s) and LTM being about a factor of 5 softer. The discrepancy in stiffness, but not in the shear modulus' frequency dependence, is expected for tracers having small adhesive contacts with the cytoskeleton, as we will discuss in more detail below.

Changes to the amplitude of the MSDs due to ATP depletion are method-dependent. Internal LTM sees an increase in MSD, suggesting that the depleted cells are more than a factor of 4 softer than control cells (Fig. 6 B, arrow 2). TPM, however, shows no significant change in amplitude at the shortest lag times corresponding to its Brownian regime (see Fig. 6 C, arrow 3), consistent with no change to the stiffness of the deep interior. External LTM also shows no significant change in stiffness, suggesting that ATP depletion alters the connection of phagocytosed tracers to the network but not the connection of externally attached tracers.

Actin filament disruption

Latrunculin A (0.1 μM) is used to disrupt the F-actin network; it works by inhibiting polymerization of G-actin monomers by binding strongly to them, competing with thymosin β, a sequestering protein, which controls prolongation of fast growing ends (21). The distribution of F-actin is determined by phalloidin staining microscopy (Fig. 4). As is common in cultured epithelial cells, these cells do not show any apparent enrichment of F-actin in the cortical region; confocal microscopy shows diffuse palloidin staining uniformly filling the cell interior. F-actin is enriched, however, in the lamellipodal region. Latrunculin A treatment causes cells to ball up slightly, and disrupts stress fibers and the diffuse staining while leaving staining at the lamellipodal perimeter and scattered punctuate sites (Fig. 4 D).

Despite a drastic change to the F-actin network, there is no change in the stiffness of the cortical region as measured with MTC (Fig. 5). F-actin disruption does, however, lead to a change in the frequency-dependent rheology, with the new exponent, β_cort = 0.06 ± .02. This indicates that the rheology of the cell cortex depends on F-actin and becomes closer to a pure elastic response when it is disrupted. A purely elastic response is frequency-independent, G* = G′ ∼ ω⁰, or β = 0. The interior of the cell shows no change upon F-actin disruption, either in functional form or amplitude as measured by LTM and TPM (Fig. 6, D–F).

Myosin II inhibition

After seeing a change in the rheology of the cortical region with latrunculin A, we investigate the role of myosin II activity. As an ATP-dependent motor protein we further hypothesized that inhibition of myosin II activity could result in some loss of non-Brownian motion, as was seen with ATP depletion. Addition of 50 μM blebbistatin has been shown to inhibit many myosin II isoforms by preventing reattachment of the myosin head after the power stroke (22). Morphologically, cells treated with blebbistatin have a similar appearance to those treated with latrunculin A. Staining shows a loss of stress fibers 2 h after the drug is administered (Fig. 4 C). Blebbistatin is dissolved in a DMSO carrier before addition to the cells, bringing the final concentration in the culture dishes up to 0.5% DMSO. (Cells incubated with only DMSO show no loss of stress fibers, unlike blebbistatin-treated cells.) The data from all four of our rheology techniques under blebbistatin treatment are unchanged relative to a blank DMSO carrier (data not shown).

Tracers with small cytoskeleton contacts move more due to applied forces

We hypothesize that discrepancies between internal LTM and TPM are due to the LTM tracers connecting to the surrounding continuum through small adhesive contacts rather than being adhered to their surroundings over their entire surfaces. Since we are only interested the qualitative scaling of the problem, we use an approach suggested by Levine and Lubensky (9) that allows us to analogize the tensorial continuum mechanical problem with a scalar, electrostatic problem, see Methods. We begin by assuming that a tracer of radius a has N small contacts with radius r_c randomly scattered over its surface. We then estimate the ratio, M, of the force required to displace a tracer with small contacts a given amount relative to a tracer having a uniform no-slip boundary condition. The computed M values collapse onto a master curve when plotted versus (Nr_c/a) (Fig. 7). Asymptotically, for small values 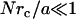, we find linear scaling, whereas for large values 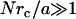, both cases have a similar force/displacement behavior, 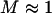. We find that spatial randomness does not affect M very much: the standard deviations of M values are smaller than the symbols plotted in Fig. 7, provided that N > 3.

FIGURE 7.

Results of our model comparing a tracer with small adhesive contacts to a tracer with a uniform adhesive boundary condition. M is the ratio of the forces required to translate both tracers by the same amount, N is the number of contacts having radius r_c, and a is the tracer radius. For small or few contacts, the force required is proportional to both contact size and number. For large or numerous contacts, the force is identical to the uniform boundary condition.

This hypothesis makes several predictions. The Brownian MSD of tracers with small contacts should be 1/M times larger than the uniform contact case. However, the MSDs should have the same lag-time dependence in both cases, since in the noninertial limit, the boundary conditions affect the viscoelastic problem in a frequency-independent manner (9). Moreover, the displacement (or strain) field around a small contact tracer has a complicated near-field solution that crosses over to a 1/r limit in the far field. In the small contact case, this far-field solution has the same form as in the uniform case, but is reduced in amplitude by a factor M relative to a uniform contact tracer displaced by the same amount. Lastly, since M is linear in the number and size of contacts when M ≪ 1, the distribution of MSD amplitudes (or apparent stiffness reported by Eq. 1) should just reflect the distributions of contact size and number.

DISCUSSION

F-actin plays a significant role in epithelial cells' cortical rheology, but not in their interior rheology

The decrease in the apparent rheology exponent, β_cort, seen by MTC measurements clearly indicates that cortical mechanics depends on F-actin. The observation that the MTC amplitude (i.e., cortical stiffness) does not change under actin disruption is interesting. That finding is consistent with the tracer-cytoskeleton contact not changing significantly (appearing to rule out contact changes for the β_cort change), but also suggests that F-actin is not the sole or even predominant structural element in the cortex (compatible with the microscopy finding that showed no F-actin enrichment there). It seems that F-actin is an integral part of the unknown mechanism that gives rise to weak power-law rheology, but is not a predominant structural element in the cortex of our epithelial cells.

Conversely, the internal techniques detect no change in the rheology of the deep cell interior, further confirming the existence of two mechanically distinct regions in cells. The fact that external LTM sees no change with actin depolymerization is not surprising given that our earlier work found that most external LTM tracers measure the interior response (8). The lack of a stiffness change in the interior is compatible with the idea that epithelial cell integrity relies upon intermediate filaments, perhaps associated with microtubules. Moreover, the lack of a change in the intracellular rheology exponent, β_int, suggests that F-actin has no role in producing power-law rheology in the interior, and, by extension, that the molecular mechanism responsible for producing it there differs from that in the cortex.

Neither myosin II cross-linking nor motor activity contribute to the noncortical mechanics of epithelial cells

In cells, myosins play two structural roles, acting as both F-actin cross-linkers and motor proteins. Our three pharmacological interventions affect these roles differently, providing additional clues regarding myosin's effect on cell mechanics. ATP depletion presumably puts myosin into rigor, retaining its cross-linking function while eliminating (or dramatically reducing) its motor sliding activity. Latrunculin A treatment inhibits both roles for all myosin isoforms through its disruption of the actin network. Finally, blebbistatin inhibits both the cross-linking and motor properties of myosin II by inhibiting its binding of F-actin. Given the null effect of latrunculin A on the cell interior, we can conclude that neither the cross-link nor sliding role of any myosin isoform plays a role there. In the cortex, given the fact that latrunculin A changed the rheology exponent, β_cort, but ATP depletion did not, it seems that myosin sliding activity is not required to maintain power-law rheology. The null blebbistatin result in the cortex suggests that myosin II cross-linking does not contribute either, but our work does not rule out a structural cross-linking role for blebbistatin-insensitive myosin isoforms in the cortex.

In addition, ATP depletion of epithelial cells results in a loss of superdiffusive behavior at long lag times, suggesting that an ATP-dependent molecular motor is responsible. However, the inhibition of neither some myosin II isoforms with blebbistatin nor all myosins by actin depolymerization affects the amplitude of the non-Brownian motion. Previously we had considered the non-Brownian forces in the deep cell interior as a consequence of a slowly evolving prestress, and supposed them to be due ultimately to actin polymerization or myosin (7). Our results indicate that a better candidate may be microtubule polymerization or its associated motors, although future studies will be needed to test this idea. The small role for myosin in the rheology is not necessarily a surprising result given the quiescent nature of epithelial cells, and may not hold for other more active cell types.

It should also be noted that none of our passive techniques unambiguously probe the non-Brownian motion within the cell cortex, so we can say little about active processes there. That is, our findings regarding the deep cell interior are not at odds with the well-known function of myosins in the cell cortex, e.g., during cytokinesis.

LTM results are influenced by tracer-network connectivity

Fig. 8 shows several possible scenarios to describe a tracer's connection to a viscoelastic continuum. Fig. 8 A shows a bead embedded in a homogenous network with a no-slip boundary condition; the situation for which the generalized Stokes-Einstein relation (Eq. 1) was derived. Fig. 8 B shows a bead surrounded by a shell having different viscoelastic properties than the bulk surroundings. In this “nonassociating” case, microrheology methods report a shear modulus intermediate between that of the shell and the bulk value (9), depending on the relative stiffness and the thickness of the shell. If the shell material and the bulk have different frequency-dependent shear moduli, the frequency-dependent response observed will differ from both of them. This is the situation that prevails in many reconstituted biopolymer systems (23). In Fig. 8, C and D, the tracer is again surrounded by a mechanically distinct layer or shell, but it is connected directly to the bulk surroundings via small holes or gaps in the shell. If the shell is also very soft compared to the bulk (e.g., fluidlike) it cannot support significant stress and this case corresponds to our simple model of a tracer with small adherent contacts.

FIGURE 8.

Schematic representations of possible connections between microrheology tracers and their surroundings. (A) Tracers lodged in a homogenous continuum with uniform no-slip boundary conditions (reports rheology of the bulk). (B) Homogenous network surrounded by a thin shell with different viscoelasticity (measures rheology of other than the bulk). (C and D) Tracers connected via distinct, finite contact areas (measures the same frequency dependence as the bulk, but with lower apparent stiffness than A).

In the cell context, our internalized LTM tracers are presumably surrounded by phagosomes, which are sometimes large enough to be obvious microscopically. If the tracers were free to explore the phagosome interior, the situation would correspond to the nonassociating case shown in Fig. 8 B, and the MSDs from LTM and TPM would either correspond precisely in lag-time dependence and amplitude (for extremely thin shells only) or would have different lag-time dependences, with the LTM response looking more diffusive (for thick shells). Alternatively, LTM tracers could adhere directly to the walls of the phagosome, perhaps via internalized transmembrane proteins. This situation would correspond to the model case (Fig. 8, C and D). The model's first two predictions, stated in Results, correspond to our findings: internal LTM reports a stiffness that is ∼5× softer than TPM (which would correspond to 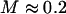), and the MSDs from internal LTM and TPM have an indistinguishable lag-time dependence.

Confirmation of our model's third prediction can be found in a study by Bausch et al. (24). They found that the cytoskeletal displacement field around a displaced phagocytosed bead (in J774 macrophages) is much smaller than expected based upon continuum mechanics and a uniform nonslip boundary condition. Translation of a 1.3-μm bead failed to induce any detectable entrainment motion of colloidal particles only 1 μm away (24). The authors explained their finding by considering that the cytoskeleton consists of densely packed and cross-linked filaments separated by soft regions. In the alternative explanation provided by our model, sketched in Fig. 9, much of the cytoskeletal strain or deformation is localized to the small tracer-cytoskeletal contacts, with the long-range displacement field being significantly attenuated (i.e., by 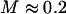) relative to the uniform boundary case.

FIGURE 9.

Cartoon of the deformation field surrounding a displaced spherical tracer. (A) A tracer with uniform no-slip, adhesive contact with its surroundings. Shading indicates the long-range deformation field in the surroundings when the tracer is translated. (B) A tracer with small contacts. Translating this tracer creates a strong deformation field near the tracer, and a much attenuated far-field deformation (compared to the first case). Darker shading indicates greater network deformation.

It has been shown that the development and maintenance of phagosomes require ATP-dependent proton pumps for acidification (25). Therefore, inhibition of ATP could result in swelling or breakdown of the phagosome, thus reducing the number or size of tracer-cytoskeleton contacts (i.e., changing from Fig. 8 C to Fig. 8 D). In such a case, internal LTM would report an artifactual softening not seen by either TPM or external LTM, just as we found (Fig. 6, A–C).

The amplitudes reported by our internalized tracers have a log-normal distribution of amplitudes, with a log-mean value of 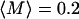and standard deviation that is a multiplicative factor of 2.2. In the range of corresponding M values we find (∼0.1–0.4), the amplitude is roughly proportional to the product of contact size and number M ∼ Nr_c (Fig. 7). This leads us to conclude that the distribution of apparent stiffnesses could be explained by a log-normal distribution of contact size, number, or both. Since log-normal distributions are frequently encountered in aggregation phenomena, we speculate that just such contact properties may be the result of adhesion receptor clustering or the heterogeneous distribution of membrane-bound receptors. Alternatively, heterogeneous discrete tracer/network contacts could result from cytoskeletal microheterogeneity at the tracer surface.

Comparison to literature results

Previous measurements using pharmacological agents for actin disruption (4,10,26), and myosin inhibition (27,28) have shown contradictory results and are difficult to compare because often different treatments, cell types, and rheology methods were used. Two studies, however, which use MTC (4) or LTM (10), found a clear increase in the rheology exponent in response to actin disruption, as opposed to the decrease found here in the cortical rheology. Of course, it is highly likely that smooth muscle cells (used in Fabry et al. (4)) will show a greater sensitivity to actin disruption and myosin inhibition. Alternatively, we find that external LTM tracers can probe the cortex, the deep cytoskeleton, or a combination of the two in a seemingly random manner that is presumably dependent on the details of tracer preparation. Therefore, when using externally attached tracers, one could find an increased exponent if actin disruption led to cortically-weighted (low exponent) tracers shifting systematically to being more interior-weighted (higher exponent).

Implications for current cell mechanical models

Currently there are three major models used to describe cellular rheology: tensegrity (29), soft glassy rheology (4), and the sol-gel hypothesis (30). The tensegrity model treats cells as a macroscopic system of tension-generating strings and compression-bearing struts, and considers the stress, or prestress, in this structure to be the primary determinant of the mechanical properties. Traditionally, the actin-myosin network is considered to be the source of the prestress and a primary component of tensegrity models (31). The rheological properties of the deep cytoskeleton are independent of both actin disruption and myosin inhibition, suggesting that this structure is either not based on tensegrity or another source of prestress generation exists in the cellular interior. Furthermore, actin disruption (32) and blebbistatin treatment (33) have both been shown to drastically decrease cellular traction forces. This suggests that a distinction should be drawn between the generation of external traction stress and any hypothetical prestress related to the deep cytoskeleton rheology.

The soft glassy rheology (SGR) model (34) was developed to explain the weak power-law rheology of pastes and foams, which is due to the rearrangement of their densely packed constituent particles or bubbles during flow. Since such rearrangements require much more than the thermal energy (k_BT) to occur, SGR assumes they are activated by nonthermal fluctuations, called an “effective temperature”, x, which is related directly to the rheology exponent by x = β + 1. In the cell context, it is supposed that the activity of molecular motors, including myosin, drives and regulates the effective temperature of cells (35) and, further, that the effective temperature might be related to the non-Brownian motion of the cytoskeleton (36). Our data show that the non-Brownian motion of the cytoskeleton is not related to the assumed SGR effective temperature, since its reduction by nearly 100-fold with ATP depletion does not affect the rheology exponent in either cell region. Since most, if not all, molecular motors should be significantly inhibited by this treatment, it seems more likely that the stress relaxation processes responsible for (epithelial) cell rheology are thermally activated.

The sol-gel hypothesis treats the cell as a gel of filamentary polymers filled with a fluid cytosol (30). Although much research has focused on the properties of reconstituted gels of actin and its cross-linking proteins (37–39), our work suggests that researchers would do well to consider intermediate-filament and microtubule-based gel networks as well. From a theoretical point of view, it is not clear how filamentary polymer gels can give rise to cell-like power-law rheology. Recent studies, however, showed that gels of actin and the cross-linking protein filamin A can produce weak power-law rheology (38,39), but with a rheology exponent (β ∼ 0.10) differing from those we find in TC7 cells. We have recently proposed a mechanism (40), however, based on cross-link proteins that undergo serial forced unfolding, that gives rise to power-law rheology generically in filamentary gels.

CONCLUSIONS

This study further underscores the utility of using multiple rheology methods, and TPM in particular, on a single type of cultured cell. This approach allows us to identify and avoid artifacts and ambiguities associated with difficult-to-quantify tracer-cytoskeleton contacts. We can now unambiguously infer that, in TC7 epithelial cells at least, neither F-actin nor any myosin isoform contributes to the stiffness of the deep intracellular cytoskeleton, its non-Brownian motion, or the unknown mechanism creating its power-law rheology. For the cortex, we find that F-actin (and potentially blebbistatin-insensitive myosin isoforms) play a role in the mechanism responsible for the cortex's power-law rheology, but neither F-actin nor any myosin isoform contribute significantly to the cortical stiffness.

More generally, distinct molecular mechanisms appear to be responsible for power-law rheology in different cell regions, suggesting a complicated rather than unitary explanation for its origin. Our results suggest that existing cell rheology models, which are often linked to the biophysics of actin and myosin, will need to be reworked to model the mechanics of the deep cell interior. Future work to dissect that mechanical response will need to focus on microtubules, their motors, and the intermediate filament cytoskeleton.