Protonation of Excited State Pyrene-1-Carboxylate by Phosphate and Organic Acids in Aqueous Solution Studied by Fluorescence Spectroscopy

Abstract

Pyrene-1-carboxylic acid has a pK of 4.0 in the ground state and 8.1 in the singlet electronic excited state. In the pH range of physiological interest (pH ∼5–8), the ground state compound is largely ionized as pyrene-1-carboxylate, but protonation of the excited state molecule occurs when a proton donor reacts with the carboxylate during the excited state lifetime of the fluorophore. Both forms of the pyrene derivatives are fluorescent, and in this work the protonation reaction was measured by monitoring steady-state and time-resolved fluorescence. The rate of protonation of pyrene-COO⁻ by acetic, chloroacetic, lactic, and cacodylic acids is a function of ΔpK, as predicted by Marcus theory. The rate of proton transfer from these acids saturates at high concentration, as expected for the existence of an encounter complex. Trihydrogen-phosphate is a much better proton donor than dihydrogen- and monohydrogen-phosphate, as can be seen by the pH dependence. The proton-donating ability of phosphate does not saturate at high concentrations, but increases with increasing phosphate concentration. We suggest that enhanced rate of proton transfer at high phosphate concentrations may be due to the dual proton donating and accepting nature of phosphate, in analogy to the Grotthuss mechanism for proton transfer in water. It is suggested that in molecular structures containing multiple phosphates, such as membrane surfaces and DNA, proton transfer rates will be enhanced by this mechanism.

INTRODUCTION

The equilibrium parameters of most biological reactions are dependent upon pH. Yet, one is hard pressed to find any example of an enzyme-catalyzed reaction rate that is limited by the rate of protonation or deprotonation. Based upon the initial observation by de Grotthuss (1) and corroborated many times later, the rate of proton transfer in aqueous solution is faster than what one expects for an ion diffusing in water (2). Even so, the rates of protonation for reactions in biological fluids are further enhanced by the presence of proton donating and accepting groups (3). Phosphate, which can act as donor and acceptor of three protons, is a major anion in living systems. Its concentration in extracellular and intracellular fluids is in the 0.5–2 mM range, with the concentration being closely regulated. In this article, we examine the role of phosphate in proton donation and contrast phosphate with carboxy-acids and cacodylic acid, which are single proton donors.

Fluorescence of molecules with suitable pK values can be used to study proton transfer rates. The basis of the fluorescence assay is that pK values are different for excited and ground state aromatic compounds (4). Light-induced deprotonation reactions for excited state aromatic hydroxy and amino compounds have been extensively studied and reviewed (5–12). Light-induced protonation reactions for aromatic carboxylic acids are also well-known (10,13). Pyrene-1-carboxylic acid has a pK of 4.0 in the ground state, whereas the excited state molecule has a pK of 8.1 (14). In the pH range of physiological interest (pH ∼5–8), the ground state compound is largely ionized as pyrene-1-carboxylate, but the excited state molecule will become protonated if a donor can transfer a proton to the carboxylate during the excited state lifetime of the fluorophore.

As shown in this article, the rate of protonation of pyrene-COO⁻ by weak acids is a function of ΔpK, as predicted by Marcus theory (15). At low concentrations of carboxy acids and cacodylic acid, the rate is dependent upon acid concentration. However, at high concentrations, the rate becomes independent of concentration, since the reaction becomes limited by formation of the reactive complex and proton transfer. However, this pattern is not seen for phosphate. For phosphate buffer the rate constant of transfer increases with increasing phosphate concentration. The high rate of proton transfer in water is attributed to dual proton donating and accepting character of water, and its ability to H-bond (16,17). We considered the possibility that the rate of proton transfer at high phosphate concentration is likewise related to the ability of phosphate to be simultaneously both a proton donor and acceptor.

MATERIALS AND METHODS

Materials

Water was deionized by reverse osmosis and then glass-distilled. Pyrene-1-carboxylic acid was obtained from Fluka Chemie (Deisenhofen, Germany). Na₃PO₄-12H₂O, Na₂HPO₄-7H₂O, NaH₂PO₄ were Baker-analyzed reagent grade. MP Biomedicals (Solon, OH) supplied the sodium salt of cacodylic acid ((CH₃)₂AsO₂H). Sodium salts of acetic acid (CH₃CO₂H), lactic acid (CH₃CHOHCO₂H), and monochloroacetic acid (CH₂ClCO₂H) were obtained from Sigma (St. Louis, MO).

The pH values of solutions were measured using a glass electrode that was calibrated with standard buffers. The stock solution of salts used to carry out titrations and the starting solutions were adjusted to desired pH by addition of HCl or NaOH. At the ending of the titration the pH was checked to make sure the pH remained at the starting value.

Spectroscopy

A Hitachi Perkin-Elmer U-3000 absorption instrument (Hitachi Instruments, Danbury, CT) was used to take the UV-visible absorption spectra.

Fluorescence emission spectra were measured with a Fluorolog-3-21 Jobin-Yvon Spex Instrument (Edison, NJ) equipped with a 450 W continuous Xenon lamp for excitation and a cooled R2658P Hamamatsu photomultiplier tube for detection (Hamamatsu Photonics, Hamamatsu City, Japan). All measurements were made with 90° geometry. Wavelength of excitation was 333 nm. Slit width was set to provide a band-pass of 2 nm for excitation and for emission. The concentration of pyrene-carboxylate was adjusted to an absorbance of 0.05 at the excitation wavelength. This corresponds to a concentration of 2 μM.

The fluorescence intensity decay profiles of pyrene-1-carboxylic acid in water were measured using the time-correlated single-photon-counting FluoTime200 fluorometer (PicoQuant, Berlin, Germany). This instrument, equipped with a microchannel plate on the detector, and a pulsed 334-nm LED for excitation, is capable of resolving lifetimes that are 100 ps and longer. Rotation-free polarization conditions (magic-angle polarizer orientation) were used to avoid the effects of Brownian rotation. The emitted light was isolated using a monochromator.

Analysis of fluorescence

In Fig. 1 we show a Förster cycle diagram for the case when pK is higher in the excited state than in the ground state molecule. We consider a system of two molecular forms, pyrene-COO⁻ and pyrene-COOH. At a given pH value, excitation with a δ-pulse leads to an initial populations of both forms and 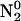in the excited states (pyrene-COO⁻* and pyrene-COOH*, respectively) that depends upon the pK value of the ground state molecules and relative extinction coefficient of both forms at the excitation wavelength. In the excited state, the pK value changes, forcing proton transfer. As given in Fig. 1, the rate constant for protonation to pyrene-COO⁻* is k₁ and the rate constant for deprotonation from pyrene-COOH* is k₂. The decay of molecules of pyrene-COO⁻* and pyrene-COOH*, at any given moment of time, can be respectively represented by

(1)

and

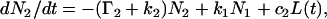(2)

where L(t) is the excitation function and c₁ and c₂ coefficients proportional to the number of molecules in forms 1 and 2 in ground states and their respective extinction coefficients at the excitation wavelength. The values N₁ and N₂ are numbers of molecules in forms 1 and 2 at any given moment of time; Γ₁ and Γ₂ represent the sum of radiative and nonradiative deactivation rates as shown in Fig. 1. The measured lifetime at extreme pH, where no excited-state proton transfer occurs, is τ₁ = 1/Γ₁ and τ₂ = 1/Γ₂.

FIGURE 1.

Schematic of protonation reaction of pyrene-1-carboxylate. Γ₁ = k_f1 + k_nr1; Γ₂ = k_f2 + k_nr2.

As given by Laws and Brand (12), the solution of this system of equations for decay of molecules according to Scheme 1 can be represented by

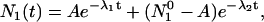(3)

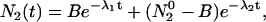(4)

where

(5)

and

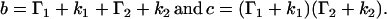(6)

A and B are amplitude terms given by

(7)

and

For samples in the absence of salt at pH 2 and 9.4, the emission spectra contained only one emitting species and the intensity decay was single-exponential. In this case, the data were fit to an exponential using FluoFit software (FluoFit V.4; PicoQuant, Berlin, Germany). In the presence of salts of weak acids, proton transfer occurred, and the emission composed of contribution from both forms. In this case, the decay profiles were obtained at 381 and 420 nm. The deconvolved intensity decays were fit globally to Eqs. 3 and 4 using MathCad 2001i Professional minimization routine (Adept Scientific, Bethesda, MD). For simplification, we used the intrinsic rate constant (Γ₁ and Γ₂) as determined for the pure forms at pH 2 and 9.4 as fixed parameters, and fit the intensity decays to determine protonation and deprotonation rate constants k₁ and k₂, and the relative amplitudes of forms 1 and 2 (A and B in Eqs. 3 and 4).

The pseudo first-order rate constant, k_q, was also evaluated by the steady-state intensity, I, of pyrene-COO⁻ according to

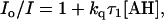(8)

where I_o is the intensity of pyrene-COO⁻ in the absence of proton transfer (18). The wavelength used was 381 nm. At high concentration of buffer, the intensity at 381 nm contains contribution from the pyrene-COOH form. This was corrected by taking a linear combination of the intensities at 420 and 381 nm, the contribution of the pyrene-COOH form subtracted from the intensity at 381 nm.

RESULTS

Fluorescence spectra and lifetime of pyrene-carboxylate and pyrene-carboxylic acid in the absence of added buffer

Absorption and fluorescence spectra of pyrene-COO⁻ and pyrene-COOH are shown in Fig. 2. Lower energy emission spectrum for the acidic form indicates a higher pK of the excited state molecule relative to the ground state molecule, as predicted by the Förster cycle (4,19). The maximum emission for pyrene-COOH is 415 nm and the maximum for pyrene-COO⁻ is 380.5 nm. This corresponds to an energy difference of 2185 cm⁻¹, for a calculated pK* of 8.67, close to the experimental value of 8.1 found by Van der Donckt (14). Pyrene derivatives are known to form excited state dimers in a reaction that is dependent upon diffusion (20,21). In Fig. 2, unstructured emission in the range of 450–550 nm (characteristic of the pyrene exciplex) is not seen. Furthermore, we examined the emission of pyrene-COO⁻ at 10-times the concentration used in Fig. 2; there was no evidence of pyrene-pyrene exciplex formation. The fluorescence intensity of pyrene-COOH was monitored between pH 1 and 2 and for pyrene-COO⁻ between 10 and 11. There was no change in fluorescence intensity in this range, showing that H⁺ and OH⁻ are not quenchers of fluorescence.

FIGURE 2.

Spectra of pyrene-1-COO⁻, pH 9.2 (solid line) and pyrene-1-COOH, pH 2.0 (dotted line) in water. A is the absorption; F is the fluorescence emission using 333 nm for excitation. NaOH and HCl used to adjust pH. Units on absorption and fluorescence (y axis) are arbitrary. Fluorophore concentration: 2 μM; temperature: 20°C.

Fig. 3 shows the fluorescence intensity decay of the two samples at extreme pH values that insure that pyrene-COO⁻ and pyrene-COOH are the sole emitting species. The lifetimes are 32.5 and 5.4 ns, for pH 9.4 and 2.0, respectively. The decays are single exponential ( between 0.9 and 1.1). The goodness of fit to a single exponential function is evident from the coincidence of the experimental data and the calculated fit curve. At pH 5.0 the decay can be fit with two exponential functions, with lifetimes the same as the acid and base forms. The pK of pyrene-COOH is 4.0 and at pH 5.0 the solution contains both forms. The amplitudes of the fluorescent components are comparable to the relative contribution of the carboxylate and carboxy-acid in the ground state. This shows that these forms do not interconvert during the excited state lifetime and indicates that the hydronium ion at a concentration ∼10⁻⁵ M does not act as a proton donor for excited state pyrene-COO⁻. Lifetimes are summarized in Table 1.

FIGURE 3.

(a) Fluorescence intensity decay of pyrene-1-COO⁻ in water at pH 9.4 observed at 381 nm. τ = 32.5 ns. (b) Fluorescence intensity decay of pyrene-1-COOH in water at pH 2 observed at λ_em = 420 nm. τ = 5.4 ns for single exponential fit. The instrument lamp function is indicated. Fluorophore concentration: 2 μM; temperature: 20°C. The calculated fit curves are the dark line, which appears superimposed over the shaded data points.

TABLE 1.

Exponential analysis for fluorescence intensity decays of pyrene-1-carboxylic acid in water

λemis, nm	Temperature	pH	τi, ns	αi
381	20°C	9.4	32.5	1.00	1.112
420	20°C	2.0	5.4	1.00	0.962
381	20°C	5.0	5.9, 36.3	0.13, 0.87	1.053
420	20°C	5.0	5.2, 36.0	0.26, 0.74	1.076

Addition of salts of weak acids

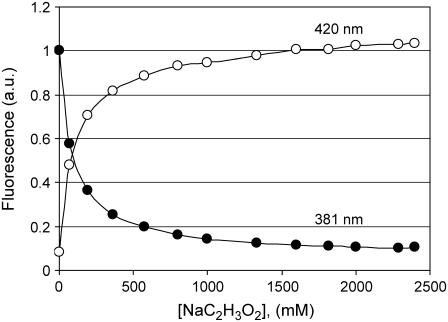
The addition of Na-acetate to the solution of pyrene-COO⁻ at pH 5.0 decreases the fluorescence contribution of the basic form and increases the fluorescence of the acidic form. Spectra of pyrene-COO⁻ with Na-acetate added are shown in Fig. 4. As Na-acetate increases, the decrease in fluorescence of pyrene-COO⁻ occurs in parallel with the increase in pyrene-COOH, as is documented in Fig. 5 where the intensities of fluorescence at 381 and 420 nm are compared. At high Na-acetate concentration there is a saturation effect; for example, between 1.5 and 2.4 M Na-acetate there is little change in the spectra.

FIGURE 4.

Fluorescence spectra of pyrene-1-COO⁻ in water, pH 5 at 20°C as a function of Na-acetate. Concentration of added Na-acetate was 0 (indicated), 0.065, 0.19, 0.364, 0.572, 0.8, 1.0, 1.33, 1.6, 1.82, 2.0 2.29, and 2.4 (indicated) M. Fluorophore concentration: 2 μM.

FIGURE 5.

Changes in fluorescence intensity 2 μM pyrene-1-COO⁻ in water, pH 5 at 20°C as a function of added Na acetate measured at 381 nm (solid circles) and at 420 nm (open circles). Data taken from Fig. 4.

The fluorescence change that occurs when Na-acetate is added depends upon pH. The titration of NaC₂H₃O₂ was compared at pH 5.0, 5.5, and 7. The acetic acid was calculated based upon the pK of Na-acetate and the pH. At pH 7, there is no conversion of the basic form even at 2.5 M. At 1 M, at pH 5 the concentration of acidic acid is 0.365, at pH 6 the concentration is 0.054, and at pH 7 this value is 0.0057 M. The concentration dependence of fluorescence change strictly followed the acid concentration, not the acetate. Based upon the lifetime and the initial slope of the curve, the bimolecular rate constant is 8.5 × 10⁸ M⁻¹ s⁻¹ for acetic acid.

The Stern-Volmer plots for the Na salts of lactic, cacodylic, and monochloroacetic acids are given in Fig. 6. At low concentrations, the quenching effect is linear with salt concentration. In the cases where it was experimentally feasible to go to high concentration, it could be seen that the Stern-Volmer plots approached saturation. At very high concentration of bases, photo-acids react at a rate which is the intrinsic proton transfer rate (22).

FIGURE 6.

Fluorescence quenching of 2 μM pyrene-1-COO⁻ in water at 20°C. Data plotted according to Eq. 8. Total buffer concentration is given on the abscissa. Na-acetate (solid circles), Na-lactate (open triangles), Na-cacodylate (open squares), and Na-monochloroacetate (open circles) at pH 5. Solid diamonds give values for Na-acetate at pH 7.

In the experiments described above, the cation concentration as well as the anion concentration is changing. We considered the possibility that shielding of charges by cations could be affecting the reaction. The experiments were repeated at 0.5 M NaCl and Na-acetate was varied. We saw no difference in the effect of proton donation by acetic acid (data not shown).

Addition of phosphate

Phosphate acts as a proton donor to pyrene-COO⁻*. This is documented in Fig. 7, A–C, for Na-phosphate salts at pH 5, 6, and 7.2, respectively. Proton transfer is the highest at pH 5, as seen by the increased conversion to pyrene-COOH. At pH 7.2, phosphate had very little effect on the yield. The pK of 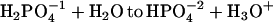is 7.21. Therefore, at pH 7 the solution contains approximately half . Yet there is no detectable proton transfer at pH 7.2, whereas, at pH 6, pyrene-COO⁻ is transformed to pyrene-COOH. This observation eliminates both 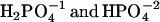as significant proton donors. For 1 M phosphate, at pH 7.2, the concentration of H₂PO₄ is <10⁻⁵ M, for pH 6, the value is 1.2 × 10⁻⁴ M, and at pH 5, the concentration is 1.3 × 10⁻³ M. The pH profile indicates that H₃PO₄ is the major proton donor.

FIGURE 7.

Fluorescence spectra of pyrene-1-COO⁻ in water at 20°C as a function of phosphate. (A) The pH was 5. Phosphate concentration was 0, 0.03, 0.09, 0.17, 0.26, 0.37, 0.46, 0.54, 0.62, 0.74, 0.84, 0.93, 0.98, 1.06, and 1.11 (indicated) M. (B) The pH was 6. Phosphate concentration was 0 (indicated), 0.33, 0.95, 0.18, 0.29, 0.4, 0.5, 0.59, 0.67, 0.8, 0.91, 1.0, 1.08, 1.14, and 1.2 (indicated) M. (C) The pH was 7.2. Phosphate concentration was 0, 0.95, 0.18, 0.29, 0.4, 0.5, 0.59, 0.67, 0.8, 0.91, 1.0, 1.08, 1.14, and 1.2 (indicated) M.

Stern-Volmer plots for the data at pH 5, 6, and 7.2 are shown in Fig. 8. Unlike acetate, the Stern-Volmer plot shows an upward slope as a function of phosphate. The upward slope is especially apparent at pH 5.

FIGURE 8.

Fluorescence quenching of 2 μM pyrene-1-COO⁻ in water by phosphate at 20°C. Data plotted according to Eq. 8; pH 5 (solid circles), pH 6 (open circles), and pH 7.2 (solid squares).

Time resolution of the emission

The fluorescence decay was examined in the presence of salts of weak acids. The decay profiles for the sample in the presence of 1 M Na phosphate are given in Fig. 9 using 381 and 420 nm as emission wavelengths. It was not possible to choose a wavelength that isolates either of the pyrene derivatives' spectra as fluorescence at either wavelength contains contribution of both species. The contribution of the protonated form was subtracted in Fig. 9 A. The decrease in the lifetime of pyrene-1-COO⁻ and the rise time and then decay of pyrene-1-COOH are apparent in the figure.

FIGURE 9.

Time-intensity profiles of 2 μM pyrene-1-carboxylate in water. (A) Emission at 381 nm in the absence (a) and the presence (b) of 1 M Na-phosphate pH 5. Contribution of the fluorescence from pyrene-1-COOH was subtracted from the decay curve. (B) Emission at 420 nm representing pyrene-1-COOH. Dark lines are the best fit to a double exponential analysis. Values for the fits are given in Tables 1 and 2.

The analyses of the data at both wavelengths for forward (k₁) and reverse (k₂) rate constants are given in Table 2 for phosphate and acetate. As expected, the forward rate constant is very dependent upon the concentration of buffer. In going from 0.1 M to 2 M Na-acetate, the forward rate constant increases by a factor of ∼20. The increase is consistent with the decrease in the fluorescence of pyrene-COO⁻ seen in the steady-state spectra (Fig. 7). The reverse rate constant also increases with Na-acetate or Na-phosphate, but the effect is less.

TABLE 2.

Fluorescence decay of pyrene-1-COO⁻ in the presence of Na acetate and Na phosphate salts (aqueous solution pH 5, 20°C)

Conditions Concentration of Na salt	Analysis for exponential decay				Analysis for excited state reaction*
		λemis, nm	τi, ns	αi		k1, s−1	k2, s−1	A	B
0.1 M acetate	381	4.5, 19.5	−0.24, 0.76	1.031	2.6 × 107	3.8 × 107	0.90	0.096
0.1 M acetate	420	4.7, 19.3	−0.34, 0.66	1.045	2.4 × 107	1.2 × 107	0.92	0.08
0.5 M acetate	381	4.0, 9.4	−0.42, 0.58	1.005	1.1 × 108	4 × 107	0.80	0.20
0.5 M acetate	420	3.9, 9.4	−0.45, 0.54	1.049	1.2 × 108	4.8 × 107	0.87	0.13
1.0 M acetate	381	2.8, 7.51	−0.43, 0.57	1.001	2.2 × 108	6.7 × 107	0.75	0.25
1.0 M acetate	420	2.74, 7.47	−0.46, 0.54	1.051	2.2 × 108	6.5 × 107	0.82	0.18
2.0 M acetate	381	1.83, 6.7	−0.41, 0.59	0.993	4.1 × 108	8.8 × 107	0.70	0.30
2.0 M acetate	420	1.81, 6.63	−0.44, 0.557	1.038	4.1 × 108	9.2 × 107	0.74	0.26
0.5 M phosphate	381	4.5, 23.6	−0.21, 0.79	1.053	1.4 × 107	2.8 × 107	0.94	0.06
0.5 M phosphate	420	4.5, 23.5	−0.35, 0.65	1.04	1.5 × 107	4.4 × 107	0.96	0.04
1.0 M phosphate	381	3.7, 14.6	−0.34, 0.66	0.968	6.1 × 107	7.9 × 107	0.87	0.13
1.0 M phosphate	420	3.6, 14.6	−0.43, 0.57	1.000	6.0 × 107	7.0 × 107	0.89	0.11

^*Values for Γ₁ and Γ₂ obtained from the lifetime values given in Table 1 for pH values 2.0 and 9.4 at 20°C; A and B are defined by Eq. 7.

Marcus behavior

Pseudo bimolecular rate constants were obtained from the data in Table 2 by dividing the rate constant k₁ by the concentration of acid. The bimolecular rate constants obtained from the steady-state and time-resolved spectra are given in Table 3. A very good correspondence between the two independent measurements was seen for the determination of rate constants.

TABLE 3.

pK of acids in water and bimolecular rate constants at 20°C, pH 5.0

	pK*	ΔpK	kq, M−1 s−1†	kq, M−1 s−1‡
Acetic acid <0.1 M	4.76	−3.34	8.50 × 108	–
Acetic acid 0.1 M		−3.34	6.9 × 108	6.8 × 108
Acetic acid 0.5 M		−3.34	4.1 × 108	6.1 × 108
Acetic acid 1 M		−3.34	3.1 × 108	5.9 × 108
Acetic acid 2 M		−3.34	1.2 × 108	5.5 × 108
Monochloroacetic acid	2.85	−5.25	7.65 × 109	–
Lactic acid	3.86	−4.24	2.03 × 109	–
Cacodylic acid	6.19	−1.91	7.96 × 107	–
H3PO4 0–0.1 M	2.12	−5.98	1.54 × 1010	–
H3PO4 0.1–0.6 M		−5.98	2.63 × 1010	2.2 × 1010
H3PO4 0.6–1.0 M		−5.98	3.79 × 1010	–
H3PO4 1–1.5 M		−5.98	5.47 × 1010	4.6 × 1010
	7.21	−0.89	1.07 × 107	–

^*The pK values are obtained from the CRC Handbook of Chemistry and Physics (32).

^†Values obtained from steady-state measurements.

^‡Values obtained from time-resolved measurements.

The log rate of transfer versus the ΔpK is plotted in Fig. 10. It can be seen that the rate is a function of ΔpK as predicted by Marcus (15). Four values for the rate constants of H₃PO₄ are plotted; these values correspond to different concentration ranges given in Table 3.

FIGURE 10.

Marcus plot of the log of rate constants for the fluorescence quenching of pyrene-1-COO⁻ in water by mono-chloroacetic acid (1), lactic acid (2), acetic acid (3), cacodylic acid (4), sodium phosphate (lower solid circle), and phosphoric acid (upper solid circles) versus ΔpK (i.e., pK of the acid minus pK of excited state pyrene). Data given in Table 3.

DISCUSSION

In this work pyrene-1-carboxylate is used to study proton transfer rates in aqueous solution from phosphate and from acetic, lactic, and cacodylic acids.

Pyrene-1-carboxylic acid as a fluorescent molecule to measure protonation reactions has some advantages over previously used probes. Its decay is strictly single exponential in the absence of proton transfer (Fig. 3). Exponential greatly simplifies the analysis of the proton transfer. Furthermore, the two forms of pyrene-COOH have distinct emission spectra (Figs. 2 and 3).

We show that excited state pyrene-carboxylate accepts a proton from acids at a rate that is related to ΔpK, as predicted by Marcus. This relationship was also shown for the deprotonation reaction of 2-naphthol with anions (23). The Marcus relationship can also be invoked to explain why H₃PO₄ is the best phosphate proton donor. The ΔpK-value is larger for H₃PO₄ than for 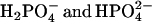, providing for greater driving force. We note that there is also a statistical factor: the acid form has three protons that are potential donators, but this cannot account for the large difference in rate. The Marcus relationship also explains why proton from water does not contribute. The high pK of water (∼14) and the low concentration of H₃0⁺, which is ∼10⁻⁵ M in our experiments, rules out the possible proton donation from water.

The most interesting result from our study is that proton transfer involving phosphate does not show saturation at high concentrations, but in fact shows enhanced rate.

A model for proton transfer is shown in Fig. 11. The special effect of phosphate is that it can be both a proton donor and acceptor. The model is analogous to proton-conducting pathways hypothesized for water. The Grotthuss effect shows that water has an anomalously high proton conductance and, although details of the mechanism remain an area of continuing research (24), the ability of water to conduct protons rests on its ability to H-bond to H₃O⁺ in a fashion such that the σ-bond of O-H and the H-bond between O and H can transiently exchange. For phosphate, if protons transfer between water and phosphate, then at high phosphate concentration, proton transfer rates will increase.

FIGURE 11.

Model for phosphate-assisted proton transfer. The picture represents value structures for phosphate in gas phase calculated by GAUSSIAN98. The angles are as follows: 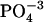is 109°, tetrahedral; 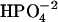is 97.7° between HO-P-O where the H is close to the other O; 104.9° between HO-P-O for the other two O-values, and 115.0° between the other three O-P-O bends; 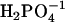is 100.5° between HO-P-OH, and 125.2° between O-P-O.

Pyrene-1-carboxylic acid has heretofore not been studied in detail as a probe for proton acceptance, but 1-hydroxypyrene has been used as a photoactivated proton donor (25). It would be especially interesting to compare the proton donation and acceptance functions as a function of time. Proton donation reactions exhibit a fast kinetic phase and then a slower reaction (26,27). A fast reaction and upward curve in the Stern-Volmer plot is predicted from diffusion theory when, after excitation, it takes time for the diffusion gradient to be established (28,29). These features have been demonstrated for pyrene exciplex formation (21). An interesting prospect will be to compare the fast proton donation and acceptance functions of similar probes in aqueous solutions.

Phosphate ion is a major buffering ion in biological tissues and the reactions of the cell are strongly dependent upon pH. The concentration of phosphate physiological fluids is not high enough so that the pyrene probe would detect the cooperative effect. However, this is a function of the lifetime of the excited state; the effect may be apparent when slower reactions, such as the turnover time of most enzymes, are studied. Furthermore, at local sites, rapid proton transfer by phosphate could be significant. Phosphates are crucial for the stability of DNA and RNA structures. Phosphorylation of enzymes is a common regulatory mechanism of metabolism, and changes in cellular pH values influence metabolism in a dramatic fashion. Membranes are composed of phospholipids and phosphates are at the lipid/water interface of all membranes. Proton transfer along the membrane surface, if abetted by a Grotthuss-type mechanism, would also occur at rates faster than diffusion rate (30,31).

SUMMARY

Protonation of excited state pyrene-carboxylate by carboxy-acids occurs at a rate that is consistent with the Marcus theory. Phosphate shows quenching rates that become faster as phosphate concentration increases. We suggest that this is due to the ability of phosphate to be both a donor and acceptor of H and to the H-bonding nature of phosphate and water.