Dynamics and Diffusion in Photosynthetic Membranes from Rhodospirillum Photometricum

Abstract

Photosynthetic organisms drive their metabolism by converting light energy into an electrochemical gradient with high efficiency. This conversion depends on the diffusion of quinones within the membrane. In purple photosynthetic bacteria, quinones reduced by the reaction center (RC) diffuse to the cytochrome bc₁ complex and then return once reoxidized to the RC. In Rhodospirillum photometricum the RC-containing core complexes are found in a disordered molecular environment, with fixed light-harvesting complex/core complex ratio but without a fixed architecture, whereas additional light-harvesting complexes synthesized under low-light conditions pack into large paracrystalline antenna domains. Here, we have analyzed, using time-lapse atomic force microscopy, the dynamics of the protein complexes in the different membrane domains and find that the disordered regions are dynamic whereas ordered antennae domains are static. Based on our observations we propose, and analyze using Monte Carlo simulations, a model for quinone diffusion in photosynthetic membranes. We show that the formation of large static antennae domains may represent a strategy for increasing electron transfer rates between distant complexes within the membrane and thus be important for photosynthetic efficiency.

INTRODUCTION

Anoxygenic purple bacteria are capable of photosynthesis using a particularly simple and well-characterized system (1). Light energy is initially absorbed by light-harvesting antennae complexes and then transferred to an RC where a photochemical charge separation takes place. Some of the antennae complexes (LH1) and the RC are closely associated and form a core complex to ensure the efficiency of this energy transfer. The photochemically generated electron is used to reduce a membrane-soluble quinone molecule, which, after being doubly reduced and protonated, diffuses to a cytochrome bc₁ complex where it is reoxidized with a concomitant transfer of protons from the cytoplasm to the periplasm. The electrons are then returned to the RC via soluble periplasmic electron carriers, typically c-type cytochromes or sometimes high-potential iron-sulfur proteins. The protons pumped across the cytoplasmic membrane return to the cytoplasm through an F₀F₁ ATP-synthase, in the process forming ATP from ADP and phosphate. This system uses four different membrane protein complexes: the peripheral antenna or LH2 complex, the core complex that contains the RC and associated LH1 antennae, the cytochrome bc₁, and the ATP-synthase.

These different proteins of the photosynthetic apparatus are organized in specialized photosynthetic membranes; however, their organization and structure varies somewhat between species. Recently, atomic force microscopy (AFM) (2) has been used to visualize the organization in membranes of several different organisms (3–10), extending previous electron microscopic analysis (11–13).

In Rhodospirillum (Rsp.) photometricum, monomeric core complexes are arranged in a disordered mixture with LH2, whereas additional LH2 complexes synthesized in cells grown with low illumination levels form two-dimensional (2D) paracrystalline arrays (7,9–10). This growth-condition-dependent arrangement has been confirmed in the native photosynthetic membranes of Phaeospirillum (Phsp.) molischianum (4). In Rhodobacter (Rb.) sphaeroides (14–16) and Rb. blasticus (5), core complexes are dimeric, containing two reaction centers (RCs) and an S-shaped aggregate of core antennae proteins. These core complexes are in Rb. sphaeroides apparently organized in short chains (3,17), whereas in Rb. blasticus the arrangement is more disordered (18). In Rhodopseudomonas (Rps.) palustris the organization is again different: core complexes are once again monomeric but arranged partly in a disordered mixture and partly in (2D) crystalline arrays, and the LH2 and low-light LH2 are similarly separated into a part mixed with core complexes and a part organized in crystalline arrays (6). In all these studies, and in those of the LH2-deficient Blastochloris (Blc.) viridis (8), where monomeric core complexes form hexagonally packed arrays, neither of the other two integral membrane protein components of the photosynthetic apparatus, namely the cytochrome bc₁ complex and the ATP-synthase, have been observed. This poses something of a paradox, as both these proteins are necessary for photosynthetic growth and function of the photosynthetic machinery.

The function of the photosynthetic membrane depends on two difficultly compatible requirements. On the one hand high connectivity is essential for excitation transfer between the light-harvesting system and the RC, and on the other hand high connectivity for quinone/quinol diffusion between the RCs and the cytochrome bc₁ complexes must be assured. These two different connectivities are both constrained to the membrane plane, the first by the stable association of pigments with integral membrane proteins and the second by the use of a membrane-soluble electron transporter diffusing in the middle of the membrane (19), although the two connectivities operate on rather different timescales. One obvious solution to these competing requirements is the formation of supercomplexes containing RC and cytochrome bc₁ (20), which though they have not yet been observed directly (3–5) have been strongly suggested by functional measurements on certain bacteria such as Rb. sphaeroides (21–23). However this solution does not seem to have been adopted in Rsp. photometricum and several other species, where the RC-containing core complex appears to be embedded in the light-harvesting system and separated from the cytochrome bc₁ complex (4,6–9). It is thus of great interest to consider how such a system is optimized and what advantages this organization could offer over an organization in supercomplexes.

In higher plants, plastoquinone diffusion in the thylakoid membrane confronts similar problems, particularly in stacked granal membranes where there is a physical separation between the photosystem II RCs and their associated antennae in the granal lamellae and the cytochrome b₆f complex (functionally equivalent to the bacterial cytochrome bc₁ complex) at the granal periphery. This situation leads to an important control on photosynthetic flux by plastoquinone diffusion (24).

Diffusion in 2D is a surprisingly complex phenomenon. The most popular current model for protein diffusion in the dilute lipid membrane is based on the analysis of Saffman and Delbrück (25) in which the mobility of the protein depends on the interplay between membrane and outer-liquid viscosity, the membrane thickness, and the particle radius. However in biological membranes, as opposed to pure lipid membranes, mobility will be strongly influenced by molecular crowding.

Theoretical investigations of the effects of molecular crowding on 2D diffusion have essentially relied on lattice models and random walks to understand how self-diffusion and tracer diffusion evolve with obstacle concentration (26–34). Particular emphasis has been made in these studies on understanding fluorescence recovery after photobleaching experiments, which can provide an experimental measure of lateral diffusion in biological membranes on a scale of several hundreds of nanometers.

Randomly distributed obstructions have been shown to produce anomalous subdiffusion on length scales shorter than the characteristic length of the average size of the clusters of obstructing objects (30). Above a characteristic obstacle concentration, a percolation threshold is reached, at which point long-distance diffusion becomes impossible. Recent investigations have examined the structure of thylakoid membranes containing light-harvesting systems. Cytochrome b₆f and RCs and the influence of their architecture on the diffusion of plastoquinone through these membranes using lattice-based Monte Carlo simulations (33–34) have suggested the necessity of specific supramolecular organizations in this system.

Recently higher resolution techniques including high-speed single particle tracking (35–37) and fluorescence correlation measurements (38) have been used to investigate diffusion in eukaryotic membranes. These studies have shown hop diffusion, in which after a period trapped in a particular domain the tracer hops rapidly to another domain. This type of diffusion is characterized by a pair of diffusion constants and a confinement area. While trapped within a particular area, the molecules show a corralled diffusion. However long-distance diffusion persists but is slow and controlled by the rate of hopping between these domains of confinement.

To gain insights into photosynthetic membrane properties and the equilibrium between excitation transfer and quinone diffusion, we have investigated the structure and the diffusion dynamics of the pigment protein complexes in membranes of Rsp. photometricum. These experimental measurements were complemented by lattice-free Monte Carlo simulations to elucidate the possible effects of the observed structure and dynamics on migration of quinones in the photosynthetic membranes. Our results provide insight into the optimization of the bacterial photosynthetic architecture and the nature of diffusion through a biological membrane.

MATERIALS AND METHODS

Bacterial culture and membrane preparation

Rsp. photometricum (DSM 121) was grown photoheterotrophically on modified Hutner media 27 under low-light (10–20 Wm⁻²) or high-light (100 Wm⁻²) conditions, as described previously (7,9,10). Cells were harvested and washed two times with 1 mM Tris-HCl, pH 7.0, before being broken by one passage through a French pressure cell. Lysates were loaded directly onto 5%–60% sucrose gradients and centrifuged for 1.5 h. The membranes corresponding to the major pigmented band sedimented to ∼40% sucrose and contained the different proteins of the photosynthetic apparatus. The membranes were washed with 1 mM Tris-HCl, pH 8, in a centrifugal concentrator and kept at 4°C for AFM analysis.

Atomic force microscopy

Mica prepared as described (39) was freshly cleaved and used as support. The mica was immediately covered by 40 μl of adsorption buffer containing 10 mM Tris-HCl, pH 7.3, 150 mM KCl, 25 mM MgCl₂. Subsequently, 2 μl of membrane solution was injected into the adsorption buffer drop on the mica surface. After 1 h the sample was rinsed with 10 volumes of recording buffer containing 10 mM Tris-HCl, pH 7.3, 300 mM KCl. Imaging was performed with a commercial Nanoscope-E contact-mode AFM (from Digital Instruments, Santa Barbara, CA) equipped with a low-noise laser and a 160-μm scanner (J-scanner) using oxide-sharpened Si₃N₄ cantilevers with a length of 100 μm (k = 0.09 N/m; Olympus, Tokyo, Japan). For imaging, minimal loading forces of ∼100 pN were applied at scan frequencies of ∼6 Hz (∼1200 nm/s) using optimized feedback parameters. The piezo precision was determined on protein 2D crystals at scan ranges between 100 nm and 300 nm, and errors in x- and y-dimensions <2% were found.

Monte Carlo simulations

Different model membranes were constructed containing circular obstacles as described previously (9) and equilibrated with periodic boundary conditions before being compressed or expanded over ∼10⁶ Monte Carlo steps to obtain the desired surface occupancy. Simulations of tracer diffusion in model membranes were performed by randomly inserting 1000 tracer molecules into free sites in the model membranes. The time evolution of the system was then investigated by attempting to move each tracer and accepting or rejecting the move. With a hard disc potential, the move was rejected if the tracer entered a disk. For each simulation, between 65,000 and 100,000,000 Monte Carlo steps were performed on each of the 1000 tracers and results accumulated. Estimated long-distance diffusion rates were obtained by fitting diffusion rates over distances >0.5 obstacle diameters to an exponential function.

RESULTS AND DISCUSSION

Protein diffusion

We have previously investigated the structure of photosynthetic membranes from the bacterium Rsp. photometricum using AFM (7,9). These investigations showed that the membrane is organized in two structurally distinct domains: disordered domains containing LH2 and core complexes, and paracrystalline LH2 antenna domains. The size and nature of the various objects observed in Rsp. photometricum membranes discussed in this article are collected in Table 1. These membranes are able to efficiently harvest light energy to support photosynthetic electron transfer, indeed functional measurements on membranes isolated from Rsp. photometricum, and the closely related and similar (4) species Phsp. molischianum, indicate that cytochrome bc₁ reduction is necessary for development of a membrane potential (C. Mascle-Allemand, J. Alric, J. Lavergne, and J. N. Sturgis, unpublished data). However in both species cytochrome bc₁ reduction after flash illumination appears to be too slow to allow direct observation of the associated membrane potential changes.

TABLE 1.

Size and nature of objects observed and discussed in Rsp. photometricum membranes

Object	Size (nm)	Nature
Membrane fragments	200–500 nm	Photosynthetically competent membrane fragments isolated from the bacterium
Paracrystalline LH2 domains	20–150 nm	Regions of hexagonally packed LH2
Mixed domains	200–500 nm	Disordered regions of membrane containing a constant mixture of 3.5 LH2/core complex
Core complex	11.5 nm	Annular complex composed of a reaction center surrounded by 16 LH1 αβ heterodimers, large rings
LH2	7.5 nm	Annular complex of 9 LH2 αβ heterodimers, small rings
Quinone	0.5 nm	Lipid soluble electron carrier ubiquinone10

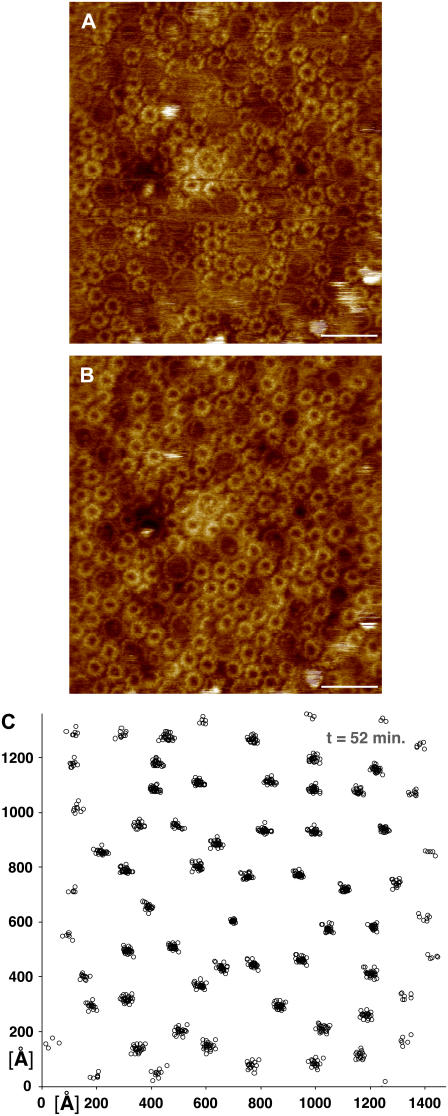
To investigate the dynamics of these different membrane domains, we repeatedly imaged several areas of membrane, from both high-light- and low-light-grown cells at high resolution to allow easy identification and measurement of the different complex positions with high precision. Pairs of such images are shown in Figs. 1 and 2. Fig. 1, A and B, shows a mixture of core complexes and LH2 complexes in high-light-adapted membranes rich in disordered regions. The individual complexes in this set of images were located and identified, and then each series of images was aligned to minimize the average of the root mean squared (rms) deviations of all the observed complex positions, as is shown in Fig. 1 C in which the core complex positions from a series of 31 topographs obtained of the membrane area shown in Fig. 1 A over a period of 52 min are shown.

FIGURE 1.

Mobility of the photosynthetic complexes in high-light-adapted membranes of Rsp. photometricum. (A, B) Two subsequent topographs of the same area of the photosynthetic membranes (scale bar, 20 nm; full color scale, 3 nm). (C) Core complex position map from 31 aligned topographs acquired over 52 min, including the images in panels A and B.

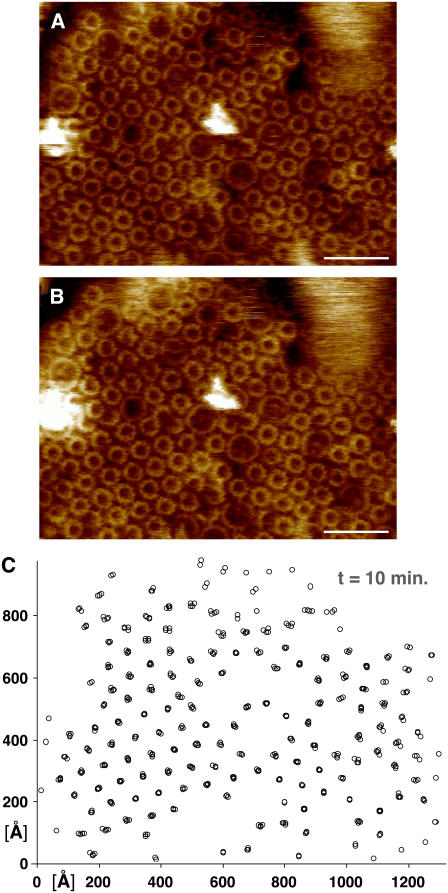
FIGURE 2.

Mobility of the photosynthetic complexes in low-light-adapted membranes of Rsp. photometricum. (A, B) Two subsequent topographs of the same area of the photosynthetic membranes (scale bar, 20 nm; full color scale, 3 nm). (C) LH2-complex position map from five aligned topographs acquired over 10 min, including the images in panels A and B.

In Fig. 2 we show a similar pair of images and correlated complex positions for a different membrane area. This figure shows a sample region of a low-light-adapted membrane containing many paracrystalline LH2 complexes that we imaged continually over a period of 10 min. From the image in Fig. 2 C it is readily apparent that the complexes in a crystalline environment are much less mobile than the complexes in less ordered environments.

As is immediately apparent, the individual complexes are easily identifiable and do not migrate very far. This is in marked contrast to what has previously been observed for purified and reconstituted F_O rings of Ilyobacter tartaricus (40), where some complexes were observed to undergo rapid lateral diffusion. Qualitatively the images appear to show that each complex rattles slightly about its equilibrium position but there is no long-distance movement. It is important to note that the movements that we see in noncrystalline regions are much larger than our measurement accuracy of ±6 Å, as judged by repeatedly analyzing the positions of a complex in the same image.

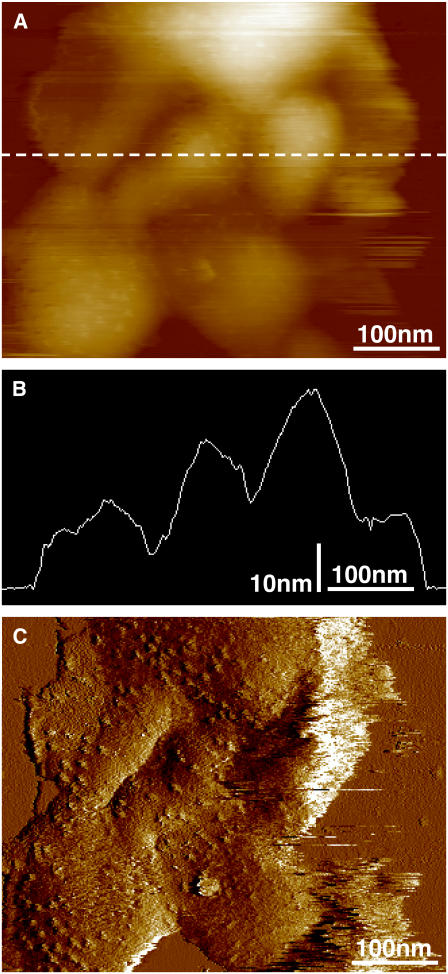
A particular advantage of Rsp. photometricum for such investigations is that the membranes form relatively robust closed sacks, similar to grana in higher plants. Thus the complexes imaged are not directly attached electrostatically to the mica support but are resting on the other surface of the sack, which is in turn attached to the mica, as we have previously described (9), and is illustrated in Fig. 3. The membranes sacks are ∼12-nm thick (Fig. 3 B), which is slightly over twice the thickness of a single photosynthetic membrane on a mica surface (6). The feedback error signal in Fig. 3 C, and to a lesser extent the height signal in Fig. 3 A, shows the roughness associated with the RC H subunit, confirming that we are imaging the cytoplasmic surface. We thus conclude that we are imaging membrane sacks deposed on the mica surface with an exposed cytoplasmic surface. The sack-like vesicle structure avoids direct interactions between the imaged complexes and the mica support perturbing the dynamics of the complexes. It remains, however, possible that interactions between the two membranes perturb the dynamics. We do not believe this to be the case, in particular as the geometry and organization of the complexes is native.

FIGURE 3.

Membrane overview of low-light-adapted membranes showing their organization on the mica surface. (A) Image of sample height. (B) Cross section along the dotted line in panel A. (C) The error feedback signal of the same image that highlights the surface roughness.

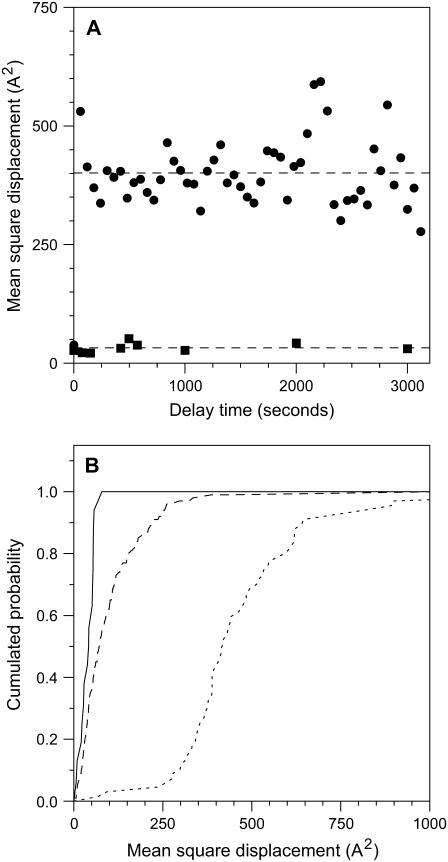
To better examine the movement of complexes, we calculated for each complex its mean square displacement (msd) as a function of time. This analysis has been performed for core complexes, which are always in disordered regions, for LH2 complexes in paracrystalline close packed regions, and for LH2 complexes as a whole. In Fig. 4 A we show the evolution of the msd with time for core complexes and LH2 complexes in paracrystalline regions. As can be seen in the time range accessible to our measurements (75–3000 s), there is no evolution of the msd with time for either type of complex; thus there is no long-range diffusion and each complex is confined to its original position. In the case of the core complexes, the variations in position are considerably greater than those that can be attributed to instrument stability and thus can be attributed to short-range diffusion in the membrane. In the case of LH2 complexes located in paracrystalline regions of the membrane, the measured msd is at all times comparable to the measurement accuracy, strongly suggesting that these complexes are static. We were unable to observe any relationship between the msd and complex position, suggesting that image stability did not significantly decline at the edges of the zone examined.

FIGURE 4.

Analysis of mobility of complexes in photosynthetic membranes. (A) Evolution of msd, averaged over complexes, with time for core complexes in mixed membrane regions (circles) and LH2 complexes in paracrystalline regions (squares). The dashed lines show the average msds of 401 and 33 A². (B) Distribution of individual complex mobilities (msd), averaged over delay times, for LH2 complexes in crystalline regions (solid line); all LH2 complexes (dashed line); and core complexes (dotted line).

The situation we observe for core complexes in Fig. 4 A is typical for corralled diffusion in which a molecule rattles around rapidly in a space slightly larger than it is. This situation is characterized by the diffusion constant within the confinement zone and the area of confinement. Unfortunately, we do not have access to the diffusion constant within the confinement zone, as we do not see any deviation of the msd from the constant value at the shortest delays, which are nevertheless many tens of seconds. Thus in each image we simply sample a random position for each complex within its confinement zone. The msd observed under these circumstances gives a measure of the area of confinement; thus the centers of the core complexes in the disordered membrane areas are confined to zones with an area of 4 nm². As we have measured the average distance between two Rsp. photometricum core complexes in contact to be 11.5 nm (9), this gives a diameter for the confinement area of ∼13.7 nm (11.5 + 2 × √(4/π)) and an area of 150 nm². More simply viewed, each complex is separated from its nearest neighbors by a distance that varies with time of the order of 1 or 2 nm.

In Fig. 4 B we show the cumulative probability as a function of msd for different complexes. This panel shows very dramatically the restricted dynamics of LH2 complexes in crystalline regions (solid line msd = 33 ± 20 A²) and the much greater mobility of core complexes (dotted line msd = 400 ± 200 A²). The third (dashed) line corresponds to all LH2 complexes in low-light membranes (Fig. 2); this line shows that many of these complexes are much more mobile than the complexes in crystalline regions, even if there are few LH2 complexes as mobile as core complexes. Thus about half the complexes have mobilities intermediate between those observed in crystalline regions and those of core complexes. A simple interpretation of this intermediate mobility is that these complexes partition between crystalline regions and noncrystalline regions, and thus the average mobility measured is a time-weighted average of the low mobility crystalline region and the higher mobility disordered regions.

These observations have several important consequences in the context of the observed membrane structure with its very high protein density. To measure the protein density in disordered membrane regions, we have calculated from several different images the total number of complexes of each type imaged, the area imaged, and the number and area of hexagonally packed complexes (9). These measurements coupled with the sizes of the complexes established from the pair distribution analysis (9,10) allow us to determine the protein surface occupancy of the membrane in close packed and disordered regions. As expected from the geometry in close packed regions, we find proteins occupy ∼91% of the surface area. In disordered regions we find that the fraction of the surface area occupied by the various complexes is 73% ± 5%. It is important in this context to remember that these systems appear to be self-organizing and are in contact with lipid-rich membrane areas both in Rsp. photometricum (7) and other species (6).

The ordered LH2 domains are static, and thus any lipids or quinones they might include will be trapped on a metabolically relevant timescale of several hundred milliseconds; thus all the metabolically active quinones will be restricted to the disordered regions. The second consequence is that the mobility of the disordered mixed domains will prevent the formation of percolation clusters for small molecule diffusion since spaces between molecules are continually opening up and closing, thus allowing passage of small molecules such as quinones.

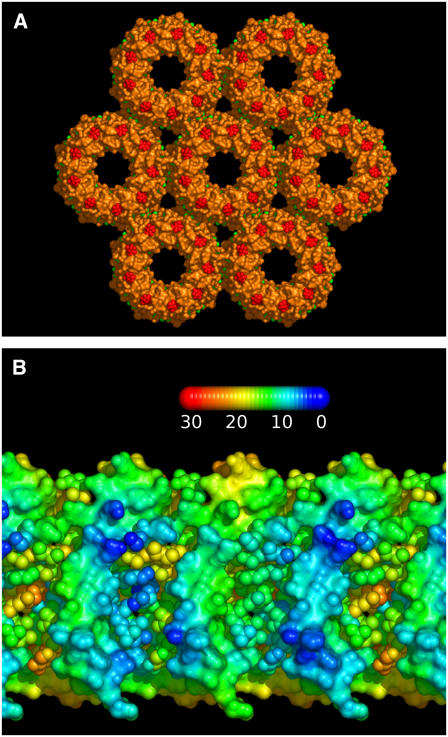
Indeed, it is possible that the hexagonally packed regions are so dense that not only do they exclude metabolically active quinones but they exclude all quinones. Based on the biological unit of the nonameric Rps. acidophila LH2 (41) (Protein Data Bank (PDB) code 1KZU) and the 7.5-nm lattice spacing measured by AFM from crystalline LH2 regions (9), we have constructed a simple model of the packing. In Fig. 5 A we show a representation of a membrane normal view of the molecular surface, which illustrates the closeness of the packing and the lack of space available for intercalating lipid molecules. Indeed based on the available surface area at this packing density there is only space for two phospholipids (or one cardiolipin) on each side of the membrane in the interstices between rings, thus a total of eight phospholipids per nonameric complex. In Fig. 5 B we show a projection of the surface of the central complex in the aggregate colored according to the shortest distance to the neighboring complex. This representation reinforces the observation that the complexes in this organization are in contact through the entire depth of the membrane, leaving no room for infiltration of quinones. This is all the more apparent when one realizes that the structure obtained from the PDB lacks parts of the cofactors on the surface of the molecule that are not observable in the electron density, notably part of the carotenoid molecules. These chains can thus further seal the interface between complexes. This structural modeling suggests that LH2 are able to form, relatively easily, a close packed lattice through which diffusion of quinones and membrane lipids will be almost impossible, and the isoprenoid, phytyl, and carotenoid chains on the surface of the complexes will be in contact. This interaction may be partly responsible for the formation of LH2 antenna regions, as we have suggested before (4).

FIGURE 5.

Model of LH2 organization in crystalline membrane regions. (A) Model constructed from the Rps. acidohila LH2 structure (PDB code 1KZU) using the 7.5-nm lattice spacing determined from AFM microscopy of Rsp. photometricum membranes. The group of hexagonally arranged complexes has been rendered to show the molecular surface and illustrate the lack of space between complexes; the protein is shown in orange, the carotenoids in red, and the bacteriochlorophyll molecules in green. (B) Cylindrical projection of part of the membrane-spanning region of the central complex in panel A colored to show the distance between atoms and the nearest atom on the neighboring complex. The distances vary according to the scale shown in angstroms. The polypeptide chains are shown as a continuous surface and the cofactors as individual balls. These illustrations were prepared with the PyMOL molecular graphics package (www.pymol.org).

The lack of space between LH2 molecules might seem at odds with the observed dark areas surrounding the LH2 molecules in the topographs; however this is not the case. It must be remembered that in AFM images we observe only the surface topology and not the electron density as in x-ray diffraction measurements. Thus a gap between the surface topologies can be perfectly in agreement with close packing of the intramembrane molecular surfaces.

It is worth noting that the exclusion of quinone from crystalline LH2 regions will effectively confine the quinone to paths running close to the core complexes, since the core complexes induce the necessary disorder in the packing. This can perhaps be related to the situation in Rb. sphaeroides where quinone molecules appear to be confined to the vicinity of core complexes (21,22) and the LH2 again may form paracrystalline arrays (3).

Tracer diffusion simulations

To better understand diffusion through a protein-lipid mixture, we have examined, using Monte Carlo simulations, diffusion of small tracer molecules through assemblies of discs resembling the photosynthetic membrane. Very similar studies have been previously undertaken by Tremmel et al. (33); however, the methods and assumptions that we have made for our simulations are different from those previously reported. In the study we report here, our objective was to investigate the distance-dependent diffusion through a crowded membrane to better understand how quinones can shuttle electrons between the core complexes and the cytochrome bc₁. A major effect of obstacle dynamics on small molecule diffusion in a membrane is the disappearance of the percolation threshold (33). This is because any dead ends are only temporary, and thus long-range diffusion will always be possible by a hop diffusion mechanism between temporary confinement zones, as has been previously commented (33). To model such a dynamic system with mobile obstacles and tracers at high obstacle density is difficult, and different approximations can be made.

Previous investigations have essentially used lattice models and a priori parametrization of diffusion coefficients (26–29,33). We have chosen a different approach and examine the diffusion of a zero size tracer through a static arrangement of discs. We choose this approximation as it avoids parametrization of the model, as the model contains only one distance, the obstacle size, and one speed, the free tracer diffusion rate. Our argument for choosing this approximation to represent the diffusion of real molecules of nonzero size through the dynamic photosynthetic membrane is that the rate of hopping from one space to the next will depend on the chance of gaps opening to a sufficient size to let the molecule pass. This opening probability depends on the dynamics and organization of the obstacles. The size of the average gap around the protein can be estimated from the confinement zone size to be 1–2 nm. However the quinone headgroup is small (0.5 nm) relative to this average gap size, suggesting that it should be able to squeeze between the proteins relatively easily and frequently; thus the zero size tracer approximation seems reasonable for examining quinone diffusion. Clearly if the frequency of reorganization is too slow the proteins will form a percolation cluster, and long-distance diffusion of quinones to the presumed peripheral location of the cytochrome bc₁ complex will be impossible.

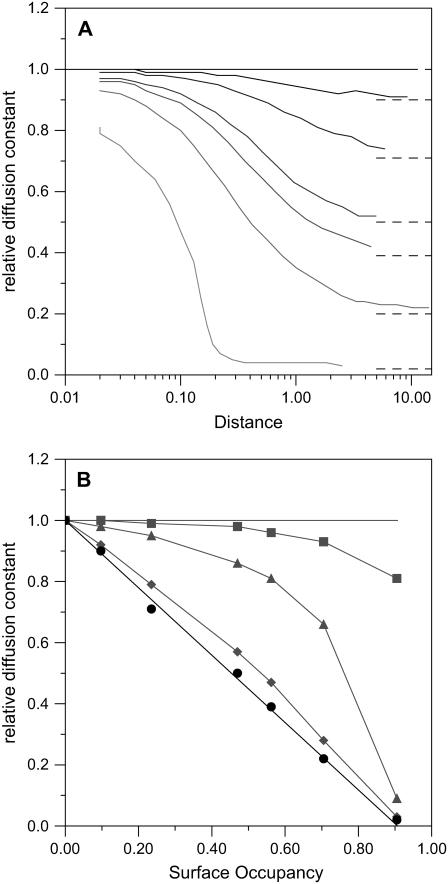
As a first study we examined the effect of obstacle concentration on the lateral diffusion in model membranes. These model membranes contained as obstacles randomly distributed nonoverlapping discs at various densities; this organization corresponds to a hard disc interaction potential. In this system the diameter of the discs defines the length scale of the model, and the hard disc potential ensures that at all the densities studied the obstacles form a single continuous phase (42). In Fig. 6 A we show the distance dependence of the apparent diffusion constant, relative to a membrane without obstacles, for several obstacle densities. This figure provides a representation of diffusion over different length scales and clearly illustrates regimes of normal diffusion (horizontal segments) and anomalous diffusion (diagonal segments). The different lines correspond to obstacle densities varying between 0 and very close (0.905) to the hexagonal close packed limit (π/(2 × √3) ≈ 0.907). In agreement with the work of Saxton (26) on lattice systems, we find that diffusion is normal at short distances (where the chance of meeting an obstacle is small), followed by a transition to an anomalous diffusion regime at intermediate length scales where the tracer is confined between obstacles. However, as expected, there is no percolation threshold, and apparently normal long-distance diffusion is possible at all the obstacle densities. This normal long-distance diffusion is not unexpected as it follows a hop diffusion mechanism and is thus governed by the rate that the tracer can jump between zones of confinement. Indeed our results compare well with those obtained by Tremmel et al. (33) using dynamic obstacles with a lattice simulation. This is particularly satisfying as the two different models—with different assumptions and defects—are coherent, suggesting that the conclusions are relatively robust. The rate of diffusion depends on the concentration of obstacles (Fig. 6 B). At short distances only very high obstacle concentrations modify the diffusion. However in the long-distance limit the relative diffusion rate declines linearly, with obstacle concentration reaching zero at the hexagonally close packed limit.

FIGURE 6.

Modeling the diffusion of a tracer in a crowded membrane. (A) Observed evolution of the relative diffusion constant with rms distance traveled. The solid lines, from darkest to palest, correspond to Monte Carlo calculations with obstacle surface densities of 0, 0.097, 0.235, 0.470, 0.563, 0.705, and 0.905. In these calculations a distance of 1 corresponds to the obstacle diameter. On the graphs dashed lines indicate the estimated long-distance relative diffusion constants at the various surface densities. (B) Evolution of the relative diffusion constant with surface obstacle density, from panel A. The gray squares, triangles, and diamonds correspond to distances of 0.02, 0.2, and 2 times the obstacle diameters, respectively, and the gray lines are aids to the eye. The black circles correspond to the estimated long-distance relative diffusion coefficients (∼20 diameters and beyond) and the black line to a linear decline between free diffusion and no long-distance diffusion in hexagonally close packed membranes.

The difficulty experienced by even zero-sized tracers to diffuse long distances in ordered crystalline regions reinforces the suggestion that the static crystalline LH2 antenna domains that we have observed in photosynthetic membranes (9) can effectively exclude metabolically active quinone molecules.

We show, as expected, that the protein concentration in photosynthetic membranes (a surface occupancy of 0.73) is so high that diffusion of even the smallest molecule in the plane of the membrane will be seriously perturbed but remains possible, albeit at a reduced rate.

Architecture optimization

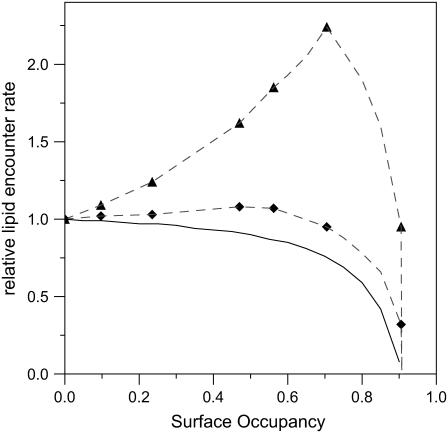
It is important to remember that molecular crowding has two opposing effects: on the one hand decreasing diffusion and kinetics due to the presence of impermeable obstacles, and on the other hand increasing concentrations and encounter probabilities due to a reduced accessible volume or, in the case of a membrane, surface area (43). Thus as the obstacle density in the membrane increases—though the long-distance diffusion constant decreases linearly—the chances of an encounter with a particular protein, if the tracer is at the right distance, increases—also linearly—since the tracer is concentrated in the spaces between obstacles. Thus the reduction of the diffusion constant is in some way compensated for by an increase in encounter probability. In Fig. 7 we show the resulting effects of crowding on encounter probability at three different distances. At long distances (solid line) crowding always reduces encounter probability; however at shorter distance scales, obstacles can have possibly dramatic effects, increasing encounter probabilities.

FIGURE 7.

Effect of membrane crowding on encounter rates. Evolution of the encounter rate for lipid-soluble molecules with surface occupancy for several obstacles' different distance scales. The gray triangles and diamonds correspond as in Fig. 5 B to distances of 0.2 and 2.0 obstacle diameters, the dashed lines are guides for the eye, and the solid black line is calculated from the linear fit to the long-distance relative diffusion coefficient.

From this we can conclude that the 73% surface occupancy observed for the disordered phase of the photosynthetic membranes examined here represents the limit for packing the membrane without serious compromising reactions of quinones and quinols at a long distance from their regions of production. This would appear to be necessary as we have not observed the cytochrome bc₁ in membranes containing many RCs. At this density, encounter probabilities for quinones within the lipid phase will be reduced to ∼2/3 that in uncrowded membranes.

If paracrystalline LH2 regions are able to exclude quinones, their formation can act as a boost to performance by further concentrating quinone in the disordered regions. However this might be expected to be counteracted by their adverse effect, as obstacles, to diffusion. However, we can use our simulations and the results presented in Figs. 6 and 7 to examine the effect of these obstacles, at least qualitatively. To do this we must change our interpretation of the meaning of the discs and the spaces. Now we consider the discs as (circular) paracrystalline LH2 domains and the gaps between as disordered regions containing mixed LH2 and core complexes. In this context we must reconsider the length scale of the diffusion. The circular photosynthetic membrane discs typically have diameters of 300 nm (see Table 1). If we assume that the cytochrome bc₁ is at the edge of the photosynthetic membrane discs, which represents the farthest that it could be from the RCs, the average distance between an RC in the membrane surface and a cytochrome bc₁ will be ∼45 nm. The LH2 paracrystalline domains are typically about twice this size; thus in this context the length scale of diffusion is ∼0.5. We can see immediately from Fig. 7 that over length scales of this order moderate crowding can significantly increase the encounter probability. The surface occupancy of paracrystalline LH2 domains, which we have observed in Rsp. photometricum membranes, is in the range of 0–0.5 (9). Thus the formation of large crystalline regions can be considered an optimization of the photosynthetic architecture for electron transfer, since the size of these crystalline regions is large relative to the distances between RC and cytochrome bc₁ complexes. This optimization depends on the ability of LH2 to form close packed paracrystalline arrays. It is perhaps pertinent that similar ordered LH2 regions appear to be a general phenomenon and have also been observed in the other species examined, namely Phsp. molischianum (4), Rps. palustris (6), Rb. blasticus (5), and Rb. sphaeroides (3).

CONCLUSIONS

In this work, we have analyzed the dynamics within specialized domains of photosynthetic membranes from Rsp. photometricum by time-lapse AFM imaging and Monte Carlo simulations. We observed that the disordered core-containing domains are much more dynamic than the paracrystalline LH2 domains. Monte Carlo analysis of diffusion in such membranes suggests that hop diffusion over long distances is possible in dynamic domains but not in static hexagonally close packed domains. Analysis of the diffusion observed in models of photosynthetic membranes suggests that the density of disordered domains is such as to allow the maintaining of relatively high turnover rates for the cytochrome bc₁ and core complexes if these exist within the same domain. The formation of large crystalline LH2 domains will further aid quinone and quinol migration in membranes if these exclude metabolically active quinones. The formation of such LH2 domains might be expected to reduce light-harvesting efficiency as photons absorbed in these large domains may get lost before finding an RC. This effect is perhaps less important than expected because the long (from 500 ps to 1 ns) bacteriochlorophyll fluorescence lifetime of light-harvesting complexes (44–46) and short time (∼1–5 ps) spent by the excitation on a complex between hops (46–47) mean that excitations are able to efficiently travel relatively long distances between absorption and trapping. Thus the observed architecture would seem to provide an alternative to supercomplexes in optimizing photosynthetic efficiency against the competing constraints of efficient energy transfer and quinone diffusion.

The suggestion that quinones cannot diffuse through crystalline regions of LH2 raises the question of how crystalline regions of core complexes, such as those observed in Blc. viridis, can function (8). Two possible solutions come to mind: 1), either the elliptical core complex shape and rotational motions are sufficient to maintain fluidity and quinone diffusion or, alternatively, 2), these arrays of core complexes are not fully metabolically active but function as a light-activated condenser providing a large light-induced membrane potential on their initial turnovers, which is stabilized thanks to the rapid rereduction of the primary acceptor by the bound tetrahaem cytochrome; but subsequently, as quinone escape is restricted from complexes trapped in crystals, these complexes remain closed and play a light-harvesting role for more peripheral or cytochrome bc₁-associated complexes that are fully metabolically active for cyclic electron transfer. The resolution of this problem needs further experimental work.

In membranes from eukaryotic cells, hop diffusion is usually interpreted as arising from trapping of molecules by the underlying cytoskeleton (35). Here we see that another mechanism, equally possible in eukaryotic membranes, could also be responsible for modulating diffusion of proteins and lipids in the membrane—namely molecular crowding in a dynamic system, where the continual movement of obstacles prevents the appearance of a percolation threshold even at high obstacle densities. It is interesting to note that in eukaryotic membranes such obstacles could include, beyond proteins and protein complexes, membrane microdomains or lipid rafts. Indeed in a membrane composed of dynamic phase-separated microdomains our results indicate that one could observe simultaneously multiple different long-distance hop diffusion systems in the same membrane, each system associated with a different membrane phase. Indeed multiple diffusion regimes in the same membrane have already been observed (38).