Abstract
Muscle contraction underlies many essential functions such as breathing, heart beating, locomotion, regulation of blood pressure, and airway resistance. Active shortening of muscle is the result of cycling of myosin cross-bridges that leads to sliding of myosin filaments relative to actin filaments. In this study, we have developed a computer program that allows us to alter the rates of transitions between any cross-bridge-states in a stochastic cycle. The cross-bridge states within the cycle are divided into six attached (between myosin cross-bridges and actin filaments) states and one detached state. The population of cross-bridges in each of the states is determined by the transition rates throughout the cycle; differential equations describing the transitions are set up as a cyclic matrix. A method for rapidly obtaining steady-state exact solutions for the cyclic matrix has been developed to reduce computation time and avoid the divergence problem associated with numerical solutions. In the seven-state model, two power strokes are assumed for each cross-bridge cycle, one before the release of inorganic phosphate, and one after. The characteristic hyperbolic force-velocity relationship observed in muscle contraction can be reproduced by the model. Deviation from the single hyperbolic behavior at low velocities can be mimicked by allowing the rate of cross-bridge-attachment to vary with velocity. The effects of [ATP], [ADP], and [Pi] are simulated by changing transition rates between specific states. The model has revealed new insights on how the force-velocity characteristics are related to the state transitions in the cross-bridge cycle.
INTRODUCTION
In muscle contraction, the relationship between shortening velocity and the load on the muscle can be approximated mathematically as a rectangular hyperbola (1). The relationship succinctly summarizes a muscle's mechanical performance. With a two-state cross-bridge model, A. F. Huxley (2) has demonstrated that the inverse relationship between force and velocity is a reflection of the fundamental steps governing the interaction between the myosin cross-bridges and the actin filaments. The actomyosin interaction is believed to be stochastic, that is, each step (either a physical transition or a chemical reaction) within the cross-bridge cycle influences the probability of occurrence of the following steps (3–6). The force-velocity relationship is known to be affected by intracellular concentrations of substrate (ATP) and metabolites (ADP, inorganic phosphate, H+), and these effects can be interpreted in terms of direct perturbation on the mechanical transitions in the cross-bridge cycle by chemical forces (5,7–13). Details regarding how the events within the cross-bridge cycle shape the force-velocity relationship, however, are not entirely clear. To further our understanding of muscle contraction at the molecular level, increasingly complex models are being used to explain the force-velocity relationship and how it can be changed under different conditions (2,6,14,15). In this study, we have developed a seven-state model to specifically address the question of how ATP and its metabolites alter the transitions within the cross-bridge cycle and hence modify the characteristics of the force-velocity relationship. In this study, we also investigated the biphasic behavior of velocity in muscles shortening at near-maximal load (16–18) and explained the behavior in terms of velocity-dependence of transition rates. Another major component of this study is the development of a rapid computational method for obtaining exact solutions of simultaneous equations from a cyclic matrix of any size. This new tool is particularly suited for analyzing cyclic interactions or reactions, such as those found in the muscle cross-bridge cycle. One major advantage of this tool is that it allows investigators to formulate the cross-bridge cycle with virtually unlimited number of states and monitor the flux of cross-bridges in and out of each state in real-time, because of its high computational efficiency. Another advantage of this method compared to conventional numerical methods is that it does not have a nonconvergence problem where numerical iterations do not lead to a solution, and can handle stiff matrices (matrices with widely varying rate constants) that need to be used in the cross-bridge cycle simulation.
METHODS
The cross-bridge cycle
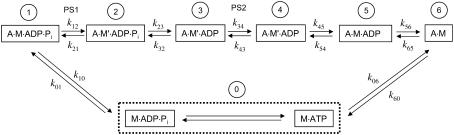
The cross-bridge cycle (Fig. 1) used in simulating the force-velocity behavior of muscle is essentially the same as those proposed previously by us (3,5,14) and by others (2,6,9–13,15,19). The biochemical basis of the cross-bridge cycle is based on the model of Lymn and Taylor (20). The force-velocity relationship as first described by Hill (1) is a steady-state muscle property, as opposed to the non-steady-state properties such as velocity (21) and tension (19) transients. The cross-bridges occupy both the attached and detached states. Two power strokes per cycle are assumed based on the findings of Dantzig et al. (9,10) and of Wang and Kawai (11,12). The first power stroke is assumed to occur before the phosphate release (Fig. 1), and a second one is assumed to occur after the phosphate release. This is consistent with the finding that inorganic phosphate inhibits force production in skinned muscle fibers (8). For simplicity, cross-bridges occupying the attached states before the first power stroke are assumed to generate no force, and the cross-bridges occupying the attached states after the second power stroke are assumed to generate twice as much force as those do in states between the first and second power strokes. The release of ADP is assumed to be after the second power stroke, because detention of ADP release has been found to increase muscle force (5,22). The rigor bridges (A·M, Fig. 1) are assumed to be force-bearing bridges because detention of cross-bridges in that state by lowering ATP concentration has been found to increase muscle force (5,22).
FIGURE 1.
A seven-state model of biochemical cycle of actomyosin interaction. The states are labeled 0–6 in circles. M, myosin; A, actin. A·M, actomyosin complex; and A·M′, A·M after an isomerization step. The dot between letters denotes ionic bonding. Power strokes (PS1 and PS2) are assumed to happen between States 1 and 2, and States 3 and 4. The rate constants under isometric conditions (ki) are assigned the following values (s−1): k01 = 40; k10 = 70; k12 = 140; k21 = 80; k23 = 150; k32 = 15; k34 = 20; k43 = 0.2; k45 = 10; k54 = 0.1; k56 = 25; k65 = 0.25; k60 = 200; and k06 = 50. It is assumed that there is a fast equilibrium between M·ATP and M·ADP·Pi (in dotted rectangle) with near infinite forward and backward rates. Note that under nonisometric conditions, some transition rates are assumed to vary with the sliding velocity of myosin relative to actin filaments; these rates as functions of velocity are specified in Fig. 2 and Table 1.
States 1 and 2 (Fig. 1) are chemically identical, but State 1 is assumed to be different from State 2 in two ways; one is that there is an isomerization step between the two states that enables the cross-bridges in State 2 to generate force (power-stroke 1), and the other is that the cross-bridges in State 1 can readily detach from actin filaments at high sliding velocities. This second feature is used to account for the lower energy consumption rate observed at high velocity of shortening (23) and is consistent with the model of Huxley and Simmons (19,24). States 3–5 are also chemically indistinguishable; a conformational change in myosin (power-stroke 2) separates States 3 and 4, and an isomerization step separates States 4 and 5. The isomerization step is added to account for actomyosin isomerization observed in biochemical experiments (25), and to account for some unique characteristics observed in tension transients (14) that can be explained by a delay due to the isomerization step. This isomerization step in isometric contraction is considered to be the rate-limiting step and minimally reversible (10) in the cross-bridge cycle and is assigned the slowest value for its transition rate. State 0 includes two complexes (M·ATP and M·ADP·Pi) in rapid equilibrium. It is assumed in this model (Fig. 1) that the rate of ATP hydrolysis is much faster than any transition rates in the cycle and therefore M·ATP ↔ M·ADP·Pi (within the dotted rectangle, Fig. 1) collapses into a single state (i.e., State 0).
Cyclic matrix and mathematical solution
One important assumption made in the simulation model is that each step or transition in the cycle is a separate stochastic process, so that the rate of each transition is simply the product of the fraction of cross-bridges in the starting state multiplied by the rate coefficient (either a constant or a function) for that transition. As described above, cross-bridges are assumed to cycle through all states. A linear first-order differential equation is used to describe the rate of change of the fraction of cross-bridges in each state. The rate of change in a particular state is taken as the difference between the rates at which cross-bridges move into and out of the state. The following set of equations describes the rate of change in each state illustrated in Fig. 1,
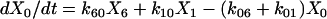 |
(1a) |
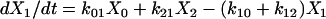 |
(1b) |
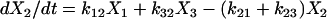 |
(1c) |
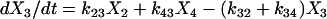 |
(1d) |
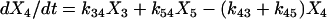 |
(1e) |
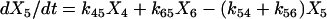 |
(1f) |
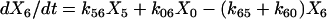 |
(1g) |
where the term Xi represents the fraction of cross-bridges in the State i. The sum of all state fractions equals 1. By definition, all the transition rates are zero in steady state. By setting Xi/dt in Eq. 1 to zero, however, it would result in an ill-posed problem with no unique solution. This problem can be avoided by replacing one of the above equations with
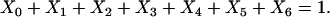 |
(2) |
The steady-state fraction of the cross-bridges can then be obtained by solving this new system of equations.
To obtain exact solution from a large set of simultaneous equations using conventional methods is slow and becomes impractical when the matrix size is >∼10. Numerical methods are usually used to solve large matrices. For a stiff matrix with widely varying constants (such as the one required for the cross-bridge cycle simulation), a potential problem is that the numerical iterations may not converge and produce a solution. (Note that there are special methods for better handling of stiff matrices, such as the Gear Method (26).) For large matrices with hundreds or even thousands of simultaneous equations, numerical methods can also be slow. An extremely fast computational method specifically for solving cyclic matrices of any size has been developed by us (see Appendix). This method allows instant updates of state fractions of cross-bridges in the computer simulation as soon as the rate constants or functions are changed. This method may become indispensable in the future if the cross-bridge cycle is divided into thousands of steps to simulate atomic interactions between the protein surfaces of myosin and actin during the processes of attachment, power stroke, and detachment.
Rate functions
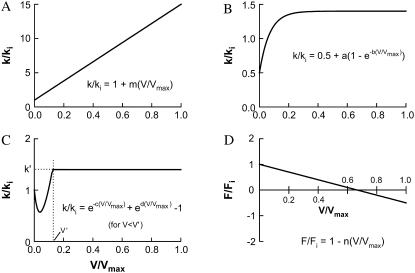
In our simulation, some of the transition rates used (indicated in Fig. 1) are constants, and some are functions of shortening velocity. The transition rates used to simulate isometric contraction are all within the range used by Dantzig et al. (9,10) and that specified by Wang and Kawai (11,12) and Galler et al. (13). There are three types of functions used to describe the dependence of transition rates on velocity, as depicted in Fig. 2 (A–C). In Table 1, the constants that defined each function for velocity-dependent transitions are listed. For single hyperbolic force-velocity relationship simulation, the attachment rate (k01, Fig. 1) is constant (i.e., velocity-independent). For simulation of reversal of curvature of force-velocity curve at low shortening velocities, k01 varies with velocity as described by the function shown in Fig. 2 B. For simulation of double hyperbolic force-velocity relationship, k01 varies with velocity as described by the function shown in Fig. 2 C. The transition rates k10, k12, k23, k34, k45, k56, and k60 all depend on velocity as described by the linear function shown in Fig. 2 A.
FIGURE 2.
Velocity-dependent rate functions (A–C) used in the simulation of cross-bridge cycle and force-velocity relationship in muscle. Function A (linear) is used for the forward transitions (clockwise, Fig. 1) between all attached states and the transition from State 6 to State 0, and from State 1 to State 0 (Fig. 1). Function B is used to simulate reversal of force-velocity curvature at low velocity. Function C is used to simulate the double hyperbolic feature of force-velocity relationship at low velocity. Function D depicts the relationship between shortening velocity and force exerted by cross-bridges in states 2–6. The value Fi and ki denote force and rate constants under isometric conditions, respectively. The ki-values are listed in Fig. 1 legend. V and Vmax are velocity and maximal velocity of muscle shortening, respectively. The constants for the rate functions (a, b, c, d, m, and n) are specified in Table 1.
TABLE 1.
Velocity-dependent rate functions used in some transitions within the cross-bridge cycle
| Transition/state | ki (s−1) | Function | Function parameters |
|---|---|---|---|
| 0-1 | 40 | k/ki = 1 (for single hyperbolic curve) | |
| 0-1 | 40 | k/ki = 0.5 + a(1−e−b(V/Vmax)) (for curvature reversal at low V only) | a = 1.2; b = 22 |
| 0-1 | 40 | k/ki = e−c(V/Vmax) + ed(V/Vmax) −1 (for double hyperbolic curve only, maximum value of k/ki is capped at 1.4) | c = 20; d = 7 |
| 1-0 | 70 | k/ki = 1 + m(V/Vmax) | m = 70 |
| 1-2 | 140 | k/ki = 1 + m(V/Vmax) | m = 14 |
| 2-3 | 150 | k/ki = 1 + m(V/Vmax) | m = 14 |
| 3-4 | 20 | k/ki = 1 + m(V/Vmax) | m = 14 |
| 4-5 | 20 | k/ki = 1 + m(V/Vmax) | m = 14 |
| 5-6 | 10 | k/ki = 1 + m(V/Vmax) | m = 14 |
| 6-0 | 20 | k/ki = 1 + m(V/Vmax) | m = 14 |
| 2 | — | F/Fi = 1 − n(V/Vmax) | n = 0.57 |
| 3 | — | F/Fi = 1 − n(V/Vmax) | n = 0.57 |
| 4 | — | F/Fi = 1 − n(V/Vmax) | n = 0.86 |
| 5 | — | F/Fi = 1 − n(V/Vmax) | n = 1.43 |
| 6 | — | F/Fi = 1 − n(V/Vmax) | n = 1.43 |
Note: Transitions not listed in the table are velocity-independent and the rate constants are listed in Fig. 1 legend.
SIMULATION
In simulating the force-velocity behavior observed in muscle contraction, velocity is used as an independent variable, varying from 0 to maximum velocity (Vmax). The absolute value of Vmax obtained from the simulation depends on the rate constants/functions used. Therefore, in different simulations, Vmax can have different absolute values. Zero velocity corresponds to the isometric condition where force generated by the muscle is maximal (Fmax). The value Fmax is determined by the sum of fractions of cross-bridges in the states after the power stroke transitions, i.e., from State 2 to State 6 in Fig. 1. Force generated by the cross-bridges in States 2 and 3 (i.e., the states between the first and second power-stroke) is assumed to be proportional to the sum of the cross-bridge fractions in those states (i.e., X2 + X3). Force generated by the cross-bridges in States 4–6 (i.e., the attached states after the second power stroke) is assumed to be proportional to the sum of the cross-bridge fractions in those states multiplied by a factor of 2 (i.e., 2(X4 + X5 + X6)). The value Fmax, therefore, is proportional to [X2 + X3 + 2(X4 + X5 + X6)]. At each increment of velocity, the velocity-dependent rate functions (Table 1) are evaluated and the new rates are used to calculate the state fractions (Xi-values) in the cross-bridge cycle. It is assumed that the transitions governing the second power stroke and ADP release are cross-bridge strain-dependent (15,27); it is also assumed that the transitions governing the first power stroke and Pi release are strain-dependent. Hence the transition rates k12, k23, k34, k45, k56, and k60 (Fig. 1) are all assumed to be velocity-dependent in a manner depicted in Fig. 2 A, with the slopes (m) specified in Table 1 for each transition. The detachment rate (k10) is also assumed to be velocity-dependent (Table 1). Force generated by the cross-bridges in all force-generating states (States 2–6) is assumed to be a linear function of shortening velocity, as depicted in Fig. 2 D, so as to simulate the scenario that, at high velocity of shortening, some of the bridges remaining in those states are able to generate negative force. The idea of negatively strained bridges at high shortening velocity was first proposed by Huxley (2). In this model simulation, the decrease in force is due to two factors—one is the reduction in the fraction of attached bridges (because k10 increased with velocity) and the other is the accumulation of negative-force bridges. These two features mimic those in the model of Huxley and Simmons (19).
Hyperbolic and other features of force-velocity curve
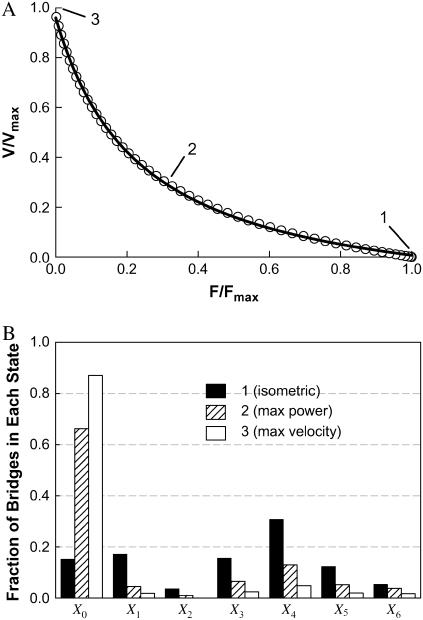
An inverse relationship between shortening velocity and force (against which the muscle shortens) can be generated by the model outlined in Fig. 1. By assuming that k01 (rate of cross-bridge attachment) is constant (i.e., velocity-independent), and using values of rate constants and functions listed in Table 1 and Fig. 1 legend for other transitions, a curvilinear, inverse relationship between velocity and force is obtained (open circles, Fig. 3). This relationship can be described well by a rectangular hyperbolic function (solid line, Fig. 3) of the form
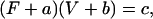 |
(3) |
where F and V are force and velocity, respectively, and a, b, and c are constants. At V = 0,
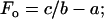 |
(4) |
and at F = 0,
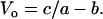 |
(5) |
The value for the normalized constants obtained from a nonlinear curve fit (SigmaPlot 8.0, Systat Software, Point Richmond, CA) is a/Fo = b/Vo = 0.23 (Fig. 3, solid line). Note that Fo and Vo are different, respectively, from Fmax and Vmax in that the former parameters are obtained from curve fitting, the latter parameters are muscle properties.
FIGURE 3.
Simulated force-velocity relationship (open circles, data generated by model) fitted with a hyperbolic curve (A). See text for fitting parameters. Snapshots of fractions of cross-bridges occupying each state at zero (1), medium (2), and maximum (3) shortening velocity (corresponding respectively to conditions where isometric force, maximum power, and maximum velocity are generated) are shown in panel B. The value Xi corresponds to states indicated in Fig. 1.
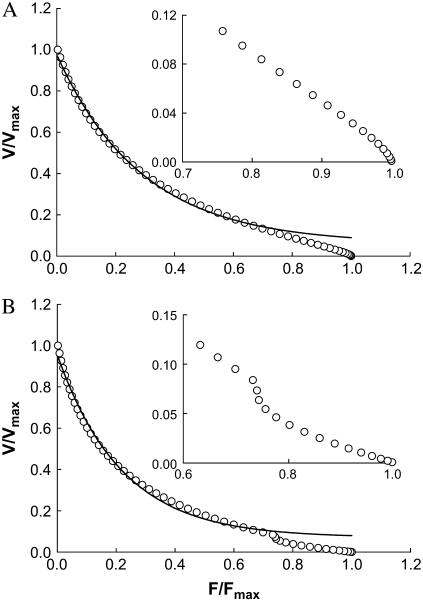
To simulate the reversal of curvature of the force-velocity curve at the low velocity region observed in smooth muscle (18), exactly the same model parameters that produced the rectangular hyperbolic force-velocity curve in Fig. 3 are used except that k01 is assumed to be velocity-dependent as depicted in Fig. 2 B. The simulated force-velocity curve is shown in Fig. 4 A.
FIGURE 4.
(A) Simulated force-velocity relationship (open circles) with a reversal of curvature in the low velocity region. Model parameters used in the simulation are the same as those in Fig. 3 except that the attachment rate constant (k01) is replaced with a rate function depicted in Fig. 2 B. Inset shows magnified low velocity region. (B) Simulated force-velocity relationship with double hyperbolae. Model parameters used in the simulation are the same as those in Fig. 3 except that the attachment rate constant (k01) is replaced with a rate function depicted in Fig. 2 C. Inset shows magnified low velocity region. Solid curves are hyperbolic fits only for data range 0–0.75 Fmax.
To simulate the double hyperbolic force-velocity curve at the low velocity region observed in intact skeletal muscle (17), exactly the same model parameters for the single hyperbolic force-velocity curve (shown in Fig. 3) are used, except that k01 is assumed to depend on velocity as depicted in Fig. 2 C. The simulated force-velocity curve is shown in Fig. 4 B.
Curvature in force-velocity curve
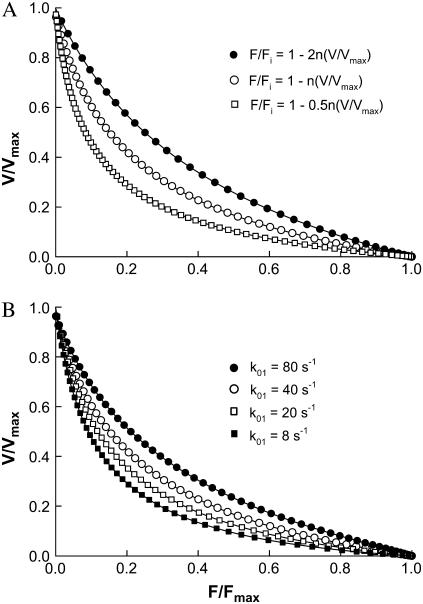
The curvature of the simulated force-velocity curve can be altered by changing the slope (n) of the linear function that specifies the magnitude and direction of force of individual cross-bridges in the force-generating states as a function of velocity (Fig. 2 D). A steeper decline in force with velocity produces more negative-force bridges at moderate to high velocities; this has an effect of decreasing the curvature of the force-velocity curve.
The curvature of the simulated force-velocity curve can also be altered by changing the rate constants (or functions) at various transitions in the cycle (Fig. 1). One feature observed in the simulation is that an increased curvature is often associated with an increased cross-bridge fraction in the detached state (X0). An example is given in Fig. 5. As the attachment rate constant (k01) is decreased, which causes the cross-bridges to accumulate in the detached state, the curvature of the force-velocity curve is increased. By reducing other transition rates such as k12 and k23, accumulation of bridges in the detached state also occurs, and leads to an increased curvature of the force-velocity curve (results not shown). Reducing k01 has the most dramatic effect because it has the most direct effect on the state fraction X0.
FIGURE 5.
(A) Normalized force-velocity curves from simulation with various slopes (n) for the linear function (F/Fi = 1 − n(V/Vmax), Fig. 2 D) that specifies force generated by individual cross-bridges in the post-power-stroke states. (B) Normalized force-velocity curves from simulation with various rates of attachment (k01).
Changes in force-velocity relationship due to variations in concentrations of ATP, ADP, and inorganic phosphate
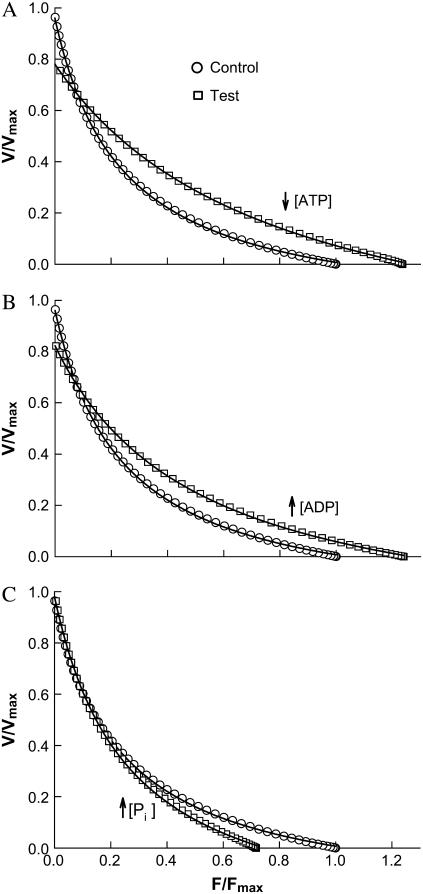
Based on the cross-bridge cycle outlined in Fig. 1, the effect of an increase in [ADP] is simulated by reducing k56. The same effect can also be simulated by changing both k56 and k65, but for simplicity, only the forward rate is changed. The value k56 is a linear function of velocity, as indicated in Table 1. By reducing the value of k56 in the isometric state from 25 s−1 to 5 s−1, isometric force (Fmax) increases by 24.0%, maximal shortening velocity (Vmax) decreases by 14.4%, and the ratio of a/Fmax increases from 0.230 to 0.402 (see Fig. 6 B and Table 2). By adding 4 mM MgADP to their regular contracting solution that contained 4 mM MgATP, Cooke and Pate (22) observed a 35% increase in isometric force and a 50% decrease in velocity in skinned rabbit psoas fibers. With the same muscle preparation, Seow and Ford (5) observed a 25% increase in isometric force, a 35% decrease in velocity, and a 55% increase in the value of a/Fmax after raising MgADP concentration from 0 to 2 mM in the presence of 5 mM MgATP. The findings from experiments with rabbit psoas therefore agree qualitatively with the model predictions resulting from only one change in a single model parameter. It is not clear, though, how the changes in MgADP concentration in the experiments correspond exactly to the changes in the value of k56 in the model.
FIGURE 6.
Simulation of the effects of decreased ATP concentration (↓[ATP]) in panel A, increased ADP concentration (↑[ADP]) in panel B, and increased inorganic phosphate concentration (↑[Pi]) in panel C. Force and velocity in test conditions (altered substrate and metabolite concentrations compared to control) are normalized to the control Fmax and Vmax. Changes in force-velocity properties are summarized in Table 2.
TABLE 2.
Summary of changes in force, velocity, and curvature in simulation of the effects of ↓[ATP], ↑[ADP], and ↑[Pi ]
| Transition rate change | (Fmax)t/(Fmax)c | (Vmax)t/(Vmax)c | (a/Fmax)t/(a/Fmax)c |
|---|---|---|---|
| (k60)t/(k60)c = 0.1 (↓[ATP]) | 1.237 | 0.788 | 2.650 |
| (k56)t/(k56)c = 0.2 (↑[ADP]) | 1.240 | 0.856 | 1.746 |
| (k23)t/(k23)c = 0.2 (↑[Pi]) | 0.718 | 1.000 | 1.505 |
Note: The subscripts c and t denote control and test, respectively. The control parameters are derived from the force-velocity curve shown in Fig. 3 that possesses initial k values as indicated in Fig. 1 legend. The only change made to produce a test curve (shown in Fig. 6) is by changing one transition rate as indicated by the ratios listed in the first column of this table.
The effect of a decrease in [ATP] is simulated by reducing k60. The linear function of k60 is listed in Table 1. By reducing k60 from 200 s−1 to 20 s−1, Fmax increases by 23.7%, Vmax decreases by 21.2%, and the ratio of a/Fmax increased from 0.230 to 0.609 (Fig. 6 B). The effect of low [ATP] on the force-velocity properties is very similar to that of high [ADP], except that a 10-fold change in [ATP] is required to match the effect of a fivefold change in [ADP] in terms of force increase (see Fig. 6, A and B, and Table 2). By reducing MgATP concentration from 4 mM to 2 mM, Cooke and Pate (22) observed a 19% increase in isometric force and a 46% decrease in shortening velocity. Lowering MgATP concentration from 10 mM to 2 mM, Seow and Ford (5) found qualitatively similar results—a 23% increase in isometric force and a 31% decrease in shortening velocity. Furthermore, they found an increase of 17% in the a/Fmax ratio (5).
The effect of an increase in [Pi] is simulated by reducing the rate constant k23. By reducing k23 from 150 s−1 to 30 s−1, Fmax decreases by 28.2%, Vmax is unchanged, the ratio of a/Fmax increases from 0.230 to 0.346 (see Fig. 6 C and Table 2). By adding 12 mM inorganic phosphate in their regular contracting solution, Cooke and Pate (22) observed a 30% decrease in isometric force and no change in shortening velocity. The model prediction (Fig. 6 C) also agrees with the findings by Hinken and McDonald (28) in cardiac myocyte when isometric force is normalized.
DISCUSSION
We have demonstrated that the characteristic force-velocity relationship observed in muscle contraction can be simulated mathematically in a seven-state model of cross-bridge cycle where the transitions between states are assumed reversible and where some of the transition rates are assumed dependent on shortening velocity (Fig. 1). The absolute values for the rate constants and functions are found to be somewhat unimportant in our model simulation, because the relative changes in the force-velocity properties are determined by relative magnitudes of transition rates throughout the cycle, and not by the absolute values of these rates. The slowest forward (clockwise) transition under isometric condition is assumed to be the transition between States 4 and 5 (an isomerization step, Fig. 1), as identified by Dantzig et al. (10). The value k45 is assigned a value of 10 s−1. Because there is a large range of values used for transition rates found in literature (9–13), in our simulation, average values for these rates are chosen using k45 as a reference. Many features of the force-velocity curve can be mimicked by changing the transition rates. However, two key components have to be incorporated into the model for it to correctly predict experimental results. The first component involves the assumption that the second power stroke is associated with greater force per cross-bridge (compared with that associated with the first power stroke). This assumption is necessary to account for the effect of blockade of the Pi release step (between States 2 and 3) that is known to decrease isometric force. The factor of 2 chosen to differentiate the force per bridge from the first and second power strokes is, however, arbitrary. The second component involves the assumption that negative force is generated by some bridges when cycling at high rates. Without this assumption, the model would have no internal brake and would generate a force-velocity curve that approaches Vmax asymptotically (i.e., Vmax = ∞).
Rectangular hyperbola and other features of the force-velocity curve
In simulating the force-velocity behavior characterized by a single rectangular hyperbola (Fig. 3), only constants and linear functions (of velocity) for transition rates are used. In simulating the curvature reversal at the low velocity region (Fig. 4 A), instead of a constant, the attachment rate (k01) is made to rise exponentially to a maximum as velocity increases (see Fig. 2 B for the rate function used). This velocity-dependent rate increase can be interpreted as an increase in the probability of detached myosin cross-bridges finding binding-sites on actin filaments, when sliding movement between myosin and actin filaments is allowed (16). This increased probability of attachment, however, is soon offset by the increase in the rate of detachment (k10) as velocity increases. This explains why the curvature reversal is confined in the low velocity region, as found in smooth muscle by Wang et al. (18).
In simulating the double hyperbolic feature of force-velocity relationship observed by Edman et al. (15), a transient decrease in k01 as a function of velocity (Fig. 2 C) is necessary. This is somewhat opposite to the k01 function used in simulating the curvature reversal described above. The simulation results also possesses opposite characteristics in terms of local concavity at the low velocity region of the curve (Fig. 4). Edman et al. (15) explained the relatively large decrease in force during low-speed shortening as due to detachment of highly (positively) strained cross-bridges. In the model by Duke (6), a different explanation is offered: At loads approaching the maximal isometric force, the low sliding velocity diminishes the probability of cross-bridges going through the power-stroke transition. The lack of power strokes in turn reduces the sliding velocity. This self-reinforcing process thus leads to a sharp decrease in velocity with increasing loads (6). Our model offers yet another explanation that does not involve detachment of high-strain bridges (15) or accumulation of bridges in the states before the power stroke transition (6). Our model indicates that a transient decrease in the rate of cross-bridge attachment in a muscle shortening at low velocity (against a near maximal load) can produce a force-velocity relationship with a biphasic feature. In muscle contraction, the probability of cross-bridge attachment is likely partially determined by the flexibility of individual cross-bridges and by how the binding sites on the thin filaments are spaced. These determinants probably play less of a role when sliding velocity is high.
It is not clear why different muscles possess different force-velocity characteristics at the high force region (15,18). It is well known that different myosin isoforms are associated with different muscle types; it is possible that cross-bridges made of different isoforms possess different spring stiffness or flexibility, and that this difference in molecular rigidity determines the shape of the force-velocity curve at the low velocity region. One puzzle is that the biphasic force-velocity relationship is not always observed. For example, in skinned skeletal muscle fibers, there is no evidence for the biphasic feature (7,8,22,29) or at least the feature was not prominent enough to be noticed.
Curvature of the force-velocity curve
Besides Fmax and Vmax, another important parameter that determines the general shape of a force-velocity curve is the curvature described by the ratio a/Fmax, if the force-velocity relationship is approximated by a rectangular hyperbola. (Note that a lower value of the a/Fmax ratio indicates a greater curvature). It is therefore of interest to find out, in a cross-bridge cycle, how the curvature is affected by the transition rates. As shown in Fig. 5 A, increasing the slope (n) of the velocity-dependent force function for the post-power-stroke states (F/Fi = 1 − n(V/Vmax), Fig. 2 D) corresponds to a decreasing curvature of the force-velocity curve. This is because, by increasing the slope (n), lower velocity is required to drive the bridges to the negative-force region; this effectively truncates the high-velocity, low-force part of the force-velocity curve and results in an apparent decrease in curvature. As shown in Fig. 5 B, decreasing the value of attachment rate constant (k01) corresponds to an increasing curvature. This also leads to an increase in the fraction of detached cross-bridges, under all loads. In our simulation, perturbations of the cross-bridge cycle that have led to retention of bridges in the detached state (X0) often result in an increase in the curvature. The connection between the fraction of bridges in the detached state and the force-velocity curvature is not obvious. However, by examining the changes in the state fractions at various velocities, it is noticed that the increase in the number of detached bridges at high velocity comes as a consequence of a disproportional decrease in the bridges occupying States 5 and 6—the last two attached states that produce mostly positive force at low velocity and mostly negative force at high velocity. Therefore, the condition that results in an increase in the fraction of detached bridges also leads to a decrease in the number of negative-force bridges, especially at high velocities. The reduced number of negative-force bridges means that fewer positive-force bridges are required to cycle at low loads and to maintain high velocity of shortening. The shift in balance favoring positive-force bridges increases Vmax because it delays the occurrence of net zero force, and this leads to an increase in the curvature of the force-velocity curve.
There is a common belief that what determines the curvature of a force-velocity curve can be understood in terms of overlapping processes governing the decrease in force and increase in velocity (30). It has been reasoned that as velocity increases, the number of positively strained bridges decreases while the number of negatively strained bridges increases. At low velocities, how quickly the positive-force bridges detach will determine the slope of the force-velocity curve in the high-force region. At high velocities, it is the rate of detachment of negative-force bridges that determines the slope of the curve in the low-force region (30). Our model has no conflict with this line of reasoning; it suggests, however, that the curvature is governed by many more subtle aspects of the cross-bridge cycle that can only be appreciated with a comprehensive modeling with at least seven states in the cross-bridge cycle.
It has been argued that the curvature of a force-velocity curve is related to the thermodynamic efficiency of the muscle (31). This is consistent with our model prediction that a greater curvature is usually associated with a smaller fraction of negative-force bridges at high velocity of shortening, assuming that equal number of positive-force bridges is required to negate the effect of negative-force bridges.
Modification of force-velocity curve by altered transition rates due to changes in [ATP], [ADP], and [Pi]
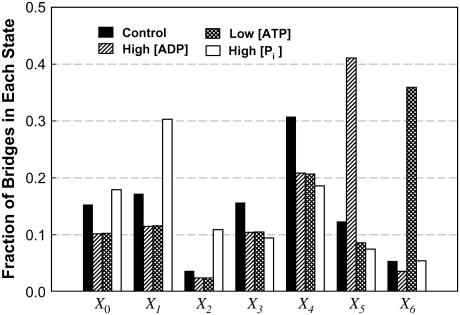
In skinned skeletal muscle fibers, we and others have shown that lowering [ATP] or raising [ADP] in the bathing solution decreases shortening velocity and increases force produced by the muscle fiber, and also decreases the curvature of the force-velocity curve (5,7,22,32). In our simulation, all these changes can be reproduced simply by reducing the rate of transition between States 6 and 0 (to mimic the effect of low [ATP]) (Fig. 6 A) or by reducing the rate of transition between States 5 and 6 (to mimic the effect of high [ADP]) (Fig. 6 B). In our experiments with skinned fibers, it has been found that a large change in [ATP] is required to produce a moderate change in force or velocity (5). This feature is also found in our simulation. Recall that a 10-fold change in k60 (which governed the rate of ATP binding, Fig. 1) produces approximately the same effect as a fivefold change in k56 (which governed the rate of ADP release, Fig. 1). By examining the fractions of cross-bridges occupying each state (Fig. 7), it becomes clear that the explanation is in the small initial cross-bridge population in State 6 (due to large initial value for k60). To cause a sufficient accumulation of bridges in that state, k60 has to be reduced drastically. Because in State 5, the initial cross-bridge population is relatively large (due to a relatively small initial value for k56), a moderate decrease in k56 is sufficient to cause significant accumulation of bridges in State 5. This insight was not available to us in our early studies (5). The agreement between experiment results and model output is another confirmation that, in a cross-bridge cycle, ADP release precedes that of ATP binding.
FIGURE 7.
Fraction of cross-bridges occupying each state under isometric conditions at simulated low substrate and high metabolite concentrations shown in Fig. 6 and Table 2.
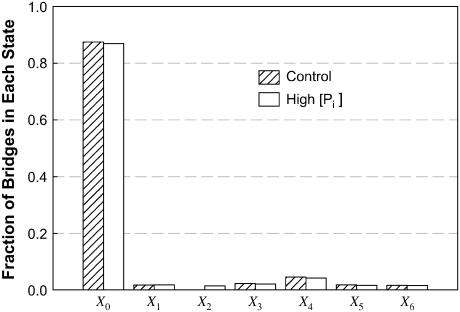
It has been shown in skinned skeletal muscle fibers that an increase in [Pi] is associated with a decrease in force and no change in maximal (unloaded) shortening velocity (8,22,28). In our simulation, a 10-fold reduction in k23 leads to a large decrease in force with no change in velocity (Fig. 6 C). The simulation therefore agrees with experimental results. The simulation results also suggest that there must be another power stroke after phosphate release, because without such a power stroke, reduction in force could not be accomplished by lowering k23. It is not difficult to understand intuitively that by blocking the transition associated with Pi release in the cross-bridge cycle, force can be reduced. However, it is not easy to explain how such a block does not lead to a reduction in shortening velocity. A closer examination of the state fraction of bridges (Fig. 7) reveals that partial blockade of the transition between States 2 and 3 (↑[Pi ]) results in a large increase in the cross-bridge population in State 1. Because of the large value for k10 and the steep dependence of k10 on velocity (Table 1), as well as the fast equilibrium (large values for k12 and k21) between States 1 and 2, most of the detained bridges (seen under isometric conditions) detaches without going through the power strokes at high shortening velocity. As shown in Fig. 8, at maximal velocity of shortening, although there is evidence of bridges being detained in State 2 (X2) in our simulation of ↑[Pi ], the perturbation does not alter significantly the overall distribution of the state fraction of bridges, and therefore should not change Vmax significantly, because Vmax is determined by the balance of positive-force and negative-force bridges mainly in the high-force states (States 4–6).
FIGURE 8.
Fraction of cross-bridges occupying each state at maximal velocity of shortening. Although X2 under conditions mimicking ↑[Pi ] is more than four-times greater than that of the control (too small to be seen on the graph), the overall distribution of the bridges in other states is largely unaffected by the partial blockade of the transition between State 2 and State 3 at maximal velocity of shortening.
CONCLUSION
Unique features of force-velocity relationship found in both striated and smooth muscle contraction can be reproduced by a mathematical model based on steady-state solutions of a 7 × 7 cyclic matrix that describes cross-bridge transitions in a seven-state model with two power strokes. Model predictions regarding altered substrate (ATP) and metabolites (ADP, Pi) concentration in muscle contraction qualitatively matched the results from experiments on skinned skeletal muscle fiber and cardiac myocyte. Insights into the mechanisms underlying changes in force-velocity properties can be gained by examining the distribution of state fractions of cross-bridges in the model under different conditions.
Acknowledgments
This work was supported by an operating grant from the Canadian Institutes of Health Research (CIHR) to C.Y.S. (grant No. MT-13271). C.Y.S. is a senior investigator of CIHR/BC Lung Association. J.J.F. acknowledges partial support by The Petroleum Research Fund, administered by the American Chemical Society, by the Natural Sciences and Engineering Research Council, the Canada Research Chair program, and the Canada Foundation for Innovation.
APPENDIX
Many biological events occur in repeating stochastic steps and are often modeled as transitions between discrete states arranged in a circle. Cycling of the muscle cross-bridges is a good example. To understand the kinetics of these chemical and physical transitions, a system of simultaneous differential equations can be derived based on a cyclic model. Solution to the model depends on solving the associated cyclic matrix. For large matrices (i.e., large number of states in the model), existing methods for exact solutions are too slow and numerical methods are usually the only option. A major disadvantage of using numerical methods is that the iterations sometimes converge slowly or not at all, especially when the matrix is stiff (i.e., with widely varying coefficients), as most of the matrices derived from biological systems are. Here we describe a method specifically designed for solving cyclic matrices. This highly efficient method is particularly suitable for matrices derived from analysis of the cross-bridge cycle; it obtains exact solutions for matrices of any size rapidly, and it does not have limitations associated with numerical methods.
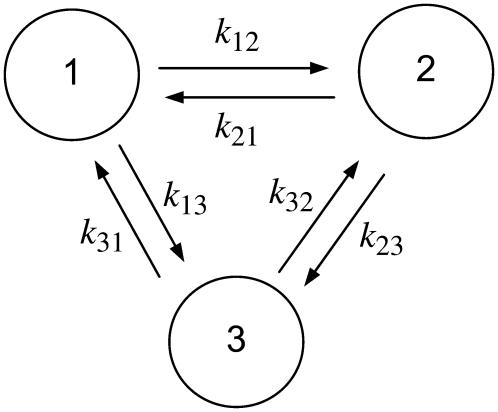
To help describe the method, we use a three-state model as an illustration (Fig. A1). Using actomyosin interaction as an example, the rate of change in a particular state is taken as the difference between the rates at which cross-bridges move into and out of the state. That is,
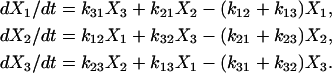 |
(A1) |
FIGURE A1.
A three-state model with forward and reverse transition rates (k-values). The fractions of the enzyme population in each conformation are designated as X1, X2, and X3, with X1 + X2 + X3 = 1.
Under steady state, dXi/dt = 0, where Xi is the fraction of cross-bridges in the state i. Solving the expressions in Eq. A1 under steady state will result in an ill-conditioned problem with no unique solution. This problem can be avoided by replacing one of the above equations with X1 + X2 + X3 = 1. For generality, let us consider an M-state model that gives rise to a linear system with the following matrix form:
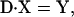 |
(A2) |
where
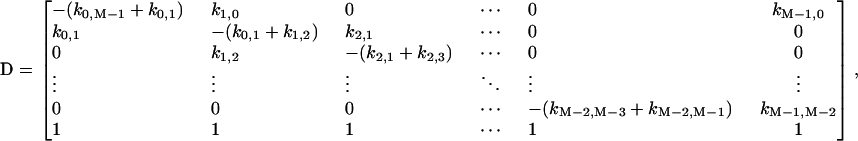 |
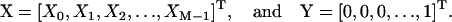 |
Instead of Cramer's rule, we use a simple graphical representation that leads to a formula for the exact solution for the linear system. Let us look at Fig. 1 but imagine that we have M states instead of 3. On the linkage (arrows between two states) we write the rate constants ki,i+1 from state i to state i + 1, and ki+1,i from state i + 1 to i as in Fig. 1. After observing the structure of exact solutions at small M, we propose the following form of solution:
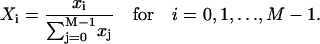 |
(A3) |
Here, 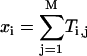 and Ti,j is defined in the following paragraph. Note that the denominator only serves to normalize the solution so that
and Ti,j is defined in the following paragraph. Note that the denominator only serves to normalize the solution so that 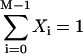 .
.
For a given i, we go over all the other states, denoted by j. For each j, imagine that we break the linkage between states j and j + 1, and then go from state j and j + 1 toward state i along the intact links, accumulating products of the rate constants along the clockwise and counterclockwise routes:
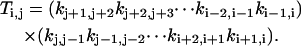 |
(A4) |
Note that all the subscripts should be mapped onto [0, M−1] due to periodicity once they exceed this range.
In the following, we will show that Eq. A3 is indeed the solution of Eq. A2. It can be verified that Ti,j has the following properties:
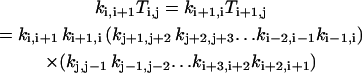 |
(A5) |
for i, j = 0,1, …, M=1 and j ≠ i;
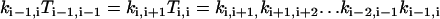 |
(A6) |
for i = 0,1, …, M−1; and
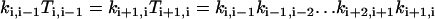 |
(A7) |
for i = 0,1, …, M−1.Considering Eqs. A5–A7, we can arrive at the following equation:
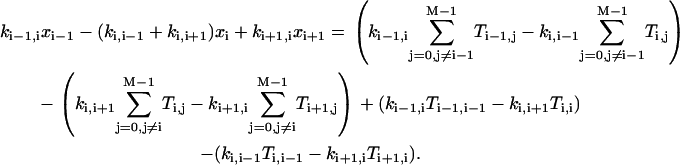 |
(A8) |
Now the second bracket on the right-hand side amounts to 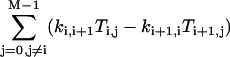 , which vanishes by virtue of Eq. A5. Similarly, the first bracket vanishes as well, since it is the same as the second after replacing i symbolically by i+1. Finally, the third and fourth brackets are zero because of Eqs. A6 and A7, respectively. Thus
, which vanishes by virtue of Eq. A5. Similarly, the first bracket vanishes as well, since it is the same as the second after replacing i symbolically by i+1. Finally, the third and fourth brackets are zero because of Eqs. A6 and A7, respectively. Thus
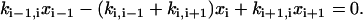 |
(A9) |
Since Xi differs from xi only by a constant scaling factor (compare to Eq. A3), Xi will satisfy Eq. A9 as well. For i = 0,1,…, M−2, these constitute the first M−1 expressions in Eq. A2. The Mth equation is satisfied automatically by the normalization in Eq. A3:
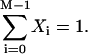 |
(A10) |
Thus, we have demonstrated that Xi as defined above is the exact solution of Eq. A2. Solution of the linear system of Eq. A1 is only a specific case of Eq. A3 with M = 3.
It is extremely easy to solve Eq. A3 for virtually any M with a short computer program (with <15 short lines of codes!). This allows instant display of modeling results and provides modelers instant feedbacks regarding the effect of a change in rate constants on the steady-state distribution of state fractions. As the model of biological processes becomes more and more realistic, the number of states in the model will undoubtedly increase in the future. As the state number approaches hundreds or even thousands, the method outlined here will become indispensable.
References
- 1.Hill, A. V. 1938. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B Biol. Sci. 126:136–195. [Google Scholar]
- 2.Huxley, A. F. 1957. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7:255–318. [PubMed] [Google Scholar]
- 3.Seow, C. Y., and L. E. Ford. 1993. High ionic strength and low pH detain activated skinned rabbit skeletal muscle cross-bridges in a low force state. J. Gen. Physiol. 101:487–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brokaw, C. J. 1995. Weakly-coupled models for motor enzyme function. J. Muscle Res. Cell Motil. 16:197–211. [DOI] [PubMed] [Google Scholar]
- 5.Seow, C. Y., and L. E. Ford. 1997. Exchange of ATP for ADP on high-force cross-bridges of skinned rabbit muscle fibers. Biophys. J. 72:2719–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Duke, T. A. J. 1999. Molecular model of muscle contraction. Proc. Natl. Acad. Sci. USA. 96:2770–2775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pate, E., and R. Cooke. 1985. The inhibition of muscle contraction by adenosine 5′ (β, γ-imido) triphosphate and by pyrophosphate. Biophys. J. 47:773–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cooke, R., K. Franks, G. B. Luciani, and E. Pate. 1988. The inhibition of rabbit skeletal muscle contraction by hydrogen ions and phosphate. J. Physiol. 395:77–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dantzig, J. A., M. G. Hibberd, D. R. Trentham, and Y. E. Goldman. 1991. Cross-bridge kinetics in the presence of MgADP investigated by photolysis of caged ATP in rabbit psoas muscle fibres. J. Physiol. 432:639–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dantzig, J. A., Y. E. Goldman, N. C. Millar, J. Lacktis, and E. Homsher. 1992. Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. J. Physiol. 451:247–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang, G., and M. Kawai. 1996. Effects of MgATP and MgADP on the cross-bridge kinetics of rabbit soleus slow-twitch muscle fibers. Biophys. J. 71:1450–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang, G., and M. Kawai. 1997. Force generation and phosphate release steps in skinned rabbit soleus slow-twitch muscle fibers. Biophys. J. 73:878–894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Galler, S., B. G. Wang, and M. Kawai. 2005. Elementary steps of the cross-bridge cycle in fast-twitch fiber types from rabbit skeletal muscles. Biophys. J. 89:3248–3260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Slawnych, M. P., C. Y. Seow, A. F. Huxley, and L. E. Ford. 1994. A program for developing a comprehensive mathematical description of the cross-bridge cycle of muscle. Biophys. J. 67:1669–1677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Edman, K. A., A. Mansson, and C. Caputo. 1997. The biphasic force-velocity relationship in frog muscle fibres and its evaluation in terms of cross-bridge function. J. Physiol. 503:141–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Edman, K. A., L. A. Mulieri, and B. Scubon-Mulieri. 1976. Non-hyperbolic force-velocity relationship in single muscle fibres. Acta Physiol. Scand. 98:143–156. [DOI] [PubMed] [Google Scholar]
- 17.Edman, K. A. 1988. Double-hyperbolic force-velocity relation in frog muscle fibres. J. Physiol. 404:301–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang, J., H. Jiang, and N. L. Stephens. A modified force-velocity equation for smooth muscle contraction. J. Appl. Physiol. 76:253–258. [DOI] [PubMed]
- 19.Huxley, A. F., and R. M. Simmons. 1971. Proposed mechanism of force generation in striated muscle. Nature. 233:533–538. [DOI] [PubMed] [Google Scholar]
- 20.Lymn, R. W., and E. W. Taylor. 1971. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 10:4617–4624. [DOI] [PubMed] [Google Scholar]
- 21.Podolsky, R. J., A. C. Nolan, and S. A. Zaveler. 1969. Cross-bridge properties derived from muscle isotonic velocity transients. Proc. Natl. Acad. Sci. USA. 64:504–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cooke, R., and E. Pate. 1985. The effects of ADP and phosphate on the contraction of muscle fibers. Biophys. J. 48:789–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hill, A. V. 1964. The effect of load on the heat of shortening of muscle. Proc. R. Soc. Lond. B Biol. Sci. 159:297–318. [DOI] [PubMed] [Google Scholar]
- 24.Huxley, A. F. 1973. A note suggesting that the cross-bridge attachment during muscle contraction may take place in two stages. Proc. R. Soc. Lond. B Biol. Sci. 183:83–86. [DOI] [PubMed] [Google Scholar]
- 25.Sleep, J. A., and R. L. Hutton. 1980. Exchange between inorganic phosphate and adenosine 5′-triphosphate in the medium by actomyosin subfragment 1. Biochemistry. 19:1276–1283. [DOI] [PubMed] [Google Scholar]
- 26.Gear, C. W. 1971. Numerical Initial Value Problems in Ordinary Differential Equations. Englewood Cliffs, NJ, Prentice-Hall.
- 27.Eisenberg, E., and T. L. Hill. 1985. Muscle contraction and free energy transduction in biological systems. Science. 227:999–1006. [DOI] [PubMed] [Google Scholar]
- 28.Hinken, A. C., and K. S. McDonald. 2004. Inorganic phosphate speeds loaded shortening in rat skinned cardiac myocytes. Am. J. Physiol. Cell Physiol. 287:C500–C507. [DOI] [PubMed] [Google Scholar]
- 29.Seow, C. Y., and L. E. Ford. Shortening velocity and power output of skinned muscle fibers from mammals having a 25,000-fold range of body mass. J. Gen. Physiol. 97:541–560. [DOI] [PMC free article] [PubMed]
- 30.Woledge, R. C., N. A. Curtin, and E. Homsher. 1985. Energetics aspects of muscle contraction. Academic Press, London, UK. [PubMed]
- 31.Woledge, R. C. 1968. The energetics of tortoise muscle. J. Physiol. 197:685–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stienen, G. J. M., W. J. van der Laarse, and G. Elzinga. 1988. Dependency of the force-velocity relationship on Mg ATP in different types of muscle fibers from Xenopus laevis. Biophys. J. 53:849–855. [DOI] [PMC free article] [PubMed] [Google Scholar]