Excitation Energy Transfer and Charge Separation in Photosystem II Membranes Revisited

Abstract

We have performed time-resolved fluorescence measurements on photosystem II (PSII) containing membranes (BBY particles) from spinach with open reaction centers. The decay kinetics can be fitted with two main decay components with an average decay time of 150 ps. Comparison with recent kinetic exciton annihilation data on the major light-harvesting complex of PSII (LHCII) suggests that excitation diffusion within the antenna contributes significantly to the overall charge separation time in PSII, which disagrees with previously proposed trap-limited models. To establish to which extent excitation diffusion contributes to the overall charge separation time, we propose a simple coarse-grained method, based on the supramolecular organization of PSII and LHCII in grana membranes, to model the energy migration and charge separation processes in PSII simultaneously in a transparent way. All simulations have in common that the charge separation is fast and nearly irreversible, corresponding to a significant drop in free energy upon primary charge separation, and that in PSII membranes energy migration imposes a larger kinetic barrier for the overall process than primary charge separation.

INTRODUCTION

Photosystem II (PSII) is a large supramolecular pigment-protein complex embedded in the thylakoid membranes of green plants, algae, and cyanobacteria. It uses sunlight to split water into molecular oxygen, protons, and electrons. PSII is conventionally subdivided into 1), a core consisting of light-harvesting complexes CP43 and CP47 and the reaction center (RC), where excitation energy is used to create a charge separation (CS) that is stabilized by secondary electron transfer processes; and 2), an outer antenna of chlorophyll (Chl) a/b binding proteins, containing the majority of the light-harvesting pigments. The latter proteins, of which the trimeric light-harvesting complex II (LHCII) is by far the most abundant, are not only required for the efficient absorption of light and the transfer of excitation energy to the RC under light-limiting conditions, they also play essential roles in several regulation mechanisms of the photosynthesis process under light-saturating conditions, like state transitions and nonphotochemical quenching (see, e.g., Pascal et al. (1)).

The overall quantum efficiency of the CS process depends on the relative rate constants of various processes: 1), excitation energy transfer (EET) from chlorophylls in the light-harvesting antenna to the chlorophylls in the RC that perform the CS; 2), CS and charge recombination in the RC; 3), stabilization of the CS by secondary electron transfer; and 4), trivial relaxation or loss processes of the excited state: intersystem crossing, internal conversion, and fluorescence.

It is important to know which of the above-mentioned processes determine the overall rate of CS in open, fully functional PSII (with an RC in which the secondary electron acceptor Q_A is oxidized). This knowledge is needed for a detailed understanding of the kinetics of regulation processes like nonphotochemical quenching. For a long time it has been assumed by many authors that the charge separation process in PSII is trap-limited, i.e., the excitation energy diffusion through the antenna to the RC is much faster than the overall CS time. Since the 1980s the so-called exciton/radical-pair-equilibrium model (2,3) has been a popular way to interpret time-resolved and steady-state fluorescence data of PSII containing preparations. More recently, Klug and co-workers concluded from the study of a whole range of PSII containing preparations possessing different antenna sizes that the CS is indeed trap limited (4). However, from singlet-singlet annihilation studies on LHCII trimers and aggregates it was concluded that the excitation diffusion within the outer antenna is relatively slow (5) and that CS in LHCII-containing PSII systems cannot be entirely trap limited (6,7). Also Jennings and co-workers came to the same conclusion (8).

At the moment a large number of experimental data are available on the charge separation kinetics of isolated PSII RCs and PSII core complexes (9,10). In PSII RC and CP47-RC preparations (which contain 6 and 22 chlorophylls, respectively, and 2 pheophytins, but do not contain the secondary electron acceptor Q_A) the kinetics were strongly multiexponential. They could be explained by three reversible radical pair states, of which the first is nearly isoenergetic with the singlet-excited state of the primary electron donor (P680*), in combination with the absence of severe kinetic limitation for the EET between CP47 and the RC (11). PSII core complexes (with 35 chlorophylls and 2 pheophytins) do contain Q_A, and in open centers (with Q_A oxidized) the decay kinetics are dominated by a major phase in the 30–60 ps time range and a minor phase of ∼200 ps (12–14). The energy difference between the first radical pair state and P680* is probably much larger than in PSII RC and CP47-RC preparations (14).

It is unknown to which extent these systems give kinetics compatible with more native-like systems like chloroplasts, thylakoid membranes, and PSII membranes (the so-called BBY preparations). Most studies on entire chloroplasts or thylakoid membranes suggested average values for the trapping time in PSII in the range from ∼300 to ∼500 ps (15–17). However, fast PSI fluorescence may partly mask faster PSII decay processes for these preparations. Moreover, unconnected light-harvesting complexes may be present in the stroma lamellae, which can further complicate the identification of the PSII fluorescence (18).

PSII grana membranes (BBY preparations) do not contain PSI or stroma lamellae, but do contain a much larger antenna than PSII core particles. Due to the presence of trimeric and monomeric Chl a/b-containing complexes, these membranes contain ∼150 Chls a per PSII, ∼4 times more than isolated PSII core particles (19). The kinetics in these membranes were described by a single lifetime of ∼210 ps (20) or with a major lifetime of 140 ps and a minor lifetime of 330 ps (12). A number of other studies revealed slower kinetics, which can be explained by a ‘contamination’ of closed centers (with Q_A single or double reduced).

In this work we present new time-resolved fluorescence data on BBY preparations and propose a coarse-grained model in which previously reported antenna and RC kinetics can easily be incorporated, allowing a comparison with the obtained fluorescence kinetics of PSII in grana membranes. To this end we make use of available knowledge about the supramolecular organization of PSII (19). The results reveal a number of essential differences in primary CS in isolated RCs, PSII cores, and PSII membranes and stress that diffusion of the excitation energy in the membranes contributes significantly to the overall CS kinetics. The presented framework will facilitate new studies that are directed at the contributions of individual complexes to the overall kinetics by using mutant preparations with altered PSII composition or organization.

MATERIALS AND METHODS

Sample preparation

PSII membranes (BBY particles) were prepared according to Berthold et al. (21) from fresh spinach leaves. An analysis by diode-array-assisted gel filtration chromatography, performed as described previously (22), showed that the preparations contained at most 1–2% of PSI.

Time-correlated single photon counting

Steady-state fluorescence spectra were measured with a Fluorolog-3.22 (Jobin Yvon-Spex, Edison, NJ) at room temperature. Time-correlated single photon counting (TCSPC) measurements were performed at magic angle (54.7°) polarization as described previously (23). The BBY particles where diluted to an optical density of 0.08 per cm in a buffer of 20 mM Hepes pH 7.5, 15 mM NaCl, and 5 mM MgCl₂. The repetition rate of excitation pulses was 3.8 MHz, and the excitation wavelength was 430 nm. Pulse energies of sub-pJ were used with a pulse duration of 0.2 ps and a spot diameter of 1 mm. The samples were placed in a 3.5-mL and 10-mm light path fused silica cuvet and stirred in a temperature-controlled (20°C) sample holder. In combination with the low intensities of excitation, this guaranteed that close to 100% of the RCs stayed open (see also Results) and significant buildup of triplet states was avoided. The full-width at half-maximum (FWHM) of the system response function was 60 ps with a resolution of 2.51 ps per channel. The dynamic instrumental response function of the setup was obtained from pinacyanol in methanol with a lifetime of 10 ps. The following interference filters were used for detection: 671, 679, 688, 693, 701, 707, 713, and 724 nm (Balzers, Liechtenstein model B40). Data analysis was performed using a home-built computer program (24,25). A fast component (∼5 ps) was needed in most cases to fit the time range around the rising edge of the excitation pulse, but this component is not relevant for this study and is omitted in the further modeling.

Synchroscan streak-camera

For the streak-camera measurements the BBY particles were diluted to an optical density of 0.7 per cm in a buffer of 20 mM BisTris pH 6.5 and 5 mM MgCl₂. Ferricyanide (1 mM) was added to keep the RCs open; and 400-nm excitation pulses of ∼100 fs were generated using a Ti:sapphire laser (VITESSE, Coherent, St. Clara, CA) with a regenerative amplifier (REGA, Coherent). The repetition rate was 150 kHz, and the pulse energy was 1 nJ. The excitation light was focused with a 15-cm focal length lens, resulting in a focal diameter of 150 μm in the sample. To refresh the sample between the excitation pulses, the sample was placed into a 2-mm-thick spinning cell of 10 cm diameter, rotating at a speed of 20 Hz. The fluorescence was detected in a direction at 90° from the excitation beam through a detection polarizer at magic angle, an orange sharp cutoff filter glass, a Chromex 250IS spectrograph, and a Hamamatsu C 5680 synchroscan streak-camera (Hamamatsu Photonics, Hamamatsu, Japan). The streak images were recorded with a cooled, Hamamatsu C4880 CCD camera. The FWHM of the overall time response of the experiment was 5 ps. Global analysis was applied, using a model with a number of parallel decaying compartments, which yields decay-associated spectra (DAS) (26).

RESULTS AND DISCUSSION

Time-resolved fluorescence measurements

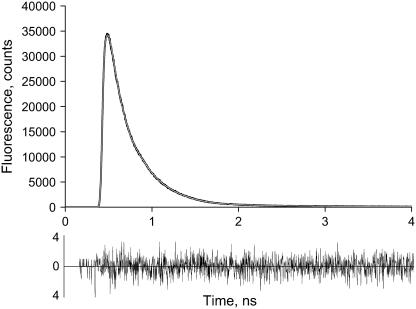
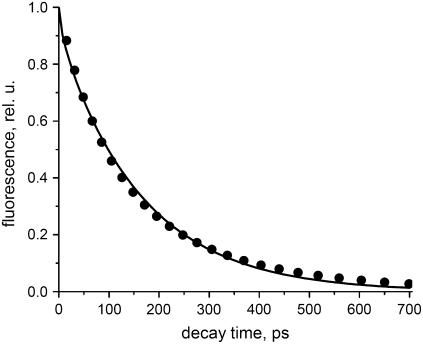
In Fig. 1 a typical TCSPC decay curve for PSII grana membranes with open RC and Chl a excitation (430 nm) is shown. To obtain a good multiexponential fit, at least four decay times are needed. The contribution of a 2.9-ns component is very small (<0.5%) and is probably due to very small amounts of PSII with closed RCs, free Chl, and/or detached pigment-protein complexes. Most of the decay can be described by two major components and a minor one: 77 ps (41%), 206 ps (56%), and 540 ps (3%). The excitation intensity was low enough to avoid excitation annihilation (singlet-singlet or singlet-triplet) or accumulation of closed RCs. Increasing the excitation intensity with a factor of 10 led to identical decay kinetics, whereas an increase with a factor of 1000 led to substantially longer decay times because of the closure of RCs (data not shown).

FIGURE 1.

Room temperature fluorescence decay curve (measured with TCSPC) for open BBY preparations together with a fit. The sample was excited at 430 nm and fluorescence was detected at 693 nm. The decay times and their relative amplitude are 77 ps (41%), 206 ps (56%), and 540 ps (3%). Also shown are the residuals (difference between data and fit).

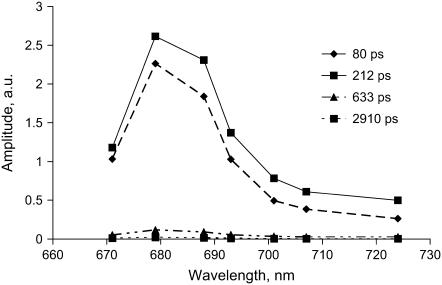
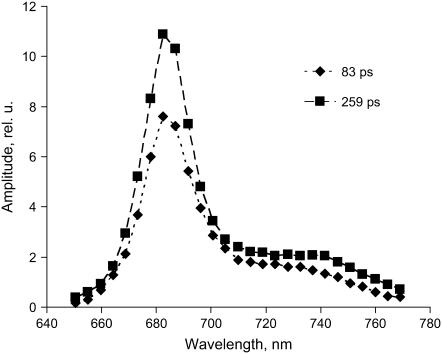
Decay curves were measured at different detection wavelengths, and the decay times were very similar in all cases. The result of a global analysis of all decay curves is given in Fig. 2, showing DAS. At all detection wavelengths the two longest decay times are nearly absent. The fitted decay times are 80 ps and 212 ps for the two major components. The contribution from a 633-ps component is small and the 2.9-ns component has negligible amplitude. The DAS are dominated by a main fluorescence band peaking between 680 and 690 nm and show small vibronic bands above 700 nm. The average lifetime of 150 ps is significantly shorter than previously estimated values for chloroplasts and thylakoid membranes (300–500 ps), but it is closer to the values obtained for BBY by Schilstra et al. (20) and Van Mieghem et al. (12). To determine whether processes are present that are faster than the time resolution of the photon counting setup, the experiments were also performed with a streak-camera with 3-ps time resolution. The results are shown in Fig. 3. The data are rather similar; the decay is dominated by two components with lifetimes 81 ps (60%) and 258 ps (40%). No short-lived component was resolved. Note that the times are similar but not identical to those obtained with the TCSPC measurements. This is mainly due to some variability in the samples. However, this variability is irrelevant for the main conclusions drawn in this work and leaves some uncertainty in the presented parameters. Note that the difference in excitation wavelength can also cause some variability but it is less outspoken (work in progress).

FIGURE 2.

Decay-associated fluorescence spectra (measured with TCSPC) of BBY preparations at room temperature. The sample was excited at 430 nm.

FIGURE 3.

Decay-associated fluorescence spectra (measured with streak-camera) of BBY preparations at room temperature. The sample was excited at 400 nm.

Modeling of the fluorescence kinetics

The overall average CS time τ can be considered as the sum of two times, the first passage time or migration time τ_mig representing the average time that it takes for an excitation created somewhere in PSII to reach the RC (primary donor) and the trapping time τ_trap (7,27). The trapping time is the product of the intrinsic CS time τ_ιCS (when the excitation is located on the primary donor) and the probability that the excitation is located on the primary donor after Boltzmann equilibration of the excitation over PSII. In a system with N isoenergetic pigments, this would mean that τ_trap = Nτ_ιCS. Note that τ_mig can be split into an equilibration time in the antenna and a transfer-to-the-trap time (7,27); but this approach is not needed here.

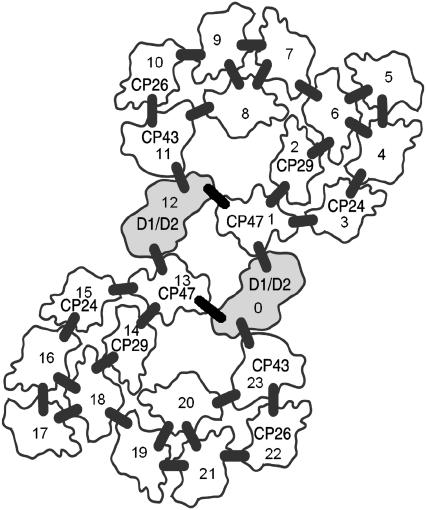
First we introduce a simple basic model to describe the overall CS kinetics in PSII in terms of the CS kinetics in the RC and EET in the antenna complexes. Thereafter, we show how the results are affected when the model is extended. In Fig. 4 we show the dimeric supercomplex of PSII (28) that is used for our coarse-grained modeling. It is a basic unit that can be further associated in different ways to form larger organization patterns (19,29). Besides two RCs it contains two CP47, two CP43, two CP24, two CP26, and two CP29 monomers and four LHCII trimers. We define a hopping rate k_h for transfer between all neighboring monomeric complexes and/or subunits that are connected via a bar in Fig. 4. It is worth mentioning that EET between monomeric LHCII subunits in the trimer is also modeled in that way. The reason we take the same hopping rate in all cases is that all outer antenna complexes are rather homologous and energy transfer is largely determined by the transfer within the complexes (see also below). The situation may be different for hopping from CP43 or CP47 to the RC and this case will be discussed separately. Forward and backward rates between complexes have been adjusted by rescaling the single hopping rate in accordance with the differences in the Chl a numbers (see Appendix for the details and Fig. 4 for the number of Chl a molecules). The outer antenna complexes all transfer their excitations to the RC via CP47 or CP43. Excitations can leave the RC again into the antenna.

FIGURE 4.

Membrane organization of PSII that is used for our coarse-grained modeling. Besides two RCs (D1/D2) (2 Phe a and 6 Chl a per RC), this dimeric supercomplex contains 1 CP47 (16 Chl a), 1 CP43 (13 Chl a), 1 CP24 (5 Chl a and 5 Chl b), 1 CP26 (6 Chl a and 3 Chl b), 1 CP29 (6 Chl a and 2 Chl b) monomer, and 2 LHCII (8 Chl a and 6 Chl b per LHCII monomeric subunit) trimers per RC. LHCII trimers are represented by 4-5-6, 7-8-9, 16-17-18, 19-20-21. Also indicated are added putative energy transfer links (short thick bars) between the light-harvesting pigment-protein complexes.

It should be noted that we also examined the effect of increasing the number of (connected) supercomplexes, based on the various models for megacomplexes (dimeric supercomplexes) that have been detected thus far (19). However, no essential differences were observed. Therefore it is sufficient to consider the basic unit with only two RCs. All complexes are taken to be isoenergetic (30).

At first we assume that irreversible CS takes place in the RC, which in our definition consists of the six central chlorins in the RC, with a rate k_CS. Note that this is different from the intrinsic CS rate k_iCS. The two peripheral Chls in the RC are assumed to be part of the antenna system, and one of them is assigned to CP47 and the other to CP43. This is justified because the distance of these peripheral chlorophylls to the nearest chlorophylls in CP47 or CP43 is shorter than to the nearest central chlorin in the RC (31). In the simplest (but nonrealistic) case of six isoenergetic central chlorins in the RC with primary CS occurring from one pigment, k_iCS would be equal to 6 k_CS.

Fig. 4 shows two LHCII trimers per RC, but it is known that on average four LHCII trimers are present per RC (7). The other two trimers can be in a different membrane layer organized in such a way that they can still transfer the excitation energy to the RCs (29), but they can also be located close to a PSII-LHCII supercomplex in the same layer, in particular in membranes without ordered arrays of PSII. Because it is unknown how the extra two LHCIIs are connected to the RC, it is only possible to guess their contribution to the overall trapping time. We consider two extreme cases. If these four LHCII trimers per PSII would be in the same membrane layer as the RC, the overall τ_mig would become close to 160 ps, as was concluded from singlet-singlet annihilation (5). The only assumption in that case is that the connectivity between the additional light-harvesting complexes and the others is the same as between the ones that were already present. The important point is that the migration time increases. The value of 160 ps is approximately equal to the observed average lifetime for BBY preparations, which would imply that the CS is nearly diffusion limited. Although we cannot rule out this possibility, it seems highly unlikely. We will return to this point later.

As another extreme case we assume that a regular two-dimensional lattice with 100 sites (the approximate number of Chl a per RC in the supercomplex shown in Fig. 4) is extended to a regular three-dimensional lattice with 148 sites (two extra trimers) with the same hopping rates. This reduces τ_mig by ∼10% (27). The same hopping rates may not be realistic, but energy transfer between membranes in a grana stack will very likely occur within the excited state lifetime (32,33). On the other hand, τ_trap increases by 48% because the equilibrium distribution of excited states is shifted further toward the antenna. For the purpose of this work it is not necessary to discuss explicitly all the different possible organizations. They will be discussed implicitly by considering different combinations of the hopping rates and charge separation rates.

The overall fluorescence decay (reflecting decay of excited-state population) can now be calculated for the model system in Fig. 4 for any initial excitation distribution (see Appendix). It can be compared to the fluorescence kinetics of PSII membranes with open centers (Figs. 1–3). In other words we reconstruct the experimental decay by including only the dominating components and the minor component of 633 ps (Fig. 2). We assume an initial distribution between the various complexes which is proportional to the number of Chls a per complex. Fig. 5 shows the reconstructed decay and the best fit of the above model over the time range 0–700 ps for the TCSPC data. This simple model provides a good description of the kinetics. The fitted hopping rate is (17 ps)⁻¹ and the CS rate is (1.2 ps)⁻¹. It should be noted that the experimentally observed nonexponentiality in this case is not modeled because it is explicitly assumed that CS is irreversible. We will show the effect of including charge recombination below. In this way nonexponentiality is introduced. However, it is also possible that the nonexponentiality is due to some structural heterogeneity, and in this case one might expect to obtain a distribution of trapping times and the fitted value should be considered to be an average trapping time.

FIGURE 5.

Reconstructed BBY fluorescence decay (dots) using the three main decay components (80, 212, and 639 ps) and the best fit (line) assuming irreversible CS (see text) over the time range 0–700 ps. The fitted hopping rate is (17 ps)⁻¹, and the CS rate is (1.2 ps)⁻¹.

Before we discuss more realistic models and the uniqueness of the fit, it is worthwhile to look at the consequences of these rates. The hopping rate (17 ps)⁻¹ is rather slow and corresponds to a value of τ_mig of 130 ps (see Appendix for method of calculation). The charge separation rate k_CS of (1.2 ps)⁻¹ is the effective rate for the whole RC, i.e., the central six chlorins. If primary CS occurs from one specific Chl, then k_iCS = (1.2 ps)⁻¹/6 = (0.2 ps)⁻¹ in the case of isoenergetic pigments. This would mean that τ_trap = τ_ιCS × N = 0.2 ps × 100 = 20 ps if an organization as in Fig. 4 is considered, or τ_trap = 0.2 ps × 150 = 30 ps if the Chl a content in PSII membranes is considered. Clearly, in this case the overall trapping time is dominated by the migration time. The streak-camera data were modeled in the same way and led to k_h = (17.5 ps)⁻¹ and k_CS = (0.4 ps)⁻¹. The observed differences in the fluorescence lifetime can easily be explained by some variability in the preparations. At this point it is not useful to discuss the differences in fitting results because the fitting outcome is not unique (see below).

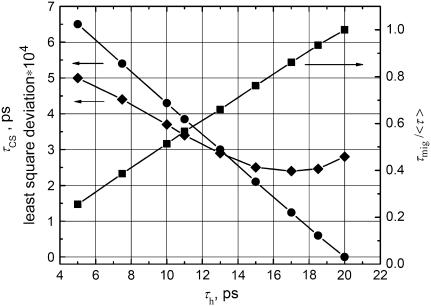
The given rates do not uniquely describe the data within the context of the above model. In Fig. 6 we show different combinations of k_h and k_CS that lead to a reasonable description of the TCSPC data. The results were obtained as follows: We chose a particular value for 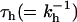and looked for the best fit of 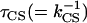. Varying for instance τ_h from 10 to 20 ps leads to fits for which the quality is rather similar (see Fig. 6), τ_mig varies from 77 to 150 ps whereas the CS time varies from 4.3 to 0 ps. A slower migration toward the RC requires a faster CS to obtain the same experimentally observed decay rates. It is clear that different combinations of hopping and CS times can explain the observed kinetics. Given the approximate nature of the modeling, no strong conclusions can be drawn from the differences between the simulated and the experimental curves.

FIGURE 6.

Different combinations (circles) of k_h and k_CS that lead to the best description of the BBY decay kinetics, assuming irreversible CS (see text). The numbers were obtained as follows: We chose a particular value for 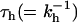and looked for the best fit of 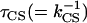. Indicated are also the difference between the model and the experimental BBY curve defined as sum of least squares of the deviates (diamonds). The squares indicate the fraction of the trapping time that is due to migration at a particular value for the hopping time. The arrows indicate which vertical axis corresponds to which curve.

Modulating excitation energy transfer from CP47 or CP43 to the RC

In the above model we assumed that CP47 can transfer energy to two different RCs (see Fig. 4). It is not entirely clear from the crystal structure whether this really is the case. Therefore, we also considered the case that CP47 can transfer to only one RC. Then a hopping time of 15.2 ps is obtained for the best fit and a CS time of 0.23 ps. Because there are fewer routes for reaching the RC, one needs to speed up the transfer and CS process to arrive at a good fit. The migration time is 147 ps, i.e., the contribution from the migration time remains dominant. This illustrates the fact that the outer antenna determines to a large extent the total migration time. However, in this case the CS becomes unrealistically fast and in the following we consider the situation that CP47 is connected to two RCs.

Although it has been argued that energy transfer from CP47 or CP43 to the RC is relatively slow (7,34), we also consider a rather extreme case in which this transfer time is three times shorter than the general hopping time. This would be in agreement with measurements on RC and CP47-RC preparations, which indicated that the energy transfer between CP47 and RC is not rate limiting (11) and that the connecting chlorophylls of CP47 and CP43 are optimally oriented for fast energy transfer (35). The best fit now requires a value of τ_h of 24.8 ps and τ_mig is 100 ps, meaning that the migration time is still dominant.

Reversible charge separation

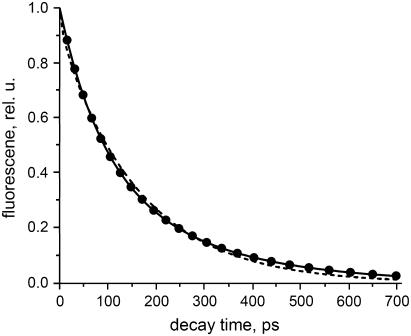
Above we made the assumption that the CS is irreversible. Although it leads to a satisfactory description of the data, it contrasts with the general opinion that substantial charge recombination occurs. Therefore, we extended our model by including recombination and a second charge separated state. It is not required for the fitting to specify the nature of such a second charge separated state but it might, for instance, be the reduced Q_A in combination with the oxidized primary donor. The electron back-transfer rate (k_bCS) to the primary donor is related to the intrinsic charge separation rate from this primary donor via the detailed balanced relation k_bCS/k_iCS = e^−ΔG/kT where ΔG is the drop in free energy upon primary CS, k is the Boltzmann constant, and T is the absolute temperature. The rate and time constant of secondary CS are called k_RP and τ_RP, respectively. The data can now be fitted in different ways, depending on the starting values of the different fitting parameters. Two fits are shown in Fig. 7. The dashed line corresponds to a slow hopping time (17 ps). In this case the times for primary and secondary CS are 1.24 and 13.3 ps, respectively, and ΔG = 2380 cm⁻¹. The solid line is a fit with an extremely fast hopping time (1.3 ps). The times for primary and secondary CS are 6.6 and 168 ps, respectively, and ΔG = 890 cm⁻¹. The crucial point is that although the rates of hopping and secondary CS cannot be separately estimated from these fits, fast primary CS in combination with a large drop in free energy is needed to describe the data.

FIGURE 7.

The BBY kinetics (dots) is fitted with reversible CS into a primary charge separated state and subsequent irreversible CS into a secondary charge separated state. The solid line is a fit with a slow hopping time (17 ps). In this case the times for primary and secondary CS are 1.24 and 13.3 ps, respectively, and ΔG = 2380 cm⁻¹. The dashed line is a fit with an extremely fast hopping time (1.3 ps). The times for primary and secondary CS are now 6.6 and 168 ps, respectively, and ΔG = 890 cm⁻¹.

Comparison with charge separation in isolated reaction centers and core complexes

We make a comparison with models for CS that have been presented in the literature based on measurements on isolated PSII RC and core complexes. We inspect what happens to the calculated trapping kinetics for BBY particles when CS in the PSII RC is described according to these models. We restrict ourselves to the most recent ones that can be directly incorporated into the above framework.

The model of (open) PSII core complexes from Vassiliev et al. (13) is given in Fig. 8 (model 3). It is characterized by many fast electron transfer steps, the first one being the intrinsic CS rate from the presumed lowest exciton state of the “special pair” or two accessory chlorophylls. This model is incorporated into our initial description above, i.e., instead of a unidirectional CS step in the RC with τ_CS = 1.2 ps, we use the CS scheme from Fig. 8 c. The first step in the latter scheme is slowed down by a factor of 6/4 because CS can take place from four out of six chlorophylls. The results are given in Fig. 9 b (thick, solid line). The hopping time is taken to be 17 ps, i.e., the time that we found in the best fit of the first model. The simulated kinetics shows a slightly faster initial decay and a larger contribution from a slow decay component when compared to the experimentally observed decay for BBY preparations. We inspected how we could bring the model into accordance with the BBY data by keeping everything the same except the first rate of CS and the corresponding change in free energy. It was possible to obtain a very good fit (not shown) by changing τ_CS from 0.15 ps into 0.75 ps and ΔG from −464 cm⁻¹ into −826 cm⁻¹, respectively, with a hopping time of 17 ps. The CS is slowed down to match the initial part of the decay curve and the drop in free energy is increasing, making the CS less reversible, leading to smaller contributions from slow components. It is exactly this lack of a slow component in the BBY data that requires a large drop in free energy upon fast CS. The presence of two additional trimers per RC will shift the equilibrium further toward the excited states, leading to even more fluorescence at longer times in the modeled curve, i.e., to a greater discrepancy.

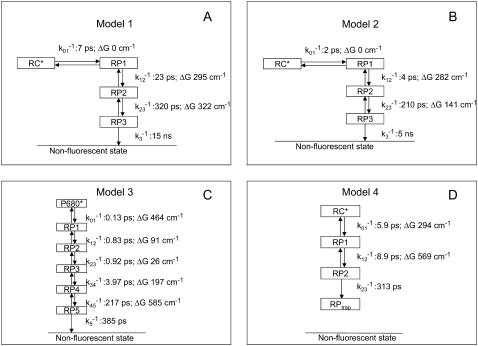
FIGURE 8.

Models for CS in the PSII RC taken from the literature. These models are based on measurements on isolated RCs, (a) model 1 (11) and (b) model 2 (43) and on measurements on PSII cores, (c) model 3 (13), and (d) model 4 (39).

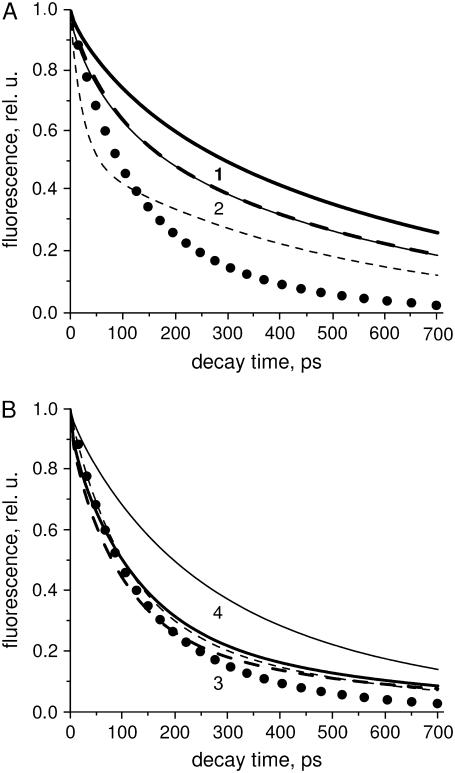
FIGURE 9.

(a) Solid circles represent reconstructed experimental fluorescence kinetics (TCSPC) of BBY (see text for details). Solid and dashed lines represent simulated decay curves, using the two RC models of Fig. 8, a and b. Electron transfer to the quinone is implemented by assuming irreversible transfer from RP2 with a rate constant of (200 ps)⁻¹. The thick lines (1) refer to model 8 (a), the thin ones (2) to model 8 (b). For the solid lines a hopping time of 17 ps is taken and an infinitely fast hopping time for the dashed ones. (b) Solid circles represent reconstructed experimental fluorescence kinetics (TCSPC) of BBY (see text for details). Solid and dashed lines represent simulated decay curves, using the two core models of Fig. 8, c and d. The thick lines (3) refer to the model in Fig. 8 c, the thin ones (4) to the model in Fig. 8 d. For the solid lines a hopping time of 17 ps is taken. For the dashed lines a hopping time of 13.4 ps is taken for case 3 (thick dashed) and 0 ps for case 4 (thin dashed).

Alternatively, we tried to fit their PSII core model to the BBY data by optimizing the hopping rate. The result can also be seen in Fig. 9 b (thick, dashed line) and the fitted hopping time in this case is 13.4 ps. The fit is better than in the first case above, but the decay remains too fast at early times and the contribution of the slow component is too large. So independent of the details of the model, the large drop in free energy upon initial CS appears to be essential to describe the BBY data. It is unclear whether the core preparations contain a fraction of complexes in which the lifetimes are too long, or whether the drop in free energy in (cyanobacterial) core particles is indeed less pronounced than in BBY particles. The latter possibility could arise from a different ligation of the pheophytin that serves as electron acceptor. The residue that is involved in an H-bond with pheophytin is a Gln in cyanobacteria and a Glu in higher plant PSII, which can give rise to a shift of the redox potential of the pheophytin by ∼30 meV (36–38).

Very recently, new data on isolated cores were obtained and a different model was proposed by Miloslavina et al. (39). The model assumes ultrafast energy transfer from CP47 and CP43 to the RC, and the authors conclude that the kinetics are trap limited in these complexes and that CS can be described by a scheme that includes reversible CS to several radical pair states (Fig. 8 d). When we incorporate this scheme for CS into our model (hopping time 17 ps), the resulting kinetics are far too slow (Fig. 9 b, thin, solid line). Even when we assume the EET throughout the antenna to be infinitely fast, the resulting kinetics are still too slow (Fig. 9 b, thin, dashed line). To improve the fit, as before, a larger drop in free energy is needed (648 cm⁻¹ instead of 294 cm⁻¹) and the CS time should decrease: 2.1 ps instead of 5.9 ps. It should be noted that the scheme of Miloslavina et al. does not include the fitting of a 111-ps component (amplitude 10%) that was observed in their experiments. Incorporating this component into the model would further increase the discrepancy.

Other models have been proposed that were based on the measurements of isolated PSII RC complexes. Two recent ones are represented in Fig. 8, a and b. They cannot be compared directly to the BBY results because the isolated RCs do not contain the electron acceptor Q_A. Therefore, we tested the hypothesis that the initial CS kinetics/energetics in isolated RCs is the same as in the open BBYs. We used the models as presented in Fig. 8, a and b, up to state RP2, whereas electron transfer to Q_A was modeled by an irreversible decay of state RP2 with rate constant (200 ps)⁻¹. With a hopping time of 17 ps the modeled kinetics are far too slow for both models (Fig. 9 a, solid lines). Even when the hopping is assumed to be infinitely fast, the simulated kinetics is still much slower. Again, the agreement between the BBY data and the RC model can only be improved by using a fast CS in combination with a large drop in free energy. However, a fast CS and a large drop in free energy are not in agreement with the measured fluorescence kinetics of isolated PSII RC complexes. Note that the inclusion of back transfer of an electron from the Q_A would only increase the discrepancy.

One might compare the RC in isolated PSII RCs (without Q_A) with closed RCs in Q_A-containing PSII preparations. It was already observed many years ago (40) that closed RCs show considerably slower fluorescence kinetics than open RCs, which could be modeled by a sixfold slower rate constant for CS and a 400 cm⁻¹ higher energy of the primary radical pair (3). The slowing down of the primary CS reaction was explained by electrostatic repulsion due to the negative charge on Q_A, but other authors suggested that the charge on Q_A has a minor effect on the energy level of the primary radical pair (4,14). The relative importance of electrostatic repulsion for slowing down CS was demonstrated by Van Mieghem et al. (12), who found a considerable difference in CS kinetics between centers with singly and doubly reduced Q_A in PSII membranes (where the fluorescence kinetics and integrated emission yield in centers with doubly reduced Q_A was just in between those with oxidized and singly reduced Q_A) but not in PSII core particles. In conclusion, the RC in isolated PSII RCs has indeed a closer resemblance to closed RCs in Q_A-containing PSII complexes, already at the level of primary CS despite the absence of a reduced Q_A.

Contribution of the migration time to the overall trapping time

It was recently suggested that the overall CS process cannot be entirely trap limited in grana membranes (41). From singlet-singlet annihilation studies (5) on LHCII trimers and aggregates, it was apparent that the spatial equilibration time per trimer is several tens of picoseconds. A value of 48 ps was determined for trimers, whereas this number was ∼32 ps per trimer in lamellar LHCII aggregates. It was argued (6) that the latter time might be faster because excitations have the tendency to be located at the outside of the trimer, thereby facilitating energy transfer and thus annihilation in aggregates. The fact that the annihilation in trimers is slower than in aggregates indicates that it is not limited by hopping between different complexes but by relatively slow transfer within the complexes, in agreement with pump-probe and photon-echo data (6,42).

Therefore, the contribution of the time of transfer in or between LHCII trimers to the overall migration is approximately equal to the number of trimers per RC multiplied by the equilibration time per trimer, provided that they are in “intimate contact” within one plane. The supercomplex in Fig. 4 contains two LHCII trimers per RC which each contribute ∼32 ps to the τ_mig (5). Moreover, CP24, CP26, and CP29 each show high homology to an LHCII monomer, and together they add another ∼32 ps. For CP47 and CP43 these numbers are less well known, but they are probably faster. The overall migration time would thus be around 100 ps, which constitutes a large fraction of the overall trapping time. This number would even be larger when the two “missing trimers” are located in the same plane, but if they would be in a different layer this value might be slightly smaller (see above). In the simulations that we showed above, it was found that a hopping time of 17 ps leads to a total migration time of 130 ps. To arrive at a migration time of 100 ps, the hopping time has to be decreased proportionally, i.e., from 17 ps to (100/130) × 17 ps = 13 ps. At the moment it is uncertain to what extent the excitation migration times determined for isolated LHCII trimers and lamellar aggregates are directly applicable to the BBY preparations. The organization of the complexes will have some influence, although it was argued above that migration is to a large extent determined by migration within the individual complexes. Also the details of the annihilation process from which the migration times were determined have some influence. This issue will be addressed in a future study.

Of course, the proposed modeling procedure for BBY is approximate. However, it provides an easy way to incorporate existing knowledge and models for individual complexes, and despite remaining uncertainties it is demonstrated that valuable conclusions can be drawn about both the EET and the CS. The exact contribution of excitation diffusion (migration time) to the overall CS remains somewhat uncertain, which results in uncertainty in τ_CS. However, the relation and consequences are transparent and can easily be extracted. It is also clear that CS should be rather fast and is accompanied with a large drop in free energy. This contrasts with existing models for primary CS in isolated PSII RCs without quinone and in PSII RCs with quinone as present in core preparations.

Possible future experiments include preferential excitation of different pigments to study the effect on the overall kinetics. Mutants are available that are lacking specific pigment-protein complexes, and the kinetics can be measured and modeled. Moreover, the effect on the fluorescence kinetics by introducing quenchers in different positions can be predicted and tested in case of the occurrence of nonphotochemical quenching. As such, the proposed method offers a way to study PSII performance as a whole in a directed way, which hopefully contributes to a gradual improvement of the knowledge about PSII functioning.

APPENDIX

In this appendix, it is demonstrated how the excited-state population is calculated as a function of the time after excitation. This population kinetics is compared to the fluorescence kinetics in the text. A so-called coarse-grained model is used in which energy transfer between individual pigments in an antenna or RC complex is not considered, but only an effective hopping rate between different pigment-protein complexes. Such a hopping rate thus represents both energy transfer within and between complexes. The complexes form a superlattice of “supersites” (individual complexes) as represented in Fig. 4 for which we consider a random walk of excitations.

The time course of the excitation population follows the Pauli master equation:

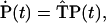(A1)

where 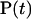stands for the vector of supersite occupancies at time t. The dot above it represents the time derivative. The transfer matrix 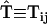is related to the adjacency matrix via 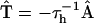. The nonzero elements of the matrix 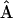conform to the energy transfer steps depicted by bars in Fig. 4 and are defined as follows:

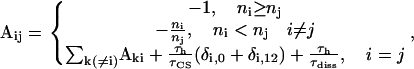(A2)

where 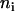is the number of chlorophyll a molecules in complex i and 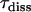is the time of excited-state decay in a complex in the absence of intercomplex energy transfer. This time is typically a few nanoseconds (44) and it is neglected in the simulations because it is much longer than the fluorescence decay time under consideration. Differences in numbers of molecules per complex introduce a retardation effect for the energy transfer step from the larger (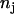) complex to the smaller one (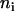). It can be simply assimilated into the activation term by a change in entropy

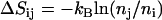(A3)

for the presumably isoenergetic complexes (eight) resulting in rescaling of the hopping rate as given in Eq. A2. The solution of Eq. A1 can be presented in the following matrix form:

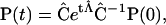(A4)

where 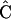is a matrix of eigenvectors, 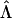is a diagonal matrix 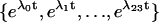of eigenvalues of the transfer matrix 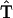, and vector 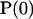stands for the initial population of the supersites. The mean lifetime of the excited system 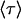can then be expressed as

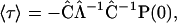(A5)

where 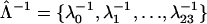is a diagonal matrix with the inverse eigenvalues on the diagonal.

This model contains just two free parameters to be determined: 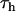, hopping time (we assume that all the intercomplex transfer rates are similar) and 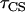,charge separation time in the reaction center (sites Nos. 0 and 12 in Fig. 4). The intrinsic charge separation time 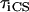from a single Chl molecule is N times shorter (if the pigments are isoenergetic), where N is the number of chromophores in the RC. From the hopping time, one can calculate the first passage time or migration time 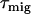to the RC by assuming an infinitesimally small charge separation time:

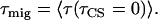(A6)

This provides the splitting of the mean lifetime into the migration and trapping components via

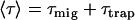(A7)

and it is useful in estimating the dominant process in the trapping process.

To simulate the reversible charge separation in the RCs, the transfer matrix 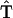in the Pauli equation (A1) is augmented as follows:

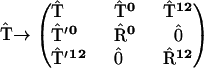(A8)

Symmetric matrices 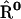and 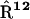describe the reversible radical pair relaxation in the RCs (labeled with 0 and 12) corresponding to the kinetic RC models presented in Fig. 8 . stands for matrices with zero elements. The dimensions of these matrices are determined by the number of the radical pair states taken into account. Rectangular matrixes 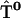, ,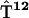, 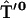and 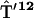containing just one nonzero matrix element per matrix couple the excited primary electron donor to the first radical pair RP1:

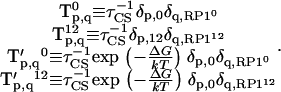(A9)

Here 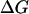stands for the drop in free energy upon primary charge separation.