Measurement of Monomer-Oligomer Distributions via Fluorescence Moment Image Analysis

Abstract

We present higher-order moment analysis of fluorescence intensity fluctuations from individual laser scanning microscopy images applied to study monomer-oligomer distributions. We demonstrate that the number densities and brightness ratios of a mixed population of monomers and oligomers can be determined by analyzing higher-order moments of the fluorescence intensity fluctuations from individual images for specific ranges of densities and particle brightness ratios. Computer simulations and experiments with fluorescent microspheres and cells were performed to illustrate the detection limits and accuracy of this statistical approach. The simulation results show that the concentration of the dimer or oligomer population should be less than or equal to the monomeric concentration for the method to provide accurate results, and that the upper density detection limit of the population of monomers is one order-of-magnitude higher than the concentration of the oligomers. We implemented this technique to resolve two populations of fluorescent microspheres with different brightness ratios and we also applied the moment-analysis method to examine the distribution of aggregation states of PDGF-β receptors in human fibroblast cells. The method was able to resolve a tetrameric population of the PDGF-β receptors relative to the background distribution of nonspecifically bound fluorophore.

INTRODUCTION

Intermolecular interactions play a fundamental role in almost all biochemical reactions. Oligomerization of biological molecules occurs during many processes such as cell growth, migration, metabolism, shape change, and differentiation (1). The molecular mechanisms that regulate these functions are not completely understood, but it is known that they often involve ligand receptor binding and clustering of cell surface receptors with other biomembrane molecules (2). Furthermore, the activation steps of signal transduction pathways are believed to involve receptor oligomerization, as membrane receptor dimerization is thought to be a key part of transduction of signals across the membrane (3). However, there are some studies which question the assumptions of the dimerization model and suggest a role for higher-order oligomerization states of these receptors (4). Thus it is of fundamental importance to quantitatively characterize distributions of receptor oligomerization states in intact cells to test current proposed models for signal transduction.

A group of microscopy-based techniques that involve statistical analysis of fluorescence intensity fluctuations was developed to measure dynamic molecular transport and aggregation. The most widely used, fluorescence correlation spectroscopy (FCS) (5), has proven sensitive to molecular transport and aggregation (6–8). FCS is able to differentiate two populations of fluorescent particles based on size if their diffusion coefficients are sufficiently different in magnitude. However, for membrane species, there is a weak logarithmic dependence of the lateral diffusion coefficient on aggregate size (9), so diffusion measurements are not the most sensitive approach.

A single-molecule microscopy approach was developed to quantitatively determine local stoichiometries based on quantitative criterion for assigning a defined number of fluorophores to each observed individual fluorescence peak (10). The method was successfully applied to measure aggregation of biotin-streptavidin complexes linked to phospholipid membranes. This technique was shown to be able to measure local stoichiometries of associates beyond the diffraction limit which makes it a powerful tool to study co-associations in biomembranes. However, the approach is limited to low density systems in which individual fluorescence peaks from macromolecular complexes can be resolved.

The photon counting histogram method (11) and the fluorescence-intensity distribution analysis (12), which relies on histogram analysis of the distributions of detected fluorescence photons, were proposed to overcome this problem. These temporal domain techniques are able to distinguish molecular species in solution or cells by differences in their molecular fluorescence yields (13).

In cellular systems, membrane proteins have slow transport dynamics or can be immobilized by binding to the cytoskeleton or confined in membrane domains. Image correlation spectroscopy (ICS) was introduced as an imaging extension of FCS, which is able to measure protein densities and dynamics in biomembranes (where transport or flow is slow) or receptor distributions in chemically fixed cells (14–16). This method has been adapted for use with two-photon fluorescence microscopy (17,18). An alternative, spatial high-order autocorrelation technique has also been introduced. Using TIRF microscopy and a CCD detector to image the fluorescence intensity across a planar membrane, distributions of IgE clusters in a lipid bilayer were resolved (19,20).

In ICS, the magnitude of the spatial intensity fluctuation autocorrelation function contains information about the number of independent fluorescent molecules in the correlation volume defined by the focus of the laser beam. However, for polydisperse samples, it is not possible to resolve the number densities together with the relative fluorescent yields with only one correlation function. One way to overcome this difficulty is to carry out spatial intensity fluctuation autocorrelation analysis of higher orders.

High-order autocorrelation has been used for the characterization of fluctuations of various types of measured signals. The approach has been applied for studies of molecular aggregation (21,22), analysis of ion channel kinetics (23), image recognition (24), and nonequilibrium thermodynamics (25–27). Higher-order FCS can detect the presence of submicroscopic clusters (28), and in some special cases it can provide quantitative measurements of the number densities of different cluster sizes present in multicomponent samples (29). The method is also able to differentiate relative fluorescence yields of the species with different molecular weights (21).

A similar technique, fluorescence cumulant analysis, which is related to the photon counting histogram method, was introduced to resolve heterogeneous mixtures of biological molecules that possess fast dynamics (30). With fluorescence cumulant analysis, it is possible to characterize the molecular brightness together with the number of molecules per observation volume for each fluorescent species present.

Although the application of high-order moment (31) and correlation analysis is not new, its accuracy, precision, and detection limits in the presence of noise have not been studied extensively. In the current work, we analyze higher-order moments of the spatial intensity fluctuations from individual laser scanning microscopy (LSM) images and characterize the dynamic range in concentration for which this approach can be applied to resolve monomer-oligomer distributions. We programmed and ran simple numerical algorithms to generate simulated LSM images of systems containing two populations of subdiffraction limit size point emitters with different brightness yields and number densities. We analyzed the simulated images by moment analysis and compared the recovered results for the densities and yields to the set parameters. The simulations were used to systematically study the accuracy and the precision of the moment approach. We also implemented the moment analysis on a simple experimental system. We prepared samples of fluorescent microspheres deposited in a monolayer on glass coverslips. We could artificially create two populations of different brightness yields by selecting microspheres with appropriate excitation/emission spectra and using selected dichroic/emission filters. We generated samples with brightness ratios of 2:1 and 6:1 and applied the higher-order moment analysis to images of the microspheres to test the method experimentally on a controlled system. Finally we implemented the moment analysis to study distributions of PDGF-β receptor cluster distributions sampled within confocal LSM images of fixed immunolabeled AG01523 human dermal fibroblasts and measured a tetrameric distribution for these receptors.

THEORY

Moments of fluorescence intensity

For a single fluorescent entity excited in the focus of the laser beam of an LSM, the integrated fluorescence intensity collected from this observation volume is given by

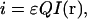(1)

where ɛ is the molar absorptivity coefficient, Q is the fluorescence quantum yield of the fluorophore, and I(r) is the excitation point spread function of the fluorescence optical microscope. This relation does not take into account the effect of bleaching of fluorophores excited by a laser beam. This becomes an important issue in the case of temporal moment analysis in which the integrated intensity changes due to the photobleaching process. However, in the present work, we are dealing only with single-scan LSM images of fixed samples, so that photodegradation of the fluorophores does not contribute significantly to the integrated intensity. For an equilibrium system containing a single molecule, the probability of finding this molecule in the focus is inversely proportional to the total sampling volume. Using the probability density function, we can write the intensity expectation value as

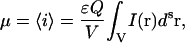(2)

and the n^th order intensity moments as

(3)

where the angular brackets represent the statistical averaging, V is the total sampling volume, s is the number of spatial dimensions, and n is a positive integer. The effects of self-quenching are not included in Eq. 3 so there will be an upper limit at high fluorophore densities where the approach we present will fail. At high packing densities, Eq. 3 would have to be modified to incorporate a quenching term to account for this.

If we assume there are multiple identical and independent particles present in the illumination volume, the probability function will depend on the total number of fluorescent species, so that the n^th moment for the integrated fluorescence intensity in this case will be

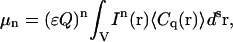(4)

where C(r) is the local concentration of fluorescent species at position r.

We assume that all fluorescent species in our system are oligomers containing q = 1, 2, 3, …, q_max subunits (monomers). One independent oligomer containing q protein subunits is called a q-mer. In this case, the overall integrated intensity will simply be the sum of the contributions from all oligomers present in the system

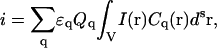(5)

where C_q represents the concentration of q-mers, and Q_q and ɛ_q are the fluorescent yield and the molar absorptivity coefficients, respectively. For simplicity, we assume that the fluorescent yield (Q₁) and the absorptivity coefficient (ɛ₁) of monomers are unaffected by the number of subunits present in an oligomer, so that

(6)

A q-mer contributes to the collected intensity as a single independent species, even though it contains q-subunits, because the positions of the subunits within the q-mer are not independent and are therefore correlated.

Higher-order fluctuation moments

A series of normalized high-order (n^th) moments of the spatial fluorescence intensity fluctuations within a single LSM image are given by

(7)

In practice, moments of orders higher than the fifth contribute little to the analysis. The higher-order moments are so sensitive to sampling fluctuations that they become dominated by random noise (31). In our studies, we compute only the first three normalized moments to resolve two populations of fluorescent particles.

We have to expand the higher-order moments given by Eq. 7 in terms of fluctuations of lower orders. Cumulants are usually more applicable than moments for computing the statistics of a fluctuating signal (32,33). Cumulants are important because the n^th cumulant of a sum of independent random variables is simply the sum of the n^th cumulants of the summands. The cumulant approach has already been successfully applied in fluorescence fluctuation temporal studies (30,34), and we follow a similar approach for the spatial analysis of images. The expressions for cumulants of particular orders can be constructed from the cumulant generating function, defined in terms of the probability distribution characteristic function (35). For moments about the mean, the first seven expressions for cumulants are

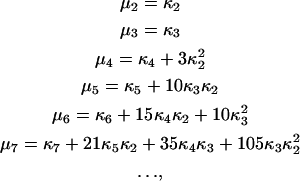(8)

where κ_n is the n^th order cumulant. One can notice a recursive relation between moments and cumulants (36).

Assuming that the number of particles in the small beam focal volume obeys Poisson statistics, we can write down the fluctuation moments in Eq. 7 as cumulants of the random variable using Eq. 8:

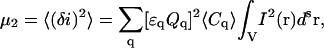(9)

(10)

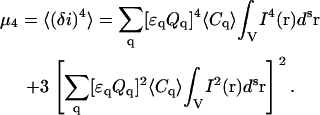(11)

Substituting Eq. 5 into the normalized second-order moment ɛ₁ yields

(12)

Dividing both the numerator and the denominator in Eq. 12 by ɛ₁Q₁, and defining the relative fluorescent yield (relative to the monomeric species) as

(13)

we can rewrite Eq. 12 as

(14)

Following the derivations performed in earlier high-order FCS work (21), we define

(15)

and

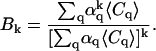(16)

Substitution of Eqs. 15 and 16 into Eq. 14 with k = 2 gives

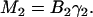(17)

Similarly we write the expressions for the third- and fourth-order moments:

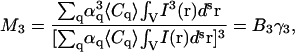(18)

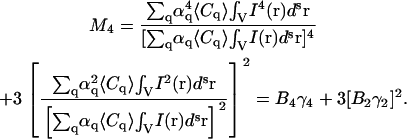(19)

Analysis of aggregate distributions

To characterize aggregation of multicomponent systems quantitatively, we need to know the spatial excitation laser intensity profile I(r). We can assume that the sample is illuminated by a focused laser beam of Gaussian transverse intensity spatial profile (37). This is a reasonable assumption as we do not observe the outer rings of the Airy disk above the background noise in our images. For a two-dimensional system, the profile is given by

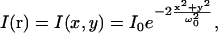(20)

where ω₀ is the e⁻² beam radius in the lateral direction. Since the Gaussian beam dimensions are small compared to the total image size, we can extend the integration limits in Eq. 15, so that

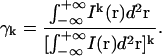(21)

Making the substitution of Eq. 20 into Eq. 21 we obtain

(22)

Due to the fact that the γ_k factor is an independent integral, one can obtain its value for certain experimental conditions from a separate experiment. A point source emitter can be imaged with the LSM and the value of γ can be obtained simply by numerical integration of Eq. 15. The same method can be applied for non-Gaussian illumination profiles.

For each value of M_n, a new quantity B_k can be determined, which contains information on the average concentration of particles of different species in the multicomponent sample. The system of equations for the B_k values can be written as

(23)

If there are two different species of aggregates present in the system, M₂, M₃, and M₄ must be obtained to determine α₂, 〈C₁〉, and 〈C₂〉 by solving the system of equations given by Eq. 23. Thus from a single fluorescence microscopy image we can measure the population densities and the fluorescent yield ratio for a two-population system via calculation of the first three higher-order normalized moments. For LSM images of a two-dimensional system, the concentrations will effectively be particle numbers per beam area (N_i/BA), which is what we work with in the rest of this article.

MATERIALS AND METHODS

Simulations

Simulated images were created by convolving point emitters distributed in a two-dimensional matrix with a Gaussian convolution function using a set of custom routines written in MatLab (The MathWorks, Natick, MA) and the image processing and optimization toolboxes. These images simulated fluorescence LSM images of two-dimensional systems in which two populations of point emitters of different yields are present and we generated them using the procedure previously reported (38). For each population, a separate image matrix was created of N_x × N_y pixels with N_q number of q-mers per simulated Gaussian beam area, and the x and y coordinates of all oligomers were randomly generated. The image matrices were created with yield values of α_q (see Eq. 13) at the q-mer locations and zeros for all other pixels. The two population matrices were summed pixel-by-pixel and convolved with a Gaussian function given by Eq. 20. To examine how the background noise contributes to our analysis, a noise matrix with normally distributed random numbers was generated. The mean of the distribution was zero, and its standard deviation was 1. The absolute values of the numbers were taken. The noise matrix was then scaled by a coefficient and added to the image matrix giving a final image with a given signal/background ratio (S/B). The resulting image matrix was normalized by 2^b, where b is the number of bits typical for the analog-to-digital conversion of the signal from the light detectors of our microscope imaging systems. All of the simulated images in this work were generated as 12-bit per pixel intensity matrices.

Fluorescent microsphere sample preparation

To experimentally generate two populations of fluorescent entities with controlled molecular brightness ratios, we used mixtures of two types of fluorescent microspheres with different excitation/emission properties. Carboxylate-modified fluorescent microspheres (FluoSpheres, 100 nm diameter, catalog No. F8801 (red), F8800 (orange), and F8803 (green) designed to absorb/emit at 580/605 nm, 540/560 nm, and 505/515 nm, respectively) were obtained from Molecular Probes (Eugene, OR) to prepare the two-dimensional samples. Fluorescent spheres in solution were sonicated for 60 min before use.

The differences in the collected emissions (see Confocal Microscopy, below) gave us values of relative fluorescent yields of 2.2 ± 0.4 and 6 ± 2 for the microsphere mixtures of orange with red and green with red, respectively. The red fluorescent microspheres were taken as a model of a monomeric population due to the fact that their integrated emission per microsphere was lower by a factor of approximately two or six as compared to the orange and green spheres, respectively, because their emission spectrum was shifted away from the maximum of the collection filter. Thus the brightness ratio represents an integrated intensity ratio per individual fluorescent particle.

Microscope slide samples were prepared by labeling polylysine-coated coverslips with fluorescent microspheres. The coating provides a strong electrostatic attraction for the surface of carboxylate-modified latex beads. The microscope coverslips (22 × 22 mm, No. 1.5; Electron Microscopy Sciences, Hatfield, PA) were obtained from CEDARLANE Labs (Hornby, ON). The coverslips were cleaned in pure lab-grade acetone and 70% ethanol for 10 min and then rinsed with double-distilled water. Cleaned glass substrates were immersed into poly-d-lysine solution (0.2 mg/mL in phosphate-buffered saline (PBS) 7.4, Sigma-Aldrich, St. Louis, MO) (39) at room temperature and gently shaken for 30 min. Due to the observed degradation of the coating in air, the coverslips were kept in the solution until time of use.

Next, 15 μL of FluoSphere PBS solutions of variable concentrations were applied to the poly-d-lysine coated coverslips and incubated for 5 min at room temperature followed by rinsing of the glass substrates with ddH₂O. The poly-d-lysine coating allowed for strong adhesion of the polystyrene microspheres in a uniform monolayer on the glass coverslips. The coverslips were then mounted on microscope slides for LSM imaging.

Cell culture and immunofluorescence labeling

Human foreskin fibroblasts (AG01523, NIA Aging Cell Culture Repository, Camden, NJ) were cultivated in Dulbecco's modified Eagle's medium, supplemented with 4 mM L-glutamine, 10% fetal bovine serum, 100 units/mL penicillin, 0.1 mg/mL streptomycin, and 0.1 nM nonessential amino acids. Cells were passaged twice per week, and maintained in a humidified, 5% CO₂ atmosphere at 37°C. Cells were plated in petri dishes with a bottom coverslip insert (No. 1.5; MatTek, Ashland, MA). After incubation with 50 ng/mL human PDGF BB (R&D Systems, Minneapolis, MN) for 60 min at 37°C, followed by washing three times in PBS (pH 7.4), the cells were fixed for 30 min at room temperature with 4% paraformaldehyde dissolved in PBS.

Post-fixation, cells were labeled for 40 min with primary monoclonal anti-PDGF-β receptor antibody (catalog No. P 7679; Sigma) at a concentration of 4.3 mg/mL. After incubation with the primary label, the samples were rinsed extensively with PBS. Subsequently, cells were incubated with 4.7 mg/mL anti-mouse IgG FITC-conjugated antibody (Sigma) specific for the Fab portion of the primary antibody. Immunofluorescence staining was followed by rinsing the cells three times with PBS. The secondary antibody control samples (cells labeled with secondary antibody and no primary) were prepared along with the regular cell samples.

Confocal microscopy

The bead and cell samples were imaged using an Olympus FluoView FV300 (Olympus America, Melville, NY) confocal laser scanning microscope coupled to an Olympus IX71 inverted microscope equipped with a 60× 1.4 NA oil immersion objective lens (Olympus PlanApo/IR). The fluorophores were excited with a 40 mW multi-argon laser (458/488/515 nm, Melles Griot, Carlsbad, CA) using the 488-nm line. An Olympus FV-FCBGR dichromatic beamsplitter together with the emission filter BA510IF (Chroma, Rockingham, VT) were used to efficiently reflect 488 nm wavelength and pass the emission wavelengths. All images of the bead mixtures were collected in a single detection channel. All images were 1024 × 1024 pixels in size, with a pixel size of 0.046 μm.

The dichroic and filters selected allowed us to generate images with fixed fluorescence yield ratios of 2.2 ± 0.4 and 6 ± 2 for the orange/red and green/red microsphere samples, respectively. These values were measured by isolating individual microspheres in low density images and calculating integrated intensities of each microsphere type.

Data analysis

For all images, the mean intensity of the background noise was calculated from empty regions in the images. A MatLab subroutine was written to calculate the n^th order intensity moments of spatial fluorescence intensity fluctuations of LSM images using Eqs. 7 and 3. For each individual pixel, the n^th power of the intensity value was calculated. A spatial average of all these iⁿ values was calculated and then normalized by the spatial average intensity of the image taken to the same power (n). The normalized moments of orders 2, 3, and 4 were calculated from the background-corrected images and were input into the system of equations given by Eq. 23. This system was then solved for the fluorescence yields and the population densities. The standard deviations of the recovered mean values were obtained from the analysis of multiple simulated or LSM images of the same sample type.

RESULTS AND DISCUSSIONS

Simulations

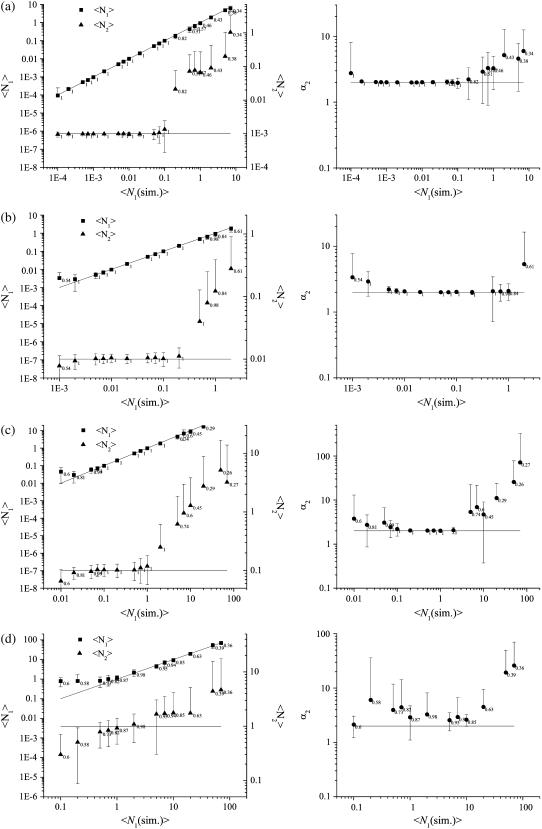
Simulated LSM images of two mixed populations of species with different densities and molecular brightness values were generated (see Fig. 1 a). The image size, pixel size, and e⁻² Gaussian convolution radius were set to be typical for standard CLSM collection on cells. We first tested the ability of the method to resolve monomer-dimer distributions using simulated image sets. The first three higher-order moments (M₂, M₃, and M₄) were calculated from the simulated images and the values of 〈N₁〉, 〈N₂〉, and α₂ were obtained for five different sets of 100 images (see Fig. 2). The mean value of the parameters measured from each set of images was plotted as a function of the set concentration of population 1 and the results are shown in Fig. 2. For the case of a simulated monomer-dimer distribution with the total particle density 0.1 particle per BA and higher, the density of the monomeric particles must be equal to or greater than the density of the dimer population to retrieve accurate values using the moment method. If the density of monomeric population is below this threshold, then systematic errors occur and the results obtained can deviate by an order of magnitude from the set values. The results obtained for the dimeric population are accurate as long as it is not more than an order-of-magnitude less dense than the monomeric population. In addition, there is a general decrease in the accuracy of the method as the total particle density increases. It ranges from roughly a 10% accuracy for very low density samples (<0.001 particle per BA) (see Fig. 2, a and b) to ∼50% when the total density reaches one particle per BA (see Fig. 2, c and d) for a 1024 × 1024 image size. When the molecular brightness ratio of the two species in the sample is >2, the accuracy and dynamic range of the higher-order moment analysis increase significantly. Simulated images for a brightness ratio of 8 were also generated and analyzed (see Fig. 3). In certain cases, the analysis failed to converge to physically valid results. For some sets of values of 〈N₁〉, 〈N₂〉, and α₂, the system of equations given by Eq. 23 returned nonphysical negative and/or complex solutions. A similar problem was reported in molecular aggregation studies using high-order FCS (21). The reason for such nonphysical solutions of the nonlinear equations is still not fully understood but typically occurs when we exceed the detection limits of the technique. Fortunately, it is immediately apparent when this occurs so we excluded nonphysical results from the analysis. For each data point on Fig. 2, we specify the percentage of physically valid solutions out of the total number of simulated LSM images generated under identical experimental conditions so only data from real and positive solutions are shown.

FIGURE 1.

Simulated and LSM images of spatial distributions of point emitters and fluorescent microspheres. (a) Simulated LSM images of mixed populations of two point emitters with different concentrations and brightness yields. The intensity yields of the first and second populations was set to α₁ = 1 and α₂ = 2, respectively, for all images shown. The numbers above the graphs show the number densities per beam area (BA) of populations 1 and 2, respectively. The images were 1024 × 1024 pixels² in size and were integrated with a Gaussian convolution function with an e⁻² radius of five pixels; (b) CLSM images of a mixture of orange and red 0.1-μm diameter fluorescent microspheres on a coverslip excited by a 488-nm laser line. The images were acquired in a single collection channel with the emission filter BA510IF which provided the brightness ratio of 2.2 (see Materials and Methods). The images were 1024 × 1024 pixels in size, with a pixel size of 0.046 μm.

FIGURE 2.

Moment analysis of simulated LSM images of mixed monomer dimer populations. Plots of the measured densities of two populations of point particles and their relative intensity yields as a function of the set value of the density of the monomeric population. The relative brightness ratio was set to 2 for all the data sets. The images were 1024 × 1024 pixels² is size, and the e⁻² radius of the Gaussian convolving function was set to five pixels. The error bars were calculated as the standard deviation from the analysis of results from 100 identical image simulations. The solid lines represent the set values for the simulations. The labels shown for each data point represent the fraction of physically meaningful results (real and positive) out of the total number of simulated images. (a) N₂ = 0.001 per BA; (b) N₂ = 0.01 per BA; (c) N₂ = 0.1 per BA; and (d) N₂ = 1 per BA.

FIGURE 3.

Moment analysis of simulated LSM images of mixed monomer octamer populations. Plots of the measured densities of two populations of point particles and their relative intensity yields as a function of the set value of the density of the monomeric population. The relative brightness ratio was set to 8 for all the data sets. The images were 1024 × 1024 pixels² is size, and the e⁻² radius of the Gaussian convolving function was set to five pixels. The error bars were calculated as the standard deviation from the analysis of results from 100 identical image simulations. The solid lines represent the set values for the simulations. The labels shown for each data point represent the fraction of physically valid results (real and positive) out of the total number of simulated images. (a) N₂ = 0.01 per BA; (b) N₂ = 0.1 per BA; (c) N₂ = 1 per BA; and (d) N₂ = 10 per BA.

As has been demonstrated previously for spatial ICS (38), the dimensionless parameter that characterizes the statistical sampling is a ratio between the laser beam area (BA) and the image size. Not surprisingly, an increase in this ratio also yields an improvement in the accuracy of the moment method. In Fig. 4 the dependence of the relative error in the measurement of the number densities and the brightness ratios of two populations is shown as a function of the image size for fixed convolution Gaussian e⁻² radius. The data indicate that an image size of 100 BAs yields a 10% accuracy in a noise-free simulation. From a practical point of view, in a typical LSM system with an e⁻² laser beam radius of ∼5 pixels, a minimum 128 × 128 pixels size image would be necessary for sufficient spatial sampling to resolve a monomer-dimer distribution from the image. When the brightness ratio is higher there is a significant improvement in the accuracy of the method. A brightness ratio of 6 reduces this error by one order of magnitude. However, the influence of background noise must still be considered.

FIGURE 4.

Plot of the relative error obtained with high order moment analysis of simulated image intensity fluctuations as a function of spatial sampling: image area per beam area (IA/BA). The data were calculated for N₁ = 1 and N₂ = 0.1. For each data point, 200 identical images were generated and analyzed via moment analysis. The images were 1024 × 1024 pixels² in size and were integrated with a Gaussian convolution function with an e⁻² radius of five pixels.

Background noise such as from scattered light and detector dark counts, present in real LSM images naturally affects the accuracy and precision of the results recovered with higher-order moment analysis. The existence of noise reduces the mean relative intensity fluctuations resulting in overestimation of the number densities and underestimation of the relative intensity yield. Using the same algorithm as previously implemented for ICS studies (38,40), we simulate noise as the absolute value of random, normally distributed numbers with a variable standard deviation added to the noise-free images. The signal/background ratio (S/B) is calculated by dividing the maximum intensity value of the image before adding the background noise by the standard deviation of the noise distribution. The plots showing the accuracy of higher-order moment analysis as a function of S/B of the image are shown in Fig. 5. The data suggest that S/B is the limiting parameter in resolving a monomer-dimer distribution from LSM images in which the background noise contributes to the spatial intensity fluctuations. The remaining noise counts after the mean background correction reduces the magnitude of the relative fluctuations due to the increase in the image mean intensity value. From a practical standpoint, a S/B ratio of 10³ or higher would be required to precisely resolve a monomer-dimer distribution. For values of α₂ ≥ 3 or greater, a typical LSM image must have S/B ratio of 10² or higher to achieve a 10% accuracy in the analysis.

FIGURE 5.

Plot of the relative error in the measured number densities and brightness yields as a function of S/B for two populations obtained with high-order moment analysis of simulated images. For each data point, 300 identical images were generated and analyzed via moment analysis. The images were 1024 × 1024 pixels² in size and were integrated with a Gaussian convolution function with an e⁻² radius of five pixels. The data were calculated for N₁ = 0.1 and N₂ = 0.01 per BA, the brightness ratio was set to (a) α₂ = 2; (b) α₂ = 4; and (c) α₂ = 8.

Resolving two populations of fluorescent microspheres

Next we tested the moment analysis method on real images of fluorescent microsphere samples. Using mixtures of subdiffraction-limit size fluorescent microspheres of different emission wavelengths, deposited on glass coverslips, we were able to set emission ratios approximating that of a monomer-dimer and monomer-hexamer mixtures. The protocol we employed would homogeneously distribute the fluorescent beads on the coverslip surface to produce a two-dimensional, two-population sample (see Materials and Methods).

We experimentally confirmed that microsphere solutions of different concentrations yielded coverslips with a constant two-dimensional surface density by analyzing CLSM images of the samples via conventional spatial ICS. Using spatial ICS, we were able to independently measure the density of the microspheres on the coverslip. We produced a calibration curve that relates two-dimensional density on glass to bulk concentration in solution for the different types of beads used (see Supplementary Material). Almost identical calibration curves were obtained for the green, orange, and red fluorescent microspheres. We performed linear regression fits on the three data sets and the mean slope was 5.4 ± 0.2. This calibration establishes that a set surface density can be prepared for each type of microsphere. This control experiment was needed to ensure linearity in concentration of the preparation method before attempting high-order moment analysis of the two population microsphere samples.

We made a series of samples containing two populations of fluorescent microspheres with concentrations determined from the calibration controls and assumed that the binding properties of green, orange, and red fluorescent spheres are not altered in the two-dimensional samples with mixed compositions. Fig. 1 b shows typical CLSM images of different mixtures of orange and red spheres with similar simulation images in Fig. 1 a for comparison purposes. The results of the analysis for green and red fluorescent spheres with a measured brightness ratio of 6 are shown in Fig. 6. The results obtained for the mixtures of orange and red fluorescent beads (α₂ = 2.2) are shown in Supplementary Material.

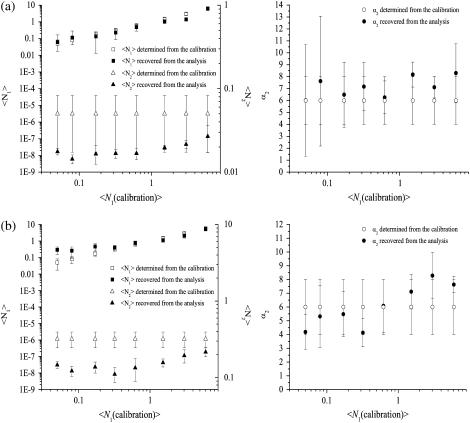
FIGURE 6.

Plots of the results of spatial high-order moment analysis applied to LSM images of two-dimensional samples of fluorescent beads. Green and red fluorescent microspheres and emission detection using the BA510IF filter were used to provide the value molecular brightness equal to 6 (see Materials and Methods). The two-dimensional densities (〈N₁〉 (calibration) and 〈N₂〉 (calibration)) were determined from the calibration experiment (see Supplementary Material) and shown as open squares and triangles, respectively. The recovered densities of two populations (〈N₁〉 and 〈N₂〉) and their relative fluorescence intensity yield (α₂) are shown as solid data points. The error bars were calculated by estimating the accuracy of the background noise measurement taking into account the standard deviation of five images acquired at different locations in the sample. All the images were 1024 × 1024 pixels², with a pixel size of 0.046 μm. For each graph, 〈N₁〉 was varied (the x axis) and 〈N₂〉 had a fixed value: (a) 〈N₂〉 = 0.005 particles/BA; (b) 〈N₂〉 = 0.05 particles/BA.

The range of the surface number densities explored in the experiments was selected based on the results of the simulations. The recovered densities of both populations agree well with the expected values from the calibration measurement. The moment analysis method applied to the images of microsphere samples follows the trends expected from the simulation results. The S/B ratio of ∼100 for the CLSM images of microspheres was too low to resolve the monomer-dimer brightness ratio by moment analysis (see Supplementary Material) as expected from the simulation results (Fig. 5 a). The results obtained for the green and red microsphere samples with the higher brightness ratio (α₂ = 6) (see Fig. 6) show that there was a systematic underestimation in the measured value of 〈N₂〉, as compared to the calibration measurement although the yield ratio and the values of 〈N₁〉 were recovered within a small error as predicted by the simulation data shown in Fig. 5, b and c.

Moment analysis of PDGF-β receptor distributions on fibroblast cells

To illustrate applicability of the spatial high-order moment approach for measurements of membrane receptor clustering, we applied the method to CLSM images of immunolabeled PDGF-β receptors on the surface of human AG01523 fibroblasts. In Fig. 7 a, a typical CLSM image of an immunolabeled fibroblast cell is shown. Fig. 7 b shows a higher zoom image, which was one selected for analysis. The estimated S/B ratio based on our definition ranged from 70 to ∼120 for the cell measurements. When applying the moment analysis to the images, we assumed that two populations of labeled receptors with different yields were present in the sample. We made this assumption based on the fact that fluorescent spots of different intensities could be seen in the images of cells labeled with both primary and secondary antibodies, and the intensity differences were greater than those expected for Poisson distributed counts. Table 1 shows results for high-order moment analysis of two sets of images of regular (primary and secondary antibodies) and two sets of control (only secondary antibodies) samples. For each sample, 60 individual cells were imaged and analyzed. The two-population moment analysis failed to provide physically valid results for the control fibroblast samples. However, when we assumed only one population to be present in the control images, the analysis recovered the same number density as the value of 〈N₁〉 obtained from the images of regular samples. These results suggested that the first population density (〈N₁〉) recovered from the moment analysis of the regular images corresponds to homogenously distributed secondary antibody nonspecifically bound on the surface of the fibroblasts.

FIGURE 7.

CLSM images of indirectly FITC immunolabeled PDGF-β receptors on the surface of a human AG01523 fibroblast. (a) Confocal image showing an overview of an AG01523 cells, taken with a pixel size of 0.115 μm; (b) a higher zoom image of a subregion of plasma membrane sampled for moment analysis. The image was taken with a pixel size of 0.057 μm.

TABLE 1.

The results of spatial high-order moment analysis applied to background-corrected CLSM images of immunolabeled PDGF-β receptors on the surface of human AG01523 fibroblasts

Sample	〈Ncontrol〉	〈N1〉	〈N2〉	Brightness ratio (α2)
A	7 ± 3	7.3 ± 2.8	0.25 ± 0.19	7.9 ± 1.9
B	7 ± 2	8.4 ± 2.8	0.22 ± 0.30	8.0 ± 2.0

For each sample, 60 individual cells were imaged and analyzed. All the number densities are expressed in particles per BA. Samples A and B were prepared in an identical manner.

We also assumed that two secondary antibody molecules bind to the two Fab portions of each primary antibody (Fab specific IgG), which was also an assumption in a previous ICS study of the same receptor system (16). We also posited that most of nonspecific fluorescence is due to individual anti-mouse IgG FITC-conjugated secondary antibodies binding nonspecifically at the cell surface. Our technique measures the distribution of what we actually detect, which is fluorescence from the secondary antibodies. To obtain the actual receptor distribution, we divide the recovered value of the brightness ratio by two given the assumption that there are two secondary IgG-values per primary antibody. If the labeling is one-for-one (as would be the case for a GFP-labeled protein), we would get the receptor aggregation distribution directly. Based on these assumptions, and also assuming no quenching between FITC molecules within a single cluster, we conclude that PDGF-β receptors exist mainly in a tetrameric state under these experimental conditions.

The aggregation state of PDGF-β receptors in unstimulated fixed dermal fibroblasts was previously measured in this cell line with a mean aggregate size of tetramers being detected via a cell population spatial ICS analysis (16). The results obtained for the same system in the presence of PDGF-BB ligand showed no detectable change in the state of the receptor aggregation, suggesting that treatment with growth factor has no effect on the aggregation state of receptors that are already clustered (41). In the current study, we also measured a mean aggregate size of tetramers after pretreatment with PDGF-BB based on the brightness ratio recovered from the moment analysis, which is in accord with the previous measurements. An advantage of the new approach is that the specific and nonspecific label populations could be individually resolved within each cell sample. In recent studies, a tetrameric state for the EGF receptor on the surface of BaF/3 cells was also reported (4). One possible explanation of these results can be the existence of membrane domains which function as platforms for bringing together cellular machinery necessary for intracellular propagation of signals (42).

CONCLUSIONS

Studies of signal transduction mechanisms and the underlying role of receptor clustering on cell surfaces require techniques that are able to resolve molecular oligomerization states. In this work, we introduced high-order moment analysis of spatial fluorescence intensity fluctuations in images as a method to resolve distributions of fluorescently labeled macromolecules in such biological systems.

The theoretical basis of the spatial higher-order moment analysis has been discussed for systems containing multiple populations of particles with different ratios in concentration and molecular brightness. Even though the theoretical relationships between the normalized high-order moments and the number densities and quantum yields of different fluorescent species in polydisperse systems has been studied previously, the detection limits have not been explored extensively. By analyzing simulated image data where all the physical parameters are set to known values and comparing the results recovered from the moment analysis with the set values, we were able to evaluate the dynamic range of the method, and obtain estimates of the error that can be expected for measurements on real samples. We performed numerical simulations to explore the experimental conditions for which the analysis yields accurate values and also reported the accuracy and precision of the method. We found that it was not possible to resolve the two components of the system when the aggregates of different sizes (yields) have densities within certain concentration ranges. Our results showed that the density of the brighter population should be less than or equal to the monomeric density for the method to provide accurate results. The upper density limit of the population of monomers is one order-of-magnitude higher than the concentration of the brighter oligomers. For such density ranges, the technique is able to provide statistically valid results for systems containing fluorescent molecules distributed as monomers and higher-order oligomers assuming the S/B is sufficiently high. However, our simulations showed that although the number densities could be measured for monomer-dimer distributions, the brightness yield ratio could not be resolved at any reasonable S/B ratio.

We created a protocol to prepare two-dimensional fluorescent bead samples that contained particles with a priori known values of concentration and with set molecular brightness ratios determined by the fluorescence spectra and collection parameters. Analysis of the moments calculated from CLSM images of those samples gave results that were quantitatively consistent with the values predicted from the sample preparation for suitable density ratios selected based on the simulations.

We also applied our analysis to CLSM images of FITC immunofluorescently labeled PDGF-β receptors in fixed human foreskin fibroblast cells. We could resolve two oligomerization states of the label on the cells: one for the specifically bound label and the other for nonspecifically bound label. The recovered value of the relative fluorescent yield suggests that PDGF-β receptors mainly exist in a tetrameric state, which is in good agreement with previously published results.

We have demonstrated that higher-order moment analysis of spatial fluorescence intensity fluctuations from individual LSM images can provide useful information about populations of fluorescently labeled molecular species under certain conditions. The method should prove to be useful in studying signal transduction in cells and the present study provides a guide for conditions in which the method will return reliable results.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.