Inference of Intramural Wavefront Orientation from Optical Recordings in Realistic Whole-Heart Models

Both computer simulations and experiments have shown that fluorescent signals recorded in optical mapping experiments originate from a widely distributed three-dimensional volume of tissue located beneath the detection site (1). Scattering of photons from within this volume, which we term the scattering volume, leads to blurring of the optical signal and to a prolongation of the optical action potential upstroke duration (2,3). The duration of the optical action potential upstroke depends sensitively upon the dimensions of the scattering volume, determined by the optical coefficients of the tissue for scattering and absorption at both illumination and emission wavelengths (4). Recent studies have suggested that optical action potential upstroke morphology contains useful information regarding wavefront propagation beneath the surface. Specifically, studies by Hyatt et al. (3) suggest that the potential level at which the rate of rise of the optical upstroke is maximal (Vf*) depends upon the angle φ, the angle of wavefront direction with respect to the imaged tissue surface. Under the particular conditions chosen in the Hyatt et al. (3) simulations, where both wavefront propagation beneath the epicardial site and tissue surface are purely planar, wavefront direction is either perpendicular or parallel to the surface. This is due to the large planar stimulus used, along with the simple slab geometry with uniform fiber orientation over which simulations were performed. The value of Vf* at a particular recording site is directly related to the local orientation of the wavefront with respect to the imaging surface. Since for planar wavefronts local orientation beneath the detection site is the same as global wavefront orientation throughout the tissue volume, the direction of global wavefront propagation can be directly inferred from Vf*. However, as described in Pertsov et al.'s comment in this issue of the journal, when considering nonplanar wavefronts, two propagation patterns with significantly different global wavefront directions could lead to similar local wavefront orientations beneath a recording site, giving similar optical upstrokes and Vf*. What information regarding wavefront direction could then be obtained from the upstroke of the action potential, and Vf* in particular, in optical maps of a whole heart, an organ of complex geometry and fiber orientation?

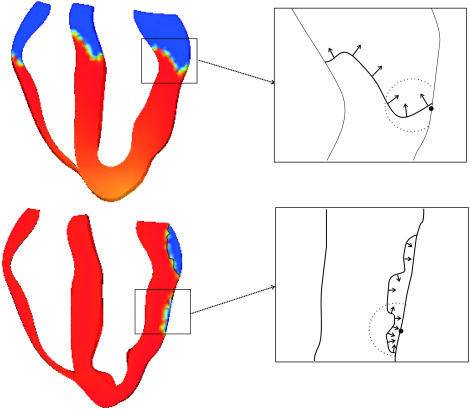
In our study published in the April 15th issue of Biophysical Journal (4) we show that the use of a physiologically realistic model of electrical excitation produces wavefront propagation with a high degree of complexity. The bidomain representation of the myocardium employed in this study provides an accurate description of the interaction between tissue and surrounding bath, which affects the nature of wavefront propagation in the vicinity of the epi- and endocardial surfaces. The use of anatomically realistic geometry and fiber orientation, combined with realistic stimulation scenarios, produce wavefronts that spread throughout the volume of the ventricles with a highly nonplanar, “jagged” appearance. As shown in Fig. 1 A, after both apical (top) and endocardial (bottom) stimulation protocols, the local angle of wavefront orientation with respect to the epicardium changes dramatically within the scattering volume (indicated by the solid circle), rotating by >90° between different points along the wavefront. Furthermore, the wavefront itself is of intrinsically three-dimensional nature, and thus, variations in local wavefront orientation, such as those shown in Fig. 1, will be even more complex in three dimensions. In our simulations of propagation through the three-dimensional rabbit ventricles, wavefronts of high degree of complexity arise without the inclusion of small-scale tissue heterogeneities (blood vessels, fatty and connective tissue, etc.), which are thought to further increase wavefront “jaggedness”. In addition, the dynamic nature of excitation propagation results in a constant change in the shape of the wavefront as it passes through the scattering volume beneath the recording site, and therefore the local orientation of the wavefront within the scattering volume changes over the course of the action potential upstroke.

FIGURE 1.

Wavefront propagation after apical (top) and endocardial (bottom) stimulus. Different wavefront propagation directions are shown by black arrows in the insets. The optical detection site on the epicardium is shown by a solid circle, with the approximate scattering volume depicted by a dashed circle.

Hyatt et al. (5) successfully addressed the problem of a varying local wavefront angle within the scattering volume by the inclusion of the concept of an optically weighted mean angle of wavefront orientation with respect to the tissue surface (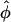). The angle 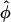represents a weighted-average of the local angles of wavefront orientation with respect to the surface, with points closest to the detection site having the greatest weight, and weights decreasing with the distance from the site. However, in situations of complex wavefront orientations constantly evolving with time, such as those shown in Fig. 1 A, it is an open question as to what useful information could be derived from the morphology of the experimentally measured optical action potentials. Of particular interest would be the application of the mean optically weighted angle-calculation algorithm to such scenarios. The important issue here is the relationship between the value of 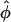and the complex shape of the wavefront beneath the recording site. Would it be possible to infer the complexity of the wavefront shape from a single number, 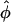? In particular, could the same value of 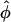result from different wavefront distributions within the scattering volume, and if so, how different could they be? Finally, could optical detectors record at a sufficiently high frame-rate to accurately and reliably determine the value of Vf*, given that the optical action potential upstroke is only ∼10-ms long?

Optical action potentials undoubtedly contain useful information regarding the excitation patterns below the recording surface. We believe, however, that the utility of optical action potential upstroke morphology as a tool for interpreting subsurface wavefront distributions in whole-heart preparations requires further study and validation.