Abstract
Background.
Pushing and pulling tasks account for 20% of occupational low-back injury claims. Primary torso muscle groups recruited during pushing tasks include rectus abdominis and the external obliques. However, analyses suggest that antagonistic co-contraction of the para spinal muscles is necessary to stabilize the spine during flexion exertions. The study quantified co-contraction and spinal load differences during isometric flexion and extension exertions. The goal was to provide insight into the mechanisms requiring greater co-contraction during trunk flexion exertions compared to extension exertions.
Methods.
Electromyographic (EMG) signals were recorded from the trunk muscles of healthy volunteers during isometric trunk flexion and extension exertions. A biomechanical model was implemented to estimate total muscle force from the measured EMG and trunk moment data. A similar model estimated the muscle forces necessary to achieve equilibrium while minimizing the sum of squared muscle forces. The difference in these forces represented co-contraction. Spinal load attributed to co-contraction was computed.
Results.
Average co-contraction during flexion exertions was approximately twice the value of co-contraction during extension, i.e. 28% and 13% of total muscle forces respectively. Co-contraction accounted for up to 47% of the total spinal load during flexion exertions. Consequently, spinal compression during the flexion tasks was nearly 50% greater than during extension exertions despite similar levels of trunk moment.
Interpretation.
Co-contraction must be considered when evaluating spinal load during pushing exertions. Results underscore the need to consider neuromuscular control of spinal stability when evaluating the biomechanical risks.
Keywords: Low-back, Spine, Co-contraction, push
1. Introduction
The primary torso muscle groups recruited for generation of a flexion exertion during pushing tasks are the rectus abdominis and the external obliques. Lumbar para spinal and posterior internal oblique muscles provide little mechanical potential for the generation of a flexion moment (McGill, 1996). However, if the para spinal muscles are not recruited during flexion exertions then the spine maybe come unstable under the compressive loads on the spine (Bergmark, 1989). Stability describes the ability of the musculoskeletal system to maintain equilibrium in the presence of small kinematic or control disturbances. Crisco et al. (1992) illustrated that the lumbar spine is incapable of stabilizing compressive loads in excess of 88 N without the support of para spinal muscle activation. Spinal compression during occupational pushing tasks has been estimated at 600-1400 N (Schibye et al., 2001). This is greater than the maximum stable load for the unsupported spine. Therefore, lumbar para spinal muscle activity during flexion exertions maybe necessary to maintain spinal stability (Gardner-Morse et al., 1995).
Stability analyses suggest that co-contraction during pushing tasks must be greater than during trunk extension exertions (Appendix A). Biomechanical analyses using a one-segment model of the spine reveal that muscle forces recruited to establish equilibrium also contribute to stability. These models suggest that spinal stability during flexion or extension exertions can be achieved with limited antagonistic co-contraction (Cholewicki et al., 1997). Conversely, stability analyses that include a multi-segment model of the spine (Granata and Wilson, 2001), require recruitment of the para spinal muscles to maintained stability regardless of whether the exertion direction is flexion or extension. During extension exertions activity in the para spinal muscles serve the dual role of maintaining equilibrium and stability. During flexion exertion the abdominal and para spinal muscles must be simultaneously active in separate roles of equilibrium and stability respectively. This requires greater co-contraction in trunk flexion than during extension exertions (Granata and Bennett, in press). Empirical measurements of torso muscle co-contraction are necessary to confirm this hypothesis.
Antagonistic co-contraction is operationally defined as muscle recruitment including force components acting in opposition to the desired trunk moment. EMG measurements have quantified lumbar co-contraction during extension exertions (Marras and Mirka, 1992; Zetterberg et al., 1987) while biomechanical analyses reveal that co-contraction contributes markedly to spinal load (Granata and Marras, 1995b). Therefore, neglect of co-contraction during flexion or extension exertions will result in estimates of spinal load that underestimate actual values. We are unaware of any study to quantify the difference in co-contraction recruitment during trunk flexion exertions versus trunk extension exertions.
The goal of this study was to quantify torso muscle co-contraction and spinal compression during trunk flexion exertions compared with data recorded during trunk extension exertions at similar levels of force. We hypothesize that co-contraction measured during trunk flexion exertions will be greater than co-contraction during extension exertions. As a result of the co-contraction we also hypothesize that spinal compression during flexion exertions will be greater than during trunk extension exertions of similar moment magnitude. Empirical data were recorded using surface EMG, measured external forces and kinematics. These were inputted into a bio-mechanical model to quantify co-contraction.
2. Methods
2.1. Experiment
Fourteen healthy volunteers with no history of low-back disorders participated in this experiment. Subjects included 7 males and 7 females with mean (standard deviation) age of 22.5 (3.2) years. Anthropometric characteristics are provided in Table 1. All participants provided informed consent approved by the Virginia Tech human subjects review board before participation in the experiment.
Table 1.
Subject characteristics
| Subjects |
||
|---|---|---|
| Male | Female | |
| Number | 7 | 7 |
| Age (yrs) | 23.7 (3.4) | 21.9 (2.6) |
| Height (cm)* | 180.3 (7.6) | 166.2 (7.2) |
| Bodymass (kg) * | 74.9 (9.7) | 64.3 (8.8) |
Indicates significant difference between genders.
The protocol required subjects to maintain an upright trunk posture against an external flexion or extension load applied to the trunk. Subjects were secured to a frame designed to restrict the motion of the pelvis and lower body while in a standing posture. A chest harness and cable system attached the subject to an isotonic load such that cable tension applied external horizontal forces of 100, 135, and 170 N at the T10 level of the trunk. When the load was attached to the anterior aspect of the chest harness the cable tension applied a flexion force thereby requiring isometric extension effort by the subjects to maintain an upright posture. Flexion exertions were achieved by attaching the load to the posterior aspect of the chest harness.
Once subjects confirmed they were at steady state with respect to the applied force, isometric EMG data were recorded. EMG signals were collected using bipolar surface electrodes (Delsys, Boston, MA, USA) on the left and right rectus abdominis (RA), lumbar para spinals (LP), internal oblique (IO), and external oblique muscles (EO). Electrodes for the RA were placed 3 cm lateral and 2 cm superior to the umbilicus; LP 4 cm lateral to the L3 spinous process; posterior IO 8 cm lateral to the midline within the lumbar triangle at a 45 ° with respect to vertical; and EO 10 cm lateral to the umbilicus with an orientation of 45 ° to vertical (Marras and Mirka, 1992). The bipolar 10 × 1 mm silver bar electrodes are spaced 10 mm apart and supported by electronics with 80 dB common mode rejection ratio and 1015 Ω input impedance. All EMG data were band-pass filtered in hardware between 20 and 450 Hz and sampled at 1000 Hz. The EMG signals were rectified and filtered using a 5 Hz, low-pass, seventh-order Butterworth filter in post-processing software (Matlab, Natick, MA, USA). Force-plate and trunk angle data were similarly filtered to avoid process-induced phase shift discrepancies between kinematic, kinetic and EMG signals. EMG values from each muscle were normalized with respect to their maximum values recorded during isometric maximum voluntary contraction (MVC) in flexion, extension, right and left lateral twist exertions (McGill, 1991).
Trunk moments were calculated about the L5/S1 joint using inverse dynamic analyses from ground reaction forces as described in the literature (Granata et al., 1995). Although subjects maintained an isometric upright trunk posture, 3-D kinematics of the trunk were recorded from electromagnetic sensors (Ascension Technology, Natick MA, USA) taped to the skin over the S1 and T10 vertebrae and at the manubrium (Granata and Sanford, 2000). Processed EMG data, trunk kinetics and kinematics were inputted into a biomechanical model to estimate co-contraction and spinal load during the flexion and extension exertions.
2.2. Biomechanical model
A three-dimensional, two-segment model was implemented to compute muscle force and spinal load (Granata and Wilson, 2001) (Fig. 1). The two-segment geometry allowed assessment of equilibrium and spinal stability while retaining simplicity for interpretation of results and assignment of muscle forces. Twelve muscle equivalents were represented including the right and left RA, EO, IO, and a three component para spinal muscle on both the right and left sides. The para spinal muscles included one- and two-segment muscles, e.g. inter-transversus and longisimus thoracic equivalent muscles. Anthropometric origin, insertion and cross-sectional area of each muscle were established from published anatomy(Jorgensen et al., 2001; Marras et al., 2001) and described elsewhere (Granata and Wilson, 2001). The moment generating capacity of each muscle was determined from the vector product between the unit vector direction of muscle force, Fi, and the muscle origin, ri, for each muscle i =1, ..., 12. This was scaled by the muscle force magnitude, fi, to determine muscle moment. The sum of muscle moments must achieve equilibrium with respect to the measured external moments (Eq. (1))
| (1) |
| (2) |
| (3) |
Magnitude of force in each muscle (Eq. (2)) was determined from the product of muscle activation, αi, muscle cross-sectional area, Areai, muscle Gain, and modulating factors to represent physiologic effects of force-length, f(Leni), and force-velocity, f (Veli) as described in our previous spine models (Granata and Marras, 1995a). Recognizing that the exertions represented an isometric upright posture, the force-length and force-velocity values were set to unity. Gain represented force capacity per unit cross-sectional area of the muscles and were calibrated for each subject. To be physiological valid the predicted Gain values must lie between 30 and 100 N cm -2 (McGill and Norman, 1986; Reid et al., 1912).
Fig. 1.
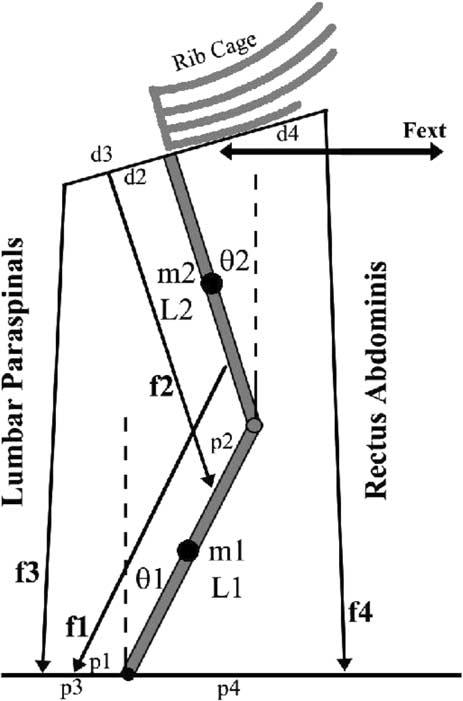
Schematic representation of trunk musculature used to quantify trunk co-contraction during trunk flexion and extension. For clarity, the external obliques and internal obliques muscles have been omitted but were included in the computational analysis.
Co-contraction was determined from muscle forces by solving for activations, αi, from measured EMG and comparing them with the values necessary for equilibrium. In the EMG-assisted approach equilibrium was achieved by determining the Gain value necessary to satisfy Eqs. (1) and (2) with constraints requiring that αi must be equal to normalized EMGi for each muscle i =1, ..., 12. Activation values of the musculature including the three components of the LP muscle were determined by methods of EMG-assisted optimization as described by Cholewicki and McGill (1994). Note that muscle forces determined from this EMG-assisted approach include components necessary to achieve equilibrium plus the effects of co-contraction, Fi_Total.
The set of muscle forces minimally necessary to achieve equilibrium without co-contraction, Fi_Equil, were estimated by means of linear programming using the model described above. Specifically, the set of αi were determined to minimize the sum of squared muscle force with equilibrium equality constraint (Eq. (1)) and activation boundary constraints (Eq. (3)). The Gain contributes to the force magnitude determined from this analysis and was therefore calibrated prior to estimation of αi by setting it equal to the Gain value computed from the EMG-assisted model described above. As per the methods of Hughes (Hughes et al., 2001) and Choi (2003) co-contraction was determined by comparing the muscle forces from these two analyses,
| (4) |
The co-contraction ratio represented the percentage of total muscle force attributed to Fi_Co-Contr
| (5) |
Spinal load at the L5/S1 level was computed as the vector sum of external loads and muscle forces. These spinal loads included separate components attributed to co-contraction and equilibrium muscle forces.
Repeated measures ANOVA were performed to determine the effects of flexion versus extension and exertion level (100 N, 135 N, 170 N) on the dependent variables of co-contraction and spinal compression. Effects were considered significant at a < 0.05. Post-hoc analyses were used to compare differences among significant treatments.
3. Results
Mean (standard deviation) measured trunk moments calculated at the L5/S1 level using inverse dynamics was 68.9 (10.9) N m. The experimental protocol applied similar horizontal external forces to the trunk during both flexion and extension exertions, so it is not surprising that trunk moments were not significantly(P < 0.412) different in flexion and extension exertions, mean values of 69.5 (6.1) N m and 68.4 (6.5) N m respectively(Table 2). Trunk moment increased significantly(P < 0.05) with exertion level from 59.3 (6.8) N m during 100 N load conditions to 80.8 (5.2) N m during conditions at 170 N loads. Accuracy and validity of the EMG-assisted model has been presented extensively elsewhere (Granata and Marras, 1993; Granata and Marras, 1995a; Granata and Wilson, 2001). The moments predicted by the EMG-assisted model were similar to the experimentally measured trunk moments, i.e. average error 1.2% during flexion and 2.1% during extension exertions. Predicted values of the muscle gains provided insight to the performance of the model. The average gain was 47.5 N/cm2 (ranging from 32.3 to 79.2) and well within the physiological accepted range of 30-100 N/cm2.
Table 2.
Model predicted spinal compression (N) from total muscle forces, task muscle forces, and co-contraction during all three load levels
| Load level (N) |
|||
|---|---|---|---|
| 100 | 135 | 170 | |
| Measured moment (Nm) | |||
| Flexion | 57.3 (4.3) | 68.9 (5.2) | 82.3 (9.5) |
| Extension | 55.1 (5.4) | 70.9 (6.3) | 79.2 (9.1) |
| Spinal compression (N) | |||
| Compression from total muscle force | |||
| Flexion | 995 (162) | 1501 (215) | 2066 (352) |
| Extension | 675 (108) | 1028 (165) | 1407 (230) |
| Compression from equilibrium muscle force | |||
| Flexion | 769.6 (75) | 1039.8 (95) | 1312 (165) |
| Extension | 619.1 (99) | 912.8 (153) | 1131.4 (270) |
| Compression from co-contraction | |||
| Flexion | 225.4 (98) | 461.2 (151) | 754 (210) |
| Extension | 55.9 (23) | 115.2 (41) | 275.6 (37) |
The effect of load level (P > 0.05) and load direction (P > 0.05) were both statistically significant on spinal compression. Measured moment were not significantly( P < 0.712) with respect to load direction. Measured moment was significantly( P < 0.05) different with respect to load level.
EMG activity was significantly greater during the iso-metric flexion exertions than during the isometric extension exertions in three of the four muscle groups. RA activity was greater during flexion than during extension, 15.3% and 10.5% MVC respectively (P < 0.05). IO activity increased from 7.5% MVC during extension trials to 10.4% during flexion exertions (P < 0.05). EO increased from 5.3% MVC during extension to 9.3% MVC during flexion (P < 0.01). Despite the expectation that LP activity should be greater during isometric trunk extension than in flexion efforts, muscle activity of the LP was not statistically different between flexion and extensions trials, 12.5% and 15.2% respectively. EMG increased significantly with respect to load level in all muscle groups. During flexion exertions RA and EO activity increased significantly(P < 0.02) with exertion level but during extension exertions the EMG from these muscles were not statistically influenced by exertion level. Lumbar para spinal EMG activity increased with isometric trunk extension effort (P < 0.02) but were not influence by exertion effort during flexion trials. These results indicate that RA and EO are the primary muscles generating the flexion moment. EMG values from the LP and IO suggest notable antagonistic co-activation during the flexion exertions.
Co-contraction ratio was significantly (P < 0.01) greater during flexion exertions than during extension exertions (Fig. 2). Although the EMG data provide in-sight into recruitment patterns it was necessary to implement a biomechanical model to relate the recruitment levels to minimum requirements of equilibrium and muscle force in order to quantify co-contraction. The average co-contraction force during flexion was approximately twice the value during extension, 27.9 (10.4)% and 13.3 (5.8)% respectively. Co-contraction increased significantly(P < 0.01) with exertion level, ranging from mean levels of 12.1 (8.0)% at 100 N load to 30.9 (9.3)% during conditions at 170 N load. There was no significant interaction between exertion level and flexion/extension (P = 0.783).
Fig. 2.
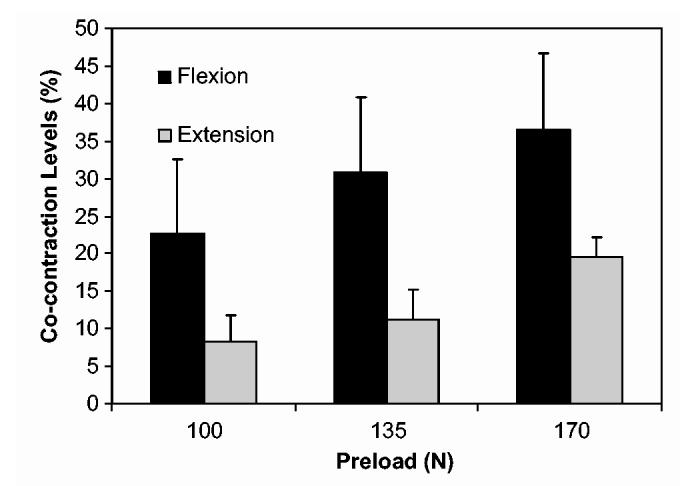
Co-contraction levels were significantly higher during flexion exertions (P < 0.01). Co-contraction levels were significantly higher with respect to load (P < 0.01). There was no significant interaction between load direction and load (P = 0.783).
Recognizing that co-contraction was greater during flexion exertions than during extension one must expect differences in spinal load attributed to the muscle forces. One might be tempted to predict reduced spinal compression during flexion exertions due to a slight mechanical advantage or moment arm of the RA and IO when compared to the trunk extensor muscles. However, when one accounts for co-contraction effects spinal compression was significantly(P < 0.05) greater during the flexion exertions than during extension exertions despite similar trunk moment magnitudes (Fig. 3). Average spinal compression during flexion was 1520.7 (250.3) N while the average spinal compression during extension was 1037 (172.1) N (Table 2). Spinal compression increased significantly(P < 0.05) with respect to exertion level, from a mean value of 835 (89) N during 100 N load conditions to 1736 (289) N during 170 N load conditions. Recall that the force in each muscle included components necessary to achieve equilibrium, FEquil, plus the force attributed to muscle co-contraction, FCo-contr. The compressive load attributed to the equilibrium components of muscle force, FEquil, was not significantly (P = 0.312) influenced by flexion/extension. Compressive load attributed to co-contraction, FCo-contr, was significantly(P < 0.01) greater during flexion exertions than during extension exertions. FCo-contr (P < 0.01) contributed to increased spinal compression with increased exertion level.
Fig. 3.
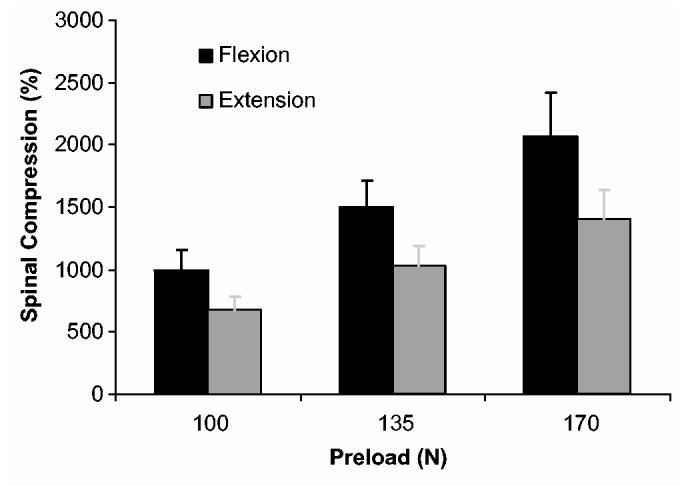
Spinal compression was significantly higher during flexion exertions (P < 0.05). Spinal compression was significantly higher with respect to load (P < 0.05).
4. Discussion
Co-contraction during trunk flexion exertions was approximatelytwice the level of co-contraction during equivalent extension tasks. Results represent co-contraction of the lumbar musculature but agree with similar analyses of the musculature surrounding the cervical spine (Choi, 2003). In the current study the mean co-contraction accounted for approximately 28% and 13% of the total muscle force during flexion and extension exertions respectively. Choi (2003) reported mean values of 35% and 12% for flexion and extension in the cervical spine. Specific values of co-contraction maybe influenced by exertion levels and by the complexity and assumptions of the model. However, theoretical analyses (Appendix A) suggest greater co-contraction during flexion exertions will remain regardless of model complexity. Controllability analyses in Appendix A provide analytical description whether or not it is possible to achieve stability of a specified system. When simulating isometric control of a single-segment spine stability can be achieved without notable differences in co-contraction during flexion and extension exertions. However, when simulating isometric control of a multi-segment spine the controllability analyses demonstrate that stability is mathematically infeasible during flexion exertions without coactive para spinal muscle forces. Thus, measured trends agree with published studies and theoretical analyses of control to conclude that recruitment of co-contraction is greater during isometric trunk flexion exertions than during extension exertions.
Why compute co-contraction using a biomechanical model instead of direct comparison of EMG data between flexion and extension exertions? When recording EMG activity during voluntary exertions the coactivity in antagonistic muscles can be determined by a priori characterization of muscle function (Granata et al., 2001; Granata and Orishimo, 2001). However, when comparing results between different tasks and moment directions, one must account for the fact that most muscles generate moments about more than one anatomic axis. Therefore, biomechanical analyses are required to characterize muscle function as agonist, antagonist, and equipoise (Hughes et al., 1994). Moreover, when estimating trunk moment from EMG activity of separate muscles one must consider the relative moment arm and size of the muscle groups with respect to the respective flexion and extension exertions. Thus, it is reasonable to quantify co-contraction by means of a biomechanical model in order to gain insight into the role of neuromuscular recruitment during pushing, pulling and lifting tasks (Marras and Granata, 1997). However, results must be considered in light of model limitations. Passive tissues mechanics were neglected as research indicates they contribute little to the stability of the trunk when in an upright posture (Cholewicki et al., 1997; Dolan et al., 1994). The model included a simplified representation of spinal geometry that was necessary to permit the control analyses (Appendix A) and EMG-assisted analyses of co-contraction (Marras and Granata, 1997). The model included three components of each para spinal muscle but EMG signals were recorded from a single surface electrode over each of the lumbar para spinal muscles. Therefore, force in the LP muscles was estimated from EMG-assisted optimization approach validated elsewhere (Cholewicki and McGill, 1994; Granata and Wilson, 2001). This may under-estimate the severity of co-contraction during flexion exertions. Thus, the model was designed to achieve a balance between the multi-component complexity sufficient to explain the empirical data versus the number of muscle actuators measurable by EMG and EMG-ssisted optimization techniques (Choi, 2003; Hughes et al., 1994). Similar trends wherein co-contraction is greater during isometric flexion than during extension can be shown with more complex models, but analyses reveal that this behavior cannot be observed with simpler model designs.
Co-contraction contributes to spinal load. Estimates of spinal load that neglect co-contraction may under estimate compression by as much as 45% during lifting tasks (Granata and Marras, 1995b). Nonetheless, estimates of spinal load during pushing tasks often neglect co-contraction. Chaffin and colleagues implemented a single-equivalent muscle model to estimate spinal loads associated with workplace pushing tasks (Andres and Chaffin, 1991; Lee et al., 1989; Resnick and Chaffin, 1995). Discussing their model of pushing, Lee et al. (1989) noted that the “solution assumes that only one muscle at a time is active to stabilize the torso (i.e. no antagonism exists)” and that single equivalent models that ignore co-contraction “may not be appropriate for the estimation of muscle forces in the lower back”. Results from the current study illustrate that up to 46.7% of the spinal load during flexion exertions are attributable to co-contraction. Consequently, spinal compression during the flexion tasks was nearly50% greater than during extension exertions. This is in contrast to published studies that report less spinal compression during pushing tasks than typically observed in lifting exertions (deLooze et al., 1995; Schibye et al., 2001). In those studies the reduction in spinal load was attributed the fact that trunk moment magnitude during pushing tasks were small when compared to lifting tasks. The protocol described in the current study examined flexion and extension exertions with similar trunk moment magnitude. Therefore, we conclude that co-contraction and associated spinal load during flexion exertions is greater than trunk extension exertions when moments magnitudes are similar. However, further analyses are necessary to investigate the role of co-contraction during simulated workplace tasks involving pushing and pulling wherein trunk moments magnitudes are different in pushing and pulling exertions.
Co-contraction and spinal load increased with exertion effort. Primary agonist muscle activation, muscle force and spinal load increase with trunk moment (Schultz and Andersson, 1981). This was evident in the results wherein the spinal load attributable to equilibrium specific muscle forces, FEquil, increased with exertion level. However, co-contraction increased with exertion effort as well. During 100 N load conditions the mean co-contraction was 12% of the total muscle force whereas during 170 N load conditions the co-contraction was nearly31% of the total muscle force. Theoretical analyses predict that stabilizing antagonistic co-contraction should decline with increased trunk moment (Cholewicki et al., 1997) but published empirical measurements of stability document increased co-contraction with external load (Granata and Orishimo, 2001). To describe this stabilizing control behavior it is necessary to implement nonlinear models. Although further research is necessary to understand this behavior the results are consistent with published data. Results suggest that analyses of workplace pushing and pulling exertions must consider the role of exertion effort on the co-contraction contributions to spinal load.
Trends in co-contraction, including the data presented in the current study maybe explained by recruitment patterns necessary to maintain spinal stability (Granata and Orishimo, 2001). Results suggest greater potential risk of spinal instability from motor control error during trunk flexion tasks than during extension exertions (Granata and Bennett, in press). However, data in this study did not empirically quantify spinal stability. Although insight can be achieved from motor control assessments of seated balance (Cholewicki et al., 2000) and biomechanical models of spinal stability (Cholewicki and McGill, 1996; Gardner-Morse et al., 1995) there are no existing empirical measures of spinal stability. To understand neuromuscular risk of low-back injury it will be necessary to develop quantitative empirical assessments of spinal stability. Moreover, the analyses described here represent static exertions. Further research is necessary to quantify the role of dynamic flexion tasks on muscle recruitment, spinal load and stability.
In conclusion, co-contraction during isometric lumbar flexion exertions is greater than co-contraction during extension exertions. This has been attributed to spinal stability requirements. Results underscore the need to consider neuromuscular control of spinal stability and coactive recruitment when evaluating the biomechanical risks of trunk flexion and extension exertions.
Acknowledgements
This research was supported in part by a grant R01 AR49932 from CDC/National Institute for Occupational Safety and Health. We wish to thank G. Slota for his assistance in the data collection and Mike Diersing for experimental coordination and scheduling.
Appendix A
Controllability analyses can be used to determine whether specified actuators, fi, can successfully stabilize and control the associated system. It is shown that by using a two-segment spine model that antagonistic para spinal muscle activation during flexion exertions is necessary for stability whereas antagonistic co-contraction during trunk extension exertions is not necessary if the muscles are sufficiently stiff. Results from this analysis provide the theoretical basis and motivation for the experimental measurements described above.
The two-dimensional model of the spine included four muscle actuators representing three muscle slips of the lumbar para spinal muscles, f1, f2, f3, and a fourth actuator representing the rectus abdominis, f4 (Fig. 1). Muscle origins and insertions were assigned to vector locations pi and di respectively for muscles fi, where i =1, ..., 4. The spine was represented as two-segment inverted pendulum. Unlike the biomechanical model (see Methods) the controllability analysis was limited to a sagittal plane representation of dynamics. The controllability analysis also ignored the internal oblique and external oblique muscles, but the system can be expanded to demonstrate similar results if these muscle groups are included. This two degree-of-freedom, 4 actuator model is sufficient to demonstrate a need for co-contraction during flexion exertion and can be generalized to demonstrate similar results in models of greater complexity, higher degrees-of-freedom and biofidelic muscle anatomy.
System dynamics were determined by Lagrange analyses with arbitrary values of segment mass, m1 and m2, and center of mass. The torso mass was included with the second (upper) segment. The equations of dynamics result in a set of two simultaneous equations of motion including segment angle, θ1, θ2, angular velocity, and angular acceleration .
| (A.1) |
| A.2 |
M(θ1, θ2) represents a 2-by-2 matrix of inertia that is a function of equilibrium geometry, θ1, θ2. Bold characters represent matrices. Values C(θ1, θ2), FExt(θ1, θ2) and G(θ1, θ2) represented the 2-by-2 matrix of velocity coefficients, the 2-by-1 external force vector, and the 2-by-1 gravity vector. Actuation torques Qh1(θj, fi) and Qh2(θj, fi) were expressed as a product of the momentarm matrix Q(θ1, θ2) and the vector of actuator (muscle) forces, .
The second-order equations of dynamics were linearized about the equilibrium posture, θ1, θ2, and expressed as a first-order state space equation (A.3) with respect to the state vector . This state-space representation included actuation forces, , with components of both equilibrium forces, and perturbation forces, fk.
| (A.3) |
where A and B are 4 × 4 matrices resulting from the manipulation of and , respectively. The linearization process eliminated the velocity coefficient matrix C(θ1, θ2), and reveals an equilibrium constant that must be balanced by the actuation equilibrium moment, i.e. revealing the system
| (A.4) |
In order to achieve stability a controllability matrix Cm is formed (Nise, 2004). The system is controllable if Rank(Cm) = 4, where Cm =[B, A · B, A2 · B, A3 · B] indicating that the actuator (muscle) design and placement is sufficient to control and stabilize the system. No assumptions regarding muscle models were required other than the fact that muscles can generate force and that the muscles can establish equilibrium. If one assumes the perturbation forces, fk, is proportional to the system state,, i.e. muscle force from stiffness and damping, , then the dynamic response about the equilibrium state can be expressed as
| (A.5) |
The system is stable if the real component of all eigenvalues of [A + B · K] are less than zero where the eigenvalues are equivalent to the system poles. Thus, muscle recruitment patterns necessaryfor spinal stability can be investigated by analyses of the system poles. Three cases of control behavior will be evaluated including analyses of trunk flexion and extension exertions with and without co-contraction.
Case 1: Flexion exertion utilizing only abdominal muscle group f4
| (A.6) |
where g is the gravitational constant, g = 9.8 m/s. Note that the first three columns of B are zero. This represents the condition wherein the para spinal muscles, f1, f2,and f3 are zero. B has been represented symbolically because its entries are long and complicated. Nonetheless, from the form of these matrices, specifically the placement of zeros in the B matrix, it is clear that Rank(Cm) 6 2. Therefore, this system is not controllable and subsequently not stabilizable. Hence, without para spinal muscle co-contraction the multi-segment spine cannot be stabilized during a flexion exertion.
Case 2: Flexion exertion utilizing abdominal muscle group f4 and lumbar para spinal muscles f1. The A matrix is identical to case 1 above, but the B matrix includes nonzero elements in column 1 to permit actuation of f1
| (A.7) |
Note that Rank(Cm) = 4 thereby demonstrating that the system is controllable only if antagonistic muscle co-contraction in the para spinal muscles are recruited.
Case 3: Extension exertion utilizing para spinal muscle groups f1 and f2 with no abdominal muscle activation. The A matrix is identical to case 1 above, but the B matrix includes nonzero elements in columns 1 and 2 to permit actuation of f1 and f2
| (A.8) |
Terms in column 4 are zero to eliminate any possible antagonistic co-contraction in the abdominal muscles. Note that Rank(Cm) = 4 thereby demonstrating that the system is controllable despite the fact that co-contraction of the flexor muscles is prohibited in this scenario. Optimized actuator performance can be achieved by permitting recruitment of f3. However, to be stable the eigenvalues of [A + B · K] must be less than zero, thereby requiring sufficiently large values of K.
This analysis requires perturbation muscle forces, fk, that can achieve both positive and negative values with respect to equilibrium forces f0. In so far as f0 is greater than zero, this criteria is physiologically valid. Specifically, the biomechanical impedance of active muscle permits the muscle force to become greater than the equilibrium force value when stretched or to be less then the baseline equilibrium force when shortened. However, if f0 were approximately equal to zero, i.e. inactive muscle, then a negative value with respect to equilibrium would indicate negative muscle force. Clearly, negative muscle force in infeasible. Therefore, results further suggest the requirement of baseline activityin the para spinal muscles, f0 > 0, to achieve controllability. Although these analyses demonstrate controllability, if one wishes to accurately predict specific values of active muscle force and co-contraction nonlinear muscle models and nonlinear control analyses must be implemented. None-the-less, the analyses demonstrate that co-contraction is necessary during trunk flexion exertions and suggests the co-contraction during flexion exertions must be greater than co-contraction during extension exertions.
More complex models of the musculoskeletal control can be investigated. With the implementation of a muscle model, it is possible to increase muscle stiffness by increasing muscle force; thus, the above K found for stability can be achieved through increasing muscle force. Previous analyses (Cholewicki et al., 1997; Gardner-Morse and Stokes, 1998; Granata and Orishimo, 2001) illustrate that if K is insufficiently large, then antagonistic co-contraction in the flexor muscles can be used to augment the extensor muscle stiffness and contribute to the system stability. Antagonistic co-contraction contributes to the magnitude K. Moreover, in order to maintain the equilibrium posture in the presence of antagonistic activity the agonist muscle groups must be further recruited activate to reject the antagonistic moment. This also contributes to the stiffness matrix. Therefore, co-contraction during trunk extension exertions maybe recruited to augment stability but is necessary only if the system is insufficiently stiff. Conversely, co-contraction during trunk flexion exertions is a necessary condition for stability.
References
- Andres RO, Chaffin DB. Validation of a biodynamic model of pushing and pulling. J. Biomech. 1991;24:1033–1045. doi: 10.1016/0021-9290(91)90020-n. [DOI] [PubMed] [Google Scholar]
- Bergmark A. Stability of the lumbar spine: a study in mechanical engineering. Acta Orthop. Scand. Suppl. 1989;230:1–54. doi: 10.3109/17453678909154177. [DOI] [PubMed] [Google Scholar]
- Choi H. Quantitative assessment of co-contraction in cervical musculature. Med. Eng. Phys. 2003;25:133–140. doi: 10.1016/s1350-4533(02)00151-0. [DOI] [PubMed] [Google Scholar]
- Cholewicki J, McGill SM. EMG assisted optimization: a hybrid approach for estimating muscle forces in an interdeterminate biomechanical model. J. Biomech. 1994;27:1287–1289. doi: 10.1016/0021-9290(94)90282-8. [DOI] [PubMed] [Google Scholar]
- Cholewicki J, McGill SM. Mechanical stability on the in vivo lumbar spine: implications for injury and chronic low back pain. Clin. Biomech. 1996;11:1–15. doi: 10.1016/0268-0033(95)00035-6. [DOI] [PubMed] [Google Scholar]
- Cholewicki J, Panjabi MM, Khachatryan A. Stabilizing function of trunk flexor-extensor muscles around a neutral spine posture. Spine. 1997;22:2207–2212. doi: 10.1097/00007632-199710010-00003. [DOI] [PubMed] [Google Scholar]
- Cholewicki J, Polzhofer GA, Radebold A. Postural control of trunk during unstable sitting. J. Biomech. 2000;22:1733–1737. doi: 10.1016/s0021-9290(00)00126-3. [DOI] [PubMed] [Google Scholar]
- Crisco JJ, Panjabi MM, Yamamoto I, Oxland TR. Euler stability of the human ligamentous lumbar spine. Part II Experiment. Clin. Biomech. 1992;7:27–32. doi: 10.1016/0268-0033(92)90004-N. [DOI] [PubMed] [Google Scholar]
- deLooze MP, Stassen ARA, Markslag AMT, Borst MJ, Wooning MM, Toussaint HM. Mechanical loading of the low back in three methods of refuse collecting. Ergonomics. 1995;38:1993–2006. doi: 10.1080/00140139508925246. [DOI] [PubMed] [Google Scholar]
- Dolan P, Mannion AF, Adams MA. Passive tissues help the back muscles to generate extensor moments during lifting. J. Biomech. 1994;27:1077–1085. doi: 10.1016/0021-9290(94)90224-0. [DOI] [PubMed] [Google Scholar]
- Gardner-Morse MG, Stokes IAF. The effects of abdominal muscle coactivation on lumbar spine stability. Spine. 1998;23:86–92. doi: 10.1097/00007632-199801010-00019. [DOI] [PubMed] [Google Scholar]
- Gardner-Morse MG, Stokes IAF, Laible JP. Role of muscles in lumbar stability in maximum extension efforts. J. Orthop. Res. 1995;13:802–808. doi: 10.1002/jor.1100130521. [DOI] [PubMed] [Google Scholar]
- Granata KP, Bennett BE. Low-back biomechanics and stability during pushing. Hum. Factors. doi: 10.1518/001872005774859962. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granata KP, Marras WS. An EMG-assisted model of loads on the lumbar spine during asymmetric trunk extensions. J. Biomech. 1993;26:1429–1438. doi: 10.1016/0021-9290(93)90093-t. [DOI] [PubMed] [Google Scholar]
- Granata KP, Marras WS. An EMG assisted model of biomechanical trunk loading during free-dynamic lifting. J. Biomech. 1995a;28:1309–1317. doi: 10.1016/0021-9290(95)00003-z. [DOI] [PubMed] [Google Scholar]
- Granata KP, Marras WS. The influence of trunk muscle coactivity upon dynamic spinal loads. Spine. 1995b;20:913–919. doi: 10.1097/00007632-199504150-00006. [DOI] [PubMed] [Google Scholar]
- Granata KP, Orishimo K. Response of trunk muscle coactivation to changes in spinal stability. J. Biomech. 2001;34:1117–1123. doi: 10.1016/s0021-9290(01)00081-1. [DOI] [PubMed] [Google Scholar]
- Granata KP, Sanford AH. Lumbar-pelvic coordination is influenced by lifting velocity and task weight. Spine. 2000;25:1413–1418. doi: 10.1097/00007632-200006010-00014. [DOI] [PubMed] [Google Scholar]
- Granata KP, Wilson SE. Trunk posture and spinal stability. J. Biomech. 2001;16:650–659. doi: 10.1016/s0268-0033(01)00064-x. [DOI] [PubMed] [Google Scholar]
- Granata KP, Marras WS, Fathallah FA. A method for measuring external trunk loads during dynamic lifting exertions. J. Biomech. 1995;29:1219–1222. doi: 10.1016/0021-9290(96)00018-8. [DOI] [PubMed] [Google Scholar]
- Granata KP, Orishimo K, Sanford AH. Trunk muscle coactivation in preparation for sudden load. J. Electromyo. Kinesiol. 2001;11:247–254. doi: 10.1016/s1050-6411(01)00003-7. [DOI] [PubMed] [Google Scholar]
- Hughes RE, Chaffin DB, Lavender SA, Andersson GB. Evaluation of muscle force prediction models of the lumbar trunk using surface electromyography. J. Orthop. Res. 1994;12:689–698. doi: 10.1002/jor.1100120512. [DOI] [PubMed] [Google Scholar]
- Hughes RE, Bean JC, Chaffin DB. A method for classifying co-contraction of lumbar muscle activity. J. Appl. Biomech. 2001;17:253–258. [Google Scholar]
- Jorgensen MJ, Marras WS, Granata KP, Wiand JW. MRI-derived moment-arms of the female and male spinal loading muscles. Clin. Biomech. 2001;16:182–193. doi: 10.1016/s0268-0033(00)00087-5. [DOI] [PubMed] [Google Scholar]
- Lee KS, Chaffin DB, Waikar AM, Chung MK. Lower back muscle forces in pushing and pulling. Ergonomics. 1989;32:1552–1563. doi: 10.1080/00140138908966924. [DOI] [PubMed] [Google Scholar]
- Marras WS, Granata KP. The development of an EMG-assisted model to assess spine loading during whole-body free-dynamic lifting. J. Electromyo. Kinesiol. 1997;7:259–268. doi: 10.1016/s1050-6411(97)00006-0. [DOI] [PubMed] [Google Scholar]
- Marras WS, Mirka GA. A comprehensive evaluation of trunk response to asymmetric trunk motion. Spine. 1992;17:318–326. doi: 10.1097/00007632-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Marras WS, Jorgenson MJ, Granata KP, Wiand B. Female and male trunk geometry: size and prediction of the spine loading trunk muscles derived from MRI. Clin. Biomech. 2001;16:38–46. doi: 10.1016/s0268-0033(00)00046-2. [DOI] [PubMed] [Google Scholar]
- McGill SM. Electromyographic activity of the abdominal and low back musculature during the generation of isometric and dynamic axial trunk torque: implications for lumbar mechanics. J. Orthop. Res. 1991;9:91–103. doi: 10.1002/jor.1100090112. [DOI] [PubMed] [Google Scholar]
- McGill SM. A revised anatomical model of the abdominal musculature for torso flexion efforts. J. Biomech. 1996;29:973–977. doi: 10.1016/0021-9290(95)00148-4. [DOI] [PubMed] [Google Scholar]
- McGill SM, Norman RW. Partitioning the L4-L5 dynamic moment into disc, ligamentous, and muscular components during lifting. Spine. 1986;11:666–678. doi: 10.1097/00007632-198609000-00004. [DOI] [PubMed] [Google Scholar]
- Nise SN. Control Systems Engineering. fourth ed. John Wiley & Sons; Hoboken, NJ: 2004. Controllability; pp. 735–739. [Google Scholar]
- Reid JG, Costigan PA, Comrie W. Prediction of trunk muscle areas and moment arms by use of anthropometric measures. Spine. 1912;3:273–275. doi: 10.1097/00007632-198704000-00015. [DOI] [PubMed] [Google Scholar]
- Resnick ML, Chaffin DB. An ergonomic evaluation of handle height and load in maximal and submaximal cart pushing. Appl. Ergon. 1995;26:173–178. doi: 10.1016/0003-6870(95)00014-4. [DOI] [PubMed] [Google Scholar]
- Schibye B, Sogaard K, Martinsen D, Klausen K. Mechanical load on the low back and shoulders during pushing and pulling of two-wheeled waste containers compared with lifting and carrying of bags and bins. Clin. Biomech. 2001;16:549–559. doi: 10.1016/s0268-0033(01)00039-0. [DOI] [PubMed] [Google Scholar]
- Schultz AB, Andersson GB. Analysis of loads on the lumbar spine. Spine. 1981;6:76–82. doi: 10.1097/00007632-198101000-00017. [DOI] [PubMed] [Google Scholar]
- Zetterberg C, Andersson GB, Schultz AB. The activity of individual trunk muscles during heavy physical loading. Spine. 1987;12:1035–1040. doi: 10.1097/00007632-198712000-00015. [DOI] [PubMed] [Google Scholar]


