A comparison of naïve and sophisticated subject behavior with game theoretic predictions

Abstract

We use an extensive form two-person game as the basis for two experiments designed to compare the behavior of two groups of subjects with each other and with the subgame perfect theoretical prediction in an anonymous interaction protocol. The two subject groups are undergraduates and advanced graduate students, the latter having studied economics and game theory. There is no difference in their choice behavior, and both groups depart substantially from game theoretic predictions. We also compare a subsample of the same graduate students with a typical undergraduate sample in an asset trading environment in which inexperienced undergraduates invariably produce substantial departures from the rational expectations prediction. In this way, we examine how robust are the results across two distinct anonymous interactive environments. In the constant sum trading game, the graduate students closely track the predictions of rational theory. Our interpretation is that the graduate student subjects' departure from subgame perfection to achieve cooperative outcomes in the two-person bargaining game is a consequence of a deliberate strategy and is not the result of error or inadequate learning.

The two-person game we use is motivated by and derived from the following two-stage game studied by Berg et al. (1): a group of subjects in room A are each given 10 one-dollar bills. Each is paired anonymously at random with another subject in room B. A subject in room A can send any amount of money—$0, $1, $2, … , $10—to their paired counterpart in room B, with the understanding by both parties that the sum sent will be tripled. Thus, if $10 is sent, the recipient in room B receives $30. Subjects in room B are then given the opportunity to return any part, including none, of the amount they receive.

The second stage of this game is a dictator game (2). If people in room B are strictly self interested, they should keep all the money. Understanding that this is the case, individuals in room A should send nothing. This is a pure investment trust game with net potential gains of 200% from reciprocity exchange if a person in room A is trusting and, if their counterpart is trustworthy, some of those gains can be used to reward the trusting investor. Subjects in room A give substantially more than subjects in one-stage dictator games offering no gains from exchange, even when performed double blind so that the experimenter, the subjects, and anyone who sees the results will be unable to identify the action of any subject (3). Furthermore, those in room B reciprocate by sending back surprising portions of what they receive (“surprising” relative to the game theoretic prediction), especially to those who are the most trusting, who send the entire $10.†

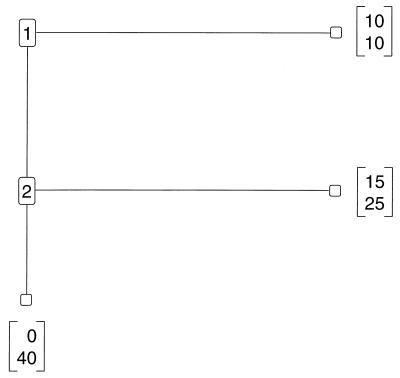
These results led us to examine the much-simplified reduced abstract extensive form of this game shown in Fig. 1, the invest $10 trust game. Player 1, who moves first, can move right, in which case the game ends, and the payoffs are (player 1, player 2) = ($10, $10). If player 1 moves down, player 2 can either move right, giving $15 to player 1 and $25 to player 2, or move down, giving $0 to player 1 and $40 to player 2. This version of the above game is equivalent to investing $10, which becomes $30, and then player 2 can split it equally (move right) or take it all (move down). But this story line does not accompany the display of the decision tree in Fig. 1 to the subjects. The equilibrium of the game, played by self-interested players using the principles of dominance and backward induction, is the subgame perfect (SP) outcome ($10, $10).

Figure 1.

Trust game. In this two-person trust game, player 1 can move right and end the game, resulting in a payout of $10 to each. Alternatively, player 1 can move down, trusting player 2 to move right (reciprocate), resulting in a payout of $15 to player 1 and $25 to player 2. Although trust and reciprocity can improve the gains from exchange to both players, player 2 faces the temptation to play down in order to get $40, leaving player 1 with nothing. Will player 1 give up a certain $10 and play down given player 2's incentives?

Our analysis of the game is different from the above and takes the perspective of a player applying her own interactive social experience to the game. The hypothesis is that people have a “natural ability” to apply the principle of reciprocity in their interactions with others in ordinary social exchange, although we expect this common propensity to be significantly compromised in anonymous one-shot interaction.‡ Reciprocity is the process of trading favors, services, and commodities across time with others. Thus A gives something of value to B at time t, receiving nothing tangible in return except a social obligation captured by the common phrase, “I owe you one,” although B at some time t + 1 may return the favor in some form. Such trades are common in human social life, yielding benefits because of the resulting gains from exchange, and those benefits reinforce the survival of the trait in populations.§ They occur to a large extent below conscious awareness, which helps to explain their survival even in anonymous interactions. In pure trust games, reciprocity is strictly positive; i.e., there is no possibility of punishing defections on the offer to cooperate. Thus, in Fig. 1, a move down by player 1 is an offer to cooperate to achieve (15, 25), but player 1 has no recourse if player 2 responds by playing down at the second node.¶

Cooperation in one-shot trust games can be explained, of course, also in terms of individual utility for other as well as own reward (for example, ref. 10). But this interpretation begs the question of the origin of interdependent utilities. We prefer the reciprocity-exchange interpretation, which can be said to help justify utility as an immediate motivation for cooperation, but is richer, we think, in terms of providing a process framework for generating testable hypotheses. Also, the exchange interpretation links up with ethnographic field data showing that social exchange in hunter-gatherer societies with no monetary exchange system supports a division of labor capable of creating significant surpluses and accounting for the growth and development of our human and protohuman ancestors long before barter, money, and the introduction of long-distance trade (11, 12).

In Fig. 1, if player 1 believes that his anonymous counterpart is a reciprocator and that player 2 will move right at node 2, then he will be tempted to play down. If P is the probability of reciprocation, the expected payoff to player 1 is 15P, which is greater than $10 for any P > 2/3. Hence, a down move by player 1 suggests a remarkably strong expectation of (signal for) trustworthy behavior under anonymous interaction.

Game theory hardwires into the analysis of play by other players the assumption that each player believes the other will apply the principles of dominance and backward induction; this rules out reciprocity behavior as “irrational,” although both players substantially increase their payoffs if they consummate an exchange. In all the matching protocols (single play, repeat play random pairing, same pairs, and so on) and games reported in ref. 8, those subjects who cooperate always earn on average at least as much as those who play the SP equilibrium and therefore cannot be said to be irrational. Also note that equity or “fairness” in the sense of a preference for an equal split payoff is not a confounding issue. If player 1 goes for an exchange, he must forego the equal split of $20. Consequently, we interpret a move down by player 1 as a self-interested attempt by him to increase payoffs by 50%, a move that is counter to both SP and a utilitarian preference for equity. However, such an expectation is reasonable from reciprocity analysis because the action increases player 2's payoff by 150%, and the intent signaled by this move is unambiguous: it is not credible that player 1 would move down if he knew that his counterpart would defect. Hence, playing down strongly signals the intention to achieve cooperation through positive reciprocity.

Experimental Design and Hypotheses

We report two experiments using the game in Fig. 1. Experiment 1 uses 24 subjects recruited from the undergraduate body at the University of Arizona. These subjects are generally naïve with respect to knowledge of game theory. We test two research hypotheses.

Hypothesis 1.

Players 1 will play right in accordance with the SP prediction. The null alternative is that subjects have only a one-half probability of playing right. Rejection of this null hypothesis will be interpreted as supporting SP, whereas failure to reject it will be interpreted as supporting the reciprocity hypothesis [see ref. 8 for a Bayesian treatment of Bernoulli trials with an extreme research hypothesis such as Prob (SP) = 1].

Hypothesis 2.

Conditional on players 1 moving down, players 2 will move down in stage 2 in accordance with the game theoretic prediction that dominant strategies will be chosen. The null alternative is a one-half probability of a move right by players 2, which supports the reciprocity hypothesis.

Experiment 2 uses 28 subjects drawn from groups of advanced graduate students as described below. This experiment consists of two sequential plays of the trust game in Fig. 1, by using the same matched pairs in the same player role for both play periods. Game theory predicts the SP outcome in each period. Our prior hypothesis, given the results of experiment 1 reported below, was that the period 1 frequency of down moves by players 1 should be greater than the period 2 frequency. Similarly, the period 1 frequency of down moves by players 2 should be smaller than the period 2 frequency. This is because we predict short-term reputation building in repeat interaction with the same partners. We think that some players 1, who would play SP in a single play, will offer to cooperate in period 1, then defect in period 2. Similarly, some players 2 who would defect in a single play of the game will cooperate in period one, building reputation, then defect in period 2. But the more common norm will be to invoke reciprocity play in both periods. We expect these features to be exhibited in only two repeat periods, although such a short horizon strongly implies the SP outcome in both periods by the logic of game theory.

Hypothesis 3.

Let f_ij = frequency with which players i move down in period j. Then the reciprocity research hypothesis has two parts: (i) f₁₁ > f₁₂, and (ii) f₂₁ < f₂₂ (game theoretic play implies that f₁₁ = f₁₂ = 0, and f₂₁ = f₂₂ = 1).

Because the subjects in experiment 2 are game theoretic savvy compared with those in experiment 1, this implies:

Hypothesis 4.

Comparing the second period play in experiment 2 with experiment 1, the frequency of players 1 choosing SP moves right in experiment 2 will exceed that in experiment 1, whereas the frequency of defection moves down by players 2 in experiment 1 will be less than that in experiment 2. Letting F_mn be the frequency of choice of the game theoretic dominant strategy (SP for player 1, defection by player 2) by player m in experiment n, the hypothesis has two parts:

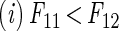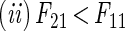Experiment 1 with Naïve Subjects

Design.

We conducted a single play of the game in Fig. 1 with subjects from the undergraduate population of the University of Arizona. Four groups of 12 subjects were run, n = 24 pairs. Each subject received $5 when appearing for the experiment and was assigned to a computer terminal monitor. Each subject was paired at random with one of the other 11 subjects in the room, one member in each pair was randomly assigned the player 1 role, and the other subject, player 2. After all subjects had finished reading the generic instructions for a two-person game tree, players were shown a game with the payoffs as in Fig. 1. By using a mouse, each player 1 clicked on right or down arrows. This move information was then displayed to player 2, who clicked on the right or down arrow. When all pairs were finished, the experiment ended, each pair learned the outcome, and the subjects were called out of the room one at a time, paid privately, and dismissed. The total time required from arrival to dismissal of the last subject was less than 30 min for each experiment.

Results: Tests of Hypotheses.

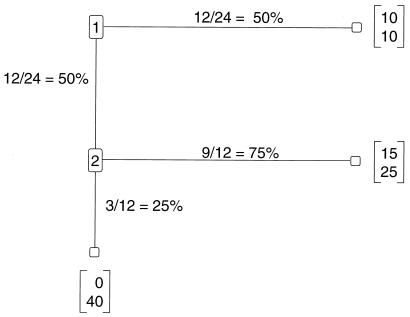
The outcomes by payoff box are shown on the move paths in Fig. 2. Players 1 in 12 of the 24 pairs moved right and 12 down or 50%. Players 2 in 9 of the 12 pairs who played stage 2 moved right for the cooperative outcome, 75%, whereas 3 moved down, 25%. Because P > 2/3, on average players 1 gained relative to the SP outcome. Specifically, the realized expected payoff to a player 1 from moving down was 0.75(15) = $11.25, which was a gain over the SP outcome, $10. In both hypotheses 1 and 2, we clearly cannot reject the null alternative to the SP prediction. We can say, however, that up to half the population of subjects are game theoretic players when subjects are paired anonymously. This result makes it clear that traditional noncooperative game theory is relevant for much of the behavior we report.

Figure 2.

Trust game. Single play by undergraduates; n = 24 pairs. Contrary to the one-shot noncooperative game theory prediction, discussed in the paper, half of our undergraduate subjects play down, of whom 75% experience reciprocity . Is this because undergraduates lack the sophisticated training in game theory to properly formulate their strategy or, as hypothesized in this paper, does their behavior reflect a ubiquitous human ability to engage in social exchange?

Experiment 2 with Sophisticated Subjects

Design.

In each of the years 1995–1997, we conducted workshops in experimental economics for graduate students from the United States and Europe. The typical graduate student was in his or her third or fourth year of study and all had been exposed to game theory, for many of whom it was a major field of concentration. The workshop extended for 5 days divided into half-day modules. Each half-day began with a laboratory experiment to introduce the topic for the session. The subjects paid their own food and lodging expenses by using money earned in the experiments, which was parameterized for an average yield of about $100 per day for two or three laboratory sessions. This provided an opportunity to conduct experiments with substantial payoffs, all of which were salient ($5 fees for arrival were not needed).

Results: Tests of Hypotheses.

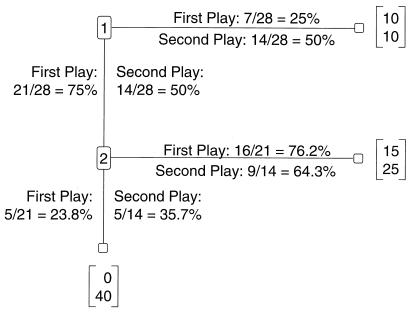
The outcomes for experiment 2 are shown on the move paths in Fig. 3. Players 1 in only 7 of the 28 pairs moved right, or 25%, whereas 21 moved down in period 1. Players 2 in 16 of the 21 pairs who played stage 2 moved right for the reciprocity outcome, or 76.2%, whereas 5 moved down, 23.8%. On average, players 1 earned 0.762(15) = $11.43, gaining relative to the SP outcome.

Figure 3.

Trust game. Played twice by advanced graduate students; n = 28 pairs. Graduate student subjects with extensive training in game theory face the same dilemma playing the two-person trust game twice with the same counterpart as the undergraduates discussed in Fig. 2. The continued use of trust and reciprocity exhibited by these subjects provides additional support for the social exchange hypothesis.

In period 2, 14 of 28 players 1 moved down, or 50%, whereas of the 14 playing in stage 2, 5 moved down, or 35.7%. On average, in period 2 players 1 earned 0.643(15) = $9.64, only slightly less than the SP payoff.

Testing the reciprocity hypothesis 3i by using the two-sample binomial test with f₁₁ = 0.75 > 0.50 = f₁₂, we reject the null alternative (P < 0.05). In hypothesis 3ii, we have f₁₂ = 0.238 < f₂₂ = 0.357 as predicted, but the difference is not significant, so that we are unable to reject the null hypothesis. Hypothesis 4i is clearly rejected; SP receives the same, not more, support in experiment 2 compared with experiment 1. Defection increases from 25% in experiment 1 to 35.7% in experiment 2, but the difference is not significant.

We conclude that undergraduates, naïve with respect to the formal apparatus of game theory, do not predominantly support the predictions of SP equilibrium theory. There is too much cooperation: half are trusting, while three-quarters of their counterparts are trustworthy. Yet game theory is relevant for half the players 1 and one-quarter of the players 2. Moreover, it cannot be claimed that the graduate students are any more likely to follow game theoretic principles than the undergraduates, in spite of the former's knowledge of those principles.

Asset Trading with Sophisticated Subjects

In stock market trading in laboratory experiments by using a 15-period horizon, it is well documented that undergraduates, business persons, and even market makers produce bubbles, with prices starting below the rational value, increasing to a peak above this value, then crashing sometime after period 9 or 10; such bubbles are largely extinguished with twice previously experienced subjects (13, 14). For these subjects, common information on true value does not induce common rational expectations. In view of the trust game results reported above, it is of particular interest to ask whether the departure from theoretical predictions by the graduate student behavior reported above applies also to the asset market. If it does, then we would have to suspect that the behavior of graduate students is impervious to their training in both environments and, because the asset trading experiment is a constant sum game, the behavior described above is not evidently related to the reciprocity and gains-from-exchange features of the bargaining game. If, however, they behave rationally in the asset-trading experiment, it suggests that they know and understand both games: their departure from the dictates of subgame perfection in the simple trust game is an intentional deliberate strategy based on expectations of reciprocity by the first mover, whereas the second mover feels an obligation not to violate the first mover's trust, without which there could have been no enhancement to the second mover's payoff.

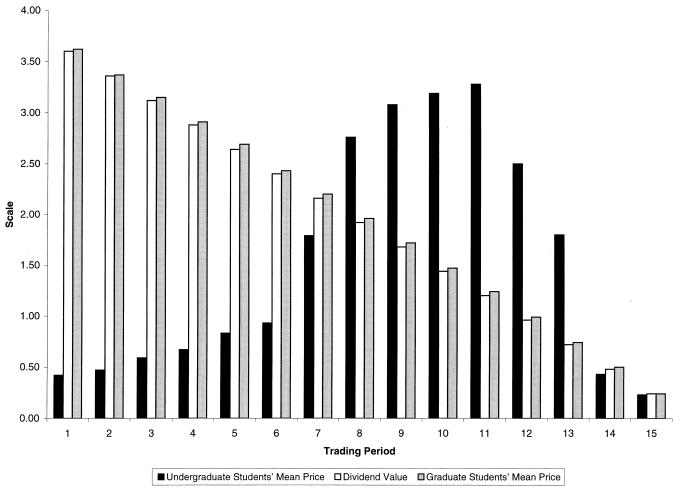
In one of the workshops described above, with 22 graduate students, we conducted a declining dividend (or “holding value”) asset trading experiment, with expected dividend $0.24 per period for 15 trading periods. (Dividends are 0, 8, 28, and 60 cents each with probability 1/4). Hence, fundamental value declines from $3.60 (15 × $0.24) in $0.24 increments, to $0.24 in the last period.

Fig. 4 uses bar graphs to chart the declining value of the asset (white bars) and mean double auction contract price by period, respectively, for a typical undergraduate sample (black bars) and for the graduate students (gray bars). As is typical, the mean deviations from fundamental value are very substantial for the undergraduates. But the deviations are miniscule and confined to the interval [0, $0.05] for the graduate students. Individual subjects among the latter not only have rational expectations, but they also attribute rational expectations to others. Common information about asset value is sufficient to induce common rational expectation in their first-time experiment, whereas undergraduates require two previous trading sessions before approaching the rational expectation prediction.

Figure 4.

Comparing graduate and undergraduate behavior in an intertemporal asset market with no induced gains from exchange shows that training in game theory may have a strong effect on behavior when there is no gain from exchange.

Fig. 4 suggests that the graduate students discern the zero-sum nature of the asset trading game, trade rationally, and when they depart from SP play in the trust game, they do so deliberately as a means of achieving the substantial gains from exchange that can be obtained through reciprocity.

Conclusions

The trust game we study provides a strong game theoretic incentive for players 1 to choose the SP equilibrium. This is because defection by player 2 is very costly to player 1, leaving him nothing. Moreover, the SP payoff is symmetric, thereby appealing to any player who is attracted to outcomes that are fair in the utility-for-equity sense. A player 1, however, who leans to reciprocity even under anonymity can send a strong and clear signal to play according to reciprocity principles. Such a move by player 1 offers to double the size of the pie and foregoes equity to give player 2 a payoff reward two-thirds larger than that of player 1. We find that half of our undergraduate players 1 move for cooperation in experiment 1, and 75% of their counterpart players 2 reciprocate.

In experiment 2, we vary subject sophistication by using advanced graduate students cognizant of game theoretic principles, who know that others in the group have similar exposure. The claim, often argued, that game theory is about sophisticated players implies that the SP prediction will be favored in experiment 2. But we observe no difference in players' 1 behavior in experiment 1 compared with players' 1 behavior in the second and final period in experiment 2. In the latter, the defection rate by players 2 does increase in period 2, in comparison with period 1, as expected of more sophisticated players, but the increase from 25% to 35.7% defection is too small to be statistically significant. Subjects in experiment 2 build short-term reputational capital in accordance with reciprocity tempered with a touch of game theoretic principles; i.e., the frequency of moves down by players 1 and right by players 2 is greater in period 1 than in period 2 play, although this difference is not significant. Game theory alone cannot accommodate this result—backward induction implies 100% SP outcomes in both periods. As we interpret it, some players 1 who would be inclined not to move down in single play are motivated to try it in a two-period game to build short-term reputational capital, induce their counterparts to move down in the second period, then defect. Consequently, friend-or-foe type uncertainty leaves room for game theoretic strategic manipulations. What is remarkable is that the defection rate increases from 25% in the first play to only 35.7% in the second play.

In asset markets, however, unlike undergraduates, various business groups, and stock traders, our graduate student subjects' behavior closely tracks rational fundamental value, as predicted by theory. From this comparison, we conclude that in the trust game, subjects' departure from SP play represents a deliberate propensity, consistent with reciprocity principles, to achieve the greater gains afforded by cooperation.

Why is the propensity for cooperative moves so strong under anonymous interaction, even in experiment 2? Our hypothesis is that reciprocal social exchange among like-minded individuals is an imperative powerful enough to overcome instruction in game theoretic principles in the context of anonymous one-on-one personal exchange, and that its power derives from its constant practice in day-to-day ordinary experience in stable societies. In half or more of our sample, this imperative overcomes anonymous matching. This is not a sentimental proclivity but rather a characteristic of realistic assumptions that players make about each other on the basis of lifestyle long-term self interest. A utility for other reward is not needed for the manifestation of this behavior. In our view, what is more appropriate for addressing the full range of our and other data in two-person extensive form bargaining are game theoretic cultural and biological evolutionary models of social exchange as, for example, in Roberts and Sherrett (13).‖

We close by emphasizing that up to half of our subjects in both population samples are dependable game theoretic players, which argues strongly against abandoning game theory, at least in anonymous interaction protocols that give SP its best shot. But a glass that is half full is also half empty. The need is for game theory to formally recognize that humans believe that other humans are capable of reciprocity even in anonymous interaction. The uncertainty in the trust games we study concerns the type with which one is matched. Is it friend or foe? Those who assume “friend” are not, on average, disadvantaged.

Abbreviation

SP

subgame perfect