Pupillary Evaluation of Retinal Asymmetry: Development and Initial Testing of a Technique

Abstract

Glaucomatous damage to upper and lower retina is often unequal. We have developed a rapid, objective, quantitative measure of asymmetry of retinal sensitivity, using infrared pupillometry and pairs of large stimuli that are symmetric about the horizontal meridian. Results for a group of eleven young subjects free of eye disease indicate that the distribution of asymmetry is close to a normal distribution centered near upper/lower symmetry. Some subjects showed modest amounts of asymmetry, which was relatively uniform within each eye, and between the two eyes, of the subject. This approach to determination of asymmetry within an eye is potentially applicable to testing patients with glaucoma. The narrowness of the distribution should make it possible to detect asymmetries caused by disease.

1. Introduction

Static automated perimetry is generally regarded as the “gold standard” for assessment of glaucomatous visual field defects. However, like many subjective tests, perimetry is demanding, performance is related to experience, and the results can be influenced by factors such as anxiety, alertness and a patient’s desire to give negative results. Because conventional perimetry measures the luminance increment threshold with a considerable number of small stimuli, it is usually relatively slow (a test may take from 5–7 minutes up to 10 minutes for one eye, depending on the test employed (Choplin & Edwards, 1995; Bengtsson, Heijl & Olsson, 1998; Bengtsson & Heijl, 1998)). Perimetric results can show relatively large test-retest variability, especially in damaged areas, and differentiation between true progression of glaucoma and random variation can require many tests (Chauhan & Johnson, 1999; Flammer, Drance & Zulauf, 1984; Heijl, Lindgren & Lindgren, 1989; Wall, Kutzko & Chauhan, 1997).

Because of these factors, efforts have been made to develop alternatives to visual fields that are objective, easy to perform, rapid to administer, and reliable. For example, one objective test which has been used recently in the clinical evaluation of glaucoma is the visual evoked potential (e.g., the multifocal VEP (Hood et al, 2004)). However, the small signal amplitude requires averaging over many repetitions to obtain distinguishable responses, prolonging the test. Another approach to developing an objective functional test is the use of the pupillary light reflex (PLR) to assess retinal function. The PLR has been shown in many studies to serve as an indicator of retinal status, (Johnson, Hill & Bartholomew, 1988; Lagreze & Kardon, 1998; Loewenfeld & Rosskothen, 1974; Lowenstein, Kawabata & Loewenfeld, 1964; Thompson, Montague, Cox & Corbett, 1982).

“Pupil perimetry”, a technique employing infrared pupillometry, was developed more than a decade ago as a way of evaluating visual fields objectively (Fankhauser & Flammer, 1989; ; Hong, Narkiewicz & Kardon, 2001; Kardon, 1992; Kardon, Kirkali & Thompson, 1991; Ukai, 1985; Wilhelm, Neitzel, Wilhelm, Beuel, Ludtke, Kretschmann & Zrenner, 2000; Yoshitomi, Matsui, Tanakadate & Ishikawa, 1999). Most studies of pupil perimetry employ a stimulus arrangement similar to that of conventional perimetry. (Wilhelm’s technique employs a stimulus similar to multifocal electroretinographic (ERG) stimuli.) Instead of measuring thresholds, the PLR amplitude is measured, using a spot stimulus of fixed suprathreshold luminance, presented at each test location. The subject’s task in pupil perimetry—staring at a fixation point—is easy to perform; subjects do not have to make judgments about stimulus visibility. However, current pupil perimetric tests are still quite lengthy (about 30 to 40 minutes), due to the nature of the stimulus layout, and defects may not be well correlated with perimetry in cases of glaucoma (Kardon, 1992). As with psychophysical perimetry, a substantial amount of within- and between-subject variability has been reported in results with pupil perimetry (Turtschi, Bergamin, Dubler, Schotzau & Zulauf, 1994).

The experimental design that we have developed is somewhat similar to the design of the “swinging flashlight test”, which has long been a useful clinical test to detect relative afferent pupillary defects (RAPD) between the two eyes (Levatin, 1959). The swinging flashlight test detects an RAPD as a significant asymmetry between the two eyes. In our test, instead of making a comparison between the two eyes, the relative pupillomotor sensitivity is determined for corresponding superior and inferior retinal territories within the same eye.

In human retina, the distribution of nerve fiber bundles is relatively symmetric about the horizontal meridian (Vrabec, 1966). During the progress of glaucoma, damage to nerve fibers is often asymmetric in upper vs. lower retina (Aulhorn & Karmeyer, 1976; Hart & Becker, 1982; Heijl & Lundqvist, 1984; Katz, Quigley & Sommer, 1995). Asymmetric functional changes characteristic of glaucomatous retinal nerve fiber damage may be detectable as asymmetries in relative sensitivity of the PLR in the upper and lower hemifield. This is somewhat similar to the “glaucoma hemifield test” (GHT), which also tests for visual asymmetry between upper and lower retina; however the GHT starts with data from conventional perimetry, and processes those data to determine patterns of asymmetry (Asman & Heijl, 1992a; Asman & Heijl, 1992b; Katz et al., 1995).

The present approach measures asymmetries of the PLR using large stimuli, which may be thought of as using the same retina as a control. An internal control of this sort could potentially reduce test-retest variability. This paper describes the new methodology and its initial application to normal subjects.

2. Methods

2.1. Apparatus

The instrumentation consisted of a stimulus display monitor (Radius PressView 21SR, Miro Displays, Inc., Germany) driven by a Power Macintosh G3 computer, and a PC-based infrared pupillometer (ISCAN EC-101, ISCAN, Inc., Burlington, MA).

The Macintosh computer controlled the stimulus display. Software was developed using the Psychophysics Toolbox (Brainard, 1997) with Yi-Zhong Wang’s interface in Matlab 5.2 (The MathWorks). This provides high-level access to the C-language VideoToolbox (Pelli, 1997). Stimulus shape, fixation point, intensity of the stimulus and background, and temporal frequency of the stimulus were selected from a menu. Three digital I/O lines connected the Macintosh and the PC. One line turned pupillometer recording on and off. The other two digital lines carried signals indicating timing of the stimulus; these two lines were recorded together with the pupil data.

The display monitor was a 21” CRT monitor with 38.0 x 27.8 cm active area, resolution 832 x 624 pixels, and frame rate 75 Hz. The monitor was 75 cm from the recorded eye. The visual angle subtended at the eye was 29.1° horizontally and 21.8° vertically.

The infrared pupillometer was a PC-based dark-pupil system, consisting of a resident card, a video camera and monitor, and an infrared spotlight. The infrared light source and video camera were placed at approximately the same distance from the subject as the display monitor, and appropriately aligned so that a pupil signal was observed on the PC. The subject’s eye could also be observed by the experimenter on the video monitor. The pupillometer recorded the horizontal diameter of the pupil 60 times/second; data were saved in both software-specific raw data files and ASCII files.

The luminance distribution of the display monitor was calibrated using a luminance meter (LS-100, Minolta, Japan). Calibrations were obtained for several locations on the monitor, expressing luminance as a function of DAC number output to the monitor. (All guns were driven equally.) One DAC level was selected from the middle of the log-linear portions of these functions, and monitor luminance was then determined at a grid of 9x7 positions for that particular nominal luminance. Each “stimulus” (see below) actually consisted of a pair of stimuli, one above and one below the horizontal meridian. For a particular experimental stimulus pair, set at a uniform nominal luminance, an estimate of relative pupillomotor effectiveness was obtained as follows: The standard curve of luminance vs. DAC value was used to set one DAC value used for the entire stimulus. The nominal luminance thus produced was multiplied by a correction factor for each grid point, determined from the grid measurements, giving an estimate of actual luminance at each grid location. Since pupillomotor sensitivity is not uniform across the retina, these numbers were multiplied by another set of scale factors relating pupillomotor sensitivity at each location to sensitivity at a central location (the “pupillary hill of vision”) (Bouma, 1965; Kardon et al., 1991; Kardon & Thompson, 1994). These numbers were summed over the set of grid points inside each member of the particular stimulus pair, giving one final number for each of the members of the pair. The final two numbers, give an estimate of the relative pupil sensitivity to the two stimuli to be expected as a result of asymmetries in the apparatus, as well as nonuniformity of pupillomotor sensitivity. The values found by this procedure gave very small estimates of differences in sensitivity (0.001–0.005 log units), and inhomogeneities of screen luminance were not considered further.

2.2. Stimuli

During the progress of glaucoma, focal damage of retinal ganglion cells often affects vision in paracentral, Bjerrum, and peripheral nasal regions of the visual field (Fig. 1(a)). The form of the most likely regions for small visual field defects, and also the boundaries of larger defects, tend to reflect, approximately, the retinal nerve fiber bundle layout (Aulhorn & Karmeyer, 1976; Hart & Becker, 1982; Heijl & Lundqvist, 1984; Weber & Ulrich, 1987, 1991). This provided the basis for the stimulus design used in the present study. Three stimuli -- paracentral, “Bjerrum”, and peripheral -- were designed to cover much of the central visual field, an area 30º wide (20º nasal to 10º temporal) × 20º high (Fig. 1(b)). For paracentral and Bjerrum stimuli, the fixation point was in the center of the screen; for the peripheral stimulus, the fixation point was moved 6º temporally, so that the peripheral stimulus extended out to 20º eccentricity in the nasal field.

Fig. 1.

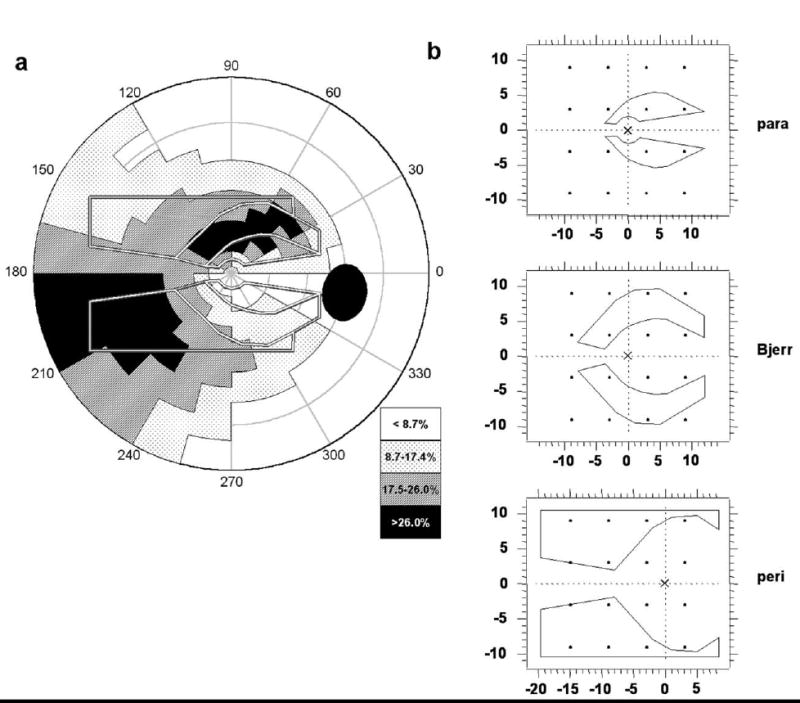
(a) Frequency distribution of focal retinal regions of glaucomatous damage (adapted from Aulhorn and Karmeyer, 1976). Gray/white lines are the outlines of the three stimulus pairs used in the present study: paracentral, Bjerrum, and peripheral. Key to shading scale indicates percent of instances of loss in an area. (b) Stimulus layout on the display monitor. All stimuli are for a right eye; the fixation point is indicated by an “X”. The dots represent the test grid for threshold perimetry (6º offset grid); dot size is Goldman size III stimulus size to scale.

Achromatic stimuli were used to elicit pupil responses. Each stimulus consisted of two parts, located in upper and lower visual field, that were mirror images about the horizontal meridian (Fig. 1(b)). For each experimental trial, the two parts of the stimulus were turned on and off alternately in the upper and lower visual field. The luminance of the lower portion of a stimulus pair was fixed at 40 cd/m², and the luminance of the upper portion cycled over three luminance levels: 24, 34, and 48 cd/m². (The middle luminance of the upper portion was less than the fixed luminance of the lower portion because, in preliminary experiments with 3 subjects, we found indications that the pupillomotor sensitivity of superior retina was less than that of inferior retina.) The luminance of each stimulus was 0.01 cd/m² when it was turned off. Outside of the stimulus boundaries was a uniform background (5 cd/m²). During stimulus presentation, first, the upper part was turned on for one second while the lower part was turned off; then the lower part was turned on for one second while the upper part was turned off, and so on. (The sequence is shown schematically in Fig. 3a.) At each transition, the pupil constricted. A complete stimulus cycle lasted 6 sec, and the stimulus cycle was repeated three times per trial, so one trial lasted 18 sec.

Fig. 3.

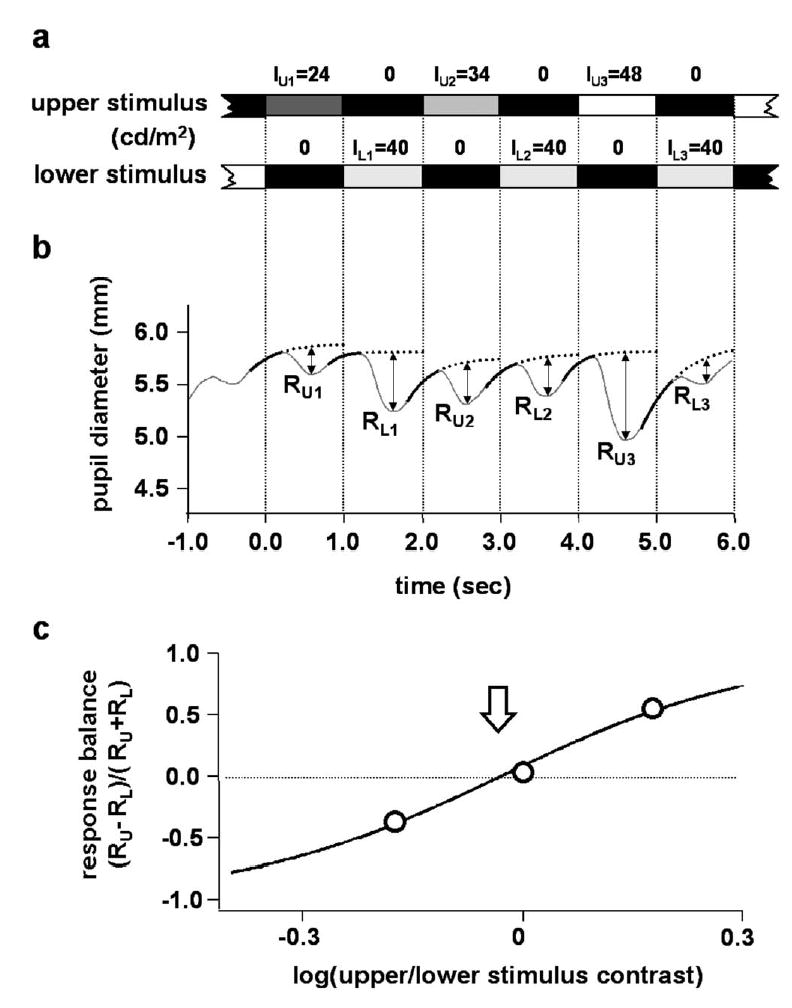
Example of data analysis. (a) Stimulus timing. (b) Pupil record. Heavy solid lines are the fitted curves (exponential functions); dotted lines are the extrapolations of the fitted curves. Amplitudes of pupil constrictions are represented by straight lines labeled R. (c) Response balance values (circles) plotted against log(upper/lower stimulus contrast). Solid line is the fitted sigmoid curve. The sigmoid fit gave log contrast balance = −0.030 (indicated by the arrow), equivalent to a contrast balance (x₀) of 0.93.

Each subject was tested in two sessions, separated by 1–3 weeks, to assess between-session variability. During each session, a complete set of six trials was performed (three stimuli for each eye); after a break of approximately 30 min, the six conditions were repeated in a different sequence to assess within-session variability.

The stimulus sequence, and the order of eye tested, were counterbalanced to minimize any effect of sequence (e.g., fatigue or practice effects). One stimulus sequence consisted of three trials presented to one eye, using each of the three stimuli. (There were six possible sequences.) Across all subjects, each sequence was used 13–16 times. If the first test of a particular subject began with the left eye, the second test in that session would begin with the right eye; in the second session for that subject, the sequence would be reversed. The first eye tested for each subject in their first session was alternated between the two eyes from one subject to the next.

2.3. Subjects

There were 11 subjects (6 males and 5 females), aged 25 to 40 years old (29.7 ± 5.2). The subjects were recruited from the community at SUNY State College of Optometry. All subjects had passed a general ocular examination at the University Optometric Center. Inclusion criteria were: best corrected visual acuity 20/25 or better, intraocular pressure less than 21 mmHg, normal slit-lamp and direct ophthalmoscopy exams, spherical refractive error less than ±5.0 D and cylindrical refractive error less than ±3.0 D. Exclusion criteria were: a primary relative with glaucoma, or medication that would have an effect on pupil function. The study was approved by the SUNY College of Optometry Institutional Review Board (IRB), and written informed consent was obtained from each subject after the nature of the experiment was explained in detail.

2.4. Protocol

Subjects sat in an examination chair with a head rest, adjusted to align the subject with the stimulus display and the eyetracker system. The eye not being tested was covered with an opaque eye patch. After the pupillometer signal was stable, a stimulus was presented on the display monitor, with a red cross as a fixation point. The subject was asked to fixate the red cross, and the experimenter checked for a pupil signal. Usually, the pupil gave a large response at the onset of the stimulus, and after several cycles reached steady oscillatory behavior. After such responses were observed on the PC, the experimenter alerted the subject, and then began recording. Pupil diameter and a digital signal of the stimulus timing were recorded for the 18 second duration of a trial (see Stimuli). After data were obtained from one eye for the three stimuli, the subject was instructed to switch the eyepatch, and the other eye was studied. A complete set of tests (all three stimuli for both eyes) typically took approximately 5 minutes.

Blinking reduces the amount of light entering the eye and contaminates the pupil record. Subjects were asked to make a moderate effort not to blink during the recording periods, and were told that it was fine to blink all they wanted at other times. If a subject blinked more than three times within one trial, the data were discarded and the same condition was repeated.

2.5. Analysis of pupil records

A software program was developed to analyze the pupil responses using Igor Pro 4.0 (WaveMetrics, Inc., Lake Oswego, OR). The data analyzed consisted of horizontal pupil diameter and timing signals of the stimulus (see above).

Initial processing of pupil data consisted of blink detection and removal, followed by digital filtering of the pupil diameter signal. Blinks were detected by differentiating the pupil diameter signal (2-point difference) and using a rate-of-change threshold. The end of a blink was located with an algorithm using pupil diameter and rate-of-change. Once demarcated, each blink was replaced with a linear data segment connecting the values before and after the blink. Filtering employed the binomial smoothing algorithm in Igor Pro, with a corner frequency at approximately 5 Hz.

Determination of Pupil Response Amplitudes

Under the luminance conditions of the present study, if one of the stimuli was turned on and remained on at a constant luminance, the pupil would typically begin to constrict 200–400 ms after stimulus onset, and reach peak constriction at 600–800 ms after stimulus onset. After that, the pupil would gradually redilate and reach a steady state at about 1200 ms. In this simple situation, the amplitude of the pupil response is the difference in pupil diameter between peak constriction and the pre-stimulus level. However, if a second stimulus is presented before the pupil reaches steady state, the second response begins before the first has reached a steady level. This makes determination of the appropriate baseline level for the second stimulus response difficult. This was generally the case for the stimuli used in the present experiments.

To deal with problem noted above, we developed a way of determining a baseline level: a portion of the pupil curve was considered--from the peak of pupil constriction to a point about 400 ms later, amounting to a window from about 800 to 1200 ms after stimulus onset. This portion of the redilation was fitted with a decaying exponential function, and the fitted exponential was extrapolated to the time of the next peak of pupil constriction. The difference between the next peak and the fitted curve was used as the amplitude of the next pupil constriction (Fig. 2 and Fig. 3 (b)). (It is important to note that 400 ms after one peak -- the end of the data window used for the extrapolation -- precedes the beginning of the next pupil response.)

Fig. 2.

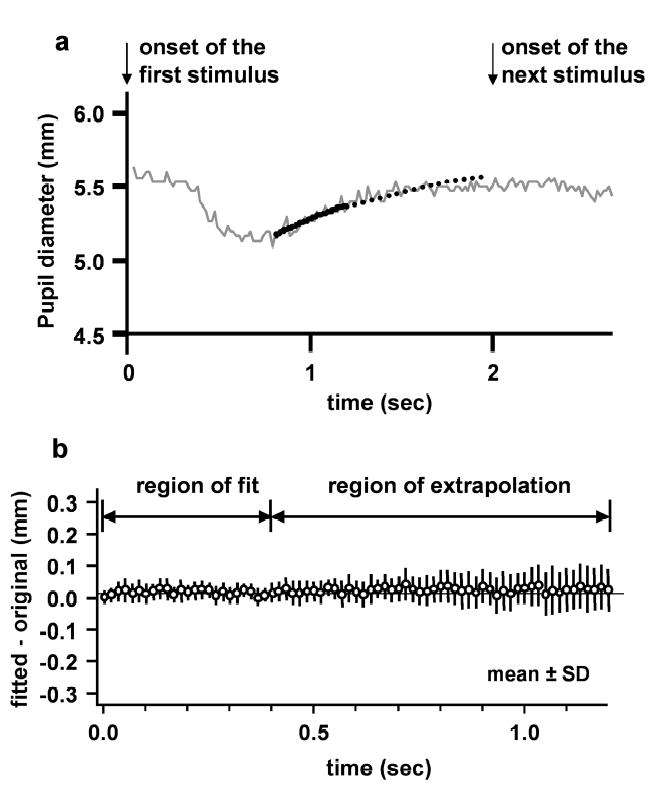
Testing the exponential fit used to estimate “baseline”. (a) Example of curve fitting for one stimulus presentation (pupil data are from average of 3 repeat cycles). Stimulus was modified so that each stimulus presentation lasted 2 sec, instead of 1 sec. Thick solid line is the fitted curve. Thick dotted line is the extrapolation of the fitted curve. Arrows indicate stimulus onset. The fit is made to a sample of pupil data from 800–1200 ms after stimulus onset. (1 sec is the time of the next stimulus onset for the standard stimulus used in the present experiments.) The difference between the fitted and extrapolated curve and the pupil record was determined at each time interval (60/sec). (b) Mean ± SD of the difference (fitted – actual) between fitted curve and actual pupil record. The data were taken from exponential fitting to the averaged pupil constriction for one trial using each of the three stimuli (paracentral, Bjerrum and peripheral stimuli; subject YN1). For the averaged data from each trial, fitting was carried out at each of the 6 stimulus onsets. (Each mean and SD is based on 3 x 6 = 18 samples.)

In order to test the accuracy of the fitting process, we modified the stimulus so that each part of the stimulus appeared for two sec instead of one sec (Fig. 2). In this case, there was enough time for the pupil to reach a steady level before the next constriction began. As with the standard stimulus timing, a 400 ms sample from the interval 800–1200 ms after an onset of upper or lower stimulus was used to perform an extrapolation. It was now possible to compare the extrapolation to the pupil record at times near 1600 ms after stimulus onset. (With the standard stimulus timing, this is the approximate time of the peak constriction to the next stimulus onset.) Figure 2 shows the mean and SD (18 trials) of the difference between the fitted and the actual data at each sample time, for subject YN1. The mean differences are close to zero, indicating that there was little tendency for the fitted curve to be larger or smaller than the actual data. The mean magnitude of the difference between fitted curve and actual data, across all stimuli, was 0.04 mm. To evaluate the significance of this, a segment of the pupil record 1500 – 2000 ms after stimulus onset was used to estimate the noise. (The pupil reached steady state about 1200 ms after stimulus onset.) The SD of pupil diameter for this segment of the data was 0.04 mm. Thus, the error in estimating the baseline was comparable to the noise level in the pupil measurements. This procedure for validating the baseline extrapolation was repeated in another subject with similar results.

Determination of “Response Balance”

For the three luminance pairs in one stimulus trial: each stimulus presentation (S) gave a pupil constriction (R). This allowed determination of a “response balance” value for each pair of stimuli (Fig. 3), where

$${\text{Response balance}}_i=(R_{Ui}-R_{Li})/(R_{Ui}+R_{Li})$$ (2)

• L_i (i=1, 2, 3): i^th stimulus presented in the lower visual field

• R_Li (i=1, 2, 3): pupil constriction resulting from L_i

• U_i (i=1, 2, 3): i^th stimulus presented in the upper visual field

• R_Ui (i=1, 2, 3): pupil constriction resulting from U_i

One trial consisted of three upper/lower stimulus values, giving three response balance values.

Determination of “Contrast Balance”

We define “contrast balance” as the relative contrast of upper to lower stimulus required to give equal (“balanced”) pupil responses, i.e., a response balance of zero. We used the response balance data from a trial to estimate the contrast balance (Fig. 3(c)): the response balance data were fitted with a sigmoid function:

$$F(x)=\frac{{(x/x_0)}^a-1}{{(x/x_0)}^a+1}$$ (3)

where x is the contrast of upper stimulus relative to lower and x₀ (the contrast balance) is the contrast that gives a response balance of zero and “a” is related to the sigmoid function slope. (Differentiation of eq(3) shows that the slope at x = x₀ is equal to a/2.) If upper and lower retina are functionally symmetric, the contrast balance should on average be 1. In the present study, the data have been interpreted on a scale of log contrast balance, and symmetry would give log contrast balance = 0. Log contrast balance is the key experimental quantity extracted from the data in the present experiments; the intent is to compare any given measurement to the distribution for normal eyes. The sign of log contrast balance indicates whether a measured asymmetry results from less sensitive lower or upper retina (positive or negative values, respectively). The contrast “x” may be thought of as the ratio: (upper stimulus luminance)/(lower stimulus luminance), or as the ratio (upper stimulus “on” luminance/upper stimulus “off” luminance)/(lower stimulus “on” luminance/lower stimulus “off” luminance), or as the ratio (upper stimulus “on” luminance/background luminance)/(lower stimulus “on” luminance/background luminance). These three expressions are equivalent, since the “off” luminances were uniform and the background luminance was uniform.

Several algorithms were developed to fit the pupil data and determine the contrast balance (see details of curve fitting in Appendix).

2.6. Statistics

The normality of the distribution of log contrast balance values for the group of subjects was evaluated with (a) the Kolmogorov-Smirnov normality test (K-S test, D less than $1.36/\sqrt{N}$ indicates a distribution that does not differ from normal at the p = 0.05 level), and (b) the Shapiro-Wilk (S-W) test. Correlation between the two eyes was evaluated with linear regression, and both correlation between the two eyes and within-session and between-session variability were evaluated with analysis of agreement (Bland & Altman, 2003).

3. Results

3.1. Pupil responses to alternating stimuli

The alternating stimuli used in the present work elicited a pupil constriction each time one part of a stimulus pair turned on and the other part turned off. The smallest response occurred after onset of the dimmest upper stimulus, and the largest response occurred after onset of the brightest upper stimulus. Each trial consisted of three 6-second stimulus cycles (see Methods) and it was often the case that the three 6-second segments of data were approximately the same. On some trials, a slow drift of average pupil size during the trial was observed, usually with pupil size decreasing over the course of the trial. Even in the presence of such drifts, the shape of each response remained fairly constant, and the average of the three cycles usually provided reasonably clean data.

The data shown in Fig. 3 are reasonably representative of the data found on many trials with the subjects in the present experiments. An important feature of the data is the rapid shift in balance of responses to the two stimuli as their relative luminance was changed. (Upper/lower stimulus luminance ratio was 24/40 for the leftmost response pair, and 48/40 for the rightmost response pair.)

3.2. Distribution of “contrast balance” values

Fig. 4A shows the contrast balance data (mean ± SD) grouped by subject (all 24 trials from each subject grouped together). Individual average values of contrast balance for the 11 subjects ranged from −0.15 to +0.23 log units. At the bottom of Fig. 4A are the data for the entire subject group (all individual trial results pooled). The smooth curve with the histogram is the best-fit normal distribution, which has center = 0.019 and SD = 0.162. The frequency distribution was normal according to a Kolmogorov-Smirnov test (d = 0.034, p > 0.2); a Shapiro-Wilk test suggested a slight deviation of the center towards the positive side, probably resulting from a group of points at the positive end of the distribution, visible in the histogram. It is apparent that the data for each subject generally form a somewhat narrower distribution than the data for all subjects pooled. (For 9 out of 11 subjects, the SD for each subject was smaller than that for the whole subject group; the other 2 subjects had SD’s equal to, or slightly larger than, the group SD.) The broader curve for the entire subject group is clearly the result of different subjects having different mean values. (The SEM values for Fig. 4A were typically no larger than the symbol size; thus, subjects with means near one end of the group differed significantly in their mean values from subjects with means near the other end.)

Fig. 4.

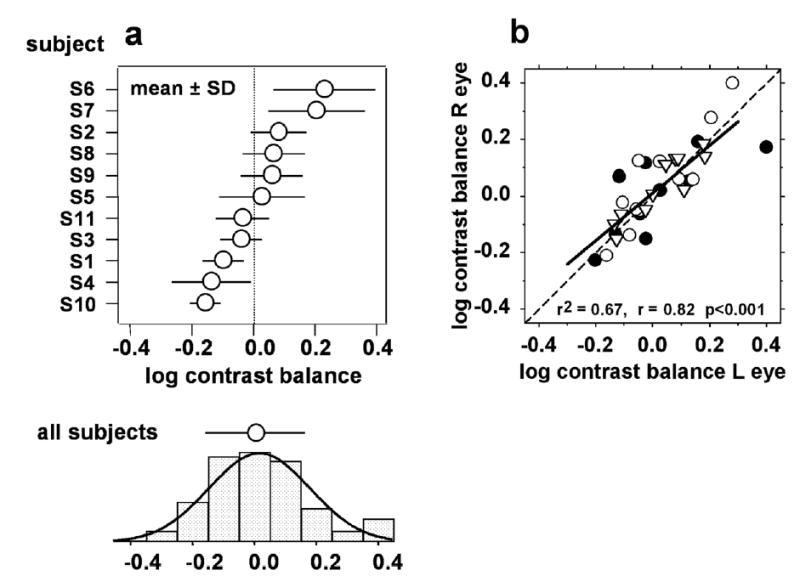
Contrast balance distributions for the subject group. (a). Contrast balance distributions for all individual trials from each subject, grouped by subject (mean ± SD). There were generally 24 trials for each subject, so most SEM error bars would not be larger than the symbol size. The distribution and mean ± SD shown at the bottom are for pooled data from all subjects. The smooth curve is the best-fit normal distribution for the pooled data: the data are not significantly different from a normal distribution according to a K-S test (d=0.07, p>0.05). With a S-W test, the distribution deviates from normal (W=0.97, p<0.05), due to the small cluster of points at the positive end of the distribution. (b). Comparison of the two eyes in each subject. The mean ± SD for each stimulus in each subject’s right eye is plotted against the mean ± SD for the left eye. Filled circles: paracentral stimulus; open circles: Bjerrum stimulus; inverted triangles: peripheral stimulus.

In a related finding, linear regression analysis showed that the average contrast balance for a subject’s right eye was correlated with (and nearly equal to) that for the left eye (r=0.82, r²=0.67) (Fig. 4B). Analysis of agreement (not shown) found no significant difference between eyes: the distribution of differences between the two eyes was Gaussian (K-S: D=0.13, p > 0.05) and centered at 0.007 log units with SD = 0.085 log units (95% CI = −0.160 to 0.174 log units). When the data for the different stimuli were separated, the correlation was somewhat poorer for the paracentral stimulus (filled circles; r = 0.74) than for the Bjerrum stimulus (open circles; r = 0.89) and the peripheral stimulus (inverted triangles; r = 0.91).

Grouping results for each of the three stimuli across subjects, it was found that there were no significant differences in the contrast balance among stimuli (1-way ANOVA, F = 0.4, p = 0.7); the average log contrast balance was approximately zero for each stimulus. (Variances for the three stimuli ranged from 0.02 to 0.03, so our sample size was adequate to detect a 0.2 log unit difference between two stimuli with a power of 0.80 at confidence level p < 0.05.)

3.3. Within-session and between-session variability

Within-session variation was taken to be the difference between log contrast balance values found for two repeat test trials performed during the same session (test 1 minus test 2) (Fig. 5, top). Data from the first session were used for the analysis of within-session variability; if data were not available from the first session for a particular stimulus condition, data from the second session were used. Within-session variation was distributed approximately normally (K-S: D=0.12, p >0.05; SW: W=0.94, p=0.001). Fig. 5 (top left) shows the difference between log contrast balance values plotted against the average of the two (Bland & Altman, 2003). The center of the distribution of within-session variation was approximately zero, and the 95% confidence interval was −0.30 to +0.28 log units (Fig. 5, top). Since it is also useful to have an estimate of the size of the variation, independent of sign, we also calculated the amount of within-session variation (absolute value of difference between log contrast balance values for the two tests); the average value of this for each of the three stimuli varied between 0.07–0.14 log units, with a mean of about 0.10 log units.

Fig. 5.

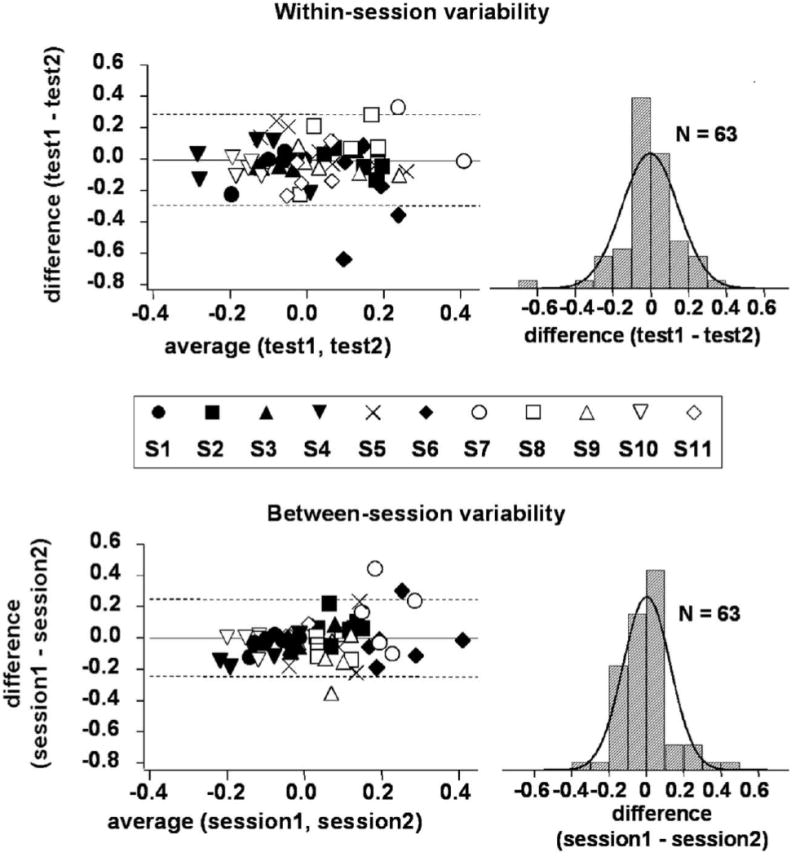
Within-session and between-session variability in the log Contrast balance. For within-session variability, the difference used is (test 1 - test 2) from a single session; for between-session variability, the difference used is (session 1 average - session 2 average). At left are scatter plots of difference vs. average (Bland and Altman, 2003). Dashed lines indicate the 95%CI. At right are the distributions of the differences; neither distribution differed significantly from normal according to Kolmogorov-Smirnov and Shapiro-Wilk tests.

Between-session variation was taken to be the difference between the log contrast balance values for the two sessions (session 1 minus session 2). For each session and each stimulus, the value used was the average of the two trials for that session. Data for between-session variability are plotted in Fig. 5 (bottom); as for within-session variability, between-session variation was distributed approximately normally, with a center close to zero (K-S: D=0.15, p>0.1; SW: W=0.93, p=0.003). The 95% confidence interval for between-session variation was −0.25 to +0.25, which is slightly smaller than that for within-session variation. As before, we also calculated the size of the variation: the average value of the amount of between-session variation (absolute value of difference between log contrast balance values for the two sessions) for each stimulus was approximately 0.07–0.12 log units, with a mean of about 0.09 log units.

The difference vs. average plots of Fig. 5, for within-session and between-session variation, were also tested for trends by linear regression; the within-session data did not show a significant probability of a trend; the between-session data showed a borderline-significant probability of a small trend. The absence of any substantial trend means that the variability did not depend systematically on the amount of up/down asymmetry.

The data of Fig. 5 were also plotted as magnitude of difference (absolute value of first minus second) vs. absolute value of average (not shown). As was the case for the plots of signed differences, these plots did not show any significant trends. Thus, the data do not show any indication of increased variability for cases of greater pupil asymmetry.

3.4. Sample data from patients with glaucoma

Fig. 6 shows data from two experimental trials of two patients with glaucoma. (The two examples were chosen to illustrate deep visual field defects which were vertically asymmetrical.) The data are shown in a form analogous to the pupil records of Fig. 3. Along with the pupil data are shown the visual fields of the tested eyes, with the outline of the pupil stimulus superimposed. A comparison of the visual field data with the pupil data shows that the areas of retina with the visual field defects produced pupillomotor signals that were much weaker than the signals from the areas of retina giving relatively normal visual field results.

Fig. 6.

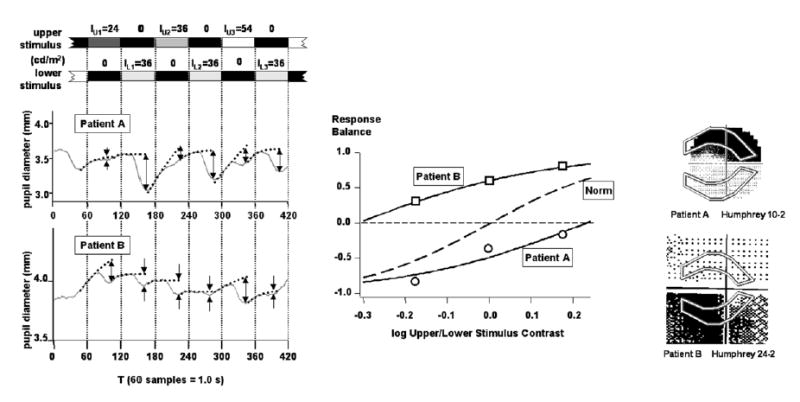
(Left) Data from two experimental trials of two patients with glaucoma, using the Bjerrum stimulus. Each data record consists of data from a single trial, averaged over the repeated stimulus cycles as in Fig. 3.

(Center) Response balance data and fitted sigmoid functions for the two trials. Dashed curve labelled “Norm” is the average sigmoid function for the group of normal subjects in the present study. Data from Patient A (circles) gave log contrast balance = +0.23; data from Patient B (squares) gave log contrast balance = −0.31.

(Right) Grayscale visual field data from the same eyes of the same patients, taken from each patient’s most recent clinic visit. The stimulus is superimposed at the same scale as the visual field data. The upper visual field used a 10-2 protocol; the lower visual field used a 24-2 protocol, and the diagram has been cropped. [Patient A: 67 y.o., MD: −13.7, PSD: 14.5 ; Patient B: 69 y.o., MD: −11.2, PSD: 11.3]

4. Discussion

In the present study, we have developed a method for determining the amount of functional asymmetry between regions of upper and lower retina, using the pupillary light reflex. In the present form, the test typically took about five minutes for all three stimuli in both eyes. The data suggest functional near-symmetry between superior and inferior retina in normal eyes, with the population mean very near to symmetry but some individuals having asymmetries which were mild in extent but consistent in both eyes and for all stimuli.

4.1. Design of the stimulus

In the present experiments, large stimuli were used because they offer the possibility of rapid testing. The PLR has the property of almost unlimited spatial summation (Schweitzer & Bouman, 1957): when a stimulus covers a large retinal area, the entire area contributes to the pupil response. The intent of these studies is to apply the techniques to patients with glaucoma; however, one potential problem is that, with a large stimulus, the pupil response will only show a significantly reduced response if a substantial fraction of the participating ganglion cells covered by the stimulus are damaged. We selected stimuli which should be sensitive to the kinds of asymmetry which are often present in early stages of glaucoma.

The short duration of the present test also depends in part on the use of suprathreshold stimuli. Working at suprathreshold levels may avoid problems commonly encountered with threshold measurements, such as low values of signal/noise, different definitions of threshold in different studies, and the time required to estimate the threshold using psychophysical algorithms.

In determining the experimental responses (see Methods), we treated the stimulus presentation as a sequence of three upper/lower stimulus pairs. Although the pairing might seem arbitrary, it is important to note that in the stimulus sequence U1/L1/U2/L2/U3/L3 (where L1=L2=L3), in the stimulus pair U1/L1, each stimulus follows the other stimulus in the pair. (U1 follows L3 which is identical to L1). The same type of symmetry holds for pairs U2/L2 and U3/L3. This symmetry is an important feature of the stimulus presentation. (There is an assumption made that still-earlier stimuli do not significantly affect the results; e.g., that the U2 stimulus that precedes the L2 that precedes the U3 does not affect the response to U3.)

4.2. Light scatter

Since the pupillary light reflex integrates light over large areas of visual space, it is important to consider to what extent light scatter could have contaminated or altered our results. We were particularly concerned about this issue, which was our motive for having a bright background — our brightest stimulus was only one log unit brighter than our background luminance. This is a very conservative choice of background; in pupil perimetry studies, the stimulus luminance has generally been at least two log units brighter than the background (Kardon, 1992; Kardon et al, 1991; Yoshitomi et al, 1999).

Another aspect of the present experiments that reduces likelihood of light scatter effects involves the mode of stimulus presentation. In an experimental trial using a Bjerrum stimulus pair for example, the background provides considerable “defense” against effects of light scatter into paracentral and peripheral areas. Light from the upper Bjerrum stimulus does scatter into the territory of the lower stimulus, but the amount of light is much less than when the lower stimulus is turned on. Thus, the simultaneous offset of the lower stimulus and onset of the upper stimulus results in a drastic lessening illumination of the retinal area of the lower stimulus. (In contrast, if the lower stimulus were off for some time, and then the upper stimulus turned on, there would be an increment in illumination within the territory of the lower stimulus due to light scatter.) Further evidence against a large role of light scatter in the present experiments may be seen in Fig. 6: areas of retina which (from the evidence of perimetry) were badly damaged, gave substantially less signal to the light reflex. The agreement between visual loss and pupillomotor loss shown in Fig. 6 argues against any very large “smearing” effect due to light scatter.

A final factor that works to reduce light scatter effects is the large stimulus size used in the present experiments; if light scatter can be considered to occur primarily within some angle θ_scatter of a ray’s direction, then extent of spread expressed as a fraction of stimulus size will be greater for a small stimulus than a large stimulus.

4.3. The use of extrapolation to determine baseline levels for pupil responses

One aspect of our data analysis which deserves further comment is the use of extrapolation to determine the baseline value for each response (see Methods and Figs. 2 and 3). We introduced this technique to cope with situations in which small responses follow larger ones. In such cases, the smaller response may appear as an inflection (see Fig. 3, response R_L3). If such a response is measured as the difference between the pupil diameter just prior to the beginning of the response and the peak of the response, the measured amplitude may be small or even zero, in spite of the fact that examination of the record shows that a response has clearly occurred. As discussed in detail in Methods, we estimated baseline levels for each response by fitting curves to portions of the pupil record. This approach gave reasonable values for the effective amplitudes of small responses, while making little difference in the measured amplitudes of larger responses. This is particularly important in situations of unbalanced pupillomotor sensitivity expected in many cases of glaucoma, where one member of a stimulus pair, falling on damaged retina, is likely to give a relatively weak response (Fig. 6). In such a case, measuring response amplitudes without using extrapolated baselines would underestimate the amplitude of the response from damaged retina, and this would have two major disadvantages: (i) By underestimating responses from the more damaged retina, the estimate of contrast balance would be shifted in the direction corresponding to greater damage, so that damage will be overestimated. (ii) Overestimating the damage would complicate the important task of developing a meaningful scale for describing the extent of damage.

We also assessed the value of the extrapolation technique in some control experiments: using several normal subjects, we ran trials using stimulus values which were either [upper=24,36,54 / lower=24], or [upper=24 / lower=24,36,54]. These choices gave response sequences which closely resembled response sequences obtained with symmetric stimuli in the presence of moderate lower or upper visual field defects (moderately damaged upper or lower retina), respectively. However, unlike situations of actual retinal damage, the contrast balance values determined for these two types of trials are estimates of the relative sensitivity of the same two areas of retina; therefore, if the stimulus luminances are taken into account, they should give the same result. We compared the results obtained by using amplitude measurements with and without extrapolated baselines. On average, the use of extrapolation was found to produce less spread in the estimations of contrast balance.

It might be thought, from the considerations relating to Fig. 2, that the need for baseline extrapolation could be avoided by using 2-sec instead of 1-sec stimulus presentations. This was not done for two reasons: (a) With 2-sec presentations, trials would have lasted 36 sec instead of 18 sec, an unreasonably long time during which to request minimal blinking. (b)The effectiveness of the test at comparing afferent signals may on partial cancellation of the offset of one stimulus by the onset of the next (see section 4.5 below).

4.4. The distribution of “contrast balance” for normal younger subjects

The approximately normal distribution of values of the log contrast balance (Fig. 4) provides the potential for detecting deviation of contrast balance from mean normal. Although the present study indicates that different subjects can have different values of average contrast balance, there tended to be less variation for a single subject in regard to differences between the two eyes, across the different stimuli, and across sessions. Therefore, in addition to assessment of deviation from mean normal by comparing a contrast balance value to the distribution for the normal population, this intra-subject homogeneity may make further assessments possible, e.g. by comparing differences between eyes and between stimuli for a single eye.

The center of the distribution of log contrast balance values was slightly positive (Fig. 4A, bottom), which suggests that, for pupil constriction, superior retina (stimulated by the inferior stimulus in the pair) is slightly more sensitive than inferior retina for the population. However, for some subjects the average log contrast balance was approximately zero, while for others it was displaced positively or negatively from zero (Fig. 4A). Differences in pupillomotor sensitivity between superior and inferior retina have been observed in other studies, though the results have not been uniform. In the present results, the average balance was very close to symmetry. Some other work, with 11 and 9 subjects, respectively, found average response amplitudes were 14% and 7 % greater for inferior retinal stimuli (superior visual field) (Wilhelm et al., 2000;Yoshitomi et al., 1999). Our finding that subjects can have mild idiosyncratic amounts of imbalance may potentially explain the variability of findings: if the degree of imbalance is normally distributed between subjects, as suggested by Fig. 4A, results from small samples could easily vary.

A number of studies of visual function have indicated greater sensitivity of superior retina, for absolute threshold sensitivity (Krill, Smith, Blough & Pass, 1968), contrast sensitivity (Skrandies, 1987), short-wavelength automated perimetry (SWAP) (Sample, Irak, Martinez & Yamagishi, 1997), pattern electroretinography (ERG) and critical flicker fusion frequency (CFF) (Skrandies, 1987). Standard perimetry has also indicated greater sensitivity of superior retina (Fig. 5 of Heijl, Lindgren & Olsson, 1987). The differences in sensitivity varied from about 0.04 log units to as much as 0.4 log units — amounts which should be apparent with our technique. Since results with the pupillary light reflex indicate near-balance or favor superior retina only slightly (see above), the visual asymmetry favoring superior retina does not appear to be present in the pupillomotor system as assessed from our small sample.

Although much is known about the anatomical substrate for the pupillary light reflex, there are still areas of uncertainty. Histological studies of macaque monkey indicate that approximately 10% of retinal ganglion cells have axons projecting to the superior colliculus and pretectum (Perry & Cowey, 1984; Rodieck, 1998), and that neurons in the pretectum mediate the PLR (Clarke, Zhang & Gamlin, 2003a; Clarke, Zhang & Gamlin, 2003b; Gamlin, Zhang & Clarke, 1995; Hultborn, Mori & Tsukahara, 1978; Trejo & Cicerone, 1984). Recent studies have shown that a small subset of retinal ganglion cells is intrinsically photosensitive and participates in the pupillary light reflex pathway (Lucas, Hattar, Takao, Berson, Foster & Yau, 2003). There is no evidence as yet as to whether the ganglion cells responsible for pupillomotor signals have a different retinal distribution from those responsible for visual signals, or whether the paths of their axons to the optic nerve are the same. (It has been suggested, for example, that the paths of retinal M-cell axons might differ somewhat from the axons of other ganglion cells in their path to the lamina cribrosa (Wyatt, 1992).) To the extent that uncertainties remain concerning the degree of similarity of the early afferent pathways for vision and for the pupillary light reflex, anatomical differences may exist which could explain the observed functional differences.

In the present experiments, the fixed luminance of the lower stimulus was higher than the middle luminance level of the upper stimulus. This was based on preliminary results, noted in Methods, suggesting stronger pupil responses from inferior vs. superior retina; thus, it was anticipated that the distribution of log contrast balance values would be centered at a negative value. Given the finding that the distribution actually centered near zero, a symmetric range of stimulus contrast may be preferable for future studies. However, given the method of determining contrast balances, modest shifts of the set of stimulus contrasts are not likely to change the distribution of contrast balances found.

4.5. Within- and between-session variability

Within-session variability was defined as the variability of a measurement repeated within a short time interval. The present study found the mean magnitude of within-session variability to be 0.10 log units.

Between-session variability is the variability of the measurement between two sessions. The assessment of between-session variability is important for determining whether changes in test results are typical fluctuations or reflect actual pathologic change. The present study found the mean magnitude of between-session variability to be 0.09 log units.

The values found for the magnitudes of both within-session and between-session variability amount to a small fraction of the estimate of the 95% confidence interval for this subject group (0.64 log units). This suggests that variability should not be a major obstacle to determining the extent to which a subject’s data deviate from mean normal. Also, as noted in Results, there was very little indication of a dependence of variability on the amount of asymmetry.

The relatively low variability observed with the present test may result from several factors:

1. The objective nature of the test, based on the pupillary light reflex, may avoid performance biases commonly encountered in subjective tests, such as learning effects, fatigue, variations in attentiveness, etc. Averaging over three stimulus cycles will tend to increase the signal-to-noise ratio (Fankhauser & Flammer, 1989). The pupil control system is not perfectly stable -- pupil size fluctuates with the level of autonomic neural activity (Lowenstein & Loewenfeld, 1969; Stark, 1969; Thompson, 1975) -- but the nature of the test (see below) seems likely to remove much of the effect of such fluctuations.

2. The stimuli used here covered large retinal areas -- much larger than used in conventional perimetry. In perimetry, relatively large stimuli are associated with lower test-retest variability, both in conventional perimetric studies employing larger than normal stimuli (Gilpin, Stewart, Hunt & Broom, 1990; Wall et al., 1997) and also in studies of new techniques such as frequency doubling perimetry (Chauhan & Johnson, 1999). In the case of conventional perimetry, it has been suggested that because a small stimulus stimulates fewer ganglion cell receptive fields, stimulus displacement resulting from head tilt or microfixation shifts can change the receptive fields stimulated. Also, if receptive fields of cortical neurons (involved in a subjective test) are constructed from signals from fewer retinal ganglion cells, the variability of the response is likely to be high (Felius, Swanson, Fellman, Lynn & Starita, 1996; Pearson, Swanson & Fellman, 2001).

3. In the present test, the pupil reacts to simultaneous onset of one retinal stimulus and offset of another. There is evidence that the signals from the two retinal stimuli show a degree of algebraic summation at some point in the pupil pathway (i.e., the onset and offset signals partly cancel each other) (Wyatt & Musselman, 1981). This means that, to a degree, one afferent signal is subtracted from the other, facilitating a comparison of relative strength and the detection of a “relative afferent defect” -- in this case, between local retinal areas. The present test could be thought of as a “swinging flashlight test” performed within one eye, using well-controlled stimuli. Because the approach employed in the present test essentially uses the same eye at almost the same time as a control, variability caused by fluctuations in the pupil system may be reduced.

With conventional perimetry, test-retest variability has been found to increase with increasing retinal damage (Chauhan & Johnson, 1999; Chauhan, Tompkins, LeBlanc & McCormick, 1993; Flammer et al., 1984; Heijl et al., 1989; Katz et al., 1995; Wall et al., 1997). This is vexing, because it means that the greater the defect, the less reliably can conventional perimetry describe, follow the progress of, and evaluate treatment of the disease. It is possible that the “built-in” control in the present test may make it more resistant to this problem.

A final question regarding variability is to what extent the variability of the contrast balance can be thought of as a consequence of independent fluctuations of upper and lower responses. To provide a preliminary assessment, we calculated within-session and between-session variability in two additional measurements: variation in response amplitude (Δ amplitude/mean amplitude) and variation in response balance. The variation in response balance was calculated simply as (Δ response balance) for the middle pair of stimuli in the stimulus sequence, noting again that response balance = (response to upper − response to lower)/(response to upper + response to lower). The results are given in Table I. The last column is an estimate of the SD of the distribution of (Δ response balance) if upper and lower retinal amplitudes vary independently; it is equal to (1/√2) times the amplitude SD. (Note that the amplitude is the difference divided by the average, while the response balance is the difference divided by the sum.)

Table I.

Variability of Response Amplitude and Response Balance

	Within-Session
Stimulus	SD [Δ Amp/mean Amp]	SD [Δ RespBal]	Estd SD[Δ RespBal]
Paracentral	0.73	0.80	0.52
Bjerrum	0.55	0.47	0.39
Peripheral	0.62	0.35	0.44
mean:	0.63	0.54	0.45
	Between-Session
Paracentral	0.60	0.52	0.42
Bjerrum	0.40	0.32	0.28
Peripheral	0.39	0.29	0.28
mean:	0.46	0.38	0.33

The values in Table I suggest that it is plausible that independent variations in responses to upper and lower stimuli underlie the variation in the response balance. We have not attempted to extend this to a prediction of variation in contrast balance, but contrast balance is closely related to response balance. If fluctuations in upper and lower retina were strongly correlated, response balance would be expected to vary less than the prediction in Table I, and this was not the case. If the variability of the response balance is taken as about 0.5, and the slope of the sigmoid function near the zero intercept is taken as 1.6 (the average value for the subject group), then the variability of the contrast balance would be expected to be roughly 0.6 times the variability of the response balance, or about 0.3. In fact, the mean and SD of the log contrast balance were about 0.0 and 0.1 log units, respectively. (On a linear scale, mean contrast balance was about 1.0 with SD about 0.21–0.26.) Thus, a rough calculation suggests that the data are consistent with independent variations in upper and lower retina.

4.6. Potential application of the technique to patients with glaucoma

As pointed out in Results, modest changes in the relative strength of the two stimuli in a pair can make substantial changes in the balance of the responses elicited by the stimulus pair (Fig. 3). This has been observed in normal subjects, and it is hoped that this sensitivity will also apply to imbalances due to retinal damage. It is clear from Fig. 6 that a large amount of imbalance due to retinal damage can result in a substantial response imbalance; it remains to be seen how sensitive the technique is in situations of more modest damage. This will depend mainly on (a) the distribution of log contrast balance values for normal older subjects, and (b) the log contrast balance found for a particular patient with glaucoma. In the trials shown in Fig. 6, the log contrast balance values were +0.23 and −0.31, and these values would have z-scores of roughly 1.5 and 2 with respect to the distribution shown for the subjects of the present work in Fig. 4 (lower left). Clearly, these data should be compared to a distribution determined from older normal subjects; using the same protocol as the subjects in Fig. 6, preliminary data for older normal subjects indicates a distribution somewhat narrower than that of Fig. 4.

In work currently underway, we are studying patients with glaucoma and older non-glaucomatous subjects. Among the issues we are focussing on are those of test-retest variability and the degree of correlation of pupillometric with perimetric findings in the same patients.

Although glaucoma often results in asymmetric damage to retinas (with differences above and below the horizontal meridian), it is widely believed that some “diffuse” damage also occurs in at least a proportion of cases (Caprioli, 1987; Funkhouser, 1991; Henson, Artes & Chauhan, 1999). If an eye suffered truly uniform damage, assessment of the contrast balance, as described in this paper, would not indicate abnormality. For this reason, we have also been studying the amplitudes of the responses to the stimuli employed; in each trial, we have taken separate averages of the three upper-stimulus response amplitudes and the averages of the three lower-stimulus response amplitudes. The amplitudes conform reasonably well to a log normal distribution; i.e., the log amplitudes are normally distributed, with an SD of about 0.2–0.3 log units. Preliminary analysis suggests that the amplitudes of the responses can provide an additional method for assessing the status of an eye. In work with patients and older normal subjects, underway at present, we plan to assess the effectiveness of such measures as well as the balance measures.

4.7. Contrast Balance vs relative response amplitude

In developing the present technique, we considered the use of relative response amplitude to a stimulus pair of equal strength as the primary measure. Pilot experiments suggested that using contrast balance led to less variability, and that measure was used. Contrast balance is closer to a constant-criterion measure, such as a threshold. The apparently greater stability may also arise from the broader stimulus range employed in the present approach. However, it is worth noting that the greater speed of a test employing a relative response measure might make it appropriate for situations in which speed is the critical factor, such as a screening paradigm.

Appendix Fitting Sigmoid Functions to Response Balance Data

This section describes, in more detail, the process for determining fits of sigmoid functions (eq.3) to response balance data from a trial.

Generally, both parameters of the function (slope “a” and contrast balance “x₀”) were allowed to vary to obtain a best fitting sigmoid. This approach, which we call a “free fit”, was successful in fitting sigmoid functions to the response balance data from most trials (e.g. Fig. 3).

In some cases, the free fit was not able to provide a successful fit, even though the data provided a clear indication of retinal function. For example, all three response balance values were occasionally either negative or positive, indicating a relatively weak pupil response from superior or inferior retina. Free fits of sigmoid functions were less reliable in such situations. Although such an occurrence was rare in normal subjects, such situations are more likely to occur in glaucoma patients, where functional asymmetry between upper and lower retina is expected. To deal with situations in which free fits were unreliable, we developed a “constrained fitting” technique, in which the slope of the fitting function was fixed at the mean value of successful free fits in the subject group, and only the contrast balance (x₀) was allowed to vary in Eq. 3. (This amounts to selecting the average curve shape and sliding it along the x-axis to find the best fit.)

There were several situations in which data from a constrained fit were used for subsequent analysis: (1) Data from a trial did not permit a free fit. (2) A free fit gave a slope or contrast balance value (“a” or “x₀”) outside a defined range. The defined range for slope was taken as +0.5 to +5.0, which included most of the “a” values found from successful free fits for individual trials. The choice for the defined range of contrast balance (x₀) was based on the luminance range of the stimuli in addition to the extrapolation range that was believed to be reliable. From the stimulus luminance sequence used in the present study (24, 34, and 48 cd/m²), we estimated a reasonable luminance range for extrapolation to be 17 to 68 cd/m². (The values 24, and 48 cd/m² are −0.15 and +0.15 log unit steps from the middle luminance, respectively; a second 0.15 log unit step corresponds to 17 and 68 cd/m², equivalent to an upper/lower contrast range of −0.37 to +0.23 log units (the lower stimulus luminance was 40 cd/m²)). The contrast range allowed from free fits was finally set to be −0.35 to +0.35 log units for the present subject group, extending somewhat further than +0.23 log units in the positive direction. This choice simplified processing and appeared to be reasonable, based on careful examination of the behavior of free fit data in the upper tail of the distribution.

When a constrained fit gave an unusually large or small contrast balance value, that value was “clipped” to a value outside which it was felt that numeric values would be unreliable. The contrast range used to limit constrained fits was −0.35 to +0.35 log units, the same as used to shift from a free fit to a constrained fit. The value that was assigned to the “clipped” data was −0.40 or +0.40 log units, depending on which limit was exceeded. This is a conservative approach, given that the limits are much more likely to be exceeded for patients with glaucoma than for normal subjects. It was felt that it would be inappropriate to use specific numerical values beyond the range of reasonably accurate extrapolations.

Because the contrast balance for a trial is obtained indirectly from the sigmoid curve fitted to the trial data, it was of interest to know how well the sigmoid fitted the data. In the present study, the square root of mean squared deviation (SRMSD) of the fitted curve to the response balance data was used as a measure of fit quality. SRMSD is similar to standard deviation for a one-dimensional distribution.

$$SRMSD=\sqrt{\frac{{(R_1-F(L_1))}^2+{(R_2-F(L_2))}^2+{(R_3-F(L_3))}^2}{3}}$$ (5)

• R_i: i=1,2,3, response balance obtained from raw data.

• F(L_i): i=1,2,3, sigmoid function at each contrast level

When the distribution of SRMSD’s was examined for free fits to data from all individual trials for which it was possible to carry out free fits, 97.2% were smaller than 0.5. Based on this, it was decided to reject data from trials for which both free and constrained fits gave SRMSD’s greater than 0.5. For the subjects in the present work, these criteria gave a data rejection rate of 7% of all individual trials.

It should be stressed that it was rare that data from normal subjects were clipped or rejected due to large SRMSD values. We were interested in setting up a general protocol for data analysis that could be applied to data from patients as well as data from normal subjects. Thus, clipping would tend to narrow the distribution of data from abnormal retinas much more frequently than it would affect the distribution from normal retinas. This is an appropriately conservative position, making it more difficult for patients’ data to fall at large distances from the center of the distribution of normal subjects’ data.