Smoothing Spline-based Score Tests for Proportional Hazards Models

Summary

We propose “score-type” tests for the proportional hazards assumption and for covariate effects in the Cox model using the natural smoothing spline representation of the corresponding nonparametric functions of time or covariate. The tests are based on the penalized partial likelihood and are derived by viewing the inverse of the smoothing parameter as a variance component and testing an equivalent null hypothesis that the variance component is zero. We show that the tests have size close to the nominal level and good power against general alternatives, and we apply them to data from a cancer clinical trial.

1 Introduction

For regression analysis of censored survival data, Cox's proportional hazards model (Cox, 1972) is unquestionably the most popular framework. The assumption of proportional hazards may not always be realistic, however; e.g., Gray (2000) notes that effects of prognostic factors in cancer often do not exhibit proportional hazards, and we have found the assumption questionable in many cancer and cardiovascular disease data analyses. Accordingly, this assumption should be critically evaluated and alternative models considered if necessary.

A situation in which the proportional hazards assumption may be suspect is in the analysis of covariate effects on survival in Cancer and Leukemia Group B (CALGB) Protocol 8541, a randomized clinical trial comparing three doses (high, moderate, and low) of chemotherapy (cyclophosphamide, doxorubicin, also known as adriamycin, and 5 fluorouracil, abbreviated CAF) in women with early stage, node-positive breast cancer. The primary analysis found no difference in survival between high and moderate doses, both of which were superior to the low dose. Based on long-term follow-up, subsequent interest focused on whether certain patient characteristics are prognostic for survival. Figure 1a shows estimated survival curves and the log-negative-log of survival curves for the 1437 patients for whom Estrogen Receptor (ER) status was available (520 ER-negative and 917 ER-positive, respectively). Under proportional hazards, the log-negative-log survival curves should be parallel, which is obviously not the case; in fact, the two curves cross on the interval (0, 1) year. Figure 1b shows the Schoenfeld (1982) residuals, which, on average, should be zero if proportional hazards were adequate but exhibit a noticeable trend away from zero. Formal evidence supporting the visual impressions from the figures would be valuable to the data analyst assessing whether the Cox model is an appropriate framework for inference.

Figure 1.

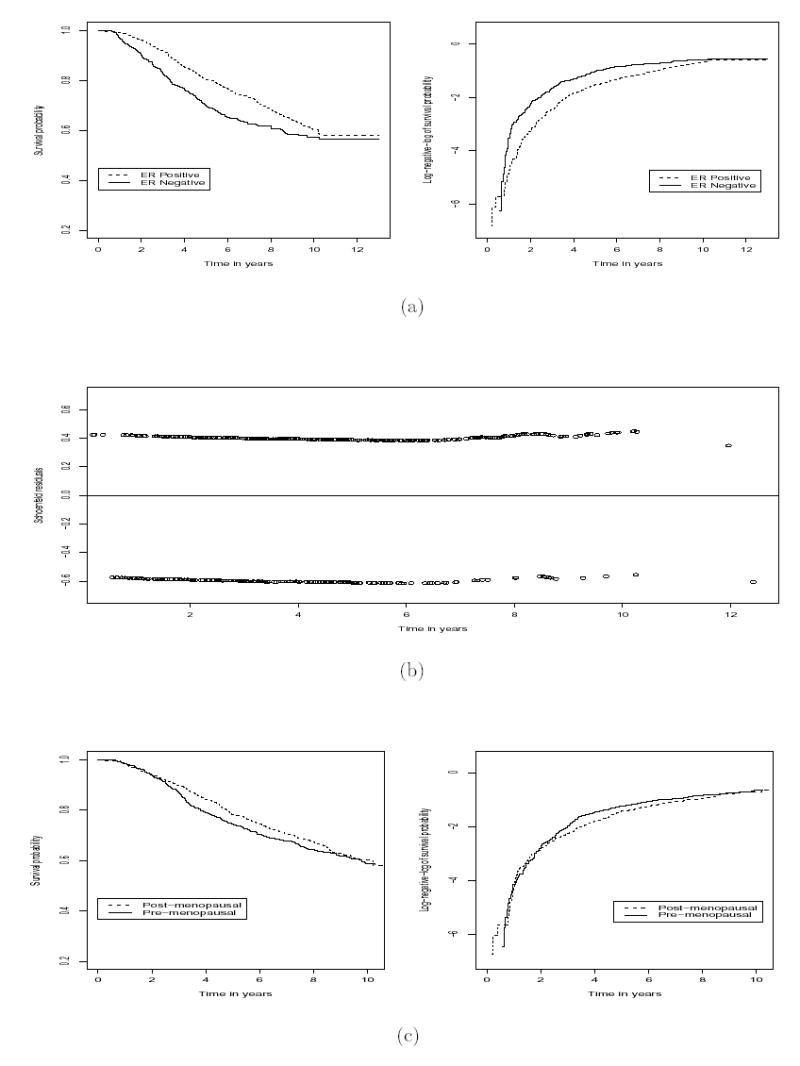
CALGB 8541: (a) Survival and log-negative-log of survival distribution by ER status estimated by Kaplan-Meier method. (b) Schoenfeld (1982) residuals of ER status obtained from SAS proc phreg. Residuals above and below the horizontal line are for ER-positive and ER-negative patients, respectively. (c) Estimated survival and log-negative-log of survival distribution by menopausal status.

Many approaches have been advocated for assessing the relevance of the proportional hazards assumption; e.g., Fleming and Harrington (1991, sec. 4.5), Klein and Moeschberger (1997, secs. 9.2 and 11.4), and Therneau and Grambsch (2000, Chap. 6) discuss procedures such as including a function of time [e.g., log(t)] as a time-dependent covariate in the linear predictor, plots of and smoothing of Schoenfeld (1982) residuals (e.g., based on assumed time-dependent coefficient models), partitioning the time axis into disjoint intervals in each of which the model is fitted and the results compared, and so on. There is also a large literature on formal testing approaches (e.g., Pettitt and Bin Daud, 1990; Gray, 1994). O'Sullivan (1988), Hastie and Tibshirani (1990), Zucker and Karr (1990) and authors referenced therein discussed estimation in the proportional hazards model with nonparametric covariate or time-varying coefficient effects using smoothing splines in a penalized partial likelihood approach. Gray (1992, 1994) proposed spline-based tests for parametric covariate and time effects using fixed knot splines. Numerical results suggest that the tests perform well in moderate samples, but they require the smoothing parameter to be finely tuned according to the true alternative to achieve good power properties, which may not be realistic in practice.

Indeed, there is a rich literature in which nonparametric smoothing is used as the basis for testing and diagnostics in general statistical models. Cox et al. (1988) was among the first major works in this spirit; these authors developed a locally most powerful test for parametric effects in generalized spline regression models for independent normal data by taking a Bayesian view; see Liu and Wang (2004) and Liu, Meiring, and Wang (2005) for related work and extensions. Barry (1993) and Eubank et al. (1995) developed tests for additivity of nonparametric regression functions. Guo (2002) proposed likelihood ratio testing for nonparametric functions in smoothing spline ANOVA models. Gu (2004) discussed model diagnostics for such models using Kullback-Leibler geometry.

A theme of some of this work (e.g., Guo, 2002) is to exploit explicitly the connection between random effects models and smoothing splines; Ruppert, Wand, and Carroll (2003) provide a comprehensive overview of this connection. Using these ideas, Zhang and Lin (2003) proposed a penalized likelihood approach to deriving a score test for nonparametric covariate effects in generalized additive mixed effects models, based on regarding the inverse of the smoothing parameter as a variance component. The test has low degrees of freedom and, moreover, does not require fitting of the model under the alternative, which can be computationally intensive; it also enjoys valid size and good power properties in practice. Score tests have also been applied with great success to testing homogeneity of odds ratio in sparse 2 × 2 tables by Liang and Self (1985), to testing variance components in generalized linear mixed models by Lin (1997), and to testing homogeneity in a frailty proportional hazards model by Commenges and Andersen (1995) and Gray (1998).

The success of these procedures leads us in this paper to adapt the Zhang and Lin (2003) strategy to testing departures from proportional hazards, described in Section 2. Another problem of interest is testing for covariate effects in the Cox model; i.e., testing whether the functional form representing the effect of a covariate on survival time is a fixed-degree polynomial. We show that this can be addressed similarly in Section 3. We report empirical results for both tests in Section 4, and apply them to the data from CALGB 8541 in Section 5.

2 Score Test for Proportional Hazards

For subject i, i = 1, …, n, let T_i and C_i be survival and censoring times; X_i a (p × 1) vector of covariates; and S_i a scalar covariate of interest, where T_i and C_i are independent given ( $X_i^T,$S_i)^T. The observed data are V_i = min(T_i, C_i), Δ_i = I (T_i ≤C_i). Cox's proportional hazards model (Cox, 1972) for the hazard function given ( $X_i^T$, S_i)^T, λ(t|X_i, S_i), is

$$\lambda (t | X_i,S_i)={\lambda }_0(t)exp\{X_i^T\beta +S_i\theta \},\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\beta (p\times 1),$$ (1)

with regression coefficients β and θ (scalar) and unspecified baseline hazard λ₀(t). Model (1) implies for any X that λ(t|X, S_k)=λ(t|X, S_l) = exp{(S_k – S_l)θ} independent of time, the “proportional hazards” assumption, which, as suggested by Cox (1972), may be evaluated by including in the model a time-dependent covariate that is the product of S and a function of time and testing if its coefficient is different from 0. Rather than adopting a known such function, which limits the scope of possible departures from (1), we consider the alternative

$$\lambda (t | X_i,S_i)={\lambda }_0(t)exp\{X_i^T\beta +S_i\gamma (t)\},$$ (2)

where γ(·) is an arbitrary smooth function of time. Because γ(·) is infinite-dimensional, we follow Gray (1994) and estimate it along with β by maximizing the penalized partial log-likelihood

$$l_p\{\beta ,\gamma (\cdot ),\eta \}=l_c\{\beta ,\gamma (\cdot )\}-(\eta /2)\int {\{{\gamma }^{(m)}(t)\}}^{2}dt,$$ (3)

where l_c {β, γ(·)} is the usual Cox partial log-likelihood, m ≥ 1 is an integer, and η > 0 is a smoothing parameter controlling the roughness of γ(t) and the goodness-of-fit of the model.

Following Zhang and Lin (2003), we consider the smoothing spline representation of γ(t) of Kimeldorf and Wahba (1971). Denote by $t^0={(t_1^0,\dots ,t_r^0)}^T$ the (r × 1) vector of ordered, distinct V_i’s with Δ_i = 1 (i.e., all failure times) and by γ the corresponding vector of γ(t) evaluated at each element of t⁰. Without loss of generality, assume $0<t_1^0<\cdots <t_r^0<1.$ As l_c {β, γ(·)} depends on γ(·) only through γ, it is well-known that maximizing l_p{β, γ(·), η} leads to a natural smoothing spline of order m for the estimator for γ(t), expressed as

$$\gamma (t)=\sum _{k=1}^m{\delta }_k{\phi }_k(t)+\sum _{l=1}^r{a}_{l}R(t,t_l^0),$$ (4)

where {δ_k} and {a_l} are constants; ${\{{\phi }_k(t)\}}_{k=1}^m$ is a basis for the space of (m – 1)th order polynomials; and $R(t,s)={\int }_0^1{(t-u)}_{+}^{m-1}{(s-u)}_{+}^{m-1}/{\{(m-1)!\}}^{2}du,$ where x₊ = x if x > 0 and 0 otherwise. The function R(t, s) is easily calculated, especially for small m; e.g., when m = 1, R(t, s) = min(t, s). Writing δ = (δ₁, . . . , δ_m)^T and a = (a_1, . . . , a_r )^T , ∫{γ ^(m)(t)}²dt = a^T ∑a and γ = Hδ + ∑a, where

$$H=\left[\begin{array}{ccc}{\phi }_1(t_1^0)& \cdots & {\phi }_m(t_1^0)\\ {\phi }_1(t_2^0)& \cdots & {\phi }_m(t_2^0)\\ ⋮& \ddots & ⋮\\ {\phi }_1(t_r^0)& \cdots & {\phi }_m(t_r^0)\end{array}\right],\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\Sigma }=\mathrm{\hspace{0.17em} }\left[\begin{array}{ccc}R(t_1^0,t_1^0)& \cdots & R(t_1^0,t_r^0)\\ R(t_2^0,t_1^0)& \cdots & R(t_2^0,t_r^0)\\ ⋮& \ddots & ⋮\\ R(t_r^0,t_1^0)& \cdots & R(t_r^0,t_r^0)\end{array}\right];$$ (5)

e.g., in the case m = 1,

$$H={\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right]}_{r\times 1},\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\Sigma }=\left[\begin{array}{ccccc}{t}_1^0& t_1^0& t_1^0& \cdots & t_1^0\\ t_1^0& t_2^0& t_2^0& \cdots & t_2^0\\ t_1^0& t_2^0& t_3^0& \cdots & t_3^0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ t_1^0& t_2^0& t_3^0& \cdots & t_r^0\end{array}\right]$$

Thus, writing τ = 1/η, (3) may be represented as l_p(β, δ, τ, a) = l_c{β,γ(δ, a)} − a^T ∑a/(2τ), where the Cox partial log-likelihood is now

$$l_c\{\beta ,\gamma (\delta ,a)\}=\sum _{i=1}^n{\mathrm{\Delta }}_i\left[X_i^T\beta +S_i{c}_i^T(H\delta +\mathrm{\Sigma }a)-log\left\{\sum _{j\in R(t_i^0)}exp\{X_j^T\beta +S_j{c}_i^T(H\delta +\mathrm{\Sigma }a)\}\right\}\right].$$ (6)

Here, R(t) is the risk set at time t; and c_i is an (r × 1) vector of all 0’s except when Δ_i = 1, when it has a 1 in the position corresponding to the failure time $t_i^0$ for subject i.

Note then that exp{l_p(β, δ, τ, a)} = exp[ l_c{β, γ(δ, a)}] exp{−a^T ∑a/(2τ )}, which has the form of the partial likelihood, depending on a, times a N (0, τ ∑⁻¹) density up to a constant. This suggests viewing a as a N (0, τ ∑⁻¹) random vector, with τ as a “variance component,” and exp[ l_c{β, γ(δ, a)}] as a partial likelihood “conditional” on a. Under this perspective, a plays a role similar to that of a frailty, so we follow the spirit of Commenges and Andersen (1995, sec. 2) and consider a “marginal partial likelihood” for (β^T , δ^T , τ)^T as

$$L(\beta ,\delta ,\tau )=exp\{l(\beta ,\delta ,\tau )\}=\int exp[l_c\{\beta ,\gamma (\delta ,a)\}]{\varphi }_r(a;0,\tau {\mathrm{\Sigma }}^{-1})da,$$ (7)

where ϕ_r is the density of an r-dimensional normal distribution.

The natural spline representation of γ(t) in (4) implies that γ(t) is an (m − 1)th order polynomial if and only if a = 0, which in (7) is equivalent to H₀ : τ = 0. Thus, testing whether γ(t) is a constant as in (1) versus the broad alternative (2) may be addressed by setting m = 1 and testing H₀. Following Zhang and Lin (2003), we propose a “score-type” test for H₀ as follows. Making the transformation u = τ ^−1/2∑^1/2a in (7), and using L’Hôpital’s rule, algebra shows that the “score" for τ based on (7) takes the form

$${\frac{\partial l(\beta ,\delta ,\tau )}{\partial \tau }|}_{\widehat{\beta },\widehat{\delta },\tau =0}={\frac{1}{2}\left\{\frac{\partial l_c\{\beta ,\gamma (\delta ,0)\}}{\partial {\gamma }^T}\mathrm{\Sigma }\frac{\partial l_c\{\beta ,\gamma (\delta ,0)\}}{\partial \gamma }+\text{tr}\left(\frac{{\partial }^2{l}_c\{\beta ,\gamma (\delta ,0)\}}{\partial \gamma \partial {\gamma }^T}\mathrm{\Sigma }\right)\right\}|}_{\widehat{\beta },\widehat{\delta }},$$ (8)

where $\widehat{\beta },\widehat{\delta }$ are the usual maximum partial likelihood estimators for β, δ found by maximizing (6) under H₀ : a = 0. The second term on the right hand side of (8) is approximately the negative of the mean of the first (see the Appendix), and our simulations show that variation in the second term is negligible relative to that in the first. We thus follow Zhang and Lin (2003), who considered an analogous test of covariate effects in generalized additive mixed models, and base our test statistic on the first term in (8). Letting S_γ {β, γ(δ, 0)} = ∂/∂γ[ l_c{β, γ(δ, 0)}], we consider basing the test on

$$U_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}=S_{\gamma }^T\{\widehat{\beta },\gamma (\widehat{\delta },0)\}\mathrm{\Sigma }{S}_{\gamma }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}.$$ (9)

In the Appendix, we argue heuristically that, for n large, n⁻¹U_τ $\{\widehat{\beta },\gamma (\widehat{\delta },0)\}$ can be expected to behave like a certain weighted sum of independent ${\chi }_1^2$ random variables whose distribution can be approximated by that of a scaled chi-square using the Satterthwaite method. Based on this heuristic reasoning, for matrices $\widehat{W}$ and $\widehat{V}$ given in the Appendix, we propose the test statistic $T=U_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}/K,$where $K=\text{tr}\left\{{(\widehat{W}\widehat{V}{\widehat{W}}^T\mathrm{\Sigma })}^2\right\}/\text{tr}(\widehat{W}\widehat{V}{\widehat{W}}^T\mathrm{\Sigma }),$ and we reject H₀ at nominal level α if T > ${\chi }_{\nu ,1-\alpha }^2,$ where ${\chi }_{\nu ,1-\alpha }^2$ is the 100(1 − α)th percentile of the ${\chi }_{\nu }^2$ distribution, with $\nu ={\{\text{tr}(\widehat{W}\widehat{V}{\widehat{W}}^T\mathrm{\Sigma })\}}^2/\text{tr}\{{(\widehat{W}\widehat{V}{\widehat{W}}^T\mathrm{\Sigma })}^2\}.$ In Section 4.1, we demonstrate empirically that this test has reliable operating characteristics.

3 Score Test for Covariate Effects

We use the same setup as in Section 2 but consider instead the general alternative

$$\lambda (t | X_i,S_i)={\lambda }_0(t)\mathrm{\hspace{0.17em} }exp\{X_i^T\beta +\gamma (S_i)\},$$

where the unknown function γ(·) represents the effect of covariate S_i on outcome. We wish to test the functional form of γ(·); specifically, the null hypothesis is H₀ : γ(·) is an (m−1)th order polynomial. Two cases of special interest are that of m = 1, corresponding to a test for no effect, and m = 2, the situation of a linear effect of S_i.

Using the same smoothing spline technique employed in Section 2, we estimate γ(·) along with β by maximizing the penalized partial log-likelihood

$$l_p\{\beta ,\gamma (\cdot ),\eta \}=l_c(\beta ,\gamma (\cdot )\}-(\eta /2)\int {\{{\gamma }^{(m)}(s)\}}^{2}ds.$$ (10)

Denote by $s^0={(s_1^0,\dots ,s_r^0)}^T$ the (r × 1) vector of ordered, distinct S_i's and by γ the corresponding vector of γ(s) evaluated at each element of s⁰. Again assuming $0<s_1^0<\cdots <s_r^0<1$, maximizing l_p{β, γ(·),η} leads to a natural smoothing spline of order m for the estimator for γ(s). We again have ∫{γ^(m)(s)}²ds = a^T ∑a and γ = H δ + ∑a, where H (r × m) has (l, k) element ${\phi }_k(s_l^0),$ and ∑ is positive definite with (l, l′) element $R(s_l^0,s_{l^{\prime }}^0).$ Equation (10) can be represented as l_p{β, δ τ, a} = l_c{β, γ (δ, a)} − a^T∑ a/(2τ), where the Cox partial log-likelihood now has a different form given by

$$l_c\{\beta ,\gamma (\delta ,a)\}=\sum _{i=1}^n{\mathrm{\Delta }}_i\left[X_i^T\beta +c_i^T(H\delta +\mathrm{\Sigma }a)-log\left\{\sum _{j\in R(V_i)}exp\{X_j^T\beta +c_j^T(H\delta +\mathrm{\Sigma }a)\}\right\}\right].$$

Here c_i is an (r × 1) vector of all 0's with the exception of a 1 in the position corresponding to the covariate value $s_i^0$ for subject i.

Taking the same perspective as in Section 2, treating a as N (0, τ ∑⁻¹) and obtaining the "marginal partial likelihood," we may cast the null hypothesis as H₀ : τ = 0 and derive a similar test statistic. For reasons of identifiability, the first component of δ must be absorbed into the baseline hazard so that only the remaining components need be estimated under H₀. By arguments analogous to those in the Appendix, for m > 1, the test of H₀ is the same as in Section 2, with the only difference being in the form of l_c. A special case is testing for no effect of S_i. The null model is $\lambda (t | X_i,S_i)={\lambda }_0(t)\mathrm{\hspace{0.17em} }exp(X_i^T\beta ),$ so m = 1, and, because δ has only one component, it is absorbed into λ₀(t), which is equivalent to δ = 0, so that we only need to estimate β under H₀. The "score" for τ takes the same form as in (8) except now the expression is evaluated at ( $\widehat{\beta }$, 0, 0), so that the test is based on $U_{\tau }\{\widehat{\beta },\gamma (0,0)\}=S_{\gamma }^T\{\widehat{\beta },\gamma (0,0)\}\mathrm{\Sigma }{S}_{\gamma }\{\widehat{\beta },\gamma (0,0)\}.$By similar arguments, the test statistic is as in Section 2, where now the matrix $\widehat{W}\widehat{V}{\widehat{W}}^T$ is defined differently; see the Appendix.

4 Simulation Evidence

4.1 Test for Proportional Hazards

We carried out simulations to evaluate the performance of the proposed test for the proportional hazards assumption. The cases we considered are similar to those in Gray (1994).

To evaluate size, failure times were generated under the null model λ(t|S_i) = λ₀(t) exp{S_iδ₀}, i = 1, 2, . . . ,n, with λ₀(t) = 1 and δ₀ = 0, 1, or 2. Values of S_i were equally spaced on the interval (0, 1) with equal numbers of subjects having each distinct S_i value; e.g., if “number of distinct covariate values” is 2, then half had S_i = 0 and half S_i = 1. We considered two censoring distributions: the unit exponential and a uniform distribution on (0, 2); the former gave minimum (maximum) censoring probabilities of 0.12 (0.50), which were 0.07 (0.43) for the latter. Sample sizes were n = 100 and 200, and N = 2000 samples were generated for each scenario. Empirical size was estimated as the proportion of N samples rejected by the nominal 0.05-level test. Table 1 shows that empirical size is very close to the nominal level for all scenarios, in most cases within sampling error. Larger differences from the nominal level are seen under unit exponential censoring, as censoring probability in that case is higher.

Table 1.

Empirical sizes of the proposed spline-based nominal 0.05-level tests for proportional hazards of S_i in the model λ(t|S_i) = λ₀(t) exp{S_iδ₀}, i = 1, 2, . . . , n, expressed as percent. λ₀(t) = 1; values of S_i are equally spaced on the interval (0, 1) with an equal number of subjects having each distinct S_i value. Results are based on 2000 simulations for each scenario. The binomial (N = 2000, p = 0.05) standard error for the entries is 0.49%.

		True value of δ0
		n = 100			n = 200
Censoring distribution	Number of distinct covariate Si values	0	1	2	0	1	2
Unit exponential	2	5.10	5.70	6.10	6.20	5.40	4.95
	4	5.70	6.05	5.10	5.60	4.65	4.85
	10	5.70	6.30	5.95	6.40	5.00	5.30
	20	5.60	6.35	5.85	6.40	4.75	4.85
	50	5.90	6.20	6.00	6.45	4.65	4.60
	100	5.70	6.60	5.95	6.35	4.65	4.60
	200				6.40	4.90	4.70
Uniform (0,2)	2	5.20	4.45	5.20	5.60	4.60	4.35
	4	5.55	4.55	4.55	4.85	4.75	4.25
	10	5.35	4.10	5.20	5.00	4.45	4.75
	20	5.30	4.30	4.50	4.95	4.95	4.75
	50	5.35	4.15	4.90	4.85	4.70	4.60
	100	5.40	4.30	4.90	4.80	4.65	4.45
	200				4.80	4.85	4.55

To evaluate power, failure times were generated under the alternative λ(t|S_i) = λ₀(t) exp{S_iγ(t)}, i = 1, 2, . . . ,n. Here, S_i was a single binary covariate defining two groups of equal size, and the true log hazard ratios for the two groups, γ(t), were given by

$$\begin{array}{llll}\text{Curve\hspace{0.28em}}1:\hfill & \gamma (t)=log\left\{.75t\right\}\hfill & \text{Curve\hspace{0.28em}}4:\hfill & \gamma (t)=log\left\{{(t-.75)}^2\right\}\hfill \\ \text{Curve\hspace{0.28em}}2:\hfill & \gamma (t)=log\{2/(1+5t)\}\hfill & \text{Curve\hspace{0.28em}}5:\hfill & \gamma (t)=log\left\{e^{I(t\ge 1)}\right\}=I(t\ge 1)\hfill \\ \text{Curve\hspace{0.28em}}3:\hfill & \gamma (t)=log\left\{e^t\right\}=t\hfill & \hfill & \hfill \end{array}$$

where I(·) is the indicator function; these curves are shown in Figure 2a. Curves 1, 2, and 4 were considered by Gray (1994) with the same setup of failure and censoring times. Again λ₀(t) = 1; thus, failure times when S_i = 0 were unit exponential and those for S_i = 1 were generated via the appropriate transformation to obtain the required hazard ratio. Censoring was uniform on (0, 2), yielding censoring probability 0.43 for S_i = 0. For each scenario, N = 1000 samples of size n = 200 were generated, and empirical power was estimated as the proportion of samples rejected by the nominal 0:05-level test. For comparison, we also computed power for several 1-degree-of-freedom score tests as follows. Under the model λ(t|S_i) = λ₀(t) exp{β₀S_i+β₁S_ig(t)}, the “linear”, “quadratic”, “log” and “optimal” tests are the score tests of H₀ : β₁ = 0 with g(t) = t, t², log(t), and γ(t), respectively. The “optimal” test is based on the true γ(·) so provides an upper bound on the power of the other tests.

Figure 2.

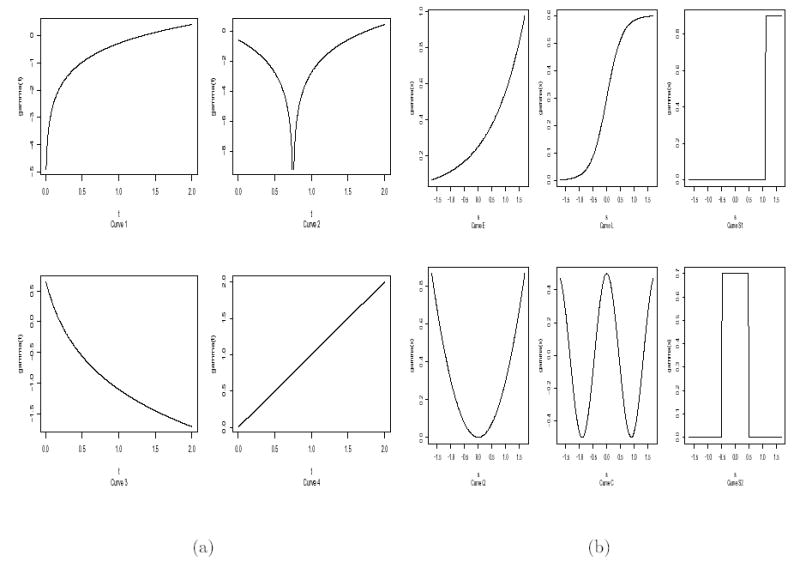
(a) Curves used in the simulation evaluating power of the tests for proportional hazards. Curve 1: γ(t) = log{.75t}; curve 2: γ(t) = log{2/(1 + 5t)}; curve 3: γ(t) = log{e^t} = t; curve 4: γ(t) = log{(t – .75)²}; curve 5: γ(t) = log{e^I(t≥1)} = I(t ≥1). (b) Curves used in the simulation evaluating powers of the tests for covariate effects. Curve E: γ(s) = .25 exp{.8s}; curve L: γ(s) = .6 exp{3.5s}/(1 + exp{3.5s}); curve S1: γ(s) = .9I(s > 1.1); curve Q: γ(s) = .3s²; curve C: γ(s) = .5 cos(3.5s); curve S2: γ(s) = .7I(|s| < .5).

Results are given in Table 2. For smooth monotone alternatives (curves 1, 2, and 3), power of our test is very close to that of the “optimal” test. These alternatives are either linear or close to linear, hence the “linear” test also provides good power for detecting them. For non-monotone (curve 4) or non-smooth (curve 5) alternatives, power is inferior to that of the “optimal” test. However, for curve 4 our test out-performs all others, while for curve 5 has power close to those of the “linear” and “quadratic” and much higher than that of the “log” test. That our test has better power for monotone than nonmonotone alternatives may be a consequence of the fact that it tends to be dominated by linear combinations of the S_γ given by the eigenvectors corresponding to the largest eigenvalues of ∑, where the eigenvector corresponding to the largest eigenvalue is positive and monotone; see the Appendix. Also, as our test is based on the penalized partial likelihood, it considers broader alternatives than any specific parametric test. The penalty function penalizes non-smooth alternatives more than smooth ones, hence power is focused toward smoother alternatives. Overall, then, the proposed test provides some power for non-monotone or non-smooth alternatives, while providing good power for very smooth alternatives, so is “robust” in the sense of providing good protection against a wide variety of alternatives.

Table 2.

Estimated powers of nominal 0.05-level tests for proportional hazards of S_i in the model λ(t|S_i) = λ₀(t) exp{S_iγ(t)}, i = 1, 2, . . . , n, expressed as percent. λ₀(t) = 1; S_i is a single binary covariate defining two groups of equal size; γ(t) is the true alternative; n = 200. Censoring distribution is uniform on (0, 2). Tests and alternatives are as described in the text. Results are based on 1000 simulations for each scenario. The maximum binomial (N = 1000, p = 0:50) standard error for the entries is 1:58%.

	Alternative
Test	Curve 1	Curve 2	Curve 3	Curve 4	Curve 5
Spline-based	90.8	78.4	47.6	37.3	28.6
Linear	90.5	78.8	51.4	10.1	30.4
Quadratic	79.7	65.3	50.0	13.8	36.6
Log	93.3	75.8	37.4	32.1	15.5
Optimal	93.3	81.7	51.4	91.5	46.6

Gray (1992, 1994) discussed methods based on fixed-knot splines in the Cox model setting. In particular, Gray (1994) presents three statistics for testing proportional hazards: a penalized quadratic score statistics Q_s, a penalized likelihood ratio statistic Q_l, and a Wald-type statistic Q_w. Examining the results Gray (1994, Sec. 4) presents for his tests and the results we obtained for our test, we find that our test and Gray’s Q_s and Q_l tests have empirical sizes close to nominal, whereas the empirical size of Gray’s Q_w test deviates markedly from the nominal level in certain cases. For smooth monotone alternatives, power of our test is comparable to that of Gray’s. For non-monotone or non-smooth alternatives, his test can have better power if an optimal degrees-of-freedom (df) is used; however, this optimal df often needs to be tuned based on the unknown true alternative, which is unrealistic in practice, while our test requires no such tuning. Our tests are essentially the limit of Gray’s when the smoothing parameter → ∞, or, equivalently, the df of his test → 0, if the distinct failure times are used to construct his basis functions. This gives some insight into why the performance of our test can be similar to his low-df test.

4.2 Test for Covariate Effects

Simulations were also carried out to evaluate performance of the proposed score test for covariate effects. We considered testing both for no covariate effect and for a linear effect.

For size, failure times were generated under the null model λ(t|S_i) = λ₀(t) (no covariate effect) and λ(t|S_i) = λ₀(t) exp{S_i}(linear effect), i = 1, 2, . . . , n, with S_i values the same as in the size simulation in Section 4.1, and λ₀(t) = 1. Censoring was unit exponential and uniform on (0, 1.5); censoring probabilities were 0.50 for testing no effect and between 0.27 and 0.50 for testing the linear effect for the former and 0.518 for no effect and between 0.24 and 0.52 for the linear effect for the latter. Sample sizes were n = 100 and 200, with N = 2000 samples generated for each scenario. From Table 3, the sizes of the proposed test are again very close to the nominal 0.05-level for testing both no and linear effect. In fact, with n = 200, all sizes are within the binomial standard error (0.49%) of the nominal level.

Table 3.

Empirical sizes of the proposed spline-based nominal 0.05-level tests for covariate effects of S_i in the model λ(t|S_i) = λ₀(t) (no effect) and λ(t|S_i) = λ₀(t) exp{S_i} (linear effect), i = 1, 2, . . . , n, expressed as percent. λ₀(t) = 1; values of S_i are as in Table 1. Results are based on 2000 simulations for each scenario. The binomial (N = 2000, p = 0.05) standard error for the entries is 0:49%.

		Null hypothesis
		n = 100		n = 200
Censoring distribution	Number of distinct covariate values	No effect	Linear effect	No effect	Linear effect
Unit exponential	4	5.25	4.65	5.10	4.90
	10	5.20	4.35	5.00	4.60
	20	5.15	4.60	5.05	4.50
	50	5.05	4.45	4.95	4.60
	100	5.15	4.25	5.00	4.80
	200			4.95	4.70
Uniform (0,1.5)	4	4.90	4.80	4.50	4.65
	10	5.30	5.15	5.10	5.05
	20	5.00	5.50	4.60	4.90
	50	5.05	5.60	4.50	4.95
	100	5.00	5.70	4.70	4.95
	200			4.70	4.85

For the power simulation, we used the same setup as in the simulation study of Gray (1994). Failure times were generated under the alternative λ(t|S_i) = λ₀(t) exp{γ(S_i)}, i = 1, 2, . . . , n, where n = 200, and we were interested in testing H₀ : γ(·) = 0 and H₀ : γ(·) is a linear function, respectively. The following six curves for γ(·) were used for both cases:

$$\begin{array}{llll}\text{E\hspace{0.28em}}(\text{exponential}):\hfill & \gamma (s)=.25\mathrm{\hspace{0.17em} }exp\left\{.8s\right\}\hfill & \text{Q\hspace{0.28em}}(\text{quadratic}):\hfill & \gamma (s)=.3s^2\hfill \\ \text{L\hspace{0.28em}}(\text{logistic}):\hfill & \gamma (s)=.6\mathrm{\hspace{0.17em} }exp\left\{3.5s\right\}/(1+exp\{3.5s\})\hfill & \text{C\hspace{0.28em}}(\text{cosine}):\hfill & \gamma (s)=.5cos(3.5s)\hfill \\ \text{S1\hspace{0.28em}}(\text{step\hspace{0.28em}}1):\hfill & \gamma (s)=.9I(s>1.1)\hfill & \text{S2\hspace{0.28em}}(\text{step\hspace{0.28em}}2):\hfill & \gamma (s)=.7I(| s |<.5).\hfill \end{array}$$

Plots of these curves are given in Figure 2b. The S_i values were equally spaced on [−1.719, 1.719] with step 0.0173 (hence standardized to have mean 0 and variance 1). Censoring times were uniform on (0, 1.5), and N = 1000 simulation runs were performed for each scenario.

For testing no effect, we also calculated empirical powers of the usual 1-, 2-, and 3-degree-of-freedom score tests based on adding linear, quadratic, and cubic terms to the null model. For example, the cubic test is the score test of H₀ : β₁ = β₂ = β₃ = 0 in the model $\lambda (t | S_i)={\lambda }_0(t)exp\{{\beta }_1{S}_i+{\beta }_2{S}_i^2+{\beta }_3{S}_i^3\}.$ Similarly, for testing a linear effect, empirical powers of the usual 1- and 2-degree-of-freedom score tests based on adding quadratic and cubic terms to the null model were computed; e.g., the cubic test is the score test of H₀ : β₂ = β₃ = 0 in the model $\lambda (t | S_i)={\lambda }_0(t)exp\{{\beta }_1{S}_i+{\beta }_2{S}_i^2+{\beta }_3{S}_i^3\}.$ In both cases, the optimal test is the 1-degree-of-freedom score test for the true alternative, thus providing an upper bound on power. For testing no effect, this is the score test of H₀ : β = 0 in the model λ(t|S_i) = λ₀(t) exp{βγ(S_i)}; for a linear effect, this is the score test of H₀ : β₂ = 0 in the model λ (t|S_i) = λ₀(t) exp{β₁S_i + β₂γ(S_i)}, where γ(·) is the true curve generating the data.

Power simulation results are given in Table 4. For testing no effect, under smooth monotone alternatives (E, L) the proposed test provides good power that is close to that of the optimal test. Results are similar for the linear test because these alternatives are close to linear. For the 2-step alternative (S1), our test is better than the linear and is close to the quadratic and the cubic. For the other three alternatives, which are non-monotone (Q, C) and non-smooth (S2), our test provides some power and is better than the linear but not as good as the other tests. Note that no test except the optimal has good power for alternative (C) because of the special shape of the curve. For testing linear effect, alternatives (E, L) are close to linear so none of the tests have good power for detecting them. Our test has better power than the quadratic and the cubic for the other four alternatives except for alternative (Q) for which the quadratic is the optimal test; even in that case the proposed test has power very close to the that of the optimal. The spline test generally has better power for testing linear effect than for testing no effect, because higher order (m = 2) smoothing splines are used for testing linear effect, in contrast to that m = 1 for testing no effect. Therefore we have better approximation to the nonparametric function when testing linear effect, consequently increasing the power of the test. Again, because the proposed test is based on the penalized partial likelihood, power of the proposed test is focused toward smoother alternatives. Overall, for testing covariate effects, the proposed test provides good protection against very general alternatives.

Table 4.

Estimated powers of nominal 0.05-level tests for covariate effects of S_i in the model λ(t|S_i) = λ₀(t) exp{γ(Si)}, i = 1, 2, . . . , n, expressed as percent. λ₀(t) = 1; values of S_i are equally spaced on the interval [−1.719, 1.719] with step 0.0173; γ(S_i) is the true alternative; n = 200. Censoring distribution is uniform on (0, 1.5). Tests and alternatives are as described in the text. Results are based on 1000 simulations for each scenario. The maximum binomial (N = 1000, p = 0.50) standard error for the entries is 1.58%.

		Alternative
Null hypothesis	Test	E	L	S1	Q	C	S2
No effect	Spline-based	74.0	72.4	73.8	23.1	5.8	16.2
	Linear	74.4	71.5	68.9	4.5	4.3	4.2
	Quadratic	71.5	60.4	84.1	73.6	5.9	44.7
	Cubic	67.2	55.5	84.1	67.7	6.2	38.5
	Optimal	81.6	74.2	96.3	81.7	92.0	93.7
Linear effect	Spline-based	12.8	4.9	56.0	80.7	7.7	65.4
	Quadratic	13.7	4.9	54.0	81.7	6.9	58.5
	Cubic	12.0	7.5	54.0	73.7	6.7	46.4
	Optimal	14.2	10.5	78.3	81.7	91.9	93.8

Comparison of our results to those in Section 3 of Gray (1994) shows a similar pattern as discussed in the last paragraph of Section 4.1, so the comments there apply here as well.

5 Application to CALGB 8541

We apply the proposed score tests to the data from CALGB 8541. Data on 1479 eligible patients were available to us after long-term follow-up.

As discussed in Section 1, the proportional hazards assumption for the binary variable Estrogen Receptor (ER) status is suspect. Among the 1437 patients who had known ER status, 917 were censored (63.8%). A proportional hazards fit of time-to-death on ER gives an estimated hazard ratio of 0.768 with a p-value of 0.003. Application of the proposed testing procedure confirms the observations in Figure 1ab, yielding a p-value of < 0.001. The “linear”, “quadratic,” and “log” tests also give p-values significant at level 0.05. Thus, modification of the model is required to achieve valid inferences. As the hazard ratio appears fairly constant within the time interval [1, 8), we may fit a piecewise constant hazard ratio model with three pieces: [0, 1), [1, 8), and [8, ∞). Such a fit gives a significant (level 0.05) p-value for non-proportional hazards on ER (p = 0.003). At nominal level 0.05, the effect of ER is significant on the interval [0, 1) (hazard ratio = 0.263; p = 0.004) and [1, 8) (hazard ratio = 0.747; p = 0.003) but not significant on the interval [8, ∞) (hazard ratio = 1.589; p = 0.137), another indication that the hazards are not proportional.

Another covariate of interest is menopausal status (0=pre-, 1=post-menopausal), abbreviated “meno.” All 1479 patients had known meno, of which 947 were censored (64.0%). A proportional hazards fit of time-to-death on meno gives an estimated hazard ratio of 0.921 with a p-value of 0.347, which is not significant at level 0.05. Figure 1c shows survival and log-negative-log of survival curves by meno for 638 pre-menopausal and 841 post-menopausal patients and is similar to those for ER in Figure 1a; the pattern of Schoenfeld (1982) residuals (not shown) is also similar to that in Figure 1b. Hence, the proportional hazards assumption on meno is suspect, and the proposed test yields a p-value of 0.011, while the “linear”, “quadratic” and “log” tests have a p-value of 0.032, 0.023, and 0.175, respectively. Had we used the “log” test, we would have not rejected the null hypothesis at level 0.05.

To get a better understanding of the effect of meno, we again consider a piecewise constant hazard ratio model. The hazard ratio shows a dramatic change on the time interval [2, 3.5) but otherwise appears fairly constant, hence we fit such a model with three pieces: [0, 2), [2, 3.5), and [3.5, ∞), which yields a significant (level 0.05) p-value for non-proportional hazards on meno (p = 0.002). At level 0.05, the effect of meno is not significant on the interval [0, 2) (hazard ratio = 0.975; p = 0.905) and [3.5, ∞) (hazard ratio = 1.148; p = 0.240) but significant on the interval [2, 3.5) (hazard ratio = 0.549; p = 0.001). A biological rationale for why menopause should be associated with benefit only in the range of 2 to 3.5 years post-treatment and not afterward is not obvious. One possibility is that chemotherapy leads to suppression of ovarian function, so that any advantage conferred by menopause is lost after a time. Such an effect would be expected only among ER-positive women, whose tumors are more likely to grow in a high-estrogen environment; however, the results of fitting the piecewise model separately by ER group are entirely similar, suggesting an association with some other phenomenon. This result demonstrates the value of testing the proportional hazards assumption for revealing important relationships that deserve more detailed study.

Other covariates available to us include treatment, size of breast cancer tumor (cm), number of histologically positive lymph nodes found. As noted in Section 1, the difference in survival between the two groups treated with a moderate or high dose was not significant at level 0.05 using the log-rank test (p = 0.814). We hence grouped these two doses as one treatment, so along with the low dose, we have a binary treatment covariate. After controlling for other covariates, the smoothing spline-based test of proportional hazards of ER gives a significant (level 0.05) p-value of 0.012. Again we can fit a piecewise constant proportional hazards model on ER assuming proportional hazards on other covariates. The flexibility of the approach allows other tests to be performed. For example, the test of the null hypothesis that the effect of “number of positive lymph nodes” is linear gives a p-value of 0.457, which is not significant at level 0.05, suggesting a linear fit is adequate.

6 Discussion

We have developed score tests for the proportional hazards assumption and for covariate effects in Cox models based on the penalized partial likelihood and natural smoothing spline representation. The tests achieve size close to nominal and provide good power for general alternatives, particularly for smooth monotone alternatives. An advantage of the tests is their simplicity; the test statistic is easy to calculate, requiring only a fit of the null model. This may be accomplished by maximizing the usual partial likelihood under the null hypothesis using existing software such as SAS proc phreg or S-PLUS/R function coxph().

If the proportional hazards assumption is rejected, one can include in the predictor interactions between functions of time and covariates; a difficulty is identifying the form of the interaction. Plotting and smoothing Schoenfeld residuals may provide some insight. Alternatively one may use a stratified proportional hazards model. An advantage is that no particular form of interaction need be assumed. A disadvantage is the resulting inability to examine the effects of the stratifying covariates.

Appendix

Heuristic Argument for Test in Section 2

Throughout, assume that H₀ : τ = 0 is true, and let (β_0, δ₀) be the true values of (β, δ). Define S_β{β, γ(δ, 0)} = ∂/∂β[l_c{β, γ(δ, 0)}], the usual partial likelihood score for β. Let I_ββ{β, γ(δ, 0)} = −∂²/∂β∂β^T[l_c{β, γ(δ, 0)}], the usual observed partial information for β; I_βγ{β, γ(δ, 0)} = −∂²/∂β∂γ^T[l_c{β, γ(δ, 0)}], (p×r); I_γβ{β, γ(δ, 0)} = −∂²/∂γ∂β^T[l_c{β, γ(δ, 0)}]; and I_γγ{β, γ(δ, 0)} = −∂²/∂γ∂γ^T[l_c{β, γ(δ, 0)}], (r × r), a diagonal matrix.

Because $(\widehat{\beta },\widehat{\delta })$ are the maximum partial likelihood estimators under H₀, it follows that ${[S_{\beta }^T\{\widehat{\beta },\gamma (\widehat{\delta },0)\},\hspace{0.17em}{S}_{\gamma }^T\{\widehat{\beta },\gamma (\widehat{\delta },0)\}H]}^T=0,$ where H is defined in (5); this, along with standard expansions, yields

$$\begin{array}{l}{S}_{\gamma }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}=\left\{(0_{r\times p}{\mathcal{I}}_r)-(I_{\gamma \beta }^{*}\mathrm{\hspace{0.17em} }{I}_{\gamma \gamma }^{*}H){\left[\begin{array}{ll}{I}_{\beta \beta }^{*}\hfill & I_{\beta \gamma }^{*}H\hfill \\ H^T{I}_{\gamma \beta }^{*}\hfill & H^T{I}_{\gamma \gamma }^{*}H\hfill \end{array}\right]}^{-1}\left[\begin{array}{ll}{\mathcal{I}}_p\hfill & 0_{p\times r}\hfill \\ 0_{m\times p}\hfill & H^T\hfill \end{array}\right]\right\}\\ \times \left(\begin{array}{c}{S}_{\beta }\{{\beta }_0,\gamma ({\delta }_0,0)\}\\ S_{\gamma }\{{\beta }_0,\gamma ({\delta }_0,0)\}\end{array}\right)=W^{*}\left(\begin{array}{c}{S}_{\beta 0}\\ S_{\gamma 0}\end{array}\right)=\{(0_{r\times p}{\mathcal{I}}_r)-C^{*}\}\left(\begin{array}{c}{S}_{\beta 0}\\ S_{\gamma 0}\end{array}\right),\end{array}$$ (A.1)

say, where $I_{\beta \beta }^{*}$= I_ββ{β*, γ(δ*,0)} and similarly for $I_{\beta \gamma }^{*},I_{\gamma \beta }^{*}\hspace{0.17em}\text{and\hspace{0.17em}}{I}_{\gamma \gamma }^{*}$; β* is between β₀ and $\widehat{\beta }$; δ* is between δ₀ and $\widehat{\delta }$; and ${\mathcal{I}}_k$ is the (k × k) identity matrix,. Thus, writing $S_0={(S_{\beta 0}^T,S_{\gamma 0}^T)}^T$,

$$\begin{array}{l}{n}^{-1}{U}_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}=n^{-1}{S}_0^T{W}^{*T}\mathrm{\Sigma }{W}^{*}{S}_0\\ \approx n^{-1}{S}_0^T{W}^T\mathrm{\Sigma }W{S}_0=n^{-1}{S}_0^T{\{(0_{r\times p}{\mathcal{I}}_r)-C\}}^T\mathrm{\Sigma }\{(0_{r\times p}{\mathcal{I}}_r)-C\}{S}_0,\end{array}$$ (A.2)

where ∑ is defined in (5), U_τ is defined in (9), and W and C are W* and C* with (β*, δ*) replaced by (β₀, δ₀). Now W has the form of a “projection matrix,” where C takes account of estimation of β and δ. In other testing problems, Zhang and Lin (2003) observed that the effect of terms analogous to C on operating characteristics of the test is negligible for large n. This gives us reason to conjecture the further approximation $n^{-1}{U}_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}\approx n^{-1}{S}_{\gamma 0}^T\mathrm{\Sigma }{S}_{\gamma 0}$.

Replacing ∑ by its spectral decomposition, we may write this as

$$n^{-1}{U}_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}\approx n^{-1}{S}_{\gamma 0}^{T}P\mathrm{\Lambda }{P}^T{S}_{\gamma 0}=\sum _{i=1}^r{\lambda }_i{(n^{-1/2}{P}_i^T{S}_{\gamma 0})}^2,$$ (A.3)

where λ_i are the ordered eigenvalues of ∑ (diagonal elements of Λ) and P_i the corresponding eigenvectors (orthogonal columns of P ). As noted by Zhang and Lin (2003, app. A), the matrix ∑ has a special structure such that the λ_i decay rapidly to zero. Moreover, it has been observed empirically that the elements of P₁ are positive and monotone increasing; the first several elements of P₂ are positive and increasing, with the remaining elements decreasing and negative; and the elements of P₃ behave similarly, except that the final few increase and are positive. It is straightforward to observe that S_γ{β, γ(δ, 0)} (r × 1) evaluated at $(\widehat{\beta },\widehat{\delta })$ is the vector of Schoenfeld (1982) residuals corresponding to the covariates S_i. Thus, from Cox (1975) and Schoenfeld (1982), writing V_γγ = I_γγ{β₀, γ(δ₀, 0)}, the components of S_γ0 have mean zero and are uncorrelated, with the variance of the kth component equal to the kth diagonal element of V_γγ. Thus, roughly speaking, $P_1^T{S}_{\gamma 0}$ is a positively-weighted mean-zero sum of the components of S_γ0 (over the failure times), so that, suitably rewritten and under regularity conditions $n^{-1/2}{P}_1^T{S}_{\gamma 0}$ should behave like a normal random variable with variance $v_1\approx n^{-1}{P}_1^T{V}_{\gamma \gamma }{P}_1$. Similarly, $n^{-1/2}{P}_2^T{S}_{\gamma 0}$ behaves like a contrast of early and later components of S_γ0, and we expect it to be approximately N (0, v₂). By this reasoning, the next few terms of the form $n^{-1/2}{P}_k^T{S}_{\gamma 0},k>2,$should also behave like normally distributed contrasts. Thus, we may write (A.3) as

$$n^{-1}{U}_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}\approx \sum _{i=1}^r{\lambda }_i{v}_i^{1/2}{(n^{-1/2}{P}_i^T{S}_{\gamma 0}{v}_i^{-1/2})}^2.$$ (A.4)

Although (A.4) is a sum over the r failure times, which increases with n, because the λ_i decay rapidly to zero, we conjecture that the behavior of (A.4) is dominated by the first few summands, so that (A.4) may be viewed approximately as a finite, weighted sum of ${\chi }_1^2$ random variables. Via a standard singular value decomposition, this finite sum can be written as a finite, weighted sum of independent ${\chi }_1^2$ random variables; thus, we thus suggest using Satterthwaite's method to approximate its large-sample distribution. Treating n^−1/2P^TS_γ0 as approximately normal as above, it is straightforward to show that the mean and variance of $n^{-1}{S}_{\gamma 0}^{T}P\mathrm{\Lambda }{P}^T{S}_{\gamma 0}$ are e = n⁻¹tr(V_{γ γ}∑) and I_{τ τ} = 2n⁻²tr{(V_γγ∑)²} Matching these moments to those of a scaled chi-square, $k{\chi }_v^2$ say, we obtain k= I_{τ τ}/(2e) and ν = 2e²/I_{τ τ.} This suggests comparing the test statistic $T=n^{-1}{U}_{\tau }\{\widehat{\beta },\gamma (\widehat{\delta },0)\}/k$ to critical values from a ${\chi }_v^2$ distribution; in practice, one would substitute $(\widehat{\beta },\widehat{\delta })$ in V_γγ to form k and v.

Although the effect of C may be negligible asymptotically, results of Zhang and Lin (2003) for finite samples suggest that it may be advantageous to take into account the effects of estimating model parameters under H₀. Following their strategy, we consider a “small-sample correction” for these effects. The correction is based the approximation $n^{-1}{S}_{\gamma 0}\mathrm{\Sigma }{n}^{-1}{S}_{\gamma 0}\approx S_0^T{W}^T\mathrm{\Sigma }W\hspace{0.17em}{S}_0$, which follows from (A.2) and (A.3). This suggests applying Satterthwaite’s method to $n^{-1}{S}_0^T{W}^T\mathrm{\Sigma }W\hspace{0.17em}{S}_0$ instead. Defining V_βγ = I_βγ {β₀; γ(δ₀; 0)}, V_ββ = I_ββ {β₀; γ(δ₀; 0)}, and

$$V=\left[\begin{array}{cc}{V}_{\beta \beta }& V_{\beta \gamma }\\ V_{\gamma \beta }& V_{\gamma \gamma }\end{array}\right],$$

an argument analogous to the one above shows that the appropriate mean and variance are e = n⁻¹tr(WVW^T ∑) and I_ττ = 2n⁻²tr{(WVW^T ∑)²}. Letting $\widehat{W}$ and $\widehat{V}$ be W and V with $(\widehat{\beta },\widehat{\delta })$ substituted, we obtain the test procedure given at the end of Section 2. In fact,

$$WV{W}^T=V_{\gamma \gamma }-(V_{\gamma \beta }{V}_{\gamma \gamma }H){\left[\begin{array}{cc}{V}_{\beta \beta }& V_{\beta \gamma }H\\ H^T{V}_{\gamma \beta }& H^T{V}_{\gamma \gamma }H\end{array}\right]}^{-1}\left(\begin{array}{c}{V}_{\beta \gamma }\\ H^T{V}_{\gamma \gamma }\end{array}\right),$$

which reduces to WVW^T = V_γγ − V_γγH (H^TV_γγH)⁻¹H^TV_γγ when S_i is the only covariate in the model (so only δ is estimated), demonstrating how estimation of the parameters is taken into account. In the case of testing for no covariate effect in Section 3 with m = 1, it may be shown that $WV{M}^T=V_{\gamma \gamma }-V_{\gamma \beta }{V}_{\beta \beta }^{-1}{V}_{\beta \gamma }$. If S_i is the only covariate in the model, WVW^T = V_γγ.