Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1999 Apr 13;96(8):4414–4419. doi: 10.1073/pnas.96.8.4414

Intermediate spectra and photocycle kinetics of the Asp96 → Asn mutant bacteriorhodopsin determined by singular value decomposition with self-modeling

László Zimányi *,†, Ágnes Kulcsár *, Janos K Lanyi ‡, Donald F Sears Jr §, Jack Saltiel §,
PMCID: PMC16346  PMID: 10200276

Abstract

Singular value decomposition with self-modeling is applied to resolve the intermediate spectra and kinetics of the Asp96 → Asn mutant bacteriorhodopsin. The search for the difference spectra of the intermediates is performed in eigenvector space on the stoichiometric plane. The analysis of data at pH values ranging from 4 to 8 and temperatures between 5 and 25°C reveals significant, early partial recovery of the initial state after photoexcitation. The derived spectra are not biased by assumed photocycles. The intermediate spectra derived in the initial step differ from spectra determined in prior analyses, which results in intermediate concentrations with improved stoichiometric properties. Increasingly more accurate photocycles follow with increasing assumed complexity, of which parallel models are favored, consistent with recent, independent experimental evidence.

Application of singular value decomposition with self-modeling (SVD-SM) to the determination of the pure intermediate spectra and kinetics of a simulated bacteriorhodopsin photocycle was demonstrated in the preceding paper (1). SVD-SM is applied to real data in this paper. Bacteriorhodopsin (BR) functions as a light-driven proton pump in the cell membrane of Halobacterium salinarium. Photoexcitation results in isomerization of the all-trans-retinal chromophore and sequential structural changes of the protein moiety (photocycle), characterized in the visible range by the distinct spectra of the metastable intermediates J, K, L, M, N, and O. At the end of the photocycle, the initial state, BR, recovers. The net result is the transfer of a proton from the cytoplasmic to the extracellular side (for reviews, see refs. 2 and 3). The proton pathway in the extracellular half channel involves the Schiff base (covalently bonding the retinal and Lys-216), Asp-85, and the region of Glu-204 and Glu-194, with water molecules also playing an important role (4–13). In the cytoplasmic half channel, Asp-96 is the proton donor to the transiently deprotonated Schiff base (4, 5, 14, 15). Replacement of Asp-96 with asparagine decelerates this step by orders of magnitude, effectively preventing the accumulation of any intermediate after M, while retaining the proton pumping activity (16–18). The photocycle of the Asp96 → Asn (D96N) mutant has been the target of a number of investigations because of its relative simplicity (19–22).

Understanding the proton pump requires knowledge of the exact time evolution of the intermediates. This information can be obtained from multichannel kinetic absorption spectroscopy once the spectra of the pure intermediates are determined. Determination of the spectra is difficult, however, because of the strong temporal and spectral overlap of the intermediates. Global model fits are designed to yield the spectra and the kinetics simultaneously, but experience, in the case of BR, shows that optimization routines are plagued by local minima that hamper selection among assumed kinetics models (23).

Similar problems are general in spectroscopy and have been addressed by various algebraic methods. Principal component analysis (PCA) and SVD each yield the effective rank of the data matrix and an orthonormal spectral basis set of eigenvectors and corresponding combination coefficients with the number of significant components being equal to the effective rank (24, 25). Self-modeling originally was applied to search for the pure component absorption or fluorescence spectra in the eigenvector space by using the non-negativity criterion (26, 27). The known photophysics of a system provide additional criteria, such as the global Stern-Volmer plot optimization criterion, that allow selection of unique pure component spectra from the range permitted by the non-negativity constraint (28).

Multichannel spectroscopy on BR provides a data matrix that consists of difference rather than absolute spectra, and, because the exact fraction of the photoexcited BR molecules is unknown, these spectra cannot be converted directly to absolute spectra. PCA-SM procedures do not apply because difference spectra cannot be normalized. Instead, the search for the pure component spectra can be based on stoichiometric constraints. The details of the algorithm were elaborated and tested on simulated data resembling data measured on D96N BR (1). Treatment of noise-free simulated data recovered the known input intermediate spectra and kinetics almost exactly. With realistic noise included, the output spectra and kinetics are sufficiently close to the input spectra and kinetics to allow the fit of the same photocycle scheme as the input scheme, with very good rate constant recovery. The method reveals the correct stoichiometric behavior of the intermediates and detects the early partial recovery of the initial state included in the input kinetics.

The analysis of real data measured on D96N BR is described here. SVD confirms that these data reflect a problem with four major intermediates (K, L, M1, and M2). Determination of the stoichiometric plane (SP) reveals an early partial recovery of BR. Self-modeling is performed in the eigenvector space of data representing the first half of the photocycle, a rank-three matrix, and yields the spectra of the K, L, and M1 intermediates. The M2 spectrum is determined from direct addition of an appropriately scaled BR spectrum to one of the late difference spectra. Comparison of the pure intermediate spectra with published spectra obtained from the same data set with different methods (19, 20) reveals deceptively small shifts and amplitude changes, which result in substantial differences in the kinetics. Earlier reported deviations of the sums of the intermediate concentrations from the expected value of unity are diminished. The simplest photocycle schemes that fit these kinetics with acceptable accuracy, with the expected Arrhenius and pH dependencies of the rate constants, are either branched at the level of M substates, in accordance with the pH dependence of proton release, or involve two independent pathways. However, only the latter, parallel scheme seems to be consistent with new, photostationary state experimental evidence for the accumulation of pure M intermediate in this mutant (29).

MATERIALS AND METHODS

Experimental data analyzed in this work are described in previous publications (19, 20, 22). D96N site-directed mutant bacteriorhodopsin was purified as purple membranes as described (30). The membranes were embedded in polyacrylamide gel and were soaked in 100 mM NaCl and 50 mM phosphate buffer plus 2 mM, 200 μM, 20 μM, 2 μM, and no NaN3 at pH 8, 7, 6, 5, and 4, respectively. Azide was added to catalyze the reprotonation of the Schiff base in the absence of the proton donor group, D96. The samples were light-adapted throughout the measurements. Time resolved difference spectra were measured at 5, 15, and 25°C after excitation with a nitrogen laser-pumped dye laser, using the gated optical multichannel analyzer setup described earlier (31). Thirty-five spectra were collected in each experiment, with logarithmically equidistant time base from 70 ns to 420 ms. The gate pulse width of the detector was increased in five steps with increasing delay while the number of averaged scans per spectrum was decreased. Nevertheless, the noise content of the early spectra is higher than that of the late spectra. The potential actinic effect of the measuring light was ruled out by taking similar data at decreased light intensity. This resulted in no change of the difference spectra apart from a higher noise content. Data analysis was performed by using the method described in the previous article (1). The program, rate2.1, written by Géza Groma (Biological Research Center, Szeged, Hungary), was used to fit photocycle schemes to the kinetics of the intermediates.

RESULTS

Singular Value Decomposition.

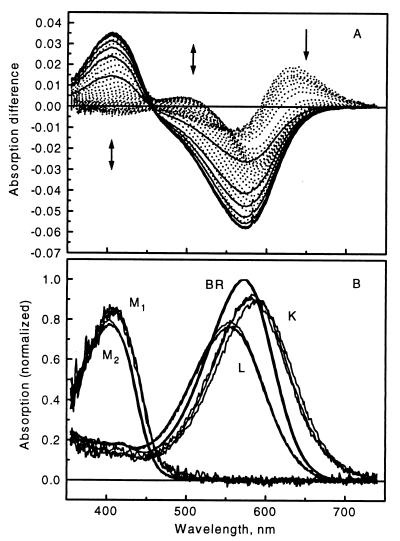
The effective ranks of the data matrices consisting of the time-resolved difference spectra measured on D96N BR at pH 8 at 5, 15, and 25°C and at pH 4, 5, 6, and 7 at 25°C were determined by SVD combined with the rotation procedure of Henry and Hofrichter (25). The latter is necessary to “pull” forward later eigenvectors based on their higher temporal autocorrelation and to reject earlier eigenvectors with higher singular values but no correlation. Experience with simulated data shows that the false ordering of some of the SVD components is a result of the uneven noise distribution in the data matrix and is removed by the rotation method (1). The rank of the data matrices is 4 at all temperatures and pH values studied. Accordingly, the original data matrices were reconstructed and thereby noise-filtered by using the first four SVD eigenvectors. For example, the SVD-reconstituted input difference spectra at pH 8, 5°C are shown in Fig. 1A. The absorption spectrum of light adapted D96N BR is shown in Fig. 1B.

Figure 1.

Figure 1

Open in a new tab

(A) Time-resolved difference spectra measured in the 70-ns to 420-ms time domain on D96N mutant BR at pH 8, 5°C. The arrows indicate the time evolution of the signal, and the solid curves correspond to the final decay phase. The spectra are reconstructed from the first 4 SVD components. (B) Intermediate absorption spectra of D96N BR calculated for 5, 15, and 25°C at pH 8.

The intermediate spectra were independently determined from the pH 8 data at the three temperatures. Pure M absorption spectra (later designated as M2) were obtained by adding appropriately scaled BR absorption spectra to difference spectra 33, 30, and 30 at 5, 15, and 25°C, respectively, each of which consists of essentially pure M2, by requiring the best possible baseline in the >540-nm wavelength range.

The Stoichiometric Planes.

The number of difference spectra before the recovery of the BR initial state was determined from truncated data matrices (λ > 540 nm), as in the case of the simulated data (1). The stoichiometric plane equation holds for the combination coefficients (elements of matrix A) up to the onset of the recovery of BR (Eq. 7 in ref. 1), where r is the rank of the data matrix, m is the total number of difference spectra, l is the number of spectra before BR recovery, Aj,k is the combination coefficient of the jth difference spectrum relative to the kth SVD spectral eigenvector, and Rk is the parameters of the stoichiometric plane as determined by least squares fit:

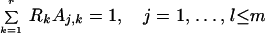graphic file with name M1.gif 1

Table 1 shows the standard deviation from unity of the left-hand side of Eq. 1 fitted to the first 11, 12, … , 35 spectral points. At all three temperatures, there is an early increase of this deviation followed by a plateau before the final increase. The number of spectra before the early recovery is estimated as 23, 19, and 17 at 5, 15, and 25°C, respectively, and the parameters of the stoichiometric planes were calculated accordingly.

Table 1.

The stoichiometric planes and BR recovery

No. of spectra Standard deviation
5°C 15°C 25°C
11 0.0114 0.0231 0.0230
12 0.0151 0.0220 0.0222
13 0.0179 0.0211 0.0223
14 0.0198 0.0205 0.0217
15 0.0202 0.0200 0.0229
16 0.0200 0.0194 0.0233
17 0.0198 0.0190 0.0237
18 0.0193 0.0185 0.0248
19 0.0194 0.0184 0.0265
20 0.0189 0.0186 0.0280
21 0.0189 0.0197 0.0318
22 0.0187 0.0214 0.0347
23 0.0186 0.0248 0.0362
24 0.0200 0.0288 0.0376
25 0.0224 0.0312 0.0380
26 0.0269 0.0343 0.0382
27 0.0312 0.0375 0.0382
28 0.0348 0.0392 0.0382
29 0.0371 0.0408 0.0377
30 0.0389 0.0427 0.0376
31 0.0427 0.0452 0.0380
32 0.0461 0.0523 0.0446
33 0.0538 0.0667 0.0581
34 0.0683 0.0878 0.0849
35 0.1038 0.1347 0.1389
Open in a new tab

Standard deviation of the stoichiometric plane fits to the combination coefficients of the first 11, 12, … , 35 difference spectra. Data are for the D96N mutant bacteriorhodopsin at 5, 15, and 25°C, pH 8. Bold numbers represent the last points considered to be on the plane and the points at which the main phase of BR recovery starts. 

Self-Modeling.

The photocycling ratio (PCR) was calculated as the average of two slightly different values obtained by two different methods. First, PCR was varied as a parameter until the best stoichiometric plane was found in the least squares sense that fits the first 23, 19, and 17 truncated difference spectra at 5, 15, and 25°C, respectively, augmented with the varied PCR scaled negative of the BR absorption spectrum, in the spectral range of 540–740 nm. Second, the dot product was calculated between the spectral eigenvectors from the SVD treatment of the first 23, 19, and 17 truncated difference spectra, respectively, and the BR absorption spectrum in the 540- to 740-nm interval, yielding its combination coefficients. Because, for any valid difference spectrum that belongs on the SP Eq. 1 holds, so it does for the −BR spectrum (equivalent in the above spectral range to M − BR) times the true PCR. Therefore, on introducing the combination coefficients of −BR into Eq. 1, we obtain 1/PCR. The PCRs, estimated in this way, are 20.2, 20.2, and 21.4% at 5, 15, and 25°C, respectively. Previous analyses of the same data (19, 20, 22) assumed that the photocycling ratios, determined from the pure M − BR difference spectra that are expected in the millisecond time range, apply also to earlier times of the photocycle. It was noted in those papers that this assumption might not be valid. The present stoichiometric analysis establishes that it is not.

The LM lines were determined as for the simulated data by using the truncated data set (1). Systematic search on the SP along directions representing decreasing amounts of K leads to points on this line by monitoring the red spectral region, where no contribution by either M or L absorption is expected. This region, identified as 697–740 nm, yields pure intermediate spectra that give the most accurate fit to the mixture input spectra. Once the truncated difference spectra on the LM line were found, the spectral region was extended to the full range of 355–740 nm, and the spectrum of M, designated here as M1, was obtained at each temperature. The extended spectra are calculated as linear combinations of the SVD eigenvectors over the full spectral range, with coefficients obtained by least squares fit of the truncated spectra with the truncated eigenvectors. The L spectrum was found by proceeding away from M along the LM line as for the simulated data until the average absorption of L in the 355- to 410-nm interval matched that of BR.

The KL line at each temperature was identified as the line connecting the vertex of L with the average of the points on the SP corresponding to the first three measured spectra. The vertex of pure K − BR was found along this line by monitoring the integral of the resulting spectrum in the 600- to 740-nm interval. This parameter was estimated by extrapolation to time zero by using the first four measured spectra and the pure L − BR spectrum (1).

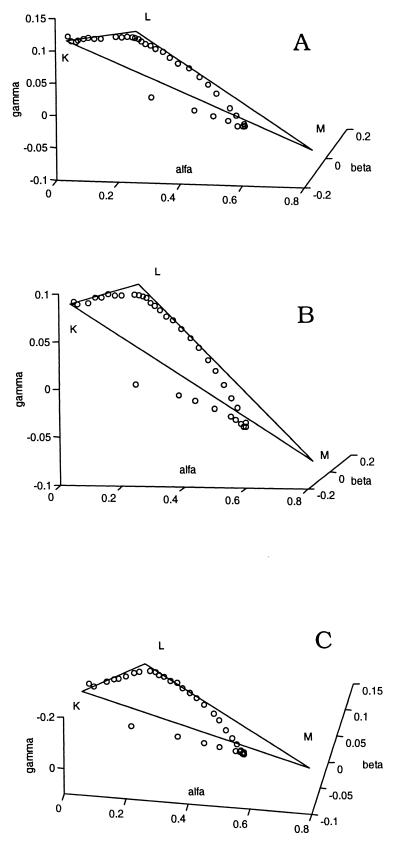
The adherence of the early spectral points to the stoichiometric planes and the biphasic deviations from these thereafter, as the BR initial state recovers, are visible when the entire spectral matrices are represented in the combination coefficient space of the first three SVD components only (Fig. 2). The intermediate spectra are plotted in Fig. 1B together with the M2 spectra, determined from the late difference spectra, and the BR spectrum. The M2 spectrum is slightly blue-shifted relative to the M1 spectrum and has a somewhat smaller amplitude. This is in accord with the small, but clearly visible, gradual blue shift of the positive band in the 400-nm region of the difference spectra in the millisecond range. There is no systematic temperature dependence of the intermediate spectra.

Figure 2.

Figure 2

Open in a new tab

Three-dimensional plots of the combination coefficients for D96N BR at 5°C (A), 15°C (B), and 25°C (C), pH 8, in the rank-3 approximation of the entire data matrix. Open circles, combination coefficients for the measured difference spectra. The stoichiometric plane is represented as the K, L, M1 triangle.

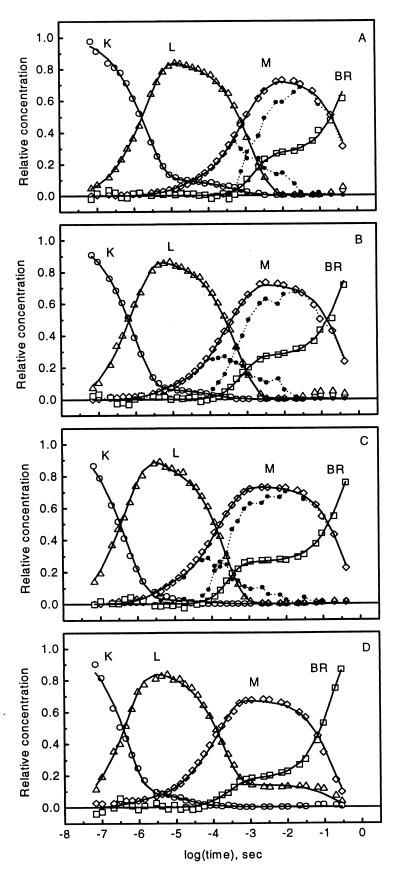
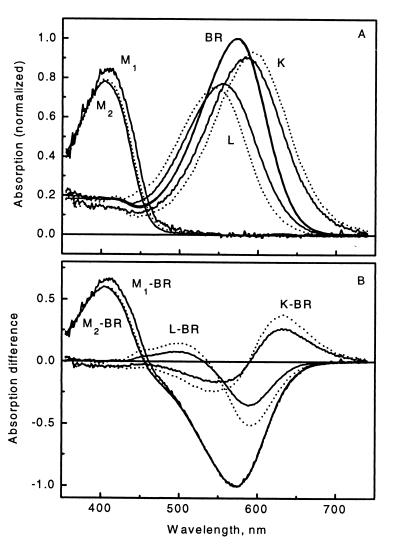
The K, L, M1, and M2 minus BR difference spectra were used in a nonnegative least squares fit to all 35 measured difference spectra at the three temperatures. The resulting intermediate concentrations are plotted in Fig. 3 A, B, and C (symbols). The kinetics of BR were obtained as 1 minus the sum of the intermediate concentrations and show the early recovery phase, as already indicated by the fit of the stoichiometric plane. Before this phase, the deviations of the intermediate sums from unity, as reflected in the deviation of the BR concentration from zero, are improved relative to earlier analyses (see Fig. 6 in ref. 20). Performance of SM on the SP ensures optimized stoichiometric behavior by the intermediates. Especially noticeable in their early evolution is that M1 appears later in this analysis. The spectra obtained in this work are compared with those from ref. 19 in Fig. 4. For this comparison, the spectra computed at the three temperatures were averaged to yield single difference (Fig. 4A) and absorption (Fig. 4B) spectral sets. A consequence of the earlier underestimation of the PCR is that the new K − BR and L − BR difference spectra are smaller in amplitude. This results in a shift of the respective absolute spectra so that the new K and L absorption bands are closer to the absorption band of the BR initial state.

Figure 3.

Figure 3

Open in a new tab

Intermediate kinetics of D96N BR calculated for pH 8, 5°C (A), 15°C (B), and 25°C (C) and pH 4, 25°C (D). Symbols represent intermediate concentrations. In A–C, the spectrally distinct M1 and M2 are represented by black dots and dotted lines. Solid lines, fits by model 1 (see text).

Figure 4.

Figure 4

Open in a new tab

Intermediate absorption spectra (A) and difference spectra (B) obtained by SVD-SM (solid lines) compared with those obtained by the grid search method from the same experimental data by Zimányi and Lanyi (19) (dashed lines). In ref. 19, only one M spectrum was resolved, which corresponds to M2 in the present work.

The averaged intermediate difference spectra were used in a non-negative least squares fit to difference spectra measured at 25°C, pH 4, 5, 6, and 7. The resulting intermediate concentrations at pH 4 are shown in Fig. 3D (symbols). They confirm the earlier-reported (22) extended lifetime of L, which gradually diminishes with increasing pH (data not shown). New is the biphasic BR recovery which is as conspicuous in the pH 4–7 range as at pH 8. The sum of the intermediate concentrations before the BR recovery (reflected in the deviation of [BR] from zero) is improved relative to earlier analysis of the same data.

Fitting of Photocycle Models to the Intermediate Kinetics.

It is tempting to seek reaction schemes that fit the kinetics in Fig. 3. A thorough analysis was not pursued because the low time resolution (35 points in time) of these data hampers identification of a unique, best model. However, the spectra of the pure intermediates determined here should be useful in fitting high time resolution single wavelength experimental data.

With the four intermediates, a minimal sequential model should consist of the K ⇌ L ⇌ M1 ⇌ M2 → BR reactions. Here, M1 → M2 corresponds to the reprotonation switch coupled to extracellular proton release so that its reverse is negligible at pH 8 (32), and M2 → BR coincides with the azide catalyzed cytoplasmic proton uptake (16, 18, 33). This model is obviously not capable of reproducing the biphasic BR recovery. Its simplest modification is a sequential BR-like form (BR1, spectrally indistinguishable from BR) between M2 and BR. With reversible reactions, except for the final BR1 → BR, this model can simultaneously reproduce the biphasic BR recovery and the non-negligible residual L as the pH is decreased. A second sequential L form improves the fit in the region of [M] rise, both in wild-type and in mutant BR (19, 34), and was interpreted as relaxation of the stress in the protein produced by the retinal isomerization (34). It results in a substantially better fit in the submillisecond range in the present study as well.

Based on mechanistic considerations, the M1 ⇌ M2 transition should split into two steps: the reprotonation switch and the extracellular proton release, whose pK was estimated as 5.8–6.0 from the [L]/[Mtotal] concentration ratio. There also should be a pathway to conclude the photocycle without the early proton release at pH lower than the above pK (22). These two internal steps have not yet been resolved, and their relationship is unknown. Hence, we attempted to fit the data with the following sequential, branched model to account for the low and high pH pathways:

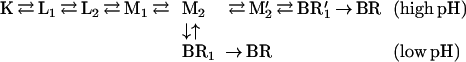graphic file with name M2.gif

The M1 → M2 and the M2 → M2′ reactions would correspond to the reprotonation switch and the (early) extracellular proton release by the terminal release group, respectively. The assumed pK = 6 of proton release was taken into account by fixing the M2 → M2′ and M2 ← M2′ rate constants. Although this model gives satisfactory fits with reasonable temperature and pH dependencies of the rates, the inclusion of the relatively fast (as compared with the recovery of BR) equilibrium between M2 and the postulated BR1 is unavoidable in both branches. This raises serious problems with the sequential schemes in view of recent experimental evidence. In the D96N/D115N double mutant (29), as well as in D96N (J.K.L., unpublished results), photostationary states are established with continuous illumination at conditions similar to our pH 8 experiments (albeit in the absence of azide). The sample can be fully converted into M whereas the fitted rate constants for the above models predict a substantial contribution by BR1.

Compatible with the photostationary accumulation of pure M is a parallel model with a rapid and a slow pathway. Good fits and meaningful temperature and pH dependencies are obtained with model 1:

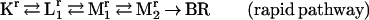graphic file with name M3.gif
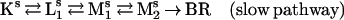graphic file with name M4.gif

In Fig. 3, solid lines show the resulting fitted kinetics at pH 8 and 4. Table 2 lists all rate constants, the ratio between the two pathways, and the χ2 parameter of the fit by model 1. The reverse of Mr1 → Mr2 is found to be negligible at all pH and temperature values, suggesting a unidirectional reaction. The contribution of the rapid pathway is 18–27%, gradually increasing with increasing pH. The photostationary accumulation of pure M can be explained by postulating a dynamic equilibrium between the rapid and slow photocycles, which would eventually deplete the rapid pathway under continuous illumination. The proton-pumping activity of the D96N mutant is probably associated with the slow pathway. This ensures an efficiency of pumping commensurable with that of the wild type because the contribution of the slow cycle under these conditions is ≈80%. The expected pH dependence of the M1 ← M2 back reaction also is attributed to this pathway, reflecting the reverse of the extracellular proton release coupled to the reprotonation switch. Some of the other rate constants also exhibit systematic pH dependencies, possibly associated with the titration of groups close to the membrane surface.

Table 2.

Logarithm of rate constants in s−1 from the fit of model 1 to the kinetics of intermediates determined by SVD-SM

pH 8, 5°C pH 8, 15°C pH 8 pH 7 pH 6 pH 5 pH 4
Kr→Lr 6.2 6.5 6.8 6.4 6.4 6.6 6.8
Kr←Lr 6.0 6.0 5.9 6.1 6.2 6.7 6.9
Lr→Mr1 4.4 4.9 5.1 4.8 4.7 5.2 6.0
Lr←Mr1 4.5 5.1 5.1 4.6 4.5 4.6 6.0
Mr1→Mr2 3.9 4.4 4.4 4.3 4.2 4.6 5.2
Mr2→BR 2.8 3.1 3.7 3.6 3.8 3.6 3.5
Ks→Ls 5.6 5.9 6.2 6.2 6.2 6.3 6.3
Ks←Ls 4.2 4.1 4.1 4.0 4.0 4.0 4.7
Ls→Ms1 2.8 3.2 3.6 3.6 3.6 3.6 3.6
Ls←Ms1 3.9 4.5 4.7 4.5 4.6 4.3 4.1
Ms1→Ms2 5.3 5.8 6.2 6.3 6.6 6.5 6.6
Ms1←Ms2 2.0 2.3 2.5 3.0 4.4 5.0 5.5
Ms2→BR 0.3 0.4 0.4 0.4 0.4 0.6 0.9
r:s 26:74 27:73 26:74 25:75 26:74 21:79 18:82
χ2(×10−2) 2.3 3.1 2.0 2.3 3.0 2.0 2.0
Open in a new tab

Output rate constants were obtained by fitting the parallel photocycle scheme, model 1, to the intermediate kinetics derived from the fit of measured difference spectra by the pure intermediate spectra from the SVD-SM analysis. Unless otherwise shown, the temperature was 25°C. 

DISCUSSION

In the preceding article (1), we introduced the method of SVD-SM to obtain pure intermediate spectra and kinetics from time-resolved multichannel absorption spectroscopic data on BR. The analysis of simulated data without noise returned the exact input data and a very good approximation of the input data with random noise included. We established that SVD-SM is capable of narrowing the range of potential solution spectra obtained earlier with a grid-search method, providing more confidence in its application to real experimental data. The method is applied here on the D96N mutant BR.

SVD of the difference spectra, measured on the D96N mutant BR, reveals that more than the three major intermediates, K, L, and M, are present. Application of the rotation procedure based on the temporal autocorrelation of the SVD kinetic vectors identified a fourth, clearly significant component. A small blue shift of the band corresponding to the M intermediate is evident in the input difference spectra, suggesting spectrally different early and late Ms, M1 and M2, consistent with published results (6). The blue shift of M2 relative to the wild-type M was attributed to the altered hydrogen bonding of the deprotonated Schiff base in the cytoplasmic direction (21). Least squares fit of the intermediate spectra, found by self-modeling, to the input difference spectra indicates small discrepancies at the very end of the photocycle: The concentrations of K and L, which had decayed to zero, appear to increase again (Fig. 3). This suggests formation of trace amounts of N and/or O. The small total accumulation of these late intermediates, ≤5% of PCR, does not allow determination of their spectra.

SVD-SM reveals a previously unnoticed early recovery phase of the initial BR state. In a former treatment of the same data, we assumed that the photocycling ratio, obtained by adding a properly normalized BR absorption spectrum to one of the late difference spectra to get a pure M spectrum (M2 in this paper), is universal. This is equivalent to the assumption that no BR recovery has taken place at the time of the difference spectrum used. One can obtain seemingly acceptable intermediate spectra in this way, but, as noted earlier, a discrepancy remains (19, 20): The sum of the intermediate concentrations deviates systematically from unity. Attempts to compensate for this discrepancy involved normalization of all concentrations (20), or the L concentration only (19), by this sum. This normalization is rendered unnecessary in the present work, in which stoichiometric constraints guide the spectral search. Optimized concentration sums naturally follow.

Model fitting to the intermediate concentrations is not expected to be decisive because of the relatively low number of difference spectra (i.e., time points) available. It is important, however, that previous models must be modified substantially to accommodate the new finding of biphasic BR recovery. The simple photocycle model used to construct simulated data (1) would describe the intermediate kinetics in D96N BR at pH 8, where because of the virtual unidirectionality of the M1 → M2 reaction, the K and L forms decay before the full accumulation of M. At lower pH, however, the simulated photocycle model is inadequate to fit the intermediate kinetics. The simplest extension is a sequential form between M and BR, which is spectrally indistinguishable from BR (designated BR1). Sequential models, which include such an intermediate, fit the data in the present work well; however, they contradict recent observations that demonstrate that 100% M intermediate can accumulate under continuous illumination in the D96N mutant (29). No quadratic term in the light-saturation curve in these experiments was found; thus, it is improbable that reexcitation of BR1 would convert it to M (L. S. Brown and J.K.L., unpublished work). Therefore, a BR-like form, in equilibrium with M, in amounts required by the above sequential models, is unlikely. Parallel models fit the present data equally well with the introduction of a rapid and a slow pathway. Assuming a dynamic equilibrium between the two pathways, the photostationary accumulation of pure M is explained by the gradual depletion of the rapid pathway. This alternative does not contradict the well established finding that, other than having a slower photocycle, D96N transports protons normally (16–18) if proton transport is linked to the slow but dominant pathway. On the basis of this fit, the spectrally distinct M forms are associated with the two pathways in the parallel model. The suggested heterogeneity and the ensuing parallel pathways are only slightly pH-dependent, unlike the reported heterogeneity in wild-type BR, arising at alkaline pH (35).

The present work validates the SVD-SM approach for the treatment of multichannel kinetic spectroscopic data. The derived, highly accurate intermediate spectra and kinetics for the D96N mutant BR are essential for the evaluation and refinement of proposed photocycle models. The previous assignment of the extracellular proton release to the M1 → M2 step is now confined to the dominant slow pathway of the parallel photocycle model. Work in progress on the SVD-SM analysis of data for the wild-type BR indicates that the early partial recovery of BR, and therefore a parallel pathway of the type suggested in this paper, is not a feature of the wild-type photocycle.

Acknowledgments

We thank Dr. G. Groma for providing the program (rate 2.1) used in the fitting of kinetic models. This work was supported by grants from the National Scientific Research Fund of Hungary (OTKA T020470) to L.Z., from the National Institutes of Health (GM 29498) and the Department of Energy (DEFG03–86ER13525) to J.K.L., and from the National Science Foundation (CHE 9612316) to J.S.

ABBREVIATIONS

BR

bacteriorhodopsin

PCA

principal component analysis

PCR

photocycling ratio

SM

self-modeling

SP

stoichiometric plane

SVD

singular value decomposition

References

  • 1.Zimányi L, Kulcsár Á, Lanyi J K, Sears D F, Jr, Saltiel J. Proc Natl Acad Sci USA. 1999;96:4408–4413. doi: 10.1073/pnas.96.8.4408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Lanyi J K. Biochim Biophys Acta. 1993;1183:241–261. doi: 10.1016/0005-2728(93)90226-6. [DOI] [PubMed] [Google Scholar]
  • 3.Ebrey T G. In: Thermodynamics of Membranes, Receptors and Channels. Jackson M, editor. Boca Raton, FL: CRC; 1993. pp. 353–387. [Google Scholar]
  • 4.Braiman M S, Mogi T, Marti T, Stern L J, Khorana H G, Rothschild K J. Biochemistry. 1988;27:8516–8520. doi: 10.1021/bi00423a002. [DOI] [PubMed] [Google Scholar]
  • 5.Butt H-J, Fendler K, Bamberg E, Tittor J, Oesterhelt D. EMBO J. 1989;8:1657–1663. doi: 10.1002/j.1460-2075.1989.tb03556.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Thorgeirsson T E, Milder S J, Miercke L J W, Betlach M C, Shand R F, Stroud R M, Kliger D S. Biochemistry. 1991;30:9133–9142. doi: 10.1021/bi00102a003. [DOI] [PubMed] [Google Scholar]
  • 7.Brown L S, Sasaki J, Kandori H, Maeda A, Needleman R, Lanyi J K. J Biol Chem. 1995;270:27122–27126. doi: 10.1074/jbc.270.45.27122. [DOI] [PubMed] [Google Scholar]
  • 8.Balashov S P, Imasheva E S, Govindjee R, Ebrey T G. Biophys J. 1996;70:473–481. doi: 10.1016/S0006-3495(96)79591-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Richter H T, Brown L S, Needleman R, Lanyi J K. Biochemistry. 1996;35:4054–4062. doi: 10.1021/bi952883q. [DOI] [PubMed] [Google Scholar]
  • 10.Balashov S P, Imasheva E S, Ebrey T G, Chen N, Menick D R, Crouch R K. Biochemistry. 1997;36:8671–8676. doi: 10.1021/bi970744y. [DOI] [PubMed] [Google Scholar]
  • 11.Dioumaev A K, Richter H T, Brown L S, Tanio M, Tuzi S, Saito H, Kimura Y, Needleman R, Lanyi J K. Biochemistry. 1998;37:2496–2506. doi: 10.1021/bi971842m. [DOI] [PubMed] [Google Scholar]
  • 12.Rammelsberg R, Huhn G, Lübben M, Gerwert K. Biochemistry. 1998;37:5001–5009. doi: 10.1021/bi971701k. [DOI] [PubMed] [Google Scholar]
  • 13.Luecke H, Richter H T, Lanyi J K. Science. 1998;280:1934–1937. doi: 10.1126/science.280.5371.1934. [DOI] [PubMed] [Google Scholar]
  • 14.Gerwert K, Hess B, Soppa J, Oesterhelt D. Proc Natl Acad Sci USA. 1989;86:4943–4947. doi: 10.1073/pnas.86.13.4943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Otto H, Marti T, Holz M, Mogi T, Lindau M, Khorana H G, Heyn M P. Proc Natl Acad Sci USA. 1989;86:9228–9232. doi: 10.1073/pnas.86.23.9228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Tittor J, Soell C, Oesterhelt D, Butt H-J, Bamberg E. EMBO J. 1989;8:3477–3482. doi: 10.1002/j.1460-2075.1989.tb08512.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Holz M, Drachev L A, Mogi T, Otto H, Kaulen A D, Heyn M P, Skulachev V P, Khorana H G. Proc Natl Acad Sci USA. 1989;86:2167–2171. doi: 10.1073/pnas.86.7.2167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Otto H, Marti T, Holz M, Mogi T, Lindau M, Khorana H G, Heyn M P. Proc Natl Acad Sci USA. 1989;86:9228–9232. doi: 10.1073/pnas.86.23.9228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Zimányi L, Lanyi J K. Biophys J. 1993;64:240–251. doi: 10.1016/S0006-3495(93)81360-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Nagle J F, Zimányi L, Lanyi J K. Biophys J. 1995;68:1490–1499. doi: 10.1016/S0006-3495(95)80321-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Zimányi L, Cao Y, Chang M, Ni B, Needleman R, Lanyi J K. Photochem Photobiol. 1992;56:1049–1055. doi: 10.1111/j.1751-1097.1992.tb09728.x. [DOI] [PubMed] [Google Scholar]
  • 22.Zimányi L, Váró G, Chang M, Ni B, Needleman R, Lanyi J K. Biochemistry. 1992;31:8535–8543. doi: 10.1021/bi00151a022. [DOI] [PubMed] [Google Scholar]
  • 23.Nagle J F. Biophys J. 1991;59:476–487. doi: 10.1016/S0006-3495(91)82241-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Warner I M, Christian G D, Davidson E R, Callis J B. Anal Chem. 1977;49:564. [Google Scholar]
  • 25.Henry E R, Hofrichter J. Methods Enzymol. 1992;210:129–192. [Google Scholar]
  • 26.Aartsma T J, Gouterman M, Jochum C, Kwiram A L, Pepich B V, Williams L D. J Am Chem Soc. 1982;104:6278–6283. [Google Scholar]
  • 27.Saltiel J, Eaker D W. J Am Chem Soc. 1984;106:7624–7626. [Google Scholar]
  • 28.Saltiel J, Sears D F, Choi J-O, Sun Y-P, Eaker D W. J Phys Chem. 1994;98:35–46. [Google Scholar]
  • 29.Brown L S, Dioumaev A K, Needleman R, Lanyi J K. Biophys J. 1998;75:1455–1465. doi: 10.1016/S0006-3495(98)74064-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Needleman R, Chang M, Ni B, Váró G, Fornes J, White S H, Lanyi J K. J Biol Chem. 1991;266:11478–11484. [PubMed] [Google Scholar]
  • 31.Zimányi L, Keszthelyi L, Lanyi J K. Biochemistry. 1989;28:5165–5172. doi: 10.1021/bi00438a038. [DOI] [PubMed] [Google Scholar]
  • 32.Váró G, Lanyi J K. Biochemistry. 1991;30:5016–5022. doi: 10.1021/bi00234a025. [DOI] [PubMed] [Google Scholar]
  • 33.Cao Y, Váró G, Chang M, Ni B, Needleman R, Lanyi J K. Biochemistry. 1991;30:10972–10979. doi: 10.1021/bi00109a023. [DOI] [PubMed] [Google Scholar]
  • 34.Gergely C, Ganea C, Groma G, Váró G. Biophys J. 1993;65:2478–2483. doi: 10.1016/S0006-3495(93)81308-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Song L, Logunov S L, Yang D, El-Sayed M A. Biophys J. 1994;67:2008–2012. doi: 10.1016/S0006-3495(94)80684-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES