Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1999 Apr 13;96(8):4420–4425. doi: 10.1073/pnas.96.8.4420

Limiting dynamics of high-frequency electromechanical transduction of outer hair cells

Gerhard Frank 1,*, Werner Hemmert 1, Anthony W Gummer 1
PMCID: PMC16347  PMID: 10200277

Abstract

High-frequency resolution is one of the salient features of peripheral sound processing in the mammalian cochlea. The sensitivity originates in the active amplification of the travelling wave on the basilar membrane by the outer hair cells (OHCs), where electrically induced mechanical action of the OHC on a cycle-by-cycle basis is believed to be the crucial component. However, it is still unclear if this electromechanical action is sufficiently fast and can produce enough force to enhance mechanical tuning up to the highest frequencies perceived by mammals. Here we show that isolated OHCs in the microchamber configuration are able to overcome fluid forces with almost constant displacement amplitude and phase up to frequencies well above their place-frequency on the basilar membrane. The high-frequency limit of the electromotility, defined as the frequency at which the amplitude drops by 3 dB from its asymptotic low-frequency value, is inversely dependent on cell length. The frequency limit is at least 79 kHz. For frequencies up to 100 kHz, the electromotile response was specified by an overdamped (Q = 0.42) second-order resonant system. This finding suggests that the limiting factor for frequencies up to 100 kHz is not the speed of the motor but damping and inertia. The isometric force produced by the OHC was constant at least up to 50 kHz, with amplitudes as high as 53 pN/mV being observed. We conclude that the electromechanical transduction process of OHCs possesses the necessary high-frequency properties to enable amplification of the travelling wave over the entire hearing range.

The discovery of electrically induced length changes of isolated outer hair cells (OHCs) (1), the so-called electromotility, provided the experimental basis for a previously proposed mechanism for the action of OHCs as putative cochlear amplifiers (2): Electrical energy from mechanoelectrical transduction in the stereocilia is converted into mechanical energy by electromechanical transduction in the cell wall. This mechanical energy, converted on a cycle-by-cycle basis, is fed back into the cochlear partition, thereby enhancing mechanoelectrical transduction. One of the most important questions concerns the frequency response of the electromotility and the mechanical force generated by the OHC (3). The frequency range of auditory signals perceived by mammals extends from several Hz to more than 100 kHz for small insect-hunting bats (4). Therefore, any mechanism proposed for amplifying mechanical signals in the cochlea, such as electromotility, must act at all frequencies in this range. Because of the capacitance of the lateral cell membrane, the OHC receptor potential, which drives the electromotility (5–8), is low-pass filtered with corner frequencies between 30 Hz for apical OHCs and 1 kHz for basal OHCs (9, 10). This electrical filtering, together with the high-frequency increase of the resistive and inertial fluid forces, is expected to cause severe attenuation of the electromotility at high frequencies in vivo. By holding the basal end of an isolated OHC in a micropipette, termed the microchamber (11), it is possible to investigate the electromotility of isolated OHCs (Fig. 1), while compensating for the high-frequency attenuation of the receptor potential by the lateral cell membrane (13). This pioneering work of Dallos and colleagues has shown that the amplitude of the electromotility remains almost unattenuated (<6 dB) for frequencies up to at least 22 kHz. On the basis of model calculations, a more recent paper from that group (14) suggested that the high-frequency response is limited by damping. By imposing a mechanical load on the cuticular plate of the OHC, the microchamber technique can be used to measure the electromechanical force produced by the OHC (15, 16). However, all published force measurements were made under quasistatic conditions (15–17) and, therefore, no information about the frequency dependence of the generated force is available. The aim of the present paper is to describe the electromechanical properties of the OHC for frequencies covering the entire hearing range. This was achieved by (i) measuring the amplitude and phase responses of the electromotility and electromechanical force up to 100 kHz; (ii) measuring the axial mechanical impedance of the cell; and (iii) deriving the damping constant and mass from the experimental data.

Figure 1.

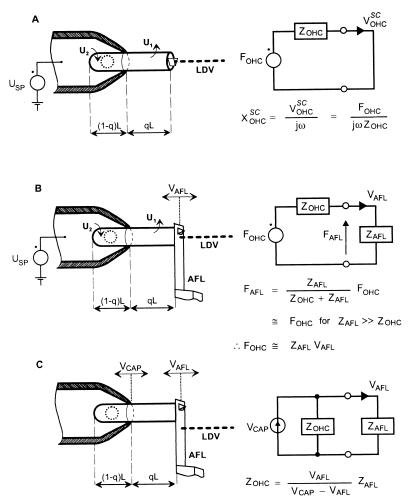
Figure 1

Open in a new tab

Experimental configurations for measuring the electromechanical properties of an isolated OHC partially inserted into a micropipette. (A) electrically induced displacement of the cuticular plate of the OHC, the so-called electromotility, XOHCSC. (B) The electromechanical force, FOHC, produced by the OHC under loaded conditions. (C) The mechanical impedance, ZOHC, of the OHC. Circuit diagrams are the electrical equivalents of OHC mechanics, with forces given as voltages and velocities as currents (12). In other words, FOHC and ZOHC are the Thévenin equivalent source force and impedance of the OHC, including extracellular fluid. For the electromotility experiment, the superscript SC is used to denote “short circuit” because, by definition, these measurements were made under unloaded conditions and we are using Thévenin equivalents. A command voltage, USP, applied to the pipette solution induces voltage drops, U1 and U2, across those sections of the cell membrane excluded from and contained in the pipette, respectively (8); U1 and U2 are of opposite phase. Voltage U1 driving the excluded length, qL, is U1 = (1 − q)⋅USP. The electromotility (A) was determined by focusing the beam of a laser Doppler vibrometer (LDV) onto the cuticular plate of the OHC and dividing the measured velocity, VOHCSC, by jω, where j = √−1 and ω is the radial stimulus frequency. FOHC (B) was determined by placing a high-impedance mechanical load, the reverse side of a lever used in atomic force microscopy (AFL), against the cuticular plate. The AFL was a silicon crystal of length 450 μm and thickness 2 μm. The velocity of the AFL, VAFL, in response to electrical induced length changes of the excluded section of the cell was measured with the LDV focused on the AFL. If the mechanical impedance of the AFL, ZAFL, is sufficiently large compared with ZOHC, so that effectively open-circuit conditions prevails, then FOHC can be approximated as ZAFL⋅VAFL. The ZOHC (C) was determined by mechanically vibrating the micropipette with a piezoelectric actuator with velocity VCAP and measuring the resulting velocity of the AFL; the impedance was calculated as ZOHC = ZAFL⋅VAFL/(VCAP − VAFL). Moreover, ZOHC can be estimated indirectly from the values of XOHCSC and FOHC determined in the electrical experiments under unloaded (A) and loaded (B) conditions, respectively: ZOHC = FOHC/jωXOHCSC.

MATERIAL AND METHODS

OHCs were nonenzymatically isolated from cochleae of adult, pigmented guinea pigs by gentle aspiration in a pipette (Eppendorf). Care and maintenance of the guinea pigs was in accordance with institutional guidelines. The cells were then transferred to a 500-μl Plexiglas chamber filled with Hanks’ balanced salt solution (Sigma, supplemented with NaHCO3 and 10 mM Hepes buffer, adjusted to 300 mOsm and pH 7.4). Only cells with a birefringent membrane, no apparent Brownian movement of their cell organelles, and the nucleus located near the basal pole were used. The basal part of the OHC (length: 32 to 108 μm) was sucked into a heat-polished glass capillary (microchamber, with inner tip-diameter of 8–10 μm), allowing calibrated electrical stimulation of the hair cell up to 100 kHz. Electrical stimuli were delivered by a custom-made voltage-clamp amplifier (phase error < 5° up to 100 kHz) and were composed of a multitone complex (58 sinusoids, 9.1 spectral points per octave) with a maximum amplitude of 2.6 mV per spectral point. Experiments were conducted at room temperature (20–22°C). The electrical corner frequency of the micropipette (fMC), which is due to the electrical access resistance and the stray capacitance of the capillary in parallel with the membrane capacitance of the electrically divided cell, was determined from measurements of the electrical input impedance of the capillary with and without the cell attached.

To measure the electromotility of the OHC (Fig. 1A), light from a laser Doppler vibrometer (LDV; Polytec 302, Waldbronn, Germany) was focused directly onto the cuticular plate to measure its velocity in response to electrical stimulation. The noise floor of the LDV decreased from 0.3 nm at 100 Hz (effective averaging time: 2 s) to 0.09 nm at 100 kHz (effective averaging time: 0.5 s). Length changes of the section of OHC projecting from the capillary (qL), due to the voltage drop across the cell membrane outside the micropipette (U1), were calculated off-line from velocity data. qL was adjusted under video control by varying the pressure inside the micropipette with a micrometer-driven syringe. q ranged from 0.32 to 0.81, with mean ± SD of 0.57 ± 0.13.

To determine the electromechanical force, FOHC, produced by the OHC (Fig. 1B), the cuticular plate of the cell was placed against the reverse side of an atomic force cantilever (AFL), with known mechanical impedance in fluid, ZAFL. For determination of ZAFL the cantilever was calibrated in water by vibrating one end with a piezoelectric actuator (20 Hz to 100 kHz) and measuring the velocity of the AFL at the free-standing end with the LDV. Using these velocity data, we then obtained ZAFL (Fig. 5C) from solution of the Euler–Bernoulli differential equations for a rectangular beam (18, 19). The velocity of the AFL, VAFL, in response to electrically induced somatic length changes of the OHC was measured with the LDV focused on the AFL. The resulting force was then calculated as FOHC = ZAFL⋅VAFL. Forces down to 1 pN could be detected. The compliance of the AFL (6–29 m/N) was much smaller than that of the OHC, enabling the force measurements to be performed under near-isometric conditions.

Figure 5.

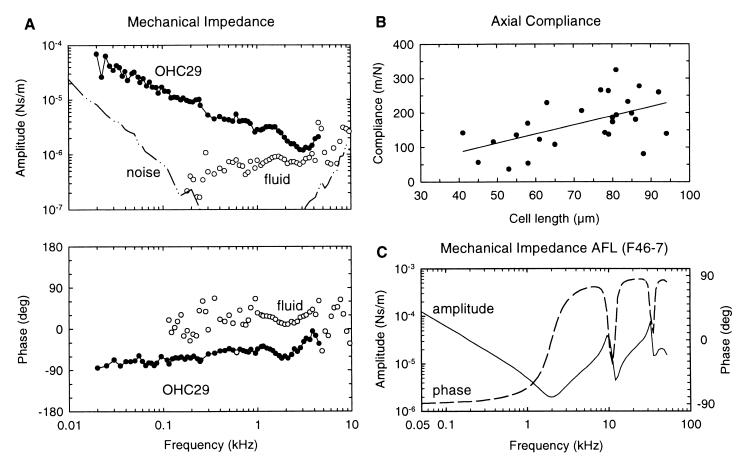
Figure 5

Open in a new tab

(A) Amplitude and phase of the mechanical impedance of the OHC, ZOHC, as a function of stimulus frequency. Up to about 3 kHz, ZOHC resembles that of a compliance with slope near −6 dB/octave (−4.8 dB/octave) and an initial phase near −90°. For higher stimulus frequencies, the impedance associated with fluid coupling (open circles) between the micropipette and the AFL constitutes an appreciable part of the measured impedance, thus preventing estimation of ZOHC above about 5 kHz. (B) Axial compliance of the OHC, COHC, as a function of cell length. COHC increases with cell length (r = 0.54, n = 26): C [m/N] = (2.37 ± 0.17)⋅106 L [m]. For the regression analysis, the axis intercept could be held constant at zero because when made variable it was found to be not significantly different from zero; C = (2.64 ± 0.83)⋅L − (20 ± 61). (C) Amplitude and phase of the impedance of the AFL (F46–7) used for the measurements of cell OHC29 (see Material and Methods for calibration details). The compliance of the AFL was 29 m/N.

To determine the axial mechanical impedance, ZOHC, of the OHC (Fig. 1C), the micropipette was vibrated with velocity VCAP, and the resulting velocity of the AFL, VAFL, was measured with the LDV. The mechanical impedance of the OHC, ZOHC, was calculated as ZOHC = ZAFL⋅VAFL/(VCAP − VAFL). The impedance associated with fluid coupling between the micropipette and the AFL was estimated by expelling the cell and repeating the measurement procedure while keeping the distance between the tip of the micropipette and the AFL constant, to mimic the original experimental conditions.

All amplitude and phase data were corrected for the measured frequency response of the LDV (20 kHz corner frequency).

RESULTS

Experiment 1: Electromotility.

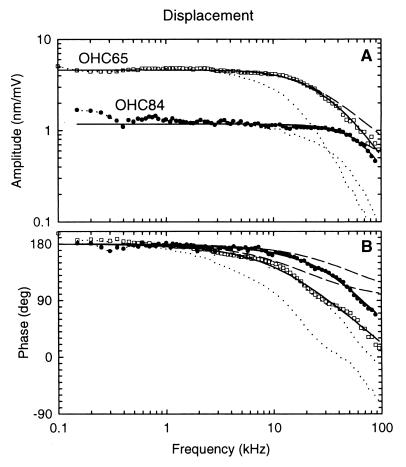
Electrical stimulation of the isolated OHC in the microchamber configuration induces phasic contractions and elongations, which were measured up to 100 kHz (Fig. 2). The amplitude and phase responses were independent of frequency up to a corner frequency, f3dB, which depended on cell length (Fig. 2). Thereafter, both decreased monotonically. The amplitude (Fig. 2A) exhibited an asymptotic slope of about −12 dB/octave, and the phase (Fig. 2B) lagged the low-frequency value by almost 180° (168°). The low-frequency phase of 180° means that depolarization produces contraction. Both the amplitude and the phase response could be best characterized with a second-order resonant system, representing a system with stiffness, damping, and mass (full lines). Alternatively, the data were examined with a first-order low-pass filter, which represents a system with only stiffness and damping (dashed lines). For all cells (n = 57), the second-order system matched the data, whereas the first-order system consistently underestimated the high-frequency attenuation (Fig. 2A) and phase roll-off (Fig. 2B). This result suggests that the high-frequency response of the electromotility of the OHC is determined by both damping and inertia.

Figure 2.

Figure 2

Open in a new tab

Displacement amplitude (A) and phase (B) of electrically induced length changes of two OHCs (□, OHC65; ●, OHC84) of different length measured under unloaded conditions (Fig. 1A). Displacement amplitudes (x[nm]), corrected for cell length and stimulus voltage (x[nm/mV] = x[nm]/[(1 − q)⋅q⋅USP]) (8), are given in nm/mV. Phase is referred to a depolarizing membrane potential and is positive for contraction; that is, for displacement away from the LDV. The data (symbols) are shown corrected for the measured electrical low-pass filter characteristic of the microchamber, with the OHC attached (dotted lines). Displacement data were fitted by the amplitude and phase responses of a second-order resonant system (full lines), representing the mechanical properties of the cell and extracellular fluid. Amplitude and phase were fitted simultaneously by using a software package in Microsoft Excel 7.0. The shape of the responses is described by only two free parameters: the resonant frequency, fOHC, and the quality factor, Q. Since Q was always less than 1/√2, the high-frequency limit was defined as the frequency, f3dB, at which the amplitude drops by 3 dB from its asymptotic low-frequency value; it was calculated from fOHC and Q by using the formula (f3dB/fOHC)2 = 1 − 0.5Q−2 + ((1 − 0.5Q−2)2 + 1)1/2. For some cases, a time delay (τ) was included as a free parameter in the fit function for the phase response. However, the estimated delay was in the range of the precision of our measurement equipment (<1 μs). For OHC65 (length = 83 μm; qL = 55.6 μm): fOHC = 38 kHz and Q = 0.41, giving f3dB = 18.6 kHz; τ = 0.7 μs. For OHC84 (length = 51 μm; qL = 24 μm): fOHC = 66 kHz and Q = 0.59, giving f3dB = 53.4 kHz; τ = 0.1 μs. For OHC65 and OHC84, the electrical corner frequencies of the microchamber loaded by the cell were 9.5 kHz and 23.3 kHz, respectively. The dashed lines are fits for another type of mechanical system: a first-order low-pass filter containing only stiffness and damping (corner frequency: 20 kHz for OHC65 and 54 kHz for OHC84). The near-perfect fit for a second-order resonant system and the poor fit for a first-order, low-pass filter demonstrate that the high-frequency response is determined not by damping alone, but also by inertia.

The frequency response never exhibited a resonance peak—it always resembled the shape for a low-pass filter with an asymptotic high-frequency roll-off of about −12 dB/octave. In other words, the quality factor, Q, which is directly proportional to the maximum stored energy and inversely proportional to the energy dissipated per cycle,† was always less than 1/√2. The Q values ranged from 0.16 to 0.6, with mean of 0.42 ± 0.09 (n = 57). Moreover, since the average value of Q was less than 0.5, the response was typically overdamped.

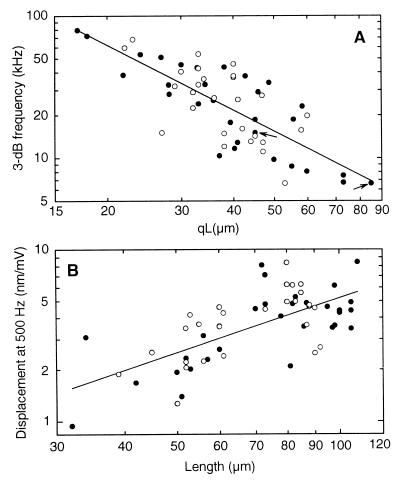
Since the response of the resonant system was low-pass, the high-frequency limit was defined as the frequency at which the amplitude of the electromotile response dropped by 3 dB (f3dB) from its asymptotic low-frequency value. There was a strong dependence of f3dB on qL (Fig. 3A): f3dB decreased in proportion to the power function (qL)−1.5, beginning at 79 kHz for qL = 17 μm and terminating at 6.6 kHz for qL = 85 μm (r = −0.76, n = 57). Moreover, the data imply that all cells, irrespective of their place in the cochlea, exhibit extremely high 3-dB frequencies, well above their place frequency. The resonant frequency of the electromotility ranged from 20 kHz to 152 kHz (data not illustrated). As for the 3-dB frequency, there was a high negative correlation between the resonant frequency and qL (for logarithmic axes, slope = −1.0 ± 0.14; r = −0.71; n = 57): doubling qL halved the resonant frequency, beginning at 152 kHz for qL = 17 μm and terminating at 20 kHz for qL = 85 μm.

Figure 3.

Figure 3

Open in a new tab

Dependence of the 3-dB frequency of electromotility on the excluded length of the cell (qL) (A) and the asymptotic low-frequency amplitude as a function of cell length (B). f3dB decreases hyperbolically with qL, with exponent of −1.5, beginning at a frequency of 79 kHz for qL = 17 μm. [Regression line: log f3dB = −(1.51 ± 0.17)log(qL) + (3.76 ± 0.3); r = −0.76, n = 57; with f3dB in kHz, qL in μm.] The two arrows indicate measurements from the same cell for different qL. The low-frequency (500-Hz) displacement amplitude is directly proportional to cell length, with proportionality constant of 4⋅10−5/mV, with L in meters and amplitude in m/mV. [Regression line: log y = (1.06 ± 0.16)log L − (1.4 ± 0.3); r = 0.67; n = 57; with y in nm/mV and L in μm.] Notice, 1.06 ± 0.16 is not significantly different from unity (P < 0.05), implying direct proportionality. Solid circles represent OHC data where the electrical corner frequency (fMC) was determined from measurements of the electrical input impedance of the micropipette with and without cell (n = 30). Open circles represent data where the electrical input impedance was not measured (n = 27); in these cases, fMC was derived by fitting the electromotile response with the mechanical filter together with a first-order low-pass filter representing the electrical properties of the microchamber configuration. Because there was no statistical difference between the two populations (P < 0.05), regression lines are for the collated data.

The f3dB value of 79 kHz for the shortest measured exclusion length of 17 μm provides a lower boundary for the frequency limit of the electromotility—thus, higher values would be expected for still shorter segments of cell. Conversely, it is of interest to know the value of f3dB for the entire length of cell membrane. This can be estimated by multiplying the measured f3dB values by q. This procedure seems valid because the resonant frequency was found to be inversely proportional to qL and the quality factor was independent of qL. These corrected values were strongly dependent on L (data not illustrated), decreasing in proportion to the power function L−1.99 ± 0.15, beginning at 58 kHz for the shortest observed cell length of 32 μm (r = −0.87; n = 57). Again, these corrected values also lie well above their place frequencies.

The low-frequency amplitude of the electromotility was directly proportional to cell length (Fig. 3B). Expressed as a proportion of cell length, the amplitude was 0.004%/mV. Proportionality is what would be expected for elementary motors connected in series and distributed homogeneously with equal density for all cells (8, 20–22). Addition of gadolinium ions, a known blocker of OHC electromotility (23, 24), lead to a pronounced decrease in the displacement amplitude of up to 30 dB over the entire frequency range (data not illustrated). This finding suggests that up to 100 kHz the measured electromotile responses are of electromechanical origin, rather than being because of electroosmosis or electrophoresis. Finally, although the amplitudes are in agreement with published electromotility data of OHCs of comparable size in the microchamber configuration (13), they are below the average value of 15 nm/mV for long OHCs measured in the whole-cell patch configuration (25). Recordings of the electromechanical transfer function of OHCs with sinusoidal or square wave stimuli (data not illustrated) demonstrated that the set-point in our experiments was not located at the steepest part on the transfer function.

Experiment 2: Electromechanical Force.

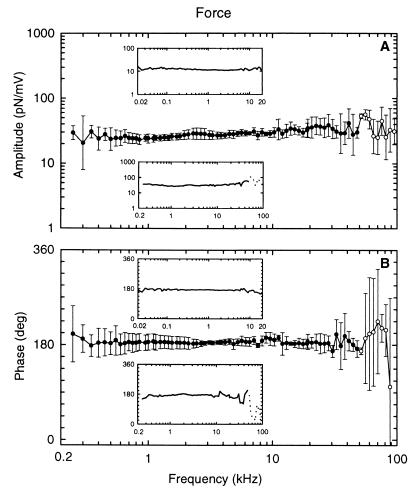
By loading the cuticular plate of the OHC with a mechanical impedance, ZAFL, much larger than that of the OHC, ZOHC, it is possible to measure the electromechanical force produced by the OHC, FOHC, under near-isometric conditions (Fig. 1B). Under these conditions, FOHC is approximately equal to that of the force-source driving the impedance, ZOHC. FOHC was found to be independent of frequency up to at least 50 kHz. Fig. 4 shows the average response of three OHCs where the force was measured up to 100 kHz. The data are complicated above 50 kHz because of unavoidable resonances in the support for the AFL at frequencies above about 50 kHz. The phase value of 180° means that depolarization generates a contractile force. For the majority of cells (n = 15), the maximum stimulus frequency was 20 kHz (Fig. 4, Upper Inset). The amplitudes ranged from 3 to 53 pN/mV, with a geometric mean of 13 pN/mV (n = 18). There was no evidence for a dependence of FOHC on cell length.

Figure 4.

Figure 4

Open in a new tab

Amplitude (A) and phase (B) of the electromechanical force generated by the OHC as a function of stimulus frequency, measured under loaded conditions (Fig. 1B). Data for three OHCs (qL = 68, 38, 28 μm), stimulated with frequencies between 250 Hz and 100 kHz, were averaged. (Lower Inset) Data for one of the averaged cells. The standard deviation of the measurement values is given by the vertical error bars. (Upper Inset) Representative example of an OHC where the electromechanical force was measured between 20 Hz and 20 kHz (qL = 15 μm). Amplitudes and phases are independent of frequency up to at least 50 kHz. Unavoidable resonances in the mechanical support for the AFL are responsible for the peaks and dips in the responses above 50 kHz (open circles), as well as the phase lag of 20° between 13 kHz and 32 kHz. The compliance of the AFL was 6 m/N.

The OHC impedance, ZOHC, can be estimated from the force, FOHC, measured under conditions of a high-impedance load (Fig. 1B) and the displacement XOHCSC, measured under unloaded conditions (Fig. 1A); namely, ZOHC = FOHC/jωXOHCSC. Since the force data clearly show that FOHC is independent of frequency up to at least 50 kHz, the frequency dependence of ZOHC is given by the frequency dependence of 1/jωXOHCSC, namely by that of the second-order, overdamped system determined from the electromotility data. For low frequencies, sufficiently below f3dB, where the amplitude and phase of XOHCSC are independent of frequency, ZOHC must be entirely compliant when driven by a frequency-independent force source. Consequently, the OHC compliance, COHC, can be estimated as COHC = Xlow/FOHC, where the low-frequency displacement amplitude, Xlow, has already been collated for 57 cells in Fig. 3B; namely, Xlow = 4⋅10−5 L (m/mV). For FOHC = 13 pN/mV, we obtain COHC = 3.1⋅106 L (m/N), with L in meters.

Experiment 3: Axial Mechanical Impedance.

The foregoing estimate of COHC was derived from Xlow and FOHC by using two different experimental configurations: without and with the AFL (Fig. 1 A and B). Therefore, ZOHC was measured directly in a third experimental series (Fig. 1C), as described in Material and Methods. For frequencies up to about 3 kHz, ZOHC resembled that for a compliance (Fig. 5A): amplitude slope about −6 dB/octave (−4.8 dB/octave) and initial phase near −90°. Fluid coupling between the micropipette and AFL prevented estimation of ZOHC above about 5 kHz (open circles in Fig. 5A). COHC was estimated from the impedance magnitude, |ZOHC| = 1/ωCOHC (at 500 Hz), and is collated for n = 26 cells in Fig. 5B. COHC showed a linear dependence on cell length: COHC = (2.37 ± 0.17)⋅106 L [m/N], with L in meters. This dependence is not significantly different from that derived by the indirect method of measuring Xlow and FOHC in separate experiments. In other words, the results of the three types of experiment are self-consistent. The compliance data are in perfect agreement with the recent data of Iwasa and Adachi (17), who report an axial stiffness per unit strain of 512 ± 103 nN; this converts to the linear dependence: COHC = (2.0 ± 0.4)⋅106 L [m/N]. Axial compliance values obtained by other groups for OHCs in the microchamber configuration (15, 16) are higher than those obtained here.

DISCUSSION

The data clearly demonstrate that OHCs are able to follow changes of membrane potential with phasic contractions and elongations of their cell body between 20 Hz and 100 kHz. We could further show that the electromechanical force produced by the OHC is constant up to at least 50 kHz. The high-frequency limit of the electromotility, defined as the 3-dB frequency, is at least 79 kHz at room temperature (20–22°C). This is the highest value reported so far and, as for the electromechanical force, significantly exceeds the hearing range in the guinea pig of 45 kHz. Because the amplification mechanism must function up to the highest frequencies audible to mammals (26), these findings have extremely important consequences for our understanding of cochlear mechanics. The authors of a recent paper (27) claimed that there is an intrinsic frequency limit for the motor molecules of about 26 kHz at 37°C, which would be far below our data for short cells. In that report, the frequency limit of the elementary motors was estimated from a frequency-dependent change in nonlinear capacitance and mechanical movements of isolated membrane patches from OHCs under voltage clamp. Their experiments were conducted at 26°C; the measured frequency limit of 16.1 kHz was extrapolated to 37°C. Assuming that the cortical lattice provides significant stiffness to the cell membrane, it might be concluded from piezoelectric models of OHC mechanics (28–30) that the corner frequency of the intact cell, in contrast to the situation in the isolated patch, should be significantly higher.

Whether the frequency response behavior of electromotility of OHCs should be described as all-pass (13), first-order low-pass (27, 31), or second-order low-pass (32) has been the subject of controversial discussion. The main reason for this controversy has been the absence of experimental data at sufficiently high frequencies. We were able to measure both the amplitude and phase of the electromotility of OHCs up to stimulus frequencies where the high-frequency asymptote is exposed. The amplitude and phase data are self-consistent and accurately described by a highly damped, second-order resonant system, and not by a single low-pass filter. Therefore, the high-frequency response is determined not only by frictional losses but also by inertia. This is consistent with a recently published model of OHC electromotility (32). The fact that there is no need for either an additional low-pass filter or a significant pure time delay to fit the frequency response of the electromotility up to 100 kHz indicates that the limiting factor for frequencies below 100 kHz is probably not the speed of the motor but fluid mechanics. Using the correlation between axial compliance and cell length, illustrated in Fig. 5B, together with the inverse relationship between resonant frequency and cell length described earlier in the paper, one can show‡ that a mass equivalent to about 6% of the cell mass is responsible for the inertial component of the response. Moreover, the mechanical resistance can be calculated‡ to be about 9⋅10−8 N⋅s/m. This resistance value is about twice that estimated from the analysis by Dallos and coworkers (14) (5⋅10−8 N⋅s/m), in which inertia was neglected.

The mean amplitude of 13 pN/mV for the electromechanical force produced by the OHC is in agreement with published data from isolated OHCs in the microchamber configuration (15, 16), but it is below the value of 100 pN/mV recently reported for whole-cell voltage clamp experiments (17). Unlike the authors in the latter report, we had no control over the membrane potential. Therefore, as for our electromotility data, the smaller forces reported here could be partially due to the set-point being located away from the steepest part of the electromechanical transfer function of the OHC. Perhaps more important than differences in absolute amplitude is that we were able to characterize the frequency response of the electromechanical force. The data clearly demonstrate that for stimulus frequencies between 20 Hz and at least 50 kHz, covering the whole hearing range, OHCs in the microchamber configuration produce approximately constant force.

One of the major problems regarding electromotility in vivo is the severe high-frequency attenuation and phase shift of the OHCs’ receptor potential, the putative driving voltage of OHC electromotility, due to electrical low-pass filtering by the basolateral cell membrane (13, 31). The mechanisms by which these losses are compensated in the organ of Corti have yet to be elucidated (11, 13, 33). Nevertheless, the present experimental data have shown unequivocally that the OHC possesses the necessary biological machinery to generate electromotile responses on a cycle-by-cycle basis, with little amplitude and phase change, well above the frequency limit of hearing.

Acknowledgments

We are grateful for discussions with M. Scherer and H.-P. Zenner and for the artwork by A. Seeger. This work was supported by the Deutsche Forschungsgemeinschaft, Klinische Forschergruppe “Hörforschung,” Project A, and by the Bundesministerium für Forschung und Technologie, Interdisziplinäres Zentrum für Klinische Forschung Tübingen (01 KS 9602) Project IA.

ABBREVIATIONS

OHC

outer hair cell

LDV

laser Doppler vibrometer

AFL

atomic force cantilever

Footnotes

This paper was submitted directly (Track II) to the Proceedings Office.

†

The quality factor, Q, is defined as the ratio of the maximum energy stored to the energy dissipated in each stimulus cycle, multiplied by 2π (12). For a second-order resonant system with compliance, C, resistance, R, and mass, M, the resonant frequency, fOHC, is 1/2π(CM)1/2 and Q at the resonant frequency is 2πfOHCM/R. For Q ≤ 1/√2, the frequency response strictly resembles that of a low-pass filter; that is, one without a resonance peak. Since the system possesses both resistance and mass, the asymptotic high-frequency roll-off is −12 dB/octave, irrespective of the value of Q. For Q < 0.5, the response to a (voltage) step is nonoscillatory and, therefore, is said to be overdamped. For all our recordings, Q was less than 1/√2 and, on average, less than 0.5.

‡

The mass and resistance of the mechanical resonant system formed by the OHC constrained in the microchamber and extracellular fluid can be estimated from experimental data as follows. All units are given as meter–kilogram–second units. From our data, the resonant frequency, fOHC, depends inversely on cell length, L, as fOHC = a/L, where a = 1.738 m/s. From Fig. 5B, the dependence of axial compliance, C, on L is C = bL, where b = 2.4⋅106 N−1. For a second-order resonant system, the mass, M = 1/C(2πfOHC)2. Therefore, expressed as a proportion of the mass of the cell, πr2Lρ, where r is the cell radius (4.5. 10−6 m) and ρ is fluid density (1,000 kg/m3), the fractional mass is 1/(4π3ρr2a2b), which evaluates to 0.055, or approximately 6%, independent of cell length. For a second-order resonant system, the resistance, R = 2πfOHCM/Q. Using our experimental data yields R = 1/(2πabQ), which evaluates to 9⋅10−8 N⋅s/m for Q = 0.42, also independent of cell length. Finally, it should be mentioned that these estimates might represent a lower limit for the values of mass and resistance because it is possible that as measurement techniques improve the measured compliance values will be found to be smaller.

References

  • 1.Brownell W E, Bader C R, Bertrand D, de Ribaupierre Y. Science. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
  • 2.Zwicker E. Biol Cybern. 1979;35:243–250. doi: 10.1007/BF00344207. [DOI] [PubMed] [Google Scholar]
  • 3.Hudspeth A J. Curr Opin Neurobiol. 1997;7:480–486. doi: 10.1016/s0959-4388(97)80026-8. [DOI] [PubMed] [Google Scholar]
  • 4.Kössl M. Naturwissenschaften. 1992;79:425–427. doi: 10.1007/BF01138579. [DOI] [PubMed] [Google Scholar]
  • 5.Santos-Sacchi J, Dilger J P. Hear Res. 1988;35:143–150. doi: 10.1016/0378-5955(88)90113-x. [DOI] [PubMed] [Google Scholar]
  • 6.Ashmore J F. J Physiol (London) 1987;388:323–347. doi: 10.1113/jphysiol.1987.sp016617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Zenner H P, Zimmermann U, Gitter A H. Biochem Biophys Res Commun. 1987;149:304–308. doi: 10.1016/0006-291x(87)91639-1. [DOI] [PubMed] [Google Scholar]
  • 8.Dallos P, Hallworth R, Evans B N. J Neurophysiol. 1993;70:299–323. doi: 10.1152/jn.1993.70.1.299. [DOI] [PubMed] [Google Scholar]
  • 9.Housley G D, Ashmore J F. J Physiol (London) 1992;448:73–98. doi: 10.1113/jphysiol.1992.sp019030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Preyer S, Renz S, Hemmert W, Zenner H-P, Gummer A W. Aud Neurosci. 1996;2:145–157. [Google Scholar]
  • 11.Evans B N, Dallos P, Hallworth R. In: Cochlear Mechanics. Wilson J P, Kemp D T, editors. New York: Plenum; 1989. pp. 205–206. [Google Scholar]
  • 12.Smith R J. Circuits, Devices and Systems. New York: Wiley; 1966. [Google Scholar]
  • 13.Dallos P, Evans B N. Science. 1995;267:2006–2009. doi: 10.1126/science.7701325. [DOI] [PubMed] [Google Scholar]
  • 14.Dallos P, He D Z, Lin X, Sziklai I, Mehta S, Evans B N. J Neurosci. 1997;17:2212–2226. doi: 10.1523/JNEUROSCI.17-06-02212.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Hallworth R. J Neurophysiol. 1995;74:2319–2328. doi: 10.1152/jn.1995.74.6.2319. [DOI] [PubMed] [Google Scholar]
  • 16.Russell I J, Schauz C. Aud Neurosci. 1995;1:309–319. [Google Scholar]
  • 17.Iwasa K H, Adachi M. Biophys J. 1997;73:546–555. doi: 10.1016/S0006-3495(97)78092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Timoshenko S, Young D H, Weaver W. Vibration Problems in Engineering. New York: Wiley; 1974. [Google Scholar]
  • 19.Scherer M P, Frank G, Gummer A W. In: Applied Mechanics in the Americas. Pamplona D, Steele C R, Weber H I, Goncalves P B, Jasiuk I, Bevilaqua L, editors. Vol. 6. Rio de Janeiro, Brazil: Am. Acad. Mechanics and Brazilian Soc. Mechanical Sciences; 1999. pp. 23–26. [Google Scholar]
  • 20.Holley M C, Ashmore J F. Proc R Soc London B. 1988;232:413–429. doi: 10.1098/rspb.1988.0004. [DOI] [PubMed] [Google Scholar]
  • 21.Dallos P, Evans B N, Hallworth R. Nature (London) 1991;350:155–157. doi: 10.1038/350155a0. [DOI] [PubMed] [Google Scholar]
  • 22.Hallworth R, Evans B N, Dallos P. J Neurophysiol. 1993;70:549–558. doi: 10.1152/jn.1993.70.2.549. [DOI] [PubMed] [Google Scholar]
  • 23.Santos-Sacchi J. J Neurosci. 1991;11:3096–3110. doi: 10.1523/JNEUROSCI.11-10-03096.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Kakehata S, Santos-Sacchi J. J Neurosci. 1996;16:4881–4889. doi: 10.1523/JNEUROSCI.16-16-04881.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Santos-Sacchi J. J Neurosci. 1989;9:2954–2962. doi: 10.1523/JNEUROSCI.09-08-02954.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dallos P. J Neurosci. 1992;12:4575–4585. doi: 10.1523/JNEUROSCI.12-12-04575.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Gale J E, Ashmore J F. Nature (London) 1997;389:63–66. doi: 10.1038/37968. [DOI] [PubMed] [Google Scholar]
  • 28.Mountain D C, Hubbard A E. J Acoust Soc Am. 1994;95:350–354. doi: 10.1121/1.408273. [DOI] [PubMed] [Google Scholar]
  • 29.Iwasa K H. J Acoust Soc Am. 1994;96:2216–2224. doi: 10.1121/1.410094. [DOI] [PubMed] [Google Scholar]
  • 30.Tolomeo J A, Steele C R. J Acoust Soc Am. 1995;97:3006–3011. doi: 10.1121/1.411865. [DOI] [PubMed] [Google Scholar]
  • 31.Santos-Sacchi J. J Neurosci. 1992;12:1906–1916. doi: 10.1523/JNEUROSCI.12-05-01906.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Tolomeo J A, Steele C R. J Acoust Soc Am. 1998;103:524–534. doi: 10.1121/1.421126. [DOI] [PubMed] [Google Scholar]
  • 33.Santos-Sacchi J, Kakehata S, Kikuchi T, Katori Y, Takasaka T. Neurosci Lett. 1998;256:155–158. doi: 10.1016/s0304-3940(98)00788-5. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES