Abstract
The image quality of a two-photon microscope is often degraded by wavefront aberrations induced by the specimen. We demonstrate here that resolution and signal size in two-photon microcopy can be substantially improved, even in living biological specimens, by adaptive wavefront correction based on sensing the wavefront of coherence-gated backscattered light (coherence-gated wavefront sensing, CGWS) and wavefront control by a deformable mirror. A nearly diffraction-limited focus can be restored even for strong aberrations. CGWS-based wavefront correction should be applicable to samples with a wide range of scattering properties and it should be possible to perform real-time pixel-by-pixel correction even at fast scan speeds.
Keywords: aberration, adaptive optics, biological tissue, deformable mirror, scattering
Resolution, signal, and contrast, especially for confocal (1) and multiphoton microscopy (2) are often degraded by refractive-index inhomogeneities in biological specimens (3–6). This degradation can be reversed if the wavefront of the incoming light is predistorted such as to cancel distortions introduced in the excitation light path, for example by the specimen. Several groups have demonstrated the usefulness of adaptive optics for both confocal and multiphoton microscopy. However, all wavefront measurement schemes (7–10) used so far are based on fluorescence and need strongly and widely stained specimens. Finding the correction parameters usually requires numerous iterations, during which the useful life of fluorophores is consumed by photobleaching and the tissue is exposed to photodynamic damage.
Here we use a wavefront measurement method, coherence-gated wavefront sensing (CGWS), that is independent of fluorescence generation (11). CGWS is instead based on backscattered light, whereby the majority of the light coming back from the sample is rejected by a coherence gate leaving only that light that has been scattered near the focus. The parameters needed for wavefront correction can thus be determined at low laser power levels and for completely nonfluorescent specimens. Here we demonstrate, in various samples, that CGWS-based adaptive wavefront correction can be used to improve signal size and resolution in episcopic two-photon microscopy.
Results
Wavefront distortions are frequently detected by using a Shack–Hartman sensor (12), which works by generating an array of foci as the beam is passed through an array of lenses (lenslets). By measuring the displacements in those foci from their positions for a plane wave, a measure of the local wavefront tilt is provided. A Shack–Hartmann sensor can also be implemented by interferometrically detecting the wavefront phase and then numerically propagating the wave through a virtual lenslet array (11). Such a “virtual Shack–Hartmann sensor” (vSHS), which was used in all of our experiments, is particularly suitable in combination with a low-coherence interferometric gate, which intrinsically provides local phase information.
A number of factors contribute to the error in wavefront measurements. Using numerical simulations we found that the reconstruction error due to photon noise is almost independent of aberration strength and scales as expected with the number of photons in the sample arm (). Due to the inherently inefficient use of photons by the vSHS the absolute error is larger (in our case 21.1 ± 1.1 times, close to the value of , expected for our configuration with 441 lenslets) than the quantum limit (13). Experimentally, we tested the vSHS with a mirror as the “sample” and confirmed that the wavefront reconstruction error is ≈30 times larger than the quantum limit, comparable to the expected value. To reach the quantum limit, a different sensing method, such as a virtual modal wavefront sensor (14) or “deterministic” phase unwrapping (15) can be used.
The appearance of optical speckle with their strong spatial intensity variations is inevitable when using elastic (coherent) backscattering from a random arrangement of scatterers. Averaging of different speckle fields (generated here by slightly moving the sample) is necessary to achieve sufficient wavefront precision. For the total wavefront measurement uncertainty using a sample containing scattering beads (see Methods), we found experimentally, for speckle-averaged (20 positions) wavefronts, a variation of 20 nm (corresponding to λ/46, all errors rms), which is dominated by speckle noise (the uncertainty due to photon shot noise should only be ≈3 nm). It should be possible to reduce the speckle noise further by averaging over a larger number of sample positions (16).
Because scattering depends on polarization, CGWS will often report erroneous astigmatism values if linearly polarized light is used. However, these errors can be avoided by the use of circularly polarized light (17). Our setup, therefore, contains a λ/4 wave-plate in the sample arm (Fig. 1), which ensures that the light is circularly polarized in the sample. Furthermore, because the polarization of the returning light is mostly rotated by 90° as it emerges from the λ/4 wave-plate, it can be almost completely redirected into the CGWS by a polarizing beam splitter, resulting in the highly efficient use of the backscattered light.
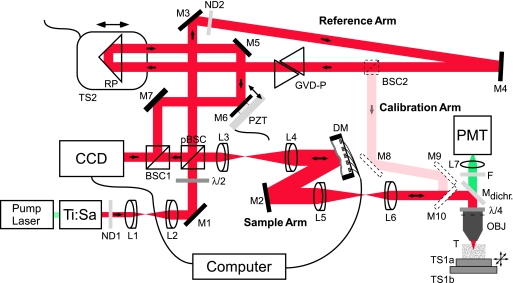
Fig. 1.
Experimental setup. The components used are Ti:Sapphire Laser (center wavelength 930 nm, coherence length 51 μm, Mira 900; Coherent, Santa Clara, CA), neutral density filters ND1 (filter wheel 0.04–3D, NT54–081; Edmund Optics, Barrington, NJ), and ND2 (1.7D, 371144; Linos, Göttingen, Germany), near-infrared achromatic doublets L1 (focal length 5 cm, NT45–803; Edmund Optics), L2 (focal length 8 cm, 322393; Linos), L3 (focal length 7.5 cm, AC254–075-B; Thorlabs, Newton, NJ), L4 (focal length 15 cm, AC254–150-B; Thorlabs), L5 (focal length 20 cm, AC254–200-B; Thorlabs), L6 (focal length 10 cm, NT45–806; Edmund Optics), silver-coated mirrors M1–7 (340525; Linos), λ/2 wave-plate (10RP42–3; Newport, Irvine, CA), polarizing beamsplitter cube pBSC (335523; Linos), nonpolarizing beamsplitter cube BSC1 (BS011; Thorlabs), DM (37 ch; Oko Technologies, Delft, The Netherlands), dichroic mirror Mdichr. (designed to reflect infrared light between 800 and 1050 nm but transmits the fluorescent light ≈525 nm; Chroma), λ/4 wave-plate (10RP44–3; Newport), objective OBJ (IR-Achroplan 63×/0.90 W; Zeiss, Jena, Germany), piezo-driven translation stage TS1a (Tritor 102 SG; Piezosystem, Jena, Germany), motorized translation stage TS1b (MP 285; Sutter Instruments, Novato, CA), blue-green filter F (BG38, 370043; Linos), lens L7 (focal length 2.5 cm, 063021; Linos), photomultiplier tube PMT (R3896; Hamamatsu, Hamamatsu City, Japan), CCD (XC-77; Sony, Tokyo, Japan), group velocity-dispersion compensation prisms GVD-P (BK7, 336615; Linos), right-angle prism RP (PS908; Thorlabs), piezo-driven translation stage TS2 (PX 400; Piezosystem Jena), and tissue sample T. Calibration arm: nonpolarizing beamsplitter cube BSC2 (BS011; Thorlabs) and silver-coated mirrors M8–10 (340525; Linos). The light-propagation directions are indicated by arrows.
The light selected by CGWS passes the specimen-induced distortions twice: on the way to the focus and on the way back. However, for wavefront correction, the aberrations due to a single-pass of the light through the distortions are needed to set the predistortions correctly. Although the backscattered waves are coherent, Monte Carlo ray tracing and analytical calculations in limiting cases show (M.R. and W.D., unpublished data) that the speckle-averaged CGWS-measured wavefront corresponds to an incoherent superposition of the backscattered waves from individual scatterers. Interference effects between those waves cancel, except for extremely high or inhomogeneous densities of scatterers (M.R. and W.D., unpublished data). Because each scatterer acts as an independent source of a spherical wave, CGWS should thus not depend on the incoming wavefront. Therefore, only the return-pass aberrations contribute to the measured wavefront. Experimentally, we found that the CGWS-measured wavefronts, after they were corrected for the influence of the deformable mirror (DM) on the backpropagating wavefront (Fig. 1, see below), do not (for scattering samples) change significantly (by only 17 nm, which corresponds to the uncertainty in the wavefront measurement) even as the incoming wavefront is varied (by up to 350 nm) with the deformable mirror. Note that, for a mirror sample, the measured wavefront is very much dependent on the incoming wave.
To obtain a diffraction-limited focus, it is necessary to send in a wavefront that is the phase conjugate of the measured wavefront. If the response properties of DM and CGWS are sufficiently well known, it is possible to set the DM in a single step, without feedback. We instead used a configuration (Fig. 1), based on the reciprocity theorem (18), where the returning light is reflected by the DM before entering the wavefront sensor and where a diffraction limited focus corresponds to a flat wavefront at the CGWS. This configuration leaves the final correction precision (but not the speed of convergence) insensitive to nonlinearities in both DM and CGWS as well as to most errors in the response matrix M of the DM (see Methods). Convergence is fast: in most cases, the deviation of the measured from the flat wavefront no longer decreased significantly beyond three iterations (Fig. 2c).
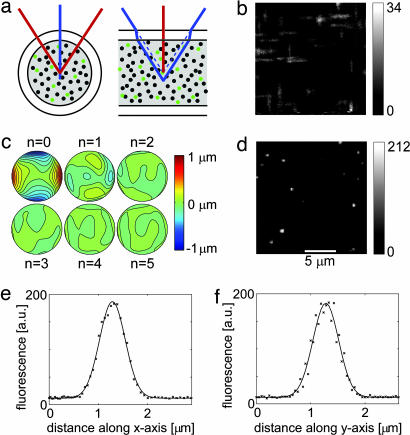
Fig. 2.
CGWS-based correction of glass capillary-induced wavefront distortion. (a) Rays in the planes orthogonal and parallel to the capillary axis form foci in different depths, leading to an astigmatic distortion. Scattering and fluorescence beads are depicted as black and green dots, respectively. (b) Single focal plane images of fluorescent beads before wavefront correction show line foci typical of strong astigmatism. (c) A sequence of wavefront distortions as measured by the coherence-gated wavefront sensor (contour lines spaced by 0.1 μm) during five correction iterations. The initial deviation was 283 nm (n = 0), measured with the mirror set to its reference shape. During the subsequent steps, the deviations were 92, 40, 30, 18, and 17 nm. At the end of this sequence the deformable mirror had reached its deflection limit. (d) Images of fluorescent beads after the final iteration step. (e and f) Fluorescence along the x (e) and y (f) axis for the brightest bead image in an image stack (20 images, spaced by 0.3 μm axially). The images in b, d, and e are corrected for the effects of the sinusoidal scan motion. Background was subtracted for the images in b and d. (Scale bar in d applies also to b.)
Correction of Glass-Capillary Induced Distortions.
To test CGWS-based wavefront correction on a sample that contains a known, well quantifiable distortion, we used a cylindrical glass capillary (Fig. 2a). Before introducing the capillary sample, we first established a reference shape for the DM by correcting (five iterations) all aberrations introduced by the optical elements of the microscope using a scattering test sample (see Methods) without capillary. Images of the capillary sample taken without correction (Fig. 2b) show a strongly astigmatic point spread function with each bead producing two intensity peaks along the z axis spaced by 3.6 ± 0.3 μm. Wavefront correction was now started and stabilized (to within 20 nm) after four iterations. The aberrations found were dominated by astigmatism (Zernike coefficient c6 = −276 ± 6 nm, which is very close to the expected value of −280 nm and corresponds to an interfoci distance of 3.6 μm). Higher-order aberrations were barely detectable (the largest was c12 with −34 nm). When comparing images taken with and without correction we find a 6-fold increase in peak fluorescence and a striking improvement in resolution (Fig. 2 b and d). In image stacks taken with the corrected wavefront the lateral widths (full width at half maximum) of a bead image were 0.61 ± 0.05 μm and 0.56 ± 0.05 μm for x and y directions (Fig. 2 e and f), respectively, comparable to values for samples without distorting elements (0.62 ± 0.05 μm and 0.53 ± 0.05 μm). This finding shows that the focus quality can be restored by CGWS-based wavefront correction. The discrepancies to the theoretical values (0.40 and 0.39 μm) for the lateral focus size are likely due to residual Brownian motion of the fluorescent beads.
Fluorescence for an Aberrated Focus.
Because focus distortion leads to a reduction in the efficiency of two-photon excitation and hence fluorescence generation, not only the peak fluorescence but also the total fluorescence generated is sensitive to wavefront aberrations. Therefore, we tested whether the experimentally determined dependence of the fluorescence signals on the strength and on the type of aberration matches what is theoretically expected for a uniformly fluorescent sample. The expected fluorescence was calculated by numerically integrating the square of the intensity distribution over the focal region (see Methods). All theory/experiment comparisons were between values normalized to those for a flat wavefront (Fig. 3).
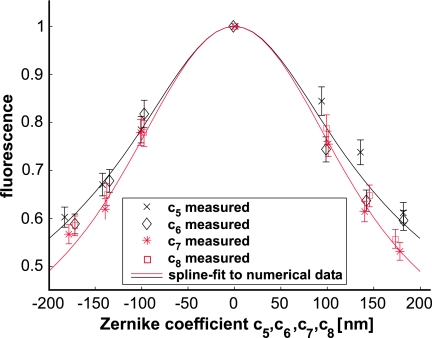
Fig. 3.
Fluorescence intensity (normalized to the maximum) with the laser focus in a “uniformly” stained sample (see Methods) as a function of astigmatism (c5, c6, black) and coma (c7, c8, red). Solid curves are spline fits to numerical calculations of the Debye integral (see Methods) for wavefronts with either astigmatism (black) or coma (red).
The measurements were performed as follows. First, we generated a flat wavefront using quadratic programming (see Methods, Eq. 2). Then we introduced a desired aberration by minimizing the deviation from the target wavefront, denoted by c⃗aberr (similar to Eq. 2, but with ||β·(c⃗aberr − c⃗(n−1)) − M·(s⃗(n) − s⃗(n−1)|| being minimized). The measured and, by reciprocity, the ingoing, wavefront then converge to the aberrated wavefront, leading to a focus with known distortion. Different sets of ingoing wavefronts, each containing only a single Zernike mode (5, 6, 7, or 8) but of different strength (±100, ±140, and ±180 nm), were thus generated.
We determined for each wavefront the average fluorescence generated while scanning the sample laterally over an area of 3 μm × 3 μm. For an aberration of c5 = −140 ± 6 nm, for example, the fluorescence varied by 3.5% between repeated correction cycles (Fig. 3). This variation is mainly due to speckle noise, which should cause a variation of ≈2%. Theoretical and experimental data agree within the error limits (Fig. 3). These results also show that neither significant astigmatism (Zernike mode 5 and 6) nor coma (Zernike mode 7 and 8) were present in the reference arm, because this would lead to a laterally shifted fluorescence vs. aberration curve.
In Vivo Wavefront Correction.
We finally tested whether CGWS-based wavefront correction can be used in living biological specimens. To this end, we imaged the developing olfactory bulb in transgenic zebrafish (Danio rerio) larvae (dlx4/6::GFP, Fig. 4a, refs. 19 and 20). In this transgenic line, GFP is expressed in a random subset of the GABAergic interneurons (granule cells and periglomerular cells) of the olfactory bulb (21). As Fig. 4c shows, the image resolution (the focus depth was ≈50 μm) was severely compromised before correction.
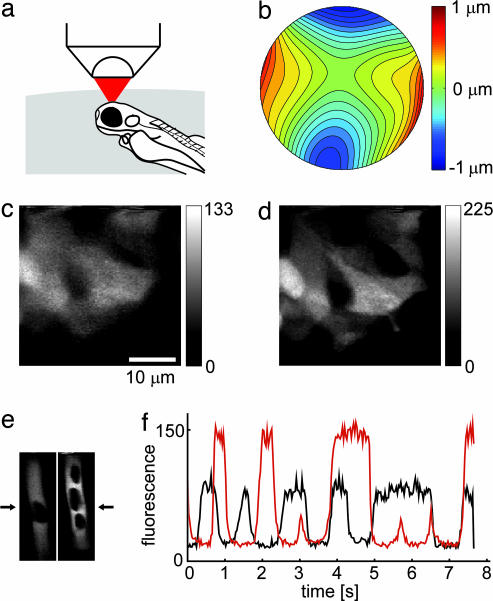
Fig. 4.
Adaptive wavefront-correction in a living animal. (a) Orientation of the zebrafish larva during imaging in the forebrain. (b) Wavefront aberrations (contour lines spaced by 0.1 μm) as measured by CGWS. (c and d) Single focal plane images (in 50 μm depth) recorded without (c) and with (d) correction (correction parameters determined while focused on the center of the image). Background was subtracted and the effects of the sinusoidal scan motion were corrected for display. (e) Single focal-plane images of blood vessels in the forebrain (depth 200 μm) recorded without (Left) and with correction (Right). Dark regions inside the blood vessel are blood cells (22). (f) Bloodflow measurements using line scans (positions as indicated by arrows in e). Plotted are the center pixel intensities as a function of time (black, without correction; red, with correction). (The scale bar in c applies also to d and e.)
For the aberrations introduced by the specimen we found mainly astigmatism (c5 = −82 nm; c6 = −306 nm) and coma (c7 = 0 nm; c8 = −79 nm). The residual aberration after correction (65 nm, after five iterations) was not limited by the measurement error but because several of the DM drive voltages had reached their limits. Even though the correction was for the center point of the image only, almost uniform improvements in image resolution and signal size were found over the whole 34 μm × 34 μm field of view (Fig. 4 c and d), indicating that most of the refractive index inhomogeneities are substantially above the focal plane, in turn suggesting skin and cartilage overlying the brain as culprits. Experiments carried out in a fixed zebrafish larva showed similar results (data not shown).
We also obtained functional (bloodflow) signals by imaging fluorescently labeled blood plasma in wild-type zebrafish. At a focus depth of 200 μm (in the forebrain), we found mainly astigmatic distortion (c5 = −24 nm, c6 = 254 nm, total deviation: 336 nm). Correction (to a final error of 95 nm after three iterations) was again limited by the DM. The time course of the fluorescence signal at the center of a blood vessel (extracted from line scans through a blood vessel, Fig. 4e) was improved almost 2-fold by wavefront correction (Fig. 4f).
Discussion
We have demonstrated that closed-loop CGWS-based wavefront correction can be applied to two-photon microscopy and allows the restoration of an almost diffraction-limited focus. Most importantly, we demonstrated that imaging in living biological specimens can be substantially improved by adaptive wavefront correction. In the current implementation, the speed of correction is limited mostly by the time needed for the numerical wavefront propagation in the vSHS. The ultimate physical speed limit depends on the number of sample-arm photons within the coherence gate, assuming that the number of averages needed to overcome speckle noise can be acquired quickly enough. The number of photons available depends on the length of the coherence gate (CG), focus depth in the sample, tissue properties (in particular backscattering efficiency), and, of course, on the intensity of the illumination light. Ideally, wavefront measurement, correction, and fluorescence imaging would occur pixel by pixel, either simultaneously or tightly interleaved. Under typical two-photon in vivo imaging conditions, we have at least a few mW, i.e., ≈1016 photons/s, of average laser power at the focus. Of those, ≈10% are scattered within the slice selected by the CG [22 μm for a coherence length of 58 μm at a mean free path (MFP) of 200 μm]. However, of those 1015 photons/s, only 1% (calculated by using the Henyey–Greenstein scattering function for an anisotropy factor of 0.95; ref. 23) are scattered in a direction that falls into the objective's acceptance cone. Scattering on the way out, at a depth of, say, five MFPs, leads to a further 100-fold reduction so that, in the end, ≈1011 photons/s are left for the CGWS. Because 105 photons are sufficient to measure the wavefront to λ/50, even when using the vSHS (13), a single wavefront measurement can, in principle, be performed in ≈1 μs. Thus, wavefront measurements would not be limited by the available light, even at pixel rates as large as 1 MHz.
Although we need at least 16 measurements at different focus positions to reduce speckle noise to below λ/50, the photons needed for a particular precision can be spread out over different focus positions, sensibly in such a way that the shot-noise error exceeds the speckle error, which occurs when the number of photons in the sample arm for one interferogram is lower than ≈103 (for a vSHS of our parameters, see Methods). The need to average out the speckle error is thus not limiting the speed as long as it is possible to change the focus position quickly enough (for example, by use of an electro-optical deflector; ref. 24) and camera frame rates are high enough.
For the photon flux given above, the appropriate frame rate would be ≈60 MHz (16 positions times four images for each interferogram every microsecond), which is still above sustained camera readout rates currently available. However, because the number of parameters needed to set the DM is much smaller than the number of camera pixels, on-chip processing (25) might ultimately provide correction parameters at MHz update rates. In any case, currently available deformable mirrors or spatial phase modulators are still considerably slower so that, at the moment, correction speeds would be limited by wavefront shaping, not measuring.
This is not a serious limitation because, as imaging in zebrafish (Fig. 4) shows, it is not necessary to provide pixel-by-pixel correction. The speed of wave shaping by some of the currently available devices (26) would be still fast enough to follow those physiological processes (such as pulsatile bloodflow) that can significantly affect the refractive index distribution and thus cause varying wavefront distortion.
Because aberrations have a particularly detrimental effect on the focus quality in high-resolution microscopy, an important area of application, in addition to two-photon and confocal microscopy, of CGWS-based wavefront correction might be modern superresolution techniques such as stimulated emission depletion (STED) fluorescence (27) and structured illumination (28, 29) microscopy.
Methods
The experimental setup (Fig. 1) combines CGWS, a wavefront correction element (in our case an electrostatically deflected membrane mirror; Oko Technologies, Delft, The Netherlands; ref. 26), and a two-photon microscope. To implement the coherence gate, we use a low-coherence interferometer. A λ/2 wave plate in combination with a polarizing beamsplitter is used to distribute the light between the reference and sample arms. The reference-arm intensity is adjusted by a neutral density filter such that the camera is operating in the shot-noise regime. Before the beam enters the interferometer, the beam is expanded by a telescope to 6.3 mm horizontally and 5.6 mm vertically (1/e2 widths). This ensures that the back aperture of the objective (IR-Achroplan 63×/0.90 W; Zeiss, Jena, Germany) is 1.25 times overfilled. Further telescopes in the sample arm (L3/L4 and L5/L6) ensure that CCD (XC-77; Sony, Tokyo, Japan), DM, and objective back aperture (4.8 mm in diameter) are optically conjugate to each other and that only the central, well controllable region (9.7 mm diameter) on the DM is used (30). To minimize the CG-length, the group delays in reference and sample arms need to be equalized, which is achieved by a length of BK7 glass in the reference arm. We used 6 cm for the test sample measurements, which is less than is needed for optimal compensation, resulting in a CG-length of 32 μm in the sample (FWHM, measured as described in ref. 31). Nearly full compensation (CG-length = 22 μm) is achieved with 20 cm of BK7 glass and was used for in vivo imaging.
A dichroic mirror in the sample arm separates the infrared light, used for two-photon excitation, from the fluorescence light, which is then focused onto a photomultiplier tube. The laser power was typically ≈8 mW at the sample during two-photon imaging, but only 60 nW during wavefront sensing. The specimen was mounted onto a piezo-driven translation stage. For scanning in x and y directions, we used sinusoidal and saw-tooth signals with periods of 30 ms and 3.8 s, respectively. Images were recorded at a digital resolution of 128 × 128 pixels.
Using the nonparaxial Debye approximation (32), the fluorescence generated via two-photon absorption within a uniformly fluorescent specimen can be calculated. A Gaussian intensity profile in the back focal plane of the objective was assumed. The integration volume was 16.1 μm × 16.1 μm × 20 μm (centered at the focus) and was sampled at intervals of 0.06 μm laterally and 0.05 μm axially.
To reduce the effect of speckle on wavefront sensing, we recorded interferograms for 20 slightly different focus positions, placed on a lateral grid with 1 μm spacing, for which the correlation between neighboring speckle patterns was experimentally determined to be 0.50 ± 0.06 (data not shown). For each position, we recorded five of the quadruplets needed for four-step phase-shifting interferometry (11, 33) to reduce photon shot noise. Phase-shifting was accomplished by displacing mirror M6 (Fig. 1) in the reference arm, using a piezo element. For each sample position, we averaged the interferograms over all five quadruplets, reconstructed the electric field of the coherence-gated sample light, and calculated the intensity distribution in the focal plane of a vSHS with 411 lenses. Then, the centroids of the intensity distributions (inside a window 15 pixels wide and centered at the peak intensity) for each of the 441 lenses within the aperture were calculated and averaged over the different focal positions. Finally, the wavefront, described as a linear combination of the first 28 Zernike modes (up to the sixth radial order; ref. 34), was reconstructed by least-squares fitting to the set of wavefront gradients measured.
The shape of the DM (again described in terms of 28 Zernike polynomials, using a set of coefficients c⃗s) depends roughly quadratically on the set of voltages that are applied to the 37 electrodes underneath the membrane (26). We, therefore, use a set of variables s⃗ = (s1, …, s37) = (v12, …, v237), whereby for each voltage 0 < vi < vmax. The shape of the mirror is then given by
where M is the response matrix describing the DM (35) and c⃗ini is the initial deviation from a flat wavefront. The matrix M was determined by interferometrically sensing the shape of the membrane in responses to each of the 37 electrodes, using the calibration arm (see Fig. 1). To allow deflections for the DM in both directions, all deflection–electrode voltages are initially set to vmax/, i.e., si = smax/2, with the resulting defocus compensated by adjusting the position of L6 (Fig. 1).
Only Zernike modes 5–28 were corrected because these correspond to aberrations that change the focus shape; tip/tilt (modes 2 and 3) and defocus (mode 4) only shift the focus. To sense all distortions in the path to the focus, the coherence gate needs to select backscattered light that originates from the focal region. Therefore, when a defocus term was detected, the length of the reference arm was automatically adjusted until the defocus was zero.
Eq. 1 would suggest that the voltage needed to correct for the measured aberrations can simply be obtained by multiplying c⃗s − c⃗ini with the (pseudo) inverse of M (30, 35). Because this frequently would call for voltages outside the available range we used instead quadratic programming [implemented by using the Matlab (The MathWorks, Natick, MA) function quadprog, ref. 36], which, like the (pseudo) inverse, minimizes
whereas, unlike the pseudo inverse, maintaining 0 < v(i) < vmax; c⃗(n−1) is the measured wavefront with s⃗(n−1) applied to the DM for the nth correction step; || || indicates the L2 norm. The parameter β determines the convergence rate and was between 0.8 and 1. Unless a different reference wavefront was specified (see below), we started with s⃗(0) = s⃗max/2, where the measured aberrations due to the DM and microscope optics were c5 = −30 nm, c6 = 63 nm, c7 = −21 nm, c8 = −10 nm, and c11 = −25 nm, c22 = 25 nm, respectively. All deviations and errors are given as rms.
Sample Preparation.
The “uniformly” stained scattering sample (mean free path, ≈550 μm) contained polysterene beads (108-nm diameter, 15 beads per μm3, 00876; Polysciences, Warrington, PA) embedded in an aqueous gel (1% low-melting point agarose, A9414; Sigma, St. Louis, MO) and also contained 100 μM fluorescein (fluorescein-sodium salt, 46960; Fluka, Sigma). The capillary for the aberration sample (270-μm outer diameter, 24-μm wall thickness) was produced from a larger capillary (1-mm diameter with 100-μm wall thickness; Hilgenberg, Malsfeld, Germany) on a micropipette puller (P-2000; Sutter Instrument Company, Novato, CA). The capillary contained scattering (108-nm diameter, six per μm3, 00876; Polysciences) and fluorescent beads (93 nm, 0.2 per μm3, yellow–green FluorSpheres; F8803; Invitrogen, Carlsbad, CA) again immobilized in 1% agarose.
Live Animal Imaging.
Zebrafish larvae (days 3–6 after fertilization) were anesthetized by immersion in 0.16 mg/ml MS-222 (A5040; Sigma-Aldrich, St. Louis, MO) and embedded in 2% low-gelling agarose (A0701; Sigma-Aldrich) with an inclination angle of the roll axis of ≈20° for better optical access (21, 37). To suppress pigment formation, embryos were treated with 0.003% N-phenylthiourea (P7629; Sigma-Aldrich) starting 10–20 h after fertilization. Spawning and raising of zebrafish larvae was performed following standard procedures (38). All animal experiments were carried out in accordance with the animal care guidelines issued by the Federal Republic of Germany.
To visualize the blood plasma of zebrafish larvae 5% (wt/vol) FITC-labeled dextran (Mr, 40,000; FD-40S; Sigma-Aldrich) in zebrafish Ringer's solution was administered to the cardiovascular system as follows: anesthetized larvae were placed sidewise under a stereomicroscope; a glass pipette was inserted into either the heart ventricle or the yolk sac, and two to three boluses of dye were ejected by an air pressure pulse. Strong labeling of the cardiovascular system was observed in most animals shortly after injection under a fluorescence stereomicroscope. Individual fluorescing larvae were mounted in agarose for imaging.
Acknowledgments
We thank Monika Reichert for preparation of zebrafish, Manfred Hauswirth, Michael Müller, and Jürgen Tritthardt for technical support, and Marcus Feierabend, Susanne Hausselt, Marcel Lauterbach, and Jürgen Sawinski for helpful discussions and comments on the manuscript. The work was supported by the Max-Planck Society and Deutsche Forschungsgemeinschaft Grants SFB 488 and GK 791.
Abbreviations
- CGWS
coherence-gated wavefront sensing/sensor
- vSHS
virtual Shack–Hartmann sensor
- DM
deformable mirror
- CG
coherence gate
Footnotes
Conflict of interest statement: W.D. has a patent on two-photon microscopy, and W.D. and M.R. have a patent on coherence-gated wavefront sensing.
This article is a PNAS direct submission.
References
- 1.Minsky M. 3,013,467. US Patent. 1961
- 2.Denk W, Strickler JH, Webb WW. Science. 1990;248:73–76. doi: 10.1126/science.2321027. [DOI] [PubMed] [Google Scholar]
- 3.Gibson SF, Lanni F. J Opt Soc Am A. 1991;8:1601–1613. [Google Scholar]
- 4.Kam Z, Hanser B, Gustafsson MGL, Agard DA, Sedat JW. Proc Natl Acad Sci USA. 2001;98:3790–3795. doi: 10.1073/pnas.071275698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Helmchen F, Waters J. Eur J Pharmacol. 2002;447:119–129. doi: 10.1016/s0014-2999(02)01836-8. [DOI] [PubMed] [Google Scholar]
- 6.Schwertner M, Booth MJ, Wilson T. Opt Exp. 2004;12:6540–6552. doi: 10.1364/opex.12.006540. [DOI] [PubMed] [Google Scholar]
- 7.Neil MAA, Juskaitis R, Booth MJ, Wilson T, Tanaka T, Kawata S. J Micros. 2000;200:105–108. doi: 10.1046/j.1365-2818.2000.00770.x. [DOI] [PubMed] [Google Scholar]
- 8.Sherman L, Ye JY, Albert O, Norris TB. J Micros. 2002;206:65–71. doi: 10.1046/j.1365-2818.2002.01004.x. [DOI] [PubMed] [Google Scholar]
- 9.Marsh PN, Burns D, Girkin JM. Opt Exp. 2003;11:1123–1130. doi: 10.1364/oe.11.001123. [DOI] [PubMed] [Google Scholar]
- 10.Booth MJ, Neil MAA, Juskaitis R, Wilson T. Proc Natl Acad Sci USA. 2002;99:5788–5792. doi: 10.1073/pnas.082544799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Feierabend M, Rückel M, Denk W. Opt Lett. 2004;29:2255–2257. doi: 10.1364/ol.29.002255. [DOI] [PubMed] [Google Scholar]
- 12.Shack RV, Platt BC. Opt Sci Center Newslett. 1971;5:15–16. [Google Scholar]
- 13.Rueckel M, Denk W. In: Advanced Wavefront Control: Methods, Devices, and Applications IV. Giles JDG Michael K., Carreras Richard A., editors. Vol 63060H. San Diego: Int Soc Opt Eng; 2006. [Google Scholar]
- 14.Lauterbach MA, Ruckel M, Denk W. Opt Exp. 2006;14:3700–3714. doi: 10.1364/oe.14.003700. [DOI] [PubMed] [Google Scholar]
- 15.Volkov VV, Zhu YM. Opt Lett. 2003;28:2156–2158. doi: 10.1364/ol.28.002156. [DOI] [PubMed] [Google Scholar]
- 16.Schmitt JM, Xiang SH, Yung KM. J Bio Opt. 1999;4:95–105. doi: 10.1117/1.429925. [DOI] [PubMed] [Google Scholar]
- 17.Rueckel M, Denk W. Adaptive Optics: Analysis and Methods/Computational Optical Sensing and Imaging/Information Photonics/Signal Recovery and Synthesis Topical Meetings on CD-ROM. Washington, DC: Opt Soc Am; 2005. AThC4. [Google Scholar]
- 18.Hardy JW. Proc IEEE. 1978;66:651–697. [Google Scholar]
- 19.Zerucha T, Stuhmer T, Hatch G, Park BK, Long QM, Yu GY, Gambarotta A, Schultz JR, Rubenstein JLR, Ekker M. J Neurosci. 2000;20:709–721. doi: 10.1523/JNEUROSCI.20-02-00709.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ghanem N, Jarinova O, Amores A, Long Q, Hatch G, Park BK, Rubenstein JL, Ekker M. Gen Res. 2003;13:533–543. doi: 10.1101/gr.716103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li J, Mack JA, Souren M, Yaksi E, Higashijima S, Mione M, Fetcho JR, Friedrich RW. J Neurosci. 2005;25:5784–5795. doi: 10.1523/JNEUROSCI.0922-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kleinfeld D, Mitra PP, Helmchen F, Denk W. Proc Natl Acad Sci USA. 1998;95:15741–15746. doi: 10.1073/pnas.95.26.15741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Henyey LG, Greenstein JL. Astrophys J. 1941;93:70–83. [Google Scholar]
- 24.Khayim T, Maruko A, Shibuya K, Morimoto A, Kobayashi T. IEEE J Quantum Electron. 2001;37:964–969. [Google Scholar]
- 25.Monteiro DWL, Nirmaier T, Vdovin GV, Theuwissen AJP. Sens J IEEE. 2005;5:976–982. [Google Scholar]
- 26.Vdovin G, Sarro PM. Appl Opt. 1995;34:2968–2972. doi: 10.1364/AO.34.002968. [DOI] [PubMed] [Google Scholar]
- 27.Hell SW. Nat Biotechnol. 2003;21:1347–1355. doi: 10.1038/nbt895. [DOI] [PubMed] [Google Scholar]
- 28.Neil MAA, Juskaitis R, Wilson T. Opt Lett. 1997;22:1905–1907. doi: 10.1364/ol.22.001905. [DOI] [PubMed] [Google Scholar]
- 29.Gustafsson MGL. Proc Natl Acad Sci USA. 2005;102:13081–13086. doi: 10.1073/pnas.0406877102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Paterson C, Munro I, Dainty JC. Opt Exp. 2000;6:175–185. doi: 10.1364/oe.6.000175. [DOI] [PubMed] [Google Scholar]
- 31.Feierabend M. PhD dissertation. Heidelberg: Univ of Heidelberg; 2004. [Google Scholar]
- 32.Born M, Wolf E. Principles of Optics. Cambridge, UK: Cambridge Univ Press; 1999. [Google Scholar]
- 33.Malacara D. In: Optical Shop Testing. Malacara D, editor. New York: Wiley; 1992. pp. 501–513. [Google Scholar]
- 34.Noll RJ. J Opt Soc Am. 1976;66:207–211. [Google Scholar]
- 35.Zhu LJ, Sun PC, Bartsch DU, Freeman WR, Fainman Y. Appl Opt. 1999;38:168–176. doi: 10.1364/ao.38.000168. [DOI] [PubMed] [Google Scholar]
- 36.Gill PE, Murray W, Wright MH. Practical Optimization. San Diego: Acadamic; 1995. pp. 177–180. [Google Scholar]
- 37.Späth M, Schweickert W. Naunyn-Schmiedebergs Arch Pharmacol. 1977;297:9–16. doi: 10.1007/BF00508804. [DOI] [PubMed] [Google Scholar]
- 38.Westerfield M. The Zebrafish Book: A Guide for the Laboratory Use of Zebrafish (Danio rerio) 4th Ed. Eugene: Univ of Oregon Press; 2000. [Google Scholar]