Abstract
Recent avian flu epidemics (A/H5N1) in Southeast Asia and case reports from around the world have led to fears of a human pandemic. Control of these outbreaks in birds would probably lead to reduced transmission of the avian virus to humans. This study presents a mathematical model based on stochastic farm-to-farm transmission that incorporates flock size and spatial contacts to evaluate the impact of control strategies. Fit to data from the recent epidemic in the Netherlands, we evaluate the efficacy of control strategies and forecast avian influenza dynamics. Our results identify high-risk areas of spread by mapping of the farm level reproductive number. Results suggest that an immediate depopulation of infected flocks following an accurate and quick diagnosis would have a greater impact than simply depopulating surrounding flocks. Understanding the relative importance of different control measures is essential for response planning.
Keywords: avian influenza, prevention and control, epidemiology, mathematical model, Netherlands
1. Introduction
Highly pathogenic avian influenza (HPAI) outbreaks have been reported worldwide since surveillance started (Alexander 2000). Virus transmission to humans has been reported, leading to fears of a new human pandemic stemming from reports of outbreaks of avian influenza around the world (Saito et al. 2001; Gilbert et al. 2006; Wee et al. 2006). In general, avian influenza viruses do not replicate efficiently in humans, indicating that efficient direct transmission of avian viruses to humans would be an event as rare as human-to-human transmission (Beare & Webster 1991). Despite this, a dramatic increase in the number of reports of avian virus transmission to humans has been observed since 1997 (Webby & Webster 2003). Moreover, it appears that the number of human infections follow a similar trend, at a smaller scale, as the avian epidemic (Koopmans et al. 2004) suggesting that human infections would be reduced when an avian epidemic is quickly controlled. This concept highlights the importance of understanding the control strategies, which would have the greatest impact in diminishing the epidemic among poultry. Should policy makers focus on a quick destruction of infected flocks? Should poultry around infected cases be depopulated? How large should the depopulation radius be?
Mathematical models provide a framework to address these questions and determine the impact of different control strategies. Although mathematical models of pandemic influenza among humans have been developed to evaluate the impact of measures such as vaccination or antiviral drugs on controlling virus diffusion (Ferguson et al. 2005; Longini et al. 2005), this approach has been rarely applied to avian influenza. To date, little detailed data about avian influenza epidemics have been published with the exception of the Dutch outbreak in 2003 (European commission 2003). To evaluate the overall effectiveness of control measures, Stegeman et al. (2004) estimated that the end of the epidemic was due to extensive culling of the susceptible population rather than to other specific control measures from the retrospective epidemic data. Questions concerning control strategies which would have the greatest impact in reducing epidemic magnitude remain unanswered. To our knowledge, no other mathematical models have been developed to explore avian influenza dynamics in poultry and candidate control measures.
The aim of this paper is to identify the strategies which would have the greatest impact on controlling avian influenza epidemics. Exposure to a virus has a spatial component that influences the spatial and temporal spread (Lemenach et al. 2005). We developed a mathematical model, calibrated on the Dutch outbreak, taking into account both spatial component and farm size. We weighed the impact of different control strategies on the forecast cumulative epidemic and performed a multivariate sensitivity analysis.
2. Methods and data
(a) Model: formulation and assumptions
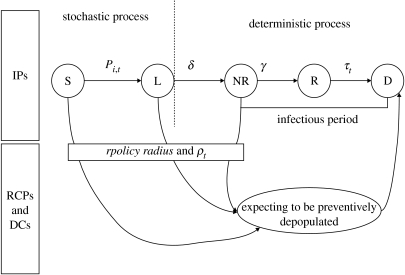
A spatial farm-based model was developed to mimic the transmission dynamics of avian influenza and the implementation of control strategies. We assumed the farm to be an individual unit because of the rapid transmission of the virus and hence animals would be kept inside holdings if an epidemic occurred (Stegeman et al. 2004). The model includes two components: a stochastic one to assess the spread among farms and a deterministic one describing the changes in the farm disease status (figure 1).
Figure 1.
Avian influenza transmission dynamics between domestic flocks. Infected premises (IPs): a farm is first susceptible (S) and may become infected by infectious farms. Once infected, a farm becomes latent (L) during δ days then infectious but not reported (NR) during γ days, becomes infectious and reported to authorities (R) before being depopulated (D) within τ days. ring-culled premises (RCPs) and dangerous contacts (DCs): farms (susceptible or infected with no specific clinical signs) that are in the vicinity or linked to an IP just revealed infected (R) would be depopulated within τ days also. The number of RCPs depends on the radius rpolicy of neighbourhood control measures and the number of depopulated DCs depends on the ratio of pre-emptive culled farm to infected IPs.
Firstly, each farm was classified as susceptible (S). The infection process was modelled stochastically using a discrete-time model formulation with a one-day-time step using Monte Carlo sampling. On day t, the probability that a susceptible farm i becomes infected is given by
This hazard-based probability depends on the farm sizes (Ni, Nj) and on the distances between farms, which are taken into account through the contact rates. The contact rates are defined as follows: is the contact rate between farms within short-range distance (aerosol dispersion, movements of poultry over pasture within the protection area), within medium range distance (contacts with neighbours and movement of workers among farms with the surveillance area) and within long-range distance (truck transport of living poultry, eggs and manure). The use of the natural log allows for large differences in the number of birds per farm to be taken into account. This scale was considered most appropriate as differences in biosecurity risks between small farms and large ones are maintained but the differences between similar industrial farms with different sizes are smoothed. Assuming a log-scaled transmission did not impose specific mathematical constrains on likelihood optimization, since the optimization as explained below was performed numerically. Thus, this approach could easily be derived to other nonlinear scaling. We also assumed the risk of being infected to be equal within each of the three transmission buffers.
Contact rate values were used at two time lags: before the virus was known to circulate (k=1, pre-control period: T1) and afterwards when control strategies, such as a national ban (i.e. all exports of live poultry and eggs were blocked and movement of live poultry was banned in the Netherlands), were put into place (k=2, control period: T2). For the ease of computation, we included a constant c to ensure estimated parameters were within reasonable bounds.
Once a farm was infected, the farm was classified as latent (L, infected but not contagious); after δ days it was classified as not reported (NR, infectious but not reported to authorities because of poor clinical expression). After γ days, the farm was classified as reported (R, infectious with explicit clinical signs reported to authorities); after τt days the farm was depopulated (D, removed from transmission chain), where τt decreases with time (table 1).
Table 1.
Values, definition and parameter bounds (bold numbers within brackets) used in the model and for the sensitivity analysis (* indicates the parameters used in the multivariate sensitivity analysis).
| symbol | definition | values (bounds) | references |
|---|---|---|---|
| T1* | silent period: before the virus is known to be circulating | 10 (5–15) days | waterfowl are highly suspected to have introduced the disease on a farm on February 18 2003. Infection was reported the 28th (European commission 2003) |
| βshort,k* | infectious contact rate at a short-range distance | T1: 0.336 (0.25–0.5) T2: 0.13 (0.1–0.2) | likelihood estimation |
| βmedium,k* | infectious contact rate at a medium-range distance | T1: 0.292 (0.2–0.4) T2: 0.162 (0.1–0.2) | likelihood estimation |
| βlong,k* | infectious contact rate at a long-range distance | T1: 0.076 (0.05–0.15) T2: 0.016 (0.005–0.05) | likelihood estimation |
| c | computing constant | 0.01 | assumed to be constant |
| δ | latent period | 2 days | (Office International des Epizooties 2004; van der Goot et al. 2003) |
| γ* | infectious, but not yet reported period | 4 (0–6) days | (European commission 2003; Stegeman et al. 2004) |
| τt* | infectious reported period | 1–6 (0–6) days | longer at onset of the epidemic (European commission 2003; Sanco 2003; van der Goot et al. 2003) |
| ρt* | ratio of preventive culled farms to infected farms | 1–5 (0–5) | (European commission 2003; Sanco 2003) |
| rpolicy* | radius of neighbourhood control policy | 1–3 km (0.5–3) | (European commission 2003; Sanco 2003) |
In addition to their disease status, farms were classified according to their control status. Farms were classified as: ‘infected premises’ (IPs) for reported farms targeted for depopulation; ‘ring-culled premises’ (RCPs) for farms in the vicinity (within a certain radius size, rpolicy) of IPs and targeted for the neighbourhood control policies, such as depopulation or vaccination; or ‘dangerous contacts’ (DCs) for farms not concerned by neighbourhood control policies but epidemiologically in contact with IPs. We let ρt denote the ratio of pre-emptive depopulated farms (RCPs and DCs) to infected farms (IPs) increasing with time. We simulated a set of DC farms, as this information was not available for the Dutch epidemic. We assumed the probability of a farm being classified as a DC to be slightly different from the risk of being infected and to decrease with distance. Since the DC status is established while investigating previous contacts of an infected farm, it does not depend as strongly on key radius zones as infected holdings. For each farm, a set of DCs was sampled using a function 1/distance.
(b) Parameter estimation and initial values
To obtain values for the spatial contact rates, (βshort, k, βmedium, k and βlong, k), we used maximum likelihood estimation (MLE) at two times: the pre-control and control periods. The likelihood of an individual farm i over the observed epidemic length T was calculated as the probability of remaining susceptible on day t multiplied by the probability of being infected the day infection was noted according to the observed data (tri). In other words, . If the farm remained susceptible over the entire epidemic duration, then tri=T+1. If the farm is pre-emptively depopulated, tri=date of depopulation+1. The individual probabilities are multiplied together to achieve a single likelihood value.
The Simplex method was used to optimize the likelihood values against observed available data. To prevent the occurrence of local minima, 1000 sets of six initial parameters were generated and the resulting optimal set was used for simulations.
All other parameters were taken from the published literature, experimental studies or previous observed epidemics (table 1). The radius distances corresponding to the three transmission buffers (less than 3 km, between 3 and 10 km and more than 10 km) and to the zone concerned by the control policy were chosen according to what is usually applied in Europe when an infected farm (Council of the European Communities 1992). The same radius distances were employed during the Dutch outbreak.
(c) Data
The model was fit to the 2003 A/H7N7 Dutch outbreak. We focused on the two most affected areas, Gelderland and Utrecht, where 185 commercials farms were infected starting from February 28 2003.
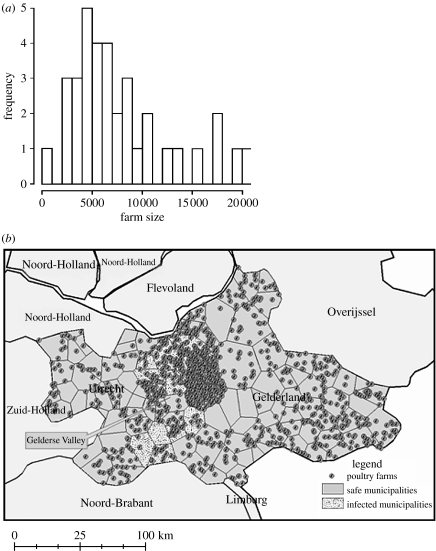
For each of the 156 municipalities in Gelderland and Utrecht in 2002, we had the number of farms (n=1136 in both regions) and the number of animals for any avian species (broiler 15.4%, layers hens 75.4%, ducks 2.2%, turkey 4.8% and other 2.2%; Statistics in Netherlands 2004). As data were not available on exact location of farms, the geographical coordinates of each farm and the number of animals within a farm were simulated at the municipal level. We first built municipal borders around its gravity centres using Voronoi tessellation, (Duyckaerts & Godefroy 2000) and then farm locations were randomly distributed within each municipality (average surface area of 40.8 km2, figure 2b). Suggested by data (figure 2a), the number of animals in each farm was assumed to follow a right-skewed distribution, i.e. a Poisson distribution parameterized by
Data on infected farms were collected through the European Commission reports published throughout the epidemic (European commission 2003). The daily incidence of infected farms and the delay between report of infection and depopulation for each of the 185 farms were provided. The dates for infection, suspicion, laboratory confirmation and depopulation were indicated as well. Data also indicate to which town, municipality and province the infected farm belongs, type and number of animals within the farm and the source of infection. The control measures were fully described as well: a national ban on poultry movement the day the virus is known to be circulating; date of implementation of the surveillance and control buffer areas; date at which pre-emptive depopulation starts (within a 1 km radius from the beginning of March 2003 and then 3 km radius from the beginning of April 2003); and date at which depopulation of dangerous contacts starts.
Figure 2.
(a) Distribution of the farm size within Ede Municipality (Netherlands). (b) Demographic inputs: simulated locations of poultry farms in Gelderland and Utrecht. Observed affected municipalities are represented by dotted surface.
(d) Model calibration
We simulated 1000 epidemics over a period of 100 days beginning with a unique index case located in Renswoude municipality where the epidemic began. The results of model simulations were then compared, by calculating the correlation coefficient, to the 5-day moving average incidence of reported cases (figure 3a). Simulations also provide spatial-kriged risk maps for the pre-control and control periods evaluating Rt values, that is the average number of secondary infected flocks by one primary infected flock (Anderson & May 1991). For each farm, Rt values were estimated by simulating infection of an initial flock and then counting the average number of secondary cases generated for the length of the infectious period. We assumed the infectious period was 10 days during the pre-control period and 6 days during the control period.
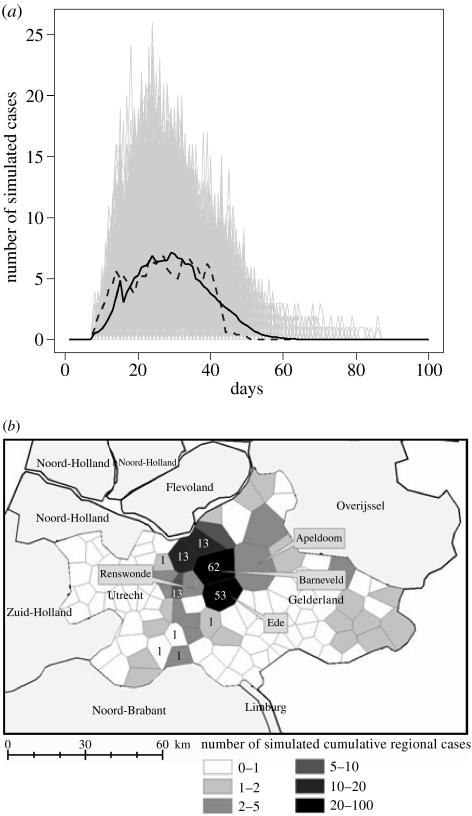
Figure 3.
Reproducing the 2003 Dutch epidemic (a) Daily cases incidence. The dashed line represents the 5-day moving average incidence of reported cases; the black line represents the mean over the 1000 simulations (light grey lines). (b) Map of simulated cases aggregated at the regional level. Figures within municipalities correspond to the count of cases during the observed epidemic.
(e) Multivariate sensitivity and uncertainty analysis
We performed a multivariate sensitivity analysis to assess the impact of control strategies and potential delays in diagnosis, reporting and implementation of control measures: (i) delay between onset of infectiousness and report to authorities γ, (ii) delay between report and depopulation τ, (iii) ratio of pre-emptive culled farms to infected farms ρ, (iv) delay before the virus is confirmed in the country and first control measures are put into place T1, and (v) radius of neighbourhood culling policy (rpolicy). These five parameters, constant over the entire duration of the epidemic, were sampled using a Latin hypercube sampling scheme (Blower & Dowlatabadi 1994) based on the assumption of statistical independence between input parameters. The distribution of infections in flocks was computed using 500 sets of parameters drawn from uniform continuous or discrete distributions, with bounds described in table 1. The partial rank correlation coefficients (PRCC) were also calculated using the 500 values for each parameter and the 500 mean cumulative number of predicted cases over the 1000 simulations (Blower & Dowlatabadi 1994).
As the Simplex method provides only point estimation values, an uncertainty analysis was performed for the contact rates using the same Latin hypercube sampling scheme, explained above. The effect of variation in contact rates values on the precision of the simulated cumulative number of infected farms was explored.
Finally, the sensitivity of the model to distances used for transmission buffers was tested by calculating the likelihood for several couple of values around the historical values (3 and 10 km) given in the literature.
3. Results
(a) Parameter estimation
Before control strategies were put to place, estimated contact rates exhibited, as expected, greater values at short distances (table 1). During the pre-control period, similar contact levels were noted for virus transmission within the protection (less than 3 km) and surveillance area (less than 10 km), but long-range contact were five times lower.
Once control strategies were implemented, the values of all contact rates decreased. The largest decreases were for long-range contacts (75% decrease beyond the surveillance area) and for short-range contacts (more than 50% in the protection area). Reduction of medium range contacts was smaller (less than 50% decrease in the surveillance area (table 1).
(b) Model fitting and spatial risk maps
Our simulation results are in agreement with the observed dynamics of 2003 (correlation coefficient=0.94, figure 3a). In the 2003 Dutch epidemic, 185 commercial farms were reported as infected and the 5-day moving average of reported cases exhibited a peak of 6.8 at day 27. The number of simulated cumulative cases was of 184, 95% empirical confidence interval (34; 294) with a peak of 7.1 reported cases at day 29.
Simulated cases were located mainly in the Gelderse valley as was the case in 2003 (figure 3b). The most affected municipalities in the simulations were Ede and Barneveld, as was also observed during the Dutch epidemic.
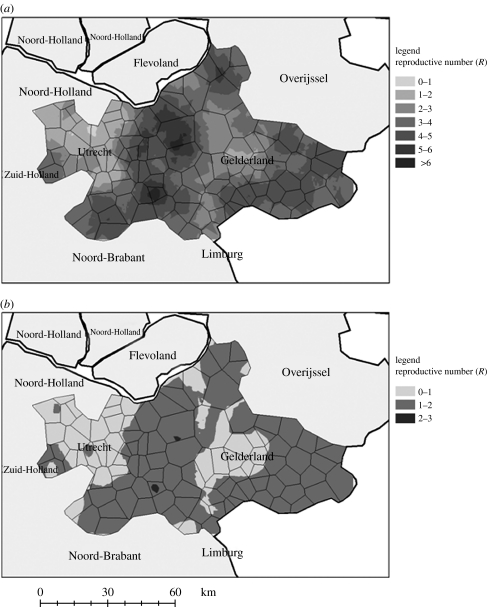
Estimation of the reproductive number identifies and quantifies high risk regions for virus spread. During the pre-control period, in the Gelderse valley, Rt values were above 4 on an average and in the north or west of Gelderland Rt values were between 2 and 5 (figure 4a). Over all regions, Rt was estimated to be 5.2 (4; 6.9) during the pre-control period. During the control period, estimated Rt values strongly decreased but remained above one in the Gelderse valley indicating the control measures alone were inadequate to halt transmission, and so the virus may have continued spreading (figure 4b). On an average, Rt was estimated to be 1.5 during the control period (1; 2.5); although the measures were inadequate to halt the spread, they may have limited the size of the final epidemic.
Figure 4.
High-risk area of virus spreading based on Rt values at two time periods: (a) pre-control period: before the virus is known circulating (b) control period: disease is confirmed and first measures are put to place.
(c) Sensitivity and uncertainty analysis
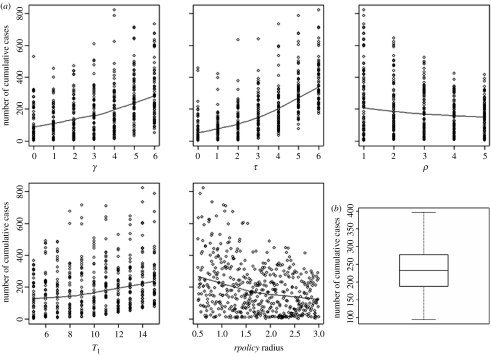
The results of the multivariate sensitivity analysis on control parameters demonstrated that the most influential parameters were first, the delay between detection and depopulation (τ, PRCC=0.85) followed by the time needed to detect an infected farm when poor clinical signs are noticed (γ, PRCC=0.73). The greater the delay between diagnosis, reporting and implementation of depopulation, larger is the epidemic (figure 5a). The duration of the pre-control period would play a minor role (T1, PRCC=0.55) but still, increasing the delay between virus importation and disease confirmation may lead to larger epidemics. Increasing the ratio of pre-emptive depopulated farms to infected ones (ρ, PRCC=−0.50) or the neighbourhood control policy radius (rpolicy, PRCC=−0.62) would both lead to fewer cases, but with less impact. The monotonic relationships between the outcome and the input variables, assumed by the sensitivity analysis, have been verified (figure 5a).
Figure 5.
Multivariate sensitivity analysis for strategy control parameters (a) impact of each of the five parameters (delay between onset of infectious period and detection within a flock: γ; delay between detection and depopulation: τ; ratio of preventive depopulated farms to reported infected farms: ρ; pre-control period, i.e. lag time between virus importation and the day the disease is confirmed in a country: T1; radius within which ring depopulation is carried out: rpolicy radius) on cumulative simulated cases. The blue lines represent non-parametric local polynomial regression fitting. (b) Impact of uncertainty of estimated spatial contact rates on the range of cumulative simulated cases.
Considering the range of spatial contact rates explored in the uncertainty analysis, the average size of epidemics was 233 cases, the 0.25 and 0.75 quantiles were equal to 188 and 277, respectively (figure 5b) and the standard-deviation was equal to 60.
The model results depend on the radius lengths that define short, medium and long transmission. The lengths used here correspond to the radius lengths implemented during the Dutch epidemic, so they have a practical interpretation. By allowing the lengths to vary, we found that a best optimization was obtained with radius equal to 1.6 km for the protection area and to 10.9 km for the surveillance area, respectively. Nevertheless as the likelihood obtained for this couple (likelihood=1015) was close to the one obtained for the couple 3 and 10 km (likelihood=1020), we decided to keep the historical values.
4. Discussion
We evaluated key control strategies in an HPAI epidemic used to control the course of the epidemic among birds and thus reduce potential transmission of the virus to humans. Unlike previous studies, our model takes into account farm size and spatial contacts.
We first estimated spatial contact rates from data describing the 2003 A/H7N7 Dutch outbreak. A sensitivity analysis was performed to evaluate the impact of control strategies and potential delays in diagnosis, reporting and implementation of control measures on the cumulative number of forecast cases.
The sensitivity analysis points out that immediate depopulation has the greatest impact in reducing avian influenza cases, as soon as a flock is reported infected (PRCC=0.85). To be effective, this strategy must be enacted quickly with a rapid detection of infection within flocks (PRCC=0.73). Further, the importance of this is evidenced by the high reproductive number during the pre-control period. These strategies have also been confirmed by field surveys (Marangon et al. 2003) and should be applied especially in layer type farms (Thomas et al. 2005). These two measures are likely to have more impact than increasing neighbourhood depopulation in HPAI epidemics (PRCC=−0.62). However, it may be necessary to apply proximity depopulation, as shown in the Netherlands where a 3 km depopulation radius was efficient in controlling the epidemic when combined with pre-existing control strategies. As illustrated in figure 4, Rt drastically decreased after the implementation of control measures. Despite the persistence of regions with Rt>1 even during the control period, the epidemic died out. This is probably a consequence of a saturation effect: no more susceptible farms were available to be infected.
Estimated spatial parameters clearly showed effective decreases in contact rates once when the disease was confirmed illustrating the impact of the control measures. Since the optimization method used here furnishes only point estimates, we explored the variation in the cumulative number of cases for contact rate values around those estimated through the uncertainty analysis. As shown in figure 5b, the range in epidemic size may be large (from 96 to 397 cases), but the likelihood, re-calculated for each set of sampled contact rates values, was set to its optimum for the estimated points. Thus, even though contact rates have an impact on the total number of cases, here we used the estimated values from data that provides the best optimization.
There are several limitations that require discussion. First, as exact data on farm location was not available; the model was based on radius buffers. Individual farms were assigned to a random location within the municipality for the purposes of the simulations. The individual-based model with random locations was preferred to a municipality metapopulation model (i.e. where the farms in a municipality were well-mixed) since transmission between farms and actual control were explicitly spatial. We tested the random placement assumption by repeating the simulations in which farms were assigned to different random locations within a municipality. Similar results were obtained for parameter estimation and epidemic curve shape, but the use of geographical information systems (GIS) to obtain more precise data concerning farms' location would help in moving to a continuous distance model. Second, we did not consider species other than domestic poultry. Waterfowl probably introduced the virus into domestic flocks in the Netherlands, but they were not presumed to play a role in the course of the epidemic afterwards. From 85 carcasses of free-living birds collected in the Gelderse valley, all were tested negative to A/H7N7 (European commission 2003). But this feature may not be relevant for all avian influenza epidemics, as during H5N1 epidemics many wild animals, birds (Ellis et al. 2004) or mammals (Kuiken et al. 2004), have been infected and may have taken part in virus spread. Even though pigs may play a major role in avian influenza dynamics through virus reassortment and transmission (Choi et al. 2004), the swine species did not seem to participate in the Dutch epidemic (European commission 2003). Therefore, no other species but domestic poultry were implemented in our model.
Detailed data on other epidemics and agricultural structures would be helpful to evaluate further the impact of other control strategies: new transmission buffer may be put into place and thus parameters could be re-estimated using the same estimation method as described in the present paper. Our results were obtained focusing only on the Dutch epidemic: what would be the most important control strategies if an epidemic occurred in another country? Vaccination using the differentiating infected from vaccinated animals (DIVA) strategy (Capua et al. 2003) coupled with a wider complex territorial strategy is recommended when there is a risk of major spread. These strategies have been successfully used in Italy between 2000 and 2003 (Marangon et al. 2003). In addition to the field studies (Lee et al. 2004), the potential impact of vaccination could be evaluated through mathematical models and used to provide important information for an A/H5N1 epidemic (Capua & Marangon 2004).
Avian influenza outbreaks cause dramatic damage in the poultry industry leading to bans on exportation and to intensive depopulations (Henzler et al. 2003). However, these epidemics also have an important impact in human societies. The primary threat is the emergence of a new pandemic after reassortment of an avian virus in humans or in other species, such as pigs. To prevent this threat, control strategies for avian outbreaks should focus on both high and low pathogenic avian influenza viruses as the virus may acquire additional virulence following antigenic drift or shift (Suarez et al. 2004). Detection of avian to human virus transmission, beyond just rare events, should be examined more thoroughly using epidemiological tools such as cluster size distribution (Ferguson et al. 2004). An efficient monitoring response in animals will help to reduce the number of infected humans, diminishing the risk of a pandemic (Webster & Hulse 2005).
The approach used here provides a framework for both mapping the risk of avian influenza and evaluating the impact of various control strategies. The model can be applied to retrospective data, as was the case here, or in theory used in real time with adequate information available on farm structures and transmission risk and with estimation of new contact parameters. The results of these simulations suggest that avian influenza risk is higher with diagnostic or depopulation delays, thereby providing important observations with clear public health implications to prevent avian virus transmission to humans.
Acknowledgments
We gratefully acknowledge the Institut National de la Recherche Agronomique de Clermont-Ferrand and the Agence Française de la Sécurité Sanitaire des Aliments de Ploufragan for their support in reviewing the manuscript.
References
- Alexander D.J. A review of avian influenza in different bird species. Vet. Microbiol. 2000;74:3–13. doi: 10.1016/s0378-1135(00)00160-7. doi:10.1016/S0378-1135(00)00160-7 [DOI] [PubMed] [Google Scholar]
- Anderson R.M, May R.M. Oxford University Press; New York, NY: 1991. Infectious diseases of humans: dynamics and control. [Google Scholar]
- Beare A.S, Webster R.G. Replication of avian influenza viruses in humans. Arch. Virol. 1991;119:37–42. doi: 10.1007/BF01314321. doi:10.1007/BF01314321 [DOI] [PubMed] [Google Scholar]
- Blower S.M, Dowlatabadi H. Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example. Int. Stat. Rev. 1994;62:229–243. [Google Scholar]
- Capua I, Marangon S. Vaccination for avian influenza in Asia. Vaccine. 2004;22:4137–4138. doi: 10.1016/j.vaccine.2004.04.017. doi:10.1016/j.vaccine.2004.04.017 [DOI] [PubMed] [Google Scholar]
- Capua I, Terregino C, Cattoli G, Mutinelli F, Rodriguez J.F. Development of a DIVA (differentiating infected from vaccinated animals) strategy using a vaccine containing a heterologous neuraminidase for the control of avian influenza. Avian Pathol. 2003;32:47–55. doi: 10.1080/0307945021000070714. doi:10.1080/0307945021000070714 [DOI] [PubMed] [Google Scholar]
- Choi Y.K, Lee J.H, Erickson G, Goyal S.M, Joo H.S, Webster R.G, Webby R.J. H3N2 influenza virus transmission from swine to turkeys, United States. Emerg. Infect. Dis. 2004;10:2156–2160. doi: 10.3201/eid1012.040581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Council of the European Communities Community measures for the control of avian influenza. Council directive 92/40/EEC, 19 May 1992. Off. J. Eur. Comm. 1992;L167:1–15. Available at http://europa.eu.int/comm/food/animal/diseases/resources/92-40.pdf (Accessed January 2005). [Google Scholar]
- Duyckaerts C, Godefroy G. Voronoi tessellation to study the numerical density and the spatial distribution of neurones. J. Chem. Neuroanat. 2000;20:83–92. doi: 10.1016/s0891-0618(00)00064-8. doi:10.1016/S0891-0618(00)00064-8 [DOI] [PubMed] [Google Scholar]
- Ellis T.M, et al. Investigation of outbreaks of highly pathogenic H5N1 avian influenza in waterfowl and wild birds in Hong Kong in late 2002. Avian Pathol. 2004;33:492–505. doi: 10.1080/03079450400003601. doi:10.1080/03079450400003601 Available at http://www.europa.eu.int/comm/dgs/health_consumer/index_en.htm. [DOI] [PubMed] [Google Scholar]
- European Commission 2003 The Netherlands: avian influenza.
- Ferguson N.M, Cummings D.A, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, Burke D.S. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–214. doi: 10.1038/nature04017. doi:10.1038/nature04017 [DOI] [PubMed] [Google Scholar]
- Ferguson N.M, Fraser C, Donnelly C.A, Ghani A.C, Anderson R.M. Public health. Public health risk from the avian H5N1 influenza epidemic. Science. 2004;304:968–969. doi: 10.1126/science.1096898. doi:10.1126/science.1096898 [DOI] [PubMed] [Google Scholar]
- Gilbert M, Chaitaweesub P, Parakamawongsa T, Premashthira S, Tiensin T, Kalpravidh W, Wagner H, Slingenbergh J. Free-grazing ducks and highly pathogenic avian influenza, Thailand. Emerg. Infect. Dis. 2006;12:227–234. doi: 10.3201/eid1202.050640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henzler D.J, et al. Epidemiology, production losses, and control measures associated with an outbreak of avian influenza subtype H7N2 in Pennsylvania (1996–98) Avian Dis. 2003;47:1022–1036. doi: 10.1637/0005-2086-47.s3.1022. [DOI] [PubMed] [Google Scholar]
- Koopmans M, et al. Transmission of H7N7 avian influenza A virus to human beings during a large outbreak in commercial poultry farms in the Netherlands. Lancet. 2004;363:587–593. doi: 10.1016/S0140-6736(04)15589-X. doi:10.1016/S0140-6736(04)15589-X [DOI] [PubMed] [Google Scholar]
- Kuiken T, Rimmelzwaan G, van Riel D, van Amerongen G, Baars M, Fouchier R, Osterhaus A. Avian H5N1 influenza in cats. Science. 2004;306:241. doi: 10.1126/science.1102287. doi:10.1126/science.1102287 [DOI] [PubMed] [Google Scholar]
- Lee C.W, Senne D.A, Suarez D.L. Effect of vaccine use in the evolution of Mexican lineage H5N2 avian influenza virus. J. Virol. 2004;78:8372–8381. doi: 10.1128/JVI.78.15.8372-8381.2004. doi:10.1128/JVI.78.15.8372-8381.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemenach A, Legrand J, Grais R.F, Viboud C, Valleron A.J, Flahault A. Modeling spatial and temporal transmission of foot-and-mouth disease in France: identification of high-risk areas. Vet. Res. 2005;36:699–712. doi: 10.1051/vetres:2005025. doi:10.1051/vetres:2005025 [DOI] [PubMed] [Google Scholar]
- Longini I.M, Jr, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings D.A, Halloran M.E. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. doi:10.1126/science.1115717 [DOI] [PubMed] [Google Scholar]
- Marangon S, Bortolotti L, Capua I, Bettio M, Dalla Pozza M. Low-pathogenicity avian influenza (LPAI) in Italy (2000–01): epidemiology and control. Avian Dis. 2003;47:1006–1009. doi: 10.1637/0005-2086-47.s3.1006. [DOI] [PubMed] [Google Scholar]
- Office International des Epizooties 2004. Available at http://www.oie.int/ (accessed March 2005).
- Saito T, Lim W, Suzuki T, Suzuki Y, Kida H, Nishimura S.I, Tashiro M. Characterization of a human H9N2 influenza virus isolated in Hong Kong. Vaccine. 2001;20:125–133. doi: 10.1016/s0264-410x(01)00279-1. doi:10.1016/S0264-410X(01)00279-1 [DOI] [PubMed] [Google Scholar]
- Sanco, D 2003 Avian influenza (AI) in the Netherlands, Belgium and Germany-chronology of main events and list of decisions adopted by the commission. Available at http://europa.eu.int/comm/food/animal/diseases/controlmeasures/avian/chronology_2003_epidemic.pdf, (accessed October 2004).
- Statistics in Netherlands 2004. Available at http://www.cbs.nl/en-GB/default.htm (accessed October 2004).
- Stegeman A, Bouma A, Elbers A.R, de Jong M.C, Nodelijk G, de Klerk F, Koch G, van Boven M. Avian influenza A virus (H7N7) epidemic in The Netherlands in 2003: course of the epidemic and effectiveness of control measures. J. Infect. Dis. 2004;190:2088–2095. doi: 10.1086/425583. doi:10.1086/425583 [DOI] [PubMed] [Google Scholar]
- Suarez D.L, et al. Recombination resulting in virulence shift in avian influenza outbreak. Chil. Emerg. Infect. Dis. 2004;10:693–699. doi: 10.3201/eid1004.030396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas M.E, Bouma A, Ekker H.M, Fonken A.J, Stegeman J.A, Nielen M. Risk factors for the introduction of high pathogenicity Avian Influenza virus into poultry farms during the epidemic in the Netherlands in 2003. Prev. Vet. Med. 2005;69:1–11. doi: 10.1016/j.prevetmed.2004.12.001. doi:10.1016/j.prevetmed.2004.12.001 [DOI] [PubMed] [Google Scholar]
- van der Goot J.A, de Jong M.C, Koch G, Van Boven M. Comparison of the transmission characteristics of low and high pathogenicity avian influenza A virus (H5N2) Epidemiol. Infect. 2003;131:1003–1013. doi: 10.1017/s0950268803001067. doi:10.1017/S0950268803001067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webby R.J, Webster R.G. Are we ready for pandemic influenza? Science. 2003;302:1519–1522. doi: 10.1126/science.1090350. doi:10.1126/science.1090350 [DOI] [PubMed] [Google Scholar]
- Webster R, Hulse D. Controlling avian flu at the source. Nature. 2005;435:415–416. doi: 10.1038/435415a. doi:10.1038/435415a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee S.H, et al. Outbreaks of highly pathogenic avian influenza (H5N1) in the Republic of Korea in 2003/04. Vet. Rec. 2006;158:341. doi: 10.1136/vr.158.10.341. [DOI] [PubMed] [Google Scholar]