Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2005 Jan 18;272(1559):187–192. doi: 10.1098/rspb.2005.2936

Resource partitioning among flower visitors and evolution of nectar concealment in multi-species communities

Miguel A Rodríguez-Gironés 1,2,*, Luis Santamaría 3
PMCID: PMC1634952  PMID: 15695210

Abstract

The plant community within which flower evolution takes place has largely been ignored. We develop two models for the evolution of nectar concealment when flowers are visited by legitimate pollinators and flower parasites. When there is a single plant species, no level of nectar concealment is evolutionarily stable: any population can be invaded by mutants exhibiting a higher level of nectar concealment. However, the presence of a second flower species with exposed nectar and not subject to evolution breaks the runaway process. In the presence of open flowers, depending on the fitness function there may be an evolutionarily stable level of nectar concealment, or more complex evolutionary dynamics, with nectar concealment fluctuating within a bounded range. Concealment of nectar from flower parasites can evolve even if it implies decreasing the accessibility of nectar to legitimate pollinators.

Keywords: optimal foraging, pollination, nectar concealment, community ecology

1. Introduction

The traditional view of floral traits is that they reflect differences in foraging preferences and morphology of pollinators, arising from tight coevolutionary processes between pairs or small groups of species. Several recent studies and reviews have, however, pointed out that plant–pollinator relationships generally show high levels of generality (Jordano 1987; Herrera 1988; Waser et al. 1996; Ollerton 1996; Elberling & Olesen 1999). The study of floral evolution should thus be approached from a community context, which takes into consideration the matrix of multi-specific, weak interactions in which it is embedded (Jordano 1987; Memmott 1999). In this paper, we study how community context affects the evolution of nectar concealment: that is, the evolution of floral traits that in any way hinder access to nectar. It is normally assumed that plant–pollinator coevolution results from selection for plant traits that enhance visitation rates and/or pollination efficiency by the most efficient pollinator (e.g. Stebbins 1974; Schemske & Bradshaw 1999). Alternatively, floral evolution may represent a compromise between attraction and defence, as proposed by Müller (1883). Several authors have indeed argued that certain flower traits may have evolved to keep non-desired visitors at bay (Waser & Fugate 1986; Galen 1999; Brown et al. 2002; Galen & Butchard 2003), although the question remains whether deterrent traits can evolve when they interfere with nectar exploitation by efficient pollinators (e.g. Irwin et al. 2004). We use a general abstract model to clarify to what extent, and under what conditions, nectar concealment can evolve.

Our evolutionary model takes into account the foraging behaviour of nectarivorous animals. For the sake of concreteness, we will refer to our model animals as bees, although nothing in the model restricts its applicability to this taxon. When species compete for resources, optimal foraging implies some degree of resource partitioning, with certain species neglecting to exploit resources that are perfectly suitable for them (Rosenzweig 1981; Possingham 1992). This theoretical principle has been confirmed for nectarivorous species, both with territorial hummingbirds (Pimm et al. 1985; Rosenzweig 1986) and non-territorial bumble-bees (Inouye 1978; Pyke 1982; Harder 1985).

Although it is becoming increasingly common to consider the effects of several animal species on the evolutionary trade-offs of flower traits (Brown 2002), it is equally important to remember that nectarivorous species interact with several plant species (Caruso 2000). Because seed set is mediated by foraging behaviour and the behaviour of flower visitors depends on the array of available options (Heinrich 1976; Inouye 1978; Pyke 1982), we cannot ignore the community in which a plant grows when we study its evolutionary history. To assess the effect of community structure on the evolution of nectar concealment, we consider two different scenarios: (i) two animal species foraging on the same plant species and (ii) two animal species foraging on two different plant species. At any point in time, we assume that bees forage optimally, and we use the results of the foraging models (Possingham 1992; M. A. Rodríguez-Gironés, unpublished data) as input for an evolutionary module. The two scenarios lead to completely different results, demonstrating the importance of ecological processes for the evolution of flower traits.

2. Optimal foraging and resource partitioning

This section provides a very concise description of a foraging model developed by Possingham (1992), on which our evolutionary model relies. We concentrate on the main ideas and basic results. Interested readers should consult the original publication.

Two bee species forage on two flower types (three in the extended model; M. A. Rodríguez-Gironés, unpublished data). MF denotes the number of F flowers open at a given time and NZ the number of Z bees, where F stands for flower type, A or B (in the model with three flower types, F=A, B or C; C flowers are open, A and B flowers belong to the same species and present nectar concealment; B represents a mutant type) and Z stands for bee species, X or Y (both species are efficient pollinators of C flowers; at A and B flowers, Y bees are efficient pollinators and X bees are (conditional) parasites) throughout this paper. Bees forage by visiting a sequence of flowers. We denote by τFZ the average time that Z bees foraging on F flowers require to complete a foraging cycle. Knowing the foraging times per flower, τFZ, the number of bees foraging at each flower type and the nectar production rates of F flowers, rF, it is straightforward to calculate the expected standing crop at F flowers, EF, the intake rate of Z bees foraging at F flowers, γFZ=EFZτFZ, and the frequency with which F flowers receive visits from Z bees, νFZ (Possingham 1992).

Following the logic of the ideal free distribution (IFD) (Fretwell & Lucas 1970), we can calculate the number of bees that must forage on each flower type so that no bee can increase its expected intake rate by switching to the other flower type (Possingham 1992; M. A. Rodríguez-Gironés unpublished data).

The key result of the model is that optimal foraging leads to resource partitioning, in the sense that at least one of the bee species will behave as specialist, visiting only one flower type (although the other species may, depending on the number of flowers of each type and the abundance of each bee species, behave as a specialist or a generalist). Possingham (1992) and M. A. Rodríguez-Gironés (unpublished data) provide closed formulas giving the number of bees that will forage at each flower type when there are two and three flower types, respectively. M. A. Rodríguez-Gironés (unpublished data) further generalizes Possingham’s results to more complex scenarios, including variable rates of nectar production, changes in the currency that foraging bees maximize and arbitrary numbers of flower types and bee species.

The qualitative results of the evolutionary models that we present below rely solely on the existence of resource partitioning, and are therefore very robust (M. A. Rodríguez-Gironés, unpublished data). The general, somewhat abstract results, will be accompanied by a specific example, based on the precise foraging model developed by Possingham (1992).

3. Evolution of nectar concealment

We assume that certain flower characteristics can make access to nectar more costly by increasing exploitation time. If nectar concealment deters legitimate pollinators, but not parasites, it will never evolve. We therefore concentrate on the case when the cost is greater for parasites than for legitimate pollinators. In what follows, we will assume that X bees are parasites and Y bees are pollinators. We assume that flower morphology can be defined by a single parameter, h, such that the time a Z bee requires to exploit an F flower, τFZ(h), is an increasing function of h, such that an increase in h has a larger impact on parasites than on pollinators (i.e. τ′FX(h)>τ′FY(h)>0, where the prime denotes the derivative with respect to h).

Let the fitness of a plant, WF, be a continuously differentiable function of visit rates,

WF=ω(υFX,υFY). (3.1)

When X bees are absolute parasites, visits by X bees decrease fitness, and visits by Y bees increase it:

∂ω∂νFX<0,∂ω∂νFY>0 (3.2)

and when X bees are conditional parasites (Thomson et al. 2000), fitness increases with visits by X and Y bees, but the positive effect of Y bees is greater:

∂ω∂νFY>∂ω∂νFX>0. (3.3)

Although we provide general results based on an abstract fitness function, figures are based on

WF=eFXνFX+eFYνFY, (3.4)

where eFX and eFY represent the per visit pollination efficiency of X and Y individuals, with eFX<0<eFY when X bees are parasites and 0<eFX<eFY when X bees are conditional parasites. (Although the fitness function in equation (3.3) can take negative values, this problem is removed with any non-negative, strictly increasing transformation of WF.)

3.1 Evolutionary dynamics in single-species communities

Let h be the level of nectar concealment for the wild-type flower morph, A. We can consider the fate of a mutant flower, B, with trait h′. To do this we calculate the frequency with which parasites and pollinators visit each flower type and compare the ensuing fitness for mutant and wild-type plants.

Regardless of whether we are dealing with absolute (Appendix A) or conditional parasites (Appendix B), the model has no evolutionarily stable strategy (ESS); whatever the value of nectar concealment in the population, h, there are values of h’=h+δh, with δh>0, such that a mutant with nectar concealment h′ can invade the populations and drive the wild-type morph to extinction. Hence, h will increase for ever unless increasing the level of nectar concealment has some additional cost not related to pollination (e.g. increased water loss with larger corolla flare; Galen et al. 1999).

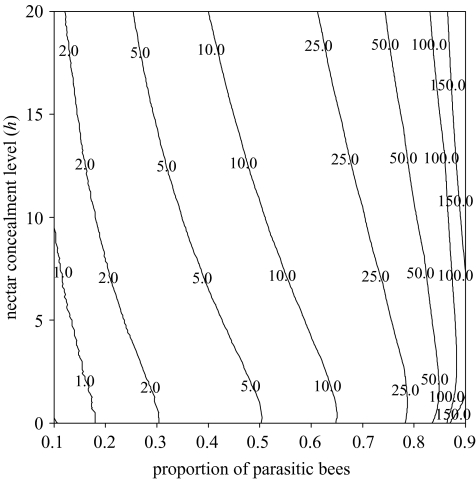
As a particular example, figure 1 shows the maximum value of δh for which the fitness of the mutant is greater than the fitness of the wild-type, regardless of the frequency of mutants as a function of the level of nectar concealment, h, of the wild-types and the proportion of parasitic bees. Figure 1 is based on Possingham’s (1992) foraging model and the fitness function of equation (3.4), with foraging times τZ=2+cZhs, with cX=1 and cY=0.5, which for h=4 s correspond to Bombus appositus (X bee) and B.flavifrons (Y bee) feeding at Aconitum columbianum (Inouye 1978). With these assumptions, we can calculate expected visit rates νFZ (Possingham 1992) and fitness (equation (3.4)) of wild-type and mutant plants. The contour lines of figure 1 were calculated numerically, using the bisection method (Press et al. 1997). When the proportion of parasitic bees is low (ca.10%), mutants can only invade if (roughly) δh<0.5, but the value of δh* increases dramatically with the proportion of parasitic bees.

Figure 1.

Figure 1

Open in a new tab

Contour plot for the maximum value of δh that can invade and drive to extinction a population as a function of the proportion of X bees and the value of h (in seconds) in the existing population. The contour lines correspond, from left to right, to δh=1, 2, 5, 10, 25, 50, 100 and 150s. The total number of bees is NX+NY=5000, r=0.0001, M=6 000 000, eX=−0.1, eY=1. Handling times are τAZ=2+cZ·h, and τBZ=2+cZ·(h+δh).

3.2 Evolutionary dynamics in two-species communities

We next study the evolution of nectar concealment in the presence of a plant species with exposed nectar rewards. Other than the plant from § 3a, with its two morphs, we now have a third flower type, C, belonging to a different species, with exposed nectar rewards. We assume that X and Y bees are equally efficient at exploiting open flowers, and more efficient exploiting open flowers than flowers with concealed rewards. We further assume that open flowers are not subject to selection and hence do not evolve. This might be the case if both X and Y bees were efficient pollinators of C flowers (Castellanos et al. 2003). We can calculate the number of X and Y bees foraging at each flower type (M. A. Rodríguez-Gironés, unpublished data) and, from them, the expected fitness of A and B plants according to equation (3.1). (We will still refer to X and Y bees as parasites and pollinators, even though they are both efficient pollinators of C flowers and X bees may be conditional parasites at A and B flowers.)

In the presence of flowers with exposed nectar, no runaway takes place. Let h* be the minimum level of nectar concealment for which all parasites forage at open flowers. If h≥h*, further increases in h are never favoured by selection and values h′ < h are always favoured if h*≤h’ (Appendix C). If h < h*, increases in nectar concealment are favoured provided that h′–h is small enough. For some fitness functions, decreases in nectar concealment may also be favoured (Appendix C). Thus, depending on the specific shape of the fitness function, either there is an ESS where the level of nectar concealment is h*, or there are complex evolutionary dynamics with nectar concealment increasing until the value of h* and then being invaded by substantially lower values. (More complex dynamics and an ESS with mixed strategies may also be possible under these circumstances, but values of nectar concealment greater than h* will never be selected.) These results apply for absolute and conditional parasites, although some fitness functions may have an ESS for absolute parasites and complex dynamics for conditional parasites.

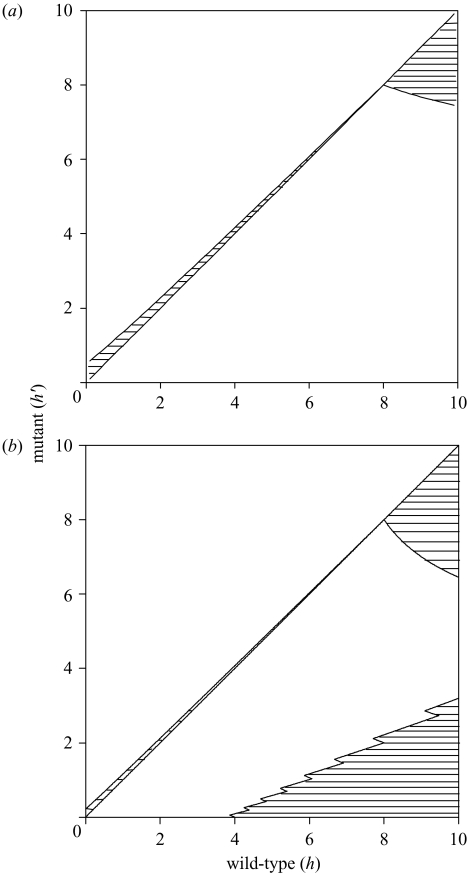
Figure 2 shows, for the fitness function of equation (3.4) and Possingham’s (1992) foraging model with foraging times per flower as in figure 1, which mutant traits h′ can invade a population where other plants have a level h of nectar concealment. (To draw the figure, we simply calculate visit rates to each flower type as in M. A. Rodríguez-Gironés, unpublished data, and substitute in equation (3.4) to see which plants attain a higher fitness. The criterion for invasibility is as in figure 1.) If X bees are absolute parasites, the system has an ESS given by the level of nectar concealment (in this case, h*=8s) that cannot be invaded by any mutant. If X bees are conditional parasites, however, no pure strategy is an ESS: whatever the value of h, there are mutants h′ that can invade the population.

Figure 2.

Figure 2

Open in a new tab

Invasibility diagram for the two-species condition when X bees are (a) absolute parasites (eX=−0.1) or (b) conditional parasites (eX=0.5). Hatched areas indicate that a mutant playing strategy h’ can invade a population playing h. NX=1250, NY=3750, r=0.0001, MA+MB=5 000 000, MC=1000000, eY=1, handling times are τAX=2+h, τAY=2+0.5 h, τBX=2+h’, τBY=2+0.5 h′ and τC=2.

Figure 3 shows, for Possingham’s (1992) foraging model with linear fitness function (equation (3.4)) and linear relationship between nectar concealment and foraging time, the ESS level of nectar concealment, h*, as a function of the proportion of absolute parasites. The ESS level of nectar concealment is (Appendix C) the minimum value of h for which all parasites forage at open flowers, and it can be calculated as the maximum value of h for which ‘type p’ solutions (Possingham 1992, table 1) exist. Setting the equal sign in the condition for existence of ‘type p’ solutions, we obtain:

h*=4NXMArA-NYMCrC2NYMCrC-N1MArA. (3.5)

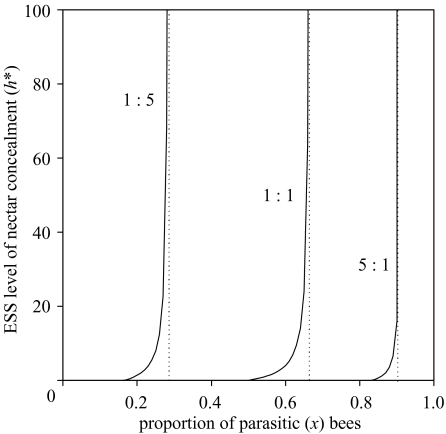
The curves of figure 3 show two threshold values. Above an upper threshold, there is a runaway process (h*=∞). This is not a general property of the ESS, and the upper threshold disappears if flowers can only hold a finite amount of nectar. However, if the proportion of parasitic bees lies below a lower threshold, no nectar concealment evolves. (To be precise: below this threshold, h*=0 in a limiting sense. If a population plays h>0, it can be invaded by any mutant playing h′ as long as h>h’>0. But if the population plays h=0, it can be invaded by mutants playing h′>0 provided that h′ is small enough: Appendix A.) This lower threshold is a general trait of the ESS: it exists because, when the proportion of parasitic bees is small enough, any value of h>0, no matter how small, ensures that all parasites forage at open flowers (Possingham 1992; M. A. Rodríguez-Gironés, unpublished data). The lower threshold increases with the proportion of open flowers and, for Possingham’s (1992) foraging model, it is reached when (Possignham 1992, table 1)

NXNY=MCrCMArA. (3.6)

Figure 3.

Figure 3

Open in a new tab

Two-species condition: level of nectar concealment (value of h, in seconds) at the ESS, as a function of the proportion of X bees. The three solid lines represent the ESS for different ratios of flowers with exposed nectar in the community (indicated above the lines as ‘exposed’ : ‘concealed’). The vertical dotted lines represent the proportions of parasitic bees above which no ESS exists. The total number of bees is NX+NY=5000, MA+MB+MC=6 000 000, eX=−0.1, all other parameters as in figure 2.

4. Discussion

The evolutionary implications of diet selection in plant–pollinator systems stem from the fact that minor changes in flower morphology may have a large impact on the matrix of interactions, and hence on plant fitness. If the change in flower morphology is small, the total number of bees exploiting that flower type will hardly be altered, but the species composition of its visitors may change dramatically. In the case of two flower types and two bee species for example, when the flowers are identical both bee species will be equally common at each flower type. A small change in the morphology of a flower type, however, may suffice to induce almost total segregation, with most bees of one species exploiting one flower type, and most bees of the other species exploiting the other flower type (Possingham 1992). Individual foraging decisions therefore amplify the effects of small morphological differences.

As an example of the importance of resource partitioning in plant–pollinator systems, we have developed a model of nectar concealment to deter parasites. Under IFD assumptions, and with a single plant species, there is a runaway process, with h increasing to infinity unless there is a stabilizing cost not included in the model (figure 1). The introduction of a second species with exposed nectar rewards completely modifies the predictions, stabilizing nectar concealment at finite values of h (figures 2 and 3). These results show the importance of considering community structure when studying the evolution of plant–pollinator systems. Although we have restricted our analysis to communities with two nectarivorous and two plant species, Possingham’s (1992) model can be extended to richer communities (M. A. Rodríguez-Gironés, unpublished data), where the same processes described here can lead to different levels of nectar concealment.

The mechanism underlying the evolutionary models is actually very simple. If a floral trait makes access to nectar more difficult for parasites than for pollinators, rare mutants showing that trait will be visited only by pollinators (Possingham 1992; M. A. Rodríguez-Gironés, unpublished data). In a community with a single plant species, all parasites will necessarily concentrate on wild-type flowers with a lower level of nectar concealment, and as a result small mutations are always favoured. In a community with several plant species, parasites may totally avoid certain plants if they are more efficient at exploiting other resources, in which case further nectar concealment presents no advantage to the already unmolested flowers (figure 3).

Nectar concealment comes in many shapes and colours. Any trait that increases the time required to reach and exploit flowers can deter flower parasites. Flowers can protect their nectar with physical barriers that visitors must overcome to obtain nectar, as is the case in the snapdragon (Antirrhinum spp.), or they can hide their nectar at the bottom of deep corollas (Inouye 1980). But if our argument is correct, nectar can be effectively protected by more tenuous barriers, such as flower colour (Waser & Price 1983; Rodríguez-Gironés & Santamaría 2004).

The models that we have developed rely on the assumption that bees are optimal foragers. There is experimental evidence showing that bees will not systematically exploit a flower type if a better option is available (Inouye 1978; Dreisig 1995; Ohashi & Yahara 2002), but bees are not error-free. Deviations from IFD predictions will be related to the cost of foraging on the less desirable option. This cost can exceed a 20% reduction of intake rate for realistic parameters (Possingham 1992), but becomes negligible when both foraging options are virtually identical. In practice, therefore, we should expect a mutant to invade only if it is favoured by selection under optimal foraging, and if it is sufficiently distinct from the wild-type to ensure nearly optimal foraging. Deviations from optimal behaviour will stabilize the system at finite values of h for the single-species case (although the values can be very large, as indicated by figure 1) and at lower values than predicted for the two-species condition.

Acknowledgments

We thank A. Traveset, C. M. Herrera and three reviewers for their critical comments on former versions of the manuscript. Funding by the Spanish Ministry of Science and Technology (project INVASRED, REN2003-06962) is also acknowledged.

Appendix A: Single species communities, absolute parasites

Initial invasion of mutants

The mutant being rare, most plants play h, and a small fraction q ≪ 1 play h′=h+δh, with 0<δh/h≪1. We call A flowers those characterized by h, and B flowers those characterized by h′. For δh to be sufficiently small, all X bees forage at A flowers while Y bees forage at A and B flowers. In the limit when δh→0: B flowers experience a higher rate of Y bee visits than A flowers, νAY<νBY, A flowers are also visited by X bees, νAX>0, while B flowers are not, νBX=0. Hence,

WA=ω(νAX,νAY)<ω(0,νAY)<ω(0,νBY)=WB (A 1)

and therefore the mutation is favoured when it is sufficiently rare that X bees restrict their foraging activity to A flowers.

Spread and fixation of mutants

When the proportion of B plants, q, increases, the population may enter a region with total habitat partition (Possingham 1992) where X bees exploit A flowers and Y bees exploit B flowers. In this region it is clear that WA<WB and therefore the mutation spreads further. When q is sufficiently large, X bees cannot entirely subsist on A flowers. In this region, X bees exploit both A and B flowers, with νAX>νBX, and Y bees forage exclusively at B flowers, νBY>νAY=0 (Possingham 1992). Although the presence of X bees reduces the fitness of B plants relative to the previous region,

WA=ω(νAX,0)<ω(νBX,0)<ω(νBX,νBY)=WB, (A 2)

and therefore the mutant continues to spread until the wild-type plant goes extinct.

Appendix B: Single-species communities, conditional parasites

We first note that total visit rates at A and B flowers become equal as the difference h′–h tends to zero. That is, for sufficiently small δh, νAX+νAY=νBX+νBY (Possingham 1992). Under these conditions, when X bees are conditional parasites, equation (3.3) implies that

νAY<νBY⇒ω(νAX,νAY)<ω(νBX,νBY). (A 3)

This means that inequalities (A 1) and (A 2) remain true when X bees are conditional parasites and, therefore, any value of h can be invaded and driven to extinction by h′=h+δh, provided that δh is small enough.

Appendix C: Two-species communities

Let h* be the minimum level of nectar concealment for which all parasites forage at open flowers.

Case h≥h*

If a mutant B has h’>h, both A and B flowers will be visited exclusively by Y bees (an increase in nectar concealment may force some pollinators to forage at open flowers, but will never make parasites to leave them). Visit rate will be lower at B than at A flowers, νBY<νAY, (although νBY→νAY as h′→h), and hence WA=ω(0,νAY)>ω(0,νBY)=WB, so mutants cannot invade.

Suppose now that a h*<h′<h. Regardless of the relative frequency of A and B flowers, the same argument developed above shows that νBY>νAY, and hence WA=ω(0,νAY)<ω(0,νBY)=WB. It follows that mutants can invade and drive the wild-type morph to extinction.

If h=h*, h’<h and h–h′ is sufficiently small, νAY≈νBX+νBY, and WB<WA, so the mutant cannot spread. If, however, h–h′ is large enough, it is possible that νAY<νBY, and, in principle (i.e. for some forms of the fitness function) the mutant might invade.

To summarize so far: if h≥h*, no mutant can invade if h′>h, all mutants with h*<h′<h can invade and, for some fitness functions, mutants with h′<h* may invade if h–h′ is large enough. Because of equation (A 3), these results hold regardless of whether we are dealing with absolute or conditional parasites.

Case h<h*

We now consider the situation where parasites do visit A flowers. A B mutant with h′>h will be visited by parasites at lower rates than the wild-type morph, and (following the steps of Appendices A and B) it can invade and drive to extinction the A morph, regardless of whether we deal with absolute or conditional parasites.

References

  1. Brown B.J., Mitchell R.J., Graham S.A. Competition for pollination between an invasive species (purple loosestrife) and a native congener. Ecology. 2002;83:2328–2336. [Google Scholar]
  2. Brown K. A compromise on floral traits. Science. 2002;298:45–46. doi: 10.1126/science.298.5591.45. [DOI] [PubMed] [Google Scholar]
  3. Caruso C.M. Competition for pollination influences selection on floral traits of Ipomopsis aggregata. Evolution. 2000;54:1546–1557. doi: 10.1111/j.0014-3820.2000.tb00700.x. [DOI] [PubMed] [Google Scholar]
  4. Castellanos M.C., Wilson P., Thomson J.D. Pollen transfer by hummingbirds and bumble-bees, and the divergence of pollination modes in Penstemon. Evolution. 2003;57:2742–2752. doi: 10.1111/j.0014-3820.2003.tb01516.x. [DOI] [PubMed] [Google Scholar]
  5. Dreisig H. Ideal free distribution of nectar foraging bumble-bees. Oikos. 1995;72:161–172. [Google Scholar]
  6. Elberling H., Olesen J.M. The structure of a high latitude plant-pollinator system. The dominance of flies. Ecography. 1999;22:314–323. [Google Scholar]
  7. Fretwell S.D., Lucas H.L. On territorial behavior and other factors influencing habitat distribution in birds. I. Theoretical development. Acta Biotheor. 1970;19:16–36. [Google Scholar]
  8. Galen C. Flowers and enemies: predation by nectar-thieving ants in relation to variation in floral form of an alpine wildflower, Polemonium viscosum. Oikos. 1999;85:426–434. [Google Scholar]
  9. Galen C., Butchard B. Ants in your plants: effects of nectar-thieves on pollen fertility and seed-siring capacity in the alpine wildflower, Polemonium viscosum. Oikos. 2003;101:521–528. [Google Scholar]
  10. Galen C., Sherry R., Carroll A.B. Are flowers physiological sinks or faucets? Costs and correlates of water use by flowers of Polemonium viscosum. Oecologia. 1999;118:461–470. doi: 10.1007/s004420050749. [DOI] [PubMed] [Google Scholar]
  11. Harder L.D. Morphology as a predictor of flower choice by bumble-bees. Ecology. 1985;66:198–210. [Google Scholar]
  12. Heinrich B. Resource partitioning among some eusocial insects: bumble-bees. Ecology. 1976;57:874–889. [Google Scholar]
  13. Herrera C.M. Variation in mutualisms: the spatio-temporal mosaic of a pollinator assemblage. Biol. J. Linn. Soc. 1988;35:95–125. [Google Scholar]
  14. Inouye D.W. Resource partitioning in bumble-bees: experimental studies of foraging behavior. Ecology. 1978;59:672–678. [Google Scholar]
  15. Inouye D.W. The effect of proboscis and corolla tube lengths on patterns and rates of flower visitation by bumble-bees. Oecologia. 1980;45:197–201. doi: 10.1007/BF00346460. [DOI] [PubMed] [Google Scholar]
  16. Irwin R.E., Adler L.S., Brody A.K. The dual role of floral traits: pollinator attraction and plant defense. Ecology. 2004;85:1503–1511. [Google Scholar]
  17. Jordano P. Patterns of mutualistic interactions in pollination and seed dispersal: connectance, dependence, and coevolution. Am. Nat. 1987;129:657–677. [Google Scholar]
  18. Memmott J. The structure of a plant-pollinator food web. Ecol. Lett. 1999;2:276–280. doi: 10.1046/j.1461-0248.1999.00087.x. [DOI] [PubMed] [Google Scholar]
  19. Müller H. The fertilisation of flowers. Macmillan; London: 1883. [Google Scholar]
  20. Ohashi K., Yahara T. Visit larger displays but probe proportionally fewer flowers: counterintuitive behaviour of nectar-collecting bumble-bees achieves an ideal free distribution. Funct. Ecol. 2002;16:492–503. [Google Scholar]
  21. Ollerton J. Reconciling ecological processes with phylogenetic patterns: the apparent paradox of plant-pollinator systems. J. Ecol. 1996;84:767–769. [Google Scholar]
  22. Pimm S.L., Rosenzweig M.L., Mitchell W. Competition and food selection: field tests of a theory. Ecology. 1985;66:798–807. [Google Scholar]
  23. Possingham H.P. Habitat selection by two species of nectarivore: habitat quality isolines. Ecology. 1992;73:1903–1912. [Google Scholar]
  24. Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. Numerical recipes in C. The art of scientific computation. 2nd edn. Cambridge University Press; 1997. [Google Scholar]
  25. Pyke G.H. Local geographic distribution of bumble-bees near Crested Butte, Colorado: competition and community structure. Ecology. 1982;63:555–573. doi: 10.1603/EN11284. [DOI] [PubMed] [Google Scholar]
  26. Rodríguez-Gironés M.A., Santamaría L. Why are so many bird flowers red? PLOS Biol. 2004;2:1515–1519. doi: 10.1371/journal.pbio.0020350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rosenzweig M.L. A theory of habitat selection. Ecology. 1981;62:327–335. [Google Scholar]
  28. Rosenzweig M.L. Hummingbird isolegs in an experimental system. Behav. Ecol. Sociobiol. 1986;19:313–322. [Google Scholar]
  29. Schemske D.W., Bradshaw H.D. Pollinator preference and the evolution of floral traits in monkeyflowers (Mimulus) Proc. Natl Acad. Sci. USA. 1999;96:11910–11915. doi: 10.1073/pnas.96.21.11910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Stebbins G.L. Flowering plants. Belknap Press; Cambridge, MA: 1974. [Google Scholar]
  31. Thomson J.D., Wilson P., Valenzuela M., Malzone M. Pollen presentation and pollination syndromes, with special reference to Penstemon. Pl. Spec. Biol. 2000;15:11–29. [Google Scholar]
  32. Waser N.M., Fugate M.L. Pollen precedence and stigma closure: a mechanism of competition for pollination between Delphinium nelsonii and Ipomopsis aggregata. Oecologia. 1986;70:573–577. doi: 10.1007/BF00379906. [DOI] [PubMed] [Google Scholar]
  33. Waser N.M., Price M.V. Pollinator behaviour and natural selection for flower colour in Delphinium nelsonii. Nature. 1983;302:422–424. [Google Scholar]
  34. Waser N.M., Chittka L., Price M.V., Williams N., Ollerton J. Generalization in pollination systems, and why it matters. Ecology. 1996;77:1043–1060. [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES